Abstract
Amplification of auditory stimuli by hair cells augments the sensitivity of the vertebrate inner ear. Cell-body contractions of outer hair cells are thought to mediate amplification in the mammalian cochlea. In vertebrates that lack these cells, and perhaps in mammals as well, active movements of hair bundles may underlie amplification. We have evaluated a mathematical model in which amplification stems from the activity of mechanoelectrical-transduction channels. The intracellular binding of Ca2+ to channels is posited to promote their closure, which increases the tension in gating springs and exerts a negative force on the hair bundle. By enhancing bundle motion, this force partially compensates for viscous damping by cochlear fluids. Linear stability analysis of a six-state kinetic model reveals Hopf bifurcations for parameter values in the physiological range. These bifurcations signal conditions under which the system’s behavior changes from a damped oscillatory response to spontaneous limit-cycle oscillation. By varying the number of stereocilia in a bundle and the rate constant for Ca2+ binding, we calculate bifurcation frequencies spanning the observed range of auditory sensitivity for a representative receptor organ, the chicken’s cochlea. Simulations using prebifurcation parameter values demonstrate frequency-selective amplification with a striking compressive nonlinearity. Because transduction channels occur universally in hair cells, this active-channel model describes a mechanism of auditory amplification potentially applicable across species and hair-cell types.
We owe the acuity of our hearing to the inner ear’s amplification of its mechanical inputs. The aural amplifier, or cochlear active process, partially overcomes the dissipation of stimulus energy due to viscous drag on the ear’s moving components (1). In response to acoustical stimulation, the amplifier additionally produces evoked otoacoustic emissions, or sounds emanating from the ear. When excessively active, the amplifier even emits sound spontaneously (reviewed in ref. 2).
In the mammalian cochlea, amplification is thought to ensue from somatic motility of outer hair cells in response to changes in their membrane potential (reviewed in ref. 3). The sensitive hearing and otoacoustic emissions of nonmammalian vertebrates without outer hair cells, however, imply the existence of an alternative form of amplification (reviewed in refs. 4–6). The most plausible source of this amplification is active, oscillatory movement by hair bundles, which has been observed in the ears of reptiles and amphibians (7–10). Two possible origins of bundle motion have been suggested. Hair bundles are known to contain several isoforms of myosin (11), at least one of which—probably myosin Iβ (12)—mediates adaptation of the transduction process. Although it is conceivable that rapid, stress-induced activation of myosin molecules produces bundle movements (reviewed in ref. 13), this mechanism would be hard pressed to account for cochlear amplification at frequencies of tens of kilohertz.
This study deals with the alternative hypothesis that bundle movements stem from the interaction of Ca2+ with mechanoelectrical-transduction channels (9, 14; reviewed in refs. 4, 5). Several lines of evidence suggest that Ca2+ modulates the activity of these channels. The decline in transduction current with increasing Ca2+ concentration (15, 16) implies that Ca2+ favors channel closure. The dependence of the electrical response on hair-bundle deflection displays an asymmetry that suggests the transduction channel has at least two closed states (15; reviewed in ref. 17), one or more of which may be stabilized by Ca2+. Consistent with this inference, a low external Ca2+ concentration or cellular depolarization retards transduction-channel closure (18). Finally, a reduced Ca2+ concentration slows and diminishes a hair bundle’s mechanically evoked transients and oscillations (10, 14, 19), which have been suggested to reflect the amplificatory process (reviewed in refs. 4, 5).
THE MODEL
When a hair bundle is deflected in the positive direction, we posit that any transduction channel may be opened by tension in the associated gating spring, presumably a tip link that connects two adjacent stereocilia along the bundle’s axis of symmetry. The open channel admits cations, dominantly K+ but also Ca2+ (20–22). We further suppose that the transduction channel, which we construe to include the pore-forming subunits and any closely linked molecules, has one or more Ca2+-binding sites on its cytoplasmic surface. When occupied by Ca2+ ions, these sites induce a molecular rearrangement that favors reclosure of the channel (9, 14). The effect of ion binding accordingly resembles that involved in Ca2+-dependent inactivation of voltage-gated Ca2+ channels (23). Consistent with experimental observations (8–10), channel closure rapidly terminates the transduction current and, by increasing tension in the gating spring, causes bundle movement in the negative direction. Because Ca2+ influx ceases upon channel closure, the local Ca2+ concentration falls, so Ca2+ eventually leaves its binding site and diffuses from the vicinity of the channel. The ion is ultimately extruded by a Ca2+ pump (24, 25). The exodus of Ca2+ primes the transduction channel for another opening under the influence of mechanical stimulation and thus for a repetition of the cycle. The mechanism is powered by the Ca2+ gradient and hence ultimately by ATP hydrolysis at Ca2+ pumps.
Local Ca2+ Concentration at the Binding Site.
If the Ca2+-binding site is a component of the transduction channel, it is reasonable to suppose that this site lies within 5 nm of the pore. Assume that an open transduction channel in a hair bundle exposed to endolymph carries a current of −6 pA, of which 3% is borne by Ca2+ (22), and that the diffusion constant for free Ca2+ is 8 × 10−10 m2⋅s−1 (26). Application of the three-dimensional diffusion equation (24) indicates that the Ca2+ concentration 5 nm from the pore reaches 35 μM, or 95% of its steady–state value, within just 5 μs of channel opening. This estimate is not significantly affected by the presence of endogenous Ca2+ buffers, for the mean distance to capture is ∼70 nm for an ion in the hair cell’s buffering environment (16, 27, 28). The Ca2+ affinity of the site therefore needs not be very great for significant Ca2+ binding to occur. Moreover, if the affinity is indeed low, the resting Ca2+ concentration in a stereocilium produces only limited occupancy of the Ca2+-binding site between channel openings.
Ca2+ Release from the Binding Site.
For the proposed mechanism to participate in the amplification of sinusoidal mechanical inputs, most channels must be able to open and reclose during each cycle of stimulation. The duration of Ca2+ binding to the effective site must therefore be sufficiently brief that a channel can reopen within one-half of a cycle after having been shut by Ca2+ binding.
Consider acoustical stimulation at a moderately high frequency such as 5 kHz. For amplification to be effective, channel reclosure should occupy no more than one-half of the oscillation’s period, or 100 μs. If Ca2+ leaves its binding site by a first-order process, the time constant for its departure from the binding site should roughly equal this interval; the off rate constant should therefore be 104 s−1 for a 5-kHz signal. If the binding of Ca2+ to the site is diffusionally limited, so that the on rate constant is ∼109 s−1⋅M−1, the dissociation constant would be 10 μM. A fast response may thus be purchased at the price of relatively low affinity.
Diffusional Clearance of Ca2+.
Even if each ion were to leave its binding site after an appropriate period, amplification would be frustrated if the local Ca2+ concentration remained sufficiently great to promote immediate rebinding of Ca2+. For the proposed mechanism to operate, the local concentration of free Ca2+ must fall rapidly after channel reclosure.
For the conditions discussed above, the Ca2+ concentration 5 nm from a transduction channel’s pore plummets from 37 μM during channel opening to only 0.1 μM within 100 μs of channel closure. If a channel binds Ca2+ for an average of 100 μs during reclosure, it follows that the probability of occupancy by a second ion after the first has vacated the binding site is quite low: for a dissociation constant of 10 μM, the binding probability is but 0.01 following a 100-μs closure.
Work Performed During Bundle Movements.
One may estimate the amount of work performed by the active process from the hair bundle’s properties and the magnitude of spontaneous or evoked bundle movements (10). Assuming that the work done against an elastic load is not recovered, the energy expended is at most ∼900 zJ or the equivalent of ∼220 kT. Even if the elastic work is wholly recovered, the work performed against viscosity nonetheless sets a lower limit on the energy expenditure of ∼100 zJ or ∼25 kT.
In the proposed mechanism of amplification, useful energy is derived from a concentration gradient, albeit not one of the ordinary, spatial type. The relevant gradient instead arises over time: the Ca2+ concentration at the binding site is hypothesized to differ significantly between occasions when the channel is open and those when it is closed. The changing Ca2+ concentration thus powers the proposed amplifier much as changing temperature drives a Carnot heat engine.
Suppose that Ca2+ binds while the cytoplasmic concentration is at the peak for the conditions given earlier, 37 μM, and unbinds after the concentration has fallen to that of a quiescent stereocilium, 0.05 μM (24). During each cycle, binding of a single ion to a transduction channel could then contribute work equal to
 |
1 |
For a hair bundle with 75 active channels (9, 29, 30), the maximal work per cycle would be ∼2,000 zJ or ∼500 kT. Even allowing for inefficiency in the system, the available energy would handily exceed that necessary to account for the observed bundle movements.
MATHEMATICAL FORMULATION OF THE MODEL
The force applied on the hair bundle may be represented by four components: the stimulus force, FSTIM, the viscous drag, the elastic force due to stiffness of the stereociliary pivots and side links, and the elastic force due to stiffness of the gating springs:
 |
2 |
in which X(t) is the displacement of the bundle’s top from rest at time t, pO(t) the transduction channel’s open probability, MHB the hair bundle’s mass, ξHB the bundle’s viscous drag coefficient, ΚSP the combined stiffness of the stereociliary pivots and associated side links, κGS the stiffness of an individual gating spring, NT the number of transduction channels, γ the geometric gain factor relating bundle displacement to gating-spring stretch, b the transduction-channel gate’s swing, XSP the displacement at which the side link and pivot forces are zero, and XGS the displacement at which the gating springs slacken. This equation resembles that for a driven damped harmonic oscillator. The gating spring introduces a nonlinear term (9), however, for the tension in the spring depends on a channel’s state, which in turn is exponentially dependent on bundle displacement.
The second-order ordinary differential equation describing hair-bundle motion may be rewritten as a two-dimensional system of first-order ordinary differential equations:
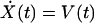 |
3 |
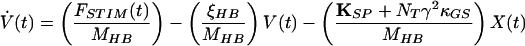 |
4 |
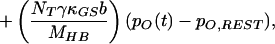 |
in which V(t) is the bundle’s velocity and pO,REST the channel’s open probability at rest. The constant offset terms for the stereociliary pivots, side links, and gating springs are equated to the last term of Eq. 4 by the boundary conditions at rest.
Ca2+-Dependent Channel Kinetics.
The present model encompasses two Ca2+-binding sites and six states of the transduction channel (Fig. 1). Let pi(t) be the probability that a channel resides in state i at time t; the open probability is then the sum of p2(t), p3(t), and p4(t). In the interest of simplicity and to maximize the amplification produced by the model, we have chosen a highly constrained system in which each of the forward (counterclockwise in Fig. 1) rate constants at rest, kF, is identical; a similar restriction applies to the reverse rate constants, kR. These conditions additionally force the rate constants for the middle gating transitions to assume an identical value, k36. Because of the computational overhead and stochastic calculations involved in explicitly determining the local Ca2+ concentration at each channel, we have represented this concentration as a step function: an open channel imposes the maximal concentration of 37 μM, whereas a closed channel yields the resting value of 0.05 μM. We have subsumed the concentration terms for the Ca2+-dependent transitions into the rate-constant prefactors.
Figure 1.
Schematic diagram of the active-channel model. Each transduction channel is posited to exist in either a closed form, C, or an open one, O. Application of a positive stimulus force to the hair bundle promotes channel opening, whereas binding of Ca2+ favors closure. The rate constants for reactions in the counterclockwise direction are designated kF, those pertaining to the clockwise direction kR, and those for the two central transitions k36. During sinusoidal stimulation or limit-cycle oscillation, the occupancy of the channel’s six states cycles in the counterclockwise direction.
We arrive at the following state equations:
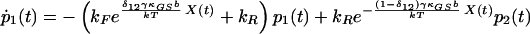 |
5 |
 |
 |
6 |
 |
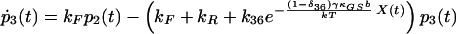 |
7 |
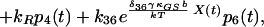 |
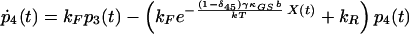 |
8 |
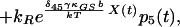 |
 |
9 |
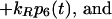 |
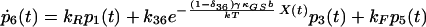 |
10 |
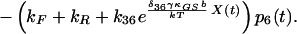 |
δij represents the reaction coordinate of gating in the closed-to-open transition between states i and j (15). The displacement-dependent terms in the exponents, which arise from the chemoelastic potential energy differences of the gating spring with the channels in their open and closed states, stem from Eyring absolute rate theory (31).
According to Eqs. 3–10, we define the state of the system as S(t) = [X, V, p1, p2, p3, p4, p5, p6]T, in which each element is implicitly a function of time. The system equations may be summarized as a vector function of state, Ṡ(t) = F[S(t)]. The system has a physiological fixed point, an equilibrium state at which all time derivatives vanish, at its rest position. Here the bundle displacement and velocity are zero and the channel populations cycle in a steady state. By the rate-constant constraints imposed above, each steady–state population is one-sixth; the fixed point therefore corresponds to S* = [0, 0, 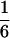 ,
, 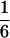 ,
, 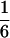 ,
, 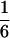 ,
, 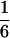 ,
, 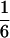 ]T.
]T.
Linear Stability Analysis.
The response of a dynamical system to stimulation is determined by the nature of its fixed points, which may be ascertained by linearizing a perturbation of the state equation around each point by Taylor expansion, and then calculating the eigenvalues of the resulting Jacobian, the gradient matrix of a vector function (ref. 32, pp. 150–159). These eigenvalues indicate the system’s stability near each fixed point and qualitatively describe its temporal evolution. The eigenvalues additionally represent the rate constants of the corresponding eigenmodes, the trajectory components along the system’s eigenvectors. Complex eigenvalues, which arise as conjugate pairs, indicate oscillatory decay or limit-cycle solutions in the neighborhood of the fixed point; the real part describes the temporal envelope and the imaginary part approximates the radial oscillation frequency. Because eigenvectors are independent and the state trajectory is the sum of the eigenmodes, the long-term behavior of the system depends primarily on the modes with the slowest decay, those with least negative real parts.
At the model system’s fixed point, the Jacobian is
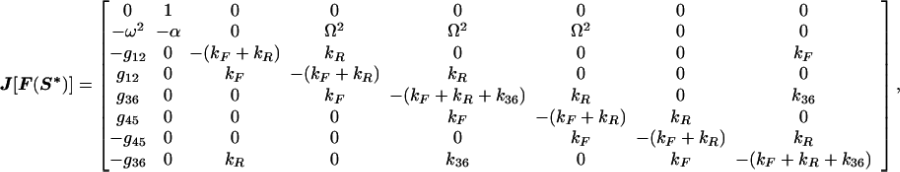 |
11 |
in which
 |
12 |
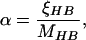 |
13 |
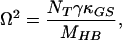 |
14 |
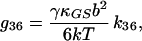 |
15 |
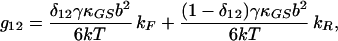 |
16 |
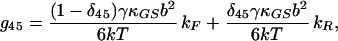 |
17 |
and all length scales are in units of b, the channel gate’s swing.
Parameter Reduction and System Dynamics.
Although the number of parameters in the model is quite large, many values may be fixed on the basis of experimental measurements. The relations between various parameters allow a further reduction in number. In particular, the constant content of filamentous actin in hair bundles along the chicken’s cochlea (33) suggests functional relations for several mechanical parameters to the number of stereocilia in the bundle, NS.
For a hair bundle of approximately rectangular cross-section in which the number of stereociliary ranks is conserved, the number of transduction channels, NT, appears in a fixed ratio to NS; NT = 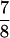 NS. Because the bundle consists largely of actin, its volume and mass are fixed as well. To the extent that stereociliary diameter remains constant, the number of stereociliary files then varies directly and the bundle’s height inversely with NS. The geometric gain factor (9), γ, is also a function of NS; γ = 2.4 × 10−3 NS. In addition, the stiffness component attributed to the stereociliary pivots and side links is directly proportional to NS and inversely related to the square of the bundle’s height; KSP = 0.98 nN × m−1 NS3. Because the bundle’s inversely related height and width imply a constant frontal area, the drag coefficient is roughly constant.
NS. Because the bundle consists largely of actin, its volume and mass are fixed as well. To the extent that stereociliary diameter remains constant, the number of stereociliary files then varies directly and the bundle’s height inversely with NS. The geometric gain factor (9), γ, is also a function of NS; γ = 2.4 × 10−3 NS. In addition, the stiffness component attributed to the stereociliary pivots and side links is directly proportional to NS and inversely related to the square of the bundle’s height; KSP = 0.98 nN × m−1 NS3. Because the bundle’s inversely related height and width imply a constant frontal area, the drag coefficient is roughly constant.
The Ca2+-cycle parameters λij, kF, kR, and k36 are independent of NS. In accordance with energy constraints, however, kF and kR occur in a constant ratio prescribed by partitioning the free energy available to the system among the transitions. The absolute value of kF or of the corresponding activation energy, ΔGF†, remains a free parameter.
RESULTS
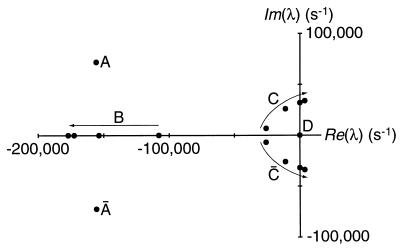
Under what circumstances can the model yield resonance with a high quality factor (Q) or even produce spontaneous oscillations? This issue may be explored by systematic variation of the parameter values, which changes the nature of the system’s eigenvalues and their positions on the complex plane (Fig. 2). As an eigenvalue crosses the imaginary axis, an oscillatory decay mode becomes a limit-cycle oscillation. The parameter set at the crossing constitutes a Hopf bifurcation (ref. 32, pp. 248–254). Because the bifurcation corresponds to an infinite Q, any neighboring set of parameters gives rise to a high-Q system. The presence of a Hopf bifurcation therefore assures the existence of a regime in which the system can act as a tuned amplifier. Although a hair bundle needs not display sustained spontaneous oscillation, the auditory system might be expected to exploit the local instability in parameter space at the Hopf bifurcation to achieve a highly resonant response.
Figure 2.
Parameter dependence of the system’s eigenvalues (λ). The eigenvalues determined for four values (108, 140, 220, and 300) of the stereociliary number, NS, are represented on the complex plane. The points designated B, C, and C̄ demonstrate the functional dependence of the system on NS; the arrows indicate the progression of eigenvalues with increasing values of this parameter. The angular frequency at the Hopf bifurcation for C and C̄, ±32,000 s−1, corresponds to a characteristic frequency of ∼5 kHz. Point D, which represents the conservation of state probability in the channel-gating cycle, remains at the origin. The conjugate pair A and Ā are independent of NS and also appear stationary. An additional conjugate pair of eigenvalues, those farthest to the left, have been omitted to permit display of the remaining points on an informative scale. The system is characterized by an eighth-degree characteristic polynomial that precludes a closed form for the eigenvalues; numerical evaluation was therefore necessary. The stability analysis and simulation programs were written in mathematica and executed on a Macintosh Quadra 800 computer (Apple Computer, Cupertino, CA) or an Indigo Impact 10000 computer (Silicon Graphics, Mountain View, CA).
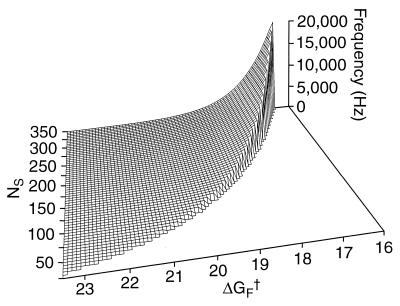
Reduction of the system to two varying free parameters, NS and ΔGF†, facilitates the search of parameter space for Hopf bifurcations. For physiologically realistic parameter values, the bifurcation locus encompasses characteristic frequencies of 0.02–20 kHz (Fig. 3). The monotonic increase in characteristic frequency with stereociliary number agrees with the observed tonotopic pattern along the cochlea, and the dependence on the activation energy of the forward rate constant accords with expectation. Over the range of stereociliary numbers observed in the cochlea of the chicken, 50–300 (34), the theoretical system is tuned to frequencies spanning the physiological range for that species, 0.05–5 kHz (35), and for mammals such as man. Mammalian species whose auditory sensitivity extends to higher frequencies have conspiciously smaller hair bundles than those considered here.
Figure 3.
Dependence of the model’s frequency selectivity on the number of stereocilia, NS, and the resting activation energy for forward transitions, ΔGF†, expressed in units of the thermal energy kT. Characteristic frequencies are calculated for points at and beyond the Hopf bifurcations, which occur along the ridge. Prebifurcation solutions, which lie to the right of the bifurcation locus, correspond to decaying responses to perturbation. The solutions near the bifurcation imply transient oscillatory components. To the left of the bifurcation locus, postbifurcation solutions represent limit-cycle oscillations.
Simulations for a 5-kHz Hair Cell.
A prebifurcation parameter set associated with a characteristic frequency of ∼5 kHz demonstrates the system’s response to resonant-frequency sinusoidal inputs. For threshold stimulation, the active-channel model displays a resonant response with a peak amplitude of 0.37 nm (Fig. 4A). An identical stimulus produces far smaller responses in two passive systems with similar mechanical characteristics: a nonlinear damped oscillator with gating springs and channels but no coupling to the Ca2+-binding cycle (Fig. 4B) and a linear system without mechanically gated channels (Fig. 4C). For threshold stimuli, the amplitude of bundle motion for the active model is 56-fold that for the nonlinear passive formulation and 117-fold that for the linear passive model. At the cessation of stimulation, both passive systems immediately return to rest; the active system, by contrast, exhibits prolonged oscillation with a Q value near 50.
Figure 4.
Modeled responses of a hair bundle to stimulation with a 5-kHz sinusoidal force 0.2 pN in amplitude (Bottom trace). (A) In the active-channel model, the bundle displays oscillations of roughly threshold amplitude upon stimulation. The system’s high Q is revealed by the gradual rise and decline of the response. (B) The response of a similar model without Ca2+-induced channel reclosure shows far less amplification and no resonance after stimulation. (C) For a passive model without channel gating, the displacement is roughly the driving force divided by the bundle’s stiffness. In each instance, MHB = 60 pg, ξHB = 100 nN⋅s⋅m−1, KSP = 9,000 μN⋅m−1, κGS = 1,200 μN⋅m−1, NS = 210, NT = 184, γ = 0.50, b = 4.5 nm, δ12 = 0.9, δ36 = 0.1, δ45 = 0.1, kF = 93,500 s−1, kR = 10,300 s−1, and k36 = 0.88 s−1. The response in B displays an offset of −2.9 nm; the system’s bistability around a resting position at which pO,REST = 0.5 emerges from fixed-point analysis.
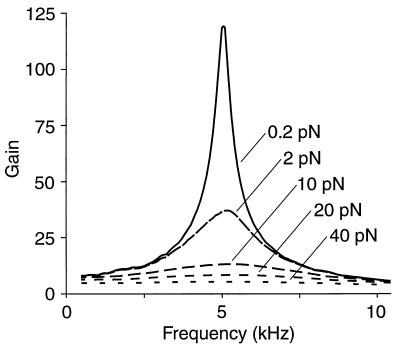
The active model displays significantly higher gain and sharper frequency selectivity at threshold than for the largest stimulus forces (Fig. 5). With increasing stimulus amplitude, the spectrum asymptotically approaches linearity. At resonance, the system’s gain shows an approximately power-law dependence upon the amplitude of stimulation. The exponent, −0.6, is similar to that of −0.7 calculated for experimental studies (reviewed in ref. 36). An active process in hair bundles may therefore contribute substantially to the compressive nonlinearity observed at the basilar membrane.
Figure 5.
Gain spectrum of the active-channel amplifier. The system’s gain, defined as the ratio of the response’s amplitude to that of the linear passive system, is greatest for stimuli near threshold. With growth of the stimulus amplitude, which is indicated for each trace, the frequency selectivity declines and the system approaches linearity. Peak response amplitudes range from 0.37 nm for 0.2-pN stimulation to 3.4 nm for a 40-pN input.
DISCUSSION
We have demonstrated that frequency-selective auditory amplification may be effectively modeled by coupling the mechanical properties of a hair bundle to a Ca2+-binding cycle that governs the open probability of mechanoelectrical-transduction channels. For some parameter values, the system additionally produces bundle oscillations that might underlie spontaneous otoacoustic emissions.
Amplitude Dependence of Amplification.
Cochlear amplification is most profound near the auditory threshold, falling steeply as the stimulus intensity increases (reviewed in ref. 36). Measured in terms of basilar-membrane displacement, the ear’s sensitivity to stimulation at a sound pressure level of 70 dB is only 1% that to a threshold stimulus of 10 dB. As a result of the decline in amplification over this 1,000-fold change in the stimulus amplitude, the basilar membrane, and presumably the hair bundle, undergoes an excursion that increases only 10-fold.
Because the proposed amplification stems from transduction-channel reclosure, the hair-bundle movement that could be produced is limited by the distance through which the transduction channel’s gate moves during channel opening, 2–4 nm (9, 30). When measurements are made at a hair bundle’s top, this motion is exaggerated by the bundle’s geometrical and mechanical properties (reviewed in ref. 17). For the outer hair cells that dominate cochlear amplification in mammals, the mechanical nonlinearity associated with transduction-channel gating (9) consequently extends to bundle deflections as great as 20 nm in amplitude (37). As shown by Fig. 5, an amplificatory process based upon transduction-channel reclosure is therefore consistent with the distance scale on which the cochlear amplifier operates.
Energetic and Kinetic Considerations.
The simplest active-channel model includes only four states and a single Ca2+-binding site. The free-energy change for ion binding in this model, 7 kT per cycle, renders the forward rate constants 5-fold the reverse. By using physiologically relevant parameter values, we have been unable to find Hopf bifurcations under these circumstances (data not shown). It should be borne in mind, however, that we have strongly constrained the system by fixing the relationship between rate constants; under less restrictive conditions, a four-state model might display resonant behavior.
The introduction of two additional states of the transduction channel, which corresponds to the addition of one further Ca2+-binding site, greatly enhances the prospects for high-Q hair-bundle resonance. When ion binding at two sites contributes 13 kT of free energy per cycle, the forward rate constants become 9-fold the reverse. More importantly, the additional states accentuate the phase separation between channel opening and closing. In the four-state model, the coincidence of a significant fraction of these transitions causes destructive interference. In addition, the Ca2+-binding step for an open channel directly competes with the channel-closing transition. Negative bundle motion caused by Ca2+-dependent closure promotes this reverse transition, limiting further occupancy of the liganded open state that underlies the active process. In the six-state model with identical binding sites, by contrast, the singly liganded state introduces a delay between the dominant gating transitions, increasing the coherence of channel gating and enhancing the transfer of force from the channels to the hair bundle. That relatively large ions traverse the transduction channel (20) suggests that its pore is formed by several molecular subunits; if so, Ca2+ binding at more than two sites might further promote coherence and force transfer.
Our model requires that the rate constants governing transduction-channel gating somehow be specified for hair cells of each characteristic frequency. Alternative splicing of the mRNA encoding this channel would potentially provide such a tuning mechanism. The Ca2+-activated K+ channels of hair cells are known to occur along the cochlea as splice variants whose differing activities adjust the frequency of electrical resonance (38, 39). In a similar fashion, transduction-channel isoforms might differ in their Ca2+ affinities, kinetic properties, or mechanical characteristics. Tuning might alternatively be regulated by such features as the geometric gain of the hair bundle, the complement and efficacy of Ca2+ pumps (25), and the effectiveness of stereociliary Ca2+ buffering (16, 24).
Limit-Cycle Oscillations in Hair Cells.
Linear stability analysis with a physiological range of parameter values demonstrates Hopf bifurcations that correspond to observed frequencies of hair-cell responsiveness. Bifurcation implies a neighboring region of parameter space in which the hair bundle behaves as a high-Q oscillator, tapping the resonant instability of the bifurcation to produce amplified mechanical responses. The existence of spontaneous otoacoustic emissions suggests, moreover, that under certain conditions the system crosses the bifurcation and achieves limit-cycle behavior.
Might limit-cycle oscillations be used in the intact auditory system? For hair cells whose outputs contribute substantially to eighth-nerve afferent activity, the transduction of continuous hair-bundle motion would inject noise into the auditory pathways. These receptors might nonetheless harbor prebifurcation amplifiers, which would enhance stimulus-driven bundle motions just as power steering facilitates turning a steering wheel. Hair cells that have little or no afferent innervation, such as mammalian outer hair cells and archosaurian short hair cells, could in contrast oscillate indefinitely without a detrimental effect on auditory signaling. A population of limit-cycle oscillators might operate independently until an external stimulus enforced coherence, whereupon synchronized bundle oscillations would promote motion of the tectorial membrane and thus excite the hair cells that communicate with the central nervous system.
Acknowledgments
We thank Dr. A. Libchaber for discussions and Drs. E. A. Lumpkin and W. M. Roberts and the members of our research groups for critical comments on the manuscript. This work was supported by Grant DC00317 from the National Institutes of Health. Y.C. is supported in part by a graduate fellowship from the National Science Foundation. M.O.M. is supported by the Mathers Foundation. A.J.H. is an Investigator of Howard Hughes Medical Institute.
References
- 1.Gold T. Proc R Soc London Ser B. 1948;135:492–498. [Google Scholar]
- 2.Probst R. Adv Otorhinolaryngol. 1990;44:1–91. doi: 10.1159/000417719. [DOI] [PubMed] [Google Scholar]
- 3.Dallos P. J Neurosci. 1992;12:4575–4585. doi: 10.1523/JNEUROSCI.12-12-04575.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hudspeth A J. Nature (London) 1989;341:397–404. doi: 10.1038/341397a0. [DOI] [PubMed] [Google Scholar]
- 5.Hudspeth A J. Curr Opin Neurobiol. 1997;7:480–486. doi: 10.1016/s0959-4388(97)80026-8. [DOI] [PubMed] [Google Scholar]
- 6.Manley G A, Köppl C. Curr Opin Neurobiol. 1998;8:468–474. doi: 10.1016/s0959-4388(98)80033-0. [DOI] [PubMed] [Google Scholar]
- 7.Crawford A C, Fettiplace R. J Physiol (London) 1985;364:359–379. doi: 10.1113/jphysiol.1985.sp015750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Howard J, Hudspeth A J. Proc Natl Acad Sci USA. 1987;84:3064–3068. doi: 10.1073/pnas.84.9.3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Howard J, Hudspeth A J. Neuron. 1988;1:189–199. doi: 10.1016/0896-6273(88)90139-0. [DOI] [PubMed] [Google Scholar]
- 10.Benser M E, Marquis R E, Hudspeth A J. J Neurosci. 1996;16:5629–5643. doi: 10.1523/JNEUROSCI.16-18-05629.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hasson T, Gillespie P G, Garcia J A, MacDonald R B, Zhao Y, Yee A G, Mooseker M S, Corey D P. J Cell Biol. 1997;137:1287–1307. doi: 10.1083/jcb.137.6.1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gillespie P G, Wagner M C, Hudspeth A J. Neuron. 1993;11:581–594. doi: 10.1016/0896-6273(93)90071-x. [DOI] [PubMed] [Google Scholar]
- 13.Hudspeth A J, Gillespie P G. Neuron. 1994;12:1–9. doi: 10.1016/0896-6273(94)90147-3. [DOI] [PubMed] [Google Scholar]
- 14.Jaramillo F, Howard J, Hudspeth A J. In: The Mechanics and Biophysics of Hearing. Dallos P, Geisler C D, Matthews J W, Ruggero M A, Steele C R, editors. Berlin: Springer; 1990. pp. 26–33. [Google Scholar]
- 15.Corey D P, Hudspeth A J. J Neurosci. 1983;3:962–976. doi: 10.1523/JNEUROSCI.03-05-00962.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ricci A J, Wu Y-C, Fettiplace R. J Neurosci. 1988;18:8261–8277. doi: 10.1523/JNEUROSCI.18-20-08261.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Markin V S, Hudspeth A J. Annu Rev Biophys Biomol Struct. 1995;24:59–83. doi: 10.1146/annurev.bb.24.060195.000423. [DOI] [PubMed] [Google Scholar]
- 18.Crawford A C, Evans M G, Fettiplace R. J Physiol (London) 1991;434:369–398. doi: 10.1113/jphysiol.1991.sp018475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Marquis R E, Hudspeth A J. Proc Natl Acad Sci USA. 1997;94:11923–11928. doi: 10.1073/pnas.94.22.11923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Corey D P, Hudspeth A J. Nature (London) 1979;281:675–677. doi: 10.1038/281675a0. [DOI] [PubMed] [Google Scholar]
- 21.Jørgensen F, Kroese A B. Acta Physiol Scand. 1995;155:363–376. doi: 10.1111/j.1748-1716.1995.tb09986.x. [DOI] [PubMed] [Google Scholar]
- 22.Lumpkin E A, Marquis R E, Hudspeth A J. Proc Natl Acad Sci USA. 1997;94:10997–11002. doi: 10.1073/pnas.94.20.10997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.de Leon M, Wang Y, Jones L, Perez-Reyes E, Wei X, Soong T W, Snutch T P, Yue D T. Science. 1995;270:1502–1506. doi: 10.1126/science.270.5241.1502. [DOI] [PubMed] [Google Scholar]
- 24.Lumpkin E A, Hudspeth A J. J Neurosci. 1998;18:6300–6318. doi: 10.1523/JNEUROSCI.18-16-06300.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yamoah E N, Lumpkin E A, Dumont R A, Smith P J S, Hudspeth A J, Gillespie P G. J Neurosci. 1998;18:610–624. doi: 10.1523/JNEUROSCI.18-02-00610.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hille B. Ionic Channels of Excitable Membranes. 2nd Ed. Sunderland: Sinauer Associates; 1992. p. 278. [Google Scholar]
- 27.Roberts W M. Nature (London) 1993;363:74–76. doi: 10.1038/363074a0. [DOI] [PubMed] [Google Scholar]
- 28.Roberts W M. J Neurosci. 1994;14:3246–3262. doi: 10.1523/JNEUROSCI.14-05-03246.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Holton T, Hudspeth A J. J Physiol (London) 1986;375:195–227. doi: 10.1113/jphysiol.1986.sp016113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Denk W, Holt J R, Shepherd G M G, Corey D P. Neuron. 1995;15:1311–1321. doi: 10.1016/0896-6273(95)90010-1. [DOI] [PubMed] [Google Scholar]
- 31.Johnson F H, Eyring H, Polissar M J. The Kinetic Basis of Molecular Biology. New York: Wiley; 1954. pp. 18–20. [Google Scholar]
- 32.Strogatz S H. Nonlinear Dynamics and Chaos. Reading, MA: Addison-Wesley; 1994. [Google Scholar]
- 33.Tilney L G, Tilney M S. J Cell Biol. 1988;107:2563–2574. doi: 10.1083/jcb.107.6.2563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tilney L G, Saunders J C. J Cell Biol. 1983;96:807–821. doi: 10.1083/jcb.96.3.807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jones S M, Jones T A. Hear Res. 1995;82:149–157. doi: 10.1016/0378-5955(94)00173-n. [DOI] [PubMed] [Google Scholar]
- 36.Ruggero M A. Curr Opin Neurobiol. 1992;2:449–456. doi: 10.1016/0959-4388(92)90179-o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Russell I J, Kössl M, Richardson G P. Proc R Soc London Ser B. 1992;250:217–227. doi: 10.1098/rspb.1992.0152. [DOI] [PubMed] [Google Scholar]
- 38.Navaratnam D S, Bell T J, Tu T D, Cohen E L, Oberholtzer J C. Neuron. 1997;19:1077–1085. doi: 10.1016/s0896-6273(00)80398-0. [DOI] [PubMed] [Google Scholar]
- 39.Rosenblatt K P, Sun Z-P, Heller S, Hudspeth A J. Neuron. 1997;19:1061–1075. doi: 10.1016/s0896-6273(00)80397-9. [DOI] [PubMed] [Google Scholar]