Adaptations of proteins to cellular and subcellular pH

Abstract

Bioinformatics-based searches for correlations between subcellular localization and pI or charge distribution of proteins have failed to detect meaningful correlations. Recent work published in BMC Biology finds that a physicochemical metric of charge distribution correlates better with subcellular pH than does pI.

See research article http://www.biomedcentral.com/1741-7007/7/69

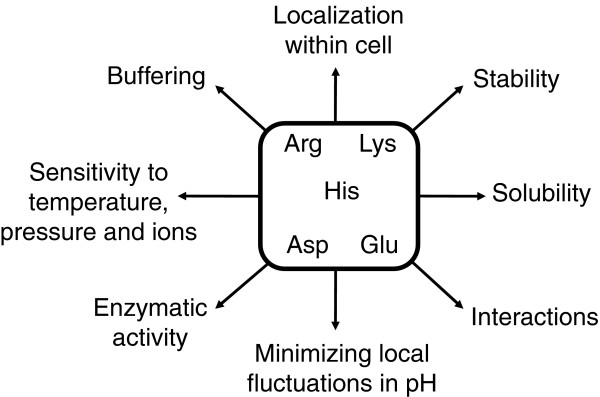
The need for tight regulation of intracellular pH is one of the most important and constant organizing principles of living systems. It is essential because the fundamental energy transduction machinery of cells runs mainly on H⁺ gradients and proton-coupled electron transfer reactions. It is also necessary because pH determines the charge state of weak acids and bases (for example, side chains of Asp, Glu, His, Lys and Arg, and so on), and the charge state in turn affects many physical and physiological properties of biological molecules, especially proteins and RNAs (Figure 1). Regulation of intracellular pH is so central to the living state that even the most primitive cells capable of energy transduction must have been able to control intracellular pH by expelling H⁺ produced from the hydrolysis of organic compounds.

Figure 1.

The distribution of ionizable residues (for example, the side chains of Arg, Lys, His, Asp and Glu) in proteins might reflect adaptations to cellular and intracellular pH. The search for these structural adaptations should consider the important roles of charged residues on the many different functional, structural, physical and biological factors that influenced the evolution of proteins, as indicated here.

How tightly is pH regulated in cells and organisms? Consider that the normal pH of human arterial blood is 7.40. Depression below pH 7.35 leads to acidosis, a condition that requires medical attention, and elevation to pH 7.50 results in alkalosis, responsible for the unpleasant symptoms of altitude sickness. Similarly small changes of 0.1 pH units in intracellular pH or within subcellular compartments can have physiological consequences. What is remarkable is that despite the need for very tight regulation, the pH in various cellular compartments varies significantly. In organs such as the human stomach, it can be extreme.

In cells, pH is nearly neutral in the cytoplasm, in the endoplasmic reticulum and in mitochondria. It is more acidic in vacuoles, lysosomes (as low as pH 5) and in the Golgi. It is more basic in the nucleus and in peroxisomes (as high as pH 8) [1]. Proteins can harness these differences in cellular and subcellular pH for physiological purposes. For example, the influenza virus requires exposure to the slightly acidic conditions in the lysosome to become activated [2]. Human hemoglobin acts similarly as a pH sensor that targets exercised tissue for delivery of oxygen by responding to local acidity [2].

The tight regulation of cellular and subcellular pH might imply that charged residues of proteins have been tailored for structural or functional purposes under specific conditions of pH. For example, the isoelectric point (pI) of proteins, which describes the balance between acidic and basic residues, might have co-evolved with the pH of the organelles in which they exist to enable or to optimize function [3]. Learning to recognize these adaptations would be useful for the annotation of proteomes and for understanding protein function and evolution. Previous bioinformatics-based searches for correlations between subcellular localization and pI or charge distribution have yielded interesting nuggets but have failed to detect a meaningful correlation [4]. The problem is that the pI is a relatively insensitive global metric of the number and types of ionizable groups; the distribution of pI values in a proteome is inherently bimodal owing to the normal differences in the pK_a (the acid dissociation constant) of the dominant acidic (Asp and Glu) and basic (Lys and Arg) residues [4,5]. Now Chan and Warwicker [5] have examined the correlation of intracellular pH with calculated electrostatic contributions to stability. Using this more physical metric of charge distribution, they found that the average pH of maximal stability for proteins in a subcellular compartment correlates better with subcellular pH than does pI. The properties of histidine residues underlie this correlation.

Effects of charge distribution on properties of proteins

Identifying further meaningful correlations between subcellular localization or subcellular pH with the number, types, distribution and properties of ionizable groups in proteins, starting from either sequence or structure, will be interesting but challenging. The problem is that the charge properties of proteins have evolved under pressure to satisfy a large number of physical and biological constraints (Figure 1). Trying to identify trends or adaptations by focusing on one or two among the many constraints is akin to examining a piece of music through statistical analysis of musical notes or their values (that is, their duration), ignoring all other attributes of the music. Averaged over their entire oeuvre, the works of Bach and Beethoven might indeed show statistically significant differences in their predilection for some notes, but it is unlikely that this will be reflected in any individual piece, that the level of discrimination will be sufficient to identify a composer from among a list of hundreds, or that this approach will improve our understanding or appreciation of music. A meaningful search for adaptations of proteins to subcellular pH should consider simultaneously some of the following structural, biological and solution properties of proteins, all of which are influenced by charged residues.

Spatial localization

The distribution of charges on a protein can be biased by the protein's location within a subcellular compartment. For example, membrane proteins tend to be more basic than cytosolic ones [4]. This might be an adaptation to facilitate interactions between positive charges on the protein and the predominantly negatively charged polar head groups of membrane phospholipids. However, to illustrate how deceptive general trends can be, consider that some proteins that interact strongly and irreversibly with membranes actually use Ca²⁺ bridges that require post-translational modifications that add negative charges to the proteins [2].

Stability

The pH dependence of stability of proteins is governed by differences in pK_a values of ionizable groups in folded and unfolded forms. Using structure-based continuum electrostatics calculations, Alexov [6] showed previously that the pI and the pH optimum for stability can be quite different. Some proteins, such as proteases in the lysosome, are clearly adapted for maximal stability and activity in the relatively low pH of this compartment. Chan and Warwicker [5] show that this correlation of the pH of maximal stability with intracellular pH is only evident when the properties of many proteins within a subcellular compartment are averaged. Their study illustrates the power of quantitative physicochemical approaches in the analysis of proteomes. The effectiveness of this approach is also illustrated by other studies of charge contributions to the stability of thermophilic proteins. Proteins from thermophilic organisms usually have a higher number of charges and ion pairs than their mesophilic homologs [7]. An analysis of the number and types of charges would conclude that charges in thermophilic proteins were selected to enhance the stability of proteins through Coulomb interactions. However, a structure-based study of electrostatic contributions to stability using a physicochemical model failed to detect any correlation between the excess charges in thermophilic proteins and increased stability [7].

Solubility

Solubility is a critical factor in the evolution of protein sequences and folds [8]. In general, charges in globular proteins are surrounded by charges of the opposite sign [9]. This would seem to reflect evolutionary tuning of surface charges to maximize stabilizing Coulomb interactions in the folded state, but it is more likely to be an adaptation to enhance solubility. Charges affect the solubility of proteins; therefore, the adaptation of charges to tune any property of a protein for a specific subcellular pH could affect solubility. Because there is no theory of protein solubility, it is impossible to determine how a specific distribution of charges affects solubility. In general, solubility correlates with pI (proteins tend to be least soluble at their pI); therefore, given the lack of correlation between pI and subcellular pH, solubility probably does not correlate well with subcellular pH. A large number of ionizable residues, especially basic ones, can enhance the solubility of a protein. However, unexpected factors can also influence solubility. For example, the solubility of folded proteins is affected by stability; a large energy gap between the fully folded, soluble form and partially unfolded, less soluble forms is needed to prevent population of aggregation-prone states. Solubility can in fact be affected by single mutations that do not alter the number of charges in the protein.

Interactions

Charges are essential both to prevent and to stabilize complexes of proteins with macromolecules and with small molecules. A correlation has been found between the pH optimum of stability of monomeric proteins and of their complexes [10]. This suggests that pH-dependent properties of the monomers and of the complexes coevolved at the same pH. The presence of a specific constellation of charges for functional interactions can bias the distribution and properties of charges in proteins. For example, regions of high density of positive charge are usually found in the faces of proteins that interact with nucleic acids. Any correlation between nuclear pH and the distribution of charges in nuclear proteins in a eukaryotic cell is likely to be a secondary consequence of these functional adaptations.

Enzymatic activity

The ionizable groups that control enzymatic catalysis usually titrate with highly perturbed pK_a values tuned for catalysis under the appropriate pH conditions. Just one of these groups with perturbed pK_a can have a dramatic influence on the pH dependence of protein stability [11]. This might be the reason that the pH optimum of enzymatic reactions is, in general, not correlated with the pH of maximum stability. The adaptation of some proteins to subcellular pH might involve tuning of the pK_a values of active-site residues. There are no computational tools that reproduce the properties of internal ionizable groups accurately, and so this essential adaptation to subcellular pH cannot yet be examined quantitatively.

Environmental conditions

Previous attempts to identify protein adaptations to subcellular pH have not considered that charges and their contribution to stability, solubility, dynamics, conformation, function, and so on are sensitive to physical variables (temperature, pressure), and to the chemical composition of their milieu (osmolytes, ionic composition, metabolites). Chan and Warwicker [5] point out that differences in the distribution of charges in proteins from extremophiles and mesophiles illustrate the important roles of charges in proteins for adaptation to specific environmental conditions. The influence of the ionic milieu on adaptations to intracellular pH deserves special mention because subcellular pH is coupled to ion homeostasis (that is, changes in intracellular pH are coupled to changes in concentration of other ions). Protein adaptations to unique ionic environments are already known. For example, hemoglobin, which is regulated physiologically by the large anion 2,3-bis-phosphglycerate, has a cleft with a high concentration of positively charged residues where the di-anion binds [2]. Another example is that of extracellular proteins or proteins that exist in vacuoles or other compartments that can have high Ca²⁺ concentrations. These proteins might be expected to be more acidic to maximize interactions of Asp and Glu residues with Ca²⁺ to enhance stability or for other purposes. Attempts to identify protein adaptations to subcellular pH should consider how the ionic milieu characteristic of a subcellular compartment might have influenced these adaptations.

Buffer capacity

The regulation of subcellular pH is partly achieved through the buffer capacity of metabolites and macromolecules. This is the reason that a correlation of protein pI with subcellular pH has been sought. However, the ability of a protein to act as a buffer in a subcellular environment will depend not just on the number of ionizable groups and their pK_a values, but also on the concentration of protein in the compartment. A meaningful correlation between pI and subcellular pH might yet be found if protein concentration and compartment volume were taken into consideration.

Biological considerations

The distribution of charges in proteins can be biased by a number of biological factors that are not linked to intra-cellular pH in an obvious way. Evolutionary history, mutational bias, AT nucleotide bias, level of gene expression and optimization of translational efficiency are some factors that will have to be examined closely.

Physicochemical considerations

Chan and Warwicker [5] have raised other interesting issues that will have to be considered when searching for protein adaptations to subcellular pH. The adaptations might not be tuned for function in the steady state intracellular pH, but rather to the transient changes in pH that might be experienced in an intracellular compartment. Chan and Warwicker also made the interesting suggestion that the dependence of the pH of maximum stability on subcellular pH might reflect the need to minimize spontaneous fluctuations in H⁺ concentration within a compartment [5]. There is clear need for a more detailed inventory of H⁺ in subcellular compartments based on the known number and calculated pK_a of weak acids and bases, and on emerging data of protein localization and concentrations. There is also need for improved understanding of the diffusion properties of protons in the osmotically complex intracellular environment, where there is no water that is not under the influence of solute, and where, formally speaking, the concept of pH is not valid.

Conclusions

Many examples of regulatory adaptations of proteins for stability or function at a specific pH are known. If charges in proteins have indeed been optimized for specific functional purposes, quite possibly they also display structural adaptations to specific subcellular conditions of pH and ionic composition. These adaptations will not be easily identified from bioinformatics analysis of proteomes using global metrics of charge distribution (such as pI). Although in general, the mean properties of proteins might be less informative than the deviations from the mean, in practice the only correlations that have been found with intra-cellular pH are with electrostatic properties calculated with physical models, averaged over many different types of proteins in a given subcellular compartment. To identify further adaptations of proteins to subcellular pH it will be useful to analyze proteomes with physicochemical models, and to consider simultaneously many of the physical and biological constraints that guided the evolution and the adaptation of proteins to the pH and ionic properties of their physiological milieu. This more integrative and physical approach might begin to reveal how different elements are combined in harmony to constitute the symphony of the cell.