Quantifying uncertainty in genotype calls

Abstract

Motivation: Genome-wide association studies (GWAS) are used to discover genes underlying complex, heritable disorders for which less powerful study designs have failed in the past. The number of GWAS has skyrocketed recently with findings reported in top journals and the mainstream media. Microarrays are the genotype calling technology of choice in GWAS as they permit exploration of more than a million single nucleotide polymorphisms (SNPs) simultaneously. The starting point for the statistical analyses used by GWAS to determine association between loci and disease is making genotype calls (AA, AB or BB). However, the raw data, microarray probe intensities, are heavily processed before arriving at these calls. Various sophisticated statistical procedures have been proposed for transforming raw data into genotype calls. We find that variability in microarray output quality across different SNPs, different arrays and different sample batches have substantial influence on the accuracy of genotype calls made by existing algorithms. Failure to account for these sources of variability can adversely affect the quality of findings reported by the GWAS.

Results: We developed a method based on an enhanced version of the multi-level model used by CRLMM version 1. Two key differences are that we now account for variability across batches and improve the call-specific assessment of each call. The new model permits the development of quality metrics for SNPs, samples and batches of samples. Using three independent datasets, we demonstrate that the CRLMM version 2 outperforms CRLMM version 1 and the algorithm provided by Affymetrix, Birdseed. The main advantage of the new approach is that it enables the identification of low-quality SNPs, samples and batches.

Availability: Software implementing of the method described in this article is available as free and open source code in the crlmm R/BioConductor package.

Contact: rafa@jhu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

A single nucleotide polymorphism (SNP) is a single nucleotide DNA variation occurring in the genomes of individuals from the same species. For most SNPs, only two bases are observed. The two possibilities are referred to as alleles. Typically, one is less common and is called minor allele. In this article, we will refer generically to the two alleles in any SNP as alleles A and B. Because we have have two copies of each autosomal chromosome (maternal and paternal), there are three possible allele combinations at each SNP: AA, AB and BB. These are referred to as genotypes. Variations in the DNA is a subject of great importance as they can elucidate, for example, how humans develop diseases and respond to treatments. Association studies enable testing for relationships between alleles and phenotypes, e.g. disease status. In the past, association studies would screen through hundreds of SNPs carefully selected to be near candidate genes. Today, microarray technology permits the screening of millions of SNPs across the entire genome and has revolutionized these studies, which are now referred to as genome-wide association studies (GWAS).

Results from large GWAS, for diseases such as bipolar disorder, coronary artery disease, Crohn's disease, hypertension, rheumatoid arthritis, Types 1 and 2 diabetes (Wellcome Trust Case Control Consortium, 2007), diabetic nephropathy (Mueller et al., 2006) and kidney dysfunction (Bash et al., 2009), have received much attention. During the last two years, we have seen a large increase of these studies and many more are in the works. Currently, the typical data analysis procedure is to genotype a large number (thousands) of cases and controls using microarrays and search for SNPs that are statistically associated with disease. However, the process of converting raw intensities into genotype calls consists of complicated statistical manipulation of noisy data and many genotype calls are uncertain. A common analysis approach is simply to perform χ²-tests to evaluate the association of the declared genotypes and disease, without accounting for uncertainty. As shown by Ruczinki et al. (http://www.bepress.com/jhubiostat/paper181) via simulation, the failure to account for genotype uncertainty properly can produce inefficient or invalid associations. Of course, a valid quantification of uncertainty is a prerequisite to using it in association studies and we focus on this aspect.

In Section 2, we outline the statistical problem and describe previous works on genotyping, focusing on CRLMM version 1, whose model is the starting point for the findings we report on this article. In Section 3, we outline the model and describe estimation procedures. In Section 4, we demonstrate the utility of our methodology with three datasets. Finally, in Section 5, we summarize and discuss our findings.

2 CONVERTING RAW INTENSITIES TO GENOTYPE CALLS

The first step, referred to as preprocessing, converts raw microarray intensities into quantities proportional to the amount of DNA in the target sample associated with each alleles A and B for each SNP. We denote these summarized intensities by I_A and I_B. We do not consider this first step and refer the reader to Carvalho et al. (2007), Affymetrix (2006), Affymetrix (2007) and Korn et al. (2008) for details. We focus on the second step (genotype calling): mapping the observed intensities, (I_A, I_B), into posterior probabilities of the three possible genotypes (AA, AB and BB) and thereby providing a confidence measure that can be used to decide which calls to omit or to introduce the appropriate genotype uncertainty when assessing association.

A naive approach to genotyping is to set confidence thresholds and call genotypes based on the Is being above or below these thresholds. For example, to call an AA genotype one might require that I_A−I_B>C. Unfortunately, the probe effect, described in detail in the microarray literature (Irizarry et al., 2003; Li and Wong, 2001a, b; Naef and Magnasco, 2003; Wu et al., 2004), requires a different cutoff for each SNP. This requirement stems from the fact that the abundance of each SNP allele is measured with different probes, having different sequences and therefore different hybridization properties, resulting in large SNP to SNP variability in the distribution of intensities I_A and I_B (Fig. 1; color version online). Competing genotype calling algorithms use different strategies for determining these SNP-specific cutoffs. Many use unsupervised clustering, like the Dynamic Model (DM)-based algorithm (Di et al., 2005) and CHIAMO (Wellcome Trust Case Control Consortium, 2007). The more successful algorithms train on data for which genotypes are known, for example, BRLMM (Affymetrix, 2006), CRLMM version 1 (Carvalho et al., 2007), BRLMM-P (Affymetrix, 2007) and Birdseed (Korn et al., 2008). For most SNPs on these training arrays, we have independent genotype calls for 270 HapMap samples (The International HapMap Consortium, 2003). These calls are based on consensus results from various technologies and are considered a gold standard.

Fig. 1.

The intensity of both the alleles is plotted against each other, i.e. I_A versus I_B, for four randomly selected SNPs. The three circles illustrate the distribution of the data for each genotype (AA: green; AB: orange; BB: violet) for the first SNP. Note that these regions are incompatible with the data for the three other SNPs. This figure illustrates that the SNP to SNP variability is much larger than the within SNP variability and that naive genotyping algorithms that define global thresholds are not appropriate.

The density of SNP microarrays has increased considerably in the last 5 years, going from a few thousands to roughly one million SNPs per chip. Nowadays it is not uncommon to find GWAS that target thousands of samples simultaneously and genotyping algorithms have gone through major modifications to accommodate such changes. CRLMM version 1 was one example of such developments, as it extended the ideas available at the time to provide means to efficiently account for various batch-related effects, outperforming competing algorithms (Lin et al., 2008). We treat it as the leading genotyping algorithm and use its model as a starting point for our work.

CRLMM uses HapMap calls to define known genotypes, which in turn permit us to define a training set. With the training data in place, Carvalho et al. (2007) describe a supervised learning approach based on a two-stage hierarchical model. Unlike other algorithms, CRLMM models M ≡ log₂(I_A/I_B) instead of the intensity pair. This choice makes CRLMM more robust to probe effects because the probe effects of the two allele probes have similar additive effects and so partially cancel. This is demonstrated by Figure 2. To account for a well-described (Affymetrix, 2006, 2007; Carvalho et al., 2007) dependence of M on the overall intensity , Carvalho et al. (2007) fit splines using a mixture model and correct the bias with the fitted curves. Then, for a given SNP, the distribution of M, conditioned on genotype, is modeled as Gaussian. To account for the remaining probe effect, each SNP i=1,…, I has a different mean μ_i and standard deviation (SD) σ_i. Sample means and SDs from the training data are used to estimate the μ_is and σ_is. However, due to low minor allele frequencies, even this large training dataset provides relatively few data points for the rare genotype in some SNPs.

Fig. 2.

The advantage of modeling M instead of (I_A, I_B): here, we plot M versus S for the same data as shown in Figure 1. The across SNP variability is smaller for M than for S. However, the probe effect is not completely removed as seen in the SNP in the bottom right panel. Note that for this SNP the cluster centers are substantially shifted.

A hierarchical model is used to improve the precision of the model parameters for these SNPs. Carvalho et al. (2007) make use of an empirical Bayes approach in which the means, conditioned on genotype, follow a multivariate normal distribution and the variances follow an inverse gamma distribution. The approach permits CRLMM to borrow strength from other SNPs. To make calls, CRLMM treats the estimated parameters as known and computes posterior probabilities for each genotype given the observed log-ratio M. The posteriors are then used as a confidence measure. Lin et al. (2008) found that the confidence measures provided by CRLMM version 1 were not optimal and proposed an ad hoc adjustment based on a training approach. CRLMM version 1 uses these adjusted confidence measures.

The strategies used to train the genotyping algorithm proposed by Carvalho et al. (2007) and the one presented on this article require an expert intervention. Currently, there is no automatic solution for this issue, but extending the algorithm to other platforms is possible, as done by Ritchie et al. (2009) for illumina infinium beadChips.

3 THE MODEL

3.1 Motivation

Procedures used in association studies are highly susceptible to problems due to inaccuracies induced by the genotyping procedures. Genotyping algorithms currently available lack methods for identifying SNPs and batches that, if not handled in the early stages of the investigation, are likely to unfavorably affect results.

The current approach to determine association between SNPs and disease is to perform an association test between genotypes and outcomes, e.g. a χ²-test for discrete outcomes. The SNPs with too low confidence scores are ‘set aside’, but the confidence cutoff is quite arbitrary and can affect results. Importantly, because there is more uncertainty associated with heterozygous calls (AB) than with homozygous calls (AA, BB), specifying a single cutoff for both (the current practice) can lead to bias due to informative missingness. Since CRLMM version 1 and other calling algorithms are model based as are assessments of association, a natural extension is to develop association tests based on genotype probabilities rather than hard calls. Marchini et al. (2007) and Plagnol et al. (2007) use such probability-based calls to combine results across different platforms. Ruczinki et al. (http://www.bepress.com/jhubiostat/paper181) demonstrate that using probability-based calls improves the power of GWAS.

The posterior probabilities provided CRLMM version 1 have three crucial limitations:

1. The posteriors are overly optimistic in favor of the genotype attaining the highest probability. The main reason for this is that the actual tails of the conditional distributions of M are longer than predicted by the Gaussian assumption. Figure 3 shows one example in which one observation has posterior of almost one and, yet, the call is wrong.

2. The statistical uncertainty of estimates from the training step is ignored, resulting in overconfident calls for minor alleles.

3. We have observed that the genotype parameters shift from batch to batch and these batch effects are not in the model used by CRLMM version 1. As a result, batches of questionable quality are not detected by the CRLMM version 1 algorithm.

Fig. 3.

An example of an SNP with three clear clusters: the calls derived from the algorithm are represented by colors (AA: green; AB: orange and BB: violet). The observation with the red circle around it was incorrectly called BB and, under the normal assumption for the residuals, the posterior was 0.999. With the assumption that the residuals follow a t-distribution, the posterior was penalized and reduced to 0.500.

The third point is particularly troublesome. A logistics problem with these large GWAS is that hybridizations need to be processed in batches. Because DNA samples are stored in 96-well plates and robots make it convenient to run all samples in a plate at once, plates are usually confounded with hybridization times. To make matters worst, it is rarely the case that a GWAS randomizes or controls for plate when storing samples. Therefore, it is common that plate and outcome of interest are at least partially confounded. Therefore, if genotyping algorithms do not appropriately assess these batch effects, it will be difficult if not impossible, to distinguish real from artifactual associations. The new methods presented in this article, successfully detect problematic batches, by simply inspecting some of the estimated model parameters.

To address these deficits, we have developed an enhancement to the model used by CRLMM version 1 that provides much improved posterior probabilities and a powerful probability-based approach to detecting problematic SNPs and batches. We demonstrate that these SNP and batch quality metrics combined with improved confidence scores can effectively identify low-quality elements and significantly improve the accuracy of the genotype calls to be used on downstream analyses.

3.2 The enhanced hierarchical model

We structure our analysis via the hierarchical model,

(1)

Index i=1,…, I represents SNP, j=1,…, J represents the batch, k=1,…, K represents the sample and g=AA, AB or BB is the genotype. The Z's are unobserved, true genotypes, the M's are the observed log-ratios, μ_i=(μ_iAA, μ_iAB, μ_iBB)^′ represents the shifts for SNP i, λ_ij=(λ_ijAA, λ_ijAB, λ_ijBB)^′ denotes batch effects associated to SNP i and batch j, σ_ig² is the SNP-specific variance for genotype g and accounts for the fact that different SNPs have different scales of variation around the predicted cluster centers, the d_g are the degrees of freedom associated to the variance, s²_g, of a typical SNP. Both d_g and s²_g are estimated from the training data using the empirical Bayes approach described in Smyth (2004).

Data exploration demonstrates that, for large and small intensity values, M for the AA and BB genotypes are shrunken toward 0 (Fig. 8 in Carvalho et al., 2007). As done by Carvalho et al. (2007), we account for this intensity-dependent bias with the deterministic function f_jkg, requiring that f_jkAB=0 and f_jkAA=−f_jkBB for all j, k. Differences across genotypes (e.g. M's for AA are on average larger than Ms for AB) are absorbed into f. These functions are estimated in a separate step, as described in detail by Carvalho et al. (2007), and are treated as known.

Fig. 8.

For Dataset A, calls were stratified by their associated posterior. For each strata the observed accuracy was computed by comparing to HapMap gold standard calls. CRLMM version 2 is compared with CRLMM version 1, which is clearly too optimistic. The dashed lines represent homozygotes, dotted lines the heterozygotes and the solid lines the overall accuracies.

The model used in CRLMM version 1 assumes that ϵ_ijkg is normally distributed. The scale factor σ_ig is needed because log-ratios for different SNPs present different levels of variation around the predicted region centers. Because, for some genotypes, some SNPs have very few observations, an empirical Bayes approach is applied to borrow information from other SNPs. The prior used for σ_ig is the inverse-χ² with d_g degrees of freedom. This is a convenient prior that provides closed form solutions. Estimation is performed as described by Smyth (2004).

Recently, we observed that outliers were common and, as a consequence, CRLMM version 1 confidence scores were overoptimistic. To avoid fitting a different error model to each SNP, we adapted the data analytic approach by changing the distribution of ϵ_ijkg from a standard normal to a t with 6 degrees of freedom. The model and fitting procedure for the scaling factor were kept the same as CRLMM version 1. We used the training data to arrive at the choice of six and this worked well in the test sets.

Note that if one has an error term and needs to add a scaling factor, in an empirical Bayes context, one needs to estimate its distribution. Regardless of the model choice, the resulting random variable is the ratio (or product) of two others. The use of the inverse-χ² distribution is both convenient and effective; other choices that provide sufficient flexibility would produce similar results.

3.3 Estimating parameters

Note that model (1) has I × (2+J) × 3 + 12 parameters. With I=906 600 SNPs, these are too many for a global estimation procedure to be practical. In this section, we describe an effective approximate modular procedure. In the first step, we take advantage of the existing training data to estimate the μ's. Then, for each new batch j, we treat the μ's as known and estimate the λ_j. Both steps implement a two-stage approach wherein robust least squares parameter estimates are produced, along with their standard errors, and then these are fed into a second stage that shrinks to improve precision. Our approach permitted us to produce priors without the need of a non-linear algorithm. This was an important feature given the size of the typical datasets: one million SNPs and several hundred samples distributed across dozens of batches. This approach resulted in a powerful software tool that outperforms the default algorithm in computation speed.

3.3.1 Estimating SNP-specific shifts

To estimate V we use an empirical Bayes approach (Louis and Carlin, 2009). We start by obtaining robust versions of the sample means and variances of the training data to estimate the μ's and σ's by and . These robust estimates are used to account for the t-distributed errors. Since the training dataset is considered the reference from which batches deviate, we assume λ=0, and thus and are unbiased estimates. Then, V is estimated by the sample variance–covariance of , producing . Note that some genotypes will have very few points available in the training data to use in estimating the μ's and σ's and the estimate will be imprecise. Now, to borrow strength across SNPs we use to shrink the using the posterior distribution formula for a multivariate Gaussian:

(2)

with W_i a diagonal matrix with entries s²_g/N_ig, g=1,…, 3 and N_ig the number of points available in the training data to estimate μ_ig. Similarly, we shrink the variance estimates (Smyth, 2004), which protects against biases that can be induced by small sample size situations:

When N_ig≤1, we simply use the posteriors s_g². These computations use the training data and most users will not have access to it. Therefore, we save the 's and N_ig's and include them as part of the software that implements CRLMM version 2.

3.3.2 Estimating batch-specific shifts

Here, we describe the two-stage approach used to estimate λ_j for each batch j=1,…, J. The general idea was to use the previously estimated SNP-specific shift parameters, 's and 's, to produce preliminary posteriors for each genotype. These were used to create a pseudo-training dataset. The λ_ij were then estimated following a procedure similar to the one used to estimate μ. Some details follow.

The first step is to obtain starting values for the posteriors by assuming there is no batch-specific shift, λ=0 and that the SNP−specific shifts μ are known:

We then assign a genotype to each SNP for each sample in the batch by simply maximizing these posteriors:

A pseudo-training dataset was created with these calls.

The expected value of M_ijk conditioned on Z_ijk=g is f_jkg(S_ijk)+μ_ig+λ_ijg. We therefore assume that the average (in practice we compute a robust average) deviation

with and N_ijg⁽⁰⁾ is the number of elements in X_ijg, is an unbiased estimate of λ_ijg.

In the second stage, U_j is estimated with the sample variance–covariance of . With Û_j, the estimate of U_j, in place, we shrink the as done in (2):

(3)

with W_i as above.

3.4 Producing posteriors

Using the CRLMM version 1, posterior calls were particularly overconfident. This is consistent with the fact that the estimated are assumed to be known. We developed a procedure that permits us to account for the uncertainty associated with estimating the SNP- and batch-specific shifts. In this section, we illustrate the idea by demonstrating the approach when there are no batch-specific shifts and the ϵ's are normally distributed. In the Supplementary Material, we describe the details needed for the full model, including the batch-specific shifts and the t-distribution assumption.

Consider the simplified model with no batch effect (thus j is omitted):

with ϵ normally distributed with mean 0 and variance σ²_ig. In our approach, we estimate with a shrunken version of the sample average, but for simplicity we will assume we used the sample average. In this case, the estimated SNP-specific shifts, , are normally distributed with mean 0 and variance σ²_ig/N_ig, with N_ig the number of points available in the training data to estimate μ_ig as in (3). We can then show that

(4)

(5)

(6)

The posterior probabilities are produced by normalizing the joint densities of the log-ratios M and genotypes g:

with ϕ_Mik|Zik=g(m) representing a normal density with mean and variance shown in Equations (4) and (6), respectively. A similar calculation, delineated in the Supplementary Material, provides posteriors for the full model.

3.5 Quality scores

Carvalho et al. (2007) present a powerful procedure for detecting problematic arrays based on the estimated f. Here, we present a quality assessment procedure for SNPs and hybridization batches. The quality of batch j can be quantified by the diagonal entries of Û_j. We demonstrate the utility of this approach in Section 4. For SNPs, we can quantify quality by assigning a posterior probability of being an outlier to each shift, i.e. μ_i or λ_ij. Using the fitted prior distributions for μ_i and λ_i, we introduce a density function h₀ for outlying μ and compute the posterior probability:

with ϕ(μ)=(2π)^−3/2|V|^−1/2exp(μ′V⁻¹μ). A practical choice for h is the 3D uniform distribution covering all possible values of μ. We perform a similar computation for λ_ij for each batch j. To illustrate the advantage of the empirical Bayes approach, we plotted the λ_ijAA versus λ_ijAB and λ_ijAA versus λ_ijBB (Fig. 4). The large number of SNPs permitted us to borrow strength across SNPs. The non-zero correlations permitted us to borrow strength across genotypes.

Fig. 4.

Plots of for a given batch. Note that they are correlated. We take advantage of this correlation to predict or improve precision of shifts when not enough training data are available. The ellipses delimit the 95% confidence regions of the estimated distribution. SNPs with points outside these regions are associated with abnormal movements and are flagged as possible outliers. (A) versus . (B) versus . The plot for versus is similar to that shown in (A).

3.6 Software

The methodology described here is available via the crlmm R/BioConductor package. To demonstrate its performance, we compared CRLMM version 2 with Birdseed, the standard genotyping tool for SNP 6.0 arrays, on the 270 HapMap samples. On this set, the maximum amount of memory used by CRLMM version 2, during preprocessing, was 3.2 GB. After preprocessing, the memory usage was reduced to 2 GB. CRLMM version 2 needed 52 min to complete the task. Birdseed used 845 MB for most of the process, increasing slowly to 900 MB and took 150 min. The comparisons were executed on a four-processors system (3 GHz Dual-Core AMD Opteron Processor 2222) with 32 GB RAM.

The implementation of this algorithm follows the standards used by CRLMM version 1: it provides the pair genotype call and confidence score for each sample at every available SNP and does not perform any type of automatic filtering, which is left to the researcher.

4 RESULTS

We assessed the performance of CRLMM version 2 with a comparison to CRLMM version 1 and Birdseed, the default algorithm is provided by the manufacturer. We use three datasets:

1. 143 HapMap samples hybridized by Affymetrix on Affymetrix SNP 6.0 arrays.

2. 55 HapMap samples hybridized at Johns Hopkins on Affymetrix SNP 6.0 arrays.

3. 3050 samples from the GoKinD dataset (Mueller et al., 2006), hybridized on Affymetrix SNP 5.0 arrays, made available through the Genetic Association Information Network (GAIN).

We used HapMap samples because knowing the ‘truth’ permitted us to effectively assess our methodology. Note that, although the same samples, the hybridizations used here were not the same as the set used to train our algorithm. Dataset C provided a large set with 34 different batches defined by the 96-well plate in which the samples were stored. To assess performance with this dataset we computed the concordance between calls obtained by running the algorithm on all samples to calls obtained by running the algorithms by batch. We obtained calls for each dataset with Birdseed, CRLMM version 1 and CRLMM version 2.

The major additions introduced by CRLMM version 2 and described below are (A) the set of metrics for the assessment of SNP (Section 4.1) and batch quality (Section 4.2) and (B) well-calibrated confidence scores. These metrics in conjunction to the Signal-to-Noise Ratio or SNR (Carvalho et al., 2007) offer a powerful set of tools for the quality evaluation of the genotyping procedure. The researcher is then able to flag low-quality SNPs, samples and batches. The appropriate use of these instruments enhances performance and reliability of the genotype calling algorithm, as the aforementioned sections in addition to Sections 4.3 and 4.4 demonstrate.

4.1 SNP quality metrics

For Datasets A and B, we computed SNP Quality Control (QC) Scores as described previously. Namely, for each SNP, we calculated the posterior probability of the estimated λ not being an outlier. This is of great importance for researchers, as it provides means of identifying SNPs whose genotype calls are very accurate. In practical terms, this means that if the investigator uses SNPs with higher scores, it is unlikely that many mistakes will be observed. To demonstrate the utility of this metric, we stratified SNPs by the quality score reported for Datasets A and B, and created Accuracy versus Drop Rate (ADR) plots for each strata, shown by Figure 5. Note, that by restricting attention to SNPs with QC scores above 0.25, we obtained near perfect results. For Datasets A and B, 98.63% and 99.18% of the SNPs surpassed this cutoff, as Table 1 shows.

Fig. 5.

ADR plots for Datasets Aand B. SNPs were stratified by their quality scores and ADR curves were produced for each stratum. The scores are shown to successfully identify SNPs with lower accuracies. The removal of such SNPs significantly increases the method's accuracy.

Table 1.

Distribution of SNPs across strata: roughly 99% of the SNPs exceed the suggested SNP QC threshold (0.25)

SNP QC	Dataset A	Dataset B
0.00–0.01	0.0063	0.0027
0.01–0.05	0.0027	0.0016
0.05–0.25	0.0047	0.0039
0.25–1.00	0.9863	0.9918

4.2 Batch quality metrics

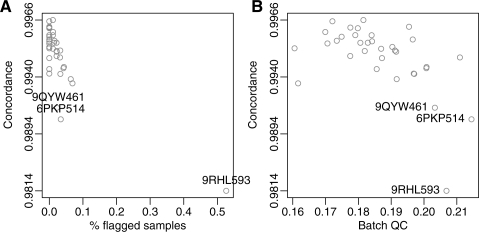
For Dataset C, we do not have reference calls to compare against, like we do for samples that are part of HapMap. Therefore, we generated calls in two ways: (i) by using and (ii) by ignoring batch information. We then computed the concordance between these two sets of calls for each batch after dropping calls whose confidence scores were below the 5th percentile. These concordances are represented on the y-axis of Figure 6A and B. We considered batches with lower concordance to be problematic. The percentage of samples with signal-to-noise ratios, as defined by Carvalho et al. (2007), below five was the best predictor of low-quality batches, as Figure 6A shows. The next significative improvement introduced by CRLMM version 2, the batch quality score predicted low quality as well, as demonstrated by Figure 6B.

Fig. 6.

Batch quality plots. (A) The concordance with a 5% drop rate is plotted against the percentage of sample flagged by the SNR score. (B) The concordance with a 5% drop rate is plotted against our batch quality score.

Our batch quality score also effectively predicted the differences in accuracy observed in Figure 7. Note that Datasets A and B had batch quality scores of 0.0337 and 0.0745, respectively.

Fig. 7.

ADR plots for Datasets A and B. For the first set, CRLMM version 2 outperforms both Birdseed and CRLMM version 1. For the second set, it outperforms the other two methods roughly at a drop rate of 6%. Also note that the accuracy on the second dataset is lower when compared with the first one, indicating significant variation on the quality of the two sets.

For each SNP, we count how many samples were classified into each genotype cluster and denote it by N_ijg. Using and N_ijg, we estimate the shift that can be attributed to each observation in that cluster by

(7)

where the term (N_ijg+1) is used to avoid division by zero. By noting that, for a fixed batch j, the individual shifts in Equation (7) can be denoted by the matrix Δ_j, we create a subset Δ_j^q, which contains only the rows of Δ_j associated to SNPs whose quality score is below q. The batch quality metric is then determined by the average variance of Δ_j^q,

(8)

for which we recommend a threshold q=0.70.

4.3 Overall accuracy

We then compared overall accuracy using Datasets A and B. We calculated accuracy, i.e. proportion of correct calls, for calls with confidence scores above a given cutoff. Various cutoffs were considered. We then plotted accuracy against the proportion of calls below the confidence cutoffs. The ADR plots, Figure 7, demonstrated that, overall, CRLMM version 2 outperformed the other two algorithms.

4.4 Posteriors

To assess the validity of the posteriors, we compared observed accuracy with reported posteriors. Specifically, we stratified calls by their associated posterior and, for each strata, we computed the proportion of correct calls. We then plotted these against each other with the expectation that they fall on the identity line. Although CRLMM version 1 does not use posteriors as a confidence measure, we obtained the posteriors by modifying its code. CRLMM version 2 improved the posteriors provided by CRLMM version 1, which clearly were optimistic (Fig. 8).

5 DISCUSSION

We have presented a multi-level enhancement to the CRLMM model described by Carvalho et al. (2007). Our sole objective is to provide accurate genotype calls, calibrated confidence scores and quality metrics based on observed intensities of SNP probes and a set of parameter estimates (location and scale) obtained from a training dataset. This strategy does not make use of any other information, like known copy number regions. Our model accounts for three levels of variability in SNP array data: (i) SNP-specific shifts, (ii) hybridization batch shifts to each SNP and (iii) heavy tailed measurement error. By explicitly modeling these sources of uncertainty, the estimated posterior probabilities are much improved as compared with those offered by CRLMM version 1. We also incorporate the variability associated with estimating model parameters with training data. Our approach produced priors with superior properties to those produced by CRLMM version 1. The refinements will improve the accuracy of downstream results obtained from probability-based association tests such as the one described by Ruczinki et al. (http://www.bepress.com/jhubiostat/paper181).

We have also described methodology useful for detecting problematic SNPs and hybridization batches. We find the latter contribution particularly important. Adapting analysis tools to deal with hybridization batch effects should be a priority of analysis groups working with GWAS data. Due to experimental logistics, GWAS rarely control or randomize for well-plate, for example, when using external controls. Therefore, an undetected problematic batch could make it difficult, if not impossible, to distinguish reported associations from artifactual ones such driven by hybridization batches. We have presented a powerful solution that predicts problematic batches and can be easily incorporated into any analysis pipeline.