Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2010 Jan;184(1):213–219. doi: 10.1534/genetics.109.110536

Estimating Breeding Values With Molecular Relatedness and Reconstructed Pedigrees in Natural Mating Populations of Common Sole, Solea Solea

Robbert J W Blonk *, Hans Komen *,1, Andries Kamstra †, Johan A M van Arendonk *
PMCID: PMC2804404  PMID: 19858283

Abstract

Captive populations where natural mating in groups is used to obtain offspring typically yield unbalanced population structures with highly skewed parental contributions and unknown pedigrees. Consequently, for genetic parameter estimation, relationships need to be reconstructed or estimated using DNA marker data. With missing parents and natural mating groups, commonly used pedigree reconstruction methods are not accurate and lead to loss of data. Relatedness estimators, however, infer relationships between all animals sampled. In this study, we compared a pedigree relatedness method and a relatedness estimator (“molecular relatedness”) method using accuracy of estimated breeding values. A commercial data set of common sole, Solea solea, with 51 parents and 1953 offspring (“full data set”) was used. Due to missing parents, for 1338 offspring, a pedigree could be reconstructed with 10 microsatellite markers (“reduced data set”). Cross-validation of both methods using the reduced data set showed an accuracy of estimated breeding values of 0.54 with pedigree reconstruction and 0.55 with molecular relatedness. Accuracy of estimated breeding values increased to 0.60 when applying molecular relatedness to the full data set. Our results indicate that pedigree reconstruction and molecular relatedness predict breeding values equally well in a population with skewed contributions to families. This is probably due to the presence of few large full-sib families. However, unlike methods with pedigree reconstruction, molecular relatedness methods ensure availability of all genotyped selection candidates, which results in higher accuracy of breeding value estimation.

To estimate genetic parameters, additive genetic relationships between individuals are inferred from known pedigrees (Falconer and Mackay 1996; Lynch and Walsh 1997). However, in natural populations (Ritland 2000; Thomas et al. 2002) and in captive species where natural mating in groups is used to obtain offspring (Brown et al. 2005; Fessehaye et al. 2006; Blonk et al. 2009) pedigrees are reconstructed. In these populations there is no control on mating structure, and typically unbalanced population structures with highly skewed parental contributions are obtained (Bekkevold et al. 2002; Brown et al. 2005; Fessehaye et al. 2006; Blonk et al. 2009). To reconstruct pedigrees, parental allocation methods are often used (Marshall et al. 1998; Avise et al. 2002; Duchesne et al. 2002). These methods require that all parents be known. For situations where parental information is not available, numerous DNA-marker-based methods for estimating molecular relatedness have been developed (Lynch 1988; Queller and Goodnight 1989; Ritland 2000; Toro et al. 2002). These relatedness estimators determine relationship values between individuals on a continuous scale. Evaluation of relatedness estimators within real and simulated data in both plants and animals (e.g., see Van de Casteele et al. 2001 ; Milligan 2003; Oliehoek et al. 2006; Rodríguez-Ramilo et al. 2007; Bink et al. 2008) has generally focused on bias and sampling error of estimated genetic variances or relatedness values. Relatively little attention has been paid to their efficiency for estimation of breeding values.

Two types of relatedness estimators are currently available: method-of-moments estimators and maximum-likelihood estimators. Method-of-moments estimators (e.g., Queller and Goodnight 1989; Li et al. 1993; Ritland 1996; Lynch and Ritland 1999; Toro et al. 2002) determine relationships while calculating sharing of alleles between pairs in different ways. A variant of method-of-moments estimators is the transformation of continuous relatedness values to categorical genealogical relationships using “explicit pedigree reconstruction” (Fernández and Toro 2006) or thresholds (Rodríguez-Ramilo et al. 2007). However, correlations of transformed coancestries with known genealogical coancestries are low (Rodríguez-Ramilo et al. 2007). Several studies have compared different method-of-moments estimators but none revealed one single best estimator (Van de Casteele et al. 2001; Oliehoek et al. 2006; Rodríguez-Ramilo et al. 2007; Bink et al. 2008).

Maximum-likelihood (ML) approaches classify animals into a limited number of relationship classes (Mousseau et al. 1998; Thomas et al. 2002; Wang 2004; Herbinger et al. 2006; Anderson and Weir 2007). For each pair a likelihood to fall into a possible relatedness class (e.g., full sib vs. unrelated) is calculated given its genotype and phenotype. ML techniques combined with a Markov chain Monte Carlo approach reconstruct groups with specific relationships jointly and are therefore more efficient than other ML approaches. To minimize standard errors, all discussed ML methods require balanced population structures, large sibling groups, and a large variance of relatedness (Thomas et al. 2002; Wang 2004; Anderson and Weir 2007). Therefore, these methods may not be suitable for natural mating systems.

Unlike parental allocation methods, a benefit from relatedness estimators is that essentially all selection candidates are maintained for breeding value estimation, even with missing parents. The question is, however, whether such relatedness estimators also give accurate breeding values to perform selection.

In this study, we test suitability of a relatedness estimator to obtain breeding values in a population of common sole, Solea solea (n = 1953) obtained by natural mating. First, we estimate breeding values using pedigree relatedness of animals for which a pedigree could be reconstructed (using parental allocation). This data set (n = 1338) is further referred to as “reduced data set.” We compare results with estimated breeding values using a simple but robust method-of-moments relatedness estimator: “molecular relatedness” (Toro et al. 2002, 2003). Next, we estimate breeding values using molecular relatedness in the full data set (n = 1953). Results show that accuracies of estimated breeding values obtained with molecular relatedness and pedigree relatedness are comparable. Accuracy increases when breeding values are estimated with molecular relatedness in the full data set. This implies that a molecular relatedness estimator can be used to estimate breeding values in captive natural mating populations.

MATERIALS AND METHODS

Data set:

Two thousand animals (age 3 years old) from a commercial production population were sampled randomly from eight tanks. All animals have been produced by natural spawning and families were mixed over tanks. The parents (n = 51) had been collected from the Dutch North-Western coastal area and were sampled at the same time as the offspring. A blood sample for genotypic analysis was taken from all offspring and available parents. However, no samples were available from six potential parents due to mortality before sampling. On all offspring, body weight, gender, tank location, and measuring team were recorded. All animals were genotyped with 10 microsatellite markers: AF173855, AF173854, AF173852, AF173849, AY950593, AY950592 (Iyengar et al. 2000), AY950591, AY950589, AY950588, AY950587 (Garoia et al. 2006). See Blonk et al. (2009) for details on DNA isolation and PCR amplification protocols.

Reconstructed pedigree relatedness:

From the offspring data set, only individuals with more than five successfully amplified markers were used for analysis. Pedigree reconstruction was performed with PAPA 2.0 software (Duchesne et al. 2002). A uniform error of 0.02 on all markers was used. To set up a reliable pedigree, allocation results were checked as follows.

Offspring that were not allocated to any parent were removed from the data set. Also, animals that were allocated to more than two parents due to equal likelihood of breeding of these parents (termed as “ambiguous” in PAPA) were removed from the data set. Further, allocated parent–offspring pairs having the single highest likelihood of breeding among all other possible pairs were checked for consistency of Mendelian allele inheritance. Allocations were considered correct only when more than five markers were allocated consistently with Mendelian inheritance. Checking of allocation results was performed using R software (R Development Core Team 2008). The remaining data set was further referred to as a “reduced data set.”

Molecular relatedness:

Genetic relationships between animals were also estimated using a relatedness estimator. To estimate molecular relatedness, we used the method described by Toro et al. (2002, 2003). Here, coancestry (f) is calculated from similarity (S) of alleles between two individuals x and y. Here 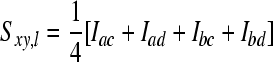Inline graphic, where at locus l, a and b are alleles of individual x and c and d are alleles of individual y (Li et al. 1993). When at Iac allele a is identical to allele c, Iac equals one, and zero otherwise, etc. According to Lynch (1988) molecular coancestry is then calculated as

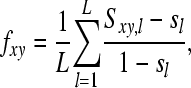graphic file with name M2.gif (1)

where L is the number of markers (markers) and sl is mean similarity (sum of squared allele frequencies, 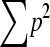Inline graphic) at locus l in the base population. Estimated relatedness r between two animals is calculated as r = 2f. When ignoring alleles that are alike in state (AIS), molecular relatedness between two individuals is calculated from coancestry as follows:

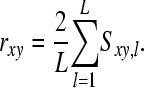graphic file with name M4.gif (2)

Consequently, values of molecular relatedness are continuous and may range between 0 (no alleles are similar) and 2 (all alleles are similar).

Genetic analysis:

To estimate heritabilities and breeding values, genetic analysis was performed with relatedness inferred from either pedigree reconstruction or molecular relatedness. The restricted maximum-likelihood method was used with ASReml software (Gilmour et al. 2006) for analysis of the following genetic univariate linear model,

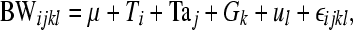graphic file with name M5.gif (3)

where BW is the response variable for body weight, μ is the mean, Ti, is the fixed effect of team i, Taj is the fixed effect of tank j, Gk is the fixed effect of gender k, ul is the random animal effect of animal l, and ɛ is the random error term.

For estimation of breeding values from the pedigree reconstruction method, the relationship matrix was calculated within ASReml software using the reconstructed pedigree. The relationship matrix from the molecular relatedness method, however, was prepared separately and offered to ASReml as a generalized inversed matrix (“GIV-file”). To obtain convergence in ASReml, before inverting, the relationship matrix was made positive definite using the bending method. Bending and inverting was done using R software (R Development Core Team 2008). Heritabilities where then calculated using the estimated additive genetic variance and the residual variance as 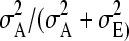Inline graphic.

Comparison of molecular relatedness and reconstructed pedigree relatedness:

Pearson correlations were calculated between relatedness values as well as between breeding values obtained from molecular relatedness and reconstructed pedigree. To evaluate how well both methods fitted the model to the data, the accuracy in predicting the phenotype was calculated using cross-validation of each method. For cross-validation, the data set was randomly divided into 100 equal sized subsets. Genetic analysis with the genetic model was then performed 100 times on all subsets jointly while successively omitting phenotype records for 1 subset at a time. In each analysis, for the subsets where observed phenotypes were omitted, phenotypes were predicted on the basis of available observed phenotypes in the other subsets.

Observed and predicted phenotypes from genetic analysis were corrected for fixed effects (referred to as “corrected phenotypes”). Accuracy of estimated breeding values (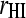Inline graphic) was calculated as

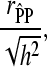graphic file with name M8.gif (4)

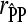where Inline graphic is the Pearson correlation coefficient between predicted corrected phenotypes and observed corrected phenotypes observed from cross-validation and h2 the heritability estimated using pedigree reconstruction. All calculations were performed using R (R Development Core Team 2008).

RESULTS

Data sets and relatedness:

DNA isolation and marker analysis was successful, with only 30 samples giving no signal. Out of 2000 samples, finally 1953 animals could be genotyped with more than five markers. This is further referred to as the “full data set.” In the full data set, on average 14.3 alleles per marker were found in the offspring. The parental data set, 13.4 alleles per marker were found.

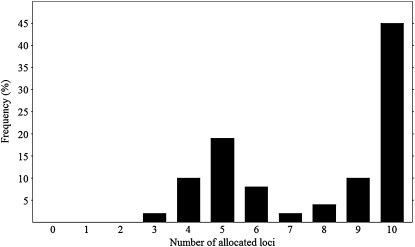
After parental allocation, all allocated parent–offspring pairs were tested for consistency of Mendelian inheritance on each marker. The number of markers following correct Mendelian inheritance patterns was counted for each pair. The frequency distribution of allocated parent–offspring pairs over the number of consistent markers is shown in Figure 1. Forty-five percent of the pairs were allocated with all 10 markers. To construct the final pedigree, only parent–offspring pairs with more than 5 markers consistent with Mendelian inheritance patterns (66%) were taken into account. This resulted in a reconstructed pedigree for 1338 offspring, referred to as a reduced data set. In the reduced data set, 21 males and 17 females contributed to the offspring producing 59 full-sib families. Parental contribution was highly skewed with six parental pairs producing 70% of the offspring. In the reduced data set, on average 13.7 alleles per marker were found in the offspring.

Figure 1.—

Figure 1.—

Open in a new tab

Frequency distribution of offspring allocated to two parents vs. number of markers that were allocated following Mendelian inheritance after pedigree reconstruction in cultured common sole (full data set, n = 1953).

Parents were assumed to be unrelated. Consequently, relatedness values between offspring pairs after pedigree reconstruction were 0, 0.25, and 0.5. This corresponds to unrelated, half-, and full-sib pairs, respectively. The average relatedness in the reconstructed pedigree was 0.1483 (σPR = 0.1865). As expected, molecular relatedness values in the reduced data set were continuous and ranged between 0 and approximately 1.5. Average relatedness was 0.5588 (σMR = 0.2100). The continuous molecular relatedness values in the full data set ranged between 0 and 1.6. Average relatedness was 0.50 (σMR = 0.2000).

Genetic analysis:

To obtain normally distributed residuals, the trait body weight was log-transformed. In the reduced data set, heritability for body weight was estimated at 0.23 (± 0.09) in a linear univariate model using relatedness inferred from pedigree reconstruction. The genetic variance was 0.56 × 10−2 g2. With molecular relatedness in the reduced data set a heritability of 0.13 (± 0.04) was observed with a genetic variance of 0.31 × 10−2 g2. In the full data set using molecular relatedness, heritability was estimated at 0.11 (± 0.03). Here, the observed genetic variance was 0.27 × 10−2 g2.

Comparison of molecular relatedness and reconstructed pedigree relatedness:

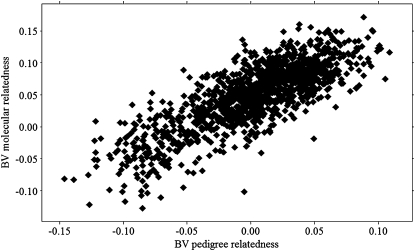
Per pedigree relationship class, the mean, standard deviation, and minimum and maximum values of molecular relatedness were calculated. Results are shown in Table 1. A large overlap of values obtained from molecular relatedness can be seen between relatedness classes of pedigree reconstruction. The Pearson correlation coefficient between molecular and reconstructed pedigree relatedness was 0.8 (P ≪ 0.000). Estimated breeding values from pedigree reconstruction were positively correlated with breeding values obtained from molecular relatedness (Figure 2). The estimated Pearson correlation coefficient was 0.77 (P ≪ 0.000).

TABLE 1.

Mean, standard deviation (SD), minimum (Min), and maximum (Max) of molecular relatedness (MR) between pairs of offspring per class of reconstructed pedigree relatedness (PR) in one generation of cultured common sole (reduced data set, n = 1338)

PR class MR mean SD Min Max
Unrelated 0 0.4337 0.1254 0.0000 1.2500
Half sib 0.25 0.6354 0.1410 0.1000 1.4286
Full sib 0.5 0.8737 1.548 0.1875 1.5000
Self 1
 1.2385
 0.1216
 1.0000
 1.6000
Open in a new tab

Figure 2.—

Figure 2.—

Open in a new tab

Relationship between breeding values estimated from molecular relatedness and reconstructed pedigree relatedness of offspring in cultured common sole (reduced data set, n = 1338).

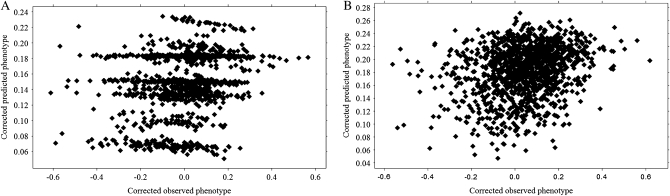
Cross-validation with 100 equal sized randomly chosen subsets resulted in similar correlations between predicted and observed corrected phenotypes in both methods. In Figure 3 relationships between predicted and observed phenotypes in both methods are shown for the reduced data set. Note that the stratified shapes of Figure 3 can be explained by presence of large sib groups in the inferred pedigree. With pedigree reconstruction, predicted and observed phenotypes correlated with 0.2577 after correction for fixed effects. Accuracy of estimated breeding values with pedigree reconstruction was 0.54. Molecular relatedness resulted in a correlation of 0.2619 (P ≪ 0.000) and an accuracy of 0.55. In the full data set, the correlation between predicted and observed phenotypes was 0.2936 (P ≪ 0.000) after correction for fixed effects. Consequently, the accuracy in the full data set was 0.60.

Figure 3.—

Figure 3.—

Open in a new tab

Relationship between predicted and observed corrected phenotypes in a linear model with reconstructed pedigree relatedness (A) and molecular relatedness (B) in one generation of cultured common sole (reduced data set, n = 1338).

DISCUSSION

In this study we tested the suitability of molecular relatedness to estimate breeding values in a commercial population of common sole, Solea solea, obtained by natural spawning of parents. Progeny and parents were genotyped with 10 microsatellite markers. Correlations of estimated relatedness and of breeding values between both methods were high. However, although relations were positive and significant, estimated heritabilities were different between methods.

In the reduced data set, accuracy of the univariate linear model was 0.54 with pedigree reconstruction and 0.55 with molecular relatedness (Figure 3). This result implies that both methods fitted the model to the data with nearly equal precision. In the full data set, accuracy with molecular relatedness increased to 0.60. These results show that in cases with missing pedigree data, molecular relatedness can be used to obtain breeding values. There was a highly skewed contribution of full-sib families to the offspring population. Therefore, the observed accuracies should be put in perspective of the maximum accuracy attainable with full-sib information (0.71). This implies that the observed levels of accuracy are high.

Prior to drawing conclusions on the optimal indicator of relationships between animals, it is useful to determine if the used forms of relationships add information to breeding value estimation at all. To this purpose, we calculated breeding values using the model (Equation 3) without any relatedness information. Estimated breeding values from this model and from the model with relationships inferred from reconstructed pedigree correlated with 0.66 (P ≪ 0.000, results not shown). This suggests that inclusion of relationships between animals alters estimation of breeding values.

Relatedness estimator:

Many authors compared relatedness estimators under different population structures, numbers of markers, and alleles (e.g., Van de Casteele et al. 2001; Oliehoek et al. 2006; Bink et al. 2008). ML estimators (Mousseau et al. 1998; Thomas et al. 2002; Wang 2004; Herbinger et al. 2006) or pedigree reconstruction methods that do not need parental information (Berger-Wolf et al. 2007; Ashley et al. 2009) were less suitable for our situation. Assumptions made by these methods, as balanced mating structures and large sibling groups, would be violated in our data set. In the data set used, skewed parental contributions were observed (data not shown). This is typical for natural spawning species in, e.g., aquaculture (Brown et al. 2005; Blonk et al. 2009).

From the literature it remains unclear which method-of-moments relatedness estimator performs best; differences are small. In this study we used molecular coancestry (Toro et al. 2002; Toro et al. 2003): among all estimators compared, molecular coancestry turned out to be relatively simple but robust.

The importance of the number of markers for the power of a relatedness estimator has been emphasized by several authors. Oliehoek et al. (2006) and Bink et al. (2008) showed that reasonable correlations (>0.7) between estimated and pedigree relatedness were found only in simulated data when using at least 50 markers and four to five alleles per marker. In contrast, in this study a correlation of 0.8 was found between estimated and pedigree relatedness using 10 markers with 13.7 alleles per marker on average. The difference in results might also be caused by the characteristics of the population under study. Relatedness estimators generally are used for natural populations in which variation of relationship structures is low. In these cases discriminative power of relatedness estimators is low with few markers. For example, Thomas et al. (2000) and Wilson and McDonald (2003) showed that 12 to 15 markers were not enough to produce reliable heritability estimates with a relatedness estimator. The tested populations (Soay sheep, Ovis aries, and rainbow trout, Oncorhynchus mykiss) showed low variation of relationship structures. Larger variation of relationship structures, i.e., larger families but also larger sample sizes, decreases bias and sampling errors of estimated relatedness (Thomas et al. 2000; Thomas et al. 2002; Rodriguez-Ramilo et al. 2007). In aquaculture populations with natural spawning in groups, generally large variation of relationship structures is found (Gjedrem 2000; Vandeputte 2005; Saillant et al. 2006). As contribution of families to the offspring population in this study was highly skewed, this may explain the success with relatively few markers.

Heritability:

In this study heritability for body weight in common sole was estimated at 0.23 (±0.09) when using pedigree relatedness. The estimated heritability is in line with values found for bodyweight in other aquatic species (Gjedrem 2000). Heritability estimated from molecular relatedness, however, was much lower: 0.11 (±0.02)–0.13 (±0.04). This suggests underestimation of genetic variance, which is likely to be caused by erroneous ascribing of relationships between offspring due to too few markers. Thomas et al. (2002) showed that, among other factors, use of fewer markers increases variance and bias of sampling error variance of estimated relatedness. With higher variance of relatedness, genetic variance and heritability decrease as 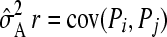Inline graphic (Falconer and Mackay 1996). This is supported by a study on genomic selection in which fewer markers led to underestimation of heritability estimates in an Angus cattle population (Hayes and Goddard 2008). A similar effect was demonstrated by Shikano (2008) in Japanese flounder, Paralichthys olivaceus. It is expected that heritability will be estimated more accurately with a higher number of markers and consequently will approach the value from pedigree reconstruction.

In our particular case of skewed contribution of parents, the observed heritabilities from molecular relatedness will have little effect on estimated breeding values and accuracies. This is because breeding values were based on family information (i.e., family means) rather than on heritabilities.

Applications for breeding programs:

Our study illustrates that pedigree reconstruction using genotyping data is an inefficient method when parental genotypes are missing. Difficulty with allocation is reflected in Figure 1. Loss of selection candidates due to ambiguous parental allocation was 33%. Comparable results (10–30%) were found by several authors in other species (Herlin et al. 2007, 2008; Pierce et al. 2008). Loss of selection candidates has major effects on costs of selection procedures in breeding programs and may lead to lower realized selection responses and increased rates of inbreeding.

As parental allocation programs often allow uncertainties to the performed allocations (Duchesne et al. 2002), mistakes in reconstructed pedigrees may occur. This increases the risk that related animals are considered as unrelated. Selection of animals using optimal contribution theory (Meuwissen 1997) may therefore unintentionally increase rates of inbreeding.

This study shows that the molecular relatedness estimator circumvents problems with pedigree reconstruction in an aquaculture population with natural spawning of groups of parents. Moreover, due to preservation of all selection candidates, a higher accuracy of breeding value estimation is achieved. The increasing amount of genetic information (e.g., number of SNPs and microsatellites) made available due to current developments in genomics (Hayes et al. 2009) will further enhance accurate estimation of genetic parameters.

Acknowledgments

The authors thank team Solea for their help in collecting the data and Piter Bijma for his helpful suggestions and advice on the genetic analysis with relatedness estimators. We thank the reviewers of Genetics for their useful comments. This study was funded by Casimir NWO, the Netherlands Organization for Scientific research), Solea bv, and Wageningen University.

References

  1. Anderson, A. D., and B. S. Weir, 2007. A maximum-likelihood method for the estimation of pairwise relatedness in structured populations. Genetics 176 421–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ashley, M. V., I. C. Caballero, W. Chaovalitwongse, B. Dasgupta, P. Govindan et al., 2009. KINALYZER, a computer program for reconstructing sibling groups. Mol. Ecology Res. 9 1127–1131. [DOI] [PubMed] [Google Scholar]
  3. Avise, J. C., A. G. Jones, D. Walker and J. A. DeWoody, 2002. Genetic mating systems and reproductive natural histories of fishes: lessons for ecology and evolution. Annu. Rev. Genet. 36 19–45. [DOI] [PubMed] [Google Scholar]
  4. Bekkevold, D. X., M. M. Hansen and V. Loeschcke, 2002. Male reproductive competition in spawning aggregations of cod (Gadus morhua, L.). Mol. Ecol. 11 91–102. [DOI] [PubMed] [Google Scholar]
  5. Berger-Wolf, T. Y., S. I. Sheikh, B. DasGupta, M. V. Ashley, I. C. Caballero et al., 2007. Reconstructing sibling relationships in wild populations. Bioinformatics 23 i49–i56. [DOI] [PubMed] [Google Scholar]
  6. Bink, M., A. Anderson, W. van de Weg and E. Thompson, 2008. Comparison of marker-based pairwise relatedness estimators on a pedigreed plant population. Theor. Appl. Genet. 117 843–855. [DOI] [PubMed] [Google Scholar]
  7. Blonk, R. J. W., J. Komen, A. Kamstra, R. P. M. A. Crooijmans and J. A. M. van Arendonk, 2009. Levels of inbreeding in group mating captive broodstock populations of common sole, (Solea solea), inferred from parental relatedness and contribution. Aquaculture 289 26–31. [Google Scholar]
  8. Brown, C. R., J. A. Woolliams and B. J. McAndrew, 2005. Factors influencing effective population size in commercial populations of gilthead seabream, Sparus aurata. Aquaculture 247 219–225. [Google Scholar]
  9. Duchesne, P., M. H. Godbout and L. Bernatchez, 2002. PAPA (Package for the Analysis of Parental Allocation): a computer program for simulated and real parental allocation. Mol. Ecol. Notes 2 191–194. [Google Scholar]
  10. Falconer, D. S., and T. F. C. Mackay, 1996. Introduction to Quantitative Genetics. Pearson/Prentice-Hall/Harlow, Essex, UK.
  11. Fernández, J., and M. A. Toro, 2006. A new method to estimate relatedness from molecular markers. Mol. Ecol. 15 1657–1667. [DOI] [PubMed] [Google Scholar]
  12. Fessehaye, Y., Z. El-Bialy, M. A. Rezk, R. Crooijmans, H. Bovenhuis et al., 2006. Mating systems and male reproductive success in Nile tilapia (Oreochromis niloticus) in breeding hapas: a microsatellite analysis. Aquaculture 256 148–158. [Google Scholar]
  13. Garoia, F., S. Marzola, I. Guarniero, M. Trentini and F. Tinti, 2006. Isolation of polymorphic DNA microsatellites in the common sole Solea vulgaris. Mol. Ecol. Notes 6 144–146. [Google Scholar]
  14. Gilmour, A. R., B. J. Gogel, B. R. Cullis and R. Thompson (Editors), 2006. ASReml User Guide Release 2.0. VSN International Ltd, Hemel Hempstead, UK.
  15. Gjedrem, T., 2000. Genetic improvement of cold-water fish species. Aquaculture Res. 31 25–33. [Google Scholar]
  16. Hayes, B. J., and M. E. Goddard, 2008. Technical note: prediction of breeding values using marker-derived relationship matrices. J. Anim. Sci. 86 2089–2092. [DOI] [PubMed] [Google Scholar]
  17. Hayes, B. J., P. M. Visscher and M. E. Goddard, 2009. Increased accuracy of artificial selection by using the realized relationship matrix. Genet. Res. 91 47–60. [DOI] [PubMed] [Google Scholar]
  18. Herbinger, C. M., P. T. O'Reilly and E. Verspoor, 2006. Unravelling first-generation pedigrees in wild endangered salmon populations using molecular genetic markers. Mol. Ecol. 15 2261–2275. [DOI] [PubMed] [Google Scholar]
  19. Herlin, M., M. Delghandi, M. Wesmajervi, J. B. Taggart, B. J. McAndrew et al., 2008. Analysis of the parental contribution to a group of fry from a single day of spawning from a commercial Atlantic cod (Gadus morhua) breeding tank. Aquaculture 274 218–224. [Google Scholar]
  20. Herlin, M., J. B. Taggart, B. J. McAndrew and D. J. Penman, 2007. Parentage allocation in a complex situation: a large commercial Atlantic cod (Gadus morhua) mass spawning tank. Aquaculture 272 S195–S203. [Google Scholar]
  21. Iyengar, A., S. Piyapattanakorn, D. M. Stone, D. A. Heipel, B. R. Howell et al., 2000. Identification of microsatellite repeats in turbot (Scophthalmus maximus) and Dover sole (Solea solea) using a RAPD-based technique: characterization of microsatellite markers in Dover sole. Marine Biotechnol. 2 49–56. [DOI] [PubMed] [Google Scholar]
  22. Li, C. C., D. E. Weeks and A. Chakravarti, 1993. Similarity of DNA fingerprints due to chance and relatedness. Hum. Hered. 43 45–52. [DOI] [PubMed] [Google Scholar]
  23. Lynch, M., 1988. Estimation of relatedness by DNA fingerprinting. Mol. Biol. Evol. 5 584–599. [DOI] [PubMed] [Google Scholar]
  24. Lynch, M., and K. Ritland, 1999. Estimation of pairwise relatedness with molecular markers. Genetics 152 1753–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lynch, M., and B. Walsh (Editors), 1997. Genetics and Analysis of Quantitative traits. Sinauer Associates, Sunderland, MA.
  26. Marshall, T. C., J. Slate, L. E. B. Kruuk and J. M. Pemberton, 1998. Statistical confidence for likelihood-based paternity inference in natural populations. Mol. Ecol. 7 639–655. [DOI] [PubMed] [Google Scholar]
  27. Meuwissen, T. H. E., 1997. Maximizing the response of selection with a predefined rate of inbreeding. J. Anim. Sci. 75 934–940. [DOI] [PubMed] [Google Scholar]
  28. Milligan, B. G., 2003. Maximum-likelihood estimation of relatedness. Genetics 163 1153–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mousseau, T. A., K. Ritland and D. D. Heath, 1998. A novel method for estimating heritability using molecular markers. Heredity 80 218–224. [Google Scholar]
  30. Oliehoek, P. A., J. J. Windig, J. A. M. van Arendonk and P. Bijma, 2006. Estimating relatedness between individuals in general populations with a focus on their use in conservation programs. Genetics 173 483–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Pierce, L. R., Y. Palti, J. T. Silverstein, F. T. Barrows, E. M. Hallerman et al., 2008. Family growth response to fishmeal and plant-based diets shows genotype × diet interaction in rainbow trout (Oncorhynchus mykiss). Aquaculture 278 37–42. [Google Scholar]
  32. Queller, D. C., and K. F. Goodnight, 1989. Estimating relatedness using genetic markers. Evolution 43 258–275. [DOI] [PubMed] [Google Scholar]
  33. R Development Core Team, 2008. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria (http://www.R-project.org).
  34. Ritland, K., 1996. A marker-based method for inferences about quantitative inheritance in natural populations. Evolution 50 1062–1073. [DOI] [PubMed] [Google Scholar]
  35. Ritland, K., 2000. Marker-inferred relatedness as a tool for detecting heritability in nature. Mol. Ecol. 9 1195–1204. [DOI] [PubMed] [Google Scholar]
  36. Rodriguez-Ramilo, S. T., M. A. Toro, A. Caballero and J. Fernandez, 2007. The accuracy of a heritability estimator using molecular information. Conserv. Genet. 8 1189–1198. [Google Scholar]
  37. Rodríguez-Ramilo, S. T., M. A. Toro, P. Martínez, J. Castro, C. Bouza et al., 2007. Accuracy of pairwise methods in the reconstruction of family relationships, using molecular information from turbot (Scophthalmus maximus). Aquaculture 273 434–442. [Google Scholar]
  38. Saillant, E., M. Dupont-Nivet, P. Haffrey and B. Chatain, 2006. Estimates of heritability and genotype-environment interactions for body weight in sea bass (Dicentrarchus labrax L.) raised under communal rearing conditions. Aquaculture 254 139–147. [Google Scholar]
  39. Shikano, T., 2008. Estimation of quantitative genetic parameters using marker-inferred relatedness in Japanese flounder: a case study of upward bias. J. Hered. 99 94–104. [DOI] [PubMed] [Google Scholar]
  40. Thomas, S. C., D. W. Coltman and J. M. Pemberton, 2002. The use of marker-based relationship information to estimate the heritability of body weight in a natural population: a cautionary tale. J. Evol. Biol. 15 92–99. [Google Scholar]
  41. Thomas, S. C., J. M. Pemberton and W. G. Hill, 2000. Estimating variance components in natural populations using inferred relationships. Heredity 84 427–436. [DOI] [PubMed] [Google Scholar]
  42. Toro, M., C. Barragán, C. Óvilo, J. Rodrigañez, C. Rodriguez et al., 2002. Estimation of coancestry in Iberian pigs using molecular markers. Conserv. Genet. 3 309–320. [Google Scholar]
  43. Toro, M. A., C. Barragan and C. Ovilo, 2003. Estimation of genetic variability of the founder population in a conservation scheme using microsatellites. Anim. Genet. 34 226–228. [DOI] [PubMed] [Google Scholar]
  44. Van de Casteele, T., P. Galbusera and E. Matthysen, 2001. A comparison of microsatellite-based pairwise relatedness estimators. Mol. Ecol. 10 1539–1549. [DOI] [PubMed] [Google Scholar]
  45. Vandeputte, M., 2005. Heritability estimates for growth-related traits using microsatellite parentage assignment in juvenile common carp (Cyprinus carpio L.). Aquaculture 247 31–32. [Google Scholar]
  46. Wang, J., 2004. Sibship reconstruction from genetic data with typing errors. Genetics 166 1963–1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wilson, A. J., G. McDonald, H. K. Moghadam, C. M. Herbinger and M. M. Ferguson, 2003. Marker-assisted estimation of quantitative genetic parameters in rainbow trout, Oncorhynchus mykiss. Genet. Res. 81 145–156. [DOI] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES