Noise-Gated Encoding of Slow Inputs by Auditory Brain Stem Neurons With a Low-Threshold K⁺ Current

Abstract

Phasic neurons, which do not fire repetitively to steady depolarization, are found at various stages of the auditory system. Phasic neurons are commonly described as band-pass filters because they do not respond to low-frequency inputs even when the amplitude is large. However, we show that phasic neurons can encode low-frequency inputs when noise is present. With a low-threshold potassium current (I_KLT), a phasic neuron model responds to rising and falling phases of a subthreshold low-frequency signal with white noise. When the white noise was low-pass filtered, the phasic model also responded to the signal's trough but still not to the peak. In contrast, a tonic neuron model fired mostly to the signal's peak. To test the model predictions, whole cell slice recordings were obtained in the medial (MSO) and lateral (LSO) superior olivary neurons in gerbil from postnatal day 10 (P10) to 22. The phasic MSO neurons with strong I_KLT, mostly from gerbils aged P17 or older, showed firing patterns consistent with the preceding predictions. Moreover, injecting a virtual I_KLT into weak-phasic MSO and tonic LSO neurons with putative weak or no I_KLT (from gerbils younger than P17) shifted the neural response from the signal's peak to the rising phase. These findings advance our knowledge about how noise gates the signal pathway and how phasic neurons encode slow envelopes of sounds with high-frequency carriers.

INTRODUCTION

Auditory brain stem neurons are endowed with distinct biophysical characteristics that impart a range of firing patterns. Neurons that show typical phasic responses have some common properties, such as short membrane time constants, precise spike timing, and small coincidence windows (Oertel 1983; Rothman et al. 1993; Svirskis et al. 2004). Phasic neurons are characterized by the absence of repetitive firing to steady current injection of high intensity (Hodgkin 1948; for review, see Izhikevich 2007 and Prescott et al. 2008). These neurons do not respond to slowly varying input, such as slow-rising ramp current (McGinley and Oertel 2006; for review, see Izhikevich 2007) or low-frequency sinusoidal current (Beraneck et al. 2007). Motivated by these studies, it is tempting to conclude that stimulus information carried by fast-changing input is important for phasic neurons while any information carried by slow-changing input is lost.

Previous studies have shown that many neuron types can encode subthreshold signals when noise of certain amplitude is added to the signal, a phenomenon commonly known as stochastic resonance (Bulsara and Gammaitoni 1996; for a neuroscience specific review, see Longtin 1993; Wiesenfeld and Moss 1995). Briefly, the addition of noise to the subthreshold signal brings the system across the firing threshold, grouping spike responses mostly around the signal's peak. It is not clear whether an analogy of a stochastic-resonance-like phenomenon exists for the phasic case. Although previous studies (Higgs et al. 2006; Lundstrum et al. 2008, 2009) show that adding noise to a constant input signal enables phasic neurons to encode the signal, the effect of adding noise to a dynamic low-frequency signal has not been directly tested. Our study combines model simulations with whole cell recordings to show that slow-varying signals can be encoded by phasic neurons in the presence of noise. Under this circumstance, the noise can be thought of as a “gate” to control the pathway of the low-frequency information.

A low-threshold potassium current (I_KLT) has been found in phasic auditory neurons, including principal neurons in the avian nucleus laminaris and magnocellularis (Rathouz and Trussell 1998; Reyes et al. 1994), the ventral cochlear nucleus (VCN) (Manis and Marx 1991), the medial (MSO) and lateral (LSO) superior olives (Barnes-Davies et al. 2004; Smith 1995), and the medial nucleus of the trapezoid body (Brew and Forsythe 1995). I_KLT is mediated mostly by Kv1.1-containing potassium channels (Pál et al. 2005; Scott et al. 2005). Apart from contributing to the phasic response properties, I_KLT can also influence the temporal coding of phasic neurons by interacting with the stimulus spectrum (Day et al. 2008). Therefore a second goal of the present study was to examine whether the presence of I_KLT affects the spike timing of phasic neurons to a slow input.

A Hodgkin-Huxley-type phasic neuron model with a I_KLT (Rothman and Manis 2003b) was used for simulations. This model and its former version (Rothman et al. 1993) were originally developed for VCN bushy cells but also have been used as point neuron models for CN octopus cells (Bahmer and Langner 2009; Hemmert et al. 2005) and MSO neurons (Colburn et al. 2009; Zhou et al. 2005). Day et al. (2008) show that by freezing the normally voltage-gated conductance of the I_KLT to its resting value, the phasic neuron model can be converted into a tonic neuron model. This manipulation emphasizes the role of the dynamic I_KLT while keeping the other properties of the model approximately the same (e.g., the resting membrane potential and input resistance). A similar tonic neuron model was used here to provide a comparison model to the phasic neuron model.

To test model predictions, whole cell recordings were performed in the MSO in gerbils aged postnatal day 12 (P12) to 22. It is known that two important parameters of the MSO principal neurons change substantially over this age range; the amount of I_KLT increases and the membrane time constant decreases (Scott et al. 2005). Recordings were also obtained from tonic-firing neurons in the LSO in gerbils aged P10-16. To further confirm the effect of I_KLT on neural responses, especially on the spike timing to a slow input, a dynamic-clamp protocol was used to simulate a virtual I_KLT and to inject this current to the recorded LSO and younger MSO neurons that appeared to have weak or no I_KLT. Dendrotoxin-K (DTX-K), a specific inhibitor for potassium channels that contains Kv1.1 units, was also bath applied during recordings of several neurons to confirm the role of I_KLT.

Countering the widely expressed view that noise in sensory systems disrupts temporal precision, our study demonstrates that noise can facilitate the encoding of signals and I_KLT can interact with stimulus spectrum to affect spike timing.

METHODS

Neuron models

We employ the model developed by Rothman and Manis (2003b) for phasic-firing AVCN bushy cells. The model contains a fast sodium current (I_Na), a high-threshold (I_KHT), and a low-threshold (I_KLT) potassium currents, a hyperpolarization-activated cation current (I_h), and a leak current (I_lk), as seen in the current balance equation

$$C_{\mathrm{m}}\frac{\mathrm{d}V}{\mathrm{d}t}=-I_{\mathrm{Na}}-I_{\mathrm{KHT}}-I_{\mathrm{KLT}}-I_{\mathrm{h}}-I_{\mathrm{Ik}}+s\left(t\right)=2·\left[-{\overline{g}}_{\mathrm{Na}}{m}^{3}h\left(V-E_{\mathrm{Na}}\right)-{\overline{g}}_{\mathrm{KHT}}\left({0.85n}^2+0.15p\right)\left(V-E_{\mathrm{K}}\right)-{\overline{g}}_{\mathrm{KL}{\mathrm{T}}^w}{}^{4}z\left(V-E_{\mathrm{K}}\right)-{\overline{g}}_{{\mathrm{h}}^{\mathrm{r}}}\left(V-E_{\mathrm{h}}\right)-{\overline{g}}_{\mathrm{Ik}}\left(V-E_{\mathrm{Ik}}\right)\right]+s\left(t\right)$$ (1)

Here, V is the membrane potential and s(t) is the current input. The parameter values are the same as those used for the type II model in Rothman and Manis (2003b) except that all the maximal channel conductances and channel time constants are multiplied by a factor of 2 and 0.33, respectively, to mimic the 32°C, temperature of the brain slices during whole cell recordings. Briefly, the membrane capacitance, C_m = 12 pF; maximal channel conductances, ḡ_Na = 1,000 nS, ḡ_KHT = 150 nS, ḡ_KLT = 200 nS, ḡ_h = 20 nS, and ḡ_lk = 2 nS; reversal potentials, E_Na = +55 mV, E_K = –70 mV, E_h = –43 mV, and E_lk= –65 mV. The model has a resting potential (V_rest) of –64 mV. The I_Na and I_KHT are basic Hodgkin-Huxley type currents that are responsible for spiking dynamics. The time constant of the activation gating variable, w, of I_KLT is ∼2 ms for the resting potential and 0.5 ms when the membrane potential was above –20 mV. Inactivation, z, is slower with a time constant that varies between 20 and 200 ms, approximately. I_h has a similar or longer time constant than z. The equations and expressions for all gating variables are identical to those in Rothman and Manis (2003b).

Figure 1 (middle) shows the responses of the phasic neuron model to step (A) and sinusoidal (B and C) current injection. The model fired one spike at the onset of the step depolarizing current (1 nA, 30 ms) and not thereafter (Fig. 1A, middle). Correspondingly, when a sinusoidal current was injected to the phasic model, the model only responded to certain combinations of frequency and amplitude. For example, when two sinusoids had the same amplitude (1 nA) but different frequency (10 vs. 100 Hz), the phasic model responded only to the sinusoid of the higher frequency (Fig. 1B, middle). For the range of amplitude tested here (0–3 nA), the phasic model did not respond to frequencies <40 Hz (Fig. 1C, middle).

Fig. 1.

A: responses of the tonic (left), phasic (middle), and weak-phasic (right) neuron models to a 30-ms step current injection. B: responses of the 3 models to a sinusoidal current with amplitude and frequency marked (bottom, *). We scale time in units of stimulus cycles to facilitate comparison. C: frequency-response maps of the 3 models. Gray-scale colors represent spiking ratios (number of spikes over number of cycles) to a sinusoid current input with varying frequency (x axis) and amplitude (y axis).

The tonic model is created by fixing the KLT channel activation and inactivation variables, w and z, at the values obtained at resting potential (Day et al. 2008). Approximately 5% of KLT channels are open at rest. The model of Day et al. (2008) fires repetitively only to a small range of step input (0.43–0.65 nA) and the peak of the steady-state action potentials only reaches –10 mV at a temperature of 32°C (not shown). For the present study, we increased ḡ_Na from 1,000 to 1,500 nS, thereby obtaining larger action potential heights (Fig. 1A, left) and a broader input range for repetitive firing (0.35–0.84 nA). This modification is made mainly for the demonstration purpose here. It was not essential in our following simulations because noisy stimuli naturally elicit larger action potentials.

Figure 1, B and C, left, shows the response of the tonic model to sinusoidal current injection, which was clearly different from the sinusoidal response of the phasic model. First, the tonic model showed low-pass filtering behaviors—the threshold did not increase at the low-frequency side in contrast to the very sharp increase in threshold of the phasic model. Second, there was a large area at the low-frequency side where the tonic model fired more than one spike in each cycle of the sinusoid.

Despite the fact that gerbil MSO neurons exhibit phasic responses as early as P11 (Svirskis et al. 2002), a fourfold increase in the KLT channels occurs from P14 to P23 (Scott et al. 2005). Consistently, we found different degrees of “phasicness” in both model simulations with varying ḡ_KLT and whole cell recordings, although the standard definition of a phasic model only requires no repetitive firing to step input. For example, when ḡ_KLT was reduced from 200 to 50 nS, the model still showed phasic responses (Fig. 1A, right), but the firing threshold rolled off at lower frequencies (Fig. 1C, right) compared with the threshold of the phasic model with a strong I_KLT (Fig. 1C, middle). The amount of I_KLT in the phasic model is several times higher than what is needed to create a phasic response. For some step current levels (e.g., 1 nA), the phasic model with a weak I_KLT showed a second small peak after the onset spike (Fig. 1A, right, red). We also observed such second peaks in some of the MSO neurons aged younger than P17. The presence of this second peak indicated that the model/neuron was barely satisfying a phasic definition, i.e., a slight decrease of the amount of I_KLT may have produced a tonic response. In the following model simulations, the phasic model with a weak I_KLT was not considered. We were interested in neurons that are strongly phasic because mature VCN and MSO neurons possess strong I_KLT (Cao et al. 2007; Rothman and Manis 2003a,b; Scott et al. 2005; Svirskis et al. 2004).

Input stimulus for model simulations

A neuron with I_KLT shows a rectified response to a sinusoidal current; that is, the hyperpolarization from the resting membrane potential in response to the negative part of the sinusoid is much more prominent than the depolarization to the positive part (Fig. 1B, middle and right). To avoid too much hyperpolarization, the 20-Hz sinusoidal signal, Asin(2πft), was multiplied by a factor of 0.5 for its negative part. The signal was kept subthreshold for both tonic and phasic models, and either Gaussian white noise (≤25 kHz for model simulations) or low-pass filtered Gaussian noise (using a 4th-order Butterworth filter) was added to make the model fire.

$$s\left(t\right)=\{\begin{array}{cc}A\sin \left(2\mathrm{\pi }\mathrm{ft}\right)+N\left(\mathrm{\sigma }\right),& \sin \left(2\mathrm{\pi }ft\right)\ge 0\\ 0.5A\sin \left(2\mathrm{\pi }\mathrm{ft}\right)+N\left(\mathrm{\sigma }\right),& \sin \left(2\mathrm{\pi }ft\right)<0\end{array}$$ (2)

σ is the power of the white noise before the low-pass filtering. The sampling frequency for the simulations was 50 kHz.

We define the signal amplitude as the peak-to-peak amplitude of the unmodified sinusoid. Two signal amplitudes were tested for the tonic model, A = 0.1 and 0.2 nA (the tonic model fired spikes for A >0.3 nA without noise). Because the phasic model did not respond to the signal over a large range of A, using the same values of A for the phasic model would have made the signal too weak to be detected. Instead, A = 1 and 2 nA were used for simulations with the phasic model. These two values were chosen so that the detectability of the signal, measured by the product of averaged firing rate and vector strength, was comparable between the two models. We remark that it is always more difficult for the phasic model to respond to low-frequency signals than for the tonic model. The goal of this study is not to compare the detectability of the two models but to compare the firing properties of the two models when the subthreshold signals are equally detectable with added noise.

To perform an accurate analysis of the stochastic response, a sufficiently large dataset was required. The simulation for each signal and noise intensity continued until the duration reached 200 s or when ∼5,000 spikes were obtained, whichever came first.

Whole cell recordings

Gerbils (Meriones unguiculatus) aged P10–22 were used to obtain whole cell recordings in horizontal brain stem slices (Jercog 2008). Borosilicate glass electrodes (1.5 mm OD) were used as patch electrodes. When filled with internal solution, their resistance ranged from 7 to 10 MΩ. The constituents of the current-clamp solution inside the glass patch pipette were (in mM) 127.5 potassium gluconate, 0.6 EGTA, 10 HEPES, 2 MgCl₂, 5 KCl, 2 ATP, 10 phosphocreatinine, and 0.3 GTP (pH 7.2). During recordings, slices (150–200 μm) were placed in a chamber with artificial cerebrospinal fluid (ACSF) containing (in mM) 125 NaCl, 4 KCl, 1.2 KH₂PO₄, 1.3 MgSO₄, 26 NaHCO₃, 15 glucose, 2.4 CaCl₂, and 0.4 l-ascorbic acid (pH 7.3 when bubbled with 95% O₂-5% CO₂) at 32 ± 1°C. DTX-K (40 nM) was added to block the I_KLT for three MSO neurons obtained from different brain slice preparations. The perfusing rate of the oxygenated ACSF in the recording chamber was 2 ml/min. An Axoclamp2A amplifier, in combination with Labview (National Instruments), was used for stimulus generation, balance of series resistance, and data acquisition. The Axoclamp amplifier allowed series-resistance compensation and capacitance neutralization. Although a full compensation of the capacitance cannot be achieved, we assured that the decay of the electrode potential settled down in <0.1 ms (the sampling rate was 10 kHz) (Svirskis et al. 2004).

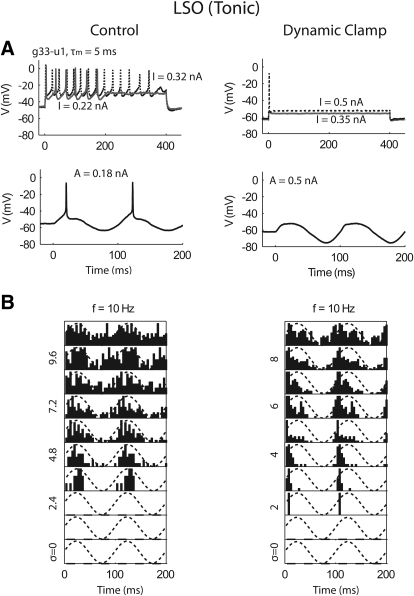
Recordings were obtained from 15 animals. The amount of I_KLT for each neuron can be roughly estimated based on whether it responded to low-frequency sinusoids (10 or 20 Hz) without noise, and whether the voltage trace for subthreshold sinusoidal input exhibited substantial rectification (see results). We separated the recorded MSO neurons into two groups for data analysis, weak-phasic MSO neurons that responded to low-frequency sinusoids for amplitude <1.5 nA, and phasic MSO neurons that do not respond up to the highest amplitude tested (1.5–3 nA) (detailed examples for the classification will be shown in Fig. 7). The phasic MSO group included 14 neurons from animals aged P13-22. The weak-phasic MSO group included four neurons from animals aged P12-16. Although the amount of I_KLT generally increases with age, both our study and the previous study by Scott et al. (2005) revealed large variations across animals. We also recorded from five tonic-firing LSO neurons (P10-16). Although phasic responses and a strong I_KLT have also been found in the LSO (Barnes-Davies et al. 2004; Kandler and Friauf 1995; Sanes 1990), no phasic responses were found in the present study possibly due to the small number of cells and our sampling bias toward a specific region in the medial limb of the LSO.

Fig. 7.

Responses of a weak-phasic (left) and a phasic (right) MSO neurons to step input (A, top), signal alone (A, bottom), and signal plus noise (B). In B, the signal amplitude was fixed (A = 0.9 nA for the weak-phasic neuron and A = 1.5 nA for the phasic neuron) and the noise intensity increased from bottom to top. Five repetitions were obtained for each condition. τ_m, membrane time constant. σ, power of the white noise before low-pass filtering (in pA).

When dynamic clamp was required for testing MSO or LSO neurons that appeared to have weak or no I_KLT, the virtual I_KLT was designed based on the neuron's V_rest, the potential for activating I_Na for spike initiation, and the membrane time constant (τ_m). The activation gating dynamics of w were expressed as

$$\begin{array}{c}\mathrm{d}w/\mathrm{d}t=\left(w_{\infty }-w\right)/{\tau }_w\\ w_{\infty }={\left[1+\exp (-\left(V-V_{\theta }\right)/S\right]}^{-1/4}\\ {\tau }_w=\varphi \cdot \{100-{\left[6\exp ((V+60)/6+16\exp (-(V+60)/45\right]}^{-1}+1.5)\end{array}$$ (3)

The voltages and time are in mV and ms, respectively. In the phasic model (Rothman and Manis 2003b), V_θ (the half activation point of w_∞) was – 48 mV and S (the steepness of w_∞) was 6, which yielded a w_∞ of 0.07 for V_rest and a w_∞ of 0.8 for the sodium-activating potential, approximately. We adjusted the values of V_θ and S for each recorded neuron to maintain similar values of w_∞ at the resting and sodium-activating potentials. τ_w was scaled by a factor of φ so that the value of τ_w at V_rest was equal to or slightly larger than the τ_m at rest. This adjustment of τ_w was necessary to ensure that the neuron can still fire to fast input but not to slow input. The slow inactivation variable, z, was kept as it was in the phasic model, except that the time constant, τ_z, was scaled by the same factor φ. We did not adjust z_∞ because it did not play a significant role in this study (see discussion).

Within each of the 0.1-ms sampling period, the membrane voltage was recorded and used by Labview to compute the artificial I_KLT, which was then added to the current stimulus to be injected to the neuron. The dynamic clamp's stability was assured by monitoring for skipped data points and saved traces of raw data (for more details, see Svirskis et al. 2004). The liquid junction potential was not measured or compensated. However, the liquid junction potential is unlikely to contribute in our dynamic-clamp approach because the parameters used in computing the virtual I_KLT are relative to the resting membrane potential and sodium-activation potential measured for each neuron.

The signal frequency was normally 10 or 20 Hz. For LSO neurons that had long τ_m, e.g., 10 ms, the signal frequency was further lowered to 5 or 2 Hz. The duration of the stimulus was 1 s. On average five repetitions were obtained for a given noise intensity for most of the recorded neurons. We used low-pass filtered noise with a cutoff frequency of 1 kHz in the recordings for two reasons. First, the membrane voltage obtained in the previous time window was used to simulate the virtual I_KLT for the next time window, which yielded a natural time delay in the dynamic-clamp protocol. Second, the capacitance of the electrode cannot be fully compensated.

In the model simulations, a fixed voltage crossing (0 mV) was used to identify action potentials, which were typically large. However, in MSO neurons, action potentials are generated in the axon and have small amplitude in the soma (e.g., 10–30 mV at P20), due to the presence of I_KLT and the inactivation of I_Na (Scott et al. 2005, 2007; Svirskis et al. 2004). Therefore a fixed-voltage threshold was likely to miss spikes during hyperpolarization or pick up fake spikes during depolarization. Figure 2 (black) shows an example of time course from an MSO neuron (P20). Instead of using a fixed voltage threshold, here we used a dynamic spike-recognition threshold, which was the membrane potential in response to the signal alone plus 25–35 mV (gray). When the membrane potential was greater than the threshold, which varied within each signal cycle, a spike was marked. We used this dynamic threshold because we can only record spikes in the soma; spikes were expected to be larger and more uniform in the axon (Scott et al. 2007).

Fig. 2.

A sample time course with the dynamic spike-recognition threshold used for the recordings. Black, membrane potential of a medial superior olivary (MSO) neuron (P20) in response to a 3-nA 20-Hz signal plus a low-pass filtered noise (σ = 28 pA). Gray, threshold for defining spikes, which was the membrane potential in response to the signal alone +35 mV.

All protocols were reviewed and approved by New York University Institutional Animal Care and Use Committee.

RESULTS

We will compare models/neurons with different firing properties, e.g., tonic versus phasic, for their noise-gated encoding of low-frequency subthreshold signals. We initially did model simulations with white noise added to the signal and made certain predictions (Figs. 3–5). We then performed whole cell recordings with low-pass filtered noise (Figs. 6–10). Because the difference between model predictions and experimental observations indicated that the frequency content of the noise might be an important parameter, we did more simulations and recordings with varying frequency content of the noise (Figs. 11–13).

Fig. 3.

Average firing rate (top), vector strength (middle), and sync rate (bottom) for the models as a function of the SD of noise (bottom axis). The upper horizontal axis shows the SD of the membrane potential for noise alone, obtained when the spiking mechanism was disabled by setting the activation/inactivation variables of the I_Na and I_KHT to their resting values. The SD of voltage was proportional to the SD of noise intensity for both models. The points and letters marked (bottom) indicate the noise σ values that are used in later examples, which were evenly distributed in σ. Current values in the legends are the peak values of the 20-Hz modified signal.

Fig. 4.

Comparisons of the tonic and phasic models for period histogram and interspike interval (ISI) histogram at different noise intensities (specified in Fig. 3). The plots in black are for signal amplitude A = 0.2 (tonic model) and 2 nA (phasic model); the period histogram in red for the phasic model shows weak phase selectivity for the smaller signal amplitude, A = 1 nA. The dotted lines in the period histogram plots represent the time course of the modified sinusoidal signal for illustration purpose. Two identical cycles of period histograms are plotted. The scale of the period histogram plots are fixed over all the panels. The scale of the ISI histogram plots are not fixed due to a large variation of values across panels.

Fig. 5.

A and B: spike-triggered average (STA) of the stimulus for the conditions marked by B in Fig. 3, bottom (A = 0.2 and 2 nA, σ = 3.8 and 9.0 pA, for the tonic and phasic models, respectively). Above A and B, the period histograms were also replotted from Fig. 4B for each condition to illustrate how the 4-ms window for signal's rising (blue) and falling (red) phases were defined. The dotted lines in the STA plots are superimposed signals preceding the spikes. In fact, the signal should be slightly shifted for each spike occurring at different time within the 4-ms window, but this shift is negligible. C: STA of the stimulus (solid lines in B) subtracted by the signal (dotted lines in B) for the phasic model. Note that time 0 was marked when the membrane potential crossed 0 mV; the sodium current that initiated an action potential was activated at the time when the stimulus STA reached its peak.

Fig. 6.

Average firing rate (top), vector strength (middle), and sync rate (bottom) as a function of noise intensity for a lateral superior olivary (LSO, left) and a phasic MSO (right) neurons. Current values (in nA) in the legends are the peak values of the modified signal. LSO: g33-u1, P11, 10-Hz signal frequency, 5 repetitions. MSO: g28-u3, P18, 20-Hz signal frequency, 6 repetitions for each signal level.

Fig. 8.

Responses of 2 phasic MSO neurons to step input (A, top), signal alone (A, bottom), and signal plus noise (B). In B, the signal amplitude was fixed at 1.5 nA and the noise intensity increased from bottom to top. Five repetitions were obtained for each condition. τ_m, membrane time constant. σ, power of the white noise before low-pass filtering (in pA).

Fig. 9.

Responses of an LSO neuron (P11) to step input (A, top), signal alone (A, bottom), and signal plus noise (B) before (left) and after (right) adding a virtual I_KLT with dynamic clamp. In B, the signal amplitude was fixed (A = 0.08 nA for the control and 0.7 nA for the dynamic clamp) and the noise intensity increased from bottom to top. Five repetitions were obtained for each condition. τ_m, membrane time constant. σ, power of the white noise before low-pass filtering (in pA).

Fig. 10.

Responses of an MSO neuron (P14) to step input (A, top), signal alone (A, bottom), and signal plus noise (B) before (left) and during (right) application of 60 nM dendrotoxin (DTX)-K. In A, the red dotted lines represent the signal scaled to match the neuron's hyperpolarizing response, so that it is clear whether a rectification of membrane potential existed in the depolarizing response compared with the shape of the signal. In B, the signal amplitude was fixed (A = 1.5 nA) and the noise intensity increased from bottom to top. Five repetitions were obtained for each condition. τ_m, membrane time constant. σ, power of the white noise before low-pass filtering (in pA).

Fig. 11.

Responses of the phasic model (A–C) and the modified phasic model with low-voltage sodium inactivation (D) to a 20-Hz signal plus white noise or low-pass filtered noise. Low-voltage sodium inactivation was created by shifting the inactivation variable, h_∞, leftward by 15 mV (Svirskis et al. 2004). The dotted lines are superimposed signals scaled to illustrate the response phase. The signal amplitude was fixed at 1.5 nA and the noise intensity increased from bottom to top. Five repetitions were obtained for each condition. σ, power of the white noise before low-pass filtering (in pA). f_cut, cutoff frequency of the noise.

Fig. 12.

Responses of an MSO neuron (P14, the same shown in Fig. 7C) to a 20-Hz signal plus noise before (left) and after (middle and right) adding a virtual I_KLT with dynamic clamp. The cutoff frequency of the noise (f_cut) was 1,000 Hz for the left and middle and 200 Hz for the right. The dotted lines are superimposed signals scaled to illustrate the response phase. The signal amplitude was fixed (A = 0.9 nA for the control and 1.5 nA for the dynamic clamp) and the noise intensity increased from bottom to top. Five repetitions were obtained for each condition. τ_m, membrane time constant. σ, power of the white noise before low-pass filtering (in pA).

Fig. 13.

Maximum membrane potential (indicated by the colors) evoked by a pulse added to the 20-Hz signal (A = 0.2 and 2 nA for the tonic and phasic models, respectively). Thick black dashed line, voltage threshold that defines an action potential.

Simulation with white noise revealed distinct temporal patterns for the phasic neuron model

Average firing rate and temporal patterns, both important features of information representation in the auditory system, will be analyzed respectively. Figure 3 (top) shows that both the tonic and phasic models had no response to the signal alone (noise σ = 0) and increased their firing rate with noise intensity. However, their firing rate showed different trends when the signal amplitude was varied. When the signal amplitude increased, the average firing rate of the tonic model remained relatively constant except at the lowest noise intensities. In contrast, the firing rate of the phasic model decreased substantially with increasing signal amplitude.

Although it was the noise that elicited spikes in both the tonic and phasic models, the spike timing can be phase locked to the signal, and the degree of phase locking depends on the noise intensity. The vector strength of responses, computed at the signal frequency (20 Hz), decreased monotonically with noise intensity for both models (Fig. 3, middle). On the one hand, the more noise added to a system, the less precise was the firing. On the other hand, the firing rate of both models decreased with increasing vector strength, suggesting that the efficiency of decoding the signal may also decrease. Therefore we computed the sync rate, the product of the average firing rate and the vector strength, to take into account of both the precision and the efficiency. Figure 3 (bottom) shows the sync rate for the two models. At very low noise intensities, the sync rate of the tonic model was low due to a low firing rate. At high noise intensities, the sync rate decreased with noise intensity due to the weakening of phase locking. The sync rate peaked at an intermediate noise intensity as a compromise between the firing rate and phase locking. In contrast, the sync rate of the phasic model continued to increase at high noise intensities because the vector strength did not decrease as fast as the vector strength of the tonic model did. Of course at very high noise intensities (well beyond physiological plausibility), the sync rate eventually dropped for the phasic model (not shown).

For neuron models with a relatively fixed action potential threshold, such as an integrate-and-fire model or the tonic model in this study, spikes are primarily determined by fluctuations of the subthreshold membrane potential caused by input currents. Therefore for a slow input signal, one can predict that the model will most likely fire near the maximum of the net input, which, in our case, was the peak of the sinusoid. In contrast, when dynamic I_KLT is present, spiking of the phasic model depends not only on the membrane potential but also on its rate of change. The difference in firing patterns of the two models can be clearly illustrated by the period histogram. Figure 4 compares the period histogram and interspike interval (ISI) of the two models at several noise intensities (marked in Fig. 3, bottom). All the plots in black were obtained with a high signal amplitude (0.2 and 2 nA for the tonic and phasic models, respectively). The two models exhibited different response features at all noise intensities (a–d), as listed in the following text.

1) When the noise intensity was low, the tonic model discharged at the signal's peak, while the phasic model discharged at the signal's rising phase. The ISI histograms show that the two models can sometimes miss cycles (13 and 60% of signal cycles had no spike for the tonic and phasic model, respectively). b) For the tonic model, responses occurred over a larger spread of phases and the period histogram followed the positive part of the signal. The ISI histogram showed that most cycles produced more than one spike. In contrast, the phasic model still showed a relatively precise spike at the signal's rising phase (in 97% of cycles); in addition, it also fired during the falling phase of the signal, although less frequently (in 54% of cycles). The middle peak of the ISI histograms indicated that in some signal cycles the phasic model fired twice, i.e., at double the signal frequency. candy d) At high noise intensities, both models had more uniformly distributed responses over each cycle with the phasic model still showing preferences at the signal's rising and falling phases.

The preceding results were obtained with the larger signal amplitude (Fig. 4, black). To explain why the phasic model showed decreased firing rate with increasing signal amplitude, the period histograms obtained with the smaller signal amplitude (1 nA) are also plotted (Fig. 4, red). The weaker signal led to less distinct features compared with those obtained with the larger signal amplitude (Fig. 4, black). For large noise intensity (b–d), the decreased firing rate with the larger signal was caused by reduced activity both at the signal's trough, due to a stronger hyperpolarization, and at the signal's peak, due to a stronger depolarization and therefore larger I_KLT.

Apart from the lack of response to the signal's peak and trough, the phasic model also showed different sensitivity to the rising, as compared with the falling, phase of the signal. To understand the cause of the difference, the spike-triggered average (STA) of the total input current, i.e., signal plus noise, was computed separately for the rising and the falling phase (Fig. 5B; noise intensity marked by b, Fig. 3, bottom). Note that spikes within a 4-ms time window centered at the midpoint of the rising or the falling phase were considered in this case, whereas in the previous analysis each group covered half of a signal cycle (25 ms). The STAs matched well to the signal (dotted lines) until 2 ms before a spike, which suggested that noise did not play a role in the earlier time window. As time approaches spike initiation, the STAs were below the signal at first and then increased abruptly to trigger a spike. Thus a significant hyperpolarizing fluctuation was required to temporarily deactivate the I_KLT before a depolarizing fluctuation for spikes on both the rising and the falling phases. However, subtracting the signal from the STAs (Fig. 5C) showed that a larger amount of hyper- and depolarizing fluctuation was required for spikes on the falling phases compared with spikes on the rising phases, which explained why more spikes occurred on the rising phases for the phasic model.

The STAs for the tonic model are also plotted in Fig. 5A for comparison. Apart from a depolarizing fluctuation required to initiate a spike, the STAs generally matched the signal. Because the conductance of the KLT channels were frozen, preceding hyperpolarizing fluctuations did not facilitate spiking as they did for the phasic model.

In summary, with white noise added to the low-frequency signal, the temporal firing patterns of the phasic model differed from the temporal patterns of the tonic model. Specifically, instead of detecting the peaks of the subthreshold signal, the phasic model was most sensitive to the signal's rising phase; at high noise intensities, it can also respond to the falling phase.

Experimental results confirmed distinct temporal patterns for phasic neurons

The preceding simulation results were obtained with white noise. In whole cell recordings, we used low-pass filtered noise with a cutoff frequency of 1 kHz (see methods). More simulations and recordings with varied noise frequency spectrum are described in the next section.

The average firing rate and phase locking of the recorded neurons generally agreed with model predictions. Figure 6 shows examples of an LSO and a phasic MSO neurons. When the signal amplitude increased from 1 to 1.8 nA, the MSO neuron showed decreased average firing rate (Fig. 6, top right) and increased vector strength (Fig. 6, middle right), similar to the phasic model's behavior (Fig. 3, top and middle right). The neuron's sync rate was approximately monotonic increasing with noise intensity as seen with the phasic model (Fig. 6, bottom right). The tonic neuron's sync rate (Fig. 6, bottom left) was erratic at higher noise intensities, so we cannot see the generally decreasing trend as found for the tonic model (Fig. 3, top left). In general, because only 5- or 6-s responses were obtained for a limited number of noise intensities in the whole cell-recordings, we will not further compare the sync rate across neurons but will focus on a comparison of the temporal spike patterns instead.

Figure 7 shows responses of a weak-phasic (left) and a phasic (right) MSO neurons to various current inputs. Similar to what is shown in the step response (Fig. 7A, top), all of the recorded phasic or weak-phasic MSO neurons did not fire repetitively. In response to a 20-Hz signal input, the weak-phasic MSO started firing when the amplitude of the signal was >1 nA (Fig. 7A, bottom left), while the phasic MSO neuron (Fig. 7A, bottom right) did not fire for all signal amplitudes tested (<1.5 nA).

Figure 7B (left) shows that when low-pass filtered noise was added to a subthreshold low-frequency signal, the weak-phasic MSO neuron behaved similar to the tonic model, that is, it responded mostly to the signal's peak. For all the four weak-phasic MSO neurons obtained in this study, a dynamic-clamp approach was applied to each of them to inject a virtual I_KLT. Each neuron's threshold was elevated to the signal with the virtual I_KLT, indicating stronger phasicness, and their response to a subthreshold signal plus noise shifted from the signal's peak to the rising phase (see Fig. 12 in next section).

In contrast, when low-pass filtered noise was added to a subthreshold signal, 13 of 14 phasic MSO neurons did not respond to the signal's peak consistent with the predictions by the phasic model. The three phasic neurons from relatively young animals (P13-14) responded to the signal's rising and falling phase (1 example in Fig. 7B, bottom right), especially for f = 10 Hz, consistent with the preceding model simulations with white noise. Although all phasic MSO neurons showed similar responses to step and sinusoidal input (Figs. 7A and 8A), 10 phasic neurons from animals aged P17 and older showed different degrees of responses in the signal's trough as well as the rising and falling phases, as represented by the two neurons plotted in Fig. 8B. Note that the membrane time constants of the three phasic neurons from young animals that did not fire in the signal's trough (τ_m = 0.7–1 ms) were longer than all of the phasic MSO neurons that did (τ_m = 0.3–0.6 ms), as membrane time constant decreases with age. We believe that the determination of the firing patterns depended on both the membrane time constant and the frequency spectrum of the noise (see next section). One of 14 phasic MSO neuron responded mostly to the signal's peak (not shown).

In addition, with the virtual I_KLT, all of the five LSO neurons were converted from tonic to phasic firing to step current injection and showed elevated threshold to the modified signal (Fig. 9A) at 2–10 Hz. The responses of four of five LSO neurons to a subthreshold noisy signal were shifted from the signal's peak to the rising phase (Fig. 9B), including one neuron that also responded to the signal's falling phase (the frequency of the signal for this neuron was 2 Hz). The fifth LSO neuron showed no shift in the firing phase. Note that the dynamic of the KLT channels is important for converting a tonic response to a phasic response. For one LSO, we also fixed the conductance of the virtual I_KLT, as we did for the tonic model. The response of the LSO remained tonic, although its membrane time constant was reduced (not shown).

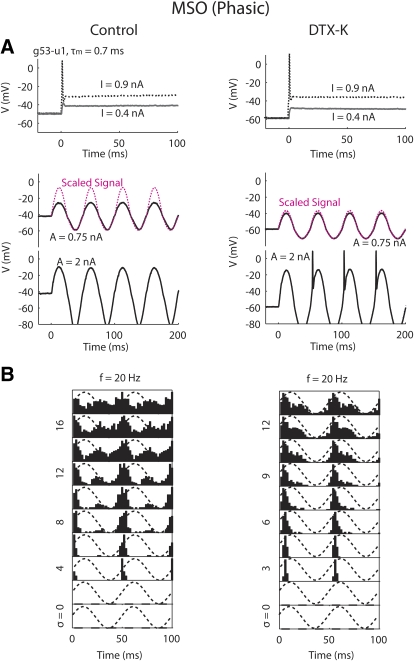
To directly test the contribution of I_KLT in creating the firing patterns observed in phasic MSO neurons, DTX-K (40 nM) was applied to three phasic MSO neurons (P14-16). We found that DTX-K increased membrane time constants (≤2 times) and action-potential heights (≤1.7 times), consistent with previous studies (Scott et al. 2005; Svirskis et al. 2002, 2004). Figure 10 shows an example neuron that was converted from phasic to weak phasic. Responses to step input remained transient after the application of DTX-K (Fig. 10A, top), likely due to low-voltage inactivation of I_Na (Svirskis et al. 2002). In the control condition, the neuron did not respond to a 20-Hz signal up to the highest amplitude tested (2.5 nA). After DTX-K was applied, the neuron started responding to the signal for A ≥1.5 nA (Fig. 10A, middle and bottom). The presence of I_KLT in the control condition can also be inferred by comparing the voltage trace (Fig. 10A, middle left, black) with the superimposed signal (red dotted). The deactivation of I_KLT during hyperpolarization led to a high-input resistance. During depolarization, I_KLT acted as a negative feedback mechanism that repolarized and shunted the membrane potential, in total preventing firing. The difference between the voltage trace and the signal was observed for all the phasic MSO neurons recorded in this study. In contrast, after the blockade of I_KLT, the membrane potential had the same shape as the signal (Fig. 10A, middle right).

In response to the 20-Hz signal with added noise, the neuron in the control condition showed distinct firing preference to the signal's rising and falling phases (Fig. 10B, left). After DTX-K was applied, the firing of the neuron shifted more toward the signal's peak and the responses at high noise intensities showed a better match to the shape of the signal (Fig. 10B, right). The other two MSO neurons showed similar behaviors. This result confirmed that I_KLT played a major role in creating the firing patterns of the phasic MSO neurons with likely contributions from sodium inactivation.

Model simulations agreed with whole cell recordings when the frequency spectrum of noise was varied

In simulations with white noise, the phasic model responded mostly to the low-frequency signal's rising phase, and at high noise intensities it also responded to the falling phase. However, our recordings with low-pass filtered noise (cutoff frequency = 1 kHz) showed that, apart from the signal's rising and falling phase, phasic MSO neurons aged P17 and older also responded at the signal's trough. One possible explanation was that if a neuron's effective time scale is fast enough compared with the temporal fluctuation of the noise, the neuron can fire in the signal's trough even though the neuron is significantly hyperpolarized. That is, the membrane can track a long duration depolarizing fluctuation to reach the firing threshold before I_KLT activates. This hypothesis was supported by the fact that the three younger MSO neurons with long membrane time constants did not respond to the signal's trough.

To further examine this hypothesis, we tested the phasic model with different cutoff frequencies of the noise. To provide a fair comparison to the whole cell recording data, instead of obtaining a large number of spikes (5,000 spikes) at each noise intensity as in the previous simulations, five repetitions of a 1-s-long stimulus at each noise intensity was obtained. Figure 11, A–C, shows the simulations with the phasic model for different noise cutoff frequencies. For white noise and low-pass-filtered noise with 1-kHz cutoff frequency, the phasic model fired mostly at the signal's rising phase and occasionally at the signal's falling phase (Fig. 11, A and B), consistent with the previous simulations. When the cutoff frequency of the noise was further lowered to 200 Hz (Fig. 11C), the model also responded at the signal's trough at high noise intensities.

If our hypothesis is correct, we should also see similar conversions in the MSO neurons by lowering the noise cutoff frequency for an MSO neuron with long membrane time constant. Figure 12 (left) shows an example of a weak-phasic MSO neuron (P14, τ_m = 2 ms), which originally responded to the signal's peak (cutoff frequency = 1 kHz). When a virtual I_KLT was added with dynamic clamp, the neuron responded on the signal's rising phase, but rarely to the signal's trough (Fig. 12, middle). When the cutoff frequency was lowered to 200 Hz, the neuron started firing in the signal's trough at high noise intensities (Fig. 12, right). We also lowered the cutoff frequency from 1 kHz to 200 and further 100 Hz for a phasic MSO neuron (P13, τ_m = 0.8 ms) and observed a similar increase of firing in the trough (not shown). We then tried increasing the cutoff frequency to 2 kHz or higher for a phasic MSO neuron (P18, τ_m = 0.4 ms); however, this neuron still responded at the signal's trough as well as the rising and falling phase.

Another possible explanation was that because MSO neurons from older animals (P15 and up) have stronger sodium inactivation than the phasic model (Svirskis et al. 2004), hyperpolarization of the neurons caused removal of the inactivation and thus promoted more firing in the signal's trough. To examine the second hypothesis, we shifted the sodium inactivation voltage sensitivity (h_∞) leftward by 15 mV (Svirskis et al. 2004) for the phasic model. The modified phasic model showed some firing to the trough at high noise intensities even for a cutoff frequency of 1 kHz (Fig. 11D). This result suggested that both sodium inactivation and a slow noise fluctuation contributed to firing during the signal's trough observed with the phasic MSO neurons (P17 and older). The fact that we could not prevent the phasic MSO neuron (P18) from firing in the trough by increasing the cutoff frequency supported our second hypothesis that sodium inactivation is also a contributing factor.

The preceding results were obtained with stochastic inputs. The stimulus STA indicated that both depolarizing and hyperpolarizing fluctuations are critical aspects of spike generation (Fig. 5). In fact, some of the trends can be observed with deterministic pulsatile inputs given at specific phases during the signal cycle (Fig. 13, top traces above each color plot). Figure 13 shows the maximum membrane potentials (represented by the color scales) occurring around the phase where a pulse of different amplitude and duration was added to the signal. The threshold in terms of pulse amplitude for eliciting a spike was marked with thick dashed lines. The tonic model (left ) showed a generally linear behavior; that is, the lowest threshold occurred at the signal's peak and the highest threshold at the signal's trough for either pulse duration. In contrast, the phasic model (right) did not fire at the signal's peak even with high pulse amplitudes. The lowest threshold occurred at the signal's rising phase, and a local minimum occurred at the signal's falling phase. When the duration of the pulse was increased from 0.1 to 1 ms, the threshold at the signal's trough was lowered.

In addition, because the input resistance at the signal's trough was the highest over all phases, action potentials occurring at the signal's trough also had the largest heights, indicated by the red/orange colors (Fig. 13). This was true for both the tonic and phasic models.

DISCUSSION

We have demonstrated with computations and in vitro experiments on auditory brain stem neurons and models how noise can enable or gate phasic neurons to respond to slow inputs that would be transparent to them when noise is absent. Tonic neurons fire in response to steady or slowly varying signals of sufficient amplitude. Phasic neurons do not fire if the signal is slow without making the amplitude unrealistically high. For slow inputs that are below a tonic neuron's threshold, noise can induce spiking near input peaks, similar to the behavior of a general stochastic resonance system. Phasic neurons resist firing near peaks of slow inputs even if substantial noise is present. We have shown, however, that noise allows phasic neurons and models to fire in the rising (and sometimes in the falling phases) of a slow signal when the membrane potential is not far from the resting potential; noise gates this responsiveness. A low-threshold potassium current, I_KLT, is the definitive mechanism underlying the phasic response properties in the model, because freezing its conductance at its resting level converts the model from phasic to tonic. We have converted neurons from tonic or weak phasic to (strong) phasic behavior and demonstrated their noise-gating properties by using the dynamic-clamp approach to inject a virtual I_KLT. Applying DTX-K to several phasic MSO neurons also revealed I_KLT as the major factor for creating the firing patterns of the phasic neurons. We have further demonstrated that the noise-gated phase-selectivity of phasic neurons and models is sensitive to the spectral profile of the noise.

Comparisons between models and recorded neurons

The phasic neuron model used here was designed for VCN bushy cells. Nevertheless, the model responses and the neuronal responses obtained in the MSO were generally in good agreement, as listed in the following text.

1) The presence of I_KLT can create phasic responses to step or low-frequency sinusoidal input, and increasing the amount of I_KLT increases the phasicness. This is supported by the model simulations, the dynamic-clamp results when virtual I_KLT was injected and the few examples involving DTX-K. In addition, the dynamic of the KLT channels is important because freezing the conductance to its resting value creates a tonic response, supported by both model simulations and dynamic-clamp data. Note that injecting a frozen I_KLT shortens the membrane time constant and hyperpolarizes a neuron, but these changes are not sufficient to convert a neuron from tonic to phasic.

2) Phasic and tonic neurons detect different features of the subthreshold low-frequency signal. The tonic neuron model, the LSO and the weak-phasic MSO neurons responded to the peak of the subthreshold signal when noise was added. In contrast, the phasic model, the majority of the phasic MSO neurons, and dynamically clamped LSO or weak-phasic MSO neurons responded to the signal's rising phase even though the signal was subthreshold to the model. The response was fairly precise, reliable, and distinct over a larger range of noise intensities. The exact firing phase of the phasic model varied slightly with signal frequency; nevertheless, the most sensitive part of a low-frequency signal (<100 Hz) was always within the rising part (not shown). The phasic model, as well as the majority of phasic MSO neurons, can also respond to the signal's falling phase at high noise intensities, although this group of spikes can sometime be smeared by the presence of spikes during the signal's trough. The stimulus STA indicated that spikes in the falling phase were caused on average by a combination of “negative-positive” fluctuations from the noise, similar to the postinhibitory facilitation proposed by Dodla et al. (2006). However, when a virtual I_KLT was injected to LSO and weak-phasic MSO neurons, spiking at the signal's falling phase was rarely found. It was possible that due to the delay caused by the dynamic-clamp procedure, these neurons were unable to benefit from post inhibitory facilitation. This argument is consistent with the fact that the one LSO neuron that fired to the signal's falling phase was tested at 2 Hz.

Note that the temperature was 32°C in the experiments and simulations. At mammalian body temperature (37°C), the model dynamics are faster and the response areas (Fig. 1, bottom) shift to higher frequencies. At 37°C, the phasic model showed highest sensitivity to the signal's rising phase ≤100-Hz signal frequency, while firing to the falling phase gradually disappeared for signal frequency >50 Hz.

3) The frequency content of the noise can affect the response patterns of a neuron with a strong I_KLT. If the membrane potential could sufficiently integrate a depolarizing noise fluctuation at a time when most of the KLT channels were inactivated, the neuron fires a spike. Our simulation (Fig. 11) and experimental (Fig. 12) results indicated that the firing at the signal's trough showed by the phasic MSO neurons aged P17 or older was partially caused by the membrane dynamics being fast enough compared with the fluctuation of the low-pass filtered noise (cutoff frequency was 1 kHz) to allow quick depolarizations that reached the firing threshold. In addition, the removal of sodium inactivation by hyperpolarizing the membrane potential can also promote firing in the signal's trough.

Role of other currents in the noise-gated encoding of signals

I_KLT acts as a subthreshold negative current feedback that repolarizes the membrane potential for slow depolarizing inputs. Its presence renders a dynamic voltage threshold for spike generations that depends not only on membrane potential or input amplitude but also on the rate of membrane fluctuations (Day et al. 2008; McGinley and Oertel 2006). We believe that I_KLT was a major contributor to the special features observed with the phasic model. Apart from the I_KLT, there are other currents in Eq. 1. I_Na and I_KHT are responsible for action potential repolarization with little effect on discharge patterns (Rothman and Manis 2003b). I_h was mostly activated below V_rest with an activation time constant of 200–300 ms, and the deactivation by membrane depolarization was on the order of tens of milliseconds. Although I_h did vary on a cycle-by-cycle base in our simulations, after freezing I_h activation variable (r) to its resting value, the phasic model maintained the characteristic features described in the preceding text (not shown). Similarly, freezing the slow inactivation variable (z) for I_KLT did not change the model behavior significantly. Therefore the fast activation variable (w) enabled I_KLT to play a key role in responding to the rising, falling, or trough phase of the signal.

It should be noted that although the VCN phasic neuron model (Eq. 1) has been used as an MSO point-neuron model (Colburn et al. 2009; Jercog 2008; Zhou et al. 2005), it does not capture all the features of MSO neurons, such as the observed substantial inactivation of I_Na at rest reported for animals aged P15 or older (Svirskis et al. 2004). The few examples involving the application of DTX-K indicated that although I_KLT was the major factor for creating the firing patterns of the phasic MSO neurons, sodium inactivation also helped to shift the response phase to a certain extent.

Phasic neurons as slope detectors

In the present study, the signal was maintained subthreshold for both tonic and phasic models. In fact, because the phasic model does not have a fixed firing threshold in terms of membrane voltage or input amplitude, it might be misleading to call the signal subthreshold based on its amplitude. McGinley and Oertel (2006) examined neurons in the ventral cochlear nucleus (VCN) using ramp stimulus with positive slopes. They found that there is a threshold in terms of rate of depolarization for bushy cells and octopus cells; ramp currents that are shallower than the threshold do not cause firing in those phasic neurons. In contrast, the firing properties of T stellate cells, which are tonic neurons, do not depend on the rate of depolarization. The fact that the phasic model and neurons in the present study did not respond to the 20-Hz signal alone indicated that even the steepest slope in the signal was below the slope threshold of the model/neurons. Therefore it might be more appropriate to call the signal subthreshold based on its frequency or slope rather than its amplitude. We showed that adding noise can make the phasic model/neurons respond to subthreshold slopes, and because input slope, not amplitude, was more meaningful for these neurons, the most sensitive part of the signal encoded by the noise was where the positive slope was adequately steep.

Phasic neurons in response to more sound-like inputs

We used low-frequency (20 or 10 Hz) sinusoidal current (with the negative part reduced by 50%) in simulations and experiments. VCN or MSO neurons are not likely to get low-frequency current inputs when responding to pure tones at very low frequencies because the auditory-nerve fibers (ANFs) are precisely locked to a particular phase of the sound, thus providing relatively fast rising EPSCs to their targets. Instead our findings are useful in predicting high-frequency (>4 kHz) MSO neurons' response to high-frequency sounds with very slow modulations. When the carrier frequency is higher than ∼4 kHz, ANFs fail to lock to the fine structure (Johnson 1980; Kiang et al. 1965; Rose et al. 1967) but can still encode the envelope (Joris and Yin 1992). Because high-frequency MSO neurons receive multiple subthreshold excitatory postsynaptic currents (EPSCs) (Smith et al. 2000) that are not synchronized to the fine structure of the sound, the summation of all the EPSCs was effectively following the envelope of the sound. Our simulations suggested that when the envelope fluctuation is very slow, MSO neurons will not respond to the sound actively unless internal noise is present. Because phase locking is essential for MSO neurons to encode interaural timing differences, we predict that the coding of interaural timing differences in a very slow envelope by high-frequency MSO neurons will benefit from the presence of noise.

It has been observed in the inferior colliculus that in response to a 10-Hz amplitude-modulated tone, one group of neurons showed the highest firing probability at the peak of the averaged membrane potential, while another group of neurons fired mainly at the rising phase (Geis and Borst 2009). Our results suggest that in the high-frequency area of the MSO, the neurons should respond mainly at the rising phase of the averaged membrane potential, which is close to the rising phase of the slow envelope.

Possible sources of noise

Possible sources of noise include channel noise (Chen et al. 2008; Chow and White 1996), spontaneous EPSCs or inhibitory postsynaptic currents (IPSCs) (Chirila et al. 2007), and even inputs that have characteristic frequencies far away from the characteristic frequencies of the majority of inputs. In any case, the noise will be filtered by one or more time scales. The intensity of the noise is also expected to be low compared with the noise levels in the preceding simulations. Therefore it is most likely that only the rising phase of the low-frequency input is encoded, creating the advantage of the unique mapping between signal phase and neural response.

The negative part of the signal caused a large hyperpolarization (lower than –100 mV) in simulations with the phasic model (Fig. 1B, middle). We do not expect inhibitory synaptic input to cause such a large hyperpolarization in response to sound. We repeated our simulations with a smaller degree of hyperpolarization by reducing the multiplication factor of the signal (see methods) from 0.5 to 0.1. The phasic model still fired most sensitively to the signal's rising and falling phases except that there was more firing in the trough at high noise intensities even with white noise. Because MSO neurons (P17 and older) have more depolarized resting potentials (V_rest = –50.6 ± 2.9 (SD), Svirskis et al. 2004) than the phasic model (V_rest = –64 mV) and a smaller signal amplitude (1.5 nA instead of 2 nA) was used for most of the recordings, the amount of hyperpolarization was generally limited (Figs. 7 and 8). In summary, a large hyperpolarization was not necessary to generate our results.

General conclusion

By adding noise to the input, phasic neurons are able to encode low-frequency information. The conventional view of phasic neurons as band-pass filters based on simple input-output relations should not be generalized to understand the information processing of these neurons because low-frequency information can be represented indirectly. Our findings have implications about how single neurons process information with varying time scales. For example, MSO neurons are known for their fast membrane and synaptic time constants. It is surprising that being sensitive to input timing on the order of tens of microseconds (Yin and Chan 1990), these neurons can still encode changes over tens of milliseconds for an input frequency as low as 20 Hz. In addition, we have discovered that phasic neurons can extract input features in a way different from tonic models; therefore phasic and tonic neurons may play different roles in representing acoustic information.

GRANTS

This project was funded by National Institute of Deafness and Other Communications Disorders Grants NIDCD-008543 to J. Rinzel and DC-006864 to D. Sanes and V. Kotak and National Science Foundation Grant DMS-0817141 to B. Doiron.