High-Amplitude Positive Spikes Recorded Extracellularly in Cat Visual Cortex

Abstract

We simulated the shape and amplitude of extracellular action potentials (APs or “spikes”) using biophysical models based on detailed reconstructions of single neurons from the cat's visual cortex. We compared these predictions with spikes recorded from the cat's primary visual cortex under a standard protocol. The experimental data were derived from a large number of neurons throughout all layers. The majority of spikes were biphasic, with a dominant negative peak (mean amplitude, −0.11 mV), whereas a minority of APs had a dominant positive peak of +0.54-mV mean amplitude, with a maximum of +1.5 mV. The largest positive amplitude spikes were recorded in layer 5. The simulations demonstrated that a pyramidal neuron under known biophysical conditions may generate a negative peak with amplitude up to −1.5 mV, but that the amplitude of the positive peak may be at most 0.5 mV. We confirmed that spikes with large positive peaks were not produced by juxtacellular patch recordings. We conclude that there is a significant gap in our present understanding of either the spike-generation process in pyramidal neurons, the biophysics of extracellular recording, or both.

INTRODUCTION

Adrian and Zotterman (1926) were the first to discover that the rate at which a sensory neuron produces action potentials (APs or “spikes”) is correlated with the magnitude of the applied stimulus. Their discovery of rate coding has been the basis of nearly a century of extraordinary progress in neurophysiology. In conventional extracellular recording from single neurons, the only relevant measure is the time at which the spike event occurs. The actual shape or polarity of the spike is irrelevant, except when one must sort multiple units recorded simultaneously with a single electrode or to identify putative “fast” spiking neurons, which are thought to be inhibitory (e.g., Barthó et al. 2004). However, it has long been apparent from traces of single-unit recordings from cat sensory cortex by pioneers like Mountcastle (1957) or Hubel (1957) that the shape and size of the extracellular AP vary greatly. Here we were interested to see whether these variations in spike shapes and amplitudes recorded by extracellular electrodes could be predicted from a biophysical model that re-creates the details of extracellular APs recorded in the CA1 region of the hippocampus in vivo (Gold et al. 2006, 2007). The model allows the average extracellular spike waveform to be used for the interpretation of intracellular features of the recorded neuron, such as conductance density of active ionic currents and the sequence of AP initiation throughout the neuron. In fact, we found that an averaged extracellular waveform recorded in vivo, for this purpose, is as good as or better than intracellular recordings made in vitro (Gold et al. 2007).

Using a recording protocol similar to that described in Hubel and Wiesel (1962), we methodically sampled the average spike waveforms of neurons in V1 of the anesthetized cat. We applied the same biophysical model to detailed reconstructions of the morphology of cat V1 neurons and so were able to make predictions as to the precise waveform and amplitude of spikes that should be produced by such neurons. Previous quantitative studies of the extracellular spike waveform of cortical pyramids (Holt and Koch 1999; Pettersen and Einevoll 2008; Pettersen et al. 2008) were based on a single pyramidal neuron from cat V1 (Douglas et al. 1991), whereas the present experiments used close to 50 different morphologies (Gold 2007). The goal of this greater effort was to estimate the sampling bias of the extracellular electrode, using the model predictions and the known density of the different types of neurons in the cortical layers (Gold 2007). We achieved this for the majority of units. However, we encountered units that had a large (>1 mV) positive amplitude spike that had not been predicted by the model. In CA1, spikes usually have negative polarity (“negative spikes”), meaning that the peak absolute voltage amplitude is in the negative phase, whereas spikes whose peak is positive (“positive spikes”) typically have only a fraction of the amplitude of negative spikes. Positive spikes could be simulated only if the AP was initiated in the distal dendrites of the pyramidal cell. However, the high amplitude of the positive spikes could not be replicated even over the widest range of plausible biophysical parameters.

METHODS

Experimental procedures

ANIMAL PREPARATIONS.

Three adult cats were used for this study. The animals were prepared for in vivo experiments carried out under authorization of the Cantonal Veterinary Authority of Zürich to KAC Martin. For a detailed description of the surgical procedure and animal maintenance see Girardin et al. (2002). Briefly, anesthesia was induced with a mixture of xylazine (0.5 mg/kg, Rompun; Bayer, Leverkusen, Germany) and ketamine (10 mg/kg, Narketan; Chassot, Bern, Switzerland) and maintained with Saffan (through a venous cannula, ∼0.1–0.2 ml·kg⁻¹·h⁻¹; Schering-Plough Animal Health, Welwyn Garden City, UK). Animals were paralyzed [mixture of gallamine triethiodide (5 mg·kg⁻¹·h⁻¹) and d-tubocurarine chloride (0.5 mg·kg⁻¹·h⁻¹)] and ventilated with a 30/70% mixture of O₂/N₂O through a tracheal cannula. Additional halothane (0.5%) was used for potentially painful procedures (e.g., durotomy) and during initial surgery (1–2%). Electroencephalograms, electrocardiograms, blood pressure, rectal temperature, and expired CO₂ were monitored continuously and kept within physiological ranges. Neutral power lenses and atropine were applied on the eyes, which were refracted and focused at a tangent screen placed 114 cm from the eyes.

RECORDING.

Recordings were made from the primary visual cortex (V1) (−3 to −6 mm posterior to the interaural plane) with high-impedance (tip size 2 microns, 5–10 MΩ, measured in normal saline) micropipettes filled with pontamine sky blue (2% in 0.5 M sodium acetate and 0.5 M sodium chloride). At least two pontamine injections were made in each penetration to reconstruct the electrode track. In each penetration the multiunit activity was recorded for 3 min at each location. The electrode was then moved down by 30 μm and sampling was repeated for the new location. When recording a high-amplitude unit, recordings were often made at shorter sampling intervals (10–20 μm) and for shorter durations (1–2 min). This was repeated until the white matter was reached. The extracellular potential was amplified with an Axoprobe amplifier (Axon Instruments) and sampled at 20 kHz and band-pass filtered (5–8,000 Hz, Kemo filter). The visual cortex was stimulated by hand with a high-contrast bar stimulus moved in all orientations and directions during the recording. The receptive field of selected single cells was plotted. Electrode resistances were measured using the standard bridge-balancing procedure.

HISTOLOGY.

At the end of the experiment the animal was very deeply anesthetized and then perfused intracardially with normal saline followed by 4% paraformaldehyde, 0.3% glutaraldehyde, and 15% picric acid in 0.2 M phosphate buffer. The fixed brains were serially sectioned (80 μm) in the transverse plane and Nissl-stained to identify the penetrations.

Computational procedures

The extracellular potential (spike) of a model neuron was calculated in two stages. First, we computed the transmembrane potential and currents for a pyramidal neuron model using the NEURON simulation environment (Hines and Carnevale 1997) as detailed in the following text. Second, we used those currents to compute the extracellular potentials.

It was previously demonstrated that the neuropil is well modeled by an isotropic volume conductor and that the electric potential in the extracellular space (V_e) is governed by Laplace's equation in the physiologically relevant range of 0–5 kHz (Logothetis et al. 2007; Plonsey 1969). For a single point source in an unbounded isotropic volume conductor, the solution is dual to the classical physics problem of point charges in free space (Coulomb's law)

$$V_e\left(r\right)=\frac{I}{4\mathrm{\pi }r\mathrm{\sigma }}$$ (1)

where I is the amplitude of a point source of current (A), r is the distance from the source to the measurement (m), and σ is the conductivity (S/m) of extracellular space. Multiple sources combine linearly (superposition).

For a continuous neuronal cable, the membrane current is proportional to the second spatial derivative of the membrane potential V_m (Gold et al. 2007; Malmivuo and Plonsey 1995). A simplified calculation of V_e, for a nonbranched cylinder, treating each compartment as a point source, is

$$V_e\left(r\right)=\frac{1}{4\mathrm{\pi }\mathrm{\sigma }}{\displaystyle \sum _{\mathrm{i}}\frac{I_m\left(i\right)}{d\left(i,r\right)}}\propto \frac{1}{4\mathrm{\pi }\mathrm{\sigma }}{\displaystyle \sum _i\frac{V_m^{″}\left(x\right)}{d\left(i,r\right)}}$$ (2)

where the subscript i indexes the compartments of the neuron, I_m is the current in each compartment, V_m(x) is the second spatial derivative of the membrane potential (x measures the path length inside the neurite), and d(i, r) is the distance from each compartment center to the measurement location. In practice such an approximation would give inaccurate results if the compartment size were not extremely fine.

For model neurons based on detailed anatomical reconstructions, spikes are calculated using the line source approximation (LSA; Holt and Koch 1999). The LSA uses a simplified continuous distribution of membrane currents by locating the net current for each neurite on a line down the center of the neurite. The current for each compartment is distributed over the three-dimensional line segments (from the morphological reconstruction) that it spans. By assuming a line distribution of current, the resulting potential has a straightforward analytic solution and is highly accurate even at short distances. For a single linear current source having length Δs, the resulting potential is given by

$$V_e=\frac{1}{4\mathrm{\pi }\mathrm{\sigma }}{\displaystyle \underset{-\mathrm{\Delta }s}{\overset{0}{\int }}\frac{Ids}{\mathrm{\Delta }s\sqrt{r^2+{\left(h-s\right)}^2}}=}\frac{I}{4\mathrm{\pi }\mathrm{\sigma }\mathrm{\Delta }s}\log \left|\frac{\sqrt{h^2+r^2}-h}{\sqrt{l^2+r^2}-l}\right|$$ (3)

where r is the radial distance from the line, h is the longitudinal distance from the end of the line, and l = Δs + h is the distance from the start of the line.

We assumed an extracellular conductivity of 0.29 S/m, corresponding to an extracellular resistivity of about 350 Ω·cm. This value is above the cortical average (∼250 Ω·cm), but is still within the normal range of variation (Hoetzell and Dykes 1979). We chose such a value because our goal was to model the high-amplitude spikes in our recordings. For our analytic calculation of maximum spike amplitude, we considered the possibility that microregions of high resistivity might exist—up to 500 Ω·cm, double the typical value.

Simulation procedures

NEURONAL RECONSTRUCTIONS.

The pyramidal neurons used in the simulations are L5 pyramidal neurons from cat visual cortex (Anderson et al. 1999; Binzegger et al. 2004; JC Anderson and KAC Martin, unpublished data). The morphological data consisted of coordinates (x, y, z) defining the paths of the dendrites and (in most cases) the axon, at intervals of a few micrometers. The soma was outlined in the morphological data with a sequence of coordinates. The soma diameter was measured at several locations, using pairs of points on opposite sides of the outline. From these measurements, a series of equivalent cylinders were constructed. The soma was modeled using a line source approximation. The difference between this approach and a point source approximation for a sphere having the same total surface area is insignificant, although our computational engine was optimized for line source neuron reconstructions. This resulted in a soma with an area-equivalent diameter of 21.7 ± 5.8 μm (i.e., diameter of a sphere with the same surface area as that of the soma).

The diameters of the dendrites at each point were provided in two cells. Diameters for the dendrites in the remaining cells were defined based on the average diameters for the cells whose dendritic diameters were measured. In the apical trunk average diameters were measured based on the distance from the soma using 10-μm sampling steps near the soma, increasing to 100-μm sampling steps in the distal apical trunk. In basal, apical oblique. and apical tuft dendrites averages were created for each branching order. A varicosity correction factor was formed by taking each neuron that had detailed diameters and comparing its total dendritic surface area using the exact diameters versus the total surface area using its own average. This resulted in a small correction of only 3%. These methods resulted in apical trunks that were initially 6 μm thick, tapering to around 2 μm thick at a distance of 500 μm. Basal dendrites were 1.6 μm thick initially and 0.8 μm thick in distal tufts. Complete details of the cell measurements are described in Gold (2007).

Numerous studies have indicated that layer 5 (L5) pyramidal cells occur in two varieties: “thick,” having thick apical trunks and extensive tuft in superficial layers, and “thin,” having narrower apical trunks that reach superficial layers but do not have extensive branching tufts (Larkman 1991; Peters and Yilmaz 1993). Because our L5 pyramidal cells with dendrite diameter measurements appear to be of the thick variety (having extensive apical tuft) we scaled the diameter measurements by two thirds for L5 pyramidal neurons that did not have extensive apical tuft (Larkman 1991). Because Meynert cells have thicker than average dendritic diameters (Feldman 1984), the one Meynert cell in our sample was not included in calculating the averages. It was simulated with its own exact diameters.

Most of the neurons included very extensive axonal reconstructions. The set of axon coordinates closest to the soma were used to define an axon hillock and axon initial segment similar to those described in Mainen et al. (1995): the axon hillock was 10 μm long and the initial segment was 20 μm long. The data also included the location of the axonal boutons. These were used to define which sections of the axon were myelinated and which were not, according to the following rules.

1. At every branch point, the axon was nonmyelinated for 1 μm before and after the branch point.

2. The axon was always myelinated for the first 50 μm after the initial segment, except for branch points.

3. Each bouton in the data (outside of the initial myelination) created 1 μm of nonmyelinated axon around it; nonmyelinated sections within 2 μm of each other were merged (i.e., the axon would not “remyelinate” unless there were >2 μm between subsequent boutons).

These rules resulted in the majority of the axons being myelinated, around 75%. Because no diameter data were available for any axons, diameters were assigned as follows: a myelinated axon was defined as having double the (internal) diameter of an equivalent section of nonmyelinated axon (Mainen et al. 1995) and the diameters used were 1 μm for nonmyelinated fibers and 2 μm for myelinated fibers (Deschênes and Landry 1980).

NEGATIVE SPIKING NEURON.

Simulations were performed in the NEURON simulation environment (Hines and Carnevale 1997) using channel models and kinetics parameters described previously (Gold et al. 2006, 2007), except for the Na⁺ channel conductance, which was modeled using a modified version of the cooperative Na⁺ channel proposed recently (Naundorf et al. 2006). Although the cooperative Na⁺ model is still a matter of debate, we observed that our use of it in our simulations had very little influence, compared with the more standard Na⁺ channel model we considered in our previous work (Gold et al. 2006, 2007). Complete details of the channel models for all types of channels are given in Gold (2007).

For the extensive reconstructed axons, we found it was required to use conductance densities in the nodes of Ranvier that were significantly lower than those in the soma. This is because the narrow axons that were mostly myelinated have a much higher input resistance than that of the soma or dendrites. Consequently, if the axonal Na⁺ densities were as large as those in the soma they would tend to be unstable because high-input resistance amplifies the effect of the Na⁺ conductance active at rest. Further, due to the high-input resistance only a small fraction of the somatic Na⁺ conductance was required for the simulated axons to have complete propagation of full-amplitude APs. Although the precise axonal Na⁺ conductance density varied from simulation to simulation the typical values were only around 20% of the density for the soma. The model for nodes of Ranvier in the myelinated axon is in contrast to the axon initial segment, where the density of Na⁺ channels is higher than that in the soma (approximately double).

SIMPLIFIED CYLINDER SIMULATIONS.

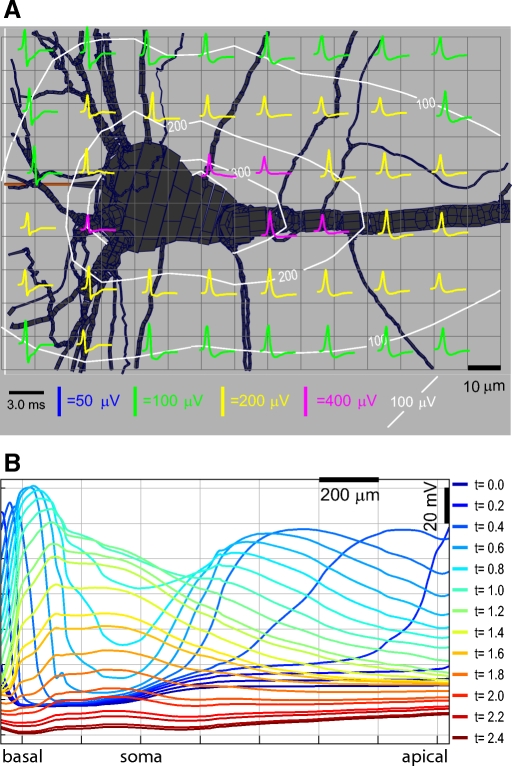
The cylinder simulations use the Hodgkin–Huxley style Na⁺ conductance kinetics described in Gold et al. (2006). The negative and positive spike-generating cylinders are modified so that they have the same total Na⁺ conductance on their surface, concentrated in the center to create the negative spike and concentrated in the ends to make the positive spike. For the negative spike cylinder, the peak Na⁺ conductance density is 0.05 and it declines (linearly) to 2% of that amount in the distal dendrites. For the positive spike cylinder the density is reversed. Other details of the simplified cylinder are the same as the simulation of cylinder “B” described in Gold et al. (2007) (see their Fig. 8).

Fig. 8.

Positive and negative spikes in a simplified model: extracellular. The axis of the cylinder is plotted vertically, with the center of the cylinder at the bottom of the plot and the distal end of the cylinder at the top. Contours show the peak amplitude, positive or negative, whichever is greater. A: extracellular potential amplitude and waveforms in a single quadrant around the cylinder with central Na⁺ and AP initiation (1st column of Fig. 7). Negative spikes of relatively high amplitude occur at the center of the cylinder. Positive spikes at lower amplitudes occur at the distal end of the cylinder. Midway down the cylinder the spikes include fast positive and negative phases of approximately equal amplitude. The highest amplitude of negative spikes occurs in a small region very close to the center of the cylinder. B: extracellular potential amplitude and waveform around the cylinder with distal Na⁺ and AP initiation. Relatively high amplitude positive spikes occur around the center of the cylinder, but the amplitude is less than that of the negative spikes due to central initiation. The spikes at the exact center are not much higher in amplitude than those 10–20 μm away. Negative spikes occur at the distal ends.

POSITIVE SPIKING NEURONS.

For the simulations of positive spikes, the parameters were altered so that the maximal Na⁺ conductance density occurred in the distal dendrites and the soma and proximal dendrites were nearly passive. We also made some modifications to the density of the K⁺ conductance to give a better match to the waveform of the positive spike recordings. The K-type K⁺ conductance was also made densest in the distal dendrites. The M-type K⁺ current was made densest in the medial apical trunk and declined to lower densities in both the distal apical dendrites and the basal dendrites, typically 10–30% of the maximum value. Compared with the negative spike simulations, the positive spike simulations were more reliant on the M- and K-type K⁺ conductances for repolarization and the total Na⁺ conductance over an entire simulated neuron was higher. For details see Gold (2007).

RESULTS

High-amplitude positive spike recordings

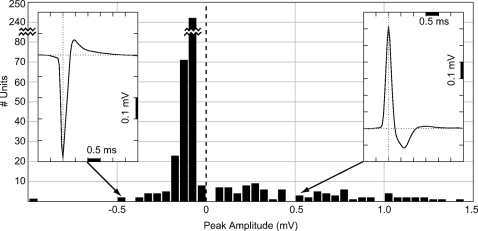
Recordings were made at 391 locations in eight separate penetrations using a glass recording pipette as detailed in methods. We identified 453 units using standard clustering techniques (Quian-Quiroga et al. 2004). The majority (74%) of these were low-amplitude spikes (50–200 μV), with a leading and dominant negative peak, as summarized in Fig. 1. This result is similar to recordings in rat CA1 (Gold et al. 2006; Henze et al. 2000) and recordings made in cat V1 using high-density silicon probes (Blance et al. 2005). However, the recordings also yielded a small number of units with amplitudes up to 1.5 mV (6.2% with peak between 0.5 and 1 mV; 3.3% with peak >1 mV). To our surprise we found that, of the high-amplitude spikes, nearly all had positive polarity (Fig. 1). The majority of these were found in deep layers, particularly L5: for positive spikes with amplitude >0.5 mV, around 60% were found in L5 and 20% in layer 6 (L6).

Fig. 1.

Distribution of recorded spike peak amplitudes in cat V1. Each bin shows the number of spikes recorded with peak amplitudes in 50-μV steps for 453 single units. The majority (74%) had leading negative peaks with amplitudes of 50–200 μV (note the discontinuous scaling of the y-axis for units with peaks between −50 and −100 μV); 9.5% of units had peaks >0.5 mV and of these virtually all had positive peaks. The amplitude (mean ± SE) of all negative spikes was −0.11 ± 0.01 mV, whereas the amplitude (mean ± SE) of all positive spikes was +0.54 ± 0.04 mV. Negative spikes accounted for 79% of the total units, whereas positive spikes of all amplitudes were 21%. Insets: examples of typical negative and positive spike waveforms. The negative spike has 2 phases: a dominant fast negative peak followed by a slowly decaying positive peak of smaller amplitude. The positive spike has 3 phases: a fast positive peak of high amplitude, followed by a negative phase of moderate amplitude and duration, and finally a much weaker, slow positive phase. In both types of spikes, the negative phase and the positive phase that follows it result from a dominance of Na⁺ current and K⁺ current, respectively, depolarizing and repolarizing the cell during the action potential (AP). The leading positive peak in the positive spike is caused by membrane capacitive current.

If spikes are recorded without inverting the polarity during amplification, the negative peak corresponds to Na⁺ current entering the site of initiation during the depolarizing phase of the AP (Gold et al. 2006, 2007; Rosenfalck 1969). Phases of positive polarity result from either a fast capacitive current preceding the Na⁺ current phase [i.e., I = C(dV/dt)], or a slower K⁺ current flowing out from the cell during repolarization (see Figs. 6 and 8, discussed in the following text). All high-amplitude positive spikes (HAPS) had a fast positive peak, followed by a smaller negative peak (Figs. 1, inset and 2), leading us to surmise that the positive peak is capacitive in nature. Many of the HAPS also had a slow positive phase after the negative phase, corresponding to K⁺ current (Fig. 1, inset). HAPS appear qualitatively similar to APs recorded intracellularly, but their fast time course indicates that they are most likely not intracellular recordings through the pipette: the mean 50% amplitude duration for positive spikes we recorded was 0.19 ± 0.09 (SD) ms, whereas it was 0.26 ± 0.06 (SD) ms for the negative spikes. A sample of neurons recorded intracellularly in cat cortex reported in the literature (Baranyi et al. 1993) had a mean 50% amplitude duration of 0.46 ms; the sample included 48 “fast-spiking” cells, presumably interneurons, which had a 50% duration of 0.25 ± 0.03 (SD) ms.

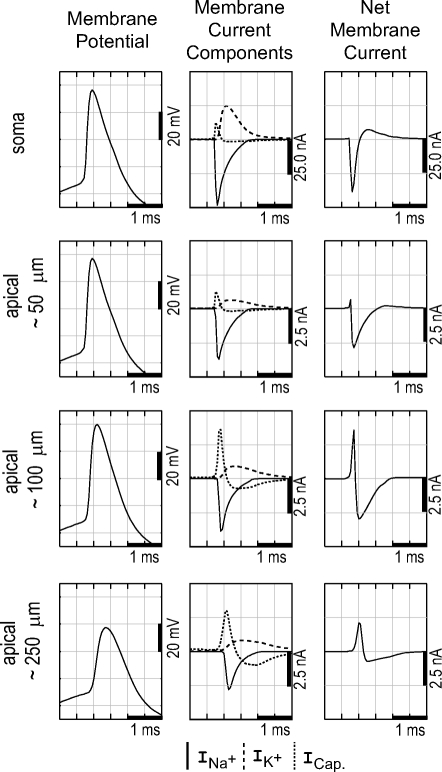
Fig. 6.

Internal details of the simulated AP in selected compartments of the model neuron of Fig. 4. First column: membrane potential. The AP initiates in the axon (not shown) a fraction of a millisecond before that in the soma, after which it spreads to the dendrites. Second column: components of the membrane current. Na⁺ current is concentrated in the axon initial segment, soma, and proximal dendrites. In distal dendrites the Na⁺ current is weaker and the capacitive current is the largest component of the membrane current. The positive current satisfies the requirement for current balance over the entire neuronal membrane. Third column: the net membrane current determines the extracellular spike. The soma has a large negative peak during depolarization, resulting from Na⁺ current, whereas the distal dendrites have a positive net current during depolarization, resulting from capacitive current.

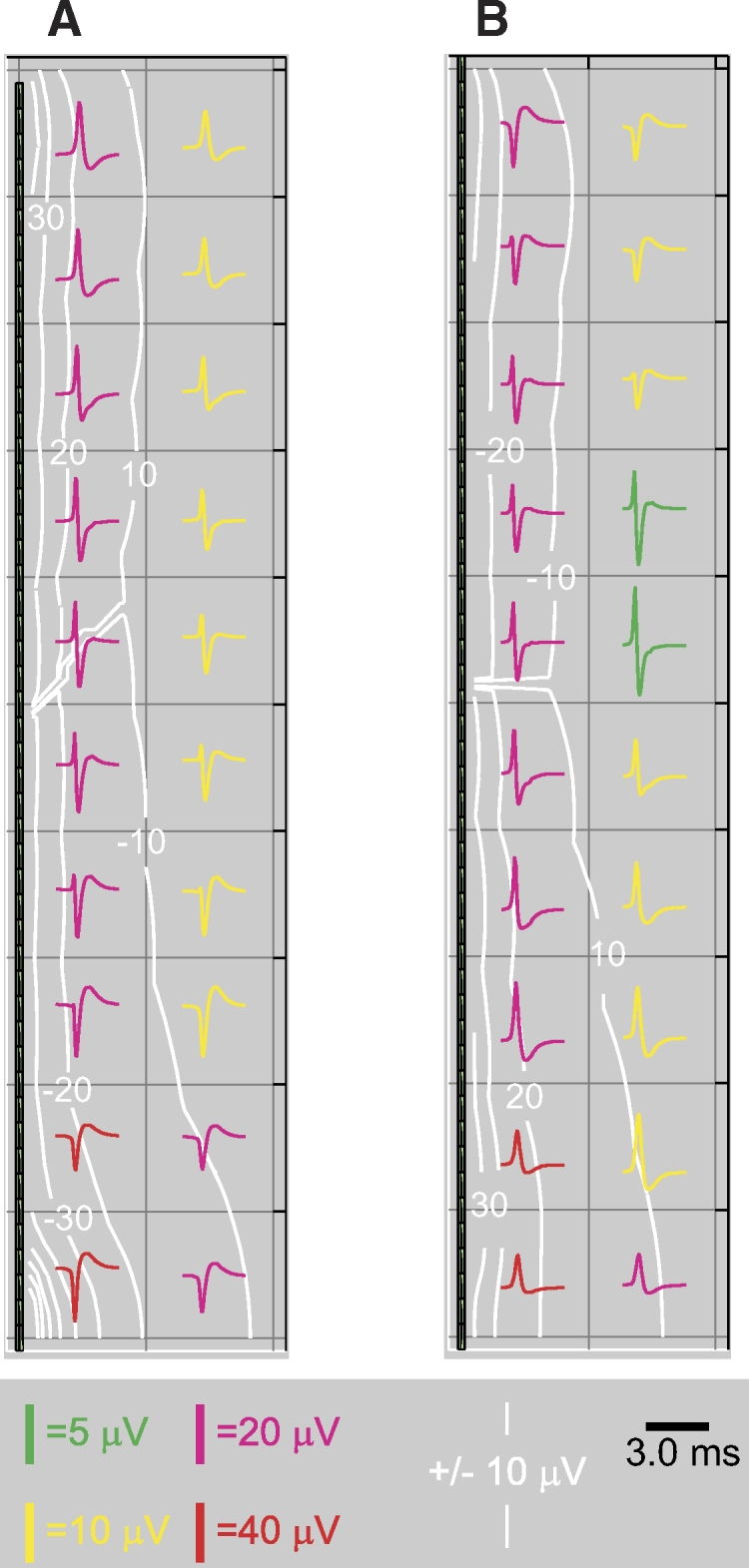
Fig. 2.

High-amplitude positive spike (HAPS). This HAPS (solid lines) was recorded as the pipette was moved progressively over a distance of 90 μm (depths below cortical surface are indicated). Identification as a single unit is based on a stable and well-defined response to a preferred stimulus orientation. During recording at the last location, the unit abruptly lost amplitude and then stopped spiking altogether. It appears qualitatively similar to an AP recorded intracellularly, but it has about 1/60 the amplitude and is sped up by a factor of 2 to 3.

HAPS tended to be very well driven by a particular orientation of the stimulus (a bar or grating) and often exhibited high-frequency bursts. We never observed a unit that changed from positive to negative polarity while a recording was made at one or more locations (around 3–15 min of recording per unit). HAPS were often recorded simultaneously with regular amplitude spikes, both positive and negative (Fig. 3). HAPS were typically recorded over tens of microns of electrode penetration, as in Fig. 2, and showed a progressive increase in amplitude followed by a progressive decrease. We recorded a total of nine HAPS units that we could track over three or more microelectrode positions; in these cases the identification as a single unit is based on a consistent well-defined response to a preferred orientation of the stimulus. The average distance over which a HAPS could be recorded was around 100 μm. The average amplitude of a HAPS when first detected was 0.3 mV and the average peak amplitude was 0.8 mV. The low profile of the pipette electrode (2 μm at the tip, as described in methods) makes it seem unlikely that the presence of a high-amplitude spike at multiple subsequent locations resulted from movement of the recorded cell and surrounding tissue by the electrode. In a few cases, the HAPS went silent after recording the peak amplitude, as in Fig. 2, and we observed a discharge pattern compatible with injury: an increased firing rate not driven by the stimulus at the same time as the amplitude declined.

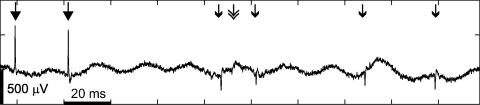
Fig. 3.

Raw data from a HAPS recording. This recording was made in Layer 5 and contains raw spikes for the average HAPS waveform illustrated in Fig. 2 (filled arrowhead). At the same time 2 negative spikes of a more typical amplitude were recorded, one with an average peak amplitude of 120 μV (single open arrowhead) and another with an average amplitude of 90 μV (double open arrowhead). Background noise of 50 Hz is visible in this unfiltered recording.

The HAPS have an amplitude greatly in excess of that predicted by standard biophysical models: as high as 1.5 mV. Our analysis, detailed in the following sections, suggests that even the largest V1 neurons cannot generate a positive spike with amplitude ≳0.5 mV. A second way in which our predictions fail to match the HAPS recording is that, according to biophysical models, the maximum positive spike potential should be restricted to a very small zone within a few micrometers of the cell. In contrast, the HAPS recording illustrated in Fig. 2 shows that a peak amplitude of >1 mV was recorded even when the pipette was moved through 40 μm. A large spatial extent for the high-amplitude peak was typical of HAPS recordings—in one case a HAPS >1 mV was recorded over >100 μm of electrode movement.

Dendritic positive spikes

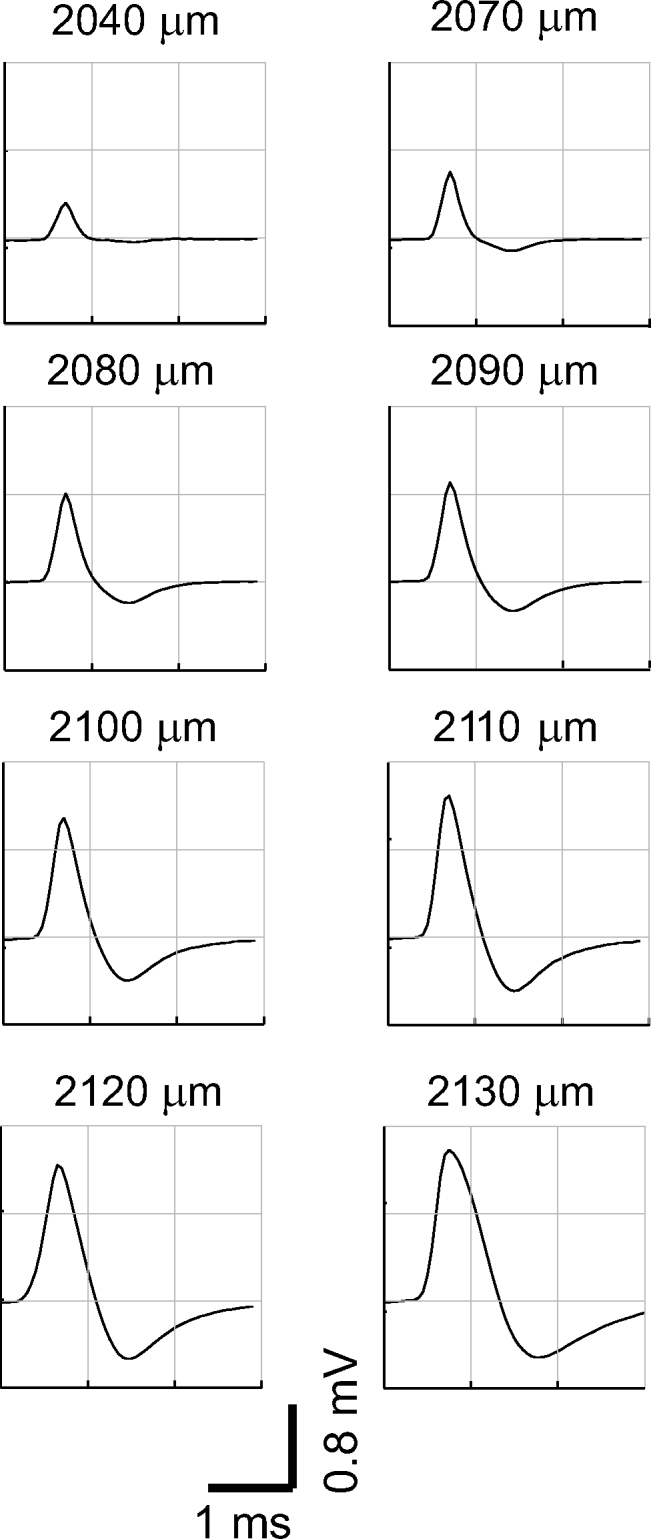
In our cortical recordings and in our previous experiments in CA1 (Gold et al. 2006; Henze et al. 2000), the majority of spikes have a negative polarity. A model re-creation of a typical negative polarity spike is shown for an L5 pyramidal neuron in Fig. 4 . The neuron was reconstructed from detailed morphological data and the model was tuned to reproduce a high-amplitude negative spike recorded in L5 (Fig. 5). The recording was made at five successive electrode placements spanning 90 μm and reaches a peak (absolute) amplitude of −1 mV. This was the highest amplitude negative spike that we recorded in our experiments and in the model this peak was best matched by assuming the electrode passed within a few microns of the soma (see Fig. 5). The different ionic current components for the model neuron of Fig. 5 are shown in Fig. 6. For cortex, our recordings and simulations suggest that negative spikes near the soma, during somatic initiation, may be in excess of 1.5 mV for large L5 pyramidal neurons that are situated in an extracellular milieu of above-average resistivity (for details see Gold 2007).

Fig. 4.

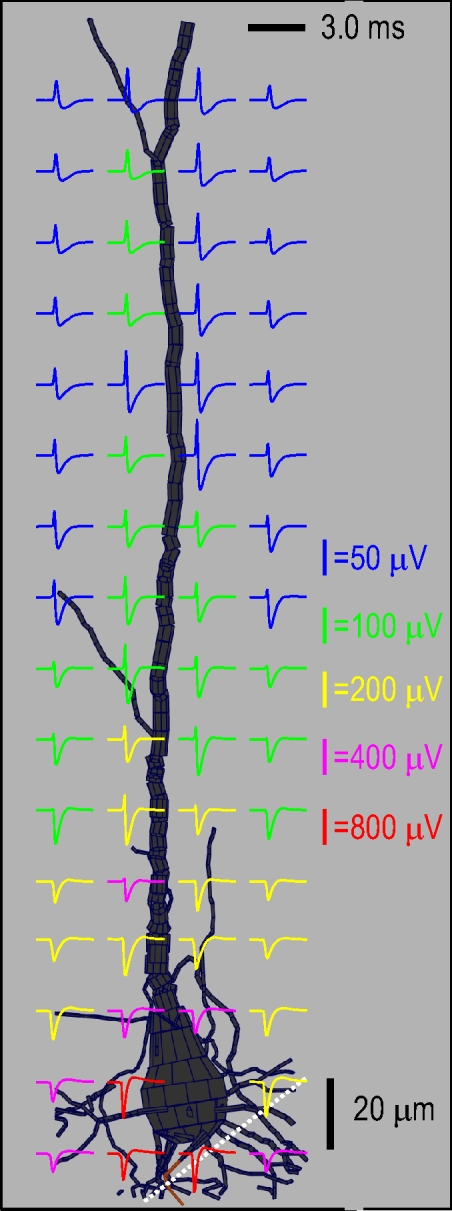
Extracellular APs (spikes) along the apical trunk of an L5 pyramidal neuron. The spikes are shown in a plane through the apical trunk. The perisomatic AP initiation results in negative polarity spikes around the soma, with a peak absolute potential of around 1 mV. The fast capacitive phase increases with distance along the apical trunk until there are positive polarity spikes along the apical trunk around 200–300 μm from the soma. The maximum amplitude for the positive spikes, at points nearly touching the apical trunk, is around 150 μV. The model was tuned to reproduce negative spikes from a single unit recorded at multiple locations (see Fig. 5); the simulated electrode track matching recordings is shown in white.

Fig. 5.

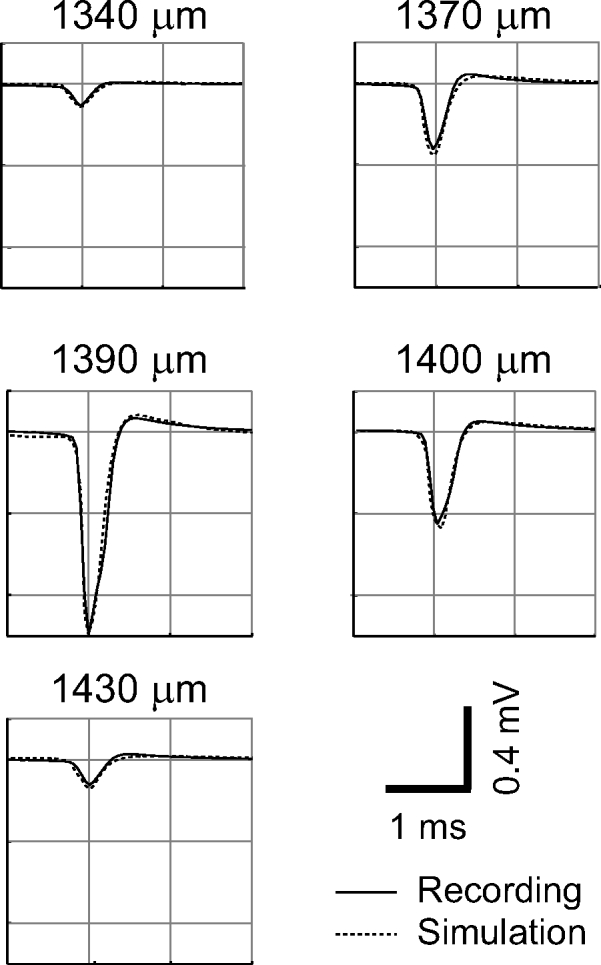
High-amplitude negative spike. The spike was recorded during a movement of the pipette of >90 μm (depths below cortical surface are indicated). The identification as a single unit is based on a well-defined response to a single preferred orientation at the 3 middle recording sites; for the first and last recording sites the 0.1-mV peak amplitude spike appeared as driven hash during recording and the unit was subsequently identified after filtering and clustering the raw data. The peak amplitude of the unit is 1 mV, at a depth of 1,390 μm, whereas in the recordings 20 μm before and 10 μm afterward the amplitude is only around 0.35 and 0.45 mV, respectively. The simulation is based on a reconstructed L5 pyramidal neuron, as illustrated in Fig. 4. The simulated recording sites chosen for comparison are based on a plausible trajectory, at a shallow penetration angle to the surface of the cortical layers (for details see Gold 2007). In the simulation, the high-amplitude negative spike at a depth of 1,390 μm is reproduced at a point just 2 μm from the soma, near the axon hillock and initial segment.

Our previously published model for extracellular recordings in CA1 suggested that positive spikes should exist in the neighborhood of distal apical dendrites of pyramidal neurons (Gold et al. 2006, 2007), but that positive spikes would be of smaller amplitude than negative spikes. This is because when an AP is initiated in the soma or the axon initial segment, the peak negative voltage is centered around the soma because inward current flow produces a negative extracellular potential. Conservation of current requires that the net membrane current over the entire neuron is zero at any given point in time, so there must be a balancing positive, capacitive current in the dendrites, resulting in a positive spike. However, Na⁺ is concentrated in the perisomatic region (including the axon initial segment) and the resulting negative voltage peak is greater in amplitude than the positive spike, which is spread over the distal tree of dendrites.

In a sample of simultaneously recorded intra- and extracellular spikes from CA1 neurons that we studied previously (Gold et al. 2006; Henze et al. 2000), we found that only 3 of 49 spikes recorded had positive polarity, with amplitude around 10, 30, and 90 μV, respectively. The 46 negative spiking units in the same sample had amplitudes ranging up to around 400 μV. However, the expected amplitude of the positive spike of a large cortical pyramidal neuron is somewhat higher than that of a CA1 pyramidal neuron: the model neuron of Fig. 5 has a positive spike present in the vicinity of the dendrites with amplitude of almost 200 μV, which is well above the effective recording threshold of 60–80 μV. Therefore we should expect to record positive spikes in cortex, although the maximum amplitude for positive spikes from a somatically initiated AP should be significantly less than the maximum amplitude of the negative spikes—e.g., 0.1–0.2 mV compared with 1–1.5 mV.

Positive spikes in a simplified model

To determine whether positive spikes could occur at amplitudes equal to those of negative spikes, we analyzed positive and negative spike generation in a simplified model: a single, long (1-mm) neural fiber (Figs. 7 and 8). The central compartments are defined as “somatic” in that they have half the membrane capacitance of the “dendrites” (>20 μm from the center in either direction), mimicking the absence of spines in the perisomatic region of a real pyramidal neuron. In the first of two simulations, Na⁺ channels are concentrated at the soma (center) of the cylinder and the AP initiates there before spreading to the distal ends. In a second simulation, the same total amount of Na⁺ channels are concentrated in the distal dendrites (ends) of the cylinder, resulting in an AP that initiates in both ends before invading the center.

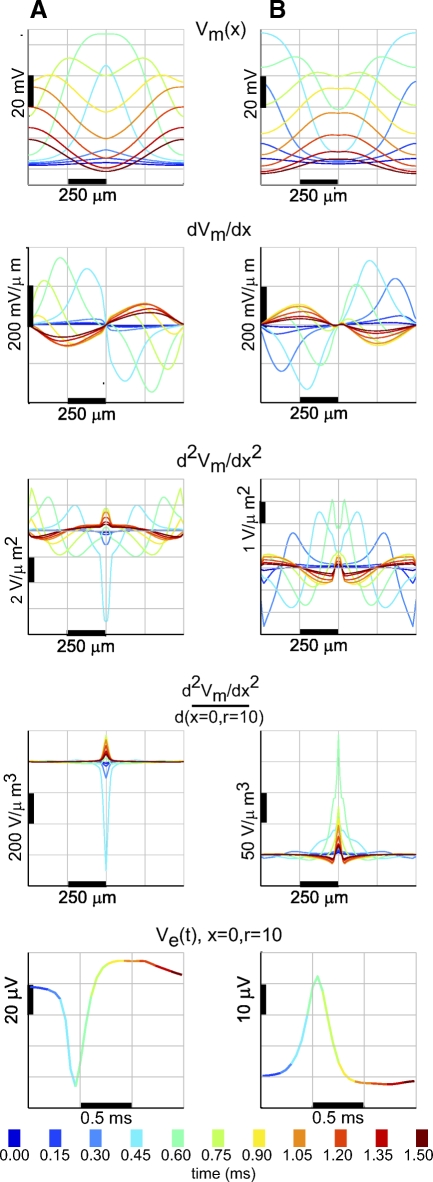
Fig. 7.

Positive and negative spikes in a simplified model: intracellular data demonstrate the relationship between the 2nd spatial derivative of membrane potential and the extracellular potential. The model “neuron” is a single cylinder 1,010 μm long and 3 μm in diameter, divided into 101 compartments. A: Na⁺ channel conductance is concentrated in the middle of the cylinder and the AP initiates in the center and spreads to the ends. B: Na⁺ channel conductance is concentrated in the ends of the cylinder and the AP initiates in the end and then spreads to the center. First row: membrane potential (V_m) as a function of position over 1.5 ms, according to the color-coded scale; 2nd row: 1st derivative of membrane potential with respect to position; 3rd row: 2nd derivative of membrane potential with respect to position. Maxima in potential result in negative 2nd derivatives, whereas minima result in positive 2nd derivatives; 4th row: 2nd derivatives scaled by the distance to a point that is beside the center of the cylinder at a radius of 10 μm. The extracellular potential at any extracellular point is proportional to the sum of the 2nd derivatives in each compartment, scaled by distance to that compartment. Bottom row: extracellular potential calculated at a point by the center of the cylinder at a radius of 10 μm. The extracellular potential at each time (color-coded) is equivalent to the integral of the corresponding scaled 2nd derivatives in the 4th row. The centralized Na⁺ channel conductance and AP initiation result in a negative extracellular spike near the center of the cylinder, whereas the distal Na⁺ channel conductance concentration results in a positive spike near the center of the cylinder.

The extracellular potential V_e around a neuron is proportional to the membrane current of the neuron, which is proportional to the second spatial derivative of the membrane potential V_m(x) (Eq. 2). This framework provides insight into the nature of positive and negative spikes. Figure 7A shows that when the AP initiates in the center of the neuron, the negative second derivatives associated with the maximum in V_m lead to a negative spike. In terms of membrane current, the negative spike corresponds to Na⁺ entering the cell at the site of initiation. Positive second derivatives dominate at the distal ends, creating positive spikes in the extracellular potential, although at lower amplitude. This corresponds to outward flowing capacitive current as the membrane is depolarized by axial current flowing from the soma. This is similar to when positive spikes of low amplitude occur outside distal dendrites, as described earlier. The positive spikes are lower in amplitude than the negative spikes for two reasons: 1) because the absolute amplitude of the second derivative at the distal ends is less than that in the center and 2) because the zones of positive second derivatives are separated at either end of the cylinder and do not combine with each other through superposition.

The amplitude of the positive spike is maximized if the AP initiates from both ends of the cable (Fig. 7B). This condition creates a single global minimum in V_m with the highest possible amplitude, rather than two separated local minima, but the positive spikes are still of lower absolute amplitude than the negative spikes in the first simulation. One reason for this is that the lower capacitance (lack of spines) at the center (soma) of the cylinder favors negative spike generation: low capacitance allows the soma membrane to be rapidly driven to high potential by a concentrated Na⁺ channel conductance, whereas the high capacitance of the spiny dendrites slows the rate at which they can follow. In the situation of distal dendritic initiation, the lower effective capacitance in the soma allows it to rapidly follow the voltage in the dendrites, reducing the gradient that leads to positive spikes.

A second reason that negative spikes can be of greater absolute amplitude than positive spikes is that negative spikes result from Na⁺ current that is an active current flowing through discrete channels. As such they can be concentrated in a small region of the neuron. Positive spikes result from capacitive current that, although fast, is a passive current distributed over the membrane. In the central initiation (Fig. 8A), high-amplitude negative spikes are concentrated close to the center, whereas in the positive spike scenario (Fig. 8B) relatively high amplitude positive spikes exist over a longer section of the cylinder, but there is no very high amplitude at the center. A final reason that positive spikes may be smaller than negative spikes is that the maximum positive spike amplitude depends on symmetric initiation in different parts of the neuron and, if the synaptic input driving the AP is unbalanced, the positive spike amplitude falls significantly. This is probably closer to the situation in a real neuron.

Somatic positive spikes from an L5 pyramidal neuron

Based on these principles, we created a model for a high-amplitude positive spike (HAPS) using a reconstruction of a large L5 pyramidal cell from cat visual cortex (Binzegger et al. 2004), as illustrated in Fig. 9. We assume that the neuron has high densities of active Na⁺ and K⁺ channels in the distal dendrites, whereas the soma and proximal dendrites have lower densities, as detailed in methods. Because the amplitude of any spike scales with the size of the soma and apical trunk¹(Gold et al. 2007), we chose a reconstructed Meynert cell—one of the largest cells in visual cortex (Feldman 1984)—for the simulation. The simulation predicts that for an L5 Meynert neuron undergoing distal AP initiation, positive spikes will be generated near the soma and apical trunk, with amplitudes ≤400 μV. Because there may be larger Meynert neurons in cat V1 than our particular cell and because there are also microregions of somewhat higher resistivity than we have assumed (Hoetzell and Dykes 1979), we conclude that in extreme cases single L5 pyramidal neurons undergoing distal dendritic initiation may generate positive spikes up to around 500 μV.

Fig. 9.

Positive spikes in an L5 pyramidal cell model. A: illustration of spike waveforms and amplitude around the soma during the simulated AP. Positive spikes dominate, with the peak amplitude reaching around 400 μV at positions nearly touching the soma. B: illustration of the membrane potential as a function of position at selected times given by the color-coded scale. Positions shown include a single basal dendrite, the soma, and the apical trunk out to the most distal tuft. The AP initiates first in the distal apical dendrite, then the basal dendrite, before invading the soma and proximal apical trunk.

Juxtacellular positive spikes

Reports of juxtacellular recording (Joshi and Hawken 2006; Pinault 1996) typically show high-amplitude (1–5 mV) positive spikes. We therefore tested whether the HAPS we recorded could be due to accidental juxtacellular recordings. During juxtacellular recordings, the electrode resistance increases by around fourfold as the electrode comes into contact with a cell and increases three- to tenfold when a seal is formed through the application of suction (Josh and Hawken 2006). (We are not aware of any reports of direct measurements of the juxtacellular seal resistance in the literature.) Given that pipette electrodes used in juxtacellular recording as well as our own electrodes have an access resistance of around 10 MΩ, we expect a resistance of around 40 MΩ if the electrode were in contact with a cell and 120–400 MΩ after a “loose patch” has formed.

Biophysical analysis of juxtacellular recording reach a similar conclusion. In juxtacellular recording the electrode measures the voltage produced by the membrane current crossing the seal resistance (for details see Gold 2007, particularly Fig. 5.4). The electrode pore diameter in our recording was around 2 μm (also see Joshi and Hawken 2006; Pinault 1996); the capacitance of a 2-μm-diameter section of membrane having a specific capacitance per unit area of 1 μ F/cm² will be 1e-6 μF/cm² × (1e-8π)cm² ≈ 31 fF. The maximum first derivative of the membrane potential during an AP is around 300 V/s (Naundorf et al. 2006). Therefore the peak membrane capacitive current within the electrode pore is 9 pA [I = C(dV/dt)]. This necessitates a seal resistance R_seal = 1e-3/0.009e-9 = 110 MΩ to obtain a +1-mV peak potential (R = V/I).

To determine whether the HAPS we recorded were produced by juxtacellular recordings, we made additional recordings from neurons in cat V1 and measured the resistance through the electrode at locations with and without HAPS. At 28 locations where we recorded a positive spike with minimum amplitude of 0.8 mV, we found the resistance of the electrode was 19.3 ± 5.1 (SD) MΩ. In comparison, at 15 locations where no HAPS were present, the resistance was 13.4 ± 5.4 (SD) MΩ. Although the difference is significant (Student's t-test, P = 0.005), the measured resistances are significantly below the level we expect for an electrode in juxtacellular contact with a cell (40 MΩ), let alone the seal that would be required to produce a 1-mV positive spike during an AP (100 MΩ). Also, when we pulsed the pipette with a positive current to measure the resistance at a HAPS location there was no evidence that the electrode current drove the cell, further contradicting the hypothesis that the HAPS we recorded resulted from a juxtacellular seal. The difference in measured resistances may be related to other aspects of the measurements, such as the fact that the electrode resistance tended to increase as the electrode proceeded in a penetration, presumably due to clogging of the tip. Whereas most HAPS were recorded in L5, 40% of non-HAPS resistance measurements were made near the start of a penetration. If we remove those early measurements and consider only those non-HAPS resistances at depths >900 μm (the shallowest penetration depth at which a HAPS resistance was recorded) the mean and SD for the non-HAPS resistance become 14.9 ± 7.3 (SD) MΩ and the difference with the HAPS measurement (19.3 ± 5.1) is not statistically significant at a high level of confidence (Student's t-test, P = 0.1). Based on these direct measurements we conclude that the HAPS we recorded did not result from juxtacellular recordings.

Analysis of maximum single-neuron positive spike amplitude

To validate our compartmental model prediction of the maximum positive spike amplitude (around 500 μV), we estimate the peak voltage depolarization produced by a passive membrane of a spherical soma of diameter R discharging capacitively. Combining Eq. 1, for the extracellular voltage change produced by a current in a purely resistive cytoplasm, with the expression for the capacitive current yields for the maximum voltage outside the cell's surface

$$V_{\max }=\rho R{C}_m{\left[\mathrm{d}{V}_m/\mathrm{d}t\right]}_{\max }$$ (4)

Here ρ is the extracellular resistivity and C_m is the capacitance per unit area of the membrane. To upper-bound this expression, we assume a very large soma size of 25 μm [the largest L5 pyramidal cells have a soma equivalent to a sphere with radius 20 μm (Gabbott et al. 1987); the neuron of Fig. 9 has an equivalent radius of around 17 μm], a C_m of 1.5 μF/cm², a maximal change in membrane potential dV_m/dt_max of 400 mV/ms (for cortical pyramidal neurons the maximal dV_m/dt is normally in the range of 250 to 300 mV/ms; Naundorf et al. 2006), and a maximum cortical resistivity of 500 Ω·cm (the average is around 250 Ω·cm; Hoetzell and Dykes 1979). This yields a maximum positive, capacitive spike of around 0.7 mV, less than half the amplitude of the largest HAPS that we recorded. Furthermore, this amplitude decreases as 1/r with distance from the soma and would not be maintained for tens of micrometers, let alone ≥100 μm. This analytic model is highly idealized because it does not provide any mechanism to drive the soma through such a rapid depolarization. For this reason, as well as those already mentioned, it probably overestimates the maximum positive spike.

We conclude that a back-of-the-envelope calculation using a few well-known biophysical parameters yields a similar result as a more complicated compartmental model. Therefore the failure of our compartmental model simulations to reproduce HAPS is not due to our choices for the model parameters—it is a result of our partial understanding of the fundamental biophysics.

DISCUSSION

Based on our previous experience and understanding of negative extracellular spikes (Gold et al. 2006, 2007), when we first observed the high-amplitude positive spikes (HAPS), we thought there was an electrode malfunction. However, careful examination of the recording equipment as well as the observation of “regular” negative spikes in the same recordings as HAPS (Fig. 3) convinced us that they are a real neuronal phenomena. We now believe that they point to a significant gap in our understanding of either spike-generation processes or the biophysics of extracellular AP generation, or both. We reached this surprising conclusion only after we carefully considered a wide variety of possible alternative explanations.

HAPS are unlikely to be intracellular spikes recorded through the pipette because they are too brief in duration and because the membrane potential does not show the DC shift expected for intracellular recording. Juxtacellular recording with a patch electrode can explain high-amplitude spikes and often show positive spike waveforms (Joshi and Hawken 2006; Pinault 1996). Our direct measurement of the electrode resistance suggests that this is not the case, but it could be argued that uncertainty in measurement of the relevant parameters led to an error in the analysis (e.g., uncertainty in the pore diameter, membrane capacitance, or maximum depolarization rate). However, further doubt is cast on the juxtacellular explanation by the fact that our protocol involved none of the careful techniques associated with forming and maintaining juxtacellular patches—i.e., careful advancement under positive pressure and then to form a high-resistance seal by application of negative electrode pressure (Pinault 1996). To record the spike shown in Fig. 2 with juxtacellular recording, we would need to have accidentally formed such an effective seal that the glass pipette dragged the cell some 90 μm, while maintaining recording quality and responsiveness (and that we accomplished similar feats repeatedly during a single experiment). This seems unlikely, unless previous descriptions of juxtacellular recordings significantly exaggerate the difficulty of the protocol.

HAPS were also recorded in cat V1 using high-density silicon probe electrodes (Blanche et al. 2005), which are not known to exhibit any form of membrane coupling. In these recordings, positive spikes made up about 15% of the total at all amplitude levels and positive spikes were typically recorded on a few neighboring channels of the multisite electrode array (TJ Blanche, personal communication). The fact that HAPS are reported to be recorded with an entirely different type of electrode is very strong evidence against juxtacellular recording as an explanation for our results. Based on all of these arguments and our many years of experience, which include both extracellular and intracellular recording techniques, it is our opinion that the HAPS recorded in these experiments were not made through accidental patching.

It is not the existence of positive spikes that gives us pause, but their large amplitude. Biophysical analysis of AP generation demonstrates that single neurons can generate positive spikes in both small and relatively large varieties, depending on whether the AP initiates in the soma or in the dendrites. However, both the analytic calculation (Eq. 4) and the compartmental model agree that for plausible values of the biophysical parameters the highest-amplitude positive spikes are only around 0.5 mV, compared with around 1.5 mV for our measured positive spikes. This mismatch between theory and experiment suggests the possibility that some of the assumptions of the biophysical model are invalid.

One possibility is that the biophysical constants used in Eq. 4 actually take much greater values than we assumed—i.e., microregions of high resistivity, cells with exceptionally high capacitance membranes, or neurons with very fast membrane depolarization. If this were the case then our analysis would underestimate the maximum positive spike amplitude. However, the accepted values for these parameters are based on years of observations by many researchers (for review see, e.g., Koch 1999). Consequently, we are hesitant to question their validity until there is more direct evidence contradicting them, as well as a theoretical explanation for how and under what circumstances the previous measurements are invalid.

Furthermore, if one of the key physical constants had an unexpected value that could explain HAPS, then it should also create negative spikes of still greater amplitude. That is, our understanding of biophysics and spike generation is in very close agreement with recordings for the maximum amplitude of negative spikes in cat V1 and rat CA1 (Gold 2007; Gold et al. 2006). So if regions of very high resistivity in cat V1 led positive spikes of 1.5 mV in amplitude, rather than the 0.5 mV we expect, then it should also on occasion lead negative spikes to be 4.5 mV rather than 1.5 mV; however, we do not observe 4.5-mV negative spikes in cat V1 and the high-amplitude negative spikes that we do observe are very well explained by the known biophysical equations and parameters. Therefore it is problematic to assume that outliers in the biophysical constants explain HAPS, unless there is an explanation for why such outliers would particularly occur in conjunction with positive rather than negative spikes.

It has been debated over the years whether the cortical gray matter has low-pass filtering properties or whether it is primarily resistive at frequencies of relevance to the neurophysiologist (from 1 Hz to a few kilohertz; Bedard et al. 2004, 2006; Gabriel et al. 1996; Hoetzell and Dykes 1979; Petterssen and Einevoll 2008). The most recent and strongest evidence based on careful and direct measurements using four electrodes in primary visual cortex of the macaque monkey concludes that the extracellular space is ohmic and anisotropic to a very good approximation over this frequency range (Logothetis et al. 2007). Although neocortical layers are known to have somewhat different resistivity (e.g., Hoetzell and Dykes 1979), the size of the layers is so large relative to that of single neurons that it will have little measurable impact on the high-amplitude spikes close to large neurons that we are studying.² We therefore have no compelling reason to depart from the standard ohmic model of extracellular resistivity, even as our findings require us to consider every aspect of such models in light of their failure to reproduce high-amplitude spikes like the ones we recorded. Of course, if the medium had low-pass capacitive filtering properties, they would only reduce spike amplitude predictions, whereas we are trying to explain unexpectedly large spikes.

The amplitudes of the extracellular fields associated with the axon are so small relative to the cortical background noise and to the potentials emanating from the cell body and dendrites that they could neither be recorded independently nor did they make a significant contribution to recorded single-unit potentials. This is mainly due to the small diameter of the axon and the fact that much of it is myelinated and passive, leading to small extracellular electrical fields. Our finding that the model requires low Na⁺ channel densities in the nonmyelinated portion of the axon outside the initial segment contributes to the small size of axonal potential predicted by our model; but even if the nonmyelinated axon had the same high Na⁺ conductance densities as those at the soma, the extracellular potential would still border on the insignificant due to the small extent of the nodes of Ranvier. This is in contrast to the axon hillock that, although small, can make a significant contribution to the single-unit potential due to its high density of Na⁺ channels, as described in Gold et al. (2006). In summary, including a model of the axon made no significant difference with respect to our modeling of HAPS.

We are left to speculate about one or more unknown processes of spike generation that may explain the HAPS. For example, synchronized positive spikes in a neuronal cluster could superimpose to create HAPS like those that we recorded (Gold 2007). However, there is no known mechanism through which the spikes of multiple neurons could be synchronized so precisely nor other direct evidence of synchronized spiking. Alternatively, it has been proposed that there are gap junctions between L5 pyramidal cells (Traub et al. 2005); maybe they exist in the dendrites so that gap junction triggered spikes have an unusually fast depolarization at the soma, leading to larger positive spikes than our model (without gap junctions) predicted, although there is as yet no proof of the existence of gap junctions between L5 pyramidal cells, nor modeling that suggests that they would lead to the necessary rapid depolarization pattern if they existed. There are probably many possible explanations of this kind, but none that we know of for which there is actually evidence.

Whatever the ultimate explanation for the HAPS, it is remarkable that after decades of recording extracellular spikes from cortex the dichotomy between positive and negative spikes has not previously been analyzed. Following the pattern set in the work on cortex by pioneers like Mountcastle and Hubel and Wiesel, the object of most physiological studies is in peristimulus time histograms or raster plots and the amplitude and sign of spikes are not even reported. In recent years, a number of groups have carried out detailed extracellular modeling of APs (Bedard et al. 2004, 2006; Gold 2007; Gold et al. 2006, 2007; Holt and Koch 1999; McIntyre et al. 2004; Pettersen and Einveoll 2008; Pettersen et al. 2008; for reviews, see Herz et al. 2006; Nunez and Srinavasan 2006). These recent advances in the modeling techniques required, combined with the publication of the core portions of our own NEURON and Matlab code (http://senselab.med.yale.edu/senselab/modeldb/), make it feasible to simulate such intriguing biophysical events in different model systems. At the very least, future physiological studies should include the sign and amplitude of the spikes that they record so that comparison can be made across different systems and preparations. The brain is a complex system that we still understand poorly—we should not be complacent about unexplained phenomena.

GRANTS

This work was supported by National Institute of Mental Health (NIMH) Fellowship 1-F31-MH-070144-01A1 and Grant MH-12403, National Institute of Neurological Disorders and Stroke Grants NS-34994 and NS-43157, the NIMH-supported Conte Center for the Detection and Recognition of Objects, the National Science Foundation, the Swiss National Fund, and European Union Grant FP6-2005-015803.