A platform for assessing chemotactic migration within a spatiotemporally defined 3D microenvironment

Abstract

While the quantification of cell movement within defined biochemical gradients is now possible with microfluidic approaches, translating this capability to biologically relevant three-dimensional microenvironments remains a challenge. We introduce an accessible platform, requiring only standard tools (e.g. pipettes), that provides robust soluble factor control within a three-dimensional biological matrix. We demonstrate long-lasting linear and non-linear concentration profiles that were maintained for up to ten days using 34.5 μL solute volume. We also demonstrate the ability to superimpose local soluble factor pulses onto existing gradients via defined dosing windows. The combination of long-term and transient gradient characteristics within a three-dimensional environment opens the door for signaling studies that investigate the migratory behavior of cells within a biologically representative matrix. To this end, we apply temporally evolving and long-lasting gradients to study the chemotactic responses of human neutrophils and the invasion of metastatic rat mammary adenocarcinoma cells (MtLN3) within three-dimensional collagen matrices.

Introduction

The hallmark characteristic of the in vivo environment is highly-regulated spatial and temporal control over the local cellular microenvironment; phenotypic changes are thought to result from an integration of complex, temporally-evolving autocrine/paracrine signaling factors, biophysical interactions, and mechanical contact with the protein-laden extracellular matrix (ECM).¹ Experimental work has confirmed that cells cultured on two-dimensional (2D) substrates tend to form monolayers of cells while even simple three-dimensional (3D) materials support cellular structures that appear morphologically similar to in vivo tissue.^2,3 These observations have spawned great interest in translating 2D assays into 3D matrices. While 3D matrices provide appropriate mechanical contact and architecture,^4-6 such scaffolds alone are not sufficient to address a critical component of the in vivo environment: the role of the soluble factor microenvironment.

The fundamental importance of biomolecular gradients during embryogenesis, cellular differentiation, and the immune response has precipitated a multitude of in vitro assays over the past thirty years.⁷ Methods such as the Transwell Assay, Zigmond Chamber, and Micropipette Assay have been widely used to qualitatively study cellular responses to soluble factors within 2D cell culture constructs.^8-10 While these traditional methods have shed light onto cellular responses and molecular signaling mechanisms, they are not able to develop the robust, predictable gradients that are necessary to draw quantitative correlations between cellular responses and soluble factor cues. Ultimately, these quantitative correlations are necessary to enable increasingly sophisticated model systems that provide accurate representations of in vivo cellular behavior.

Through the development of reproducible, predictable, and defined soluble factor gradients, microfluidic technologies have helped to overcome the limitations of traditional approaches. Microfluidic methods have been applied to quantitatively study the migratory responses of cancer cells and leukocytes, and to investigate the differentiation of neuronal cells.^11-13 While the defined environments provided by microfluidic methods have proven to be beneficial within 2D culture constructs, the development of an analogous level of control within 3D environments remains an active area of research within the community.^14-16 As the quest toward physiologically relevant model systems progresses,^17,18 the ability to create defined chemical environments becomes a valuable experimental tool that can be used to study the migration and reorganization of cell populations within a 3D matrix.

We introduce a method that provides robust soluble factor control within a 3D gel matrix. We demonstrate linear and non-linear soluble factor gradients that last on the order of days, as well as temporally-evolving pulses within the same system. These characteristics are applied to study the migratory behavior of human neutrophils within a 3D collagen matrix in response to a temporally-evolving fMLP gradient; and to study the invasion and migration of metastatic rat mammary adenocarcinoma (MTLn3) cells into a 3D collagen matrix in response to a stable gradient of epidermal growth factor (EGF) over a two day period. This functional, yet operationally simple method opens the door for 3D systems that can be widely used to study drug dose response profiles and model physiological cell responses in vitro.

Results

Gradient generation

Linear and non-linear soluble factor gradients are developed within 3D gel-filled channels by combining variable channel geometries with the principle of infinite sources and sinks. The infinite source/sink concept is an idealized case where the concentrations at either end of a system are held constant. The fixed boundary concentrations result in a steady state concentration profile between the two boundaries. The geometry of the channel connecting the source and sink reservoirs affects the steady state profile; straight channels yield linear profiles and v-shaped (”wedge“) channels produce logarithmic profiles.¹⁹

Typical embodiments of infinite sources and sinks use flowing fluids to maintain boundary concentrations.^14,20-22 While effective, these approaches require external instrumentation to continuously drive fluid flow and expend large volumes of potentially expensive reagents during long-term experiments. Our approach approximates infinite sources/sinks by using finite volume reservoirs that are periodically replenished. The geometry of the channel connecting the source and the sink defines the concentration profile that develops within the system (see ESI eqn (5)^†).

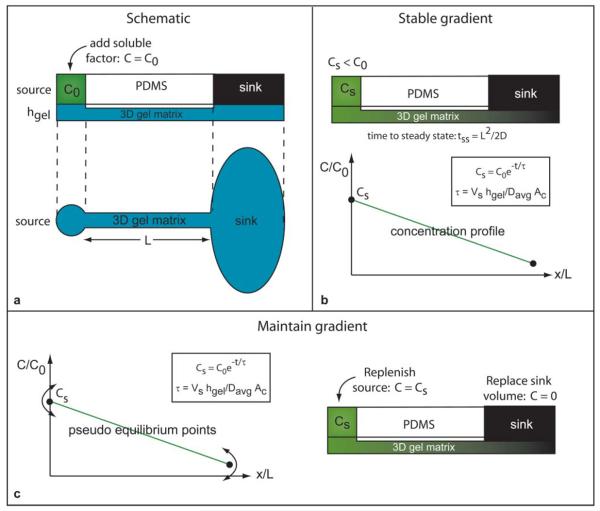
As shown in Fig. 1, an agarose-filled channel of length L is connected to source and sink reservoirs whose relative reservoir volumes are much greater than the channel volume (e.g. 3 μL source solution volume and 40 μL sink solution volume compared to a 70 nL total channel volume). The source is loaded with a solution of the fluorophore Alexa 488 (C = C₀) while the sink reservoir is filled with deionized water (C = 0). The fluorophore diffuses into the gel and creates a gradient along the length of the channel from source to sink.

Fig. 1.

(a) Schematic representation of the gel filled PDMS device. The source reservoir is loaded with the desired soluble factor at concentration C = C₀ and the sink is loaded with deionized water C = 0. (b) The added factor diffuses into the gel and, after a setup time t_ss, develops a pseudo-steady gradient from source to sink. (c) The gradient is maintained by periodically replenishing the source reservoir with a concentration of C_s < C₀. The concentration C_s rather than C₀ is used to minimize disruption of the established gradient. Established gradients were maintained for extended periods of time by periodic replenishment of the source and sink reservoirs.

During gradient formation, the finite volume source begins to deplete as the soluble factor diffuses from the source into the channel. After a setup time t_ss, the gradient reaches a pseudo-steady state profile along the length of the channel and the concentration at the mouth of the channel is in equilibrium with the source concentration C_s where C_s < C0. Because finite volume reservoirs are used, the source concentration (and consequently the concentration at the channel entrance) depletes as a function of time. The solution in the source reservoir must be replenished in an appropriate manner to maintain the developed gradient. As described below, the timing of the initial source replenishment plays an important role in defining the concentration range of the gradient.

Because the source and channel entrance concentrations are at equilibrium C = C_s, replacing the source solution with C = C₀ drives the gradient away from its pseudo-steady state and perturbs the system; the concentration in the channel gradually increases then tapers off until a shifted pseudo-steady state is reached. The source solution must be replenished at C = C_s (see eqn (1)) to minimize gradient disturbances.

$$C_{\mathrm{s}}=C_0{\mathrm{e}}^{-t∕\tau }$$ (1)

τ is defined as the source time parameter:

$$\tau =\left(V_{\mathrm{s}}{h}_{\mathrm{gel}}\right)∕\left(D_{\mathrm{avg}}{A}_{\mathrm{c}}\right)$$ (2)

V_s is the volume of solution in the source, h_gel is the height of the gel in the port, D_avg is average diffusivity of the factor in solution and in the gel, and A_c is the limiting cross-sectional area at the channel entrance. The source time is used to determine the depletion of the source concentration and consequently serves as a guide to determine the concentration at which to replenish the source reservoir to minimize disruption of the gradient (see ESI Table 1^†). The source time can be extended (therefore decreasing the amount of source depletion for a given amount of time) by increasing the volume of solution input, increasing the gel height in the port, or decreasing the limiting cross-sectional area at the channel entrance.

The source replenishment is performed by removing the old solution with a pipette and adding in a solution volume at the new concentration (calculated using eqn (1) and (2)). Care must be taken not to contact the gel with the pipette to prevent a dosing or bolus effect during loading. The fluidic resistance of the gel allows solutions to be exchanged without disturbing the gradient as long as the gel surface is not physically perturbed. The addition volume is a free parameter and can be changed during the course of the experiment if desired (as long as the replacement concentration is recalculated).

Gradient maintenance

The concentration in the source must be replenished periodically to maintain the gradient for extended periods of time. The frequency of the source solution replacement (C = C_s) is dictated by the system time parameter λ.

$$C=C_{\mathrm{s}}{\mathrm{e}}^{-t∕\lambda }$$ (3)

$$\lambda =\left(V_{\mathrm{s}}{L}_{\mathrm{t}}\right)∕\left(D_{\mathrm{gel}}{A}_{\mathrm{c}}\right)$$ (4)

L_t = L + h_gel corresponds to the total diffusion distance from the source solution to the sink. The frequency of replenishment depends on two factors: one physical and one logistical. The physical consideration is one of continued source depletion; waiting an extended period of time between replenishment affects the stability of the gradient. The logistical issue is one of convenience: requiring frequent media changes (e.g. every 3–6 h) leads to labor-intensive gradient maintenance and increases reagent usage. For demonstration purposes, the frequency of source replenishment was set between 20–24 h to coordinate with the time scale at which media is typically replenished during routine mammalian cell culture. The outer bound for replenishment is t = 0.1λ (corresponding to C = 0.9C_s) in order to minimize disturbance to the gradient (see ESI Table 2^†). The amount of deviation from the theoretical profile is directly related to the source time parameter λ.

The previous discussion pertains only to the source concentration. The sink reservoir volume is several orders of magnitude larger than the system volume, and is therefore less sensitive fluid replenishment (i.e. it acts more like an infinite sink). However, the sink solution volume is replaced at the same time as the source is refilled for convenience. While the source reservoir volume can be increased to match the sink volume we chose a small source reservoir volume to demonstrate a practical lower limit for reagent usage in long term experiments (e.g. 34.5 μL reagent solution volume required to maintain the stable exponential profile for 10 days).

Non-linear gradient generation

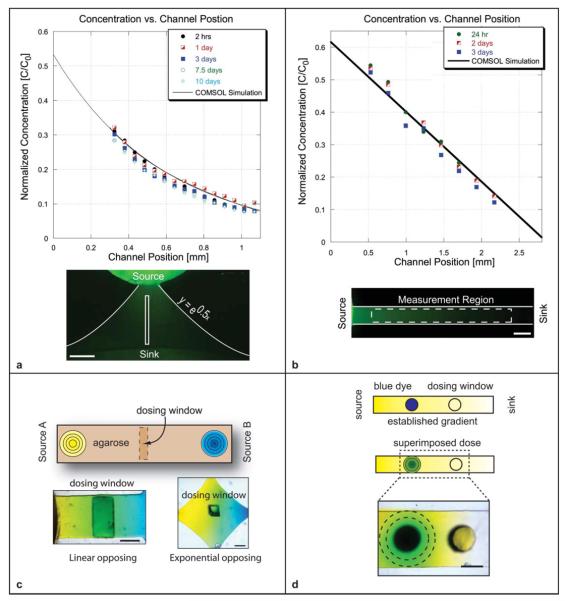
We demonstrate the development and maintenance of a non-linear (exponential) concentration profile using a 1.1 mm long channel whose profile follows the equation y = e^0.5x (Fig. 2(a)). The source and sink reservoirs were initially loaded with 3 lL of fluorophore solution and 60 μL deionized water respectively. The exponential channel geometry produced an exponential concentration profile in the channel. The initial replenishing of the source was performed 20 h after loading (t = 0.625τ) by adding 3.5 μL of concentration C = 0.53C₀ solution. Additional solution volume was added to the source to reduce the amount of depletion before the next solution change (i.e. increase τ). Subsequent replenishment was performed at 20 h intervals (corresponding to t = 0.076λ) for a total of 10 days. The COMSOL predicted profile and the experimental data are shown in Fig. 2(a). The experimental results deviated from the predicted profile by a maximum root mean squared error of 0.026. The exponential profile was maintained for 10 days and required 34.5 μL solution volume of Alexa 488 over the course of the experiment.

Fig. 2.

(a) Exponential profile was developed and maintained within an agarose-filled microchannel for ten days using a total of 34.5 μL of Alexa 488 solution. Maximum RMS error from the predicted profile was 0.026. Scale bar = 400 μm. (b) A linear concentration profile was developed and maintained within a 3D agarose gel-filled channel for three days using a total of 9 μL of Alexa 488 solution. Maximum RMS error from the predicted profile was 0.029. Scale bar = 250 μm. (c) Opposing concentration profiles of dye were created within a 3D agarose-filled microchannel. The left reservoir contained yellow dye and the right contained blue dye. The combination of diffusing yellow and blue dye molecule resulted in green coloration within the region of overlap. Linear opposing profile, scale bar = 1 mm and exponential opposing profile, scale bar = 250 μm are shown. Dosing windows are used to introduce cells or additional soluble factors to the system. (d) A stable linear gradient (in yellow dye) was established from source to sink. Blue dye was then added to one of the dosing windows. The blue dye diffusing into the channel on top of existing yellow gradient appeared as a radially evolving green gradient. Windows can be dosed at different time points to superimpose dynamic gradients in different regions of the channel. Scale bar = 1mm.

Linear gradient generation

We demonstrate the generation and maintenance of a linear concentration profile using a straight, 2.8 mm long agarose gel-filled channel connected with large volume source and sink reservoirs (Fig. 2(b)). The source reservoir was loaded with 3 μL of Alexa 488 (MW 400) solution at C = C₀ and the sink was loaded with 40 μL of deionized water C = 0. After 24 h, the source volume was replenished using the concentration defined by eqn (1) (here, τ = 51 h and C_s = 0.63C₀) and the sink volume was replenished with C = 0. The 24 h period representsthe system behavior with source replenishment performed at a conveniently spaced time period.

The source and sink concentrations were subsequently replenished every 24 h (corresponding to t = 0.03λ) to maintain the established gradient. The gradient was maintained for a total of 3 days and required 9 μL volume of Alexa 488 solution. The experimental data deviated from the model profile by a maximum root mean squared error of 0.029. Observed deviation from the predicted profile can be attributed in part to the inhomogeneity of fluorescence illumination from day-to-day and the timing of the source replenishment (determined by λ).

Opposing gradient generation

The concept of sources and sinks can similarly be used to create opposing gradients with one concentration source acting as a sink for the other concentration source (Fig. 2(c)). We demonstrate linear and non-linear opposing profiles of dye diffusing within a 3D agarose gel. Yellow dye was loaded into the left source reservoir and blue dye into the right reservoir. The yellow and blue dye molecules diffused through the gel and appeared green in the region of overlap; the deeper green coloration represented a higher degree of overlap. As expected, the linear opposing profiles exhibited a deeper green than the exponential opposing profiles where the concentration drops off exponentially moving away from each source. The centrally located dosing window in each case can be used to either superimpose additional factors onto the existing overlapping profiles or to add cells to the system. The high fluidic resistance provided by the gel helps to minimize disruption to the developed profiles during dye addition.

Temporal gradient generation

Dosing windows were photolithographically defined in the ceiling of the channel layer to provide access to the gel surface. As shown in Fig. 2(d), a gradient of yellow dye was first developed from source to sink. A new factor (blue dye) was then added to a dosing window as shown. The fluidic resistance provided by the gel maintained the developed gradient while the new factor diffused into the system. The mixing of the blue with the underlying yellow appeared as a green, radially evolving pulse. Transient doses act locally, and do not alter the steady state gradient. The evolution of the transient dose, where the concentration is initially confined to a region (−h < x < +h) is predicted by the well-known error function (see ESI eqn (6)^†). Superposition of individual dose profiles can be used to determine the degree of overlap between pulses when multiple dosing regions are used.²³

Migration assays

Neutrophil migration

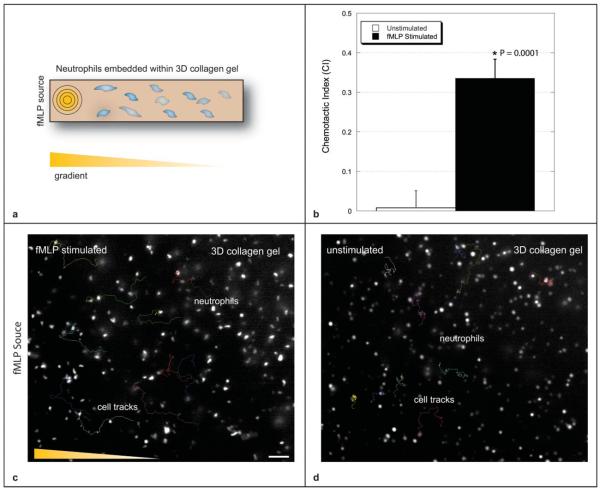
Neutrophils play an integral part of the immune response; they are recruited from the blood stream in response to foreign body invasion, and migrate to the point of insult along a biomolecular gradient produced by injured tissue and the invading agents. We quantified the chemotactic behavior of human neutrophils embedded within a collagen I matrix in response to a temporally evolving gradient of the peptide f-Met-Leu-Phe (fMLP). The polymerized collagen supported 3D distribution of neutrophils; in-plane fluorescence intensity is seen to be higher than out-of- plane fluorescence.

Migratory characteristics were assessed using the chemotactic index (CI) metric. The CI is defined as the ratio between the distance traveled parallel to the gradient and the total path length traveled. Chemotactic response in the simulated channel was compared to chemotactic response in an unstimulated control channel.

Cells in the unstimulated channel exhibited more rounded morphologies as compared to the cells within the fMLP stimulated channel. The stimulated cells exhibited classic behavior and polarized in response to the chemoattractant; a larger proportion of the stimulated cells became mobile (see ESI videos 1 and 2^†). Superimposed cell tracks, and calculated CI values are shown in Fig. 3. The chemotactic index for the stimulated case (0.336 ± 0.048) was statistically significant from that of the unstimulated channel (0.008 ± 0.041) with p < 0.0001 (n = 10). Data reported as mean ± sem.

Fig. 3.

The 3D distribution of neutrophils is visible within the collagen matrix (fluorescence intensity of in-plane cells is brighter than out-of-plane cells). (a) Cell tracks are shown for neutrophils embedded within the unstimulated channel and (b) neutrophils embedded within a channel stimulated with an fMLP gradient. Scale bar = 50 μm. Contrast has been adjusted in order to improve clarity. (c) Average CI values for the stimulated (0.336 ± 0.048) and unstimulated cases (0.008 ± 0.041) are shown (n = 10 cells, p < 0.0001). Data reported as mean ± sem. See ESI videos 1 and 2^† for migration videos with labeled tracks.

Although the chemotactic responses presented here cannot be directly compared to those found in the literature due to unmatched experimental conditions, this approach can be used to develop future studies that quantitatively compare migratory responses in 2D and 3D. As a point of reference, chemotactic indices in the range of 0.2 have been reported for human neutrophil populations in 2D in response to gradients of IL-8 using microfluidic approaches.²⁴ Future studies are required to draw a more direct comparison between 2D and 3D migratory responses.

MTLn3 invasion

The invasive behavior of metastatic cells is of great interest to oncologists looking to target tumorigenic cell populations in vivo. A 3D in vitro model for cellular response is therefore useful to test the effectiveness of therapeutic agents that inhibit or reduce metastatic behavior. Within this context, we demonstrate an assay that studies the migratory response of invasive rat mammary adenocarcinoma (MTLn3) cells to a gradient of EGF over a two day period. The assay was performed at 37 °C in a humidified environment containing 5% CO₂. Solutions were replenished every 24 h in a sterile hood using aseptic technique.

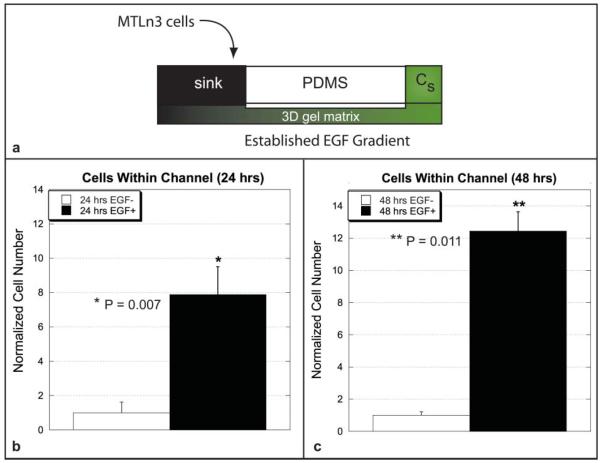
To investigate invasive MTLn3 behavior, a gradient of EGF was developed along the channel length (predicted slope of 98 nM mm⁻¹). MTLn3 cells were then added to the sink region, adjacent to the channel mouth (500–1000 cells). The cells were only able to enter the channel by migrating through the gel in the sink region. Therefore, as shown in Fig. 4, invasive migratory response to the EGF stimulus was determined by counting cells within the channels at 24 and 48 h time points for the stimulated and unstimulated channels.

Fig. 4.

(a) Schematic representation of the long-lasting gradient study using the invasive MTLn3 cancer cell line. (a) Comparison of cell numbers in the channel at 24 h post plating within the EGF-simulated and unstimulated channels. Cell numbers were normalized with respect to the unstimulated cell population and were found to be statistically significant with p = 0.007. (b) Comparison of cell numbers in the channel at 48 h post plating within the EGF-simulated and unstimulated channels. Cell numbers were normalized with respect to the unstimulated cell population and were found to be statistically significant with p = 0.011. Data reported as mean ± sem. Data tabulated from six total channels from three separate experiments. See ESI videos 3 and 4^†.

The results show that the number of cells present in the unstimulated channels were statistically different than those present in the stimulated channels at 24 and 48 h (p = 0.007 and p = 0.011 respectively). Cell numbers at 24 and 48 h within the stimulated and unstimulated channels were compared to determine if the resulting cell numbers could be a result from cell doubling alone. The differences in cell number at 24 and 48 h numbers for the unstimulated case were found to be statistically insignificant from one another (p = 0.388), while the difference in cell numbers in the stimulated channels were found to be statistically significant from one another (p = 0.027) (see ESI Fig. 1^†).

As a point of reference, CI values ranging from approximately 0.2–0.6 have been reported for MTLn3 cells migrating in 2D environments in response to EGF using microfluidic approaches.¹¹ Future work will facilitate quantitative comparisons between long-term migratory behavior of cells within 2D and 3D culture environments.

Discussion

Microfluidic methods have provided unparalleled control over the soluble factors cues presented to 2D cell culture assays; complex overlapping gradients have been demonstrated using pneumatic actuation systems,^25,26 and wide ranges of gradient profiles (e.g. linear, exponential, polynomial and step-wise) have been demonstrated using laminar flow based methods.^27,28 These methods are advantageous because of their ability to rapidly tune gradient characteristics by modulating flow rates or the frequency of valve actuation. However, the main limitations of these methods (in the realm of biologically relevant assays) are that they (i) remain confined to 2D substrates, and (ii) they require external equipment that reduces their ability to reach a widespread audience.

We demonstrate a platform that translates two-dimensional microfluidic control into a more physiologically relevant three-dimensional matrix. In doing so, we also remove the dependance of external instrumentation; the functionality of our system is designed into the system, and requires only a pipette to operate. Gradient profiles are dependant on the geometry of the channel that is used rather than on fluid flow rates. Temporal functionalities are provided by adding soluble factor pulses to the system via predefined dosing windows.

Gradient characteristics

Concentration ranges and slopes can be modified by altering the timing of the initial source volume replacement. The maximum concentration possible at the channel entrance depends upon the amount of time that system requires to reach pseudo-steady state. In order to create and maintain stable gradients, the initial replenishment is performed after the gradient becomes stable (the time to steady state can be estimated using the relation t_ss = L²/2D_gel, where L is the channel length and D_gel is the diffusion coefficient of the species through the gel). For example, in the linear gradient system, if the reservoir replenishment was made immediately after reaching steady state (~7.2 h), the left end point of the profile would be C = 0.87C₀ as opposed to C = 0.63C₀ for a replenishment made after 24 h. Thus, gradient range and slope is defined by the timing of the initial source volume change: steeper slopes are created by replenishing the source reservoir volume soon after the gradient setup time t_ss.

The use of 3D gels not only provides architecture similar to the in vivo, but also provides fluidic resistance to the system. The small diameter pores present throughout the gel volume enable fluids to be exchanged with minimum perturbation of the developed concentration profile. A similar platform containing only liquid is problematic because any differences in pressure that occur during fluid replenishment (e.g. differences in fluid height or a negative pressure head generated during solution exchange) rapidly disrupt the gradient. Design elements that add fluidic resistance (e.g. gels, porous membranes,^29,30 or constricted geometries) must be used to ensure that the gradient is not disturbed during fluid replacement.

It is likely that soluble factor signaling in vivo is made up of both long-lasting gradients and transient pulses that result from soluble factors produced by other cells or the ECM.³¹ Transient pulses are created in the system by adding the desired factor onto the system via dosing windows that access the top surface of the gel (Fig. 2(d)). This approach is useful because each dosing window can be individually addressed as desired, providing temporal and spatial control over the local soluble factor microenvironment within the system. Each dosing window is also a cell patterning window where new cell populations can be introduced in order to develop more complex in vitro model systems with spatial and temporal resolution.³² Even though the temporal dose is diffusion-based, soluble factors can diffuse quickly over short distances. For example a small molecule (D = 5 × 10⁻⁶ cm² s⁻¹) can diffuse a distance of 10 microns in ~0.1 s (assuming the factor does not react with the matrix) allowing for rapid changes to the microenvironment over cellular scale lengths.

Biological functionality

Soluble factor control within a 3D matrix opens the door to many new avenues for exploration. At the simplest level, cellular responses between traditional 2D assays and the 3D analogue can be compared to probe for changes in morphology, function, protein localization and gene expression. More complicated model systems can be used to investigate the effectiveness of a therapeutic agent, study metastatic cell response, or identify factors that produce inappropriate immune cell recruitment and inflammation.

Dosing windows, for example, could be used to guide a cell that is migrating along a stable gradient. The cell could be ”steered“ by dosing an adjacent window with a new factor or, alternatively, two windows adjacent to the cell could be dosed with different factors to create overlapping gradients on top of a stable gradient. This platform mimics in vivo functionality where cells are simultaneously exposed to multiple stimuli and choose a preferential path.³³ An assay of this type could help to elucidate signaling hierarchy between chemotactic factors.

The demonstrated neutrophil experimental setup could be modified to study the migratory responses of two cell populations embedded within the matrix; one treated with an inhibitory agent and the other wild type. More sophisticated imaging techniques (such as confocal microscopy) could be used to track cell migration in 3D. The MTLn3 experiment demonstrates the ability to create an operationally simple, quantitative, 3D analogue to the Transwell Assay in which gradient characteristics are known, and the cell count readout can be fully automated for high-throughput integration.

Conclusions

We have presented a platform that provides spatiotemporal control over the soluble factor microenvironment within a 3D gel. Long lasting gradients, coupled with transient doses, allow us to more faithfully recreate in vivo environments, and provide new capabilities for in vitro investigations. This platform can be applied to examine the conditions that affect the differentiation of stem cells, promote (or inhibit) cancer metastasis, or direct cell orientation during early development. Another advantage of our system is that of operational simplicity; the pipette-based system can readily be incorporated into life science research. Pipette-based operation also facilitates high throughput cell migration or therapeutic screening assays within 3D gel environments.

Methods

Fabrication

The system is created using standard soft-lithography techniques using polydimethylsiloxane (PDMS). As schematically shown in Fig. 1, the device is composed of two exclusion molded PDMS layers.³⁴ The bottom layer contains the channel geometry and defines the source and sink regions. The second layer defines fluid reservoirs that retain the source and sink solutions. All channel heights are 100 μm; port heights are 500 μm for the non-linear channel and 600 μm for the straight channel.

The channel and port layer is first loaded with unpolymerized gel solution. The gel in the port is leveled by removing excess liquid from the surface with a sharp razor blade prior to solidification. The second layer (containing reservoirs) is aligned over the top of the first after the gel polymerizes. Gel thickness in the ports and channels is defined by the heights achieved during the photolithography process. The source and sink reservoirs are then loaded with deionized water (or medium) and the system is allowed to equilibrate in a humidified environment for at least 1 h before the soluble factor is loaded.

Gradient profiles were quantified by creating a standard linear correlation between the measured fluorescence intensity and known sample concentrations within the gel. The measured pixel intensity was converted to fluorophore concentration using the calibration curve. Results shown are normalized with respect to the intensity of the input concentration. Modeling was performed using COMSOL Multiphysics (Burlington, MA) simulation software. All p-values reported in the text were calculated using the unpaired, two-tailed t-test with unequal variance.

Reagents

Agarose gel powder (Sigma) was mixed with deionized water to create a 2% (w/v) gel solution according to manufacturers directions. PDMS (Sylgard 184, Dow Corning) was prepared at a 10 : 1 base to crosslinker ratio and cured at 85 °C for 1.5 h. Unconjugated Alexa 488 (Molecular Probes) was diluted to the desired concentration in deionized water. Fluorescence images were captured using an inverted scope (Nikon IX70) microscope using Metamorph software (Molecular Devices). Image analysis and cell tracking were performed using ImageJ (version 1.37v). Type I Collagen solution was purchased from Sigma.

Neutrophil experiments

Primary human neutrophils were isolated from whole blood as described by Lokuta et al.³⁵ All donors were self-reportedly healthy and informed consent was obtained at the time of the blood draw. The use of human subjects was approved by the University of Wisconsin Madison, Center for Health Sciences Human Subjects Committee. The isolated neutrophils were incubated with blue fluorescent CellTracker dye (Molecular Probes) at 1 : 1000 ratio for 30 min to aid visualization.

250 μm tall channels, 600 μm wide, 2 cm long channels containing 600 μm diameter ports each end were loaded with a mixture of type I collagen gel and neutrophils (total concentration of gel was 1.33 mg mL⁻¹). The gel was allowed to polymerize incubated at 37 °C for 1 h with 7.5% ambient CO². Media was pooled around the device to reduce evaporation. After polymerization, three-dimensional distributions of neutrophils were visible.

The right port was covered with a PDMS slab to limit evaporation and possible surface tension based pumping. Devices were placed in The Box closed system (Life Imaging Services), and maintained at 37 °C while viewed on a Nikon Eclipse TE300 inverted fluorescent microscope. 2 μL of 100 nM of the chemotactic agent f-Met-Leu-Phe (fMLP) was added to the top of the left access port of the stimulated channel; blank medium was added to the access port in the control (unstimulated) channel. Images were acquired every 15 s for 15 min with a Hamamatsu cooled CCD video camera using a 20× phase objective and captured into Metamorph v7.0.

MTLn3 experiments

MTLn3 cells were a kind gift from Prof. John Condeelis and Prof. Jeffrey Segall (Albert Einstein College of Medicine). Cells were cultured in α-MEM supplemented with 5% FBS and antibiotics as described previously.³⁶ The assay was performed at 37 °C in a humidified environment containing 5% CO₂. Solutions were replenished every 24 h in a sterile hood using aseptic technique.

The channel and ports were loaded with a 1.33 mg mL⁻¹ collagen mixture in α-MEM culture media containing 35.7 mM HEPES pH 7.2 and allowed to polymerize for 2 h at 37 °C in a humidified environment. The sink reservoir was then loaded with α-MEM culture media and the source loaded with 500 nM EGF (or vehicle control) and allowed to equilibrate at 37 °C containing 5% CO₂ for 24 h. After 24 h, the source was replenished with 490 nM EGF, the sink solution was replenished, and equal numbers (500–1000) of MTLn3 cells were added to the sink reservoir. The source solution volume was replenished every 24 h. MTLn3 cell invasion and migration into the channel was monitored at 24 and 48 h post plating. Migrating MTLn3 cells were imaged every minute for 1 h.