Pacific decadal oscillation hindcasts relevant to near-term climate prediction

Abstract

Decadal-scale climate variations over the Pacific Ocean and its surroundings are strongly related to the so-called Pacific decadal oscillation (PDO) which is coherent with wintertime climate over North America and Asian monsoon, and have important impacts on marine ecosystems and fisheries. In a near-term climate prediction covering the period up to 2030, we require knowledge of the future state of internal variations in the climate system such as the PDO as well as the global warming signal. We perform sets of ensemble hindcast and forecast experiments using a coupled atmosphere-ocean climate model to examine the predictability of internal variations on decadal timescales, in addition to the response to external forcing due to changes in concentrations of greenhouse gases and aerosols, volcanic activity, and solar cycle variations. Our results highlight that an initialization of the upper-ocean state using historical observations is effective for successful hindcasts of the PDO and has a great impact on future predictions. Ensemble hindcasts for the 20th century demonstrate a predictive skill in the upper-ocean temperature over almost a decade, particularly around the Kuroshio-Oyashio extension (KOE) and subtropical oceanic frontal regions where the PDO signals are observed strongest. A negative tendency of the predicted PDO phase in the coming decade will enhance the rising trend in surface air-temperature (SAT) over east Asia and over the KOE region, and suppress it along the west coasts of North and South America and over the equatorial Pacific. This suppression will contribute to a slowing down of the global-mean SAT rise.

A near-term climate prediction covering the period up to 2030 is a major issue to be addressed in the next assessment report of the Intergovernmental Panel on Climate Change (1, 2). To make the political decisions required to solve the socioeconomic problems arising from climate change over the coming decades, we need to take into account the large-scale climate changes associated with internal climate variability as well as the global warming signals (i.e., the response to external forcing due to changes in concentrations of greenhouse gases and aerosols, volcanic activity, and solar cycle variations) (3–6). A globally averaged surface-air-temperature (SAT) forecast up to 2030 depends little on specific socioeconomic scenarios or models used in centennial climate projection experiments (7, 8). On decadal timescales, SAT changes due to internal climate variability are comparable to those associated with global warming in magnitude (9). The predictability of internal climate variations is central to validating our skills in predicting the near-term climate variations.

Prediction of internal decadal variability in the climate system represents one of the newest and toughest challenges. It is only recently that near-term climate projection experiments have been carried out focusing on internal decadal variations (10–12). Keenlyside et al. (11) have suggested that, in the coming decade, decadal-scale weakening of the Atlantic meridional overturning circulation (AMOC) can work to suppress the globally averaged SAT rise due to anthropogenic forcing. Here, we have considered that the Pacific decadal oscillation (PDO) (13) can also have large impacts on decadal-scale projections of the pan-Pacific climate and decadal-scale modulations of the global warming trend. The PDO is a dominant internal oscillation in the climate system with phase shifts developing on decadal timescales. After the end of the 1970s, for example, corresponding to the positive phase of the PDO, the upper-ocean temperatures were higher than those in the preceding decades along the west coasts of North and South America and over the equatorial Pacific, while they were lower over the western and central North Pacific (14, 15). The PDO has recently attracted much attention not only in climate studies but also in impact assessments in the areas of agriculture, water resources, and fisheries (13, 16, 17). Successful prediction of the state of the PDO over timescales of years to one decade has considerable societal benefits (18).

A near-term climate prediction requires not only good performance from the models in simulating major climate processes but also realistic estimates of initial climate states using observational data, while physics of internal variations itself and the stochastic forcing can also contribute to limiting predictability. In particular, the climate prediction community faces a major difficulty in obtaining good atmospheric and oceanic initial conditions that are compatible with both the model and the observations. Even in recent studies using coupled atmosphere-ocean general circulation models (GCMs), the El Ninõ southern oscillation, which is a dominant internal fluctuation on interannual timescales, seems only to be predictable up to at most 1 year in advance (19, 20). In the present paper, we examine the impacts of the initialization on predicting internal decadal variations and validate the hindcast skill of our coupled GCM for the PDO.

The coupled atmosphere-ocean GCM adopted here is version 3.2 of the Model for Interdisciplinary Research On Climate (MIROC) in medium resolution. Using MIROC, Nozawa et al. (2005) (21) and Shiogama et al. (2007) (6) performed 10-member ensemble simulations during 1850–2000 using the historical data of natural and anthropogenic forcing toward reproducing the 20th Century Climate in Coupled Models (20C3M) and during 2001–2030 with the A1B-type emissions scenario in the Special Report on Emissions Scenarios (22). We define these 10-member ensembles as a reference field in the present paper (referred to as NoAS). These forcing data have been used in a number of global warming studies (6, 10, 11) and we similarly use them as a boundary condition in all experiments in the present paper. Our initialization is done on the basis of a data assimilation approach together with an ensemble technique, using MIROC and the objective analyses of sea surface temperature (SST), subsurface ocean temperature, and salinity (23–25). Using the ensemble snapshots of the assimilation data as initial conditions, we perform seven sets of 14.5-year-long, 10-member ensemble hindcast experiments every 5 years between July 1, 1960 and December 31, 2004 (referred to as HCST). In a similar manner, we also perform an ensemble forecast experiment starting from July 1, 2005 up to December 31, 2030 (referred to as FCST).

Results

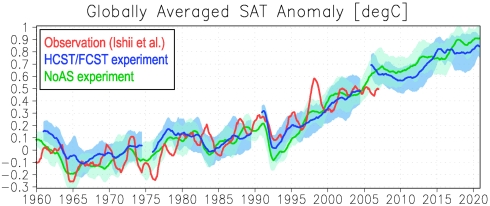
When examining the global-mean SAT variations (Fig. 1), on decadal timescales, the observed values lie within 1 SD of the HCST and/or NoAS ensembles throughout virtually all of the prediction periods. The temporal variations of the globally averaged SAT are largely controlled by the external forcing prescribed in all experiments in the same manner. The linear trends during 1961–1990 display a negligible difference between the observation (0.085 °C/10 yr) and the NoAS data (0.080 °C/10 yr). On the other hand, internal variations can contribute to the decadal-scale modulations such as the late-1970’s change in climate (26), which is defined here as the 5-year running mean during 1979–1986 minus that during 1971–1978. The magnitude of this late-1970’s change in the observations (0.149 °C) is substantially larger than that in the NoAS data (0.091 °C), when the SD of the 10 ensembles (0.078 °C) is considered. In the NoAS experiment, because the individual ensemble member should arbitrarily represent states of internal oscillations due to the absence of an initialization based on observational data, realistic phase changes of internal decadal variations are simulated by only a few ensemble members rather than an ensemble mean. It is not easy to identify a significant improvement due to initialization in the temporal evolution of the global-mean SAT (Fig. 1), whereas some differences between the NoAS and HCST/FCST data are noticeable. For example, internal variations may work to make the globally averaged SAT in the FCST-derived ensemble mean slightly lower than that in the NoAS data (Fig. 1). In fact, such a slowing down of the globally averaged SAT rise can be closely related to a significantly negative tendency of the predicted PDO phase as suggested below.

Fig. 1.

Hindcasted, forecasted, and observed time series of globally averaged SAT anomaly. Globally averaged anomalies of the annual-mean SAT (°C) relative to the averages during 1961–1990. Red, blue, and green lines represent the observation (Hadley Centre-Climate Research Unit gridded surface temperature dataset, HadCRUT3v) and the ensemble-mean values of the HCST/FCST and NoAS data, respectively. Blue and green shades represent the ranges of 1 SD of the 10 ensembles in the HCST/FCST and NoAS data, respectively. Plotted values for the HCST/FCST data are the results of hindcast and forecast experiments starting from 1960, 1975, 1990, and 2005.

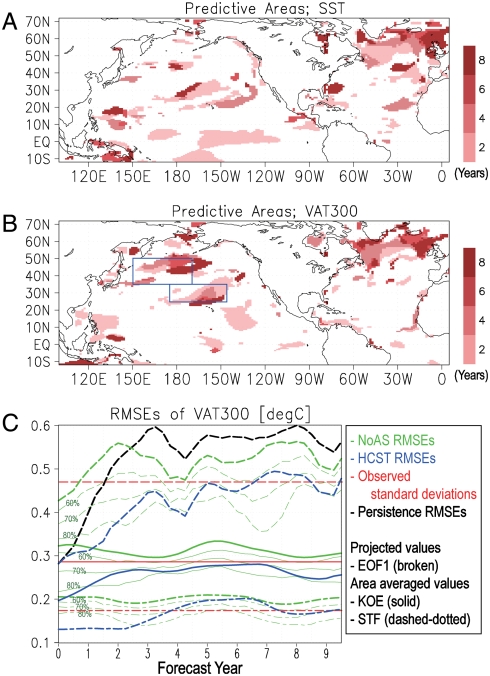
Our major interest is directed toward the predictability of internal decadal variations in the climate system, particularly the PDO. To identify and isolate internal variations from a forced variation governed by the external forcing more effectively, we analyze the HCST-derived and observed deviations from an externally forced variation (hereafter called internal components). Here, we define the externally forced variation as a leading mode obtained from a signal-to-noise maximizing empirical orthogonal function (EOF) analysis (27, 28) using the NoAS data during 1958–2017. Figs. 2A and B indicate that the internal decadal-scale variations of SST and vertically averaged ocean temperature over the upper 300 m (VAT300) are predictable almost a decade in advance in specific areas. Around the KOE (particularly its northern part and downstream), subtropical oceanic frontal (STF) and eastern off-equatorial regions of the extratropical North Pacific (see two rectangles in Fig. 2B for the KOE and STF regions), for example, the hindcasted VAT300 deviations are significantly correlated with the observation for several years (Fig. 2B). For the ensemble-mean VAT300s in the KOE and STF regions, the rms errors (RMSEs) of the HCST data are significantly smaller than those of the NoAS data during about the initial 6 and 4 years (Fig. 2C), respectively, while significance levels are limited to 70%. The SST in the midlatitude also represents a similar predictive skill (Fig. 2A). As indicated by Smith et al. (2007) (10) and Keenlyside et al. (2008) (11), in addition, the high latitudes of the North Atlantic exhibit long predictability in both SST and VAT300.

Fig. 2.

Skills in hindcasting internal decadal variations in terms of anomaly correlation coefficients at each grid point and area-averaged errors. (A) Areas where the 5-year-mean SST deviations from the externally forced variation are significantly hindcasted at 90% confidence levels in terms of the anomaly correlation coefficients at forecast years 2, 4, 6, and 8, respectively. Significance tests are conducted on the basis of a bootstrap approach using 2,000 sets of resampled ensemble-mean values (SI Text). (B) The same as (A), except for the VAT300 deviations. Two blue rectangles represent the KOE and STF regions defined in the present paper. (C) RMSEs of the 5-year-mean VAT300 deviations projected onto the leading EOF (i.e., Fig. 3A) (broken lines) and those averaged over the KOE (solid lines) and STF (dashed-dotted lines) regions, respectively. Thick blue, green, and black lines represent the errors in the ensemble-mean states of the HCST and NoAS data and the persistence prediction (for the PDO time series only), respectively. Thin green lines represent values indicating that the RMSEs in the HCST data are significantly smaller than those in the NoAS data at 60%, 70%, and 80% confidence limits, respectively (SI Text). Red lines represent the observed SDs.

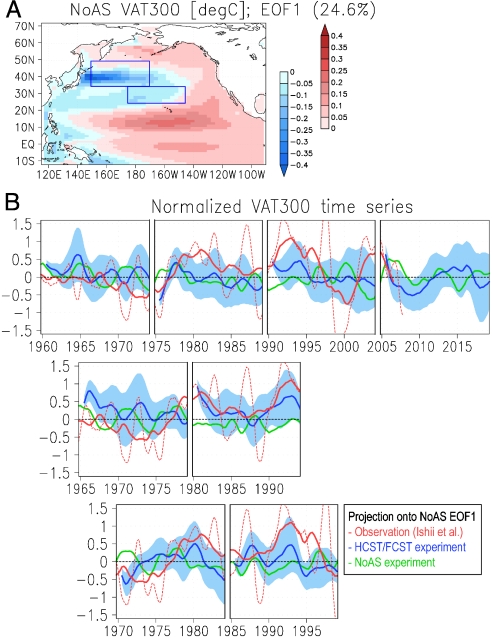
These regional but significant predictive skills in the upper-ocean temperature suggest that the initialization enables us to predict the PDO on decadal timescales, because the KOE and STF regions are the centers of action of the PDO (Fig. 3A) (29). The temporal evolution of the observed PDO, which is defined here by the projection onto the leading EOF of internal components (i.e., Fig. 3A), represents a decadal variation such as the late-1970’s change with interannual fluctuations (red lines in Fig. 3B). On decadal timescales (e.g., in 5-year-mean fields), the area-averaged VAT300 variations in both the KOE and STF regions are observed significantly correlating with the PDO time series at 90% confidence levels. Overall, the hindcasted time series of the PDO (i.e., the projection of the hindcasted VAT300 deviations) are in fair agreement with the observations, particularly in an initial few years (Fig. 3B). Fluctuations of the NoAS-derived projections would represent noise probably due to small size of the ensembles. When compared to the NoAS experiments, the RMSEs of the projected VAT300 deviations suggests that the PDO phases are predictable almost 6 years in advance at 70% confidence levels (Fig. 2C). Errors in a persistence prediction (i.e., keeping the initial conditions unchanged) grow quite rapidly to a level of the NoAS data (Fig. 2C). Over the coming decade, the projected VAT300 deviation of the FCST data indicates that the positive phase of the PDO on July 2005 rapidly shifts to a significantly negative phase within several years (Fig. 3B, Top). The observational data for recent years (2005–2008) also display this rapid phase change of the PDO. Although the time series plotted in Fig. 3B contains both interannual and decadal components, this agreement suggests that the FCST data can represent a predictive skill at least during the initial 3 years, which is consistent with the skills statistically found in the HCST data.

Fig. 3.

Hindcasted, forecasted, and observed time series of the leading mode of internal decadal variations in upper-ocean temperature over the North Pacific. (A) Spatial pattern of the leading EOF of the North Pacific VAT300 deviations from the externally forced variation in the NoAS data during 1958–2017. (B) The projections onto the leading EOF [i.e., (A)] for annual-mean VAT300 deviations in the HCST/FCST (blue lines) and NoAS data (green lines) and in the observation (broken red lines), respectively. Solid red lines are 5-year-running mean values in the observation. Blue shades represent the ranges of 1 SD of the 10 ensembles of the projected deviations in the HCST/FCST data. Plotted values are normalized using the SD of the observations.

Discussion

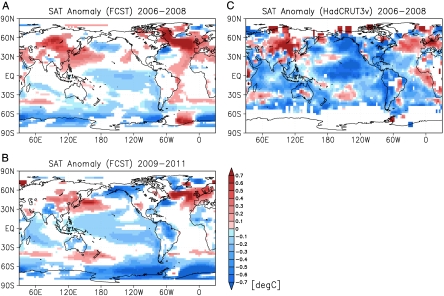
The predictability of the PDO phase can contribute to that of global climate changes on decadal timescales (e.g., global-mean SAT changes) as implied in Fig. 1. In fact, when examining the individual ensemble members of the HCST data between July 1975 and December 1989 together with the assimilation data for the preceding initialization up to June 1975, a large global-mean SAT rise is always simulated with a positive PDO tendency in the 1980s. The global-mean SAT rising rate (see Fig. 1) and changes in the PDO tendency (see Fig. 3B) exhibit a significant relationship in the averages during 1979–1986 minus those during 1971–1978; the correlation coefficient is 0.791. This suggests that the external forcing and the PDO interplay to realize the late-1970’s change in climate, and that the initialization has a great impact on the future prediction associated with global climate change as well as the PDO. Fig. 3B suggests that the PDO may also contribute to the decadal-scale climate changes in recent years. The FCST data reveal that the internal decadal variations may suppress the globally averaged SAT rise in the coming decade (Fig. 1). The SAT deviations over the initial 6 years (Fig. 4A and B) indicate that the slowing down of global warming in the FCST data is largely due to the tropical low SAT comprising a PDO-like pattern (e.g., Fig. 3A), in agreement with the observation over the initial 3 years (Fig. 4C). The rising trend in SAT is enhanced over east Asia and over the KOE region, while it is suppressed along the west coasts of North and South America and over the equatorial Pacific. The PDO-like patterns in the SAT difference shown in Fig. 4 Left are closely related to a significantly negative phase of the predicted PDO after 2007 (Fig. 3B).

Fig. 4.

Impacts of initialization on the predicted SAT in the coming decade. The FCST-derived ensemble-mean SAT deviations (°C) from the externally forced variation during (A) 2006–2008 and (B) 2009–2011, respectively. Shaded regions are the significant areas at 90% confidence levels (SI Text). (C) The same as (A), except for the observed deviation. Note that the observational dataset contains missing values, particularly over the high latitudes.

Keenlyside et al. (2008) (11) have suggested that global warming, particularly over the North Atlantic region, may slow down due to an internal change of the AMOC in the coming decade. Our results suggest that the PDO also plays a major role in modulating the global warming trend on decadal timescales. Both the PDO and the AMOC have considerable impact on the pan-Pacific and pan-Atlantic climates and can influence a globally averaged state. Over the high latitudes of the North Atlantic and Europe, our FCST experiment simulates a high SAT consistent with recent observations (Fig. 4). Although our focus in the present paper is on the PDO, physical processes influencing the Atlantic climate should be examined in more detail. Development of the initialization system by advancing the assimilation and ensemble generation techniques and by assimilating additional observational data may enable us to further improve the estimates of initial conditions. In addition, improvement of the model components may raise the level of performance in simulating major climate processes. A higher-resolution climate model should provide us with more detailed regional information.

Methods

Model Description.

We perform data assimilation and prediction experiments using the objective analyses and a coupled atmosphere-ocean model, MIROC. MIROC has been developed at the Center for Climate System Research of the University of Tokyo, National Institute for Environmental Studies, and Frontier Research Center for Global Change of the Japan Agency for Marine–Earth Science and Technology. The resolution of the atmospheric component is horizontally the same as the commonly used T42 spectral model and has 20 levels on a vertical σ-coordinate. The resolution of the ocean component is 1.4° in longitude and 0.56–1.4° in latitude (finer around the equator) and has 44 vertical levels.

Assimilation Procedure for Initialization.

Objective analyses of ocean temperature and salinity have been conducted beforehand on a monthly basis (23–25). We assimilate anomalies of the objective analyses relative to the averages during 1961–1990, because correction of model climatology by data assimilation sometimes leads to a climate drift that contaminates temporal evolutions of the internal variability of interest in predicted fields. By an incremental analysis update method (30), the model temperature and salinity in the upper 700 m depth are forced to approach the observations which contain the dominant signals of the PDO. We perform 10-member assimilation runs with different initial conditions on January 1, 1945 that are derived from the 10-ensemble snapshots of the NoAS data.

Estimates of analysis errors are also compiled in the objective analysis dataset (24), which enable us to evaluate statistical reliability of the analyses at each grid point. Using the analysis errors, we control the magnitudes of analysis increments (i.e., forcing by the data assimilation) in such a way that these become relatively large at a grid point where an objective analysis is available with high reliability. A model-to-observation ratio of analysis errors is also taken into consideration to determine the magnitudes of analysis increments. In addition, we introduce a constraint that ensures no change in global averages of both heat and salinity in the assimilation. When applying this conservation constraint for global averages, the density of ocean water is assumed to be invariant at each grid point during the assimilation interval (i.e., 1 day). Impacts of sea-ice variations on a near-term climate prediction have not been assessed so far, and an inconsistency in sea-ice cover between the model and the observations usually results in unfavorable temperature and salinity variations over the polar regions in data assimilation experiments. Within our present framework of data assimilation, the objective analyses are not assimilated at a grid point where sea ice exists in the model. In addition, at a grid point located away from the modeled sea ice within a 10° distance in latitude, the analysis increment is damped in proportion to the distance of the nearest sea ice. The data assimilation procedure described here has allowed us to prevent the model climate from unrealistic drift in subsequent prediction experiments.

Definition of the PDO.

We apply an EOF analysis to the deviations of the NoAS-derived 10-ensemble members from the externally forced variation during 1958–2017, which is defined using a signal-to-noise maximizing EOF technique (27, 28). The leading EOF should define the spatial pattern of the dominant internal variation that is not driven by the external forcing. As a whole, the leading EOF for the North Pacific (15°S-70°N, 15°E-90°W) SST, which is a good proxy for the SAT over the ocean, represents major characteristics of the spatial pattern of the observed PDO in a reasonable manner. When projected onto the leading EOF, the observed SST anomaly relative to the averages during 1961–1990 displays decadal variations similar to the so-called PDO index (13). The spatial pattern of the leading EOF for VAT300 is quite similar to that for SST and is characterized by strong signals over the KOE and STF regions of the midlatitude North Pacific (29). These leading EOFs obtained from the ensemble simulations are in good agreement with the observed counterparts.