Anisotropy of Fibrous Tissues in Relation to the Distribution of Tensed and Buckled Fibers

Abstract

Fibrous tissues are characterized by a much higher stiffness in tension than compression. This study uses microstructural modeling to analyze the material symmetry of fibrous tissues undergoing tension and compression, to better understand how material symmetry relates to the distribution of tensed and buckled fibers. The analysis is also used to determine whether the behavior predicted from a microstructural model can be identically described by phenomenological continuum models. The analysis confirms that in the case when all the fibers are in tension in the current configuration, the material symmetry of a fibrous the tissue in the corresponding reference configuration is dictated by the symmetry of its fiber angular distribution in that configuration. However, if the strain field exhibits a mix of tensile and compressive principal normal strains, the fibrous tissue is represented by a material body which consists only of those fibers which are in tension; the material symmetry of this body may be deduced from the superposition of the planes of symmetry of the strain and the planes of symmetry of the angular fiber distribution. Thus the material symmetry is dictated by the symmetry of the angular distribution of only those fibers which are in tension. Examples are provided for various fiber angular distribution symmetries. In particular, it is found that a fibrous tissue with isotropic fiber angular distribution exhibits orthotropic symmetry when subjected to a mix of tensile and compressive principal normal strains, with the planes of symmetry normal to the principal directions of the strain. This anisotropy occurs even under infinitesimal strains and is distinct from the anisotropy induced from the finite rotation of fibers. It is also noted that fibrous materials are not stable under all strain states due to the inability of fibers to sustain compression along their axis; this instability can be overcome by the incorporation of a ground matrix. It is concluded that the material response predicted using a microstructural model of the fibers cannot be described exactly by phenomenological continuum models. These results are also applicable to non-biological fiber-composite materials.

1 Introduction

Most biological soft tissues are fibrous. The fiber distribution may be either random or oriented, imparting anisotropy to the tissue. Fibrous tissues are also characterized by a much higher stiffness in tension than compression, a property commonly attributed to buckling of the fibers in compression. In the field of soft tissue mechanics, fibrous tissues exhibiting tension-compression nonlinearity have been modeled using phenomenological continuum representations, microstructural representations, or combinations thereof. The main feature of microstructural models is that they start with the formulation of a constitutive relation for a single fiber; the behavior of the tissue as a whole is obtained by characterizing its fiber angular distribution and summing (or integrating) the individual fiber responses over this distribution [1, 2]. In these types of models the material symmetry of the tissue has been assumed to depend on the fiber angular distribution. In many studies the fibrous contribution has been superposed upon that of an embedding matrix (representing a ground substance, for example), which itself may be either isotropic or anisotropic [3, 4].

Phenomenological continuum models which account for a distinct behavior in tension and compression (bimodular response) have also been examined, most commonly in the study of fiber composites. A characteristic of these phenomenological models is that they postulate material symmetries in tension and compression, then proceed to identify which material coefficients of the corresponding constitutive model are allowed to assume different values in tension versus compression. The formulation of such phenomenological models has posed a challenge in the field of continuum solid mechanics, with no consensus yet emerging. For example, some investigators have questioned whether it is possible for a material which exhibits tension-compression nonlinearity to also be isotropic [5]. Curnier et al. [6] proposed a conewise linear elasticity model whose material symmetry can be postulated independently of the state of strain; they described isotropic and orthotropic formulations of this constitutive model. One feature of their theory is that the shear modulus must assume the same value whether the material is undergoing tension or compression. In contrast, in an earlier study, Green and Mkrtichian [7] postulated that a material which is initially isotropic becomes transversely isotropic if subjected to a strain field whose principal values are a mix of tensile and compressive values. Their model allows for a jump in the shear modulus depending on the state of strain. The disparate features of these phenomenological constitutive models make it difficult to determine which, if any, is most representative of fibrous tissues.

In this study we propose to analyze the material symmetry of fibrous tissues undergoing tension and compression to better understand how it may be influenced by the relative distribution of tensed and buckled fibers. The findings of this analysis will also be used to determine whether the phenomenological continuum models of Curnier et al. [6] or Green and Mkrtichian [7], which are attractive because of their frame-invariant formulations and their intuitive yet very distinct premises, are representative of fibrous tissues.

2 Fibrous Tissue Analysis

2.1 Reference Configuration

A fundamental concept of continuum mechanics is that the symmetry groups of a material may depend on the choice of reference configuration [8]. For example, a material which is isotropic in one reference configuration may be anisotropic in another. Therefore, the choice of reference configuration κ ($\mathcal{B}$) for a body $\mathcal{B}$ may influence its material symmetry. In the study of fibrous tissues, Lanir [2] proposed that the behavior of the tissue at a point can be predicted from the weighted behavior of the individual fibers passing through that point, with the weight factor represented by a fiber angular distribution function. A consequence of this assumption is that the reference configuration of the tissue may be dependent on the reference configuration of its individual fibers.

A basic assumption adopted in the current study is that a single fiber can sustain load in tension but buckles in compression [9, 10]. A buckled fiber is idealized to have a negligible bulk modulus, so that it cannot resist any compressive load; in effect, a buckled fiber behaves as a non-existing fiber. An important but subtle consequence of this assumption is that the definition of the body $\mathcal{B}$ representing the tissue changes depending on which set of fibers are in tension and which are buckled in the current configuration. For example, consider for simplicity that the tissue consists of two fiber bundles, oriented along the unit vectors n₁ and n₂ in the current configuration κ, respectively. If the fibers along n₂ are buckled while those along n₁ are not, the tissue is effectively represented by the body ${\mathcal{B}}_1$ consisting of the fiber bundle along n₁ only. The current configuration is denoted by κ (${\mathcal{B}}_1$) and its corresponding reference configuration is κ₀ (${\mathcal{B}}_1$). The material symmetry of the tissue, relative to κ₀ (${\mathcal{B}}_1$), is determined exclusively by the fiber bundles of ${\mathcal{B}}_1$, since these are the fibers which define the tissue in the current configuration. As usual in continuum mechanics, the reference configuration may be hypothetical in the sense that the material may never assume that configuration in an actual history [8].

Since the tissue may be represented by different bodies ${\mathcal{B}}_b$ depending on which fibers are in tension in the current configuration κ, the material symmetry in the corresponding reference configuration may also differ.¹ We may define the reference configuration κ₀ (${\mathcal{B}}_b$) as that for which the fibers of ${\mathcal{B}}_b$ are subjected to an infinitesimal tensile traction along their length. Thus, the state of zero strain along each fiber corresponds to the state when the fiber is just barely loaded in tension. In the treatment which follows, the objective is to define the distribution of tensed fibers in the different bodies ${\mathcal{B}}_b$ which may be representative of the fibrous tissue, based on the strain field in the current configuration κ (${\mathcal{B}}_b$), in order to determine the material symmetry of the reference configuration κ₀ (${\mathcal{B}}_b$).

2.2 Formulation

The basic constitutive formulation for a fibrous tissue starts from the formulation for a single fiber, oriented along the unit vector n⁰ in the reference configuration [2, 11]. The state of strain in the tissue is given by the Lagrangian strain tensor E. The normal component of E along the fiber direction is denoted by E_n, where

$$E_n={\mathbf{n}}^0\cdot {\mathbf{En}}^0={\mathbf{N}}^0:\mathbf{E}{\mathbf{N}}^0={\mathbf{n}}^0\otimes {\mathbf{n}}^0$$ (1)

Here, the colon denotes the double dot product of second order tensors and ⊗ denotes a dyadic product. The symmetric tensor N⁰ represents a material texture. The basic constitutive assumption is that the strain energy density Ψ associated with a single fiber is only a function of E_n and that all fibers share the same constitutive model. Furthermore, fibers can only sustain a tensile strain.

The representation of the fiber distribution at a point has been described by many authors, in 2D [12, 13, 14] and 3D [10]. The orientation of each fiber at a point in the tissue can be represented by the angles θ and ϕ of a spherical coordinate system centered at that point, such that

$${\mathbf{n}}^0=\cos \theta \sin \varphi {\mathbf{e}}_1+\sin \theta \sin \varphi {\mathbf{e}}_2+\cos \varphi {\mathbf{e}}_3-\pi ∕2\le \theta <\pi ∕2,0\le \varphi <\pi$$ (2)

where {e₁, e₂, e₃} represent Cartesian basis vectors. The fraction of all fibers which cross an elemental area dA = sin ϕ dϕdθ on the unit sphere along the (θ, ϕ) direction can be characterized by the fiber angular distribution R (θ, ϕ) [13] (also called a density distribution function [12] or probability density function [14]), where

$$R(\theta ,\varphi )dA=\frac{\text{number of fibers crossing}dA}{\text{total number of fibers}}$$ (3)

Both R and dA are unitless quantities. The fiber angular distribution must therefore satisfy ∫_A R (θ, ϕ) dA = 1. The strain energy density dW contributed by fibers pointing along the (θ, ϕ) direction is

$$dW=R\left({\mathbf{N}}^0\right)H\left(E_n\right)\Psi \left(E_n\right)dA$$ (4)

where we have represented the dependence of R on (θ, ϕ) by the equivalent dependence on the texture tensor N⁰. Note the use of the Heaviside step function H (.) to account for the tension-only response of fibers,

$$H\left(E_n\right)=\{\begin{array}{cc}1\hfill & E_n>0\hfill \\ 0\hfill & E_n<0\hfill \end{array}\phantom{\}}$$ (5)

The total strain energy density in the tissue is thus

$$W\left(\mathbf{E}\right)={\int }_{A}dW={\int }_{-\pi ∕2}^{\pi ∕2}{\int }_0^{\pi }R\left({\mathbf{N}}^0\right)H\left(E_n\right)\Psi \left(E_n\right)\sin \varphi d\varphi d\theta$$ (6)

Both W and Ψ have the same set of units (energy per unit volume), since the remaining quantities in the integral are unitless. The second Piola-Krichhoff stress S and the Lagrangian (material) elasticity tensor $\mathcal{C}$ can be obtained by appropriate differentation of this expression,

$$\mathbf{S}=\frac{\partial W}{\partial \mathbf{E}}={\int }_{-\pi ∕2}^{\pi ∕2}{\int }_0^{\pi }R\left({\mathbf{N}}^0\right)H\left(E_n\right)\frac{\partial \Psi }{\partial E_n}{\mathbf{N}}^0\sin \varphi d\varphi d\theta$$ (7)

$$\mathcal{C}=\frac{\partial \mathbf{S}}{\partial \mathbf{E}}={\int }_{-\pi ∕2}^{\pi ∕2}{\int }_0^{\pi }R\left({\mathbf{N}}^0\right)H\left(E_n\right)\frac{\partial \Psi }{\partial E_n^2}{\mathbf{N}}^0\otimes {\mathbf{N}}^0\sin \varphi d\varphi d\theta$$ (8)

The exact forms of the strain energy density W, stress S and elasticity tensor $\mathcal{C}$ depend on the functions R and Ψ as well as the state of strain. In the next section we examine the influence of the fiber angular distribution R.

2.3 Fiber Angular Distribution

The fiber orientation in a tissue may be perfectly random, in which case the fiber angular distribution is isotropic, with R (N⁰) = 1/2π; for example, this is the case for the middle zone of the collagen matrix of articular cartilage. Clearly, lower symmetries may also be encountered. For example, if all fibers are oriented along a single direction (as in a tendon), or if fibers are randomly oriented in a sheet, the fiber angular distribution is transversely isotropic. Examples of lower symmetries may also be conjured. Two fiber bundles of equal volume fraction, subtending an arbitrary angle, exhibit orthotropic (three planes of) symmetry; this type of structure is observed in the annulus of the intervetebral disc. Two coplanar fiber bundles of unequal volume fraction, subtending an arbitrary angle (≠ π/2), exhibit monoclinic (one plane of) symmetry. At the bottom end of the spectrum is triclinic (no planes of) symmetry, as achieved for example by three fiber bundles of unequal volume fractions, subtending arbitrary angles (≠ π/2).

To represent the symmetry of the fiber angular distribution mathematically, let the planes of symmetry in the reference configuration be represented by the unit normals ${\mathbf{a}}_a^0$ and texture tensors ${\mathbf{A}}_a^0={\mathbf{a}}_a^0\otimes {\mathbf{a}}_a^0(a=1,2,\dots )$. By the definition of the symmetry of R, any orthogonal transformation Q which satisfies

$${\mathbf{QA}}_a^0{\mathbf{Q}}^T={\mathbf{A}}_a^0$$ (9)

will keep the function R (N⁰) invariant,

$$R\left({\mathbf{QN}}^0{\mathbf{Q}}^T\right)=R\left({\mathbf{N}}^0\right)$$ (10)

for all N⁰.

The first proposition that we address is as follows: If all the fibers are under tension in the current configuration κ, H (N⁰ : E) = 1 ∀N⁰, then the body ${\mathcal{B}}_T$ representing the tissue consists of all its fibers, and the material symmetry in the reference configuration κ₀ reflects the symmetry of the fiber angular distribution. This can be verified if it can be shown that

$$W\left({\mathbf{QEQ}}^T\right)=W\left(\mathbf{E}\right)$$ (11)

for any Q that satisfies Eq.(9). Consider the integrand of W = ∫_A w dA in Eq.(6), where

$$w(\mathbf{E},{\mathbf{N}}^0)=R\left({\mathbf{N}}^0\right)\Psi ({\mathbf{N}}^0:\mathbf{E})$$ (12)

Applying the transformation on the strain yields

$$w({\mathbf{QEQ}}^T,{\mathbf{N}}^0)=R\left({\mathbf{N}}^0\right)\Psi ({\mathbf{Q}}^T{\mathbf{N}}^0\mathbf{Q}:\mathbf{E})\ne w(\mathbf{E},{\mathbf{N}}^0)$$ (13)

where we have used Eq.(10). This result shows that the function w is not invariant to transformations Q that keep the fiber angular distribution invariant. Interestingly, it turns out that this conclusion does not apply to W, as will be illustrated in an example below. The question can be restated to ask whether there exists a direction m⁰ with associated M⁰ = m⁰ ⊗ m⁰ such that

$$w({\mathbf{QEQ}}^T,{\mathbf{N}}^0)=w(\mathbf{E},{\mathbf{M}}^0)$$ (14)

for every direction n⁰. Indeed, this equation can be satisfied if

$${\mathbf{m}}^0={\mathbf{Q}}^T{\mathbf{n}}^0{\mathbf{M}}^0={\mathbf{Q}}^T{\mathbf{N}}^0\mathbf{Q}$$ (15)

on the basis of the symmetry condition of Eq.(10). Since W is an integral over all possible directions n⁰, there will always be a matching m⁰ satisfying the above requirement. Thus W does remain invariant to transformations Q which keep the fiber angular distribution invariant, as long as all the fibers are in tension.

This result can be illustrated with a simple example. Consider a planar fiber distribution in the x₁ − x₂ plane such that

$$R(\theta ,\varphi )=\frac{1}{2}\left[\delta \left(\theta -\frac{\pi }{6}\right)+\delta \left(\theta +\frac{\pi }{6}\right)\right]\delta \left(\varphi -\frac{\pi }{2}\right)$$ (16)

where δ is the Dirac delta function. This distribution represents one pair of fiber bundles, oriented at ±π/6 relative to the x₁ − x₃ plane. Using Eq.(2), the unit normals in the directions of the fibers are evaluated as

$$\mathbf{n}\underset{\pm 1}{\overset{0}{}}=\frac{\sqrt{3}}{2}{\mathbf{e}}_1\pm \frac{1}{2}{\mathbf{e}}_2$$

so that

$$\left[{\mathbf{N}}_1^0\right]=\frac{1}{4}\left[\begin{array}{ccc}\hfill 3\hfill & \hfill \sqrt{3}\hfill & \hfill 0\hfill \\ \hfill \sqrt{3}\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\left[{\mathbf{N}}_{-1}^0\right]=\frac{1}{4}\left[\begin{array}{ccc}\hfill 3\hfill & \hfill -\sqrt{3}\hfill & \hfill 0\hfill \\ \hfill -\sqrt{3}\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$$

The three planes of symmetry for these fiber bundles are the coordinate planes, with ${\mathbf{a}}_1^0={\mathbf{e}}_1$, ${\mathbf{a}}_2^0={\mathbf{e}}_2$, ${\mathbf{a}}_3^0={\mathbf{e}}_3$. The strain energy density function is given by $W\left(\mathbf{E}\right)=\frac{1}{2}[\Psi ({\mathbf{N}}_1^0:\mathbf{E})+\Psi ({\mathbf{N}}_{-1}^0:\mathbf{E})]$. For an orthogonal transformation Q which satisfies Eq.(9), we have

$$W\left({\mathbf{QEQ}}^T\right)=\frac{1}{2}[\Psi ({\mathbf{Q}}^T{\mathbf{N}}_1^0\mathbf{Q}:\mathbf{E})+\Psi ({\mathbf{Q}}^T{\mathbf{N}}_{-1}^0\mathbf{Q}:\mathbf{E})]$$

There are six such transformations Q (reflections about the coordinate planes, and half-turn rotations about the coordinate axes). For example, a reflection about the x₁ − x₃ plane is given by Q = e₁ ⊗ e₁ − e₂ ⊗ e₂ + e₃ ⊗ e₃. It is straightforward to show that ${\mathbf{Q}}^T{\mathbf{N}}_1^0\mathbf{Q}={\mathbf{N}}_{-1}^0$ and ${\mathbf{Q}}^T{\mathbf{N}}_{-1}^0\mathbf{Q}={\mathbf{N}}_1^0$, from which it follows that W (QEQ^T) = W (E), thus illustrating that W is invariant to these transformations even though w is not.

2.4 Tension-Compression Nonlinearity

The tension-compression nonlinearity in the fiber response arises as a result of the state of strain. The state of strain can be expressed using the spectral representation of E,

$$\mathbf{E}=\sum _{i=1}^3{E}_i{\mathbf{m}}_i\otimes {\mathbf{m}}_i$$ (17)

where E_i are the eigenvalues of E and m_i are the corresponding eigenvectors. For convenience, let us now consider that the basis vectors of the Cartesian coordinate system are aligned with the eigenvectors of the strain, m_i = e_i (this condition is relaxed subsequently, where required). Substituting Eq.(17) into Eq.(1) and using Eq.(2) yields

$$E_n=E_1{\cos }^2\theta {\sin }^2\varphi +E_2{\sin }^2\theta {\sin }^2\varphi +E_3{\cos }^2\varphi$$ (18)

If all three eigenvalues of E are greater than zero (T case, where the tissue is represented by body ${\mathcal{B}}_T$), then E_n > 0 and H (E_n) = 1 for all directions (θ, ϕ), which implies that all fibers are in tension. In that case, the strain energy function of Eq.(6) reduces to

$$W_T\left(\mathbf{E}\right)={\int }_{-\pi ∕2}^{\pi ∕2}{\int }_0^{\pi }R\left({\mathbf{N}}^0\right)\Psi \left(E_n\right)\sin \varphi d\varphi d\theta$$ (19)

If E₁ ≤ E₂ ≤ 0 < E₃ (TC case, where the tissue is represented by body ${\mathcal{B}}_{TC}$), it is necessary to determine the range of (θ, ϕ) over which the fibers are in tension, E_n > 0. Looking at Eq.(18), it is evident that this range depends on the magnitudes of the eigenvalues of the strain. Setting E_n = 0 and solving for ϕ as a function of θ yields the roots ϕ₀ and π − ϕ₀ where

$${\varphi }_0\left(\theta \right)={\tan }^{-1}\sqrt{-\frac{E_3}{E_1{\cos }^2\theta +E_2{\sin }^2\theta }}$$ (20)

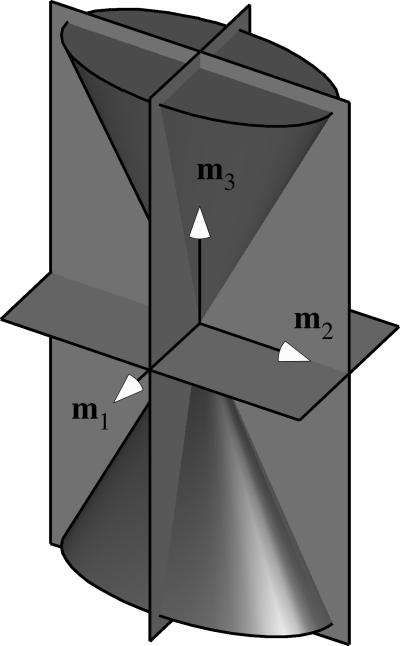
For the TC case, the range of ϕ over which E_n > 0 is 0 ≤ ϕ < ϕ₀ (θ) and π − ϕ₀ (θ) < ϕ < π.² This range describes an elliptical double cone whose apexes meet at the origin and whose axis is along the x₃–direction (Figure 1). The minor and major axes of the cone are along x₁ and x₂ and the minor and major radii of the elliptical base are proportional to $\sqrt{E_3∕E_1}$ and $\sqrt{E_3∕E_2}$. From this result we deduce that only the fibers which fall within this double elliptical cone are in tension. In this case the strain energy function is given by

$$W_{TC}\left(\mathbf{E}\right)={\int }_{-\pi ∕2}^{\pi ∕2}\left[{\int }_0^{{\varphi }_0\left(\theta \right)}R\left({\mathbf{N}}^0\right)\Psi \left(E_n\right)\sin \varphi d\varphi +{\int }_{\pi -{\varphi }_0\left(\theta \right)}^{\pi }R\left({\mathbf{N}}^0\right)\Psi \left(E_n\right)\sin \varphi d\varphi \right]d\theta$$ (21)

Using a similar reasoning, it follows that for the case E₃ ≤ 0 < E₁ ≤ E₂ (CT case, where the tissue is represented by body ${\mathcal{B}}_{CT}$) the fibers are in tension in the complementary region ϕ₀ (θ) < ϕ < π − ϕ₀ (θ) (the region outside of the double elliptical cone) and the strain energy function is

$$W_{CT}\left(\mathbf{E}\right)={\int }_{-\pi ∕2}^{\pi ∕2}{\int }_{{\varphi }_0\left(\theta \right)}^{\pi -{\varphi }_0\left(\theta \right)}R\left({\mathbf{N}}^0\right)\Psi \left(E_n\right)\sin \varphi d\varphi d\theta$$ (22)

Finally, if all three eigenvalues are less than unity (C case, where the body ${\mathcal{B}}_C$ representing the tissue is an empty set) then H (E_n) = 0 and W_C (E) = 0. This means that a purely fibrous tissue cannot resist compression along all directions. The behavior of the material is indeterminate in this case. Of course, real fibrous biological tissues have a ground substance which contributes a separate term to the strain energy function [3], which is not being considered here since the focus is on the influence of fibers on material anisotropy, but is easy to add.³

Figure 1.

Double elliptical cone of normal strain, shown with its three planes of symmetry.

The T case represents the configuration where the material symmetry matches the fiber distribution symmetry, as reviewed in the previous section. The TC and CT cases represent the configurations for which we would like to determine whether the material symmetry is different than the fiber distribution symmetry. Whereas the above equations were presented for the case where the eigenvectors of the strain are aligned with the basis vectors, it is easy to visualize the most general case when the relative orientation is arbitrary (m_i ≠ e_i). In the TC case, fibers are in tension inside the double elliptical cone whose axis is along the eigenvector m₃ and whose minor and major elliptical axes are along m₁ and m₂, whereas in the CT case fibers are in tension in the complementary region outside this double elliptical cone (Figure 1). Note that in the special case where two of the eigenvalues are equal (E₁ = E₂) the elliptical double cone becomes circular.

Fibers which are not in tension make no contribution to the tissue response, therefore the TC case can be interpreted as a fibrous tissue with fibers distributed only within the double elliptical cone, and the CT case with fibers distributed only in the complementary region. These equivalent fiber angular distributions may be represented by

$$\widehat{R}\left({\mathbf{N}}^0\right)\equiv H\left(E_n\right)R\left({\mathbf{N}}^0\right)$$ (23)

Following the reasoning of the previous section, the material symmetry is thus given by the symmetry of R̂ (N⁰). The double elliptical cone has three mutually orthogonal planes of symmetry, which are normal to the eigenvectors m_i of the strain. These are the planes of symmetry of the function H (E_n) in the TC and CT cases. If these planes of symmetry coincide with planes of symmetry of the fiber angular distribution R (N⁰), then R̂ (N⁰) shares the same three planes of symmetry. Thus, we conclude that the material can exhibit no higher than orthotropic symmetry in the TC and CT cases. Of course, in the most general case, there is no guarantee that all three planes of symmetry of the double elliptical cone will coincide with those of the fiber angular distribution. If the fiber angular distribution and elliptical cone of normal strain share only one plane of symmetry the material symmetry is monoclinic, and if they share no plane of symmetry the material symmetry is triclinic.

2.4.1 Isotropic Fiber Angular Distribution

Let us further elaborate on this point. Consider an isotropic (random) fiber angular distribution, in which case every plane is a plane of symmetry for R (N⁰). Thus it is guaranteed that the planes of symmetry of the elliptical double cone of the strain will coincide with planes of symmetry of the fiber angular distribution for any TC or CT strain state, and R̂ (N⁰) will be orthotropic. Therefore, such a fibrous material will behave as an orthotropic material when subjected to a combination of tensile and compressive strains, keeping in mind that the orientation of these planes of orthotropic symmetry may vary with the state of strain.

In the special case when two of the eigenvalues are equal (E₁ = E₂), the double elliptical cone becomes circular and the material symmetry in the TC and CT cases will be raised to transverse isotropy.

2.4.2 Transversely Isotropic Fiber Angular Distribution

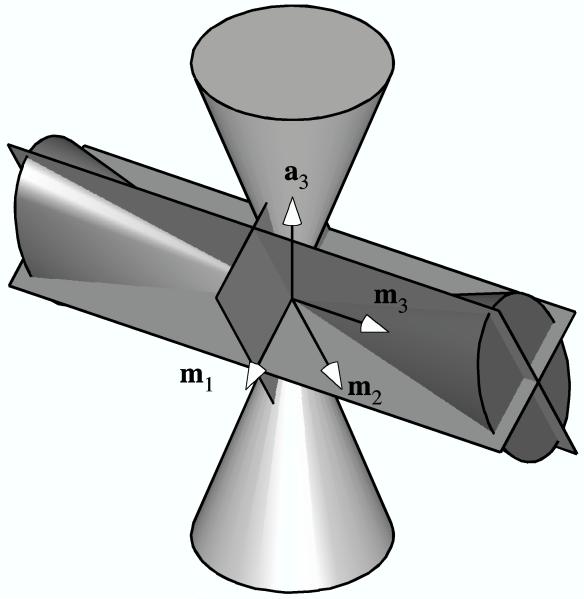
Next, consider a transversely isotropic fiber angular distribution R (N⁰). Such a fiber distribution may consist of fibers distributed inside, outside, or on the surface of a circular cone, with equal volume fractions along the circumferential direction. A special case of general interest for biological tissues would be fibers distributed randomly in a planar sheet. For this distribution R (N⁰), there are an infinite number of planes of symmetry which pass through the axis a₃ of the circular cone, and one plane of symmetry perpendicular to the cone and passing through its apex. In the TC or CT strain state, if the axis m₃ of the elliptical double cone of the strain coincides with the axis a₃ of conical fiber distribution, the three planes of symmetry of H (E_n) coincide with planes of symmetry of R (N⁰) and the material symmetry is orthotropic (Figure 2a). (Once again, as a special case when E₁ = E₂, the material symmetry would rise to transverse isotropy.) Similarly, if the axis m₃ of the elliptical double cone of the strain and either the minor (m₁) or major (m₂) axis lie in the transverse plane of isotropy of the fiber angular distribution, H (E_n) and R (N⁰) share three planes of symmetry and the material is orthotropic (Figure 2b). However, if m₃ lies in the transverse plane of isotropy of the fiber angular distribution but m₁ and m₂ don’t, there is only one plane of symmetry coinciding between H (E_n) and R (N⁰), which is normal to m₃, and the material symmetry is monoclinic (Figure 2c). Similarly, if a₃, m₃ and m₁ (or m₂) are coplanar, there is one common plane of symmetry, which is normal to m₂ (or m₁) and the material symmetry is monoclinic. For any other TC or CT strain state, there will be no common planes of symmetry between the elliptical double cone of the strain and the conical fiber angular distribution, in which case the material symmetry is triclinic (Figure 2d).

Figure 2.

The three planes of symmetry of the elliptical cone of normal strain in relation to planes of symmetry (not shown) of a transversely isotropic fiber angular distribution represented by a cone: (a) Example when all three planes coincide. (b) Alternate example when all three planes coincide. (c) Example of only one coincident plane (normal to m₃). (d) Example of no coincident planes.

The case of a single fiber direction represents a degenerate case for transversely isotropic fiber angular distributions. As long as the fiber direction falls within the double elliptical cone of normal strain (in the TC case) or outside of it (in the CT case), the fibers are in tension and the material symmetry is never lower than transversely isotropic.

2.4.3 Orthotropic Fiber Angular Distribution

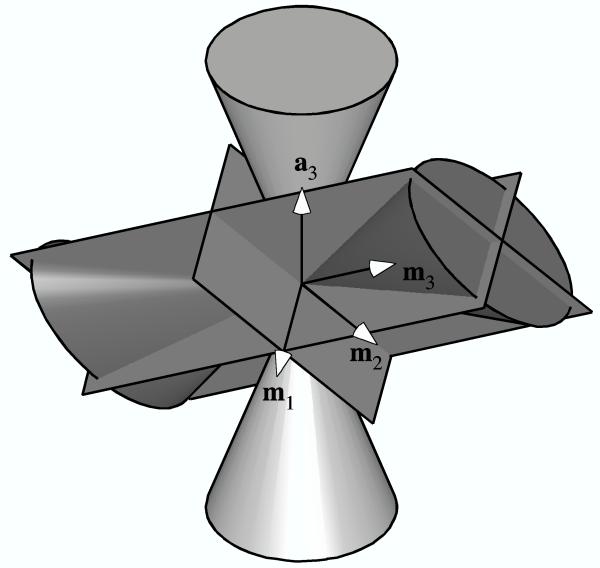
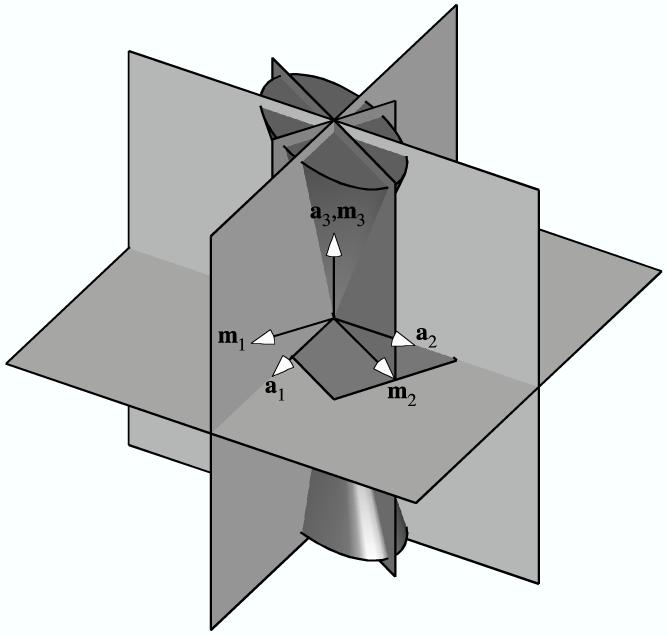
An orthotropic fiber angular distribution has three mutually orthogonal planes of symmetry. In the TC or CT strain state, if the planes of symmetry of the elliptical double cone of the strain coincide with those of the fiber angular distribution, the material symmetry remains orthotropic (Figure 3a). If only one of the planes of H (E_n) and R (N⁰) coincide the material symmetry reduces to monoclinic (Figure 3b), and if none of the planes coincide the material symmetry is triclinic (Figure 3c).

Figure 3.

The three planes of symmetry of the elliptical cone of normal strain (with unit normals {m₁, m₂, m₃}) in relation to the three planes of symmetry of an orthotropic fiber angular distribution (with unit normals {a₁, a₂, a₃}): (a) Example when all three planes coincide. (b) Example of only one coincident plane (normal to a₃ and m₃). (d) Example of no coincident planes.

Degenerate cases arise when the orthotropic fiber angular distribution results from three or two discrete fiber bundles. For example, in the case of three mutually orthogonal fiber bundles of unequal volume fractions, the strain field may place all three bundles in tension, in which case the material symmetry is orthotropic; or two of the bundles are in tension, also producing orthotropic material symmetry; or only a single bundle is in tension, in which case the material symmetry rises to transverse isotropy. Another possible orthotropic fiber bundle configuration yielding similar results consists of two fiber bundles of equal volume fraction, subtending an arbitrary angle, with a third fiber bundle of unequal volume fraction, orthogonal to the other two. Unlike the first example, this case can produce a shift in the planes of orthotropic material symmetry, depending on which fiber bundles are in tension, since two of the fiber bundles are not orthogonal to each other.

2.4.4 Monoclinic Fiber Angular Distribution

A monoclinic fiber angular distribution has only one plane of symmetry. An example of such a distribution would be a planar sheet of fibrous material (ϕ = π/2) with an asymmetric fiber angular distribution R (θ) in the plane of the sheet, and (optionally) a fiber bundle orthogonal to the sheet. Hence the only plane of symmetry is that of the sheet. In the TC and CT cases, if one of the planes of symmetry of the double elliptical cone of normal strain coincides with the symmetry plane of the fiber angular distribution, the material symmetry remains monoclinic, otherwise it reduces to triclinic.

Degenerate cases may also arise in the case of three or two discrete fiber bundles. For example, three fiber bundles of unequal volume fractions, with the first two bundles subtending an arbitrary angle and the third bundle orthogonal to the other two, produce a monoclinic fiber angular distribution whose single plane of symmetry is the plane of the non-orthogonal fiber bundles. Depending on which fibers are in tension, the material symmetry may remain monoclinic, or rise to orthotropy or transverse isotropy.

2.5 Example of an Isotropic Fiber Angular Distribution

In order to illustrate these results for a specific fiber distribution symmetry, it is necessary to formulate a constitutive relation for Ψ (E_n). The simplest function (the first relevant term in a series expansion of the strain energy density) is given by

$$\Psi \left(E_n\right)=\frac{{\lambda }_f}{2}{E}_n^2$$ (24)

where λ_f is the fiber modulus. For reasons discussed below, this example, which has the benefit of yielding a closed-form solution, is most relevant in the range of small strains. The corresponding fiber stress and elasticity tensors are

$${\mathbf{S}}^f=\frac{\partial \Psi }{\partial E_n}{\mathbf{N}}^0={\lambda }_f{E}_n{\mathbf{N}}^0$$ (25)

$${\mathcal{C}}^f=\frac{{\partial }^2\Psi }{\partial E_n^2}{\mathbf{N}}^0\otimes {\mathbf{N}}^0={\lambda }_f{\mathbf{N}}^0\otimes {\mathbf{N}}^0$$ (26)

We consider the case where the fibers are randomly oriented, which yields an isotropic fiber angular distribution where R (N⁰) = 1/2π. Since there is no preferred fiber orientation, there is no loss of generality in considering that the eigenvectors of the strain are aligned with the basis vectors. First consider the state of pure tension (all three principal strains positive). Substituting this expression for R (N⁰) into Eq.(19), using the expression for E_n in Eq.(18) and evaluating the resulting integral yields

$$W_T=\frac{{\lambda }_f}{30}[3(E_1^2+E_2^2+E_3^2)+2(E_1{E}_2+E_1{E}_3+E_2{E}_3)]$$ (27)

Given that

$$\mathrm{tr}\mathbf{E}=E_1+E_2+E_3\mathrm{tr}{\mathbf{E}}^2=E_1^2+E_2^2+E_3^2$$ (28)

this expression can also be written in the form of the strain energy function of an isotropic material,

$$W_T=\frac{\lambda }{2}{\left(\mathrm{tr}\mathbf{E}\right)}^2+\mu \mathrm{tr}{\mathbf{E}}^2$$ (29)

with material coefficients

$$\lambda =\mu =\frac{{\lambda }_f}{15}$$ (30)

The corresponding stress and elasticity tensors can be obtained from

$$\mathbf{S}=\lambda \left(\mathrm{tr}\mathbf{E}\right)\mathbf{I}+2\mu \mathbf{E}$$ (31)

$$\mathcal{C}=\lambda \mathbf{I}\otimes \mathbf{I}+2\mu \mathbf{I}\underset{-}{\overset{-}{\otimes }}\mathbf{I}$$ (32)

using the above Lamé constants. This has the form of the constitutive relation of a St-Venant-Kirchhoff material and is therefore subject to similar limitations in the range of large strains; in the range of small strains, this would yield a linear isotropic elastic material with Young’s modulus E_Y = λ_f/6 and Poisson’s ratio ν = 1/4.

For the TC case (E₁ ≤ E₂ ≤ 0 < E₃), the strain energy function is obtained by substituting Eq.(18) into Eq.(21), and using the expression for ϕ₀ in Eq.(20). Unfortunately the resulting integral cannot be solved in closed form. However, in the special case when E₁ = E₂,

$${\varphi }_0={\tan }^{-1}\sqrt{-E_3∕E_1}$$ (33)

is independent of θ and the integral can be evaluated analytically to produce the strain energy function of a transversely isotropic material,

$$\begin{array}{cc}\hfill W_{TC}=& \frac{{\lambda }^T}{2}{\left(\mathrm{tr}\mathbf{E}\right)}^2+{\mu }^T\mathrm{tr}{\mathbf{E}}^2+({\lambda }^L-{\lambda }^T)\left(\mathrm{tr}\mathbf{E}\right)\left(\mathrm{tr}{\mathbf{M}}_3\mathbf{E}\right)\hfill \\ \hfill & +\left(\frac{{\lambda }^T+\lambda }{2}-{\lambda }^L-\mu +{\mu }^T\right){\left(\mathrm{tr}{\mathbf{M}}_3\mathbf{E}\right)}^2+2(\mu -{\mu }^T)\mathrm{tr}{\mathbf{M}}_3{\mathbf{E}}^2\hfill \end{array}$$ (34)

with material coefficients

$$\begin{array}{cc}\hfill & \lambda =\frac{{\lambda }_f}{1920}(128-30\cos {\varphi }_0-95\cos 3{\varphi }_0-3\cos 5{\varphi }_0)\hfill \\ \hfill & \mu =\frac{{\lambda }_f}{3840}(256-210\cos {\varphi }_0-25\cos 3{\varphi }_0-21\cos 5{\varphi }_0)\hfill \\ \hfill {\lambda }^T=& {\mu }^T=\frac{{\lambda }_f}{30}{\sin }^6\left(\frac{{\varphi }_0}{2}\right)(19+18\cos {\varphi }_0+3\cos 2{\varphi }_0)\hfill \\ \hfill & {\lambda }^L=\frac{{\lambda }_f}{480}(32-30\cos {\varphi }_0-5\cos 3{\varphi }_0+3\cos 5{\varphi }_0)\hfill \end{array}$$ (35)

The corresponding stress and elasticity tensors are given by

$$\begin{array}{cc}\hfill \mathbf{S}=& {\lambda }^T\left(\mathrm{tr}\mathbf{E}\right)\mathbf{I}+2{\mu }^T\mathbf{E}+({\lambda }^L-{\lambda }^T)[\left(\mathrm{tr}\mathbf{E}\right){\mathbf{M}}_3+\left(\mathrm{tr}{\mathbf{M}}_3\mathbf{E}\right)\mathbf{I}]\hfill \\ \hfill & +[\lambda +{\lambda }^T-2({\lambda }^L+\mu -{\mu }^T)]\left(\mathrm{tr}{\mathbf{M}}_3\mathbf{E}\right){\mathbf{M}}_3+2(\mu -{\mu }^T)({\mathbf{M}}_3\mathbf{E}+{\mathbf{EM}}_3)\hfill \end{array}$$ (36)

$$\begin{array}{cc}\hfill \mathcal{C}=& {\lambda }^T\mathbf{I}\otimes \mathbf{I}+2{\mu }^T\mathbf{I}\underset{-}{\overset{-}{\otimes }}\mathbf{I}+({\lambda }^L-{\lambda }^T)[\mathbf{I}\otimes {\mathbf{M}}_3+{\mathbf{M}}_3\otimes \mathbf{I}]\hfill \\ \hfill & +[\lambda +{\lambda }^T-2({\lambda }^L+\mu -{\mu }^T)]{\mathbf{M}}_3\otimes {\mathbf{M}}_3+2(\mu -{\mu }^T)({\mathbf{M}}_3\underset{-}{\overset{-}{\otimes }}\mathbf{I}+\mathbf{I}\underset{-}{\overset{-}{\otimes }}{\mathbf{M}}_3)\hfill \end{array}$$ (37)

It can be verified that when ϕ₀ = π/2 we recover the tension-only case, with isotropic symmetry.

For the CT case (E₃ ≤ 0 < E₁ ≤ E₂), using Eq.(22), the analysis also yields a transversely isotropic material symmetry, with

$$\begin{array}{cc}\hfill & \lambda =\frac{{\lambda }_f}{1920}(30\cos {\varphi }_0+95\cos 3{\varphi }_0+3\cos 5{\varphi }_0)\hfill \\ \hfill & \mu =\frac{{\lambda }_f}{3840}(210\cos {\varphi }_0+25\cos 3{\varphi }_0+21\cos 5{\varphi }_0)\hfill \\ \hfill & {\lambda }^T={\mu }^T=\frac{{\lambda }_f}{1920}(150\cos {\varphi }_0-25\cos 3{\varphi }_0+3\cos 5{\varphi }_0)\hfill \\ \hfill & {\lambda }^L=\frac{{\lambda }_f}{60}{\cos }^3{\varphi }_0(7-3\cos 2{\varphi }_0)\hfill \end{array}$$ (38)

which reduces to the tension-only isotropic case when ϕ₀ = 0. It can be noted that W_TC + W_CT = W_T. We conclude that the TC and CT cases result in a loss of symmetry relative to the T case. In general, the reduction is from isotropic to orthotropic symmetry; however, in the above illustrative case where E₁ = E₂, the reduction is to transversely isotropic symmetry.

Consider a rectangular or cylindrical bar of the fibrous material in this example, being loaded in tension along x₃. Let the lateral strains be equal, E₁ = E₂. Furthermore, they are assumed to be negative while E₃ > 0, so that Eqs.(35)-(36) are applicable. The lateral and axial normal stresses are thus given by

$$\begin{array}{c}{S}_{11}=2({\lambda }^T+{\mu }^T)E_1+{\lambda }^L{E}_3\hfill \\ S_{33}=2{\lambda }^L{E}_1+(\lambda +2\mu )E_3\hfill \end{array}$$ (39)

These equations are well defined for arbitrary choices of E₁ ≤ 0 and E₃ > 0, whose ratio produces a corresponding value of ϕ₀ according to Eq.(33), which can be substituted into Eq.(35) to yield well defined values of the material coefficients. It can be verified that a strictly tensile value of S₁₁ is achieved in all cases, indicating that the fibers are pulling inward in an effort to shrink in the lateral direction upon tensile axial loading.

Interestingly, a lateral stress-free state cannot be achieved by this material for any strictly positive value of E₃. This can be demonstrated by letting S₁₁ = 0 above, solving for the ratio −E₃/E₁, substituting it into Eq.(33) and making use of Eq.(35) to produce

$$\tan {\varphi }_0=\sqrt{\frac{-5\cos {\varphi }_0-12\cos 2{\varphi }_0-3\cos 3{\varphi }_0+20}{25\cos {\varphi }_0+12\cos 2{\varphi }_0+3\cos 3{\varphi }_0+20}}$$ (40)

whose only solution (in the range 0 ≤ ϕ₀ ≤ π/2) is ϕ₀ = 0. According to Eq.(33), this solution is incompatible with a positive axial strain and negative (but finite) lateral strain. The implication from this result is that an idealized fibrous material with random fiber angular distribution and zero compressive modulus exhibits an unstable behavior, collapsing laterally under uniaxial tensile loading.⁴ The fact that real fibrous tissues do not exhibit such a collapse can be explained by the presence of a ground matrix which can sustain compression. For example, if the ground matrix is isotropic with Lamé constants λ_g and μ_g, the expressions for the lateral and axial normal stresses become

$$\begin{array}{c}\hfill S_{11}=2({\lambda }^T+{\mu }^T+{\lambda }_g+{\mu }_g)E_1+({\lambda }^L+{\lambda }_g)E_3\hfill \\ \hfill S_{33}=2({\lambda }^L+{\lambda }_g)E_1+(\lambda +2\mu +{\lambda }_g+2{\mu }_g)E_3\hfill \end{array}$$ (41)

and the corresponding equation needed to solve for ϕ₀ in the case when S₁₁ = 0 is

$$\tan {\varphi }_0=\sqrt{2}\sqrt{\frac{\frac{1}{15}{\lambda }_f(18\cos {\varphi }_0+3\cos 2{\varphi }_0+19){\sin }^6\left(\frac{{\varphi }_0}{2}\right)+{\lambda }_g+{\mu }_g}{{\lambda }_g+\frac{1}{480}{\lambda }_f(-30\cos {\varphi }_0-5\cos 3{\varphi }_0+3\cos 5{\varphi }_0+32)}}$$ (42)

This equation admits any number of solutions for ϕ₀, depending on the values of λ_g/λ_f and μ_g/λ_f. Once a solution for ϕ₀ has been obtained, the tensile Young’s modulus and Poisson’s ratio can be deduced from Eqs.(33) and (41),

$$\begin{array}{cc}\hfill E_Y=-\frac{1}{5}{\lambda }_f{\cos }^5{\varphi }_0+\frac{{\lambda }_f}{5}& +{\lambda }_g+2{\mu }_g\hfill \\ \hfill & -\frac{{[(3\cos 2{\varphi }_0-7){\lambda }_f{\cos }^3{\varphi }_0+4({\lambda }_f+15{\lambda }_g)]}^2}{240[(18\cos {\varphi }_0+3\cos 2{\varphi }_0+19){\lambda }_f{\sin }^6\left(\frac{{\varphi }_0}{2}\right)+15({\lambda }_g+{\mu }_g)]}\hfill \end{array}$$ (43)

$$\nu =-\frac{E_1}{E_3}=\frac{1}{{\tan }^2{\varphi }_0}$$ (44)

For example, for the case μ_g/λ_f = 0 (which is representative of a ground substance consisting of a charged macromolecular species, such as proteoglycans, that can resist only a hydrostatic stress [15]), a plot of ϕ₀ versus λ_g/λ_f is shown in Figure 4. The upper bound on ϕ₀ is ${\varphi }_0^{\infty }={\tan }^{-1}\sqrt{2}$ as λ_g/λ_f → ∞. This means that an increasingly stiff ground matrix helps to recruit more fibers to resist tensile loading, but at most, only those fibers which fall within a cone of angle ${\varphi }_0^{\infty }=54.7°$ relative to the loading direction will be under tension. The tensile Young’s modulus is presented in Figure 5. In the limit as λ_g/λ_f → 0, this modulus reduces to 0. In the opposite limit, as λ_g/λ_f → ∞, it tends to $E_Y^{\infty }=(9-2\sqrt{3}){\lambda }_f∕45$; this represents the tensile modulus when as many fibers as possible have been recruited for this loading configuration. The numerical value of this expression, $E_Y^{\infty }\approx 0.123{\lambda }_f$, shows that the tensile Young’s modulus of a fibrous tissue with random fiber angular orientation can never exceed one-eighth of the fiber’s modulus. (Contrast this result to the T case, where Young’s modulus is one-sixth of the fiber’s modulus.)

Figure 4.

Conical angle of fiber recruitment, ϕ₀, versus λ_g/λ_f, for uniaxial loading of a bar of fibrous material with isotropic fiber angular distribution.

Figure 5.

Tensile Young’s modulus for the example shown in Figure 4, normalized to $E_Y^{\infty }=(9-2\sqrt{3}){\lambda }_f∕45$.

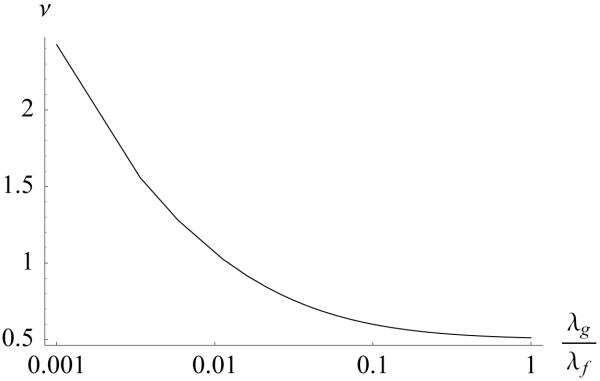
The corresponding tensile Poisson’s ratio is shown in Figure 6. In the limit as λ_g/λ_f → 0, Poisson’s ratio goes to infinity, consistent with the above explanation of a lateral collapse in the absence of a ground matrix. In the opposite limit, as λ_g/λ_f → ∞, the lower bound on Poisson’s ratio is ν^∞ = 1/2 as can be deduced from Eq.(42). The predicted range of this tensile Poisson’s ratio is consistent with experimental measurements on articular cartilage, ν ~ 0.6 – 1.9 [16, 17], and hip capsular ligament, ν = 1.4 [18], which would suggest that λ_g/λ_f ~ 0.002 – 0.1 for these tissues. Thus, a ground matrix whose bulk modulus is much smaller than the fiber modulus produces tensile Poisson’s ratios well in excess of 1/2.

Figure 6.

Apparent Poisson’s ratio ν = −E₁/E₃ = 1/ tan² ϕ₀ corresponding to Figure 4.

3 Discussion

The main objective of this study was to analyze the material symmetry of fibrous tissues undergoing tension and compression to better understand how this symmetry may depend on the choice of reference configuration in a tissue where some of the fibers may be buckled in the current configuration. The first finding, which agrees with our intuitive expectation, is that the material symmetry of a fibrous tissue for which all the fibers are in tension in the current configuration is dictated by the symmetry of its fiber angular distribution.

However, if the strain field in the current configuration exhibits a mix of tensile and compressive principal normal strains, the fibrous tissue is only defined by those fibers which are in tension; thus, the material symmetry is dependent upon the superposition of the planes of symmetry of the strain and the planes of symmetry of the angular fiber distribution. In other words, the material symmetry is dictated by the symmetry of the angular distribution of only those fibers which are in tension. In the analysis of this study we provide a straightforward approach for determining this material symmetry, which can be conveniently illustrated by 3D representations.

In the most general case, the directions of positive fiber strains at a point in the continuum fall either inside a double elliptical cone whose apexes meet at that point (TC case), or its complementary region in 3D space (CT case). These domains exhibit three planes of symmetry, normal to the conical axis as well as to the minor and major axes of the elliptical cross-section (Figure 1). If these three planes of symmetry coincide with planes of symmetry of the fiber angular distribution, the material symmetry for a non-degenerate distribution is generally orthotropic. Under special conditions, depending on the fiber distribution and the strain field as outlined in the above treatment, the material symmetry may rise to transverse isotropy. However, if only one plane of symmetry of the strain distribution coincides with a plane of symmetry of the fiber angular distribution, the material symmetry drops to monoclinic; and if no planes coincide, the material symmetry is triclinic.

We conclude from these results that the material symmetry is not only a function of the fiber angular distribution but also the strain field in the current configuration, which together determine which fibers enter into the definition of the body in the reference configuration. In effect, the apparent behavior of the tissue may be viewed as a strain-induced anisotropy which manifests itself even in the range of infinitesimal strains, which is distinct from that resulting from finite rotation of fibers under large deformations. However, from a continuum mechanics perspective, it should be understood that an idealized fibrous tissue whose buckled fibers are effectively non-existent fibers is in fact represented by different bodies, each of which consists only of fibers which are in tension, thus exhibiting their own material symmetry. The nature of the material symmetry (isotropy, orthotropy, etc.) is not dependent on the specific constitutive relation for the fiber strain energy density, Ψ (E_n). It is not dependent on the magnitude of the principal normal strains either, only on their algebraic signs (differentiating the T, TC, CT and C cases). However, the material coefficients associated with the TC and CT cases do depend on the ratio of tensile to compressive strains as manifested in the general expression for ϕ₀ in Eq.(20). As shown in the example of an isotropic fiber angular distribution in Eq.(33), ϕ₀ is a function of the ratio E₃/E₁, which represents the conical angle of the double cone encompassing fibers under tension (TC case) or compression (CT case). In general, the magnitude of ϕ₀ can vary widely even in the range of infinitesimal strains. Hence the magnitude of the material coefficients in the TC and CT cases, Eqs.(35) and (38), is very sensitive to the state of strain.

Based on the illustrative example of an isotropic fiber angular distribution where the fiber strain energy density is a quadratic function of E_n, it appears that the constitutive relations for fibrous materials represent subclasses of their respective material symmetries. In the example examined above, the Lamé constants shown in Eq.(30) are not distinct, as otherwise expected in the most general class of isotropic materials. A similar observation can be made about the material constants for transversely isotropic symmetry, shown in Eqs.(35)-(38), and this observation is expected to hold for lower material symmetries. The concept that structural models can only represent continua with fixed Poisson’s ratio is not new and has been shown by Hrennikof in the study of trusses [19]. This finding is also indirectly related to that of Billiar and Sacks [13], who noted that microstructural models may require fewer material coefficients than phenomenological models to describe the same tissue response, a proposition supported by their experimental study on aortic valve cusp.

A material consisting only of fibers, which can sustain tension but not compression, cannot be stable under all strain configurations. This is evident when all three principal normal strains are negative (C case), but also occurs under other configurations as shown in the case of uniaxial loading of a fibrous tissue with random fiber angular distribution. Even though that illustrative example was limited in its general applicability to fibrous tissues in the range of small strains, the stability problem arose from the inability of fibers to sustain compression, regardless of the magnitude of strain. Since the quadratic strain energy formulation adopted in that model would represent the first term in a Taylor series of a more general constitutive function which is convex at the strain origin, it is expected that this instability would manifest itself regardless of the general form of Ψ (E_n). As also shown in the same example, a ground matrix is essential for providing stability under all strain configurations. Therefore, in practice, microstructural constitutive models for fibrous tissues should incorporate the ground matrix, as advocated by Humphrey and Yin [3] and many subsequent authors (e.g., [20]). If the ground matrix is isotropic, all of the above conclusions regarding the strain-induced material symmetry of fibrous tissues remain unchanged. For an anisotropic ground matrix, the material symmetry of the tissue would depend on the configuration of the superposition of the planes of symmetry of the fiber angular distribution, ground matrix, and elliptical cone of normal strain, following a straightforward extension of the approach described above.

If we now place the results of this microstructural analysis in the wider context of the literature on phenomenological theories of elastic solids which exhibit different moduli in tension and compression, a number of interesting observations follow. We find that a fibrous material with isotropic fiber angular distribution cannot remain isotropic when subjected to a strain field exhibiting a mix of tensile and compressive principal normal strains. This observation confirms the speculative statement in the study of Rigbi [5], who suspected that it was not possible to have a bimodulus material remain isotropic under these conditions. It also follows from the above analysis that a fibrous tissue with isotropic fiber angular distribution is not adequately described by the bimodular isotropic half-spacewise elasticity model of Curnier et al. [6], which preserves isotropic material symmetry under a mix of tensile and compressive principal strains, but allows the first Lamé constant λ to assume different values whether tr E is negative or positive (in the case of infinitesimal strains).

Since the material symmetry of a fibrous tissue with isotropic fiber angular distribution generally reduces to orthotropy in the TC and CT cases according to the microstructural analysis of this study, we also find that the continuum model of Green and Mkrtichian [7] cannot capture this behavior since it assumes that the lowest material symmetry in these cases is transverse isotropy. However, the orthotropic octantwise elasticity model of Curnier et al. [6] is consistent with the degenerate case of three mutually orthogonal fiber bundles, since both models maintain the same three planes of symmetry under all strain states, and both allow the same material coefficients to vary depending on which fiber bundle is in tension. Nevertheless, the orthotropic octantwise elasticity model is not representative of the most general case of orthotropic fiber angular distributions, since it cannot predict material symmetries lower than orthotropy as the microstructural model does. Finally, the elasticity tensor of a fibrous material, as summarized in Eq.(8), exhibits the usual major and minor symmetries (i.e., C_ijkl = C_klij, C_jikl = C_ijkl, C_ijlk = C_ijkl) regardless of the state of strain (T, TC or CT cases), as also verified in the special example of an isotropic fiber angular distribution. Therefore the asymmetric elasticity tensor advocated by Bert [21] for fibrous composites with different properties in tension and compression is not supported by the microstructural analysis adopted here.

In summary, microstructural models of fibrous materials exhibit a range of material symmetries dependent upon the distribution of tensed and buckled fibers, with strain-dependent material coefficients, even in the range of infinitesimal strains. The behavior predicted using a microstructural model of the fibers cannot be described exactly by phenomenological continuum models, which either prescribe the material symmetry a priori, allowing some of the material coefficients to assume different values depending on the state of strain, or prescribe distinct material symmetries depending on the state of strain, each with constant material coefficients. Based purely on this theoretical argument, if fibrous tissues truly behave as predicted by idealized microstructural models, the goal of modeling their full complexity would ultimately prove futile when using purely phenomenological constitutive models. Of course, no biological tissue is expected to behave exactly as predicted by the idealized microstructural model adopted in this study. Indeed, fibers do not truly exhibit the idealized tension-only response assumed here; therefore they may sustain some amount of compression, particularly if butressed by a ground matrix. Nevertheless, the idealized model does suggest a complex interaction between the state of strain and material symmetry, which may serve as an important guiding principle in the constitutive modeling of fibrous tissues.