Perceiving parts and shapes from concave surfaces

Abstract

“A hole is nothing at all, but it can break your neck.” In a similar fashion to the danger illustrated by this folk paradox, concave regions pose difficulties to theories of visual shape perception. We can readily identify their shapes, but according to principles of how observers determine part boundaries, concavities in planar surface should have very different figural shapes from the ones we perceive. Three experiments tested the hypothesis that observers perceive local image features differently from simulated 3D concave and convex regions, but use them to arrive at similar shape percepts. Stimuli were shape-from-shading images containing regions that appeared either concave or convex in depth depending on their orientation in the picture plane. The results show that concavities did not benefit from the same global object-based attention or holistic shape encoding as convexities, and that participants relied on separable spatial dimensions to judge figural shape in concavities. Concavities may exploit a secondary process for shape perception that allows regions composed of perceptually independent features ultimately to be perceived as gestalts.

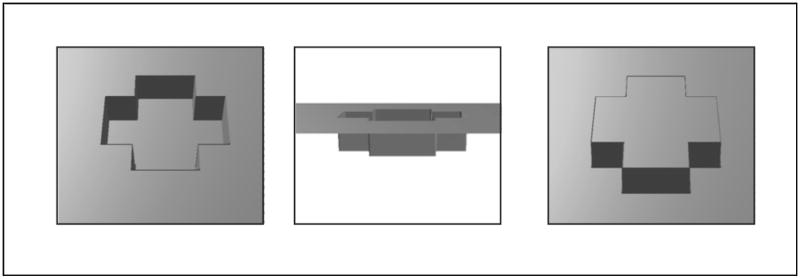
The label “hole” can be applied to numerous kinds of structures (for a philosophical review, see Casati & Varzi, 1994). This study focuses on the specific case of concave regions that are bounded by a planar surface, as in Figure 1. This kind of stimulus is useful both because it resembles the kind of common real-world hole that can break your neck (e.g. an unexpected pothole), and, more importantly, because the depth dimension is orthogonal to the 2D planar outline shape of the bounding cusp. We exploit this latter property to compare the perception of local surfaces that form either concave or convex versions of 3D shapes that project the same bounding contour (Experiment 1), and to examine how the perception of a 2D outline changes when it is defined by a 3D concavity or a 3D convexity (Experiment 2), in addition to comparing observers’ judgments of 3D concavities and convexities as whole objects (Experiment 3). In this study, depth information is conveyed using purely pictorial (monocular) cues; the transformation used to change apparent depth (rotation in the picture plane) does not alter the low-level properties of the images themselves (for example image reflectance, contrast, and spatial frequencies are unchanged), but only leads the observer to interpret them differently. Thus, any effects of depth are the consequences of the depth interpretation, and not of the distal cues themselves, thereby differing, for example, from reversing the sign of disparity in stereograms. Even though the stimuli were created purely in 2D, we use the term “3D concavity” to distinguish regions of a planar surface that appear concave with respect to depth from “2D concavities” which are the concave portions of a 2D shape boundary that lie in the plane itself. Finally, it should be noted that while these investigations focused on perceptual differences, there are other very salient functional differences between 3D concavities and convexities. For example, hand-sized solid masses and holes afford very different kinds of actions (c.f. Subirana-Vilanova & Richards, 1996; Palmer, Davis, Nelson, & Rock, 2008); even the concave and convex aspects of the same object such as a bowl require different gripping actions.

Figure 1.

The type of hole that is the focus of this study. Left: a concavity bounded by a flat plane, with a closed bounding contour. Middle: the concavity shown as an indentation in a planar sheet. Right: the concavity shown rotated 180° in depth so that it appears as a convex bulge with the same 2D bounding contour.

Surface concavities and convexities should not have the same perceived shapes according to Gestalt principles

One of the Gestalt principles for predicting which region of an image will be perceived as figure is the convexity principle (Kanisza & Gerbino, 1976). All things being equal, a 2D region bounded by convex curvature in its contour will be perceived as the figure. This principle was extended by Stevens and Brookes (1988) who found that the presence of locally concave features (concave cusps) acted over and above global contour concavity to cause regions to be identified as grounds. Since such grounds tend not to be recognized when presented later as isolated shapes (i.e. without the figural part of the original image, Palmer et al., 2008), in this case contours that are primarily concave would likely be associated with poor shape encoding.

However, the shape of the region corresponding to a concavity in depth bounded by a planar surface (as in Figure 1) appears unambiguously figural. In this 3D case, concavities can produce the same (or at least very similar) shape percepts as the solid regions that would fill these holes. Such an interpretation is similar to findings from recent research on the perception of 2D holes (apertures in planes). Indeed, when observers perceive shapes from 2D holes (apertures in planes) they remember these shapes just as well as they do solid planar shapes (Palmer et al., 2008). When the shape described by a hole’s outline is perceived, observers may perceive the hole to have the same shape as its corresponding solid object, either based directly on the shape of the empty region itself (Nelson & Palmer, 2001; Palmer et al., 2008), or indirectly based on the shape of the surrounding solid material (Bertamini & Croucher, 2003). In any case, 2D holes appear not to be perceived via the same processes as figural shapes associated with solid material. Investigations have shown that switching from a convex to a concave interpretation of a planar contour reverses the figure-ground status of the two sides of the contour (Baylis & Driver, 1993; Bertamini & Croucher, 2003), and changes the perceived part structure of a region (Barenholtz, Cohen, Feldman, & Singh, 2003; Bertamini & Farrant, 2005; Cohen, Barenholtz, Singh, & Feldman, 2005). This, in turn, leads to performance differences for solid shapes and aperture holes in different kinds of psychophysical tasks (Bertamini & Lawson, 2006). This is all in spite of the fact that regardless of whether a region is perceived to be a hole or a surface, the bounding contour is the same and thus has the potential to convey the same amount of image information (Bertamini & Croucher, 2003).

A 3D concavity is unambiguously associated with solid material (the sides and bottom of the hole) in addition to the empty space it encompasses. What may differ, then, between the perception of shape from 3D concavities and convexities is the type and amount of information that observers glean from the same image when a surface appears to encompass solid material versus empty space. The current study focuses on three key questions related to the idea that similar figural shapes are ultimately perceived from 3D concavities and convexities in spite of differences in how observers perceive their local features. Proceeding in a local-to-global order of analysis, we first ask: are the perceived relationships between local image elements in 3D concavities different from those in 3D convexities? Second, since the 2D shape projected by the bounding cusp of 3D convexities and concavities can be the same, are there differences in the perceived part structure of identical 2D shapes when they are associated with 3D concave and convex regions? Third, is the same shape gestalt in fact perceived equally well from 3D convexities and concavities?

Experiment 1

Effects of 3D depth on perceived part structure

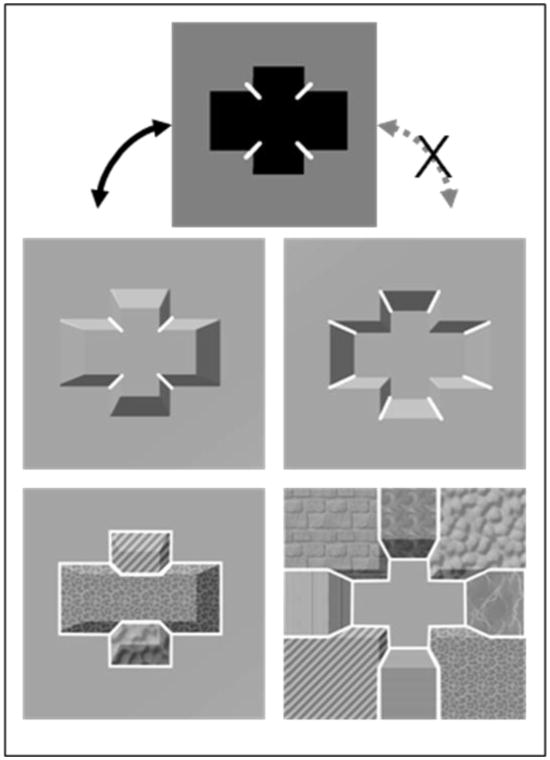
An a priori reason for believing that local shape features are encoded differently from 3D concavities and convexities comes from the minima rule of Hoffman and Richards (1984). The minima rule posits that minima of curvature are crucial to parsing objects: “Divide a surface into parts at loci of negative minima of each principal curvature along its associated family of lines of curvature (p. 74).” Essentially, an object can be divided into parts with boundaries formed on the maximally concave sections of each curved contour present on the object. A key implication of the minima rule is that similar 3D concave and convex regions ought to have different part boundaries.ⁱ The middle row of Figure 2 shows the same cross-shaped 3D region portrayed as both a concavity and a convexity. Superimposed lines indicate local minima of curvatureⁱⁱ. Note that there are twice as many minima in the concave version -- this is because the 2D cross shape itself has uneven numbers of concave and convex extrema of 2D curvature. The minima rule can be applied to 2D shapes as well as to 3D shapes, and the positions of the minima of curvature for a 3D convexity and its 2D projection align (Figure 2), but this is not the case for 3D concavities. Hence we can hypothesize that the shape of a 3D concavity will not be perceived as holistically as its 3D convex counterpart (because it is subdivided by more part boundaries), nor will it share the same general pattern of within- and between-part effects (Barenholtz & Feldman, 2003) with its 2D outline shape (in contrast to a 3D convexity).

Figure 2.

Top: Minima of curvature marked on a 2D cross shape. These minima of curvature correspond to minima that cut through the sides of a 3D convexity, but not to those of a 3D concavity, which are complementary. Middle: These minima of curvature marked on equivalent convex and concave 3D versions of the cross shape. There are twice as many minima cutting through the sides in the concave version. Bottom: Part structures (indicated by different image textures) based on the convex and concave minima and on the “shortcut rule” of Singh et al. (1999). It is unclear precisely how the concave image’s part boundaries radiate out past the cusp of the concavity. However, since the cusp itself is a maximum of curvature, the facets oriented in depth which form the sides of the concavity belong with regions of the surrounding plane, rather than with the surface forming the bottom of the hole.

Experiment 1 used a flanker task, inspired by studies of object- and part-based attention (Kramer & Jacobson, 1991; Vecera, Behrmann, & McGoldrick, 2000; Vecera, Behrmann, & Filapek, 2001; Barenholtz & Feldman, 2003), to test whether 3D concavities and convexities influence attention to local image elements differently, and, by extension, whether their surfaces are perceived more like independent parts or not. The dependent measure was a difference score comparing performance on two types of trials, congruent (both surfaces same color) and incongruent (surfaces different colors), as was used in Kramer and Jacobson’s (1991) study. The degree to which congruence between the surfaces’ colors aided performance and the degree to which incongruence hurt performance indicated how well the surfaces were perceived as an integrated unit.

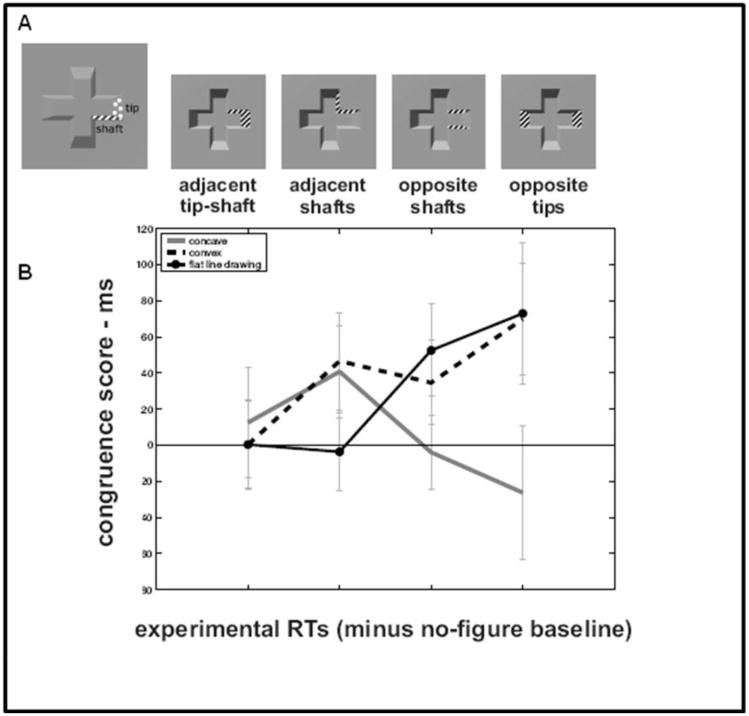
The perceptual integration of various pairs of surfaces was tested by asking participants to judge the color of a target surface while ignoring the color of a distractor surface. Each individual surface on the bounding wall of a cross-shaped region was used equally often in both roles, and both adjacent and non-adjacent pairs of surfaces appeared in the experiment. The bounding wall of the 3D cross-shaped region was composed of two qualitatively distinct types of surface: “tips” (the surfaces forming the ends of the crossbars) and “shafts” (the surfaces aligned with the long dimensions of the crossbars). Note that for a cross shape, there are necessarily twice as many shafts as tips (8 vs. 4). Accordingly, there are 8 possible adjacent tip-shaft combinations, 4 adjacent shafts combinations, 4 opposite shafts combinations, and 2 opposite tips combinations. Examples of these four kinds of surface pairings are shown in Figure 4a.

Figure 4.

A: Schematic illustration of surface pair combinations used. Only surface pigmentation was altered to highlight surfaces in the actual stimuli; hatching is drawn for clarity. B: Congruence scores based on median RTs. Scores from the no-figure baseline condition have been subtracted out. Error bars represent standard error of the mean.

Experiment 1 measured the extent to which different task-irrelevant background images imposed perceptual unity on two spatially distinct parts of the display. We hypothesized that a 3D convex background would produce a main effect of greater perceptual unity across all pairs of surfaces, in accord with the idea that attending to one region of an object facilitates attention to other spatially distant regions that belong to the object (e.g. Egly, Driver, & Rafal, 1994; Lavie & Driver, 1996). We hypothesized that such object-based attention effects would be absent with 3D concave backgrounds, and that, in this case, intervening 3D curvature minima might actually render different surfaces more perceptually independent than would be predicted based on their spatial separation alone.

Methods

Participants

20 undergraduates participated for course credit. All participants had normal or corrected vision, were between the ages of 18 and 22 and provided informed consent.

Stimuli

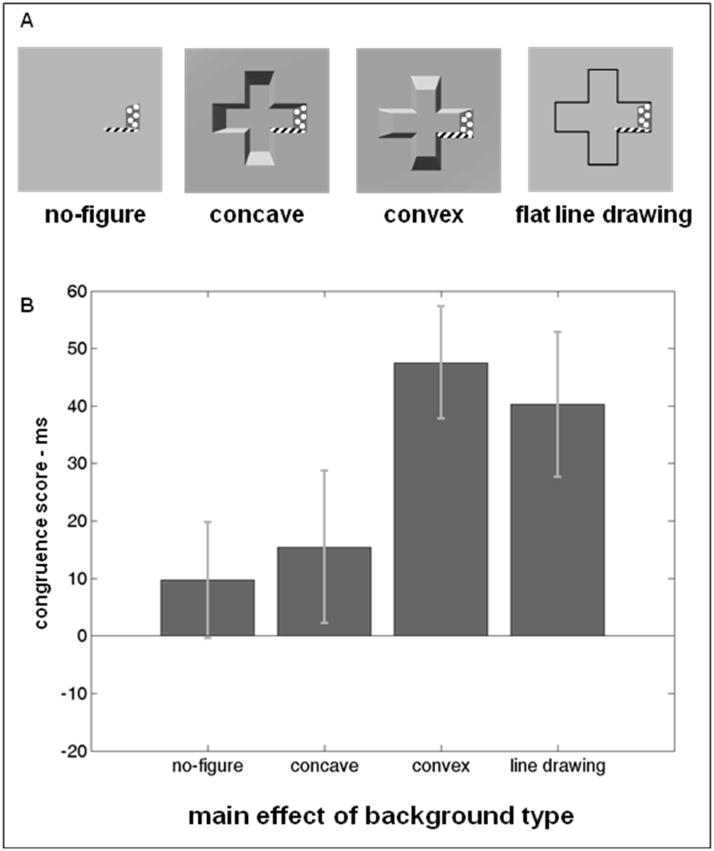
The stimuli for a given trial included three images: a background image, a cue image, and a probe image. The cue and probe images were made by adding color to the background images in systematic ways. Four background images were used, illustrated in Figure 3a: no-figure, concave, convex, and flat line drawing. The no-figure image was a blank green metallic surface rendered at a resolution of 400×400 pixels, using MATLAB (Mathworks Inc., Natick, MA). Its width and height both spanned 8 cm (approximately 9.2° at 50 cm viewing distance) on the screen. The concave background image described a cross-shaped region with equal horizontal and vertical extents of approximately 6 cm (6.9° at 50cm) on the screen, with arms approximately 2 cm (2.3°) in width. The convex background image was produced by rotating the concave background image 180° in the picture plane. Many authors (e.g. Kleffner & Ramachandran 1992) have shown that the polarity of a shape-from-shading image’s 3D depth reverses when the apparent direction of a light source is inverted. The flat line drawing image consisted of a closed black line drawn on the no-figure background that described the planar boundary of the cross-shaped region. In all background types the surface was illuminated by a simulated light source above and to the left of the figure; this position has been found to be optimal for inducing perception of depth-from-shading (Sun & Perona, 1998). The light source in the testing room (a halogen bulb desk lamp) was positioned above and to the left of the monitor.

Figure 3.

A: schematic illustration of stimulus backgrounds used in Experiment 1. Hatched and dotted regions represent differently colored surface patches for clarity. All examples show the adjacent tip-shaft surface pair for clarity of comparison. B: main effect of stimulus background on congruence scores.

The cue images were created by coloring two of the surfaces on the bounding wall of the concave region, one gold and the second white. The same cue images were used with all background types, but they were superimposed differently on the different backgrounds. The convex cue images were made by rotating the concave cue images 180° in the picture plane. The no-figure and flat line drawing cue images were made by copying the colored surface patches from a concave cue image and superimposing them on a blank or line drawing background (see Figure 3a). Note that this method preserved all of the luminance and shading properties of the colored patches that were rendered as part of a concavity. To reduce the depth-from-shading cues associated with the colored patches, these entire images were rotated 90° clockwise after the patches were added.

The gold-colored surface (henceforth the target cue) was used to indicate where a target would appear in the probe image, and the white colored surface (the distractor cue) indicated where a distractor would appear. Figure 4a shows examples of the four types of surface location relationships. Two cue images were created for each unique pair of surfaces, by counterbalancing the relative location of the target and distractor patches. Thus, for each background type, 16 total cue images were created for the adjacent tip-shaft condition, 8 for the adjacent shafts condition, 8 for the opposite shafts condition, and 4 for the opposite tips condition, for a total of 36 images. Note that in the adjacent tip-shaft condition the two surfaces were different sizes, since a tip had a larger surface area than a shaft. Since a target cue was equally likely to appear on a tip as on a shaft in the adjacent tip-shaft images, all trials involving the adjacent tip-shaft condition were binned together for analysis.

The probe images were created by the same method as the cue images, except that in lieu of gold and white, the two surfaces were colored with red and blue. A probe image could include any of the four possible permutations of the two color values. Thus for each of the 36 cue images of a given background type, 4 probe images were created. This yielded a total of 144 probe images per background type.

Procedure

The testing session consisted of two stages. In the first stage, all stimuli were the no-figure type so that performance in this stage would not be influenced by the expectancy of a global cross-shaped contour. In the second stage, concave, convex and flat line drawing trials were randomly interleaved.

During the first stage, participants’ only task was to identify the color of the target patch in the probe image. Participants were instructed to direct their attention to the gold-colored surface and to report which color this surface took on in the probe image. Participants were told that the white-colored surface indicated where an additional red or blue patch would appear in the probe image, and that this additional patch was a distractor that should be ignored.

Participants pressed a key on the keyboard to initiate a trial. The cue image appeared in the center of the screen, surrounded by a gray background, and remained on the screen for 1 second. The text “Get ready …” appeared at the bottom of the screen for the same interval. A blank screen ensued for 300 ms followed by the centrally-presented probe image which remained until the participant pressed one of two keys, which were labeled with red and blue stickers. The response and RT (relative to probe image onset) were recorded. A feedback message (“correct!” or “incorrect!”) then appeared. If the response was correct, the participant could proceed to the next trial but if not, the computer beeped, the keyboard was locked and the participant was required to wait for 5 seconds before the next trial could be initiated.

During the second stage, participants performed an additional task at the beginning of each trial: they judged the apparent depth of a background image containing no colored patches. At the start of a trial, a background image appeared and remained visible until the participant pressed one of three keys to indicate whether the background appeared to be concave, convex or a flat line drawing. This response and its reaction time were recorded. Participants used the left hand to press these three keys, in order to leave the right hand free to respond for the main task. Participants were instructed to indicate what depth the image appeared to have upon first inspection. After this first response, the background image disappeared and was replaced with a cue image. The remainder of the trial was identical to the procedure used in the first stage of the experiment.

All experiments were conducted using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) for MATLAB. Participants performed 144 trials in the first stage, with one trial for each of the possible probe images, and 432 trials in the second stage (144 trials for each of the four background types). Prior to the experiment, participants read printed instructions with diagrams, and performed 10 practice trials, randomly selected from the first stage. During the second stage, three breaks were given and, upon completion, participants were debriefed.

Results

For the first stage, trials with incorrect responses were excluded from the RT analysis. Second stage trials were excluded when either the background image response (concave/convex/flat) or the probe image response was incorrect. Participants with probe image error rates greater than 10% for all trials, or with an error rate greater than 20% for any one cell (see below), were excluded from the analyses. Four participants were excluded on this basis, leaving 16 (9 male, 7 female). The mean error rate for the remaining participants was very low (2.6%) and was not analyzed further.

The mean RTs (s.e.m.) for the preliminary task of identifying the concave, convex and flat line drawing backgrounds were 881 (91), 920 (80), and 727 (73) ms, respectively. A repeated measures ANOVA revealed a main effect of background type (F_{(2, 30)} = 17.55, p < 0.001), and a Tukey’s HSD test yielded a critical T value of 85 ms, meaning that the flat line drawing responses were significantly faster than those for the concave and convex backgrounds, which did not differ from each other. The mean accuracies for the concave, convex and flat line drawing backgrounds were very similar at 97.3%, 96.4% and 96.7%, (F_(2,30) = 0.55, p = 0.58). Any differences between the concave and convex conditions in the main task, therefore, were not attributable to longer viewing times or unequal difficulty between conditions.

A factorial repeated measures ANOVA with background type (4 levels: no-figure, concave, convex, flat line drawing), and surface relationship (4 levels: adjacent tip-shaft, adjacent shafts, opposite shafts, opposite tips) as factors was conducted with the congruent-incongruent difference score as the dependent measure. Before computing the congruence score, all trials were binned into 32 cells for the analysis (4 × 4 × 2; the last 2 indicates congruent/incongruent). These cells were the basis for excluding participants with greater than 20% errors in any single cell. The median RT for all trials within a cell was calculated, and the median congruent RT was subtracted from the median incongruent RT to obtain the congruence score. The congruence scores for the no-figure trials were used as a baseline measure of the perceptual unity of two surfaces inherent from their sizes and proximity, and were subtracted from the congruence scores for the other background image conditions. These baseline congruence scores were 20 ms (s.e.m. 20 ms) for the adjacent shafts condition, 29 ms (20 ms) for adjacent tip-shaft, 7 ms (15 ms) for opposite shafts, and −23 ms (22 ms) for opposite tips. The negative score in the opposite tips conditions may indicate that when a spatially distant pair of surfaces share the same color, the distractor may impede performance by drawing attention away from the target rather than helping by providing a redundant feature (c.f. Theeuwes, De Vries, & Godijn, 2003; Lamy, Leber, & Egeth, 2004).

The ANOVA revealed a main effect of background type (F_(2,30) = 3.42, p = 0.046). Planned pairwise comparisons revealed that the concave condition had a significantly lower congruence score than the convex condition (t₁₅ = 2.36, p = 0.033), but neither the concave versus flat line drawing (t₁₅ = 1.89, p = 0.078) nor the convex versus flat line drawing (t₁₅ = 0.62, p = 0.55) comparisons were significant. An ANOVA examining the raw RTs for these three background types showed no main effect (F_(2,30) = 1.32, p = 0.28) nor an interaction (F_(6,90) = 0.35, p = 0.91), so the congruence score effects were not likely to be byproducts of baseline performance differences for the background types. Figure 3b shows the non-baseline-adjusted congruence scores for all four conditions.

There was also a significant two-way interaction between background type and surface relationship (F_(6,90) =3.39, p = 0.0046). A post-hoc Tukey’s HSD critical T value of 89 ms showed that the only significant differences were in the opposite tips part relationship condition, in which the convex and flat line drawing backgrounds yielded higher congruence scores (i.e. greater interference from the distractor surface) than the concave background. Figure 4b shows the baseline-adjusted scores grouped by background type and surface relationship.

Discussion

3D concavities and convexities engage attention to local image elements differently, even when they define the same 2D outline shape. Two aspects of the results stand out. First, unlike the convex and 2D line drawing backgrounds, the 3D concave backgrounds added very little perceptual unity to the display on the whole, barely more than the no-figure condition (Figure 3b). Second, the concave and no-figure backgrounds both yielded negative scores in the opposite tips conditions, which may indicate these backgrounds allowed a spatially distant distractor to impede performance by drawing attention away from the target when it was congruent (c.f. Theeuwes et al., 2003; Lamy et al., 2004), in the manner of an object distinct from the one containing the target feature. Although similar 2D cross shapes can be perceived in the three figural background types, the figural goodness produced by 3D concavities does not affect visual attention in the manner of most objects.

Experiment 2

Effect of 3D depth on integration of 2D part structure

Experiment 1 showed that attention does not spread globally across 3D concavities the way it does in 3D convexities, which suggests that when figural shape is perceived in concavities, it might be perceived in a less holistic way than in convexities. To assess whether figural shape judgments differ for 3D concavities and convexities, in the next experiment participants made judgments about the shape of contours bounding 3D concave and convex regions when the 2D outlines of these shape-from-shading images were identical.

Examining judgments of 2D shape is a reliable means for assessing the perceptual ramifications of different 3D structure. In an influential series of experiments, Enns and Rensink (1990, 1991) found that visual search is efficient when 2D line drawings convey vivid 3D structure, even when similar but flat-looking drawings yield inefficient search slopes. An even stronger demonstration of the interaction between the orthogonal dimensions of 2D and 3D structure comes from Liu, Jacobs and Basri (1999), who found that concavity in a shape’s 2D outline affects how well observers integrate different parts of a shape across gaps in 3D depth. Observers were better at noticing a depth disparity separating two halves of a planar shape when the two halves were linked by a concave 2D contour (like an hourglass) rather than a convex contour (like a barrel), suggesting that surfaces connected by a convex bulge were perceptually grouped by a better gestalt. Thus a concave contour appears to allow the properties of different parts to be perceived independently, even when the properties in question are not directly related to the shape of the 2D contour itself. Conversely, we consider here whether concavity in 3D (i.e. depth) leads a 2D outline to be perceived less holistically.

Experiment 2 used the Garnerian “orthogonal insertion” task of Lederman, Klatzky and Reed (1993) to determine the integrality or separability of parts of a 2D planar shape. In this task, participants view a set of stimuli and classify them based on the value of a single stimulus dimension. After this, variability is introduced along a second dimension that is completely independent from the first dimension (“orthogonal insertion”). The participants continue to classify the stimuli based solely on the value of the first dimension, while ignoring variation along the second dimension. Poor performance after the orthogonal insertion (an “orthogonal insertion effect”) is evidence for dimensional integrality, because participants were unable to attend to the first dimension without being distracted by the irrelevant dimension. If performance remains unchanged, then the dimensions are deemed to be separable. This difference is probably quantitative rather than qualitative, since the separable-integral difference itself is probably a continuum rather than a dichotomy (Garner, 1974).

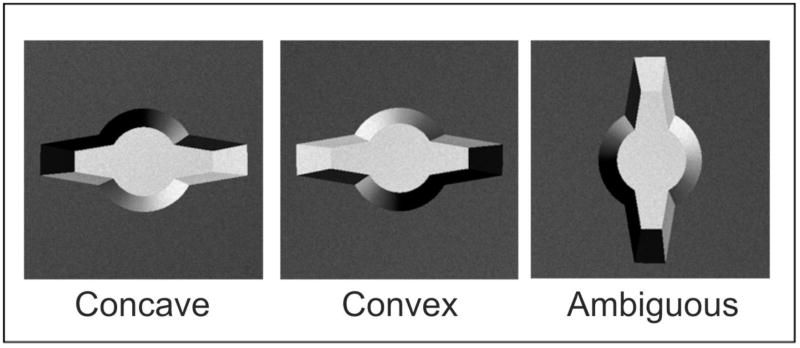
The two dimensions manipulated in this experiment were the appearance of the “arms” and the ovoid “body” of a shape (Figure 5). Participants classified the stimuli based on the arms, initially without and then with the presence of trial-to-trial variation in the body shape. Orthogonal insertion effects were predicted to be stronger for 3D convexities than for 3D concavities, reflecting greater integration of all of the 3D convexities’ features into a whole.

Figure 5.

Examples of the three 3D-rendered stimulus types used in Experiment 2. The convex and ambiguous stimuli were created by rotating the concave stimuli in the picture plane.

Methods

Participants

A total of 36 undergraduates participated for course credit. Participants had normal or corrected vision, were between the ages of 18 and 22 and provided informed consent.

Since the experiment measured how responses were affected by an unexpected change to the stimulus, each participant performed one session, viewing only a single stimulus type. Thus the experiment was conducted with stimulus type as a between-subjects factor. Three groups of participants performed the experiment: 12 participants (7 male, 5 female) saw concave stimuli, 12 (6 male, 6 female) saw convex stimuli, and 12 (6 male, 6 female) saw ambiguous (90° rotated) stimuli.

Stimuli

Stimuli were 3D rendered images of novel shapes composed of two tapered arms protruding from an ovoid body (see Figure 5). One set of images was used to portray all three 3D stimulus types: concave, convex, and ambiguous stimuli. All shapes were originally rendered as concavities recessed from a planar background surface, with light sources emanating from the top left of the shape, using a ray tracing program (POVray, copyright ©, POV-Team^™ 1991–2009). Convex stimuli were produced by rotating the concave stimuli 180° in the picture plane. The concave stimuli were rotated 90° clockwise to produce ambiguously-shaded control stimuli.

All images were rendered at a resolution of 400 × 400 pixels. Stimuli had widths of approximately 9×5.7 cm, subtending approximately 10.2×7.4° from a viewing distance of 50 cm. The surfaces within the central region had a lighter tone than the background plane, and both types of surface were finely textured. Pilot testing indicated that the concave texture cues did not prevent the images from being perceived as convex or ambiguous.

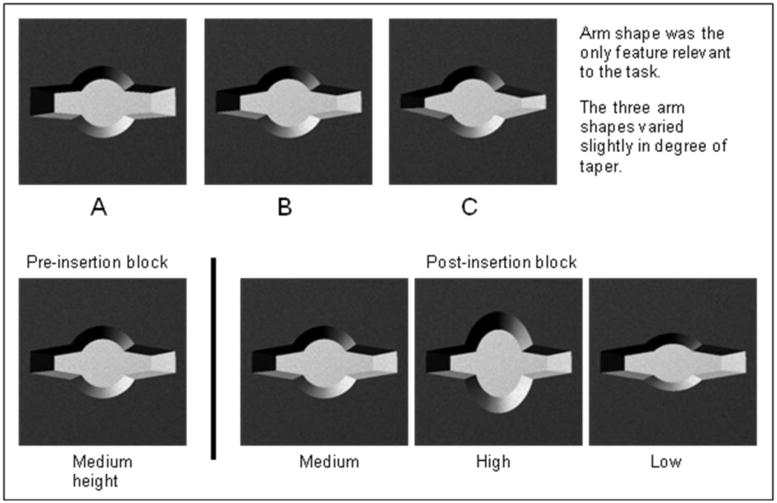
Stimuli had one of three different arm shapes (Figure 6, top row). Arm types A, B and C tapered to end thicknesses subtending 2.1°, 1.6° and 1.1°, respectively. In addition, shapes in the post-insertion portion of the experiment could also have one of three different body shapes: high (subtending 7.3°), medium (5.3°), or low (4.2°) heights (Figure 6, bottom row). All stimuli in the pre-insertion portion of the experiment had medium body shapes.

Figure 6.

Scheme for stimuli used in Experiment 2. Top row: the three different arm shapes that participants were instructed to identify. All three arm shapes are shown on the same (medium height) body shape for consistency of comparison. Bottom row: illustration of the orthogonal insertion manipulation of the irrelevant (body shape) dimension. During the pre-insertion block the body shape dimension did not vary; all stimuli had a medium height body. During the post-insertion block body shape changed randomly from trial to trial, uncorrelated with arm shape. All post-insertion examples shown with arm shape B for consistency of comparison.

Procedure

Participants performed a three-alternative forced choice categorization task, in which they categorized each stimulus according to its arm thickness. Participants first studied a display of sample stimuli that illustrated each arm type (all had medium body shape) and its response label (A, B, and C), and were told that the body shape was irrelevant (Figure 6). Responses were made with the right hand on the keyboard using three adjacent keys. Verbal and written instructions informed participants about the depth (concave or convex) that the stimuli were supposed to portray. Ambiguous stimuli were simply described as “computer-generated images.”

Participants performed a block of 18 practice trials (6 for each arm type). A stimulus appeared and remained until participants made a key press response. If the response was correct, a 1000 ms intertrial interval (ITI) followed. If the response was incorrect, the word “Incorrect” was displayed in red text for 500 ms during the 1000 ms ITI. All participants correctly identified each stimulus on at least 4 out of 6 trials. Prior to the experiment itself, participants were instructed to respond both quickly and accurately.

The main task consisted of two blocks of trials. The pre-insertion block of 60 trials consisted of 20 presentations of each of the three stimuli, presented in random order. The trial procedure was identical to the practice block but no feedback was provided. At the end of the first block, the experimenter instructed the participant that the stimulus body would vary from trial to trial but that her three-way decision was still to be based only on the arm thickness. The post-insertion block began immediately following these instructions. The post-insertion block used nine different stimuli, each repeated 20 times, defined by the crossing of the three body types (low, medium and high) with the three arm types (A, B and C). After this, participants were asked whether the stimuli appeared more concave or more convex, and their responses were recorded.

Results

Two participants were excluded, one from the concave and one from the convex group since their RT or error rate, respectively, exceeded two standard deviations of the group mean. All participants in the concave and convex stimulus groups reported that the stimuli appeared to have the appropriate depth. Of the participants in the ambiguous group, 5 reported them to appear concave and 7 convex; this judgment difference did not significantly affect performance in the analyses of the data.

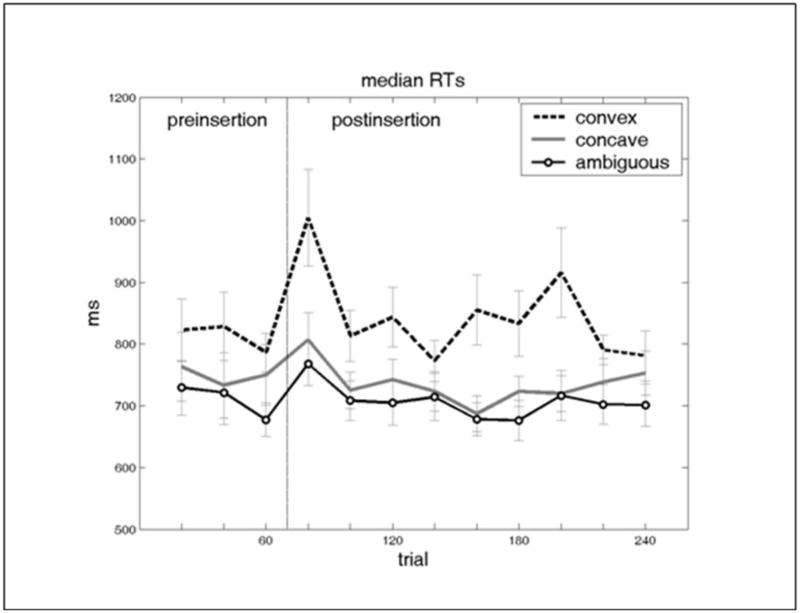
RTs from correct response trials were divided into bins of 20 trials, yielding 3 pre-insertion bins and 9 post-insertion bins, as plotted in Figure 7 (see Lederman et al. (1993) for the rationale of this analytic method). A repeated-measures ANOVA of the immediately pre- and post-insertion trials (i.e. bins 3 and 4) included stimulus type as a between-subjects factor, and time (pre/post-insertion) as a within-subjects factor. Significant main effects were found for both stimulus type (F_(2,31) = 4.51, p < 0.05) and time (F_(1,31) = 25.26, p < 0.001), as well as a significant interaction between the two (F_(2,31) = 4.10, p < 0.05). Planned paired samples t-tests revealed significant orthogonal insertion effects for the convex (t₁₀ = −3.36, p = 0.0072) and ambiguous groups (t₁₁ = −4.04, p = 0.0019), but not for the concave group (although there was a trend: t₁₀ = −2.11, p = 0.061). Also, two-sample t-tests showed that the magnitudes of the orthogonal insertion effect were significantly different between the concave and convex groups (t₍₂₀₎ = 2.30, p = 0.032) but not between the concave and ambiguous groups (t₍₂₁₎ = 0.97, p = 0.34) or the convex and ambiguous groups (although there was a trend: t₍₂₁₎ = 1.93, p = 0.067). The same ANOVA using accuracy as the dependent measure indicated lower post-insertion accuracy (F_(1,31) = 4.45, p < 0.05) and no other significant effects.

Figure 7.

Median reaction times for each bin of 20 trials, averaged across subjects for Experiment 2. The vertical line after trial 60 indicates the orthogonal insertion point dividing the pre- and post-insertion blocks. Error bars represent standard error of the mean.

The bin size of 20 trials was chosen for these analyses because it appeared to capture the peak of the orthogonal insertion effect while containing instances of all the different stimulus types. ANOVAs comparing the median RTs obtained with different bin sizes were performed using the concave and convex subject groups. The critical time by stimulus type interaction was significant for the bin sizes 10 (F_(1,26) = 4.74, p = 0.039), 15 (F_(1,26) = 5.43, p = 0.028) and 20 (as reported above; F_(1,26) = 5.08, p = 0.033), indicating that the critical finding is not specific to the bin type initially chosen.

Discussion

The results of Experiment 2 indicate that 2D figural shape may be perceived by different means when it is associated with 3D concavities and convexities, even though this depth dimension is orthogonal to the plane of the figure itself. Participants viewing the 3D convex and the 3D ambiguous stimuli showed significant orthogonal insertion effects, as measured by the RT difference between immediately pre- and post-insertion trials. In contrast, there was very little decrement in performance from the orthogonal insertion with the 3D concave stimuli; significantly less than with 3D convexities. It appears that participants perceived the 3D convex and ambiguous images in an integrated or holistic manner, since they had difficulty ignoring changes to a task-irrelevant part of the shape.

In sum, Experiment 2 suggests that figural shape perceived from 3D concavities is derived from a collection of perceptually independent partsⁱⁱⁱ, compared to the relatively holistic mode of shape perception seen with 3D convexities. 3D depth has high-level effects on perception even when it is an irrelevant and orthogonal dimension in a shape perception task. 3D depth appears to affect the process of part determination in addition to the grouping across depth disparities reported by Liu et al. (1999), and the grouping of individual surfaces found in Experiment 1.

Experiment 3

Effects of 3D depth on whole shape matching

The first two experiments showed that local surface elements of 3D concavities, as well as the parts of the 2D bounding contour shapes of 3D concavities, are perceived as independent sets of features compared to the equivalent features of 3D convexities. Continuing the local-to-global trajectory of the first two experiments, Experiment 3 investigated whether observers perceive the global dimensions of figural shapes differently with 3D concavities and convexities, and asked participants to make judgments about entire shapes, rather than to focus on specific parts of them. If observers really do perceive that 3D concavities and convexities describe similar 2D boundary shapes, do they arrive at these similar percepts via the same processes, and are they sensitive to the same global shape information in both cases?

Visual search studies indicate that 3D concave shapes, even those without distinct parts, may be represented differently from 3D convexities in the human visual system. Under many experimental conditions a 3D concave target “pops out” of an array of convex but otherwise similar shapes, but convex targets are hard to detect among concave distractors. This search asymmetry (Treisman & Souther, 1985) suggests that concavity in depth is a salient feature for capturing attention. A concave shape is an unusual “feature-present” stimulus for a search asymmetry (Kleffner & Ramachandran, 1992), since it can be constructed by physically removing material from the “feature absent” stimulus, the convex shape. However, it may be that the salient feature guiding attention is not so much the distal cues indicating concavity, but rather the greater number of psychological units (i.e. dimensions) perceived with a concavity versus a convexity. Popout for concavity has been found with 3D stimuli that have no discernible divisions into multiple surfaces or parts, as with the shape-from-shading circles used by Kleffner and Ramachandran (1992). It seems unlikely that the feature singleton guiding attention to concavities would be the presence of greater pictorial depth, because Liu and Todd (2004) found that pictorial depth tends to be greater in convexities, not concavities. If anything, this would appear to give convex targets an extra feature. One interpretation of these studies is that concave shapes are perceived to consist of a larger number of basic features than those of convexities.

Experiment 3 tests the hypothesis that observers are sensitive to different global dimensions of shapes (i.e. dimensions that span the entirety of the shape) with 3D concavities and convexities. Specifically, the hypothesis predicts that observers maintain sensitivity to the spatial extents of concavities (e.g. height or width) as separate quantities, whereas these independent dimensions are integrated into a single emergent shape dimension (e.g. aspect ratio) in the case of convexities. This hypothesis holds that the number of global shape features perceived in concavities will always be greater than the number perceived in convexities, because integrating multiple spatial dimensions reduces the number of dimensions ultimately perceived. This basic hypothesis also implies that observers will be relatively sensitive to the absolute size of 3D concave images, but will perceive 3D convex images via a more scale-invariant process.

Experiment 3 used a match-to-sample task to measure observers’ sensitivity to the global spatial extents of images and to the features that emerge when these independent dimensions are perceptually integrated; specifically, aspect ratio and surface area. Two properties of the sample images’ shapes were manipulated, the spatial extents of height and width, and distorting specific combinations of values for these properties yielded three categories of foils, corresponding to three possible schemes for identifying the stimulus: judging aspect ratio (ratio of height to width), area (product of height and width) or individual spatial extents (height and width considered as individual quantities). Each type of foil kept the stimulus’ description constant according to one of the three schemes, despite making changes to the other two schemes. For example, a same-aspect-ratio foil had a different area and also different height and width values than the sample. If participants especially relied on a given dimension to recognize the shapes, then their performance would be low when foils preserved that dimension.

Methods

Participants

Eleven undergraduates, all of whom had normal or corrected vision, were between the ages of 18 and 22 and provided signed informed consent, participated for course credit.

Stimuli

The stimuli were 3D rendered cross-shaped regions (see Figure 8) that could appear concave or convex depending on their rotation in the picture plane. The two images presented in a trial were either a sample/match pair (images identical) or a sample/foil pair (second image slightly distorted). Different sample images were created by generating cross shapes based on 4 parameters: the major axis extents of the crossbars, and their thicknesses (minor axis extents). Only the major axis extents were used as dependent variables. These parameters were obtained by randomly selecting one of 5 values for each parameter. The 5 values spanning the range from 2.5 cm (2.9°) to 6 cm (6.9°) formed the set of possible crossbar major axis extents and the five values spanning 1.9 cm (2.2°) to 4.8 cm (5.5°) formed the set of possible crossbar minor axis extents. The program for generating the images included constraints that prevented the occurrence of combinations of these parameters that resulted in impossible cross shapes (e.g. the vertical extent of the horizontal crossbar being greater than the height of the vertical crossbar). The images were rendered in MATLAB at a resolution of 400 × 400 pixels, and the images were simulated to have light sources above and to the left of the figure.

Figure 8.

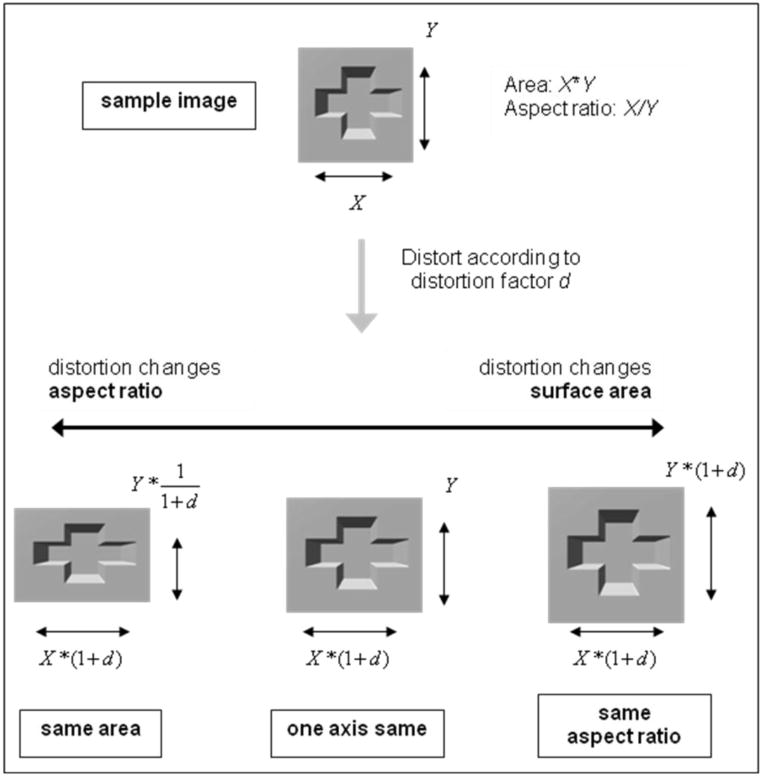
The three types of distortion used to create foils in Experiment 3. The cross shape that served as the sample image for a trial (labeled “sample image” at top) has horizontal extent X and vertical extent Y. The same-area distortion elongated one dimension and shortened the other, which changed aspect ratio X/Y, but preserved the surface area of the shape (proportional to X*Y). The same-aspect-ratio distortion elongated the shape along both dimensions equally, which significantly increased surface area but preserved the shape’s aspect ratio. The one-axis distortion produced changes intermediate to these two extremes by stretching only one axis, changing both surface area and aspect ratio moderately. Note that the one-axis distortion is the only case that kept one of the shape’s original axis dimensions constant. All of the above examples show concave images and positive values of d; negative values of d were also used. The shapes’ square backgrounds have also been distorted for emphasis, although they were not distorted in the actual stimuli.

Foil images were created by distorting these cross shapes. The magnitude of the distortions was defined by a parameter d, which was set to 0.15 after pilot testing. Both positive and negative values of d were used. The three distinct kinds of distortion described above were used (see Figure 8). For simplicity, the following descriptions mention only positive values of d.

The same-area distortion preserved the 2D surface area covered by the cross shape by stretching the shape along one axis and compressing it along the other axis. The identities of the stretched and compressed dimensions were counterbalanced, so that the horizontal and vertical extents were stretched and compressed equally often. While this same-area distortion preserved the original surface area of the shape (1+d * 1/[1+d] = 1), the aspect ratio of the horizontal and vertical extents changed significantly, by a factor of 1+d/1/(1+d) = (1+d)².

The same-aspect-ratio distortion was the converse of same-area distortion: it preserved the aspect ratio of the horizontal and vertical extents of the cross shape by changing both axes by the same amount. Aspect ratio was unchanged, 1+d/1+d = 1; surface area was changed significantly, by a factor of (1+d)².

The one-axis distortion was a condition that fell midway between the extremes of same-area and same-aspect-ratio distortion. By distorting only one axis, both the surface area (1 * 1+d = 1+d) and aspect ratio (1/[1+d]) were altered, but to a smaller degree than with the other two distortions. The horizontal and vertical axes were manipulated as the distorted dimension equally often. Because the one-axis distortion left one axis completely unchanged, unlike the other two distortions, it provided a chance to test whether participants were sensitive to the axes as independent dimensions. Our assumption was that if observers perceived the two dimensions independently, similarity between samples and foils would be reckoned according to a city-block metric encompassing these two dimensions (Garner, 1974). All three kinds of distortions affect the city-block distance between sample and foil (|width_sample−width_foil| + |height_sample−height_foil|), but the one-axis distortion produces the largest such difference. Simply put, the one-axis distortion should be hard to detect if participants perceive the two axis extents independently, because half of the relevant dimensions are unchanged. The one-axis distortion is the key test for distinguishing whether observers based their judgments on the individual spatial extents of the shapes themselves, instead of on higher-order features constructed by integrating them.

Eighty unique trials were generated, comprising 40 “same” and “different” trials apiece. Each trial was presented twice during an experimental block, in random order, for a total of 160 trials. The concave and convex blocks presented the same set of trials in different random orders. The noise mask that intervened between the presentations of the sample and match/foil images was a 400×400 pixel image composed of 1600 randomly colored 10×10 pixel squares tiling the image.

Procedure

3D depth (concave or convex) was treated as a within-subjects factor. All stimuli within a block had the same 3D depth, and the order in which the conditions were viewed was counterbalanced across participants. Participants performed 10 practice trials followed by a block of 160 trials for each depth condition. Following a key press, the sample image appeared on the computer monitor, centered on the screen against a gray background, and remained there for 1 s. A noise mask of 500 ms duration replaced the sample. The match or foil image replaced the mask and remained on the screen until the participant responded using keyboard keys labeled “same” and “different.” After this key press the match/foil image was cleared from the screen and a feedback message (“correct!” or “incorrect!” the latter accompanied by a beep) appeared for 1 s. Response RT and accuracy were recorded by the computer.

Modeling

A simple computational model was used to evaluate the data further in light of the hypothesis that the major axis extents of the cross shapes were either perceived by integrating these dimensions into the single property of aspect ratio (in the case of convexities) or by perceiving them as separable dimensions (concavities). The difficulty of each “different” trial was modeled by calculating the dissimilarity between representations of the stimulus shapes. Dissimilarities were measured in terms of proportional difference (Weber fraction) ΔX/X. Aspect ratio (integral dimension) dissimilarities were thus computed with the formula |AR_sample−AR_foil|/AR_sample, while a city-block dissimilarity measure (separable dimensions model) used the formula (|width_sample−width_foil| + |height_sample−height_foil|)/(width_sample + height_sample). The changes in aspect ratio and the city-block distance measure that occurred in each experimental trial were measured and averaged with respect to the same factors used in the behavioral RT ANOVA.

Results

Separate analyses were performed for the “same” and “different” trials, since the effects of the three types of foil distortion (same-area, one-axis, same-aspect-ratio) could only be compared in “different” trials. Repeated measures ANOVAs of the “same” trials found no significant effect of 3D depth with either RT (concave mean 984 ms [s.e.m. 67 ms], convex 991 ms [76 ms], F_(1,10) = 0.01, n.s.) or error data (concave mean 14% [3%], convex mean 13% [2%], F_(1,10) = 0.15, n.s.).

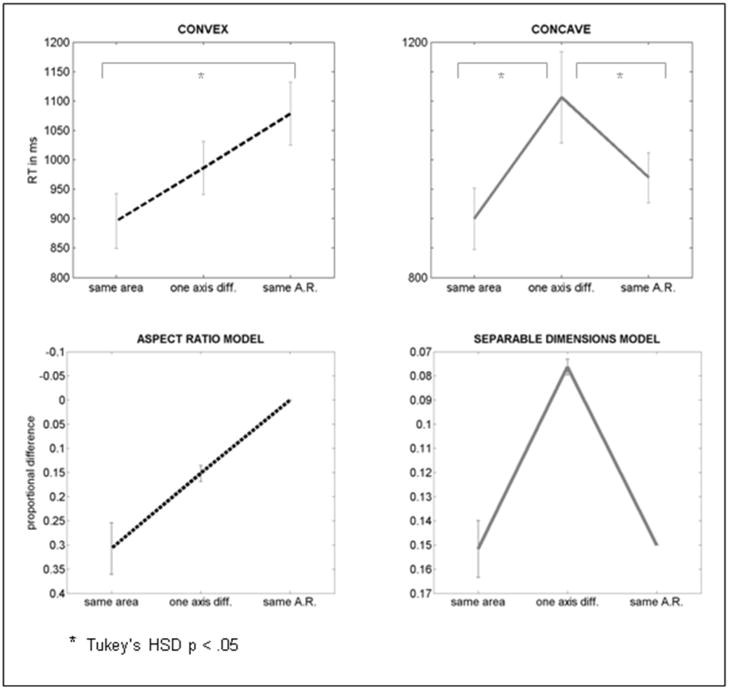
Repeated measures ANOVAs were performed on the RT and error data from the “different” trials, using two within-subjects factors: 3D depth (two levels: concave and convex) and distortion type (three levels: same-area, one-axis, and same-aspect-ratio). The RT analysis (Figure 9) showed a significant effect of distortion type (F_(2,10) = 7.17, p < 0.005) and an interaction between distortion type and 3D depth (F_(2,20) = 9.91, p < 0.001), but no main effect of 3D depth (F_(1,10) = 0.03, n.s.). A post-hoc Tukey’s HSD critical T value of 151 ms revealed that the mean RT for the same-area distortion type (898 ms, [s.e.m. 48 ms]) was significantly faster than means for both the one-axis type (1046 ms [56 ms]) and the same-aspect-ratio type (1024 ms [44 ms]). The Tukey’s HSD critical T value of 114 ms for the distortion type by 3D depth interaction indicates that the one-axis distortion type mean was significantly higher than both the same-area and same-aspect-ratio means in the concave data, but only the same-area and same-aspect-ratio means differed in the convex data. The only significant difference between the concave and convex groups was in the one-axis distortion, which had a higher mean with concave stimuli.

Figure 9.

Top row: mean of individual subjects’ median RTs for Experiment 3. Error bars represent standard error of the mean. Bottom row: differences in modeled shape representations for the three distortion types, based on representing shapes by aspect ratio (left) by a city-block model in which differences were calculated by considering length and width as separable dimensions (right). Error bars represent standard deviations for the set of stimulus dimensions used in the trials of the experiment. Ordinates for the model data have been inverted so that small shape differences compare to higher RT in the behavioral data graphs.

The error analysis showed a strong main effect of distortion type (F_(2,20) = 12.99, p < 0.001), but no main effect of 3D depth (F_(1,10) = 0.27, p = 0.61), nor any significant interactions. A Tukey HSD critical T value of 15.5% for the distortion type main effects revealed that the mean error rate for the same-area distortion type (4.7%) was significantly lower than means for both the one-axis type (25.2%) and the same-aspect-ratio type (21.8%). It is unclear why a distortion type effect, but not an effect of 3D depth, was found in the error rate data. In any case, the pattern of the distortion type effects (i.e. collapsed across 3D depth) are closely corresponding for both the RT and the error rate data.

The changes in aspect ratio and in the city-block distance measure that occurred during each experimental trial were measured and are plotted below the RT data in Figure 9. These two models reproduced the ordinal patterns of the RT results. To test how well the two models fit the concave and convex RT data, regressors based on the two models were used in a linear mixed effects regression. The model included binary indicator variables for the fixed effect depth (concave or convex); random effects terms for the aspect ratio and city-block distance model values for each trial; and the interactions of depth with these two model terms. Individual subjects were modeled as random factors using the linear mixed effects model function of the R statistics package.

The aspect ratio regressor was highly significant (t₍₁₆₅₉₎ = −2.68, p < 0.01), confirming that a greater difference in aspect ratio led to lower RTs. This effect did not interact with stimulus depth, as seen from the non-significant beta weight for the interaction between aspect ratio and concave depth (t₍₁₆₅₉₎ = 0.57, p > 0.1). Concavity itself was not associated with higher RTs in the regression analysis (t₍₁₆₅₉₎ = 0.57, p > 0.1), nor was the city-block distance regressor significant (t₍₁₆₅₉₎ = −0.99, p > 0.1). However, the concavity by city-block interaction term was significant (t₍₁₆₅₉₎ = −2.06, p < 0.05), meaning that observers were attuned to height and width as independent dimensions only when viewing concave stimuli.

Discussion

Observers appear to have relied on different dimensions to judge the concave and convex shapes. Observers’ performance with convex images closely followed the linear pattern across distortion types predicted by the aspect ratio model, indicating that this single, integrated dimension accounts for convex shape perception very well. In contrast, concave performance followed the pattern of the city-block model, indicating that observers were able to perceive the major axis extents separably. This V-shaped pattern of results indicates that no one integrated dimension, either aspect ratio or surface area, can account for the results.

The principle that concavities are perceived in terms of relatively independent features applies to global dimensions as well as to surface- or part-based ones. Observers appeared to use the major axis extents of 3D concave regions to judge their shapes, rather than limiting their analysis to features (e.g. aspect ratio) that result from the integration of these one-dimensional spatial quantities. This qualitative difference between the perception of 3D concavities and convexities is an important complement to the results of Experiments 1 and 2, which comprise mainly quantitative differences on measures of perceptual unity and holistic processing. It seems unlikely that asymmetries in the perception of depth from pictorial cues (e.g. the great depth perceived with pictorial convexities; Liu & Todd, 2004) could have produced the results of Experiment 3.

Two questions that were not addressed directly by this experiment deserve mention. First, the shapes were very simple and were designed so that their global structure could be captured by a minimal number of spatial parameters. It is unknown what limits there are to the number of independent spatial dimensions that observers might be able to use to judge the shapes of 3D concavities, and how their performance might change when there are many simple dimensions to attend simultaneously. Perhaps one would rely instead on a holistic mode of perception identical to that used to perceive 3D convexities. Indeed, it may be difficult for observers even to perceive complex 2D regions as having concave depth. Nelson and Palmer (2001) reported that when planar holes described familiar and meaningful shape outlines, they were more likely to be perceived as solids rather than holes. The very compelling “hollow face illusion” (Hill & Bruce, 1993, 1994, 1996) can prevent even the structure of face masks with physical (not just apparent) 3D concavity from being perceived properly. It seems likely that simply perceiving an image to be convex would be sufficient to produce the holistic perception effects seen here with convex stimuli, regardless of the actual structure of the distal stimulus. It is important to note, however, that visual guidance of action is not affected by such illusions of convexity, as shown recently (Kroliczak, Heard, Goodale, & Gregory, 2006).

Performance in the same-area condition was superior to same-aspect-ratio performance with concavities, and the regression term for the aspect ratio model was significant with respect to concave stimuli. This indicates some sensitivity to aspect ratio akin to that found with convexities. There are at least two possible sources for sensitivity to aspect ratio with concavities. First, it could be that observers encode aspect ratio in addition to separable spatial dimensions, although they rely primarily on the latter. Alternatively, they could use the separably-encoded dimensions themselves as input to construct a representation of aspect ratio, as a subsequent process in a serial chain. These alternatives may be weighed as possible solutions to the problem of how observers ultimately perceive phenomenologically similar figural shapes with concavities and convexities. The results of Experiment 3 do not answer this question directly, but provide new data to constrain possible answers.

General Discussion

This study found that observers analyze the local and global properties of 3D concavities and convexities differently, in spite of the fact that these images portray the same figural shape. The results of three experiments suggest that there may be two pathways for perceiving figural shape in the human visual system, which operate differently on figures whose local elements are or are not grouped by overall 3D convexity.

Experiment 1 examined how well participants could focus attention on one small region of an image without being influenced by features of other local parts. Performance with concave and convex stimuli was only significantly different when these regions were maximally distant from each other. This is somewhat in contrast to the findings of Vecera and colleagues (Vecera et al., 2000; Vecera et al., 2001), who found that participants were more accurate at reporting two object attributes when they belonged to the same part than to different parts of the same object. It is difficult to compare those studies with the present one, since they used markedly different stimuli (non-polygonal stick-figures) and tasks. Nonetheless, it appears that 3D concavities and convexities differ in terms of the degree of global object-based attentional spreading (facilitation or inhibition due to properties of distant regions of the same figure), but not necessarily in terms of local, part-based attention.

Experiments 2 and 3 determined that a specific distinction between the processes for perceiving figural shape in 3D concavities and convexities is the use of separable versus integral dimensions. Participants could ignore variation in task-irrelevant regions of 3D concave shapes, whereas they showed significant signs of holistic shape perception when viewing convexities and ambiguously-oriented 3D images. Also, since observers in Experiment 2 identified parts of the 2D figural shape’s outline equally well with concavities and convexities during the pre-insertion block, the differences found between concavities and convexities in Experiment 1 were not likely the result of weaker figural percepts with concavities.

The results of Experiment 3 and the common perception of figural shape from 3D concavities would seem to indicate that the final outcome of figural shape perception in 3D concavities and convexities is identical. However, Experiment 3 did not test that hypothesis exhaustively. Experiment 3 assessed subjective shape perception more directly than Experiments 1 and 2 because participants were explicitly instructed to judge entire shapes.

Experiment 3 showed that the subjective similarity between the perceived shapes of 3D concavities and convexities is belied by qualitative differences in how observers perceive them. However, Experiment 3 assessed simple discrimination abilities, and not subjective reports of perceived shape. There are many other conceivable aspects of recognition performance that could also distinguish the processes for perceiving shape with concavities and convexities, including, for example, viewpoint dependence of recognition (Biederman & Gerhardstein, 1993; Tarr, Williams, Hayward, & Gauthier, 1998) and the precision of categorization boundaries for different shapes (Siddiqi, Tresness, & Kimia, 1996). Furthermore, the cross shapes used in Experiment 3 were designed to limit the number of dimensions along which exemplars varied. It will be necessary to investigate performance using complex concave shapes to determine whether such concavities, especially depictions of familiar objects, rely on the same separable dimension processes found here (and also whether the dimensions of their convex versions are integrated to the same extent). Shape cues related to familiar objects may recruit different processes (Peterson, Harvey, & Weidenbacher, 1991; Peterson & Gibson, 1994; Peterson, de Gelder, Rapcsak, Gerhardstein, & Bachoud-Levi, 2000). It also appears to be difficult to perceive veridical concavity with complex shapes in the first place (Nelson & Palmer, 2001), especially for stimuli that evoke strongly holistic perception, as in the hollow face illusion (Kroliczak et al., 2006). If a hollow face could ever be reliably perceived as concave, would observers perceive it less holistically, or even as a face?

This study rejected the hypothesis that observers rely on the same process to perceive 2D shape from 3D concavities and convexities, but it remains to be determined exactly how a subjective figural gestalt is assembled from the separable elements observers encode from concavities. We propose a hypothetical model of shape perception that is based on the existence of parallel processes for images that meet different perceptual grouping criteria. The model proposes that the local organization (e.g. structure of individual vertices and surfaces) and simple global organization (including discrimination of concave from convex regions) of both 3D convexities and concavities is determined in early occipital areas. This assertion is in accordance with the research on shape-from-shading perception in agnosic patients (e.g. Humphrey, Symons, Herbert, & Goodale, 1996) which shows that even in the absence of object recognition abilities, patients can distinguish shading-defined concavities and convexities. This ability is almost certainly the result of activity in occipital areas (Humphrey et al., 1997; Lee, Yang, Romero, & Mumford, 2002), although dorsal visual regions are sensitive to shape from shading cues as well (Taira, Nose, Inoue, & Tsutsui, 2001).

The model proposes that only stimuli that meet certain criteria, notably global convexity, would eventually engage relatively anterior occipitotemporal areas for shape analysis (Farah, 1992; Goodale & Milner, 1992; Malach et al., 1995; Logothetis & Sheinberg, 1996; Tanaka, 1996; Grill-Spector, Kourtzi, & Kanwisher, 2001; Kourtzi, Erb, Grodd, & Bulthoff, 2003). There, local image elements would undergo additional perceptual organization involving the integration of different intra-object spatial features. This would render the global aspects of the figure more salient, the local elements harder to perceive independently, and the specific metric dimensions of the figure less salient. 3D concave regions, and possibly planar holes as well, fail to meet these criteria. Instead, their local features would be analyzed in a way that preserves the salience of their spatial properties (e.g. location, extent).

3D concavities do meet at least one grouping criterion that indicates perceptual coherence above that of a disjoint collection of surfaces or of an image composed of multiple discrete objects -- the presence of a closed boundary contour. Stimuli that fail to meet the convexity criteria but do meet this closure criterion could then form the input (in the form of the separable spatial dimensions of their component features) for distinct holistic shape perception processes, which would transform this input into figural shape percepts. In this way, two ultimately similar holistic shape perception processes could operate on either: one, the output of lower-level visual areas that meet reliable criteria for objecthood (convexity); or two, on the output of higher-level analysis of the spatial properties of features grouped by a closed contour. A good candidate locus for such processing is the dorsal visual pathway, which has been found to play an important role in perceiving spatial dimensions of objects such as position, size and orientation (Ungerleider, Galkin, & Mishkin, 1983; Goodale, Milner, Jakobson, & Carey, 1991; Valyear, Culham, Sharif, Westwood, & Goodale, 2006). The idea that the perceptual grouping of image features is not a unitary process has been proposed in several domains related to figure-ground parsing and shape perception (Peterson et al., 1991; Behrmann & Kimchi, 2003; Palmer, Brooks, & Nelson, 2003). Our hypothetical second process, which remains to be investigated, would thus constitute a “second chance” for perceiving figural shape from concave stimuli: an alternative way to recover valuable figural shape information from images that contain more global grouping cues than collections of distinct objects or unorganized features, but which differ significantly from the image properties of solid objects.

In summary, this study found that the similar figural percepts observed with 3D concavities and convexities are belied by very different processes for encoding their shape information. Observers perceive 3D concavities to be composed of visual elements that are markedly more local than those of equivalent 3D convexities, and perceive the spatial extents of 3D concavities as separable, not integral dimensions. These results help to explain the paradox of how figural shape is perceived from holes, and suggest that shape perception, in general, may consist of two distinct processes. These experiments motivate a hypothetical model of dichotomous shape perception processes that can be tested in future studies.