Abstract
A new approach, based on the hierarchical soft correspondence detection, has been presented for significantly improving the speed of our previous HAMMER image registration algorithm. Currently, HAMMER takes a relative long time, e.g., up to 80 minutes, to register two regular sized images using Linux machine (with 2.40GHz CPU and 2-Gbyte memory). This is because the results of correspondence detection, used to guide the image warping, can be ambiguous in complex structures and thus the image warping has to be conservative and accordingly takes long time to complete. In this paper, a hierarchical soft correspondence detection technique has been employed to detect correspondences more robustly, thereby allowing the image warping to be completed straightforwardly and fast. By incorporating this hierarchical soft correspondence detection technique into the HAMMER registration framework, the robustness and the accuracy of registration (in terms of low average registration error) can be both achieved. Experimental results on real and simulated data show that the new registration algorithm, based the hierarchical soft correspondence detection, can run nine times faster than HAMMER while keeping the similar registration accuracy.
1. Introduction
Deformable registration is important for comparing medical images across different subjects. So far, various image registration algorithms [1–19] have been proposed in the literature. Most registration methods are based on matching simple image information such as intensities, while other methods use features for image registration. Features can be local features [4, 20] such as image boundary or curvature, or regional features such as geometric moment invariants (GMIs) [21, 22], wavelet coefficients [23], multiple-scale histogram features [24], local descriptor features [25], or combinations of various local features [25]. In the image registration, besides maximizing the matching of image features, the estimated dense deformation field is required to be smooth as well. This can be achieved by using a Laplacian smoothness constraint [21, 22], an elastic energy [8], or even the statistical deformation constraint learned from the training samples [26].
We have previously developed a hierarchical image registration algorithm, called HAMMER [21, 22]. There are two novel ideas in this algorithm. First, an attribute vector is defined for each point in the image, in order to characterize and better distinguish this point from its neighboring points; the image registration can be accordingly formulated as a problem of attribute vector matching or correspondence detection. Second, a strategy for hierarchical approximation of energy function is used to reduce the chance of local minima in the registration. In particular, the registration algorithm is designed to focus initially on the registration of only a small set of active points (with distinctive attribute vectors). This process implicitly selects only a small number of major energy terms in the whole energy function for optimization, thus potentially achieving global optimization for the new energy function. With the progress of registration, more and more points with less distinctive attribute vectors are added into the set of active points for actively driving the image registration, once these less distinctive points have been moved close to their targets and become stable for registration. In the final registration stage, all points in the images are considered as active points to drive image registration, which means that all energy terms in the whole energy function will be finally considered for optimization. By using this hierarchical registration strategy, we can improve the performance as well as the speed of registration. Also, since not all points are initially considered as active points to drive image registration, thus effectively reducing the scale of image registration problem and becoming fast and robust to complete.
HAMMER has been successfully applied to many large clinical research studies and clinical trials involving over 5,000 MR brain images. These applications include one of the largest longitudinal studies of aging in the world to date - which involves an 18-year annual follow-up of 150 elderly individuals [27], a relatively large schizophrenia imaging study involving 148 participants [28], a study of cocaine-exposed children [29], a morphometric study of children with genetic abnormalities [30], a large study of the effects of organolead-exposure on the brain [31], and a study of effect of sustained, heavy drinking on the brain [32, 33]. Many of these studies are the leading studies in their respective fields, and have received ample international attention.
To further improve the performance of HAMMER, various research works have been performed. In order to improve the performance of correspondence detection using attribute vectors, the best-scale geometric moment invariants (GMIs) have been learned for registration [34]. Also, the separate sets of best features have been specially learned for different parts of brain, since it is believed that different types of features have different functions in characterizing image points, and different parts of brain need different sets of best features to distinguish themselves. Moreover, by learning the normal brain variations from a set of brain image samples, we can use this learned information to constrain the image registration, thus improving the robustness of registration [25, 26].
It is worth noting that all previous improvements were focusing on improving the robustness and accuracy of registration in HAMMER, e.g., using the average registration error. Less attention has been paid to increasing the registration speed. Currently, HAMMER takes up to 80 minutes for registering two MR brain images with the size of 256×256×124, which might be too long for some applications. Therefore, it is important to design methods to improve the speed of registration algorithm.
One reason that HAMMER needs a relatively long time for registration is that the correspondence detection results, used to guide image registration, can be ambiguous in some complex structures, and image warping has to be performed conservatively and thus slow. Many advanced correspondence detection methods have been proposed in the literature [35, 36]. Traditionally, one to one correspondence is established for each point in the image, which we can call as hard correspondence detection. Some advanced methods such as in [35, 36] allow to identify correspondences in a soft way, e.g., each point can be have multiple points as candidate correspondences, each assigned with a possibility. The total possibility is equal to 1. This is called soft correspondence detection. In the initial correspondence detection procedure, candidate correspondences can have similar amount of probability, indicating the uncertainty is high. With the progress of correspondence detection process, it will allow only a single correspondence or several candidate correspondences having the high probability and others close to zero, which increases the specificity of correspondence detection.
In this paper, we propose to detect soft correspondences [35, 36] for active points selected during the registration procedure. Thus, correspondence detection can be robust and allows the image warping to perform fast. Moreover, soft correspondence detection can be implemented hierarchically to render the registration both robust and accurate. For example, in the initial registration procedure, the distant points with high attribute similarity can also contribute significantly to the soft correspondence detection, thus potentially increasing the robustness of correspondence detection. With the progress of registration, the distant points even with high attribute similarity decrease gradually their contribution to the soft correspondence detection, thus effectively increasing the specificity of final correspondence detection results. By mathematically formulating this soft correspondence detection idea into the HAMMER registration framework, the speed of the final registration algorithm is reduced to only the one-ninth of original computational cost required by HAMMER, without affecting much for registration performance. In particular, the proposed registration algorithm can complete the alignment of two 256×256×124 images in about 9 minutes using Linux machine (with 2.40GHz CPU and 2-Gbyte memory).
The structure of this paper is organized as follows. In Section 2, the definitions for attribute vector and similarity, a new energy function for registration, and details for implementation are all discussed one by one. In particular, the ideas of how to mathematically allow each active point to have multiple correspondences in the other image, and how to make soft correspondence detection strategy robust as well as accurate are also explained in detail. In Section 3, various experiments on simulated and real data are conducted to confirm that the performance of the proposed registration method is not decreased much even with the significant deduction of computation cost. This paper concludes in Section 4.
2. Method
Image registration problem is formulated here as an iterative process of detecting soft correspondences for the active points. The active points are selected according to the distinctiveness of their attribute vectors, which include image intensity, edge type, and geometric features from the neighborhood. The active points are also selected hierarchically during the registration procedure, e.g., initially a small set of active points with the most distinctive attribute vectors and gradually a larger and larger set of active points by including less distinctive points. The dense correspondences in the entire image domain are interpolated by the mean correspondences estimated in the active points.
The correspondence for each active point is softly determined. Instead of one-to-one correspondence detection, each active point is allowed to have multiple correspondences detected in the other image; each detected correspondence is assigned with a probability ranging from 0 to 1, and all the detected correspondences have a total probability of 1. The location of soft correspondence is determined as a statistical mean location of all detected correspondences. Note that, if a point v is considered as a correspondence of an active point x, the respective probability is determined by evaluating not only the similarity of attribute vectors of points v and x, but also the similarity of attribute vectors of all points in their neighborhoods. To increase the speed of detecting candidate correspondences and measuring their probabilities, the evaluation of the similarity of attribute vectors of the two points can be performed first, in order to select only a small set of candidate points {v} to perform the computation-consuming comparison of attribute vectors in the whole neighborhoods.
It is worth noting that the soft correspondence detection is more robust than the one-to-one correspondence detection, thus the robustness of registration using the soft correspondence detection can be improved. In the initial registration procedure, both local and distant points with similar attribute vectors can contribute to the correspondence detection. Gradually, in the later registration procedure, only the most similar points are allowed to contribute to the correspondence detection. By using these strategies, we can achieve both the robustness and the accuracy for the registration results.
In the following, we first briefly summarize the definitions for attribute vectors and their similarity, which are the same as in HAMMER [21, 22]. Then, we give a definition of new energy function for the proposed registration algorithm. Finally, we provide the detailed descriptions of the soft correspondence matching within the original HAMMER registration framework.
2.1 Attribute Vector and Similarity
Definition
An attribute vector is defined for each point x in the image, to better distinguish one point from its neighboring points and also to identify its corresponding points in the other image by matching attribute similarity. The attribute vector a(x) includes three parts of information, i.e., edge type a1(x), image intensity a2(x), and Geometric Moment Invariants (GMIs) a3(x) that are calculated from the structure in the neighborhood. Hence, a(x) = [a1 (x) a2 (x) a3 (x)]; each of these three sub-vectors is explained one by one in the next three paragraphs.
For the hard tissue segmentation case [37] as employed in this paper, a1(x) is a 1×1 vector, which takes one of 7 discrete values corresponding to 7 edge types such as non-edge and six combinations of edges between grey matter (GM), white matter (GM), and CSF. In the fuzzy segmentation case [38], a 3×1 fuzzy vector [CWM, CGM, CCSF]T is typically used to represent the probability of WM, GM, and CSF on an image point x, where CWM, CGM, and CCSF all take a value between 0 and 1 and CWM + CGM + CCSF = 1.0. Thus, in the fuzzy segmentation case, a1(x) is designed as a 3×1 vector to measure the maximal direct difference (3×1 vector) of the tissue segmentation results between the image point x and any neighboring points.
a2(x) represents direct information on the image point x, which can be image intensity, tissue segmentation result, or both. In this paper, a2(x) is selected as a 1×1 vector to represent the intensity on the image point x, which has been normalized between 0 and 1.
For the brain images, the vector a3(x) comprises the GMIs of the respective GM, WM, and CSF, calculated from the multiple-scale spherical neighborhoods around the image point x. For a particular scale and tissue type, thirteen rotation invariants can be calculated from the zero-order, second-order, and third-order 3D regular moments [39]. Therefore, a3(x) can be a vector with K=3×13×L, where L is the number of scales used. Four rotation invariants that are formulated from the zero-order and the second order moments are listed next, while other nine rotation invariants, formulated from the third-order moments and both the second-order and the third-order moments, can be found in [39].
Note that the first GMI corresponds to the volume of a certain tissue.
Similarity
As mentioned above, there are three parts of attributes included in each attribute vector, with different parts of attributes having different contributions to the overall similarity of attribute vectors. For example, a1(x) represents the edge type, which provides important information for matching the same type of boundary points in the two individual brain images. a3(x) provides the geometric features, to allow the detailed comparison of geometric similarity between two images. Moreover, the sizes of these three different parts of attributes are different. Thus, we can first compare the similarity of short vectors of important attributes, such as a1(x), in the two attribute vectors, in order to avoid comparing the similarity of long vectors of attributes, such as a3(x), if the similarity on short vectors is low. In this way, we can significantly reduce the overall computation time for similarity measurement. In particular, the dissimilarity of two attribute vectors, a(x) and a(y), of two points x and y can be defined as:
If |a1 (x) − a1 (y)| is larger than ε, the overall dissimilarity d (a(x), a(y)) is one. In the hard tissue segmentation case, ε is equal to zero; in the fuzzy segmentation case, ε is a certain value that should be determined in the experiments. c([a2 (x) a3 (x)],[a2 (y) a3 (y)]) is the similarity of the second and the third parts of the two attribute vectors in a(x) and a(y). To be strict on the similarity measure, each element in a2 and a3 is first normalized into a range from 0 and 1, and then compared and further integrated as a way described next:
where is the i-th element of a3 (x) which has total K elements.
2.2 Energy Function
The goal of image registration is to best align a template image T (x) with a subject image S(y) by maximizing the similarity of attribute vectors on the corresponding points. If a template point x is corresponding to a subject point y, their attribute vectors aT (x) and aS (y) should be as similar as possible, i.e., d (aT (x), aS (y)) should be as small as possible. On the other hand, the estimated deformation field {h(x), x ∈ ΩT}, where ΩT denotes the template image domain, should be able to warp the template point x very close to its corresponding subject point y, i.e., h(x) = y.
It is important to allow each active point to have multiple correspondences detected in the other image, in order to increase the robustness of overall registration algorithm. This is significant particularly when the one-to-one correspondence detection is difficult. Accordingly, in this paper, each active point x in the template is allow to have multiple points {v} detected in the subject image as correspondences, with {px,v} representing the probability of a template active point x and a subject point v as a pair of corresponding points. The deformation field h(x) in the template point x can be thus estimated as a statistical mean location of all correspondences detected in the subject, i.e., . Note that the soft or fuzzy correspondence will be progressively forced to the one-to-one correspondence during the registration procedure, thus achieving not only the robustness but also the accuracy of registration. The robustness is achieved by initially allowing all points with similar attribute vectors to contribute to the correspondence detection, while the accuracy or the specificity of registration is achieved by finally allowing only the most similar points to contribute to the correspondence detection.
Our registration algorithm can be accordingly formulated as an iterative optimization process involving three steps. The first step is to select active points from both template and subject images, with the number of active points progressively increased during the registration. The second step is to detect multiple candidate correspondences and respective probabilities for each active point; candidate points can be selected initially from a large neighborhood and later from a small or even immediate neighborhood. The third step is to calculate the mean deformation for each template active point based on the detected correspondences, and also to interpolate the mean deformations in the other locations of the template image domain and make them smooth spatially. By iteratively performing these three steps, the registration algorithm can register images robustly and accurately.
The energy function is defined next to facilitate the iterative performance of these three steps in the registration procedure.
Energy terms
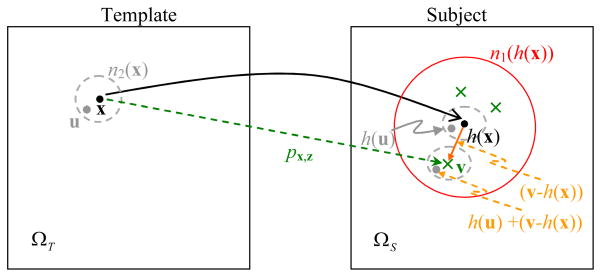
The first term in the whole energy function describes the overall cost of matching a template image with a subject image (see Fig. 1 for reference). For a template point x, its mean deformation is defined as h(x). For a subject point v in the neighborhood of h(x), v ∈ n1 (h(x)), its probability of being selected as a correspondence for the template point x is px,v. n1 denotes a searching neighborhood around the mean deformation h(x); the size of n1 is large initially, and decreases gradually with the progress of registration, in order to achieve the robustness as well as the accuracy of registration. Three types of costs need to be minimized once a subject point v is selected as a correspondence of the template point x. The first type of cost is the dissimilarity of attribute vectors of the template point x and the subject point v, i.e., d (aT (x), aS (v)). The second type of cost is the overall dissimilarity in the neighborhoods around the template point x and the subject point v, i.e., where all neighboring points {u} of the template point x, u ∈ n2 (x), are compared with the neighboring points h(u) + (v − h(x)) of the subject point v, by using attribute vector dissimilarity. n2 represents a matching neighborhood, whose size changes from an initial large size to a final small size with the progress of registration. The third type of cost is the distance of the subject point v away from the mean deformation h(x), i.e., ||v − h(x)||2. By integrating all of these three types of cost from all template points, the total cost for aligning the template with the subject images can be obtained as the first energy term in whole energy function.
Fig. 1.
Schematic explanation for correspondence detection, probability estimation, and neighborhood matching in our registration algorithm. A template point x is tentatively warped to a location h(x) in the subject. In the subject space, a neighboring point v of h(x) is considered as a candidate correspondence for the template point x, with the probability px,z calculated from the similarity of attribute vectors on points x and v, as well as the similarity of attribute vectors in the respective neighborhoods (e.g., a dotted grey circle n2 in the template and one deformed dotted grey circle around point v in the subject). The deformed dotted circle around point v is shifted by v−h(x) from the one around point h(x), which is a warped version of an original circle in the template. In the searching neighborhood n1 (red circle), only several points (green cross points) are detected as candidate correspondences for template point x.
For increasing the consistency of registration [5, 21, 22, 40, 41], we also define a cost function for matching the subject image with the template image, as described by the second energy term in the whole energy function. h−1(y) is the backward transformation from the subject to the template, which is the inverse of the forward transformation h(x). Cost definitions in the second energy term are similar to those in the first energy term.
As mentioned, by allowing each point to have multiple correspondences, the robustness of registration algorithm can be increased. Also, in order to increase the specificity or the accuracy of registration results, it is necessary to finally determine only a single correspondence for each point, or require all the detected correspondences very close to the mean deformation h(x). The latter requirement can be implemented by increasing the parameter σ (in the energy function) with the progress of registration, to constrain the distance between each correspondence (v) and the mean location of all correspondences (h(x)). Also, the progressive decrease of the size of searching neighborhood n1 ensures the selection of candidate correspondences from the nearby points. The former requirement can be implemented by adding an entropy measurement on the probabilities {px,v} and {pv,y}, which is included as the third energy term in the whole energy function. The parameter τ controls the significance of this energy term [42, 43]. By adaptively adjusting parameter τ with the progress of registration, i.e., changing from extremely large to extremely small value, we can actively allow the registration algorithm to detect multiple correspondences from an initial large neighborhood to later a small neighborhood, and also from initially even the low similarity points to latter only the high similarity points.
The last energy term evaluates the smoothness of the mean deformation field {h(x)} estimated in the entire image domain, using a Laplacian operator. Based on the multiple correspondences and the respective probabilities detected for each active point, the mean deformations {h(x)} in all active points {x} can be statistically determined and then used to refine the previous estimations in the same active points. The mean deformations in the other locations of the image can be interpolated with an interpolation kernel, e.g., a Gaussian kernel used in this paper. Finally, this updated deformation field can be made as regular as possible in the entire image domain by using a Laplacian smoothness constraint. A parameter β is used to control the importance of the Laplacian smoothness constraint in the whole energy function.
The following is the whole energy function that our image registration algorithm will minimize.
Subject to the constraints:
Hierarchical optimization
As mentioned, our registration algorithm will hierarchically select a set of active points with distinctive attribute vectors to drive the image registration. The set of active points will be progressively increased with the progress of registration by adding less distinctive points when they are deformed close to their targets and become reliable to drive the image registration. This strategy can be implemented by hierarchically assigning different values to the parameters ωT(x) and ωS (y) in the energy function, thus effectively selecting the respective template and subject points (x and y) to be actively involved in the image registration.
We can initially assign large values to the points with distinctive attribute vectors, and zero to other points in the images. In this case, the whole energy function above describes a problem of determining correspondences for those selected active points and also interpolating a smooth dense deformation field according to the mean correspondence locations determined in those active points. After solving this relative small scale problem of correspondence detection and deformation field estimation, we can increase the set of active points by including other less distinctive points, and then start to solve a relative large scale problem of correspondence detection on more active points. Since the sizes of the searching neighborhood n1 and the matching neighborhood n2 will be decreased with the progress of registration, the computational cost for detecting correspondences for more active points will not be necessarily increased as confirmed by our experiments.
In the final, by considering all image points into the energy minimization problem, we solve the exact energy function that our registration algorithm should originally minimize. Importantly, the advance of using this hierarchical optimization strategy is that we can have high chances to avoid local minima. The subsection next describes the details for implementing this hierarchical optimization strategy.
2.3 Implementation
The whole energy function above can be hierarchically minimized by iteratively estimating (1) the correspondence probabilities {px,v} and {pv,y} for the current selected active points, (2) the mean deformations in the current selected active points, and (3) the dense mean deformation field in the entire image domain. The descriptions for each of these three iterative steps are provided next.
Estimating correspondence probabilities
The probability for each pair of correspondences in {px,v} can be determined by solving an equation of ∂E/∂Px,v = 0, with the result given next. Note that the probabilities in {pv,y} can be similarly determined.
where c is a constant, m(x, v) measures the similarity of attribute vectors between a template point x and a subject point v, and mSub (x, v) represents the similarity of whole neighborhoods around the template point x and the subject point v, and mDist(x, v) measures how close two points x and v are. Expressions of these measures are given next:
The estimated probabilities {px,v} are normalized separately for each template point x as follows, in order to ensure that the total probability for detecting correspondences for the point x is 1.0.
It is worth noting that, the similarity of neighborhoods mSub (x, v) is generally expensive to compute, if the number of points {v} in the neighborhood n2 is large. To avoid this computation problem, we propose to first calculate the measurement m(x, v) for all neighboring points {v}. Then, we check whether any neighboring points have the measurement m(x, v) over a certain threshold. (Note that this threshold can be gradually adjusted with the progress of registration, e.g., from initially a large value (such as 0.8 in our paper) to later a small value.) Only for the points with the expected measurement m (x, v), their neighborhood similarity mSub (x, v) will be consequently computed. By using this strategy, we can potentially assign zero probability for many neighboring points v, thus significantly reducing the overall computational time.
Estimating the mean deformations in active points
Once the probabilities {px,v} and {pv,y} have been determined, the mean deformation, or the location of soft correspondence, for each active point can be immediately determined. By taking active points in the template image as an example, we can determine the mean deformation for each template active point x by optimizing the sub-energy term, . The solution is . This means that the new location of soft correspondence for the active point x is the statistical mean location of all correspondences detected in the subject image.
By determining the new location for each of these active points in the template and the subject images, we can deform all points in the neighborhoods of these active points by using a Gaussian kernel as employed in HAMMER [21, 22]. By selecting the standard deviation of the Gaussian kernel as small as the one-third of the size of searching neighborhood n1, we can smoothly update the deformation field without introducing possible self-intersection. Note that the entire deformation field might be not sufficiently smooth due to this independent, local updating of deformations. This necessitates the use of Laplacian smoothness constraint to regularize the entire deformation field, as briefly summarized next.
Regularizing the dense deformation field
Once deformations have been updated in active points and their neighborhoods, the last energy term, e.g., Laplacian smoothness constraint, can be used to ensure both global and local smoothness of the entire deformation field. In the discrete case, the Laplacian smoothness constraint actually requires the deformation of each point to be close to the average deformation in its immediate neighborhood. Therefore, in the implementation, we can gradually push the deformation of each point to the average deformation in the immediate neighborhood, e.g., a 3×3×3 neighborhood. By repeating this step, we can finally obtain a smooth dense deformation field {h(x)}.
3. Experimental Results
The performance of the proposed registration algorithm has been evaluated using both simulated and real data. The results on simulated data show that the proposed registration method can achieve a registration accuracy comparable to the one produced by HAMMER, while the results on the real longitudinal data indicate that the proposed registration algorithm can achieve better longitudinal consistency than HAMMER. Importantly, the speed of the proposed registration algorithm has been significantly improved, e.g., taking only about the one-ninth of computation time required by HAMMER. For example, it takes about 9 minutes for registration of two 256×256×124 brain images, using Linux machine (with 2.40GHz CPU and 2-Gbyte memory).
Three subsections next compare the performances of our proposed registration algorithm and HAMMER in registering simulated data, constructing average brains from 18 individual brains, and aligning longitudinal data of real patients, respectively. The registration is performed in the isotropic image space. Note that, all of these experimental results are provided to confirm that the performance of the proposed registration algorithm is comparable to that of HAMMER, even with the significant improvement of registration speed.
2.1 Simulated Data
The proposed registration method has been applied to the simulated data for quantitatively measuring its registration performance. The same simulated data used to validate HAMMER in [21] is used here. The simulated data was created by first randomly selecting a brain, and then using the STAR elastic warping method [8] to warp this selected brain to five individual human brains by respectively placing forces on the ventricles and the cortex. Finally, five simulated brains were obtained, which are actually the different warped versions of the same selected brain. Note that the overall shapes of these five simulated brains are similar to those five individual brains used to guide the warping.
It is worth noting that the ground-truth deformations from the selected brain to each of these simulated brains are known. Thus, by applying the proposed registration method to estimating the deformations between the selected brain and each of these five simulated brains, we can quantitatively measure the accuracy of the proposed registration algorithm by comparing our estimated deformations with the ground-truth ones. The average registration error by the proposed algorithm is 1.13mm, which is comparable to 0.97mm error produced by HAMMER. Note that, as mentioned above, the proposed algorithm took only the one-ninth of the computational cost required by HAMMER.
2.2 Average Brain
The proposed registration algorithm has been applied to 18 real brain images for constructing an average brain from these 18 normalized brain images in the template space. The same 18 brain images used in HAMMER [21] are used here for direct comparison of our constructed average brain with that by HAMMER.
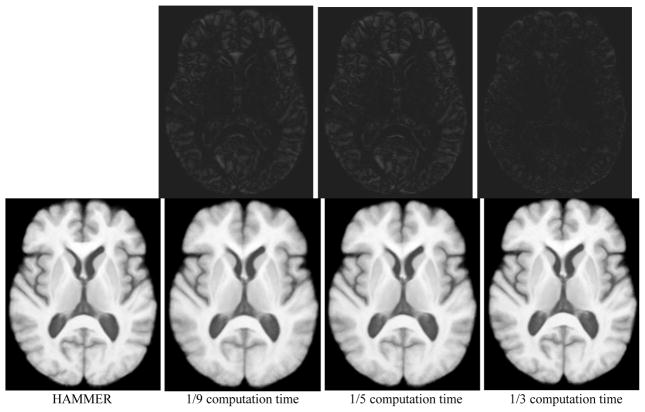
Fig. 2 show the average images constructed from 18 individual brain images using the proposed registration algorithm and HAMMER, respectively. The average brain image constructed by the proposed method (the 2nd from left in the bottom row) is relatively fuzzy compared to the one constructed by HAMMER (left). Considering that the proposed registration method takes only the one-ninth of computation time to align images, the quality of registration is still promising. If we spend a relatively long time for registration, i.e., about 1/5 or 1/3 of computation time used by HAMMER, we can obtain average brain images closer and closer to the one obtained by HAMMER.
Fig. 2.
Average brain images constructed from 18 normalized individual brain images by HAMMER, and by the proposed registration algorithm that took about 1/9, 1/5, or 1/3 computation time of HAMMER. The difference image between the result by HAMMER and each result by the proposed method is provided in the top row. These different images have been enhanced for better visual inspection.
2.3 Longitudinal Data
The proposed registration method has been applied to the longitudinal data obtained from our Baltimore Longitudinal Study of Aging (BLSA) [27], to check the longitudinal stability of our registration algorithm in aligning images of the same subject acquired at different times. In the BLSA project, SPGR MR brain images have been acquired annually by a GE 1.5T scanner for 150 elderly subjects over 13 years. We applied our registration algorithm to the first five images of the same patients (acquired in the first five years), and the performance is compared with that achieved by HAMMER.
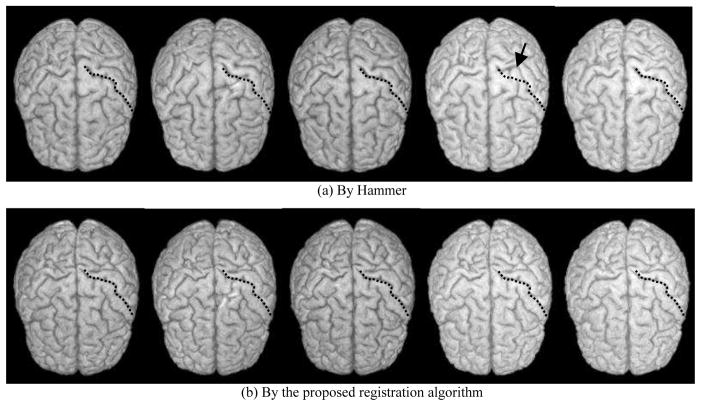
Fig. 3 shows the results of five longitudinally acquired images collected once per year for five years of the same subject. These images were spatially normalized by HAMMER (1st row) and the proposed algorithm (2nd row), respectively. Since the normalization for each time image was performed independently, the normalization results might be not longitudinally consistent. It can be observed that the normalization results by HAMMER are not consistent in the fourth time image as indicated by the arrow. In contrast, the normalization results achieved by the proposed algorithm are more stable across different times, indicating the better performance of the proposed algorithm than HAMMER in aligning longitudinal data. On the other hand, it is worth noting that the normalization results from these two methods are somewhat different, particularly in the light hemisphere sulcal patterns (right in the image). More evaluations need to be done in the future for complete comparison of the two methods.
Fig. 3.
Comparison on the longitudinal consistency of the registration on five different images of the same subject, using (a) HAMMER and (b) the proposed registration algorithm.
4. Conclusion
We have presented a new approach to significantly improve the speed of our previous HAMMER registration algorithm. This is achieved by using a hierarchical soft correspondence detection technique to replace the one-to-one correspondence detection strategy in HAMMER, thus the correspondence detection can be performed more robustly and the image warping can be conducted straightforwardly and fast. In particular, for each active point selected during the registration procedure, it is allowed initially to have multiple correspondences detected in the other image, and gradually forced to have few (or even one) correspondences detected in the other image. By using this hierarchical soft correspondence detection technique, we can achieve not only the robustness but also the accuracy of registration.
In summary, the image registration is here formulated as a process of hierarchically detecting a soft correspondence for each active point selected during the registration procedure, and also a process of interpolating and regularizing the dense smooth deformation field in the entire image domain. The experimental results indicate that, compared to HAMMER, first the speed of the proposed registration algorithm has been significantly increased without sacrificing much for the registration performance, and second the longitudinal consistency has been considerably improved.
In the future work, we will extensively evaluate and optimize all the parameters in our proposed registration algorithm, by using more real and simulated datasets with ground-truth information provided by manual raters or computer simulations. The final registration algorithm will be released publicly, as we did for the HAMMER registration algorithm, http://www.nitrc.org/projects/hammer/.
Footnotes
Dinggang Shen received all of his degrees from Shanghai JiaoTong University. He is an Associate Professor in the Department of Radiology at UNC-Chapel Hill since April 2008. He was an assistant professor (tenure-track) in the Department of Radiology at University of Pennsylvania (Upenn), from July 2002 to March 2008, and a faculty member in Johns Hopkins University from Jan 2001 and June 2002. Dr. Shen is on the Editorial Board of Pattern Recognition, International Journal of Image and Graphics, and International Journal for Computation Vision and Biomechanics. He also served as a reviewer for numerous international journals and conferences, as well as NIH, NSF and other grant foundations. He has published over 180 articles in journals and proceedings of international conferences. His research interests include medical image analysis, pattern recognition, and computer vision.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Collignon A, Maes F, Delaere D, Vandermeulen D, Suetens P, Marchal G. Automated multi-modality image registration based on information theory. In: Bizais Y, Barillot C, Paola RD, editors. Information Processing in Medical Imaging. Dordrecht, The Netherlands: Kluwer; 1995. pp. 263–274. [Google Scholar]
- 2.Alexander DC, Gee JC. Elastic matching of diffusion tensor images. Comp Vis and Image Understand. 1999;77:233–250. [Google Scholar]
- 3.Ashburner J, Friston KJ. Voxel-based morphometry: the methods. Neuroimage. 2000;11:805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- 4.Bookstein FL. Principal Warps: Thin-Plate Splines and the Decomposition of Deformations. IEEE Trans on Pattern Analysis and Machine Intelligence. 1989;11:567–585. [Google Scholar]
- 5.Christensen GE, Johnson HJ. Consistent Image Registration. IEEE Trans on Med Imaging. 2001;20:568–582. doi: 10.1109/42.932742. [DOI] [PubMed] [Google Scholar]
- 6.Collignon A. Multi-modality medical image registration by maximization of mutual information. Leuven, Belgium: Catholic Univ. Leuven; 1998. [Google Scholar]
- 7.Collins DL, Evans AC. Automatic 3D estimation of gross morphometric variability in the human brain. Neuroimage. 1996;3:S129. [Google Scholar]
- 8.Davatzikos C. Spatial transformation and registration of brain images using elastically deformable models. Comp Vision and Image Understanding. 1997;66:207–222. doi: 10.1006/cviu.1997.0605. [DOI] [PubMed] [Google Scholar]
- 9.Dawant BM, Hartmann SL, Gadamsetty S. Brain Atlas Deformation in the Presence of Large Space-occupying Tumours. Lect Notes in Comp Sci:MICCAI’99. 1999;1679:589–596. doi: 10.1002/igs.10029. [DOI] [PubMed] [Google Scholar]
- 10.Friston KJ, Ashburner J, Frith CD, Poline JB, Heather JD, Frackowiak RSJ. Spatial registration and normalization of images. Human Brain Mapping. 1995;2:165–189. [Google Scholar]
- 11.Gee JC, Reivich M, Bajcsy R. Elastically deforming 3D atlas to match anatomical brain images. Journal of Computer Assisted Tomography. 1993;17:225–236. doi: 10.1097/00004728-199303000-00011. [DOI] [PubMed] [Google Scholar]
- 12.Gerig G, Styner M, Lieberman J. Shape versus Size: Improved understanding of the morphology of brain structures. presented at MICCAI; 2001; Utrecht, the Netherlands. 2001. [Google Scholar]
- 13.Joshi SC, Miller MI, Christensen G, Banerjee A, Coogan T, Grenander U. Hierarchical brain mapping via a generalized Dirichlet solution for mapping brain manifolds. Proc of the SPIE Conf on Geom Methods in Applied Imaging. 1995;2573:278–289. [Google Scholar]
- 14.Mohamed A, Shen D, Davatzikos C. Deformable Registration of Brain Tumor Images via a Statistical Model of Tumor-Induced Deformation. presented at MICCAI; CA: Palm Springs; 2005. [DOI] [PubMed] [Google Scholar]
- 15.Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Non-rigid registration using free-form deformations: Application to breast MR images. IEEE Transactions on Medical Imaging. 1999;18:712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- 16.Thirion JP. Non-rigid matching using deamons. presented at Proc. IEEE Conf. Comp. Vis. and Patt. Recog; 1996. [Google Scholar]
- 17.Thompson P, Toga AW. A surface-based technique for warping three-dimensional images of the brain. IEEE Trans on Med Imaging. 1996;15:402–417. doi: 10.1109/42.511745. [DOI] [PubMed] [Google Scholar]
- 18.Wang Y, Peterson BS, Staib LH. 3D brain surface matching based on geodesics and local geometry. Computer Vision and Image Understanding. 2003;89:252–271. [Google Scholar]
- 19.Wells I, William M, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Medical Image Analysis. 1996;1:35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- 20.Rohr K. Image registration based on thin plate splines and local estimates of anisotropic landmark localization uncertainties. Lect Notes in Comp Sci:MICCAI’98. 1999;1496:1174–1183. [Google Scholar]
- 21.Shen D, Davatzikos C. HAMMER: Hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- 22.Shen DG, Davatzikos C. Very high resolution morphometry using mass-preserving deformations and HAMMER elastic registration. NeuroImage. 2003;18:28–41. doi: 10.1006/nimg.2002.1301. [DOI] [PubMed] [Google Scholar]
- 23.Xue Z, Shen D, Davatzikos C. Determining Correspondence in 3D MR Brain Images Using Attribute Vectors as Morphological Signatures of Voxels. IEEE Trans on Medical Imaging. 2004;23:1276–1291. doi: 10.1109/TMI.2004.834616. [DOI] [PubMed] [Google Scholar]
- 24.Shen D. Image Registration by Hierarchical Matching of Local Spatial Intensity Histograms. presented at MICCAI’04; St. Malo, France. 2004. [Google Scholar]
- 25.Wu G, Qi F, Shen D. Learning Best Features and Deformation Statistics for Hierarchical Registration of MR Brain Images. presented at IPMI; The Netherlands. 2007. [DOI] [PubMed] [Google Scholar]
- 26.Xue Z, Shen D, Davatzikos C. Statistically-Constrained High-Dimensional Warping Using Wavelet-Based Priors. presented at Proceedings of IEEE Computer Society Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA 2006); New York City, NY, USA. 2006. [Google Scholar]
- 27.Resnick SM, Goldszal A, Davatzikos C, Golski S, Kraut MA, Metter EJ, Bryan RN, Zonderman AB. One-year age changes in MRI brain volumes in older adults. Cerebral Cortex. 2000;10:464–472. doi: 10.1093/cercor/10.5.464. [DOI] [PubMed] [Google Scholar]
- 28.Davatzikos C, Shen DG, Wu X, Lao Z, Hughett P, Turetsky BI, Gur RC, Gur RE. Whole-brain morphometric study of schizophrenia reveals a spatially complex set of focal abnormalities. JAMA Archives of General Psychiatry. 2005 Nov;62:1218–1227. doi: 10.1001/archpsyc.62.11.1218. [DOI] [PubMed] [Google Scholar]
- 29.Fan Y, Rao H, Giannetta J, Hurt H, Wang J, Davatzikos C, Shen D. Diagnosis of Brain Abnormality Using both Structural and Functional MR Images. IEEE 2006 International Conference of the Engineering in Medicine and Biology Society (EMBS); NY, USA. 2006. (submitted) [DOI] [PubMed] [Google Scholar]
- 30.Shen D, Liu D, Liu H, Clasen L, Giedd J, Davatzikos C. Automated Morphometric Study of Brain Variation in XXY Males. NeuroImage. 2004;23:648–653. doi: 10.1016/j.neuroimage.2004.08.018. [DOI] [PubMed] [Google Scholar]
- 31.Stewart WF, Schwartz BS, Davitzikos C, Shen D, Liu D, Todd AC, Shi W, Bassett S, Youssem D. Tibia Lead Level is Associated with White Matter Lesions and Global and Region Specific Volumetric Measures in Former Organolead Manufacturing Workers. 2004 submitted. [Google Scholar]
- 32.Beresford Thomas P, David JA, Arciniegas B, Lori Clapp RN, Martin Brandon, Liu Dengfeng, Shen Dinggang, Davatzikos Christos. Hippocampus Volume Loss in Chronic Alcohol Dependence. Journal of Studies on Alcohol. 2005 submitted. [Google Scholar]
- 33.Beresford Thomas P, David JA, Arciniegas B, Lori Clapp RN, Martin Brandon, Beresford Henry F, Du Yiping, Liu Dengfeng, Shen Dinggang, Davatzikos Christos, Laudenslager Mark L. The Association of Hypercortisolism and Hippocampus Volume Loss In Alcoholism. Journal of Studies on Alcohol. 2005 submitted. [Google Scholar]
- 34.Wu G, Qi F, Shen D. Learning-Based Deformable Registration of MR Brain Images. IEEE Trans Medical Imaging. 2006 Sept;25:1145–1157. doi: 10.1109/tmi.2006.879320. [DOI] [PubMed] [Google Scholar]
- 35.Chui H, Rangarajan A. A new point matching algorithm for non-rigid registration. Computer Vision and Image Understanding. 2003;89:114–141. [Google Scholar]
- 36.Yang J, Williams JP, Sun Y, Blum RS, Xu C. Non-rigid Image Registration Using Geometric Features and Local Salient Region Features. presented at IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2006. [Google Scholar]
- 37.Goldszal AF, Davatzikos C, Pham D, Yan M, Bryan RN, Resnick SM. An image processing protocol for the analysis of MR images from an elderly population. Journal of Computer Assisted Tomography. 1998;22:827–837. doi: 10.1097/00004728-199809000-00030. [DOI] [PubMed] [Google Scholar]
- 38.Pham DL, Prince JL. Adaptive fuzzy segmentation of magnetic resonance images. IEEE Transactions in Medical Imaging. 1999;18:737–752. doi: 10.1109/42.802752. [DOI] [PubMed] [Google Scholar]
- 39.Lo CH, Don HS. 3-D Moment Forms: Their Construction and Application to Object Identification and Positioning. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1989;11:1053–1064. [Google Scholar]
- 40.Xue Z, Shen D, Davatzikos C. CLASSIC: Consistent Longitudinal Alignment and Segmentation for Serial Image Computing. presented at Information Processing in Medical Imaging; Colorado: Glenwood Spring; 2005. [DOI] [PubMed] [Google Scholar]
- 41.Johnson HJ, Christensen GE. Consistent landmark and intensity-based image registration. IEEE Trans on Med Imaging. 2002;21:450–461. doi: 10.1109/TMI.2002.1009381. [DOI] [PubMed] [Google Scholar]
- 42.Geman S. Seminar on MRFs, Gibbs distributions, and Simulated Annealing. presented at Joint Centers for Intelligent Control Computer Vision Workshop; Harvard University; 1987. [Google Scholar]
- 43.Kirkpatrick S, Gellatt CD, Jr, Vecchi MP. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]