Active pixel imagers incorporating pixel-level amplifiers based on polycrystalline-silicon thin-film transistors

Abstract

Active matrix, flat-panel imagers (AMFPIs) employing a 2D matrix of a-Si addressing TFTs have become ubiquitous in many x-ray imaging applications due to their numerous advantages. However, under conditions of low exposures and∕or high spatial resolution, their signal-to-noise performance is constrained by the modest system gain relative to the electronic additive noise. In this article, a strategy for overcoming this limitation through the incorporation of in-pixel amplification circuits, referred to as active pixel (AP) architectures, using polycrystalline-silicon (poly-Si) TFTs is reported. Compared to a-Si, poly-Si offers substantially higher mobilities, enabling higher TFT currents and the possibility of sophisticated AP designs based on both n- and p-channel TFTs. Three prototype indirect detection arrays employing poly-Si TFTs and a continuous a-Si photodiode structure were characterized. The prototypes consist of an array (PSI-1) that employs a pixel architecture with a single TFT, as well as two arrays (PSI-2 and PSI-3) that employ AP architectures based on three and five TFTs, respectively. While PSI-1 serves as a reference with a design similar to that of conventional AMFPI arrays, PSI-2 and PSI-3 incorporate additional in-pixel amplification circuitry. Compared to PSI-1, results of x-ray sensitivity demonstrate signal gains of ∼10.7 and 20.9 for PSI-2 and PSI-3, respectively. These values are in reasonable agreement with design expectations, demonstrating that poly-Si AP circuits can be tailored to provide a desired level of signal gain. PSI-2 exhibits the same high levels of charge trapping as those observed for PSI-1 and other conventional arrays employing a continuous photodiode structure. For PSI-3, charge trapping was found to be significantly lower and largely independent of the bias voltage applied across the photodiode. MTF results indicate that the use of a continuous photodiode structure in PSI-1, PSI-2, and PSI-3 results in optical fill factors that are close to unity. In addition, the greater complexity of PSI-2 and PSI-3 pixel circuits, compared to that of PSI-1, has no observable effect on spatial resolution. Both PSI-2 and PSI-3 exhibit high levels of additive noise, resulting in no net improvement in the signal-to-noise performance of these early prototypes compared to conventional AMFPIs. However, faster readout rates, coupled with implementation of multiple sampling protocols allowed by the nondestructive nature of pixel readout, resulted in a significantly lower noise level of ∼560 e (rms) for PSI-3.

INTRODUCTION

Active matrix, flat-panel imagers (AMFPIs) incorporating arrays with amorphous silicon (a-Si) thin-film transistors (TFTs) have become ubiquitous in the field of medicine and are accelerating the trend of digital, filmless x-ray imaging in many applications and venues. These arrays employ two-dimensional matrices of pixels with a pixel architecture consisting of an addressing TFT coupled to some form of pixel storage capacitor. Indirect detection AMFPI arrays use a storage capacitor in the form of an optical sensor that detects incident light emitted from an overlying scintillator (e.g., CsI:Tl). In direct detection AMFPI designs, a storage capacitor collects charge from an overlying photoconductive material (i.e., a-Se). While such conventional AMFPIs have proven to be highly versatile, offering good imaging performance for applications including mammography, radiography, cardiac imaging, and radiotherapy imaging, the ratio of the signal generated per interacting X ray to the electronic additive pixel noise is modest. This results in a significant reduction in detective quantum efficiency (DQE) under conditions of low exposure or high spatial frequencies¹ and is particularly pronounced for fluoroscopy^{1, 2} as well as for applications requiring small pixels, such as mammography and breast tomosynthesis.^{3, 4} In the case of fluoroscopy, it has been shown that the DQE of AMFPIs is inferior to that of image intensifiers (XRIIs) at the lower end of the exposure range (0.1–1 μR)⁵–where the limited system gain of AMFPIs results in the additive noise⁶ becoming significant relative to x-ray quantum noise.

To overcome this limitation, a variety of approaches are being pursued, all of which aim at enhancing the amount of signal generated per interacting X ray — given that significant reduction in the additive noise of AMFPIs appears unlikely. For direct detection AMFPIs, one approach involves the development of photoconductive materials offering x-ray sensitivities significantly higher (i.e., up to a factor of 10) than those offered by a-Se. The high gain materials under investigation include HgI₂, PbI₂, and PbO.^{7, 8, 9, 10, 11, 12} Another approach involves the use of a double layer of a-Se photoconductive material. While a thicker top layer acts as the converter of X rays into electrons and holes, a thinner bottom layer provides further signal amplification by means of an avalanche multiplication mechanism.¹³ In the case of indirect detection AMFPIs, one approach involves increasing the fraction of the area in each pixel that is optically sensitive through the use of a continuous photodiode design to achieve near-unity fill factor.^{3, 14} Another approach involves the introduction of a thin a-Se avalanche multiplication layer between the scintillator and the active matrix array to provide amplification of the light signal emerging from the scintillator.^{15, 16, 17}

An approach that can be applied to both direct and indirect detection AMFPIs involves the incorporation of an amplification circuit within each pixel, enhancing the pixel signal prior to readout. The use of in-pixel amplification is inspired by the successful incorporation of simple amplifiers into individual pixels of image sensors based on crystalline-silicon (c-Si) CMOS technology. Such devices, called active pixel sensors (APSs), have been extensively developed for various types of mobile imaging applications (e.g., digital cameras and cell phones) and have been investigated for use in medical imaging applications¹⁸ — although c-Si-based devices cannot provide the very large monolithic areas or very high radiation damage tolerance of a-Si arrays.^{19, 20} While early examination of in-pixel amplification using simple amplifier designs based on conventional n-channel a-Si TFTs has been reported,^{21, 22} the low carrier mobilities offered by a-Si material (∼1 cm²∕V s for electrons and ∼10⁻³ cm²∕V s for holes) is restrictive. An alternative to a-Si is polycrystalline silicon (poly-Si), which is playing an increasingly important role in a broad range of semiconductor devices, such as mobile active matrix displays and organic light emitting diode (OLED) displays.²³ Poly-Si offers the advantage of substantially higher carrier mobilities, on the order of 100 cm²∕V s for both electrons and holes, while maintaining the large area processing capability and radiation damage resistance of a-Si.²⁴ Such high mobilities enable faster TFT switching speeds and higher currents, as well as considerably more sophisticated amplification circuits based on both n-channel and p-channel TFTs. Another advantage of the high mobilities of poly-Si is the possibility of integrating additional circuitry, such as gate line drivers and data line multiplexers, on the periphery of AMFPI array substrates — reducing the density of connections as well as the amount of peripheral external electronics.

In this article, the basic design, operation, and performance of indirect detection flat-panel prototype arrays based on poly-Si TFTs are reported. The prototypes, referred to as polycrystalline-silicon imaging (PSI) arrays, employ various pixel circuits and incorporate a continuous photodiode structure.^{14, 25, 26} Two designs incorporate an amplification circuit in each pixel, which we will refer to as an “active pixel” (AP) architecture. The performance of these prototype arrays is characterized in terms of basic pixel signal and noise properties, as well as the spatial-frequency-dependent metrics, modulation transfer function (MTF), noise power spectrum (NPS), and DQE.

METHODS AND MATERIALS

Introduction to prototype PSI arrays

The three poly-Si array designs were implemented on a common wafer, a 4 in. quartz substrate. A schematic illustration of the layout of the three arrays on the wafer is shown in Fig. 1. In addition to the arrays, poly-Si multiplexers, gate drivers, and test circuits are present on the wafer. In the present study, the gate drivers on PSI-1 and PSI-2 were not used, and contact between gate lines and peripheral electronics was achieved through use of contact pads located on the opposite side of these arrays. The multiplexers, on the other hand, were used for the two array designs incorporating pixel amplification. Test circuits, which lie at the periphery of the wafer, include individual poly-Si TFTs of the types used in the array designs. Studies performed on such test circuits to investigate the radiation damage and noise properties of poly-Si TFTs have been previously reported.^{24, 27} In addition to providing a measure of the quality and performance of the poly-Si TFTs independent of the complications of array operation, empirical data obtained from these test circuits can also serve as input to circuit models simulating the signal and noise performance of array pixels.²⁷

Figure 1.

Schematic diagram illustrating the general features and layout of the three poly-Si array designs, PSI-1, PSI-2, and PSI-3, on a 4 in. wafer. The contact pads located at the periphery of the arrays were used to connect the data and gate lines to external preamplifier and gate driver circuits (not shown in the diagram), respectively. For PSI-2 and PSI-3, these contact pads connect to the array data lines via poly-Si multiplexer circuitry (labeled MUX), which reduces the number of contacts by factors of 16 and 8, respectively. The poly-Si gate line drivers located at the periphery of PSI-1 and PSI-2 were not used in the present study.

The creation of these poly-Si arrays involves a hybrid process^{28, 29} employing a continuous a-Si photodiode structure and one to five poly-Si TFTs per pixel.^{25, 26} For the TFTs, a-Si is first deposited on the substrate and later crystallized by a process involving a pulsed excimer laser.³⁰ The laser produces pulses of short wavelength (less than 400 nm), high intensity, and short duration (∼50 ns) — ensuring that the a-Si melts and solidifies rapidly without thermally damaging the substrate. The photodiodes are largely fabricated above the plane of the TFTs and consist of a patterned a-Si n-doped layer, as well as continuous intrinsic and p-doped a-Si layers.^{3, 14} The discrete n-doped layer connects to an underlying collection electrode, which defines the geometric fill factor of the pixel. Compared to the discrete photodiodes commonly employed in conventional AMFPIs, implementation of out-of-plane photodiode structures provides larger optical fill factors (defined as the fraction of the pixel surface that is optically sensitive to incident light) that are close to unity.^{3, 14} Such out-of-plane photodiode structures circumvent the competition for pixel area that would otherwise occur between the pixel TFTs of an amplification circuit and a conventional discrete photodiode.

The three prototype array designs are labeled PSI-1, PSI-2, and PSI-3, and their design specifications are summarized in Table 1. The PSI-1 array is based on a relatively simple design with a single poly-Si TFT used as an addressing switch, analogous to conventional AMFPI designs. However, unlike conventional designs, the TFT employs a dual-gate structure in order to reduce the elevated levels of leakage current that result from the higher mobilities offered by poly-Si material. The array has a pixel format of 384×256 pixels and a pitch of 90 μm, giving an active area of ∼3.45×2.30 cm². PSI-1 (which has been previously characterized)¹⁴ provides a reference for the performance of an array based on poly-Si TFTs, without in-pixel amplification. PSI-2 incorporates a single-stage, in-pixel amplifier with a pixel format of 384×256 pixels and a pitch of 90 μm, resulting in the same active area as for PSI-1. PSI-3 incorporates a dual-stage, in-pixel amplifier with a pixel format of 128×128 and a pixel pitch of 150 μm, resulting in an active area of ∼1.92×1.92 cm². An illustration of an individual pixel from each array is shown in Fig. 2.

Table 1.

Design specifications of the poly-Si arrays used in this study, including the channel type, width (W), and length (L) of the pixel transistors. Note that the geometric fill factor corresponds to the percentage of the pixel area occupied by the pixel charge collection electrode. Also note that the notation “(5+5)” refers to the length of the dual-gate structure used in some of the TFTs.

Property	PSI-1	PSI-2	PSI-3
Pixel pitch (μm)	90	90	150
Pixel format (data×gate)	384×256	384×256	128×128
Array dimensions (cm2)	3.45×2.30	3.45×2.30	1.92×1.92
Geometric fill factor (%)	∼70	∼60	∼75
TFTADDR, n-type; W×L (μm2)	10×(5+5)	8×(5+5)	8×(5+5)
TFTRST, n-type; W×L (μm2)		8×(5+5)	8×(5+5)
TFTSF, n-type; W×L (μm2)		30×10	30×10
TFTRO, n-type; W×L (μm2)		60×5	60×5
TFTAL, p-type; W×L (μm2)			10×30
TFTCSA, n-type; W×L (μm2)			437×10

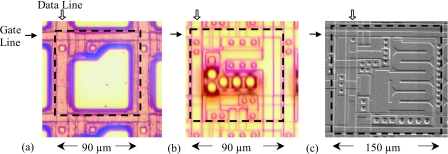
Figure 2.

Photomicrographs of a single pixel from (a) PSI-1, (b) PSI-2, and (c) PSI-3. The pixels are oriented so that gate lines and data lines run horizontally and vertically, respectively, as indicated by the solid and open arrow symbols. While the PSI-1 pixel has a simple architecture consisting of a collection electrode and an addressing TFT, PSI-2, and PSI-3 incorporate additional features corresponding to their in-pixel amplification circuits. The dashed squares appearing in the photomicrographs indicate the boundaries of one pixel. This figure is an adaptation of a figure from Ref. 25.

Array operation

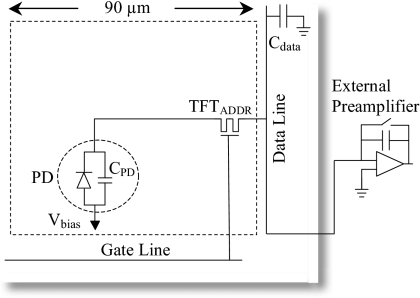
In order to understand the operation and performance benefits of PSI-2 and PSI-3, it is useful to examine the operation of PSI-1. A circuit diagram depicting a PSI-1 pixel, which consists of an addressing TFT (TFT_ADDR) coupled to a pixel storage capacitor (with intrinsic capacitance C_PD formed by the continuous photodiode structure), is shown in Fig. 3. A voltage V_bias, provided by an external supply, establishes a reverse bias across the photodiode structure. During image capture, the TFTs are kept nonconducting so that light photons produced through the interaction of incident radiation with the scintillator and detected by the photodiode result in the capture of imaging signal in the pixel storage capacitors. This imaging signal, which is proportional to the amount of incident radiation, is read out one row of pixels at a time by turning on (i.e., render conducting) the corresponding TFTs. This initiates current flow along the data lines, allowing the imaging signal to be sampled by an external charge preamplifier and subsequently digitized, while simultaneously resetting the voltage across the photodiode to its initial state.

Figure 3.

Schematic diagram illustrating the circuit for a single pixel in the PSI-1 prototype array. The circuit, surrounded by the dashed rectangle, comprises a dual-gate addressing transistor, TFT_ADDR, and a photodiode structure, PD. A bias voltage, V_bias, is applied to the photodiode, which has capacitance per pixel of C_PD. The pixel is addressed by means of a gate line and a data line (with capacitance C_data). A preamplifier circuit used to read out the pixel is located externally to the array substrate, as indicated by the shaded lines.

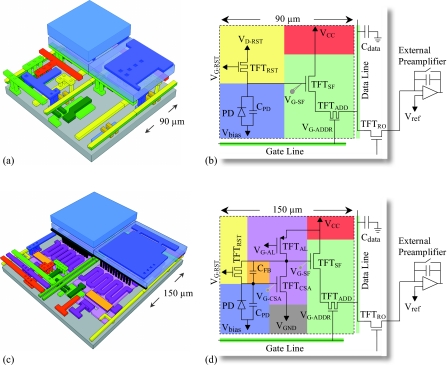
In the case of PSI-2, in addition to the photodiode and the dual-gate addressing TFT (TFT_ADDR), the pixel incorporates a reset TFT (TFT_RST) and a source-follower TFT (TFT_SF), as shown in the structural illustration and circuit diagram of Figs. 4a, 4b, respectively. Table 2 lists some of the voltages supplied to the various transistors in PSI-2 (and PSI-3) during array operation. When incident radiation is detected, the photodiode capacitance is discharged, causing the voltage at the gate of TFT_SF (V_G-SF) to drop from the initial reset voltage of V_D-RST in proportion to the imaging signal generated by the radiation. The imaging signal defined by this voltage change is then amplified by turning TFT_ADDR on, resulting in a current flow that charges the capacitance (C_data) of the corresponding data line. This current flow continues until the voltage of the data line approaches that of the gate contact of TFT_ADDR, hence the name “source follower.” The resulting charge remains stored on the data line by keeping the readout TFT (TFT_RO), located at the periphery of the array, in the off state (i.e., nonconducting). The additional signal gain provided by PSI-2 is determined by the ratio of the capacitance of the data line to that of the photodiode, C_data∕C_PD. The imaging signal stored in the data line capacitance is subsequently sampled by the external charge preamplifier via a 16 to 1 multiplexer (see Fig. 1). After sampling, the data line is reset to a reference voltage, V_ref. In order to reduce the number of control lines in the design of the PSI-2 prototype, reset of the pixel, performed by turning TFT_RST on, is achieved using the gate lines. Thus, when the voltage for a given gate line is switched to a positive value, this enables sampling of the charge from pixels along that line (by turning on the corresponding TFT_ADDR transistors) while simultaneously resetting pixels along the preceding gate line (by turning on the corresponding TFT_RST transistors). The reset action restores the gate contact of TFT_SF to its initial voltage of V_D-RST and, thus the voltage across the photodiode to its initial value of (V_bias−V_D-RST).

Figure 4.

Illustrations relating the physical structure of the prototype active pixels to their circuit diagrams, with color coding to indicate the correspondence between parts of the circuit and their physical implementation in the pixel. Three-dimensional drawings of the detailed structure of (a) PSI-2 and (c) PSI-3 pixels. Each drawing illustrates four adjoining pixels and reveals varying degree of detail. Note that dimensions in the direction perpendicular to the substrate have been exaggerated for clarity of presentation. Schematic circuit diagrams for prototype arrays (b) PSI-2 and (d) PSI-3. For each diagram, the dashed line delineates an individual pixel from other elements on the array. Each pixel design incorporates: a photodiode structure, PD, with capacitance per pixel of C_PD (in blue); a dual-gate addressing transistor TFT_ADDR and a source-follower transistor, TFT_SF, providing an amplification stage (both shown in light green); a reset transistor, TFT_RST, and its control lines (in yellow); and a readout transistor, TFT_RO, located on the periphery of the array and used to allow integration of the amplified signal on the data line capacitance, C_data, prior to sampling by an external preamplifier. For PSI-3, additional circuit elements include: a common-source amplifier transistor, TFT_CSA, and an active load transistor, TFT_AL, which together provide the first of two stages of amplification (in purple); a feedback capacitor, C_FB, (in orange), which serves as the pixel storage capacitor; and a ground line (in dark gray). V_bias represents the reverse bias voltage externally applied to the photodiode. V_D-RST and V_G-RST refer to the voltage applied to the drain electrode and gate electrode of TFT_RST in the PSI-2 and PSI-3 designs, respectively. Finally note that, for PSI-3, adjacent pixels share common lines which provide supply voltages (i.e., V_CC, V_G-AL, and V_GND along the data line direction and V_G-RST along the gate line direction). Values for these voltages are given in Table 2.

Table 2.

Parameter names and values of voltages used in the operation of the PSI-2 and PSI-3 arrays. The notations V_G-RST and V_G-ADDR correspond to the gate voltages of TFT_RST and TFT_ADDR, respectively, and the positive and negative values given correspond to the voltages used to render these TFTs conducting and nonconducting, respectively. V_D-RST and V_G-AL correspond to the voltages supplied to the drain contact of TFT_RST and to the gate contact of TFT_AL, respectively.

Array	Vbias (V)	VCC (V)	VG-RST (V)	VD-RST (V)	VGND (V)	Vref (V)	VG-ADDR (V)	VG-AL (V)
PSI-2	2.5–4	8	−3, 15	5	N∕A	2.2	−3, 15	N∕A
PSI-3	−1, 1	8	−2.5, 15	N∕A	1	2.2	−2.5, 15	4.5, 5.5

For PSI-3, each pixel incorporates a dual-stage amplification structure in the form of a common-source amplifier in series with a source-follower amplifier, as illustrated in Figs. 4c, 4d. The design is similar to that of PSI-2, except for the additional n-channel common-source amplifier TFT (TFT_CSA), the p-channel active load TFT (TFT_AL), and the feedback capacitor (C_FB) — which together constitute a first-stage amplification circuit. As incident radiation is detected, the photodiode capacitance is momentarily discharged, causing the voltage of the gate contact of TFT_CSA (V_G-CSA) to drop. Due to the very high open loop gain (∼80) of the first amplification stage, the voltage of the gate contact of TFT_SF (V_G-SF) increases until V_G-CSA is rapidly restored nearly to its initial value prior to irradiation.²⁶ This results in the voltage (and thus the electric field strength) across the photodiode remaining largely constant during array operation. Such a voltage-change limiting feature is expected to reduce image artifacts (e.g., lag and ghosting) associated with charge trapping and release in the a-Si material of the photodiode.²⁶ Amplification in the second stage of the PSI-3 pixels is provided by the same source-follower circuit as in PSI-2. The additional signal gain provided by PSI-3 is largely determined by the ratio of the data line capacitance to the feedback capacitance, C_data∕C_FB. The imaging signal stored on the data line capacitance is subsequently sampled, via an 8 to 1 multiplexer (see Fig. 1), by an external charge preamplifier. After sampling, the data lines are reset to V_ref and the pixels are reset through discharge of their corresponding capacitors C_FB by rendering the TFT_RST transistors conducting. Whereas pixel reset for PSI-1 and PSI-2 is performed one row of pixels at a time, for PSI-3 it is applied globally to all pixels prior to the delivery of radiation and the start of row-by-row readout.

For PSI-2 and PSI-3, the image information contained in the photodiode capacitor, C_PD, and the pixel storage capacitor, C_FB, respectively, is left undisturbed by readout and sampling by the external preamplifier since the pixel reset action is independent of readout. This feature allows for the possibility of more sophisticated readout protocols that can be used to reduce additive noise.

Electronic acquisition system

The PSI arrays were operated by means of an electronic acquisition system, G3,³¹ previously developed to allow detailed studies of the performance of conventional AMFPIs.^{3, 12, 32} However, in the case of the PSI-2 and PSI-3 arrays, when a given gate line is addressed, only a fraction of the 384 and 128 data lines can be read out at one time due to 16:1 and 8:1 on-array multiplexing of these lines, respectively. In order to support the multiplexed operation of these arrays using G3, supplemental control logic, based on complex programmable logic device (CPLD) chips, was implemented on an additional circuit board added to the G3 system. This board provides the substantial amount of “glue logic” between the G3 system and the arrays required to facilitate the reported studies — but at the cost of a reduction by factors of ∼16 and ∼9 in the maximum frame rate for readout of PSI-2 and PSI-3, respectively. In addition to allowing readout of multiplexed data, this glue logic also allows multiple nondestructive readout of PSI-3 whereby many frames of data were acquired following a global reset. This technique was employed to explore additive noise reduction.

The acquisition system also incorporates full-custom, low noise, 32-channel preamplifier-multiplexer chips³³ operated at two charge capacity settings, resulting in analog-to-digital conversion gains of 550 e∕ADC and 4092 e∕ADC for PSI-1 and PSI-2∕PSI-3, respectively, unless otherwise indicated. A single readout of array data by the G3 system results in a data frame. For all measurements, the system was operated so as to generate a continuous sequence of data frames with the time between consecutive frames defined as the frame time. Unless otherwise stated, the operational frame times of PSI-1, PSI-2, and PSI-3 were ∼0.28, ∼0.58, and ∼0.23 s, respectively. Data frames were acquired either in the absence of radiation (resulting in dark frames) or in the presence of radiation using X rays or optical illumination (resulting in image frames). Image frames were acquired both radiographically and fluoroscopically³⁴ with the delivery of radiation synchronized with array readout.

Experimental methodology

X-ray measurements were performed at 72 kVp using a Dunlee PX1415 x-ray tube with a tungsten target powered by a Picker MTX380 high frequency generator. The X rays generated in the tube were filtered by an inherent 3.2 mm of aluminum filtration and an additional 20 mm of Al filtration used to simulate the presence of a patient. The resulting x-ray spectrum incident on the prototype imagers has a half-value layer of ∼7 mm aluminum — corresponding to the standard x-ray spectrum RQA5 in IEC 1267. Unless otherwise indicated, the surface of each array was positioned at a source-to-detector distance (SDD) of 100 cm. The desired exposure to an imager was achieved through adjustment of tube current and exposure time. The exposure to the surface of an imager was determined by means of a calibrated ion chamber (Keithley 96035) located at the same SDD and connected to a dosimeter (Keithley 35050A). For all x-ray measurements, a phosphor screen, acting as the x-ray-to-light converter, was placed over the arrays. Two types of screens based on Gd₂O₂S:Tb were used: Lanex Regular and Lanex Fine (Eastman Kodak) with surface densities of ∼70 and 34 mg∕cm², respectively. Close contact between the phosphor and the array surface was maintained by exerting a low, uniform pressure on a thin foam plate positioned over the phosphor.

Optical measurements were performed by directly illuminating the arrays with a light source consisting of either an incandescent lamp or a flashing LED. The LED has a central emission wavelength of 568 nm, which is near the peak of the photodiode efficiency.³⁵ In order to control the amount of light received by array pixels, the LED was placed a short distance above each array and was flashed a specific number of times between frames, with each flash lasting a few microseconds.³⁴ For measurements with the incandescent lamp, there was no synchronization between light emission and array readout. In this case, the light source was continuously “on” and the desired amount of light signal per image frame was achieved through a combination of appropriate optical collimation and positioning of the light source above an array.

Signal response linearity and charge trapping

Signal response up to pixel saturation for the three prototype arrays was obtained in radiographic and fluoroscopic modes³⁴ using the LED to produce various light levels. For each light level, a total of six image frames were acquired and averaged. After dark signal subtraction, data from eight representative pixels were averaged to yield pixel response data. From these data, signal linearity was derived by applying a linear fit to the response curves using a portion of the curves corresponding to a range of signals in the first 25% of pixel saturation. The difference between the fit and the data, normalized to the pixel saturation level, yielded the magnitude of deviation from linearity.³⁴ For each prototype array, charge trapping (corresponding to the amount of charge lost following a radiographic exposure) was derived from the difference between the fluoroscopic and radiographic response curves.³⁴

X-ray sensitivity

X-ray sensitivity was determined for the three prototype arrays using the Lanex Regular screen under fluoroscopic conditions where charge trapping and charge release are in approximate equilibrium.³⁴ Measurements of x-ray sensitivity for PSI-2 and PSI-3, compared to that for PSI-1, provide a means of evaluating the magnitude of additional signal gain offered by pixel amplification. X rays were delivered continuously, resulting in a frame-time-dependent exposure level. The linear dependence of exposure on frame time resulted in PSI-1 and PSI-2 pixels receiving the same level of exposure in a given image frame, since pixel reset is performed line by line concurrently with gate line readout. For PSI-3, in which pixel reset is performed globally for the array, this dependence resulted in pixels receiving varying exposures, depending on when the corresponding gate line is read out with respect to the latest global reset action. In this case, a correction utilizing the relationship between exposure and gate line readout timing was applied to normalize all pixel signals to that of pixels along the last gate line (i.e., line 128). Sensitivity, expressed in units of signal in electrons per unit exposure and area, was determined from a linear fit to the pixel signal data obtained at exposures ranging from ∼0.03 to ∼0.7 mR. For each exposure, the signal data were determined from the median of the pixel signal distribution obtained from a block of 60×60 pixels following dark signal subtraction. The motivation for using this technique, as opposed to simply extracting data from selected pixels, is to include the effect of any spatial variations in sensitivity across an array that may occur as a result of process variations over the array surface.

Modulation transfer function

Spatial resolution of the prototype imaging arrays was characterized through determination of the presampled MTF, obtained from the Fourier transform of the line spread function (LSF). Measurements of the LSF were performed under both optical and x-ray illuminations. The x-ray measurements, which were performed to characterize the system MTF with the Lanex Regular and Lanex Fine screens, were conducted without the additional 20 mm Al filtration. The LSF data were obtained using the angled slit technique.³⁶ The slit consists of a circular, 3 cm diameter tantalum disk, 1.5 mm thick with a central opening of ∼0.007×7 mm² (Slit Camera, Nuclear Associates, Hicksville, New York). The optical measurements, which were performed to characterize the intrinsic spatial resolution of array pixels in the absence of the phosphor screen, used a collimated incandescent light source. In this case, the LSF was obtained using an optical slit, which consists of a circular, 1 in. diameter blackened stainless steel disk, 13 μm thick with a central opening of ∼0.01×15 mm² (Precision Air Slit, National Aperture, Inc., Salem, New Hampshire). The slit was attached to a 500 μm thick, black, anodized, aluminum backing plate with a central opening of ∼1×16 mm². For each MTF measurement, ten images of the slit were obtained with the slit tilted at a small angle (∼2°) with respect to the data line direction. For each measurement, averaging of the slit images, after gain and offset corrections, results in a single image from which the LSF was determined.

Noise power spectra and detective quantum efficiency

The methodology used to measure the NPS follows that described in previous publications,^{37, 38} and only specific details pertinent to the present measurements are summarized below. One-dimensional empirical NPS results were obtained from images taken in radiographic mode at a SDD of ∼134 cm for exposures ranging from 0.07 to 0.19 mR. For each prototype imager and x-ray exposure, a total of 50 dark frames (i.e., dark fields) and 50 image frames (i.e., flood fields) were acquired. The image frames served to determine the NPS associated with a given exposure while the dark frames were used to estimate the magnitude of the additive noise contribution. Each image frame was then corrected for intrinsic pixel-to-pixel variations by means of gain and offset corrections (while only offset corrections are applied to the dark frames) following data cropping to a central region of interest having minimal pixel and line defects. A 3×3 median filter was subsequently applied to correct for nonfunctioning pixels, affecting less than ∼1% of the total number of pixels. The resulting processed data frames were divided into independent, nonoverlapping blocks of pixels from which NPS results were determined using the synthesized slit technique.^{39, 40, 41} Each block consists of 154×24 and 85×24 pixels for the PSI-2 and PSI-3, respectively, with the longer direction oriented along the gate line direction. For a given block, pixel signal was summed along the data line direction to yield a realization. Following the application of a Hanning window function, realizations were Fourier transformed, normalized, and averaged to yield one-dimensional NPS data. For each prototype array and exposure, the resulting NPS was used to determine the spatial-frequency-dependent DQE employing the following equation:⁴²

$$\text{DQE}=\frac{{\overline{d}}^2{\text{MTF}}^2}{{\overline{q}}_0\text{NPS}},$$ (1)

where $\overline{d}$ is the mean pixel signal in units of electrons derived from the NPS image data, ${\overline{q}}_0$ is the average incident x-ray fluence (x-ray photons per unit area), and MTF is the measured modulation transfer function.

Noise reduction techniques

The inclusion of a reset transistor in an active pixel circuit decouples pixel signal readout from pixel initialization. Readout of signals from pixels along a given gate line therefore leaves those signals undisturbed, and thus such readout may be referred to as nondestructive — compared to conventional AMFPIs in which readout and initialization are simultaneous. Nondestructive readout was used to explore the possibility of additive noise reduction through acquisition and averaging of multiple readout frames following a single global reset on the PSI-3 array. Such studies were precluded for PSI-2 due to the use of gate lines to provide reset signals, and not because of the intrinsic design of the pixel circuit. In these measurements, the charge capacity of the external preamplifier corresponded to an analog-to-digital conversion gain of 550 e∕ADC.

RESULTS

Pixel response, linearity, and charge trapping

Pixel response

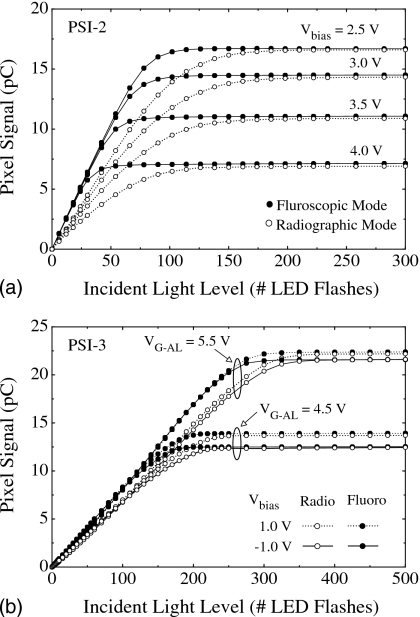
The average pixel signal is plotted as a function of LED light level up to pixel saturation for PSI-2 and PSI-3 in Figs. 5a, 5b, respectively. Results are shown for both radiographic and fluoroscopic modes. All response curves exhibit a signal increase with increasing light level before asymptotically reaching saturation. For a given light level, the radiographic signal is consistently lower than the fluoroscopic signal due to the loss of charge caused by trapping in the a-Si of the photodiodes — an effect that is less prominent in the fluoroscopic results where measurements were performed under conditions in which charge trapping and charge release are in approximate equilibrium.³⁴

Figure 5.

Pixel signal response for (a) PSI-2 and (b) PSI-3 plotted as a function of incident light level (in units of number of LED flashes) for both radiographic and fluoroscopic modes. Results are shown for V_bias values ranging from 2.5 to 4.0 V and ±1 V for PSI-2 and PSI-3, respectively. In the case of PSI-3, results are also shown for values of the gate voltage applied to TFT_AL, V_G-AL, of 4.5 and 5.5 V. For each response curve, the contribution of the dark signal has been subtracted. The lines connecting the data points in this and the remaining figures are provided to guide the eye, unless otherwise indicated.

For PSI-2, results are shown for V_bias values ranging from 2.5 to 4.0 V. This corresponds to effective values of the magnitude of reverse bias voltage V_PD (applied across the photodiode), ranging from about 2.5 to 1.0 V, since V_D-RST was set to 5 V [see Fig. 4b]. As seen in Fig. 5a, the pixel saturation level does not increase in exact proportion to decreasing V_bias, unlike the behavior of conventional indirect detection AMFPIs where direct proportionality is observed.^{14, 34} The reason for this anomalous behavior is as follows. For each V_bias setting, as signal increases (leading to decreases in V_PD) the potential on the gate contact of TFT_SF, V_G-SF (which is also the potential on the photodiode cathode), decreases from its initial value following reset (5 V). Given sufficient illumination, the pixel signal will saturate the photodiode capacitance C_PD when V_G-SF diminishes to a value equal to V_bias (corresponding to V_PD becoming approximately equal to 0 V). However, if V_G-SF drops below ∼V_ref (which is the potential of the data line before readout), then TFT_SF will not conduct during readout, and pixel saturation will be defined by the value of V_ref and not by saturation of the photodiode capacitance. As a consequence, for V_bias values of 4.0, 3.5, and 3.0 V, pixel saturation is primarily determined by the saturation of the photodiode capacitance, while for V_bias values of 2.5 V and lower, pixel saturation is limited by V_ref. For all PSI-2 results reported in the following sections, V_bias was kept at 3.0 V.

For PSI-3, results are shown for V_bias values of −1.0 and 1.0 V and V_G-AL values (the voltage applied to the gate of TFT_AL) of 4.5 and 5.5 V. In all cases, unlike the PSI-2 data in Fig. 5a, the observed saturation levels are not set by saturation of the photodiode capacitance but rather by saturation of the external preamplifier. As the incident illumination increases, the corresponding change in signal is manifested across the feedback capacitor, C_FB, and is also reflected by the change in the magnitude of V_G-SF (i.e., by the difference between the dark signal and the image signal). The magnitude of V_G-SF after reset is primarily dependent on voltages associated with the first-stage amplification elements (i.e., V_GND, V_CC, and V_G-AL). For example, as V_G-AL is reduced, the conductivity of the p-channel transistor, TFT_AL, is improved. This results in an increase in V_G-SF, which leads to a higher dark signal. This, in turn, results in a reduction in the available charge capacity within the external preamplifier, which explains the reduction in the saturation level observed in Fig. 5b at a V_G-AL of 4.5 V compared to that at 5.5 V. For a given value of V_G-AL, the higher saturation level observed at a V_bias of 1.0 V is due to a lower photodiode dark current (leading to lower dark signal) which results in a larger charge capacity available within the external preamplifier — a situation similar to that observed for the dependence of signal response on V_G-AL. In summary, although the pixel signal responses observed from the PSI-2 and PSI-3 arrays exhibit a more complex dependence upon various operational voltages than that for conventional AMFPIs, the observed behaviors are in line with expectations based on a detailed analysis of each pixel circuit.

Linearity of pixel response

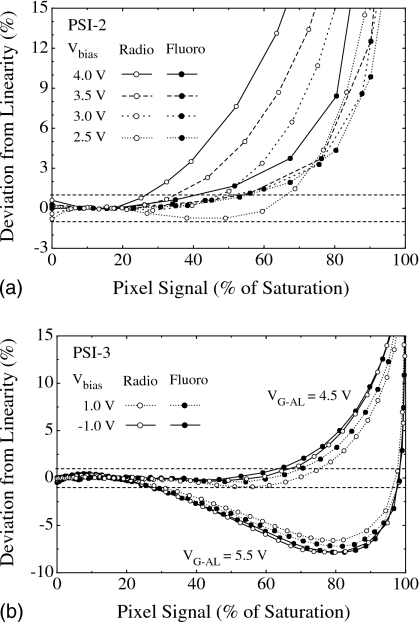
From the pixel response data of PSI-2 and PSI-3 shown in Figs. 5a, 5b, the degree of deviation from linearity, relative to pixel saturation, was determined and is plotted as a function of pixel signal size in Figs. 6a, 6b, respectively. In the case of PSI-2 [Fig. 6a], deviation from linear behavior generally becomes greater as pixel signal increases. The range of pixel signal where good linearity (i.e., deviation within ±1%) is maintained increases with decreasing V_bias (i.e., increasing V_PD) and is observed to be generally better for fluoroscopic mode — a trend similar to that observed for conventional indirect detection AMFPIs.^{14, 34} This trend is believed to originate from the loss of charge due to trapping states in the a-Si of the photodiodes. As the amount of trapping is strongly dependent on the electric field applied across the photodiode, any increase in V_bias setting or pixel signal (both of which decrease the electric field) results in increased deviation from linear behavior for radiographic mode. Fluoroscopic operation is less sensitive to this effect since charge trapping and charge release are brought to approximate equilibrium in this mode.

Figure 6.

Deviation from linearity of pixel signal response for (a) PSI-2 and (b) PSI-3, plotted as a function of pixel signal size for radiographic and fluoroscopic modes. The results were derived from the response curves of Fig. 5. The x-axis scale corresponds to pixel signal magnitude, expressed as a percentage of the saturation signal. The y-axis scale represents the percentage deviation of the pixel signal from a linear fit applied to the first ∼25% of the pixel signal range. The horizontal dashed lines represent deviation levels of ±1%.

In the case of PSI-3 [Fig. 6b], the observed trends in deviation from linearity are noticeably different from those observed from PSI-2. For example, for a given value of V_G-AL and a given mode, the results for V_bias of −1.0 and 1.0 V are similar. Furthermore, for a given value of V_bias and V_G-AL, data obtained in radiographic mode are similar to the fluoroscopic results. This independence of linearity on mode is likely the consequence of the voltage-change limiting feature of the PSI-3 circuit design, in which the electric field across the photodiode remains largely constant as signal increases. For V_G-AL equal to 4.5 V, good linearity is maintained for pixel signals extending up to ∼65% to 75% of saturation. For V_G-AL equal to 5.5 V, this range is sharply reduced to only ∼30%, suggesting a strong dependence of pixel response on the operating voltages. For all PSI-3 results reported in the following sections, V_G-AL was kept at 5.5 V. The reason for this choice is that additive noise was observed to be significantly lower at this voltage setting, most likely due to reduction in the current flowing through TFT_AL. Note that, since the measurements reported in the following sections were obtained for signal values less than ∼20% of pixel saturation, the larger deviation from linearity observed at higher signals did not affect the outcome of these measurements.

Charge trapping

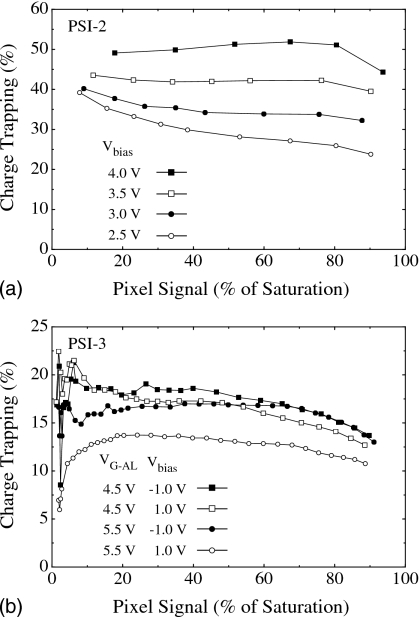
From the pixel response data of PSI-2 and PSI-3 shown in Figs. 5a, 5b, charge trapping results, derived from the difference between the fluoroscopic and radiographic data, are plotted as a function of pixel signal size in Figs. 7a, 7b, respectively. In the case of PSI-2 [Fig. 7a], charge trapping is observed to increase with increasing V_bias (i.e., decreasing V_PD) — a trend similar to that observed for conventional indirect detection AMFPIs.^{14, 34} However, the magnitude of trapping, even for the lowest V_bias (2.5 V) is ∼25% to 40%. These values are generally higher than those reported for conventional indirect detection AMFPIs operated with similar bias voltage across the photodiode,^{14, 34} but are similar to those observed for other arrays employing a continuous photodiode structure, including PSI-1.¹⁴ The higher than expected values of trapping are contrary to a simple model of trapping completely dominated by losses to metastable states in the photodiode material. The more complicated structure of the continuous photodiode, compared to the discrete photodiode in conventional AMFPIs, may contribute to additional trapping — for example, in the region between the pixels.¹⁴

Figure 7.

Charge trapping for (a) PSI-2 and (b) PSI-3, plotted as a function of pixel signal size. The y-axis scale represents the amount of signal lost to trapping, derived from the difference between the fluoroscopic and the radiographic response curves of Fig. 5 and expressed as a percentage of the fluoroscopic signal.

In the case of PSI-3, trapping is generally below 20% for all values of V_bias and V_G-AL investigated. This result is lower than that observed for PSI-2 despite the fact that V_PD is generally low — estimated to be less than 1 V at a V_bias of 1 V and a V_G-AL of 5.5 V. This favorable outcome may be the result of the voltage-change limiting feature of PSI-3, which tends to keep the electric field across the photodiode largely unchanged following illumination. This feature would be expected to lead to very low levels of trapping in metastable states-levels that should be largely independent of V_bias or pixel signal size. While independence from V_bias is observed for most of the trapping curves in Fig. 7b, as well as for that obtained at a V_bias of 0 V (not shown), the non-negligible amount of trapping nevertheless observed may be due to additional charge losses occurring between pixels. Finally, the systematically lower level of trapping at a V_bias of 1 V and a V_G-AL of 5.5 V is not presently understood.

X-ray sensitivity

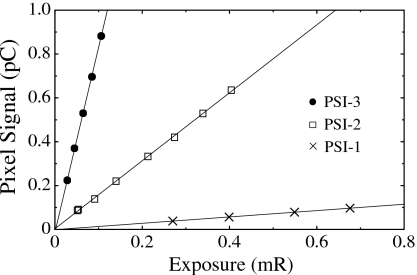
Pixel response as a function of x-ray exposure, measured in fluoroscopic mode with the Lanex Regular screen, is plotted in Fig. 8 for PSI-1, PSI-2, and PSI-3. Results are shown for exposures providing pixel signal levels up to ∼4.4% and 7.2% of pixel saturation for PSI-2 and PSI-3, respectively. Compared to PSI-1, pixel response is seen to be magnified due to the one-stage pixel amplifier of PSI-2 and further magnified due to the two-stage amplifier of PSI-3. (Note that the enhanced response of PSI-3 is also a result of its larger pixel size, 150 μm, compared to the 90 μm pitch of PSI-1 and PSI-2.) X-ray sensitivities, derived from the slope of the response data and normalized to unit pixel area, are 1.12×10⁸ e∕mR∕mm², 11.9×10⁸ e∕mR∕mm², and 23.4×10⁸ e∕mR∕mm²for PSI-1, PSI-2, and PSI-3, respectively. From these sensitivities, the relative increases in signal gain provided by the PSI-2 and PSI-3 architectures, compared to that of PSI-1, are found to be ∼10.7 and 20.9, respectively. These empirically determined values are in reasonable agreement with predicted values of ∼11 and 25 based on the ratios C_data∕C_PD and C_data∕C_FB calculated using the nominal design parameters for PSI-2 and PSI-3, respectively. The degree of agreement between measurements and theoretical expectations is reasonable given the presence of several factors that may affect the measurements. For example, it is estimated that up to 10% variations in material thickness are possible during array fabrication, affecting the capacitance of the various circuit elements and thus the gain of the prototype arrays.

Figure 8.

Pixel signal response for PSI-1, PSI-2, and PSI-3, using a Lanex Regular screen, plotted as a function of x-ray exposure. From these results, the signal gain of PSI-2 and PSI-3, relative to that of PSI-1, can be determined using the slopes of the linear fits indicated by the lines.

Modulation transfer function

Figure 9a shows pre-sampled optical MTF results obtained from PSI-2 and PSI-3. Such results provide insight into the intrinsic spatial resolution of the prototypes in the absence of an x-ray converter and can generally be represented by a sinc function corresponding to the Fourier transform of a rect function whose aperture is given by the photodiode size. In order to determine the photodiode aperture size (and thus optical fill factor) of PSI-2 and PSI-3, each measured MTF was fitted with a sinc function of the form:

$$\text{MTF}\left(f\right)=\frac{\mid \text{sin}\left(\pi a_{\text{PD}}f\right)\mid }{\pi a_{\text{PD}}f},$$ (2)

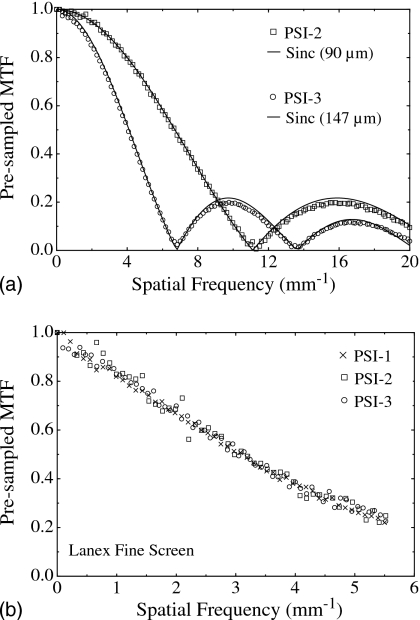
where a_PD is the photodiode aperture which is treated as a free parameter. For each data set, the fit shown in the figure corresponds to the best match with the position of the first minimum in the data. For PSI-2 the fit is for a sinc function based on a 90 μm aperture size whereas for PSI-3 the fit corresponds to a 147 μm aperture. Since the pixel pitches of PSI-2 and PSI-3 are 90 and 150 μm, the resulting optical fill factors are ∼100% and 96%, respectively (assuming equal MTF results for both gate and data line directions). Despite the fact that the geometric fill factors of PSI-2 and PSI-3 are 60% and 75%, respectively [based on the area of the charge collection electrode relative to the pixel size — see Figs. 4a, 4c and Table 1], the corresponding optical fill factors are higher and near unity. Such behavior is characteristic of continuous photodiode structures, which have been shown to exhibit near-unity optical fill factors, even for AMFPI arrays with smaller pixel pitch.^{3, 14}

Figure 9.

Pre-sampled MTF associated with PSI-1, PSI-2, and PSI-3. (a) Measured optical MTF for PSI-2 and PSI-3 obtained through illumination of the arrays with a light source. For each set of array results, a fit to the data, based on a sinc function, is indicated by a solid line. (b) Measured MTF for PSI-1, PSI-2, and PSI-3 obtained with a high-resolution phosphor screen, Lanex Fine, at 72 kVp. In order to allow direct comparisons with the results of the 90 μm pitch PSI-1 and PSI-2 arrays, the results for PSI-3 have been renormalized from a 147 μm aperture [corresponding to that inferred from the optical MTF of (a)] to a 90 μm aperture.

Figure 9b shows pre-sampled MTFs for PSI-1, PSI-2, and PSI-3 obtained under x-ray illumination using a high-resolution phosphor screen (Lanex Fine). To facilitate direct comparisons between the different prototypes, the results of PSI-3 have been appropriately normalized so as to correspond to a photodiode aperture of 90 μm. The MTF results from the three prototypes are observed to largely overlap — indicating that performance is independent of pixel circuit design and pitch. In particular, compared to the simple architecture of PSI-1, the added complexity in the PSI-2 and PSI-3 pixel circuits (including additional TFTs and control lines) is seen to have no discernible effect on the spatial resolution of these arrays. Moreover, for the irradiation conditions under which the measurements were performed, these arrays exhibited no indication of spatial resolution degradation due to charge sharing between pixels.

Noise power spectra and detective quantum efficiency

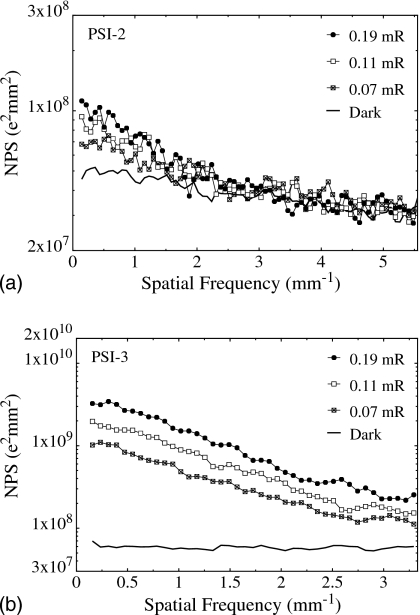
Figures 10a, 10b show NPS results obtained with a Lanex Regular screen for PSI-2 and PSI-3, respectively. For each prototype, results are shown for three different x-ray exposures, ∼0.07, 0.11, and 0.19 mR. For PSI-2 [Fig. 10a], the NPS results do not exhibit the linear increase with exposure to be expected from a system dominated by x-ray quantum noise. In this case, the increase is small at low spatial frequencies and almost nonexistent at frequencies close to the Nyquist limit of 5.55 mm⁻¹ — an indication of a noise performance dominated by electronic additive noise. As seen in the figure, the dark NPS (shown as a thick line) exhibits a magnitude that is similar to that of the radiation NPS at high frequencies. This confirms the dominance of additive noise, which is estimated from the dark NPS results to be on the order of 5500 e (rms), when referred to the input of the pixel (i.e., before pixel amplification). For PSI-3 [Fig. 10b], the NPS results exhibit a nearly linear increase with increasing exposure. In this case, the magnitude of the NPS is much higher than that of the corresponding results for PSI-2. Such behavior is the consequence of the higher signal that is made possible by the larger pixel amplification gain as well as by the larger pixel size of PSI-3. The dark NPS (shown as a thick line) corresponds to an estimated additive noise level of ∼2400 e (rms), when referred to the input of the pixel. For PSI-3, the combination of lower additive noise and higher signal results in a performance less dominated by additive noise compared to that for PSI-2.

Figure 10.

NPS measured from (a) PSI-2 and (b) PSI-3. Results are shown for three exposure levels. In addition, NPS results obtained in the absence of radiation (dark NPS) are shown and correspond to additive noise levels of ∼5500 e and 2400 e (rms) for PSI-2 and PSI-3, respectively.

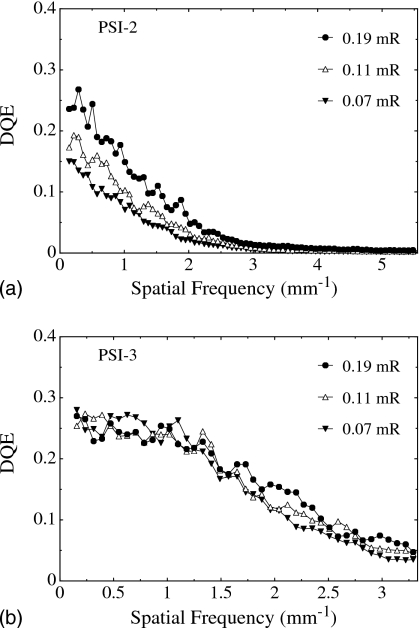
Figures 11a, 11b show DQE results obtained using the Lanex Regular screen for PSI-2 and PSI-3, respectively. These results were determined from measurements of mean detector signal, MTF, and NPS (from Fig. 10), and assume a fluence of 262690 X rays∕mm²∕mR. For PSI-2 [Fig. 11a], DQE is seen to generally increase with increasing exposure due to the diminishing contribution of additive noise relative to x-ray signal. At high spatial frequencies, however, the magnitude of DQE is strongly attenuated at all exposures due to a combination of the relatively large additive noise and the low spatial resolution of the Lanex Regular phosphor. For PSI-3 [Fig. 11b], the DQE shows only a weak dependence on exposure — indicative of input-quantum-limited operation where DQE performance is not affected by additive noise. The DQE values at low spatial frequencies are observed to converge to a limit defined by the properties of the phosphor screen — a limit set by the product of the x-ray quantum efficiency and Swank factor of the screen, ∼0.3.

Figure 11.

DQE for (a) PSI-2 and (b) PSI-3, corresponding to the NPS data reported in Fig. 10.

Sampling techniques for noise reduction

For active pixel arrays of the type examined in this study, the principal contributions to additive noise may generally be considered to originate from four sources: (1) Preamplifier noise (σ_preamp) which scales with increasing C_data and is typically the dominant noise source in conventional AMFPIs; (2) noise from array circuit elements located after the point of pixel amplification (σ_postgain) which includes the data line thermal noise and noise associated with TFTs involved in the readout (i.e., TFT_ADDR, TFT_SF, and TFT_RO); (3) reset noise associated with TFT_RST (σ_reset); and (4) other noise sources from array circuit elements located before amplification (σ_pregain) which include photodiode shot noise and shot and flicker noise from TFT_RST, as well as (in the case of PSI-3) from TFT_AL and TFT_CSA. While the additional gain provided by pixel amplification should render σ_preamp and σ_postgain negligible, the noise contributions of σ_pregain and σ_reset are not negated since their magnitude increases in proportion to the amplification gain. For these reasons, additive noise is expected to be dominated by σ_pregain and σ_reset.

The delineation of the noise sources outlined above can serve as a basis for exploring the magnitude of contributions from each source as well as examining strategies for reducing these contributions. The higher than expected noise value of 2400 e (rms) observed for PSI-3 (obtained from NPS measurements reported in Sec. 3D) suggests a large contribution from σ_pregain since σ_reset is calculated (from ${\sigma }_{\text{reset}}=\sqrt{kT{C}_{\text{PD}}}$)²⁶ to be only ∼550 e. Reduction of the frame time from 0.23 s, at which the NPS measurements were obtained, to 0.13 and 0.015 s yielded noise values of only ∼1700 e and 830 e (rms), respectively. This result indicates that, among the frame-time-dependent noise components (including photodiode leakage current, TFT transient current,⁶ and TFT 1∕f noise), one or more significantly contribute to the total additive noise. (A similar dependence of additive noise on frame time was observed for PSI-2.) While the magnitude of the noise contributions from these sources depends on the quality of the semiconductor material (and can, in principle, be reduced through improvements to the underlying fabrication process), σ_reset is a result of the pixel reset action and is thus independent of semiconductor quality. It is therefore of interest to explore readout techniques that have the potential of reducing or eliminating σ_reset as well as other noise components.

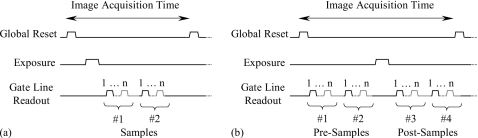
The PSI-3 array, whose design permits simultaneous, global reset of all array pixels, allowed exploration of additive noise reduction through multiple, nondestructive sampling of signals from a block of pixels. (The lack of a global reset capability in the PSI-2 design precluded such studies for this array.) In particular, the nondestructive readout of PSI-3 allows multiple frames of data to be acquired following each pixel reset, as schematically illustrated in Fig. 12a. These frames, which may be acquired after an x-ray exposure, can be used to reduce additive noise through frame averaging. This technique will, of course, only reduce the effect of the noise sources σ_pregain, σ_postgain, and σ_preamp. The effect of the other noise source, σ_reset, can, in principle, be eliminated through the application of a correlated double sampling (CDS) technique. For example, the data acquisition system could be configured to acquire, after each reset, a number of dark frames, followed by a number of image frames, as shown in Fig. 12b. The application of CDS, consisting of the subtraction of the averaged dark frames from the averaged image frames, has the potential to largely, or completely, remove the unknown common signal offset due to the reset.

Figure 12.

Timing diagrams illustrating the conceptual operation of an active pixel imager with (a) multiple sampling and (b) correlated double sampling. Both sampling techniques are allowed by the nondestructive readout capability of an active pixel array designed to permit global reset. Each sample corresponds to a frame of data obtained by reading out an array with n gate lines.

The effectiveness of frame averaging, and of correlated double sampling, on reducing additive noise for PSI-3 was explored through acquisition of 800 consecutive dark frames at a frame time of ∼0.015 s. This short frame time was achieved by reading out only a relatively small number of consecutive gate lines (and data from a contiguous block of 33×13 pixels were used in the analysis). Pixel reset was applied every eighth frame, resulting in a total of 100 sets of dark frames with each set consisting of eight frames. Each frame within a set is referred to as a “sample.” For CDS noise reduction, the samples were divided so that the first four are considered “pre-irradiation” samples while the last four are considered “post-irradiation” samples, following the nomenclature of Fig. 12b. [Although the acquisition system was not configured to allow a readout scheme that includes both dark and image frames, such as that shown in Fig. 12b, the effectiveness of CDS can nevertheless be tested using dark frames only.] For each pixel, in order to remove the effect of temporal variations in signal from set to set across the 800 dark frames, a signal drift correction, based on linear detrending, was applied.³ Noise for each pixel, referred to its input, was characterized in terms of the standard deviation in the pixel signal across the 100 sets of dark frames and is expressed in electrons.

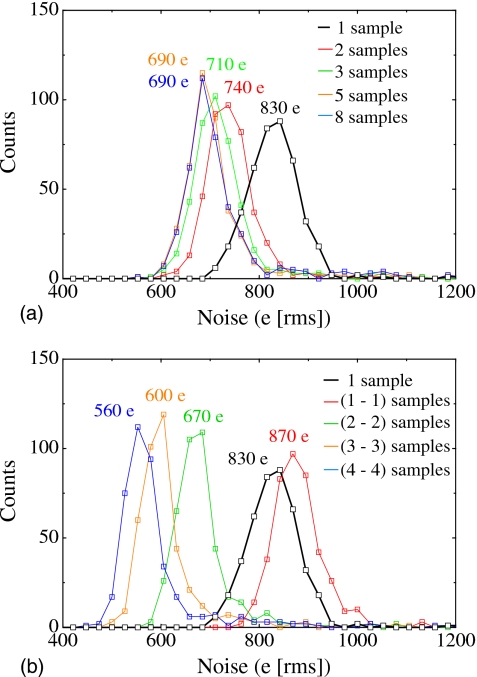
Figure 13 shows distributions of pixel noise for the selected block of pixels. When a single sample per set is used in the noise determination (“1 sample”), the median in the resulting noise distribution is ∼830 e (rms). However, as more samples per set are averaged (two to eight), the median noise decreases to an asymptotic limit of ∼690 e (rms), as seen in Fig. 13a, due to the effect of averaging on σ_pregain, σ_postgain, and σ_preamp. While such averaging does not reduce the effect of noise correlated with the reset process, the subtraction of any two samples (i.e., implementing CDS by considering a first sample to be pre-irradiation and a second sample to be post-irradiation) eliminates σ_reset. This subtraction, however, slightly increases median noise to ∼870 e [see Fig. 13b] due to an additional contribution from each of σ_pregain, σ_postgain, and σ_preamp. When a larger number of pre- and post-irradiation samples are averaged before subtraction, (i.e., 2-2, 3-3, and 4-4), median noise is progressively reduced to ∼560 e (rms). The remaining noise is likely caused by sources before amplification such as photodiode shot noise, TFT shot, transient, and 1∕f noise. For a given frame time, the contributions from these sources increase with increasing number of samples between resets.

Figure 13.

Distributions of pixel temporal additive noise for a block of 33×13 pixels from PSI-3. The results were obtained using various sampling techniques involving one or more samples acquired following a single pixel reset. (a) Distributions corresponding to a single sample (“1 sample”) and the average of multiple samples (“2 samples,” etc.) (b) Distributions corresponding to a single sample (“1 sample”) and to results obtained using correlated double sampling involving the subtraction of two samples [“(1-1) samples”] as well as the subtraction of the averages of two or more samples [“(2-2) samples,” etc.].

DISCUSSION AND SUMMARY

For over half a century, numerous medical applications have benefited from the relentless development of increasingly sophisticated transistor-based technologies-technologies often originating from consumer products. Thus, it is unsurprising that the performance of conventional, large area, flat-panel imaging arrays (employing the same a-Si TFT active matrix technology used in liquid crystal displays) could potentially be improved through incorporation of more complex circuitry (of the type used in CMOS active pixel image sensors) based on poly-Si TFTs (which are under development for mobile displays and large area OLED displays). In this article, an investigation of the properties of a pair of early prototype array designs, PSI-2 and PSI-3, incorporating pixel amplification structures with three and five poly-Si TFTs per pixel, respectively, as well as of a reference array design employing a single poly-Si TFT, PSI-1, has been reported. The PSI-2 and PSI-3 prototypes benefit from carrier mobilities considerably higher than those of a-Si, enabling relatively sophisticated circuit designs based on both n- and p-channel poly-Si TFTs. The studies were performed in the spirit of providing baseline information to assist in the future realization of more optimized designs capable of overcoming the performance limitations (originating from the relatively modest ratio of signal per X ray to additive noise) of conventional AMFPIs.

The signal results obtained from PSI-2 and PSI-3 are highly encouraging. These prototypes provided an initial, empirical demonstration that a specified level of additional system gain can be achieved through the implementation of active pixel architectures based on poly-Si TFTs. In addition, the incorporation of a novel continuous photodiode structure, located largely above the plane of the pixel TFTs (thereby maximizing the area available for other pixel circuit elements), has been shown to further increase system gain¹⁴ by providing optical fill factors that are close to unity. In addition, the added complexity of the PSI-2 and PSI-3 pixel circuits, compared to that of PSI-1 or a conventional AMFPI array, has no observable effect on spatial resolution. Generally, while the signal behaviors of the prototypes were observed to be more complex than those of conventional AMFPI arrays, they are nevertheless in line with expectations based on consideration of the design and operational conditions of the array circuits.

Compared to PSI-3, the PSI-2 design (whose pixel amplifier gain is given by C_data∕C_PD) has fewer TFTs per pixel and is somewhat simpler. However, it suffers the disadvantage that, for a given pixel pitch (which largely sets the value of C_PD), increasing the number of pixels along a data line (which increases the value of C_data) will result in increased amplification — leading to an undesirable coupling between array size and signal gain. The more sophisticated two-stage amplifier circuit of PSI-3 allows greater flexibility in this regard, since pixel amplifier gain is given by C_data∕C_FB and the value of the feedback capacitor can be varied independently of array size. Another advantage of the PSI-3 design is the high open loop gain of the first-stage pixel amplification, which allows the voltage across the photodiode to remain largely unchanged even following high x-ray exposures. Such a feature should, in principle, limit image lag and ghosting artifacts that plague conventional AMFPIs.

Although the pixel amplifiers in PSI-2 and PSI-3 provide significant enhancement of system gain relative to that of comparable, conventional AMFPI arrays, there was little or no improvement in the signal-to-noise properties of these prototypes due to their relatively high levels of additive noise. However, a relatively straightforward analysis of noise sources (identifying components σ_preamp, σ_postgain, σ_reset, and σ_pregain), along with the empirical noise studies reported in this paper, provides some guidance for additive noise reduction in future prototypes. For example, careful selection of the magnitude of the gain provided by pixel amplification should render σ_preamp and σ_postgain negligible. In addition, implementation of signal processing techniques, involving multiple, nondestructive sampling of the pixel signal and suitable averaging and subtraction of these samples, offers the potential of significantly reducing the contribution of σ_pregain as well as eliminating the contribution of σ_reset.

Improvements in poly-Si fabrication could also lead to substantial reduction in additive noise. For example, compared to the laser equipment used in the fabrication of the present prototypes, newer equipment provides greater stability in energy deposition [5% (rms) versus 15% (rms)] allowing the laser energy to be much more precisely tuned to conditions²⁸ that optimize the poly-Si crystallization process. As a result, early tests indicate that the average poly-Si grain size has increased to several microns (compared to ∼0.5 μm with the old equipment) leading to mobilities of up to ∼260 and 100 cm²∕V s (compared to less than 100 and 50 cm²∕V s) for n- and p-channel TFTs, respectively. As it is generally believed that leakage current in channels occurs between grains and 1∕f noise originates in trapping states (which are more numerous at grain boundaries), the fewer grain boundaries associated with larger grains should lower TFT shot and 1∕f noise — reducing σ_pregain and σ_postgain. Such fabrication improvements will also provide more uniform TFT characteristics across an array (due to more stable laser energy deposition) as well as allow faster circuit operation and higher frame rates (as a result of the larger currents facilitated by higher TFT mobilities).

Beyond the use of sampling techniques and improved fabrication methods, signal and additive noise performance could also be enhanced through future refinements in the design of the active pixel architectures. For example, improvements to the uniformity of the topology of the continuous photodiode structure (which is highly nonuniform in the PSI-1, PSI-2, and PSI-3 designs), as well as changes to the passivation material in the periphery of the pixels (where additional charge trapping may be occurring), could significantly reduce charge trapping as well as photodiode dark current (thereby lowering shot noise and thus σ_pregain) — as suggested by recent studies of arrays with novel photodiode structures.¹⁴ An attractive alternative to the use of continuous photodiodes is a novel discrete photodiode structure in which the bottom contact of the photodiode is positioned above the plane of the pixel TFTs — an approach that has demonstrated excellent properties in conventional prototypes but at some cost in optical fill factor.¹⁴ Finally, it is to be expected that further innovation in array design will be attempted in order to achieve desirable performance objectives — such as the introduction of selectable gain through innovative circuit modification with the goal of maximizing the exposure range over which an active pixel array can be practically operated.

Ultimately, the achievement of optimized signal-to-noise behavior in future prototypes will require improved design and fabrication of the arrays, as well as a detailed understanding and quantification of all noise sources — with the latter achieved through a combination of circuit simulations and analytical noise calculations, employing empirical data obtained from individual poly-Si TFTs.²⁷