Simultaneous Evaluation of the Magnitude and Breadth of a Left and Right Censored Multivariate Response, with Application to HIV Vaccine Development

Abstract

Both the magnitude and breadth of neutralization against multiple strains of virus are main endpoints for comparing antibody-based HIV-1 vaccine candidates in Phase I and II trials, and are key markers to be evaluated in vaccine efficacy trials as immune correlates of protection against HIV-1 infection. More generally, consideration of both magnitude and breadth is encountered when there is interest in comparing quantitative multivariate response data between groups. In this paper, we discuss two approaches to simultaneously evaluating the magnitude and breadth of a multivariate response. We suggest methods for the summarization and group comparison of multivariate response data that are subject to left and/or right censoring. Applications to data from a phase III clinical trial (Vax004) are discussed. Simulation-based sample size calculations and power analyses of the described methods also are presented.

1. INTRODUCTION

In the search for a successful HIV-1 vaccine, it is a common goal to induce potent antiviral immune responses, such as neutralizing antibody (Nab) responses against a broad range of circulating viruses. Nab responses are assessed in terms of both the magnitude and breadth of neutralizing activity, as two main endpoints for comparing HIV-1 vaccine candidates in Phase I and II trials (Mascola et al., 2005). In addition, magnitude and breadth of neutralization are key markers to evaluate in Phase III vaccine efficacy trials as immune correlates of protection against HIV-1 infection. Magnitude of neutralization refers to the relative quantity of Nabs against a single strain of virus above a pre-specified threshold that is determined by the limit of detection in the assay. Breadth of neutralization refers to the extent by which the antibodies cross-neutralize multiple strains of the virus.

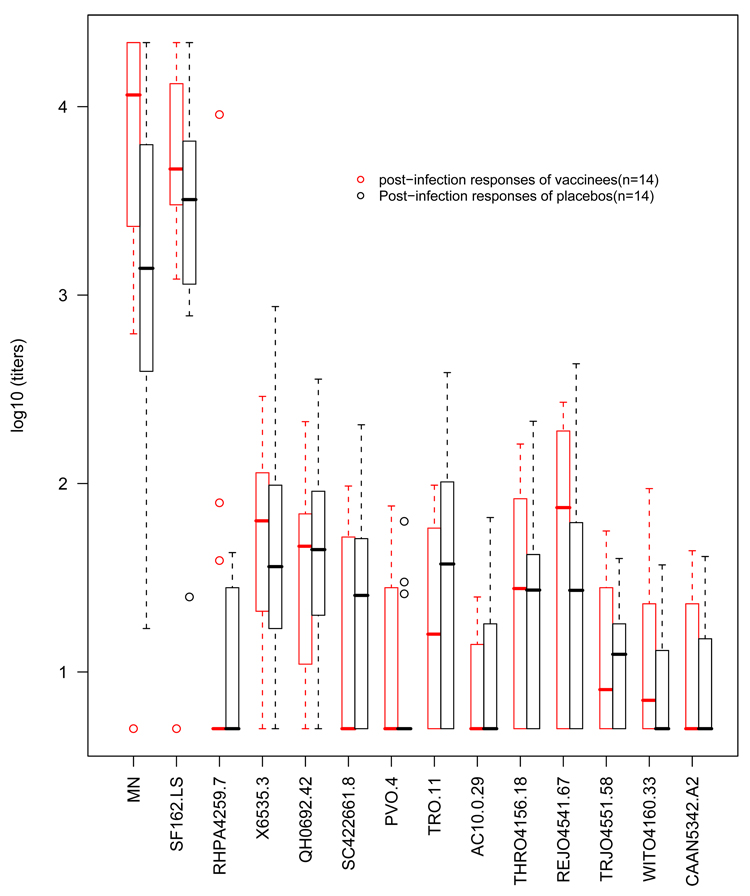
In 2003, the first two Phase III HIV-1 vaccine trials, Vax004 and Vax003, failed to show evidence of a vaccine induced reduction in HIV-1 infection rate (Flynn et al. 2005; Pitisuttihum et al. 2006). Based on sera sampled approximately 1 year after Vax004 participants were diagnosed with HIV-1 infection, Figure 1 shows Nab responses of 14 vaccinees and 14 placebo recipients against the laboratory adapted HIV-1 vaccine strains MN and SF162, as well as against 12 non lab-adapted reference strains. The MN and SF162 strains are known to be highly sensitive to neutralization. The 12 reference strains were sampled from newly clade B HIV-1 infected persons (within 3 months of the estimated date of infection) and are genetically and geographically diverse (Li et al. 2005). We can see from Figure 1 that there was no evidence for a difference in the response levels among vaccine and placebo recipients for the 12 reference strains. Such lack of Nab responses against a broader range of newly sampled viruses is consistent with the inability of the tested vaccine to prevent infections. The failure of this vaccine hence affirms the importance of simultaneous evaluation of both magnitude and breadth of vaccine-elicited multi-viral Nab responses from HIV vaccine trials.

Figure 1.

Boxplots of post-infection Nab responses to MN, SF162 and 12 reference isolates from Vax004

Nab responses directed against HIV-1 can be assessed by a luciferase reporter gene assay performed in TZM-bl cells (Montefiori, 2004). Because neutralizing antibodies protect cells from infection by blocking virus entry, antibody-mediated neutralization of HIV-1 can be measured by a reduction in virus infectivity in TZM-bl cells. Using the TZM-bl cell-based assay, neutralizing activity against a test virus can be characterized by titration experiments in which TZM-bl cells are added to cell-free virus that has been preincubated with multiple dilutions of a test serum sample. Calibration curves can hence be generated to display the relationship between the percentage reduction in virus infectivity and the corresponding serum dilution. The 4-parameter logistic function is usually adopted to fit such calibration curves, where the four parameters are the limits of the function as x → − ∞ or x → ∞, the x value at the inflection point with response midway between the two asymptotes and a slope parameter. Based on the calibration curve, it is common to quantify the magnitude of neutralization as the reciprocal titer of sera required to reduce the number of infectious virus particles by either 50% (infectious dose 50 or ID50) or 80% (ID80); both ID values fall within the linear portion of the neutralization curve (Montefiori, 2004). Alternatively, for example, the difference between the two horizontal asymptotes or adjusted ID values standardizing for the three other parameters via a regression model can also be used as a summary measure of the calibration curve. In subsequent work, the ID values are carried forward as the response variable to illustrate the statistical methods. To be more focused, in this paper we assume that ID50 (or ID80) values are estimated from the calibration curve with no error and are treated as realizations of random variables subject only to sampling variation. However, the ID50 (or ID80) values may be censored at a certain value when the calibration curve never reaches the point of 50% (or 80%) infectivity reduction within the range of pre-defined dilution levels.

Both magnitude and breadth of neutralization are principal criteria for evaluation of HIV-1 vaccine candidates. However, some current ad hoc methods of summarization and comparison based solely on either quantity do not adequately characterize the underlying difference in neutralization activity. Motivated by the need for better statistical methods that fully incorporate information from multi-viral immunological data from HIV vaccine trials, we discuss in this paper two approaches for simultaneously evaluating the magnitude and breadth of multivariate responses that are subject to left and/or right censoring. For demonstration, Nab response data is used as an example of such responses; however, the methods are applicable to other data when interest is in the evaluation of both magnitude and breadth of multivariate responses.

The outline of this paper is as follows. Real Nab response data from the Vax004 trial are briefly described in section 2. In section 3, several individual and group summary statistics and test statistics for group comparisons are discussed. These methods are then applied to the Vax004 Nab response data in section 4. In section 5, design issues including sample size calculations and power comparisons of different methods through simulations are discussed. We provide a discussion in section 6.

2. VAX004 NAB RESPONSE DATA

Vax004 was a double-blind, randomized Phase III vaccine efficacy trial conducted in North America and the Netherlands in 5417 HIV-1-uninfected volunteers (5,108 men and 309 women) with a 2:1 vaccine to placebo recipient ratio. For details of the design of Vax004, we direct readers to articles by Flynn et al. (2005), Gilbert et al. (2005), and Pitisuttithum et al. (2006). After completion of the trial, post-infection sera from 14 vaccinees and 14 placebo recipients were assayed against the 12 reference strains by the Laboratory for AIDS Vaccine Research & Development at Duke University Medical Center (Figure 1). All samples were drawn about 1 year after diagnosis and were from antiretroviral therapy (ART)-naïve participants. All responses were ID50 values. The dataset can be obtained upon request to the authors.

3. METHODS

For illustration purpose, the following notations are described for multi-viral Nab response data in ID50 values. However, the same notations can apply to other designated multivariate response variables. Let n be the number of subjects (or reagents), and m be the number of HIV-1 isolates in the testing panel. Let Y_ij, i = 1, 2, …, n, j = 1, 2, …, m be the random variable denoting the log₁₀ transformed ID50 value from subject i against virus isolate j. Within the range of experimental dilutions, the most intense sample of the minimal dilution may not incur a 50% infectivity reduction, or the least intense sample of the maximal dilution may incur higher infectivity reduction than 50%. For this reason, Y_ijis not always observed and is subject to left or right censoring. The recorded information is hence max(min(Y_ij, t_Uij), t_Lij) together with indicator variables for observed titer values, i = 1, 2, …n, j = 1, 2, …, m, where t_Lij and t_Uij (t_Lij ≤ t_Uij), respectively, are limits of observation below or above which Y_ij is not calibrated and is left or right censored. In the context of Nab response measured by titration experiments, t_Lij and t_Uij are usually controlled by investigators prior to the experiment; hence we assume that the censoring titers and the ID50 titer are independent random variables.

Following, we introduce two approaches to analyzing such Nab response data. In the first approach, we sidestep the need to estimate the correlation among isolates by introducing the notion of magnitude-breadth (M-B) curves that plot neutralization breadth as a function of neutralization magnitude. In the estimation of M-B curves, we consider two cases in terms of the censoring pattern of the data. In case I, censoring titers t_Lij and t_Uij of subject i = 1, …, n are fixed across isolates. We can therefore drop the isolate index of t_Lij and t_Uij and refer to them as t_Li and t_Ui. This case I may occur when subjects are tested against isolates of a similar range of neutralization sensitivities, and hence the investigator presets the same lower and upper dilution levels for all isolates when specifying the experiment parameters. In case II, censoring titers t_Lij and t_Uij of subject i = 1, …, n are not necessarily the same across different isolates. Case II may occur when subjects are tested against isolates of possibly different ranges of neutralization sensitivities, and hence the investigator may preset different lower and/or upper dilution levels for different isolates. In the estimation of M-B curves for case II data, we assume that for each subject i = 1, …, n, Y_i1, …, Y_im and each subject is independent and identically-distributed (i.i.d). This assumption is not necessary in case I. For both cases, we use M-B curves as building blocks upon which to summarize subject-specific or group-specific Nab response and to compare Nab responses between groups.

In the second approach, we take into account the correlation among isolates and assume that the data consist of n independent random samples from a certain m-variate distribution of Y = (Y₁,…,Y_m)'. Maximum likelihood estimates of the mean vector and variance-covariance matrix can be used to summarize the data. Readers can refer to textbooks on multivariate statistical analysis for further details of these estimates. For group comparisons of multi-viral Nab response data, due to the censoring of values, we describe several rank-based nonparametric methods and permutation tests for data sets with small amounts of censoring.

3.1. First approach case I

In the following, we define and provide estimates of M-B curves for case I data, where censoring titers of subject i = 1, …, n are fixed across isolates. We also suggest individual and group level summaries, as well as methods for group comparisons based on M-B curves.

3.1.1. M-B curves

Considering the basic parallelism between Nab response data and time-to-event data, a magnitude-breadth (M-B) curve is similar to a survival curve where the “event” of interest is neutralization and the “time-toevent” refers to the titer required to get 50% (or 80%) neutralization (i.e., ID50 or ID80). For each i = 1, …, n, the M-B curve is defined as {B_i (t) : t ∈ [0,∞)}, where B_i(t) is the expected fraction of isolates to which the i^th subject generates a response greater than t:

$$B_i(t)=\mathrm{E}((\#\text{of}\text{isolates}\text{with}{\mathrm{Y}}_{\text{ij}}>\mathrm{t})/\mathrm{m})=\mathrm{E}({\displaystyle \sum _{j=1}^{m}I(Y_{ij}>t)/m)={\displaystyle \sum _{j=1}^{m}P(Y_{ij}>t)/m,t\in [0,\infty ].}}$$ (1)

With the number of isolates (m) being fixed, the neutralization breadth at a given threshold t, B_i(t) can be interpreted as the expected proportion of “successes” from an m-variate Bernoulli distribution (i.e., (I(Y_i1 > t),…,I(Y_im > t)'~ MVB_m (P_m, 1, D)), where P_m = (P(Y_i1 > t), …, P(Y_im > t))' and D specifies the dependence structure of the m marginal Bernoulli distributions.

If sufficient numbers of independent samples from subject i are measured against each isolate j, P(Y_ij > t) and hence B_i(t) can be estimated by parametric methods that assume a parametric model (e.g., log-normal) for the neutralization titers Y or that fit a smooth function to the log-density function of Y (Kooperberg and Stone 1992). However, such data are difficult to obtain and are not the focus of this paper. In most situations when only one sample is available from each subject against each isolate, we recommend the use of non-parametric estimation of B_i(t) as a right-continuous step function of t. Specifically, for a given subject i, suppose there are m' distinct titer values t_Li ≤ t₁ < t₂ < … < t_m' ≤ t_Ui. For case I data, the indicator for I(Y_ij > t) for t ∈ {t₁,…, t_m'} can always be determined because Y_ij, j = 1,…, m, is either left censored with Y_ij ≤ t_Li ≤ t₁, right censored with Y_ij > t_Ui ≥ t_m', or exactly observed with one of the values {t₁,…, t_m'}. The non-parametric maximum likelihood estimates (NPMLE) of $B_i(t),B_i^{\mathit{\text{est}}}(t_1),\dots ,B_i^{\mathit{\text{est}}}(t_{m\text{'}})$ are then simply the proportion of isolates with observed neutralization titers greater than t₁, …, t_m', respectively. The standard error of the estimated M-B curves at each observed titer can be estimated via bootstrap methods.

The estimated M-B curve can be plotted as the estimated neutralization breadth function B^est(t) versus t (neutralization magnitude) with constant breadth between two observed titers. When there are no censored data or there is only left censoring at t_Li, the X-axis of the M-B curve spans the range of [0, t_m'] and the Y-axis (B^est) of the M-B curve starts with 1 (B^est(0)=1), drops down at each distinct titer value to a lower value and ends with 0 at the largest titer t_m' (B^est (t_m') = 0). When there is right censoring at t_Ui, the X-axis of the M-B curve spans the range of [0, t_Ui] and the M-B curve starts at 1, drops down at each distinct titer but ends flat at B^est(t_m') between the maximum observed titer t_m' and the censoring titer t_Ui.

3.1.2. Individual level summaries based on the M-B curve

Because an entire curve is needed to capture the neutralization activity of a subject, M-B curves by themselves may be cumbersome to use, for example, in group comparisons. The area-under-the M-B curve (AUC M-B) can be used to summarize the neutralization activity of a subject and to compare candidate vaccines. For example, the AUC M-B can be compared to an external threshold value (e.g., estimated from external neutralizing antibody studies), and the distribution of AUC M-Bs can be compared between vaccine arms. Because the expected value of a random variable is the area under its survival function, the AUC M-B is equal to the average of the mean responses of the m isolates. That is, for each subject i,

$$\mathit{\text{AUC}}-M{B}_i={\displaystyle {\int }_0^{\infty }{B}_i(t)dt=\frac{1}{m}{\displaystyle \int {\displaystyle \sum _{j=1}^{m}P(Y_{ij}>t)dt=}}\frac{1}{m}}{\displaystyle \sum _{j=1}^{m}E(Y_{ij}),i=1,2,\dots ,n.}$$

Therefore, the AUC M-B can be estimated either by integrating the area under the M-B curve or by the average of the observed neutralization titers. However, if some titers are left or right censored, then the AUC-MB is correspondingly left or right censored; and if both left- and right-censoring are present, then the type of censoring for the AUC M-B is indeterminate.

Alternatively, the percentiles, rather than mean responses, can be used as summary statistics, which may be preferred when there are both left and right censored values. Generally of interest is the 50^th percentile—the median of the neutralization breadth distribution. Sample percentiles are less affected by extreme values beyond the censored titers. This is especially true in case I with single value left and/or right censoring.

A third measure that serves as a compliment to percentiles is the fraction of isolates that are neutralized above a certain fixed threshold τ (i.e., B(τ), the neutralization breadth at τ). This measure is also preferred when there is censoring. Besides being easy to compute, by setting a biologically meaningful titer threshold estimated from similar studies, it renders a summary of breadth that may be more relevant for predicting vaccine efficacy. This measure is thus used as a summary statistic for sample size calculations in section 5.

3.1.3. Group level summaries and group comparisons based on the M-B curve

When different vaccine regimens are applied to several groups of subjects, we often wish to summarize the subject-specific M-B curves at the group level and/or to compare the M-B curves between these groups. An intuitive group summary based on M-B curves is the point-wise average of M-B curves. Such group-average M-B curves can be constructed by averaging the breadth at each distinct titer across all subjects within a group. Hence by averaging (1) over subjects we have

$$B^G(t)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{B}_i(t)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\mathrm{E}({\displaystyle \sum _j^{m}I(Y_{ij}>t)/m)=\mathrm{E}({\displaystyle \sum _{i,j}I(Y_{ij}>t)/mn),t\in [0,\infty ].}}}}$$

This shows that a group-average M-B curve, B^G is equivalent to the M-B curve for one subject as if his serum sample were tested against m × n isolates. Therefore, group-average M-B curves describe not only the group tendency of neutralization magnitude and breadth, but also the expected proportion of m × n responses with Y_ij > t. Because of this, B^G can be easily estimated in the same way as described in section 3.1.1 as long as every subject i = 1, ‥, n has responses censored at the same censoring titers or there are no censored values at all (case I). Otherwise, further assumptions on Y_ij are needed to achieve the MLE of B^G, which we discuss in section 3.2.

In terms of methods for group comparisons, test statistics based on the distance between group-average M-B curves can be used in tandem with permutation tests. An example of such test statistics is the maximum vertical distance between the two estimated group-average M-B curves, max|B^G_d| defined by

$$\text{max}|{B^G}_d|=\underset{t}{\text{max}}(|B^{\widehat{G}=1}(t)-B^{\widehat{G}=2}(t)|)$$

In addition, group comparisons may be based on various summaries of subject-specific M-B curves described in the previous section, such as the distribution of the AUC-MB, the percentiles of the M-B curves or the breadth at a certain threshold. Once these summary indices are computed for individual M-B curves, univariate statistical tests (e.g., the Kruskal-Wallis nonparametric test) can be used to test for differences in M-B curves between groups. Note that in the presence of both left and right censoring, the type of censoring and hence the rank of the AUC M-B is indeterminate, in which case summary statistics other than the AUC-MB are preferred for group comparisons.

3.2. First approach case II

For case II data, where censoring titers of subject i = 1, …, n are not necessarily the same across isolates, the estimate of the M-B curve is no longer simply the sample proportion of isolates with Y_ij > t, because this can be biased downward due to cases that are censored before t. To take advantage of existing methods that handle random left and/or right censoring for time-to-event data, we assume that for each subject i = 1, …, n, Y_i1, …, Y_im are i.i.d. This assumption implies that 1) intra-individual Nab responses to different isolates are uncorrelated; 2) all isolates have the same sensitivity to neutralization. Under this i.i.d assumption, together with equation (1), the neutralization breadth function of subject i for case II data is:

$$B_i(t)={\displaystyle \sum _{j=1}^{m}P(Y_{ij}>t)/m=P(Y_{i1}>t),t\in [0,\infty ],i=1,\dots ,n.}$$

First note that if only left or right censoring is present, then the K-M estimator (Kaplan and Meier 1958) and Greenwood’s formula can be used to derive the estimate of B_i(t) and its standard error. Under both left and right censoring, the NPMLE of B_i(t) can be computed using a self-consistency EM algorithm (Turnbull 1974, 1976). The estimated Fisher information matrix (Turnbull 1976) can be used to estimate the standard error of the M-B curve at each observed titer. The resulting estimator has no closed form but is analogous to the product-limit estimator. We refer readers to the listed references for more details. R code implementing this procedure is available from the first author upon request. Alternatively, readers can refer to an R package (dblcens); this package, however, treats the last right-censored and first left-censored observations as uncensored.

Individual level summaries of estimated M-B curves, such as the AUC M-B, percentiles and the breadth at a certain threshold can be defined and estimated similarly as described for case I data. Likewise, group comparisons based on the distribution of these summaries can be carried out as for case I data. The group-average M-B curves for case II data can be derived and estimated by further assuming that responses from subjects of one group are i.i.d. Consequently, test statistics for testing differences in survival functions can be adopted here. For example, when there is only left or right censoring, log-rank test statistics or a number of other well-established methods can be used (Fleming and Harrington 1991; Kalbfleisch and Prentice 2002). When there is both left and right censoring, the recently developed generalized log-rank test for mixed interval-censored and right-censored data (Zhao and Sun 2004) can be employed.

3.3. Second approach—Two-sample multivariate rank tests

For researchers who are interested in group comparisons that can take into account differential neutralization sensitivities of isolates and correlations among isolates, Nab response data can be viewed as coming from a multivariate distribution, where responses to each isolate have their own marginal distribution and their correlations are explicitly specified. In situations where the amount of censoring is small, we recommend substituting ranks for the actual observations in construction of three test statistics (Higgins 2004). Let W1' = (W1_i1, …, W1_im), i = 1, …, n₁, and W2'= (W2_i1, …, W2_im), i = 1, 2, …, n₂, denote the two vectors of ranks of the original titers, and let w̄1' = (w̄1₁, …, w̄1_m) and w̄2' = (w̄2₁, …, w̄2_m) denote the two vectors of sample means. The first test statistic is analogous to the Hotelling’s T² statistic and is defined by

$$T_w^2=\frac{n_1{n}_2}{n_1+n_2}(\overline{w}1-\overline{w}2)\text{'}{C}^{-1}(\overline{w}1-\overline{w}2),$$

where

$$C=\frac{{\displaystyle \sum _{i=1}^{n_1}(W{1}_i-\overline{W}1)(W{1}_i-\overline{W}1)\text{'}}+{\displaystyle \sum _{i=1}^{n_2}(W{2}_i-\overline{W}2)(W{2}_i-\overline{W}2)\text{'}}}{n_1+n_2-2}$$

is the pooled variance-covariance matrix based on ranks. By setting C = I, $T_w^2$ becomes a statistic based on squared mean differences of ranks.

The second test statistic is defined based on the Wilcoxon rank-sum statistics. Let W₁, …, W_m denote the sum of ranks for group 1. For the j^th isolate, let

$$Z_j^w=\frac{W_j-E(W_j)}{\sqrt{\mathit{\text{Var}}(W_j)}},\text{where}E(W_j)=\frac{n^{*}(n+1)}{4}\text{and}\mathit{\text{Var}}(W_j)=\frac{n^{*}(n+1{)}^{*}(2n+1)}{24}.$$

Then, the maximum of (|Z^w₁|, …, |Z^w_m|) can be used as a test statistic for two-sided hypotheses and the maximum of (Z^w₁, …, Z^w_m) for one-sided hypotheses.

The third test statistic is a sum statistic, W_sum = W₁ + … +W_m. For all three statistics, we can carry out permutation tests where multivariate vectors are permuted between groups and the resulting permutation statistics are compared to the original one to calculate the significance level of the test.

4. APPLICATIONS TO VAX004 NAB RESPONSE DATA

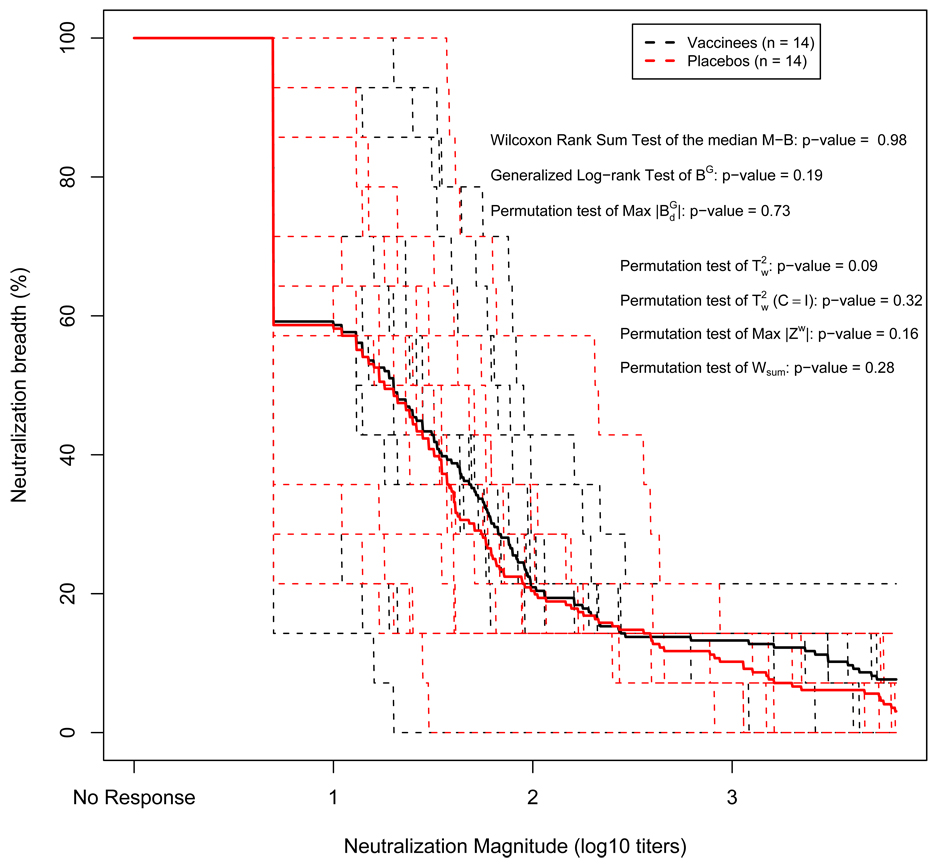
In this section, we compare the post-infection Nab response between vaccine and placebo recipients in the Vax004 trial. Univariate analyses of this dataset (Figure 1) show that a significant difference between the two groups is found in responses to the MN strain (p-value = 0.004), but not in responses to the other 13 strains (p-value > 0.1). In Figure 2, the individual estimated M-B curves and group-average estimated M-B curves for vaccine and placebo recipients are plotted. We compare the two groups by simultaneous evaluation of the magnitude and breadth of the multi-viral Nab responses. Because the data are single-value left (at log₁₀(5)) or right (at log₁₀(21870)) censored, we apply the methods described for case I data in section 3.1.3, and methods from the second approach described in section 3.3. Namely, the Wilcoxon rank sum test of the median M-B (p-value = 0.98), the generalized log-rank test of group average M-B curves (B^G) (p-value = 0.19), permutation tests of the maximum vertical distance between the two group-average M-B curves (max|B^G_d|) (p-value = 0.73), the rank-based Hotelling T² (T²_w) (p-value = 0.09), the special case rank-based Hotelling T² with C = I (T²_w(C=I)) (p-value = 0.33), the maximum absolute Z^w (max|Z^w|) (p-value = 0.16) and the sum rank statistic (W_sum) (p-value = 0.29). The p-values from the multivariate rank tests, T²_w and max|Z^w| are lower than those from other tests that do not take into account the correlations among isolates. This suggests that the multivariate rank tests are likely more sensitive to detect differences in multi-viral Nab responses that are at least moderately correlated (average pair-wise Pearson’s correlation coefficient = 0.55). More extensive comparisons of these different tests are discussed in section 5. Nevertheless, none of the tests show strong evidence of significant differences in Nab response between vaccine and placebo recipients. This lack of significant differences implies that prior vaccination did not augment either the magnitude or the breadth of natural antibody response generated by HIV-1 infection in these trial participants.

Figure 2.

Individual and Group Averaged M-B curves of Post-infection Responses of Vaccine and Placebo Recipients from Vax004

5. SAMPLE SIZE CALCULATIONS AND POWER ANALYSES OF DIFFERENT GROUP COMPARISON METHODS

In the multivariate framework, quite a few parametric approaches for sample size calculations have been proposed for continuous outcomes (Liu and Liang 1997; Jung and Ahn 2003), mostly based on a multivariate extension of the work of Self and Mauritsen (Self and Mauritsen 1998). In HIV-1 vaccine trials, however, instead of the m-component vectors of means from the multi-viral Nab response data, comparisons of neutralization breadth between different vaccine candidates are often of greater interest. In addition, classical sample size calculations are often inappropriate for multi-viral Nab response data because of censoring. Envisioning multi-viral Nab response data comprised of designated summary measures (e.g., ID50) from the neutralization calibration curve, we base the sample size calculations on the analysis of the neutralization breadth at a certain threshold τ, B^est(τ), which obviates the censoring issue. A meaningful value of τ is usually estimated from external Nab response studies. We then compare the distributions of B^est(τ) from two groups using Wilcox on rank sum tests. We use Monte Carlo simulations to estimate power and to calculate the necessary sample size to achieve 90% power.

We first describe how we simulate the data sets based on pre-specified values of a few parameters. Neutralization titers against m isolates Y = (Y₁,…,Y_m)' are assumed to be distributed according to N(μ,Σ), where μ is the m-variate mean vector and Σ is the variance-covariance matrix of dimension m × m. Because μ is often unknown and difficult to estimate with any existing data, investigators could instead specify an m-variate parameter P = (P₁,…,P_m)', the probability that isolates are neutralized above a threshold τ. For a given τ, μ_j, j = 1, …, m can be related to P_j in a way such that μ_j is the solution that minimizes the distance between P_j and Pr((Y_j−μ_j)/σ_j > τ), where σ_j is the user-specified standard deviation of Y_j. After data sets are simulated for groups with different specifications of P, the B^est(τ) are computed. The empirical power and sample size are then calculated using a Wilcoxon rank sum test, with 2-sided Type I error rate = 0.05.

In the simulations, one can vary the choices of Σ and τ for different combinations of P. It is often easier for investigators to specify the correlation coefficients ρ_ij between each pair of responses Y_i and Y_j, i, j = 1, …, m, where ρ_ij =σ_ij /σ_iσ_j. A reasonable value of τ should set a biologically meaningful bar for effective immunogenicity. In the example below, we use τ = log₁₀(400), σ_i² = 0.425 and ρ = 0.5 (or 0.9), where titer 400 corresponds to the 75^th percentile and 0.425 corresponds to the sample variance of the MN neutralization titers measured in Vax004 participants 2 weeks after receiving the third vaccination. ρ is guided by the sample correlation coefficients ranging from 0.64 to 0.89 for different antibody targets that were assessed in Vax004 (Gilbert et al. 2005).

An example of sample size calculations is provided in Table 1. Suppose a panel of 12 viruses is used, and two vaccines are tested in equal sample size, each of which generates neutralization levels to the panel of isolates according to a multivariate normal distribution specified by P, σ_i² and ρ. The two vectors of P for groups 1 and 2 are listed in columns 1 and 2. The variance of the multivariate normal distribution is set as 0.425 for all isolates and the linear correlation between log10 neutralization titers against any two isolates is 0.5 (third column) or 0.9 (fourth column). The required sample sizes were estimated using Monte Carlo simulations based on 2000 generated HIV-1 vaccine trial datasets. For example, as highlighted in Table 1, if the 12 isolates are assumed to be equally sensitive to neutralization and intra-subject neutralization levels to two isolates are assumed to be positively correlated with linear correlation 0.5, then with 30 vaccine recipients per arm there is 90% power to distinguish a vaccine that neutralizes 10% of viruses from one that neutralizes 25% of viruses. This many subjects and viruses also provide 90% power to distinguish a vaccine with neutralization probabilities ranging uniformly from 0.30 to 0.50 across the 12 isolates from a vaccine with neutralization probabilities ranging uniformly from 0.30 to 0.90 across the 12 isolates. As the number of subjects analyzed increases, smaller differences in neutralization probabilities of the 12 isolates can be detected. Furthermore, the higher the correlation between intra-subject neutralization levels to different isolates, the greater the number of subjects (or isolates in the panel) needed to achieve 90% power; the lower the correlation, the more information on breadth is contained in the isolate panel. If missing data are anticipated at the design stage, the proposed sample size can be adjusted by the percentage of expected missing data, which may be estimated from similar previous studies. Because the estimation of the ID values or other summary measures of the calibration curve is beyond the scope of this paper, the variance of those estimates is not incorporated in the calculations above. However, estimation of such variance should be straightforward from suitably replicated observations. Sample sizes corrected for measurement error can hence be derived in a similar manner with the additional variance added to the simulated multivariate data.

Table 1.

Number of participants per arm (N) required to have 90% power to detect a difference in the breadth of neutralization of two vaccine regimens, based on a panel of 12 isolates

Prob. of neutralization of the 12 isolates, group 1 (P1) (Expected % neutralized)	Prob. of neutralization of the 12 isolates, group 2 (P2) (Expected %neutralized)	N (ρ = 0.1)	N (ρ = 0.5)	N (ρ = 0.9)
Isolates equally neutralization sensitive
.10-.10 (.10)	.20-.20 (.20)	25	54	140
.10-.10 (.10)	.25-.25 (.25)	14	30	74
.10-.10 (.10)	.30-.30 (.30)	9	19	45
.40-.40 (.40)	.60-.60 (.60)	15	32	86
.40-.40 (.40)	.70-.70 (.70)	7	16	38
.40-.40 (.40)	.80-.80 (.80)	5	10	20
Isolates differentially neutralization sensitive
.05-.20 (.125)	.05-.35 (.20)	44	90	190
.05-.20 (.125)	.05-.45 (.25)	18	37	72
.05-.20 (.125)	.05-.55 (.30)	11	22	42
.30-.50 (.40)	.30-.70 (.50)	47	112	260
.30-.50 (.40)	.30-.80 (.55)	21	51	124
.30-.50 (.40)	.30-.90 (.60)	12	30	57

Note: The two numbers in columns 1 and 2 are the response probabilities for the least and most neutralization-sensitive isolates, respectively. The response probabilities for the other 10 isolates are evenly distributed between the response probabilities for the least and most sensitive isolates. For example, .10-.10 indicates that the response probabilities are .10 for all 12 isolates, and .05-.20 implies that the response probabilities for the 12 isolates are .05, .064, .077, .091, .105, .118, .132, .145, .159, .173, .186, and .20, and the expected percentage of isolates neutralized is the average of the least and most neutralization probability.

In another simulation study, we compare the proposed group comparison methods using these simulated Nab response data. In Table 2, with sample size of 30 or 50 per group and correlation of 0.1, 0.5, or 0.9, we present empirical power for two-sample comparisons using eight tests: the Wilcoxon rank sum tests of the breadth (denoted as B^est(τ) in column 5); the Wilcoxon rank sum test of the AUC M-B (AUC M-B); the generalized log-rank test of the two group-average M-B curves (B^G); the permutation test of the maximum vertical distance between the two group-average M-B curves (max|B^G_d|); the permutation test of the rank-based Hotelling T² (T²_w); the permutation test of the special case rank-based Hotelling T² with C = I (T²_w(C=I)); the permutation test of the maximum absolute Z^w(max|Z^w|); and the sum rank statistic (W_sum). We find that all eight tests have excellent power (≥90%) when ρ = 0.1, N=30 or 50 and when ρ = 0.5, N = 50. As expected, with fixed values of P₁ and P₂, power for all tests except “T²_w” always increases or maintains at the level of 1.0 as N increases and decreases or maintains at the level of 1.0 as ρ increases. For example, when P₁ = (0.05, …, 0.2) and P₂ = (0.05, …, 0.45), power for “AUC M-B” increases from 0.999 to 1.0 (ρ = 0.1), 0.979 to 1.0 (ρ = 0.5) and 0.903 to 0.973 (ρ = 0.9) as N increases from 30 to 50; power for “AUC M-B” decreases from 0.999 to 0.979 to 0.903 (N=30) and from 1.0 to 1.0 to 0.973 (N=50) as ρ increases from 0.1 to 0.5 to 0.9. In addition, when the expected percent of neutralization is similar, all tests, except “T²_w”, have higher power to detect the difference between group 1 and group 2 in the scenarios with homogeneous neutralization sensitivities of isolates (i.e., P₁ = (0.1, …, 0.1) and P₂ = (0.25, …, 0.25)) than in the scenarios with heterogeneous neutralization sensitivities of isolates (i.e., P₁ = (0.05, …, 0.2) and P₂ = (0.05, …, 0.45)). When neutralization sensitivities of isolates are homogeneous, power for “T²_w” also decreases or maintains at the level of 1.0 as ρ increases; however, this pattern is less clear when neutralization sensitivities of isolates are heterogeneous.

Table 2.

Empirical power of 8 tests for two-sample comparisons based on 1000 simulated datasets

P1	P2	N	ρ	Best(τ)	AUC M-B	BG	max|BdG|	T2w	T2w(C=I)	mmax |Zw|	Wsum
.10-.10	.25-.25	30	.1	0.997	1	1	1	0.999	1	0.972	1
		50	.1	1	1	1	1	1	1	1	1
		30	.5	0.927	0.999	0.98	0.976	0.728	0.976	0.876	0.992
		50	.5	0.99	1	1	1	0.962	1	0.99	1
		30	.9	0.541	0.962	0.674	0.653	0.332	0.726	0.656	0.798
		50	.9	0.787	0.999	0.898	0.872	0.524	0.904	0.88	0.952
.40-.40	.70-.70	30	.1	1	1	1	1	1	1	0.999	1
		50	.1	1	1	1	1	1	1	1	1
		30	.5	0.998	1	0.999	0.998	0.934	0.999	0.982	1
		50	.5	1	1	1	1	0.998	1	1	1
		30	.9	0.847	0.993	0.888	0.858	0.53	0.894	0.866	0.944
		50	.9	0.974	1	0.978	0.983	0.786	0.985	0.984	0.992
.05-.20	.05-.45	30	.1	0.988	0.999	0.999	0.998	0.975	0.996	0.877	1
		50	.1	1	1	1	1	0.999	0.999	0.989	1
		30	.5	0.832	0.979	0.83	0.835	0.746	0.918	0.766	0.902
		50	.5	0.966	1	0.97	0.966	0.968	0.991	0.962	0.982
		30	.9	0.536	0.903	0.423	0.412	0.986	0.532	0.65	0.562
		50	.9	0.746	0.973	0.63	0.629	0.998	0.784	0.904	0.768
.30-.50	.30-.80	30	.1	0.975	0.997	0.997	0.99	0.964	0.994	0.9	0.998
		50	.1	0.998	1	1	1	0.999	0.999	0.994	1
		30	.5	0.681	0.966	0.726	0.736	0.81	0.919	0.822	0.848
		50	.5	0.894	0.999	0.927	0.922	0.984	0.991	0.974	0.964
		30	.9	0.37	0.874	0.367	0.336	1	0.505	0.76	0.506
		50	.9	0.537	0.958	0.525	0.527	1	0.776	0.958	0.68

Note: The 8 tests are the Wilcoxon rank sum tests of the breadth (B^est(τ)), of the AUC M-B (AUC M-B), the generalized log-rank test of the group-average M-B curves (B^G), the permutation test of the maximum vertical distance between the group-average M-B curves (max|B_d^G|), of the rank-based Hotelling T² (T_w²),of the special case rank-based Hotelling T² with C = I (T²_w(C=I)), of the maximum absolute Z^w (max|Z^w|) and the sum rank statistic (W_sum).

Overall, “AUC M-B” has the greatest power or at least comparably good power among the eight tests. Specifically, when isolates have homogeneous neutralization sensitivities, “AUC M-B” has the greatest power followed by “W_sum”; when isolates have heterogeneous neutralization sensitivities with median correlation (ρ = 0.5), “AUC M-B” still has the greatest power but followed by “T²_w(C=I)”; when isolates have heterogeneous neutralization sensitivities with high correlation (ρ = 0.9), "T_w²" has the greatest power followed by “AUC M-B”, and “max|Z^w|” has better power than the rest of the four tests. Interestingly, by avoiding the estimation of the variance-covariance matrix, power increases substantially in “T²_w(C=I)” as compared to “T²_w” in all scenarios except when isolates have heterogeneous neutralization sensitivities with high correlation (ρ = 0.9), where a large amount of power is lost by ignoring the correlation among isolates. In summary, this power analysis study shows that in scenarios where isolates have homogeneous neutralization sensitivities or when isolates have heterogeneous neutralization sensitivities but low-to-moderate correlation, the Wilcoxon rank sum test based on the AUC M-B is preferred in comparisons of Nab responses. When isolates have heterogeneous neutralization sensitivities and high correlation, the power of the Wilcoxon rank sum test based on the AUC M-B is sacrificed and the permutation test based on the rank-based Hotelling T²_w is preferred because of its acknowledgement of the correlation among isolates.

6. DISCUSSION

We have described two approaches for the analysis of multi-viral immunological data with left and/or right censoring. One approach is based on M-B curves, which can be studied similarly to survival curves for time-to-event data. M-B curves are simple to estimate and easy to understand. This approach integrates magnitude and breadth information and provides effective tools to display, summarize, and compare multi-viral immunological data in the context of HIV-1 vaccine trials. In addition, this approach does not reply on any specific distributional forms of the data. We have found in our simulation studies that tests based on the AUC M-B have the greatest power in detecting the difference in multi-viral Nab response of vaccine candidates. However, when the direction of censoring of the AUC-MB is indeterminate in the presence of both left and right censoring, tests for group comparisons based on the second approach may be preferred.

The second approach takes into account the correlation and differential neutralization sensitivity of isolates. It is therefore appealing if the objective is to acknowledge the likely heterogeneous but inter-correlated contributions of each isolates in evaluation of Nab responses. However, in group comparisons of different vaccine candidates, all tests we studied based on the second approach render less power than the ones based on the AUC M-B except when isolates have differential neutralization sensitivity with high correlation. In this later scenario, our simulation study finds that permutation tests of the rank-based Hotelling T_w² have greater power than those tests based on the first approach. In future research, simulation studies for scenarios with a mix of high and low correlations among isolates will be of interest. However, in practice the correlation among isolates should not be so high because an objective in designing the isolate panels is to minimize the correlation so that a wide range of neutralization activities can be assessed. In general, though, knowledge of the correlation structure of a data set for analysis should be taken into account to help choose an appropriate procedure.

As a general rule for multivariate data analyses, univariate analyses should always precede any subsequent multivariate analyses that compare groups simultaneously with respect to multiple dimensions. Such univaraite analyses are useful in examining situations where responses from one group may be superior on either magnitude or breadth but inferior on the other and where responses from one group may be superior for some isolates but inferior for others. If these situations are identified, the test statistic “max|B^G_d|” that is designed to pick up differences in either magnitude or breadth should be used in the first situation and the multivariate rank test statistics, especially “T²_w” or “T²_w(C=I)” should be used in the second situation to avoid any loss of information.

The methods described in section 3 focus on using one ID value (ID50, ID80 or any other designated ID value) estimated from each individual calibration curve. Because different significance levels or different directions of conclusions could result from comparisons based on different ID values, it is important to decide which ID values to use or how to combine the results from tests of different ID values. One way to address this issue is to consider the steepness of calibration curves (e.g., the linear slope between ID50 and ID80 values). A test on the homogeneity of the steepness of calibration curves could be conducted before the comparison of the magnitude and breadth based on a specific ID value. If the null hypothesis of equal steepness is accepted, the question of which ID values to use should really depend on the objectives of the study: use ID50 if the goal is to analyze data based on maximum assay sensitivity; use ID80 if the objective is to compare stronger Nab responses that might have greater value for effective vaccination, keeping in mind that the two values might be related but on different planes of potency. If the null hypothesis is rejected, we suggest rank-based bi-variate permutation tests of (ID50, ID80) using the AUC M-B.

Lastly, there are currently many cell-mediated immunity (CMI) HIV-1 vaccines under evaluation that target multiple segments of the HIV genome. It will be an interesting exercise to apply the methods discussed in this paper to the evaluation of magnitude and breadth across the HIV genome of T-cell responses for these vaccines as well as to multivariate data from other fields. The programming code of this paper will be placed on a website, and is available upon request.