Microsecond molecular dynamics simulation shows effect of slow loop dynamics on backbone amide order parameters of proteins

Abstract

A molecular-level understanding of the function of a protein requires knowledge of both its structural and dynamical properties. NMR spectroscopy allows the measurement of generalized order parameters that provide an atomistic description of picosecond and nanosecond fluctuations in protein structure. Molecular dynamics (MD) simulation provides a complementary approach to the study of protein dynamics on similar timescales. Comparisons between NMR spectroscopy and MD simulations can be used to interpret experimental results and to improve the quality of simulation-related force fields and integration methods. However, apparent systematic discrepancies between order parameters extracted from simulations and experiments are common, particularly for elements of non-canonical secondary structure. In this paper, results from a 1.2 µs explicit solvent MD simulation of the protein ubiquitin are compared with previously determined backbone order parameters derived from NMR relaxation experiments [Tjandra, N.; Feller, S. E.; Pastor, R. W.; Bax, A. J. Am. Chem. Soc. 1995, 117, 12562–12566]. The simulation reveals fluctuations in three loop regions that occur on timescales comparable to or longer than that of the overall rotational diffusion of ubiquitin and whose effects would not be apparent in experimentally derived order parameters. A coupled analysis of internal and overall motion yields simulated order parameters substantially closer to the experimentally determined values than is the case for a conventional analysis of internal motion alone. Improved agreement between simulation and experiment also is encouraging from the viewpoint of assessing the accuracy of long MD simulations.

Introduction

Biological function often emerges from intermolecular interactions that are modulated by dynamic changes in protein conformation.¹ NMR spectroscopy can quantify protein motions on a wide range of timescales with atomic resolution.^2,3 Nuclear spin relaxation rate constants for backbone amide moieties in proteins in solution depend on the autocorrelation functions C(t) = 〈P₂[μ(0)·μ(t)]〉 of the N-H bond unit vector orientations μ(t), where P₂[x] = (3x² −1)/2 and the angle brackets denote ensemble averaging.⁴ The Lipari-Szabo (LS) model⁵ interprets experimental relaxation measurements, and hence parameterizes C(t), in terms of the overall rotational diffusion time of the protein (τ_M), as well as the generalized order parameter (S) and the correlation time (τ_e) for intramolecular motions of each N-H bond vector. The degree of spatial restriction of an N-H bond vector is quantified by 0 ≤S² ≤ 1, with high S² values corresponding to more rigid sites. Backbone amide order parameters have been measured for more than 200 proteins and used to quantify changes in conformational flexibility associated with protein folding, molecular recognition, and catalysis.⁴

Values of S ² obtained from protein molecular dynamics (MD) simulations have been compared to those obtained from experiments to validate^6,7 and improve^8,9 MD simulations, and to aid in the interpretation of experiments.^10,11 Ubiquitin is a 76-residue protein that has been used as a model system for experimental and computational studies of protein structure and dynamics.^{9,11,12,13,14,15,16} Nederveen and Bonvin¹⁴ analyzed a 0.2 µs MD simulation of ubiquitin and calculated S² values as ensemble averages over internal bond vector fluctuations (see method (2) below). In that work, calculated S² values varied extensively in the loop regions of ubiquitin depending on the timescale over which dynamics were averaged; values of S² obtained as averages over the full trajectory were much lower than found by experiments. The correlation functions C(t) also were calculated from the simulation data to assess the effect of slow internal motions on NMR spin relaxation rate constants. These analyses were hindered, however, by the limited length of the simulation, and the calculated τ_M value, 0.74 ns, was surprisingly short.

Here we compare backbone S² values calculated from a 1.2 µs MD simulation with values determined from NMR relaxation experiments¹² for ubiquitin. Simultaneous consideration of all (rather than solely internal) motions in the MD simulation is found to reduce the discrepancies between calculated and experimental S² values. In particular, the simulation reveals several loop residues that are conformationally mobile at timescales comparable to or longer than overall rotational diffusion (“tumbling”). The calculated S² values for these residues are in good agreement with the experimentally determined values only if overall motion is included in the analysis of the MD simulation (see method (3) below).

Methods

Our MD simulation of ubiquitin was based on PDB 1D3Z¹⁷, with pressure and temperature consistent with the experimental conditions used by Tjandra et al.¹² We used the OPLS-AA/SPC force field,¹⁸ with the Desmond program for MD simulations.¹⁹ Conformations were saved every 2 ps during the 1.2 µs simulation to obtain an ensemble of 6×10⁵ conformations, which represent both the overall and internal motions of ubiquitin.

We calculated S² from the MD trajectory in three ways. In methods (1) and (2), overall rotational motion of the protein is first removed by superposing all structures to a molecular reference frame. In method (1), S² is calculated as C_I (100 ns), which serves as an approximation to the long-time limit of the internal autocorrelation function C_I(t), calculated from μ(t) within the molecular reference frame of the superposed structures. In method (2), S² is calculated as P₂[(Σ_ij <μ_i(t)μ_j(t) >²)^1/2] where μ_i(t) is the i-th Cartesian component of μ(t) within the molecular reference frame.²⁰ In method (3), C(t) was calculated directly from the MD trajectory²¹ and S² was obtained by a weighted least-squares fit (as described further in the Supporting Information) of the “extended” LS model for the correlation function introduced by Clore, et al.,²² which is defined as

$$C(t)=\text{exp}\left(-t/{\tau }_{\mathrm{M}}\right)\left(S^2+(S_{\mathrm{f}}^2-S^2)\text{exp}(-t/{\tau }_{\mathrm{e}})\right)$$

The parameter $S_{\mathrm{f}}^2$ in this model accounts for a fast initial decay of the correlation function on timescales shorter than the first sampled point in the correlation function at 2 ps. The parameter τ_M was globally optimized to a value of 1.98 ns. (This simulated value of τ_M is about a factor of 2 smaller than the experimental value of τ_M,¹² consistent with the observation that the self-diffusion constant of the SPC model for water is 1.8 times larger than the value determined experimentally.²³) In all three S² calculation methods, ensemble averages were approximated by time averages over the trajectory. Sample deviations in the correlation functions were estimated using a blocking method.²⁴ Additional details on the MD simulation and the fitting analysis are provided in the Supporting Information.

Results and Discussion

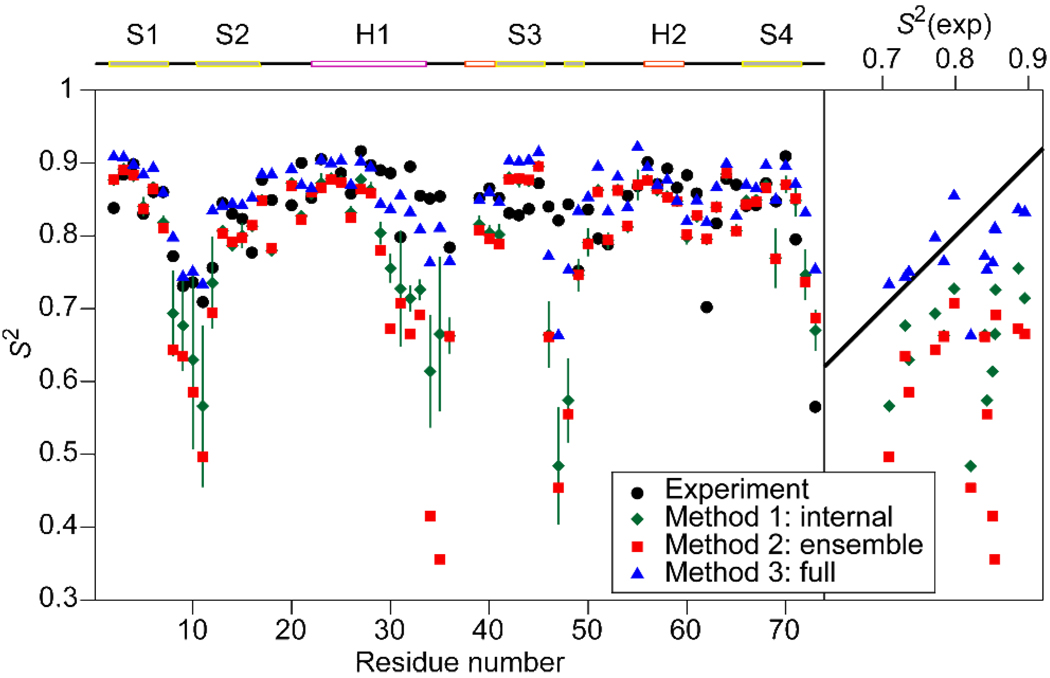
We carried out a 1.2 µs MD simulation of ubiquitin, and calculated backbone S² values from this simulation using three different methods. All analysis methods yield S² values for the β-strands and most of the N-terminal helix that are consistent with experiment (Figure 1). In the case of residues 8–11, 30–36, and 46–48, however, the S² values obtained using method (3) agree better with experimental values than those determined using methods (1) and (2). For these residues, which span three loops and part of the N-terminal helix, the average differences between experimental and simulated values of S² are 0.16, 0.23, and 0.04, and the root-mean-squared differences are 0.18, 0.26, and 0.07 for methods (1)–(3), respectively. In addition to fast ps–ns motion, these loops sample alternative conformations over periods of tens to hundreds of ns in the MD simulation.

Figure 1.

Experimental¹² and simulated backbone amide order parameters for ubiquitin. Calculated values were obtained from MD simulation using methods (1)–(3) as described in the text. The left panel shows S² as a function of amino acid residue number. Secondary structural elements are shown above the graph (H = helix; S = β strand). The right panel shows the correlation between simulated and experimental S² values for loop residues 8–11, 30–36, and 46–48. The solid line has an intercept of zero and a slope of one.

In simulation, as well as in experiment, slow internal motion will reduce C_I(t) for lag times t > τ_M. Such motion has little effect, however, on C(t) or the model parameters obtained by fitting to it, because bond-vector directions are already significantly decorrelated by tumbling for t > τ_M, explaining the improved agreement with the experimental S² values when using method (3). Like the experimental analysis, method (3) incorporates tumbling and is therefore only weakly sensitive to slow internal motion. In contrast, methods (1) and (2) give long-time fluctuations the same weight as motions faster than tumbling, leading to lower predicted S² values.

Several attempts to overcome this limitation of methods (1) and (2) have been described^8,14,25. For example, Buck et al. used a variant of method (1) in which they calculated S² as the value of the internal correlation function at 6 ns, a time comparable to the rotational correlation time of the protein lysozyme.⁸ Markwick et al. carried out several short MD simulations, each of a length comparable to the timescale of rotational motion, for the B3 domain of protein G.²⁵ In that work, S² values were calculated by applying method (2) to each individual simulation, and then averaging the resulting values over all simulations. These modifications of methods (1) and (2) yielded S² values in good agreement with experimental values, although whether these modifications could be used more generally to remove the effects of long-timescale dynamics on S² values calculated from MD simulations is unclear.

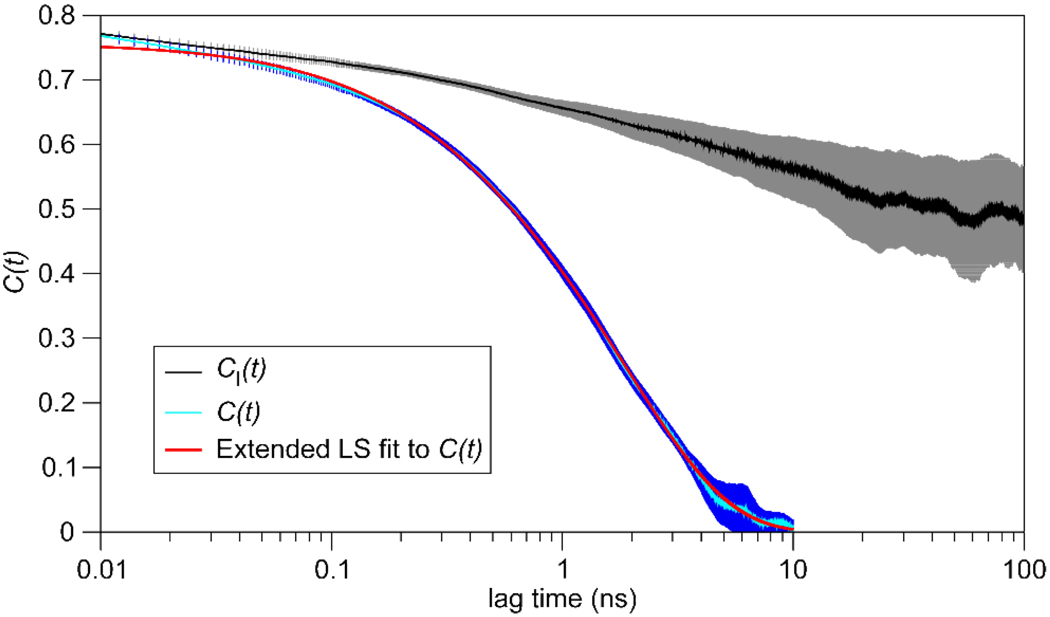
Our interpretation of the results of method (3) is exemplified by the C_I(t) and C(t) values calculated from the MD simulation for Gly47. As shown in Figure 2, the divergence between C_I(t) and C(t) beyond 50 ps reflects the decorrelation of the bond-vector direction due to molecular tumbling; the subsequent decay of C_I(t) on the ns timescale results from long-time dynamical processes that only weakly affect the calculation of S² from C(t) with method (3). For this residue, the experimental value of S² is 0.82, whereas simulated values for methods (1)–(3) are 0.45, 0.48, and 0.66, respectively. The deviation of 0.16 for method (3) is smaller by more than a factor of two compared to the other methods.

Figure 2.

Internal and full autocorrelation functions (C_I(t) and C(t), respectively) calculated from the MD simulation for the amide bond vector of Gly47. Error bars represent one standard deviation.

Any LS analysis of the full autocorrelation function, C(t), is based on the assumption (the “separability assumption”) that this function can be written as the product of two other autocorrelation functions—one depending only on internal motion, the other only on overall rotational motion. Such a decomposition of C(t) is always possible if internal motion occurs only on a timescale much faster than overall rotational diffusion.²⁶ Since several residues in our simulation display motion on longer timescales, the validity of the separability assumption might seem to be called into question. A recent analysis by Wong and Case²⁷ of a 100 ns MD simulation of ubiquitin and of a 200 ns MD simulation of the B3 domain of protein G, however, suggests that such a decomposition may be justifiable in practice even for residues that display internal motion on the same timescale as tumbling. We repeated this analysis for the present 1.2 µs trajectory, and similarly found no evidence of any substantial inconsistency with the separability assumption.

Conclusions

Protein dynamics slower than molecular tumbling can now be probed computationally using long MD simulations. The present work demonstrates that high S² values, derived from NMR relaxation experiments, are compatible with mobility on the 10–100 ns timescale, observed in long MD simulations, in the loop regions of ubiquitin. Such motions cannot currently be detected with NMR relaxation techniques.³ Residual dipolar couplings are sensitive to motions on these timescales;^16,25,28 however, at present, S² values obtained from such data depend substantially on the method of analysis (see Figure S2 in the Supporting Information) and a consensus approach awaits ongoing developments.

Our observations also highlight some of the complications that can arise in the interpretation of S² values determined by NMR relaxation experiments. In many applications, including the extraction of configurational entropies and other thermodynamic parameters from relaxation measurements,²⁹ the quantities of interest are the equilibrium bond vector fluctuations. Our results illustrate that the amplitudes of such fluctuations—quantified, for example, by the S² values calculated using methods (1) and (2)—are not always in agreement with the amplitudes extracted from NMR relaxation experiments, which instead give S² values that correspond more closely to those calculated using method (3). Because of rotational tumbling, the S² values obtained from standard relaxation experiments are not affected by long-timescale internal motion, increasing the difficulty of extracting thermodynamic information directly from the experiments.²⁹ In contrast, thermodynamic information obtained from MD simulations is limited only by the timescale of sampling and the accuracy of the force fields employed. To the extent that the results of MD simulations and NMR relaxation experiments can be reconciled within an analytical framework like that described in this paper, we expect that MD simulations will prove to be a valuable tool in the extraction of thermodynamic quantities from NMR experiments.

Finally, our results reiterate^15,30 the need for caution in assessing simulation quality from comparisons with experimental values of S² . Furthermore, the improved agreement between experiment and simulation obtained in the present work by joint fitting of internal and overall motions to the simulation trajectory justifies detailed interpretation of long MD simulations of protein function.