From patterns to processes: Phase and density dependencies in the Canadian lynx cycle

Abstract

Across the boreal forest of North America, lynx populations undergo 10-year cycles. Analysis of 21 time series from 1821 to the present demonstrates that these fluctuations are generated by nonlinear processes with regulatory delays. Trophic interactions between lynx and hares cause delayed density-dependent regulation of lynx population growth. The nonlinearity, in contrast, appears to arise from phase dependencies in hunting success by lynx through the cycle. Using a combined approach of empirical, statistical, and mathematical modeling, we highlight how shifts in trophic interactions between the lynx and the hare generate the nonlinear process primarily by shifting functional response curves during the increase and the decrease phases.

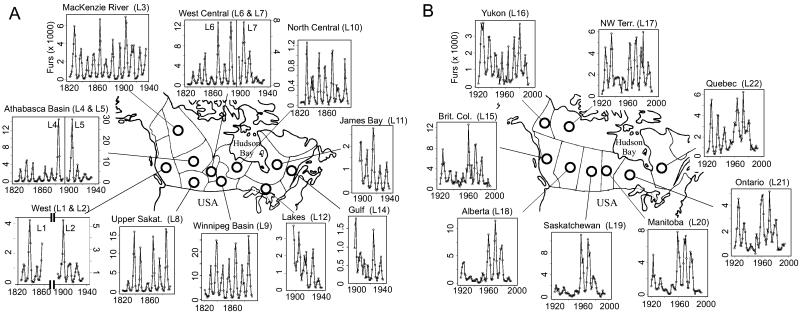
Periodic fluctuations in fur returns of the Canadian lynx (Lynx canadensis) have influenced ecological theory profoundly (1–29): these data have been used to examine concepts such as “the balance of nature,” predator–prey fluctuations, food web dynamics, chaos, and regional and community synchronization. The enigma of the lynx cycle has challenged observational and experimental (6–13), mathematical (5, 14–18, 26, 27), and statistical (25, 28, 29) ecology. Using a combined approach of empirical, statistical, and mathematical modeling (30–35), we here provide a comprehensive analysis of the lynx fur return data from the Hudson Bay Company (1) and more recent data (36, 37) from all of boreal Canada (Fig. 1 A and B). The resulting patterns are interpreted on the basis of recent experimental field studies on the snowshoe hare (Lepus americanus) and the lynx.

Figure 1.

The time series of fur returns of lynx (given on arithmetic scale) from the Canadian boreal forest (see Table 1). (A) The series L1-L12 and L14 represent the pelt counts between 1820 and 1940, as compiled by Elton and Nicholson (1). The borders on the map represent the demarcations of the regions. (B) The series L15-L22 represent data between 1920 and 1994 summarized by Statistics Canada (36, 37) for which the demarcation is given by the Canadian provincial borders. For the modern series (L15-L22), there were occasional zeros. We added one to the modern series before log-transformation.

Earlier statistical analyses of the Canadian lynx cycle have focused primarily on the MacKenzie River time series (series L3 of this paper; compare in Table 1). This series has been studied by using a variety of parametric and nonparametric models, including testing for the presence of nonlinearity, the determination of order and presence of significant lags, nonlinear prediction, and noisy chaos. It has, therefore, formed a benchmark data set for time series modeling (39, 45–57). Detailed scrutiny of a threshold autoregressive model has revealed a particularly good statistical fit to L3 (39, 49, 56–58).

Table 1.

Nonlinear autoregressive structure of old and modern time series on lynx in the Canadian boreal forest

No. remaining	Time series	Years	Threshold, θ
			NAIC		dopt optimal	Overall θ d’s	Lag-2
			d = 1	d = 2
L1	West	1825–1856	−0.493	−0.606	2	2	5.64  (0.56)
L2†	West	1897–1934	−1.789	−1.892	2	2	6.56  (0.28)
L3*	MacKenzie River	1821–1934	−1.416	−1.472	2	2	7.62  (0.29)
L4	Athabasca Basin	1821–1891	−0.367	−0.198	1	1	4.98  (0.67)
L5†	Athabasca Basin	1897–1934	−1.455	−1.356	1	1	7.54  (0.45)
L6	West Central	1821–1891	−1.621	−1.717	2	2	6.18  (0.43)
L7†	West Central	1897–1934	−1.360	−1.127	1	1	7.02  (0.36)
L8	Upper Saskatchewan	1821–1891	−0.602	−0.639	2	2	6.19  (0.75)
L9	Winnipeg Basin	1821–1891	−1.656	−1.709	2	2	8.26  (0.36)
L10	North Central	1821–1891	−1.231	−0.911	1	1	5.00  (0.33)
L11†	James Bay	1895–1939	−2.190	−2.143	1	2  (1)	6.55  (0.41)
L12†	Lakes	1897–1939	−1.890	−1.978	2	2	6.59  (0.26)
L13†	James Bay and Lakes	1897–1939	−2.291	−2.364	2	2	6.68  (0.32)
L14†	Gulf	1897–1939	−1.334	−1.292	1	1	6.22  (0.40)
	Overall weighted estimates for the Hudson Bay series§						6.646  (0.10)
	Deduced phase dependency: β1,0 ≤ β2,0 β1,1 ≤ β2,1 β1,2 > β2,2
	Empirical Bayesian estimates for the Hudson Bay series¶
	Deduced phase dependency: β1,1 ≤ β2,1 β1,2 > β2,2
L15	British Columbia	1920–1994	−1.330	−1.417	2	2	7.38  (0.26)
L16	Yukon Territory	1920–1994	−1.084	−1.188	2	2	7.25  (0.23)
L17	Northwest Territory	1920–1994	−1.462	−1.460	1	2  (1)	7.13  (0.33)
L18	Alberta	1920–1994	−1.161	−1.134	1	2  (1)	8.01  (0.43)
L19	Saskatchewan	1920–1994	−0.646	−0.697	2	2	6.51  (0.45)
L20	Manitoba	1920–1994	−1.105	−1.085	1	2 (1)	6.39  (0.51)
L21	Ontario	1920–1994	−1.960	−1.928	1	2  (1)	6.65  (0.29)
L22	Quebec	1920–1994	−2.390	−2.385	1	2  (1)	7.19  (0.27)
	Overall weighted estimates for the modern series§						7.128  (0.11)
	Deduced phase dependency: β1,0 ≈ β2,0 β1,1 < β2,1 β1,2 > β2,2
	Empirical Bayesian estimates for the modern series¶
	Deduced phase dependency: β1,1 < β2,1 β1,2 > β2,2
	Grand total weighted estimates for all series§						6.858  (0.07)
	Deduced phase dependency: β1,0 Η β2,0 β1,1 < β2,1 β1,2 > β2,2
	Empirical Bayesian estimates for all series¶
	Deduced phase dependency: β1,1 < β2,1 β1,2 > β2,2

The lower regime of the SETAR model, increase phase			The upper regime of the SETAR model, decline phase			Any trend
β1,0 (±SE)	β1,1 (±SE), direct DD	β1,2 (±SE), delayed DD	β2,0 (±SE)	β2,1 (±SE) direct DD	β2,2 (±SE) delayed DD
1.30  (1.07)	1.02  (0.17)	−0.20  (0.30)	5.83  (2.27)	1.16  (0.25)	−1.04  (0.36)	No
1.03  (1.09)	0.91  (0.16)	−0.03  (0.24)	2.54  (1.37)	1.71  (0.18)	−1.08  (0.26)	No
1.35  (0.31)	1.27  (0.06)	−0.43  (0.07)	2.68  (2.37)	1.60  (0.13)	−1.01  (0.31)	No
3.10  (2.30)	0.53  (0.30)	−0.05  (0.44)	3.52  (0.64)	1.33  (0.10)	−0.86  (0.12)	No
4.10  (1.08)	1.36  (0.16)	−0.94  (0.18)	5.39  (1.39)	1.34  (0.16)	−0.99  (0.22)	No
1.13  (0.62)	1.28  (0.08)	−0.35  (0.13)	1.71  (0.59)	1.52  (0.08)	−0.81  (0.10)	No
4.59  (1.73)	0.80  (0.25)	−0.51  (0.26)	3.97  (2.00)	1.31  (0.19)	−0.83  (0.28)	No
−0.05  (1.36)	1.08  (0.17)	0.10  (0.92)	2.90  (0.81)	1.40  (0.10)	−0.81  (0.13)	No
2.42  (0.80)	1.37  (0.09)	−0.64  (0.13)	1.91  (1.53)	1.42  (0.13)	−0.67  (0.19)	No
2.98  (1.31)	0.76  (0.19)	−0.31  (0.25)	0.48  (0.83)	1.44  (0.11)	−0.59  (0.15)	No
1.65  (0.46)	1.45  (0.09)	−0.70  (0.11)	1.60  (1.88)	1.44  (0.18)	−0.73  (0.30)	No
2.79  (0.95)	1.29  (0.16)	−0.75  (0.20)	4.79  (1.86)	1.33  (0.19)	−0.99  (0.28)	No
3.30  (1.02)	1.30  (0.12)	−0.80  (0.18)	3.68  (1.06)	1.56  (0.14)	−1.05  (0.17)	No
0.97  (1.07)	1.05  (0.18)	−0.23  (0.23)	2.09  (2.44)	0.92  (0.24)	−0.31  (0.40)	No
1.70  (0.19)	1.24  (0.03)	−0.50  (0.04)	2.63  (0.29)	1.43  (0.04)	−0.82  (0.05)
	1.25  (0.11)	−0.54  (0.13)		1.40  (0.05)	−0.79  (0.07)
−1.15  (2.21)	0.17  (0.17)	0.76  (0.29)	1.81  (1.28)	0.96  (0.15)	−0.20  (0.20)	No
3.20  (1.23)	0.79  (0.16)	−0.26  (0.21)	2.19  (1.82)	1.25  (0.13)	−0.58  (0.26)	No
6.32  (3.58)	0.53  (0.28)	−0.42  (0.43)	4.29  (0.98)	1.07  (0.12)	−0.63  (0.15)	No
1.97  (1.10)	0.88  (0.16)	−0.14  (0.18)	3.52  (1.18)	1.45  (0.13)	−0.86  (0.17)	No
4.90  (1.66)	0.27  (0.22)	−0.11  (0.23)	1.75  (0.63)	1.27  (0.13)	−0.51  (0.14)	No
2.86  (1.32)	0.76  (0.22)	−0.27  (0.24)	2.09  (0.60)	1.29  (0.12)	−0.58  (0.13)	No
5.76  (3.35)	0.51  (0.28)	−0.40  (0.41)	2.88  (0.67)	1.26  (0.11)	−0.65  (0.13)	(<0.10)
2.67  (1.33)	1.31  (0.16)	−0.70  (0.22)	4.13  (0.90)	1.30  (0.11)	−0.83  (0.14)	No
2.80  (0.54)	0.75  (0.07)	−0.20  (0.09)	2.66  (0.30)	1.24  (0.04)	−0.63  (0.05)
	0.92  (0.17)	−0.15  (0.12)		1.21  (0.13)	−0.47  (0.20)
1.83  (0.18)	1.15  (0.03)	−0.45  (0.04)	2.64  (0.20)	1.36  (0.03)	−0.73  (0.04)
	1.10  (0.20)	−0.37  (0.22)		1.32  (0.12)	−0.66  (0.17)

Assuming a SETAR(2;2,2) model, the NAIC [NAIC being AIC = −2ln(max likelihood) + 2(number of parameters) normalized by the effective number of observations] values for d = 1 and d = 2 are given together with the optimal d value, d_opt, defined as the one minimizing the NAIC over d = 1 and d = 2; in cases that the NAIC values for d = 1 and d = 2 are insignificantly different {defined by [(NAIC(d₋)−NAIC(d_opt)]/[−NAIC(d_opt)] < 0.025}, where d₋ is the nonoptimal d, both 1 and 2 are listed; d = 2 is given in bold because this is the overall most appropriate delay. The estimated parameters in the SETAR model (Eq. 1) for the lynx time series from Canada are provided by Elton and Nicholson (1) [L1-L14] and the time series provided by Dominion Bureau of Statistics and Statistics Canada (36, 37) [L15-L22]. Analyses are based on the original and not detrended data, for which the thresholds are estimated on the basis of the NAIC criterion; the same conclusions emerge if detrended data are analyzed. Detrending was done in S-plus by subtracting a fitted cubic B-spline with 4 degrees of freedom (38). The optimal threshold, θ, assuming a lag (d) equal to 2, was determined by NAIC (Ref. 39; p. 379); the threshold estimate is given together with the estimated bootstrap SE (40, 41). The column “Any trend” summarizes the results of testing the null hypothesis of a SETAR(2;2,2) model against the alternative of a “SETAR(2;2,2) + linear time trend” model. “No” indicates a rejection of the alternative at 5% level and hence suggests the adequacy of a SETAR model. The test is implemented via the method of Lagrange multiplier, also known as the score method (42). The overall weighted estimates were calculated as weighted means, Σ(μ_tw_i)/Σw_i, where μ_i are the estimated parameters for series i and w_i = 1/(SE_i)². The overall SE is given as (1/Σw_i)^1/2. The empirical Bayes estimation (43) is done via the EM-algorithm (44). All series first are normalized (linearly) so that the 30 (70) percentiles become 0 (1). Only the mean lag-1 and lag-2 coefficient estimates are given in the table because the other parameters are not invariant under the scale change. 

SE, standard error; NAIC, normalized kaike information criterion; DD, density dependent. 

^*This series was analyzed by Tong (39). 

^†Series has been interpolated for the missing observation in year 1914. 

^‡This combined series was studied by Stenseth et al. (28, 29) because this most closely corresponded to the snowshoe hare series they studied; this combined series is included here for comparative reasons but is excluded from the both sets of pooled estimates. 

^§The weighted estimates are computed under the framework that the SETAR coefficients are the same for the all of the series in a particular panel of lynx data. The numbers in parentheses are the standard errors of the weighted estimates. 

^¶The empirical Bayesian estimates are computed based on a random coefficient model that for each series the SETAR coefficients are drawn from a super-population. The numbers in parentheses are the corresponding (between-region) standard deviations of the super-population (see main text). 

We build on >40 years of statistical modeling of L3 to bridge the gap between statistical modeling of lynx data, mathematical modeling of the hare–lynx dynamics, and field studies on hares and lynx. We do so by synthesizing available time series data on the Canadian lynx within a nonlinear autoregressive statistical framework that is interpreted on the basis of an ecological model (Table 1). The statistical pattern engraved in these series is consistent with detailed experimental data from the 10-year “Kluane Boreal Forest Ecosystem Project” in the Yukon (10–13). This enables us to elaborate on the strengths and the functional forms of the interactions in the processes underlying the cycle. Earlier, Royama (25) discussed the monitoring data depicted in Fig. 1. Here, we substantially extend his analysis both by using more efficient statistical methods [the Threshold Auto-Regressive modeling approach (39)] and by interpreting the structure of the time series on the basis of new experimental findings. Statistical checks (59) on the fitted residuals of Royama’s model reveal that they cannot be seen as white noise. Thus, Royama’s original reservation about his model was well founded.

The Data

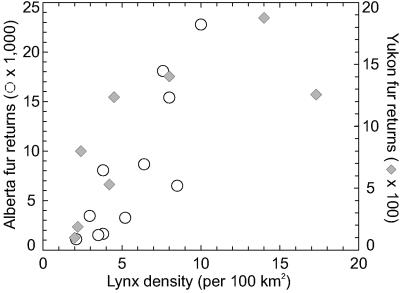
Our core data (Fig. 1) come from the Hudson Bay Company (1) and Statistics Canada (36, 37). They represent good proxies for the actual population abundances (Fig. 2). We estimatekthat, in peak years, trappers caught ≈5% of the total lynx population across Canada and, in trough years, ≈9%.

Figure 2.

The relationship between lynx fur returns and lynx density estimates obtained from intensive field studies in Alberta [1964–74; from Keith and colleague (7–9)] and in Yukon [1987–94; from O’Donoghue et al. (60, 61)]. Provincial fur returns from Statistics Canada (37).

Statistical Modeling

Previous statistical analyses have demonstrated that L3 (on a logarithmic scalel)may be adequately fitted by a nonlinear autoregressive process of order two (28, 29, 42–46, 49, 51). The nonlinearity can be modeled as a threshold process of the form (42):

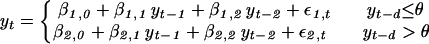1

where y_t is the log-transformed abundance of the lynx at year t [i.e., y_t =ln(Y_t)], β_i,j are statistical parameters that determine the dynamic properties of the system (i = 1 and 2 correspond to the lower and the upper regimes of the model; j = 0, 1, and 2 correspond to the constant term and the lag-1 and lag-2 coefficients, respectively), θ is the threshold applicable to the density d years earlier, and ɛ_i,t are noise-terms with independent and normal distributions, N(0, σ_i²); this model is a SETAR(2;2, 2) model (39, 49–57), i.e., a self-exciting threshold autoregressive model. [The notation SETAR(m;p₁,p₂,… ,p_m) stands for a SETAR model with m regimes, and the order of the jth regime equals p_j]. As a form of local function approximation, SETAR modeling is a computationally efficient way of approximating complex and nonlinear structures, and its statistical properties are well documented (28, 29, 39). Several nonlinear ecological models can be approximated by a SETAR model on log-scale (64) and are characterized by the entire spectrum of dynamic behavior commonly found in ecological models (65).

The optimal thresholding lag, d_opt, can be investigated statistically; Table 1 shows that d_opt = 2 is the most parsimonious choice. The lag-2 is consistent with 16 of 21 series whereas lag-1 is consistent for 11 of 21 series. Furthermore, d_opt = 2 is in agreement with the earlier reported approximate additive structure for these time series (28, 29). Analyzing the residuals demonstrates that a SETAR(2;2, 2) model provides an appropriate description of the datam.

Adopting the approach of empirical Bayes (43), and assuming a random coefficient model that specifies that the SETAR coefficients of each series are drawn randomly from a super-populationn, we may pool information across all of the older series (L1-L14), all of the modern series (L15-L22), and all series altogether (L1-L22). The empirical Bayes estimates are generally close to those obtained from simple weighted averaging (Table 1). However, for the modern series, there are some differences between the empirical Bayes estimates and the weighted average estimates of the lag-1 coefficient in the lower regime and the lag-2 coefficient in the upper regime. The between-region standard deviations of the upper regime of the older series are quite close to zero, suggesting common structure in that part of the modelo.

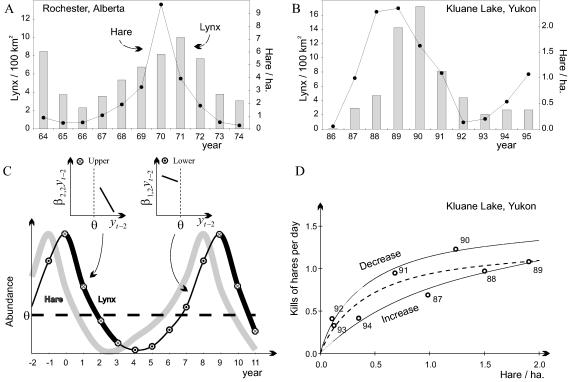
The ecological machinery behind the threshold structure of the lynx time series may be sought in the hare–lynx interaction. Fig. 3 depicts the hare–lynx cycle at Rochester, Alberta (Fig. 3A) and at Kluane Lake, Yukon (Fig. 3B); a more stylized hare–lynx cycle together with the threshold level separating the two regimes also is shown (Fig. 3C). The lower regime applies during the lynx increase, and the upper regime applies during the lynx (and hare) decrease. As a result, we call the lower regime the “increase phase” and the upper regime the “decline phase.”

Figure 3.

The pattern of fluctuation in the snowshoe hare (L. americanus Erxleben, 1777) and the Canadian lynx (L. canadensis Kerr, 1792) as recorded at Rochester, Alberta, from 1964 to 1974 (7–9) (A) and as recorded at Kluane Lake, Yukon, from 1986 to 1995 (10–13) (B). (C) The idealized pattern from the data in A and B with a schematic depiction of the phase dependency in β_2,2y_t−2 (see text) resulting from the predator–prey interaction. (D) The functional response curve of lynx feeding on snowshoe hares for Kluane Lake from O’Donoghue (60) and O’Donoghue et al. (66). Increase years (1987, 1988, 1989, and 1994) have a different functional response than decrease years (1990, 1991, 1992, and 1993), thus explaining the phase dependency in this system: the log likelihood increases by 9.19 when fitting two curves as compared with one common curve (the critical value being 3.00, i.e., 0.5*χ²_0.95(2); see ref. 67). The common model for the functional response curve {kill rate = s [hare density]/[1 + h (hare density)]} is given by the parameters s = 3.11 (±0.28) and h = 2.35 (±0.29) (RSS = 0.1937; 6 d.f.); for the decrease phase, the corresponding estimates are 3.92 (±0.38) and 2.47 (±0.36) (RSS = 0.01218; 2 d.f.) and, for the increase phase, they are 1.26 (±0.16) and 0.66 (±0.16) (RSS = 0.0073; 2 d.f.).

Fitting the SETAR model to all time series, we obtain (Table 1): (i) β_1,0, measuring the average log-transformed abundance in the lower regime, is marginally smaller than or equal to β_2,0; (ii) β_1,1, measuring the lag-1 coefficient [sometimes called the coefficient of statistical direct density dependence (25)], is smaller than or equal to β_2,1; and (iii) β_1,2 is consistently greater than β_2,2 (both negative). In absolute value, this implies a significantly weaker lag-2 effect (statistical delayed density dependence) during the increase phase than during the decrease phase. The β_i,2y_t-2-functions for regimes 1 and 2 are depicted in Fig. 3C. This is the component in which the major phase shift is located.

The full model (Eq. 1) is a density-dependent model because the lag-1 coefficient β_i,1 and the lag-2 coefficient β_i,2 are significantly different from 1 and 0, respectively (68–71). The fitted model is phase-dependent because the pattern of density dependence (β_1,. and β_2,.) varies across the cycle. The consistency across all panels of time series is conspicuous and indicates that the underlying ecological processes change through the cycle. This may be taken as a demonstration, based on time series analysis, of phase dependency in the population dynamics of the lynx; another form of phase dependency earlier has been demonstrated in the Norwegian lemming (Lemmus lemmus) (65, 72).

Mathematical Modeling

To interpret the statistical models (Table 1), we consider a predator–prey model for the lynx [P_t; y_t = ln(P_t)] and the snowshoe hare [H_t; x_t = ln(H_t)]. The following model may be seen as a Taylor-approximation to various, more specific model formulation (29) and is defined (26, 28, 29) as:

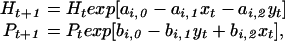2

where a_i,1 and b_i,1 determine the degree of intraspecific regulation in the hare and the lynx (within phase or regime i), respectively; a_i,2 and b_i,2 determine the strength of the trophic interaction between the two species; and a_i,0 and b_i,0 represent the “intrinsic growth rate” (corresponding to conditions without any significant intraspecific interactions and in the absence of other species). Taking logs on both sides of Eq. 2, we may, under reasonable biological assumptions (K.-S.C., H.T., and N.C.S., unpublished work), write

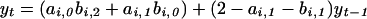3

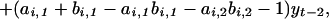which is equivalent to the statistical model given by Eq. 1. This allows us to relate the ecological parameters of Eq. 2 to the autoregressive parameters of Eq. 1. The first-order autoregressive parameter, β_i,1 = 2 − a_i,1 − b_i,1, is a function of the ecological density dependence in both the hare and the lynx (a_i,1 and b_i,1). The second-order autoregressive parameter, β_i,2 = a_i,1 + b_i,1 − a_i,1b_i,1 − a_i,2b_i,2 − 1, incorporates the strength of the trophic interaction (i.e., a_i,2b_i,2). Note that the second-order coefficient β_i,2 also may be represented as β_i,2 = 1 − ( β_i,1 + “intra”_i) − “inter”_i, where intra_i and inter_i signify the strength of the multiplicative intra- and interspecific (trophic) interactions in the system. Thus, the second-order autoregressive parameter is influenced by trophic interactions as well as the ecological density dependencies within the interacting species. Assuming that the trophic model is appropriate, this suggests that the ecological mechanism underlying the observed nonlinearity is likely to be related to the interaction between the hare and the lynx.

Models and Field Observations

The ecological model allows a link between the population-level pattern and the mechanistic processes by putting constraints on permissible ecological interactions. We need to account for the following important patterns of density and phase dependence (Table 1): (i) The lag-1 coefficient is significantly positive, but less so during the increase phase; and (ii) the lag-2 coefficient is significantly negative, and more so during the decline phase. On the basis of Eq. 3, the pattern in the lag-1 coefficient (Table 1) implies that the sum of the strengths of intraspecific interactions (a_i,1 + b_i,1) is somewhat stronger during the increase phase than during the decline phase.

During the increase phase of the hare cycle, lynx appear to be territorial (60, 61, 74–76). This intraspecific regulation disappears as territoriality within the lynx population breaks down 2–3 years after the hare peak (76). Hares exhibit a dominance hierarchy; however, the only aggressive interactions apart from those related to breeding have been observed around concentrated food sources (77–81). Given that hares browse on widely distributed shrubs during the winter when food is most scarce, it is unlikely that individual hares effectively could be excluded from food. It is known that the reproductive rate of hares starts to fall in the late increase and reaches its lowest level in the decline and low (7–10). Thus, we can account for some, but not very strong, phase dependency in the intraspecific component of the dynamics of the two interacting species (i.e., as expressed in the statistical parameters, β_i,1 and, as a result, in the ecological parameters, a_i,1 and b_i,1).

Turning to the trophic interaction, the phase dependency in the snowshoe hare is likely to arise from at least two biological processes: the hare’s change in habitat selection, which is itself a function of predation risk (82, 83), and the hare’s intrinsic responses either to predator-induced stress (10–13, 82–84) or to changes in its food supply (7–13). In lynx, it is likely to result from at least two biological processes: (i) changes in the foraging behavior of lynx as the relative abundances of hares and alternative prey fluctuate (60, 61), and (ii) shifts in the demographic structure of the lynx population. Reproductive output by lynx also declines rapidly to low levels after the hare peak (9, 10, 13), resulting in a gradual upward shift in the mean age of lynx as hares decline, and this is reversed only in the early increase (60, 61, 74–76, 85–89).

The phase dependency in the lag-2 coefficient (β_1,2 > β_2,2; Table 1) suggests that a_i,2b_i,2 is largest in absolute value during the decline phase (Eq. 3). New field observations (66) show that the kill rate per lynx at a given hare density is greater during the decline than during the increase (Fig. 3D). The functional responses of lynx were calculated based on measurements of kill rates/kilometer along lynx trails in snow, travel rates, and activity budgets (66). The probability that the four increase years all fall below the four decrease years, at given densities, is 0.014 (one-sided hypergeometric test). Separate functional response models for the increase and decrease phase also fit the data the best (see legend to Fig. 3D). This phase dependency may be caused by behavioral responses of lynx because lynx surviving into the low phase of the cycle switch to alternative prey and may have changed hunting tactics during the decrease phase. This behavioral change is known to persist into the subsequent early cyclic increase (60, 61, 77). Phase dependency in the kill rate also occurs in coyotes preying on hares (60) and thus may be a general feature of this predator–prey system. The inferred changes in a_i,1, b_i,1, a_i,2, and b_i,2 are all consistent with the estimated differences in β_i,0 between the two regimes (Table 1).

By combining field observations with statistical and mathematical modeling, we have been able to detect and interpret new patterns within the boreal ecosystem. The interplay between theory and analyses of time series data (refs. 28 and 29, and this study) has shed light on a 25-year-old prediction of May (73) and suggests that, even though we need to consider both vegetation and the predators to understand the dynamics of the hare (10, 28, 29), we need only consider the hare to understand the dynamics of the lynx. In a community context, this makes the boreal forest ecosystem—within which the hare and the lynx are main actors—a particularly interesting system to study.

Conclusion

By combining statistical modeling of 21 time series spanning 175 years with mathematical and statistical modeling and experimental data, we have demonstrated: (i) The dynamic patterns (or structure) of the Canadian lynx is both phase- and density-dependent. The density dependence involves both direct and delayed effects. The structure of the dynamics is broadly similar over time (from the early part of the 19th century until the present) and space (the entire Canadian boreal forest region). (ii) The density-dependent structure of the lynx time series is consistent with the proposition that the dynamics in the Canadian lynx is governed by processes involved in the trophic interactions between the snowshoe hare. (iii) The phase-dependent structure of the lynx time series is primarily a result of the strength of the trophic interaction between snowshoe hare and lynx changing during the cycle. And, (iv), density dependence induces the regulatory delays whereas phase dependence induces the nonlinearity. The two act in concert to produce the observed lynx cycle. Altogether, we have clarified a long-lasting controversy in the ecology of cyclic vertebrates of the North, namely that concerning phase dependence and density dependence (6). For the Canadian lynx, it is clearly not a matter of one or the other, but both.

ABBREVIATIONS

SETAR model

self-exciting threshold autoregressive model

SE

standard error

NAIC

normalized kaike information criterion

DD

density dependence