Label Space A Coupled Multi-Shape Representation

Abstract

Richly labeled images representing several sub-structures of an organ occur quite frequently in medical images. For example, a typical brain image can be labeled into grey matter, white matter or cerebrospinal fluid, each of which may be subdivided further. Many manipulations such as interpolation, transformation, smoothing, or registration need to be performed on these images before they can be used in further analysis. In this work, we present a novel multi-shape representation and compare it with the existing representations to demonstrate certain advantages of using the proposed scheme. Specifically, we propose label space, a representation that is both flexible and well suited for coupled multi-shape analysis. Under this framework, object labels are mapped to vertices of a regular simplex, e.g. the unit interval for two labels, a triangle for three labels, a tetrahedron for four labels, etc. This forms the basis of a convex linear structure with the property that all labels are equally spaced. We will demonstrate that this representation has several desirable properties: algebraic operations may be performed directly, label uncertainty is expressed equivalently as a weighted mixture of labels or in a probabilistic manner, and interpolation is unbiased toward any label or the background. In order to demonstrate these properties, we compare label space to signed distance maps as well as other implicit representations in tasks such as smoothing, interpolation, registration, and principal component analysis.

1 Introduction

Shape analysis is an important task in the medical imaging community, and for such analysis, coupled multi-shape models are powerful tools. Indeed, tissue boundaries may vary as organs press up against each other. Image segmentation typically draws upon such models as priors. For example, while the outline of one region may be difficult to discern in the image, the shape of neighboring regions that are correlated may offer important evidence for the outline location [1,2,3].

The first step in constructing such models is choosing an appropriate shape descriptor capable of accurately representing statistical variability. There are two main types of models: explicit and implicit. Splines and medial axis skeletons are two popular examples of explicit models [4,5,6,7,8,9]. While providing a reduced parametric representation, explicit models have several drawbacks. For example, they often assume a fixed shape topology, require care in distributing control points, and/or do not provide natural point correspondence unless based on object-specific models.

This work focuses on implicit models which avoid these problems. After mapping the entire volume to another space, the value of each pixel contributes to describe the shape. In this new space, arbitrary topologies may be represented, correspondences are naturally formed between pixels, and there are no control points to redistribute. However, since this shape space is often of higher dimension than the original dataset, one key disadvantage for this type of representational model is that it will usually increase the spatial and computational complexity of the analysis.

For a single object, the simplest implicit representation is a binary map where each pixel indicates the presence or absence of the object. Signed distance maps (SDMs) are another example, each pixel having the distance to the nearest boundary of the object, a negative distance being prescribed for points inside the object [3,10].

For multiple objects, vector-valued mappings are often used, an approach to which our method is most closely related. A typical approach is to simply layer the single object representations, each layer representing a different object [2], and effort has been made to reduce the spatial demands of layering by mapping to a unit hypersphere of lower dimension [11,12]. A problem with layering is that it often does not form a closed vector space, e.g. adding two signed distance maps does not necessarily yield a signed distance map. To address this, Pohl et al. [1] proposed a closed field representation with natural probabilistic interpretation and algebraic operations based upon Bayesian rationale. This representation has proven to be very versatile, but still suffers from the need of having to perform a certain normalization procedure in order to make the defined “addition” operation compatible with Bayes’ rule. Moreover, there is the problem of choosing a certain intermediate mapping which may impact the computed probabilities. See the discussion in Section 2.

1.1 Our contributions

This paper proposes a coupled multi-object representation that maps object labels to the vertices of a regular simplex, going from a scalar label value to a vertex coordinate position in a high dimensional space which we term label space and denote by ${\mathcal{L}}^n$ for n labels. Illustrated in Fig. 1, this regular simplex is a hyper-dimensional analogue of an equilateral triangle, n vertices (labels) capable of being represented in n − 1 dimensions (${\mathcal{L}}^n\subset {\mathbb{R}}^{n-1}$). This rather simple convex representation has several desirable properties: all labels are equally separated in space, algebraic operations may be done directly, label uncertainty is expressed equivalently as a weighted combination of labels or in a probabilistic manner, and interpolation is unbiased toward any label including the background.

Fig. 1.

The first three ${\mathcal{L}}^n$ label space configurations: a unit interval ${\mathcal{L}}^2\subset \mathbb{R}$ for two labels, a triangle ${\mathcal{L}}^3\subset {\mathbb{R}}^2$ for three labels, and a tetrahedron ${\mathcal{L}}^4\subset {\mathbb{R}}^3$ for four labels (left to right).

We believe that the proposed method addresses several problems with current vector mappings. For example, while the binary vector representation of Tsai et al. [2] was proposed for registration, we will demonstrate that it induces a bias sometimes leading to misalignment. On the other hand, since our ${\mathcal{L}}^n$ label space representation equally spaces labels, there is no such bias. Additionally, compared to the layered signed distance maps, the proposed method introduces no inherent per-pixel variation across equally labeled regions making it more robust for statistical analysis. Hence, the proposed method better encapsulates the functionality of both representations. Further, the registration energy proposed by Tsai et al. [2] is designed to consider each label independent of the others. In contrast, ${\mathcal{L}}^n$ label space jointly considers all labels. Next, we will show that, while lowering the spatial demands of the mapping, the hypersphere representation of Babalola and Cootes [11] biases interpolation and can easily lead to erroneous results. The arrangement of our proposed label space incurs no such bias allowing convex combinations of arbitrary labels. Lastly, referring to the work of Pohl et al. [1], we will show that label space may be regarded as a certain subset of the logarithm-of-odds space with probabilistic and algebraic interpretations. Therefore it inherits many of the advantages of this powerful approach.

2 Related representations

In this section, we describe several of the problems that may develop in shape representations which the label space approach circumvents.

The signed distance map (SDM) has been used as a representation in several studies [1,2,3,10,13]; however, it may produce artifacts during statistical analysis [14]. For example, small deviations at the interface cause large variations in the surface far away, thus it inherently contains significant per-pixel variation. Additionally, ambiguities arise when using layered signed distance maps to represent multiple objects: what happens if more than one of the distance maps indicates the presence of an object? Such ambiguities and distortions stem from the fact SDMs lie on a manifold where direct linear operations are inappropriate [14,15]. Strictly speaking because of this, linear statistical techniques such as principal component analysis (PCA) which are typically used in conjunction with the SDM representation are not rigorously applicable.

Label maps have inherently little per-pixel variation, pixels far from the interface having the same label as those just off the interface. For statistical analysis in the case of one object, Dambreville et al. [14] demonstrated that binary label maps have higher fidelity compared to SDMs. However, for the multi-object setting, the question then becomes one of how to represent multiple shapes using such binary maps?

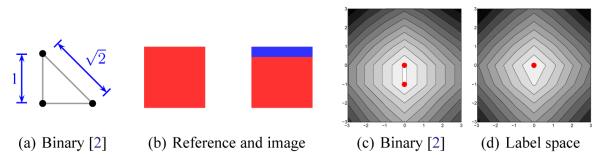
For the purpose of multi-object registration, Tsai et al. [2] have proposed layering binary maps. As Fig. 3(a) shows, this representation places labels at the corners of a right-triangular simplex; however, unlike this present work, it is not a regular simplex but has a bias with respect to the background. The background, located at the origin, is a unit distance from any other label, while any two labels, located along a positive axis, are separated by a distance of $\sqrt{2}$. For translation alone, Fig. 2 demonstrates that this bias may produce non-unique minima; the number of such local minima multiplies when considering additional alignment parameters. When smoothed, Fig. 3 demonstrates that this bias may erroneously introduce background presence.

Fig. 3.

Progressive Gaussian smoothing using binary vectors [2] and the label space. Smoothing among several labels in the binary vector representation yields points closer to background (black) while label space correctly represents the mixture at this junction.

Fig. 2.

(a) Binary vector representation [2] for two labels and background. (b) Reference template and image with extraneous region (blue). (c),(d) Energy landscapes for translation: extra strip leads to nonunique minima (red dots) using binary vectors while the unbiased label space has a unique minima.

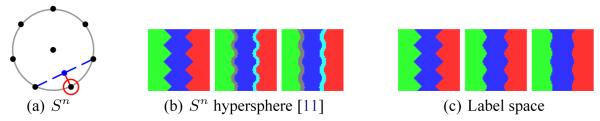
To address the spatial demands of such layered approaches, Babalola and Cootes [11] have proposed mapping labels to points on the surface of a unit hypersphere Sⁿ placing the background at the center. They demonstrate that configurations involving dozens of labels can be efficiently represented by distributing label locations uniformly on the unit hypersphere using as few as three dimensions. The fundamental assumption is that pixels only vary between labels that are located near to each other on the hypersphere, so the placement of labels is crucial to avoid erroneous label mixtures. For example, Fig. 4 indicates how simple Gaussian smoothing can introduce erroneous labels. Here, two labels far from each other are mixed and the result is attributed erroneously to other labels (see Fig. 5(a)).

Fig. 4.

Progressive Gaussian smoothing using Sⁿ hyperspheres [11] and label space. Hyperspheres develop intervening strips of erroneous labels while label space correctly captures label mixtures.

Fig. 5.

Probability of each region using inverse logistic function or label space on the final smoothed maps of Fig. 3. Color is scaled by underlying probability, black being zero probability. When using logarithm-of-odds (left), notice significant nonzero character across the domain of each region, so much so that background starts to dominate the other regions (see Fig. 4(a)).

As we mentioned, the logarithm-of-odds representation of Pohl et al. [1] provides a powerful representation for statistical shape analysis. However, in addition to the normalization requirement in the definition of the “addition” operation, the main concern when using this methodology is the choice of intermediate mapping, a choice that directly impacts the resulting probabilities. The authors explore the use of both binary vectors and layered SDMs [2]; however, both choices have certain drawbacks. For the layered SDM intermediate mapping, Pohl et al. [1] notes that the results of algebraic manipulations in the logarithm-of-odds space often produce invalid SDMs even though the logarithm-of-odds representations are still valid. Thus, computing probabilities as described in [1] may yield erroneous likelihoods.

3 Label space

Our goal is to create a robust representation where algebraic operations are natural, label uncertainty is captured, and interpolation is unbiased toward any label. To this end we propose mapping each label to a vertex of a regular simplex; given n labels, including the background, we use a regular simplex which lies in n − 1 dimensions and denote this by ${\mathcal{L}}^n$ (see Fig. 1). A regular simplex is an n-dimensional analogue of an equilateral triangle.

In this space, algebraic operations are as natural as convex addition, scalar multiplication, inner products, and norms; hence, there is no need for normalization as in [1]. The key property is that for any two points $x_1,x_2\in {\mathcal{L}}^n$ in the simplex, the point $t{x}_1+(1-t)x_2\in {\mathcal{L}}^n$, 0 ≤ t ≤ 1, remains in the simplex.

Note that label uncertainty may be expressed naturally as the weighted mixture of vertices. For example, a pixel representing labels #1, #2, and #3 with equal characteristics would simply be the point $x=\frac{1}{3}{l}_1+\frac{1}{3}{l}_2+\frac{1}{3}{l}_3$, a point equidistant from those three vertices. Using this fact, one can map any point in a probabilistic atlas to a unique point in the label space ${\mathcal{L}}^n$, i.e. given the probabilities p₁, .., p_n with ∑ p_i = 1, the corresponding representation in ${\mathcal{L}}^n$ is given by $l=\sum p_i{l}_i\in {\mathcal{L}}^n$, where $l_i\in {\mathcal{L}}^n$ is a vertex of the simplex. Thus, the above function defines a mapping similar to the logit function used in the logarithm-of-odds space [1]. Alternatively, the probability for $x\in {\mathcal{L}}^n$ being label $l\in {\mathcal{L}}^n$ is, P (x = l) = exp(−∥x−l∥²)/Z, where Z = ∑ exp(−∥x−l_i∥²) acts as a normalization constant. Taking this to define the inverse logistic function, label space becomes an element of the logarithm-of-odds space [1]. The proposed framework however has distinct advantage over the traditional logarithm-of-odds space in that it does not use logarithms, thus removing singularities in the definition of the logit function when any of the probabilities p_i is zero.

Alternatively, computing probabilities from the smoothed binary mappings may produce undesirable results. On the one hand, Fig. 3 demonstrates that smoothing can introduce the presence of background, while on the other hand the use of the exponential in the logit function leaves significant nonzero probability across the domain. Fig. 5 visualizes the probabilities for each region of the final smoothed binary and label space maps in Fig. 3. Here, the top left corner which is clearly the red region yields a probability of only P(red) = 0.475 when using the logistic function [1], while yielding a more appropriate probability of P(red) = 0.948 in label space.

We should note that generating probabilistic atlases from smoothed binary vectors (using the logistic function) could thus produce erroneous probabilities in certain regions misguiding any atlas-based segmentation method. Due to space constraints, a detailed analysis of differences in segmentation based on atlases generated using either method is outside the scope of this work.

4 Experiments

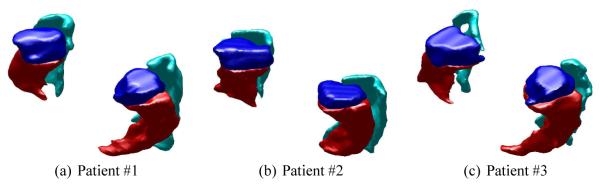
After having explored many of the properties of label space on synthetic examples, we turned to examine a set of 31 patient brains with manually segmented amygdala, hippocampus, and parahippocampus.¹ Fig. 6 shows these subcortical structures for the first three patients. Using label space as the underlying representation to eliminate bias, we performed affine registration [2].

Fig. 6.

Manually segmented amygdala, hippocampus, and parahippocampus (blue, red, cyan) from three patients.

To demonstrate the detail maintained in label space probabilistic calculations, Fig. 7 shows the conditional probabilities for the amygdala and hippocampus of the first three patients, i.e. the probability of the amygdala given the probability of the amygdala in the other patients. For visualization, one slice is taken that passes through both regions. These probabilities were computed via the exponential formula in Section 3. Conditional probabilities like this may be used to judge inter-rater segmentation. Notice the sharp tail of the hippocampus, a feature which may easily be lost in either intermediate representation used in the logarithm-of-odds approach.

Fig. 7.

For one slice, conditional probability of the presence of amygdala and hippocampus of the first three patients given the other patients (white indicates high probability). Notice the fine detail of the hippocampus, features which may be lost when using smoothed intermediate representations [1].

We then compared label space against both the SDMs and binary vectors for use in linear principal component analysis (PCA); see [2,10] and the references therein for a description of this technique. We chose to separate out a test patient, compute the PCA basis on the remaining patients, and examine the projection of the test patient onto that learned basis. As a side note, we used the eigenvectors representing 99% of the variation in the data.

We employed the Dice coefficient as a measure of percent overlap between the test map M and its projection $\widehat{M}$. The Dice coefficient is defined as the amount of overlapping volume divided by the average total volume: $D(M,\widehat{M})=2\mid M\cap \widehat{M}\mid ∕\mid M\cup \widehat{M}\mid$, where |·| denotes volume. The following table gives the mean and variance coefficient for each tissue class². We found that label space is better than SDMs because of the inherent low per pixel variance and also better than binary vectors because it can represent unbiased label mixtures; SDMs and binary vectors require thresholding to determine label ownership. Note that the parahippocampus results improve significantly when label uncertainty is taken into account³.

	SDMs	Binary vectors	Label space
Amygdala	0.783 ± 0.0031	0.825 ± 0.0014	0.855 ± 0.0004
Hippocampus	0.782 ± 0.0016	0.819 ± 0.0006	0.843 ± 0.0003
Parahippocampus	0.494 ± 0.0033	0.561 ± 0.0017	0.773 ± 0.0003

5 Conclusion

This paper describes label space, a new coupled multi-object implicit representation. For this representation, we demonstrated that algebraic operations may be done directly, label uncertainty is expressed equivalently as a weighted mixture of labels or in a probabilistic manner, and interpolation and smoothing is unbiased toward any label or the background.

It remains to perform a detailed analysis of label space in the framework of the logarithm-of-odds space [1]. However, label space can be thought of as an element of the logarithm-of-odds space, inheriting all the functionality mentioned above. For nonrigid registration, we believe that both representations are best suited because of their local descriptive nature compared to SDMs. For segmentation, these initial experiments indicate that label space may be better suited for probabilistic atlas construction.

Modeling shapes in label space does have its limitations. One major drawback to label space is the spatial demand. It might be possible to avoid hypersphere interpolation issues[11] (see Fig. 5(a)) by taking into consideration the empirical presence of neighbor pairings when determining vertex distribution.