Abstract
The successful design of biomaterial scaffolds for articular cartilage tissue engineering requires an understanding of the impact of combinations of material formulation parameters on diverse and competing functional outcomes of biomaterial performance. This study sought to explore the use of a type of unsupervised artificial network, a self-organizing map, to identify relationships between scaffold formulation parameters (crosslink density, molecular weight, and concentration) and 11 such outcomes (including mechanical properties, matrix accumulation, metabolite usage and production, and histological appearance) for scaffolds formed from crosslinked elastin-like polypeptide (ELP) hydrogels. The artificial neural network recognized patterns in functional outcomes and provided a set of relationships between ELP formulation parameters and measured outcomes. Mapping resulted in the best mean separation amongst neurons for mechanical properties and pointed to crosslink density as the strongest predictor of most outcomes, followed by ELP concentration. The map also grouped formulations together that simultaneously resulted in the highest values for matrix production, greatest changes in metabolite consumption or production, and highest histological scores, indicating that the network was able to recognize patterns amongst diverse measurement outcomes. These results demonstrated the utility of artificial neural network tools for recognizing relationships in systems with competing parameters, toward the goal of optimizing and accelerating the design of biomaterial scaffolds for articular cartilage tissue engineering.
Introduction
Tissue engineering and regenerative medicine strategies for functional articular cartilage regeneration or repair have suggested a large number of scaffolds for guiding new tissue formation.1–14 Scaffolds have included those that are prefabricated ex situ4,9,15–17 or those that may be injected,18–20 and they have been formed from a variety of natural and synthetic materials. Several studies have demonstrated that material formulation parameters affect the mechanical properties of these scaffolds as well as their ability to support chondrogenesis by encapsulated or seeded cells.7,21–31 These and other studies have demonstrated difficulty in meeting the competing requirements amongst design goals, or outcome measures, for creating an environment supportive of growing new cartilage tissue. This is largely due to the complex role that cartilage plays within the diarthrodial joint, providing important mechanical, biochemical, and biological functions32,33 that are regulated by a sparse population of one cell type. These cells are responsible for synthesizing a very specialized extracellular matrix33 that displays mechanical integrity in tension and compression, exhibits resistance to shear, and is a multiphasic, viscoelastic material.34–39 Biomaterials used as scaffold materials in cartilage tissue engineering applications must not only support these biological and mechanical roles, but must also be biocompatible, biodegradable, and able to be securely affixed within a defect,11,40–43 which has led to difficulty in simultaneously targeting all of these goals with any one tissue engineering strategy.
This competition amongst design goals, combined with the inherent difficulty in handling datasets that include both biological and mechanical information, suggested a need for a tool to rapidly and simultaneously investigate the effects of perturbations of multiple biomaterial formulation parameters on the competing outcome measures relevant to cartilage tissue engineering. Motivated by this rationale, the goal of this study is to examine the utility of one such mathematical tool, unsupervised artificial neural networks (ANNs), for identifying relationships between a range of biomaterial formulations and diverse and competing outcomes.
Chemically crosslinked elastin-like polypeptide (ELP) hydrogels were chosen as the model biomaterial for creating tissue engineering scaffold for this study. ELPs are polymeric repeats of the VPGXG amino acid repeat found in native elastin44 (where X denotes a guest residue and may be any amino acid except proline). We chose ELPs for the following reasons: (1) chondrocytes1,45 and progenitor cells46 encapsulated in ELPs promote cartilage matrix synthesis in vitro; (2) ELPs afford the ability to precisely control formulation parameters at the genetic level, which allows the effects of ELP formulation parameters on functional outcomes to be systematically investigated; (3) the elastin peptide sequence is native to musculoskeletal tissues44; (4) ELPs elicit no known antigenic response when implanted subcutaneously47; (5) ELPs are thermally responsive, and undergo a soluble to insoluble transition above their characteristic transition temperature leading to the formation of an ELP-rich coacervate phase, which promotes the formation of gels in situ.
The ELPs used here have been designed so that they may undergo chemical crosslinking to form turgid hydrogels in a biocompatible process.48 Sixteen different hydrogel formulations of ELPs were used to evaluate the ability of unsupervised neural network modeling to identify relationships amongst ELP formulation parameters and 11 different and competing outcome measures, including mechanical properties, substrates and products of glucose metabolism, accumulation of appropriate matrix components, and histological appearance.
An unsupervised form of ANN, termed a self-organizing map (SOM), was used to identify these relationships because of their ability to recognize patterns in large and diverse datasets.49 SOMs are also generally robust to noise and errors in datasets, which are common features of biological data, and they require no a priori knowledge of relationships amongst data components.49 SOMs consist most commonly of one-dimensional or two-dimensional arrays of units, or neurons, which become specifically matched to regions of input space during training, and effectively result in clusters of data based on similarities in measured parameters.49 SOMs have been used in many diverse applications including analysis and visualization of gene array data,50,51 in materials science for automation and quality control,52 and in protein engineering for computer-based molecular design.53 SOMs have also recently been shown to be useful for classifying cells based on their single-cell mechanical properties for tissue engineering applications.54
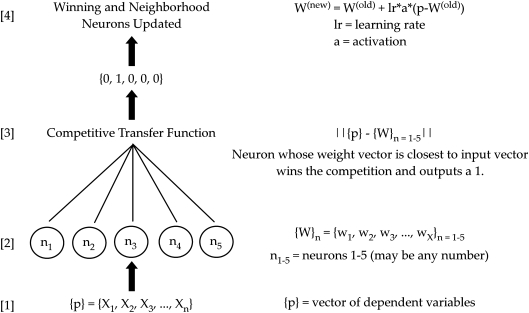
SOM networks are trained by presenting vectors of data to a network of neurons, each having an associated weight vector of the same dimension as the input vector (Fig. 1). As used here, each input vector is compared with the weight vector associated with each neuron by computing the distance between them. The neuron whose weight vector is most closely matched to a given vector of inputs receives the greatest amount of adjustment, according to the Kohonen learning rule,49 with all other neurons' weight vectors being updated according to their proximity, or distance, to this neuron, creating a topologically ordered map. The final map resembles “clusters” of input space with various regions of maximum response, such that those neurons physically close to one another in output space are the neurons that are most similar to input vectors that are near each other in input space.49 In this study, ELP formulations whose parameters had a similar effect on measured outcomes were grouped together by use of SOM, thereby allowing one to identify relationships between the formulation parameters and the measured outcomes.
FIG. 1.
Simplified schematic of self-organizing map learning. A vector of dependent variables {p} [1] is presented to a network of neurons [2] that each possesses a weight vector having the same number of components as the input vector {p}. The norm of the distance between the weight vector for each neuron and the input vector is then calculated (weighted input and net input), and a competitive transfer function [3] outputs 1 for the “winning neuron,” the neuron with the most positive net input. The neurons are then updated according to the Kohonen learning rule [4]. The winning neuron is updated to the greatest degree, followed by neighboring neurons, and then all other neurons according to scaling by the learning rate (lr) and activation (a). The learning rate decreases during training to provide coarse to fine tuning of neuron weights. Activation is 1 for the winning neuron, 0.5 for neighboring neurons, and 0 for all other neurons.
Methods and Materials
ELP synthesis
Genes for all ELPs were available from previous studies.48,55,56 The nomenclature for ELPs used here provides the stochiometric ratio of valines (V) to lysines (K) at the guest residue position (X in VPGXG) as well as the total number of pentapeptides in the polymer. For example, ELP [KV6]-112 designates an ELP with a substitution ratio of V:K of 6:1 (K-period = 7) at the guest residue position in the pentapeptide repeat VPGXG and a total of 112 pentapeptides in the ELP. Different K-containing ELP genes were chosen in this study to provide a wide variation in ELP parameters including crosslink density (determined by periodicity of K), molecular weight (MW), and ELP architecture, as shown in Table 1.57 ELPs were expressed from plasmid-borne genes in E. coli as previously described48,55,56 and purified from E. coli lysate by inverse transition cycling, a nonchromatographic purification method that exploits the inverse phase transition behavior of ELPs and their fusion proteins.58,59 Purified ELP protein concentrations were measured by UV spectrophotometry (UV mini 1240; molar extinction coefficient at 280 nm of 5690 M−1 cm−1; Shimadzu Scientific, Columbia, MD) and adjusted to 100, 150, 200, or 250 mg/mL prior to crosslinking in 25 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES)-buffered saline. A total of 16 distinctly different ELP scaffolds were generated for the study (Table 1).
Table 1.
Elastin-like Polypeptide Formulations of Eight Different Molecular Weights, Five Periods of Lysine Repeats (K-Period), and Four Different Concentrations Were Studied
| Formulation no. | ELP amino acid sequence–pentapeptide repeats | MW (kDa) | K-period | Concentration (mg/mL) |
|---|---|---|---|---|
| 1 | [KV6]-56 | 23.9 | 7 | 250 |
| 2 | [KV6]-112 | 47.1 | 7 | 150 |
| 3 | [KV6]-112 | 47.1 | 7 | 200 |
| 4 | [KV6]-224 | 93.4 | 7 | 100 |
| 5 | [KV6]-224 | 93.4 | 7 | 150 |
| 6 | [KV6]-224 | 93.4 | 7 | 200 |
| 7 | [KV6]-102 | 42.7 | 17 | 200 |
| 8 | [KV16]-204 | 84.8 | 17 | 150 |
| 9 | [KV16]-204 | 84.8 | 17 | 200 |
| 10 | [KV2F]-128 | 55.7 | 4 | 100 |
| 11 | [KV2F]-128 | 55.7 | 4 | 150 |
| 12 | [KV2F]-128 | 55.7 | 4 | 200 |
| 13 | [KV7F]-144 | 61.1 | 9 | 100 |
| 14 | [KV7F]-144 | 61.1 | 9 | 150 |
| 15 | [KV7F]-72 – [VG7A8]-64 – [KV7F]-72 | 85.2 | 12 | 100 |
| 16 | [KV7F]-72 – [VG7A8]-64 – [KV7F]-72 | 85.2 | 12 | 200 |
ELP, elastin-like polypeptide; MW, molecular weight.
Crosslinker preparation
A biocompatible, trifunctional, amine-reactive crosslinker, β-[tris(hydroxymethyl) phosphino] propionic acid (betaine) (THPP; Pierce Biotechnology, Rockford, IL),20,48,57 was dissolved in 200 μL of 25 mM HEPES-buffered saline to a final concentration of 250 mg/mL. Aliquots of this solution were stored at −80°C until further use.
Preparation of samples for mechanical testing
Each ELP solution was mixed with THPP in a 1:1 molar ratio of ELP amines to THPP (hydroxyl)methylphosphines. Solutions were then injected into custom molds and incubated at 37°C to promote crosslinking as described previously.57 Cylindrical samples (6 mm diameter × 2 mm thick, n = 6 per formulation) were incubated overnight at 37°C in a serum-free medium (Ham's F-12 culture medium; Invitrogen, Carlsbad, CA) supplemented with 5 mL of 100 × penicillin/streptomycin (Sigma, St. Louis, MO) and 25 mM HEPES buffer (Invitrogen). This procedure was followed for 13 of 16 formulations, which will hereafter be referred to as “Group 1” formulations.
Three formulations (1, 7, and 8; Table 1) formed a pipettable solution after crosslinking rather than a turgid gel and so were prepared according to an altered protocol. For these formulations, the crosslinker was added to the appropriate ELP solutions and mixed. These mixed solutions were incubated at 4°C overnight in the serum-free medium in a reaction tube to prevent ELP coacervation. These formulations will hereafter be referred to as “Group 2” formulations.
Compression testing
Sample diameters of crosslinked discs (n = 6 per formulation) were determined from their photographs (Photoshop; Adobe, San Jose, CA). Samples were mechanically tested in a 37°C, temperature-controlled phosphate-buffered saline bath. Group 1 formulations were tested in compression using a strain-controlled rheometer (ARES; TA Instruments, New Castle, DE) as previously described.10,60 Briefly, samples were subjected to compressive deformation with a nonporous upper platen (8 mm diameter). After equilibrating under a tare load (1–2 g), the samples were subjected to compressive strains in 5% increments followed by 25 min relaxation to a maximum of 20% compressive strain. Linear regression applied to the normal stress (σ) at equilibrium versus strain (ɛ) was used to determine the equilibrium compressive Young's modulus (E). The samples from Group 2 along with Formulations 9, 15, and 16 (Table 1) from Group 1 were not tested in compression because of continuous flow under compressive strain.
Shear testing
All samples (n = 6 per formulation) were tested in oscillatory shear. Group 1 samples were subjected to an oscillatory frequency sweep with angular frequencies between 1 and 20 rad/s with an amplitude of 0.05 strain (γ). The magnitude of the complex shear modulus (|G*|) and loss angle (δ) were obtained at a frequency of 10 rad/s because frequency dependence of these ELPs was observed to be minimal.
For Group 2 formulations, sample thicknesses were estimated (∼1.194 mm) based on a sample diameter of 8 mm (top platen diameter) and a fixed volume of 60 μL. The samples (60 μL) were pipetted onto a preheated bottom platen and immediately underwent a temperature-driven phase transition. The upper platen was then lowered to a gap thickness of 1.194 mm and then further compressive strain was applied to generate a corresponding 20% strain level (0.955 mm), to be consistent with Group 1 formulations and to prevent slippage during testing. Five minutes of equilibration were then allowed before oscillatory shear was applied. Shear was applied at a strain amplitude of 0.05, and the magnitude of the complex shear modulus (|G*|) and loss angle (δ) were then obtained at 10 rad/s in the same manner as for Group 1 samples.
Chondrocyte isolation and encapsulation in ELP hydrogels
Primary porcine chondrocytes were isolated and encapsulated in crosslinked ELP as previously described.57 Briefly, cells (100 × 106/mL) were mixed with each ELP solution, THPP was added, and solutions were crosslinked in custom molds as described for mechanical testing of samples. Each sample (4 mm diameter × 2 mm thick, n = 6 per formulation) was cultured in a separate vial containing 1.5 mL Ham's F-12 culture medium (Invitrogen) supplemented with 10% fetal bovine serum (Hyclone/ThermoFisher Scientific, Waltham, MA), 50 μg/mL l-ascorbic acid 2 phosphate (Sigma), 5 mL of 100 × penicillin/streptomycin (Sigma), and 25 mM HEPES buffer (Gibco/Invitrogen, Carlsbad, CA). Media was not changed for the first 7 days (see section “Measurement of Media Metabolites”) so that cumulative metabolite levels could be measured, and 50% volume changes were made every 3–4 days following for 28 days. The samples of ELP containing no cells served as assay controls.
Measurement of media metabolites
The concentrations of glucose, lactate, and pyruvate were measured from conditioned media on day 4 as previously described57 (CMA Microdialysis, North Chelmsford, MA). The difference between the value of the concentration of each metabolite in media from cell-containing samples and the value for that metabolite in cell-free media, incubated for an equivalent time period and analyzed in the same batch, was calculated for each sample.
Determination of biochemical content (DNA, sulfated glycosaminoglycan, and hydroxyproline)
In a related study57 of the relationships between measures of short- and long-term cultures, the cell content (via DNA) and the concentration of accumulated sulfated glycosaminoglycans (sGAG) and hydroxyproline (OHP) were determined for papain digests of samples cultured for 28 days (n = 6 per formulation)57 according to established protocols. Briefly, DNA content was determined using the PicoGreen® dsDNA Assay Kit (Molecular Probes/Invitrogen, Carlsbad, CA), using a standard curve generated from standard DNA provided in the assay kit. sGAG was determined using the dimethylmethylene blue assay61 and a standard curve generated using commercial chondroitin-4-sulfate (Sigma). OHP content was determined after acid hydrolysis (6 M HCl, 110°C)62 using a 96-well plate format and a standard curve generated using commercial hydroxyl-l-proline (Sigma-Aldrich, St. Louis, MO). Mean absorbances (or fluorescence) for each cell-free ELP formulation were subtracted from corresponding ELP samples for each assay to obtain values for the concentrations of DNA, sGAG, and OHP for each formulation.
Histological analysis
On day 28 of culture, samples (n = 2 or 3 per formulation) were embedded in Tissue-Tek® O.C.T. Compound (Sakura Finetek U.S.A., Torrance, CA) flash frozen in liquid nitrogen and then stored at −80°C until further use. Eight-micrometer-thick frozen sections were stained with safranin-O to visualize negatively charged proteoglycans or were processed for immunohistochemical labeling of types I (C2456; Sigma) and II (II-II6B3; Developmental Studies Hybridoma Bank, Iowa City, IA) collagen using the HistoStain Plus Broad Spectrum staining kit (Invitrogen).
Following staining,57 all samples were photographed, and images were randomized and graded by two blinded readers according to a histological grading scheme adapted from the work of O'Driscoll et al. and from the International Cartilage Repair Society Visual Histological Assessment.63,64 The scheme includes categories that describe the number and distribution of cells, as well as the abundance and type of matrix, and each category was graded on a 0–3 or 0–4 point scale. The blinded readers reached consensus for all samples and categories. Histological scores were analyzed using principal component analysis65 to obtain a weighted contribution of histological categories to the overall data set (factor 1 and factor 2) (MatLab; The MathWorks, Natick, MA).
Unsupervised ANN simulation
Altogether, 11 experimental outcomes were measured for cartilage regeneration in vitro and were assembled into a vector, or array of values, to be fed to an ANN model as an “input vector” for each sample (Fig. 1) as follows:
INPUTS = {Glu, Lac, Pyr, δ, DNA, E, |G*|, OHP, sGAG, Factor 1, Factor 2}.
Thus, as this vector contains experimental outcome measures, it is indeed fed to the ANN as an input vector. Each sample of each formulation gives rise to a single input vector. These input vectors were entered into the training simulation for an unsupervised ANN (SOM), to identify relationships between the 11 outcomes of in vitro cartilage regeneration and the controlling biomaterial parameters. The unsupervised ANN consisted of a one-dimensional array of five “neurons” (“newsom,” Neural Network Toolbox) which was trained using the “train” command in the MatLab Neural Network Toolbox.
In developing this model of a one-dimensional array of five neurons, a parametric study was undertaken to determine the optimal number of neurons and number of samples required to train a network with excellent repeatability. This was accomplished by iteratively varying the sample number and then the number of neurons, followed by network training for each iteration. Statistical analyses were then performed on the clusters resulting from each iteration to determine the sample number and neuron number that resulted in the greatest number of statistically significant clusters and correctly classified samples (a correctly classified sample is one that maps to the neuron containing the majority of samples for that formulation). With this dataset, neuron numbers greater or less than 5 did not yield correctly classified formulations for a majority of formulations. Further, the number of mismatched samples was minimized when at least 10 data examples were used. Because data were collected here for only n = 6 samples, we followed methods established in ANN modeling of biomaterials,66 which use Monte Carlo methods to obtain pseudoexperimental data points for each measurement outcome to achieve the target of n = 10 data examples. We generated pseudoexperimental data using a previously developed method, based on generating a normal distribution of the experimental data for n = 6 data examples, and random sampling of the normal distribution to yield n = 10 data examples. Given that pseudoexperimental data points are sampled from the same statistical distribution as experimentally determined samples, clustering on these data should not affect conclusions drawn from network analysis.
Statistical analysis
For experimental outcomes, analysis of variance (ANOVA) and Tukey's post hoc tests were used to determine the effects of K-period and starting ELP concentration on each measured parameter, including mechanical properties, metabolite concentrations, cell content, and sGAG and OHP accumulation at a significance level of 0.05. Testing for an effect of ELP MW or a starting ELP concentration of 250 mg/mL was not performed because of insufficient statistical power.
For modeling outcomes, custom code was used to probe each neuron for a list of samples, mean values, and standard deviations of all ELP formulation parameters and measured parameters contained therein. The number of samples in each neuron was also obtained. ANOVA and Fisher's post hoc tests were used to test for an effect of clustering on means of each ELP formulation parameter and measured outcome in each neuron at a significance level of 0.05. Because of the high number of significant comparisons in each case, statistics are not represented on plots. The map was also evaluated for “quality” by determining the number of mismatched samples per formulation. Statistical analysis was performed using JMP Software (SAS, Cary, NC).
Results
Mechanical testing
Statistical analysis revealed that both ELP concentration (ANOVA, p < 0.05) and K-period (ANOVA, p < 0.01) significantly affected compressive modulus and loss angle, but only K-period (ANOVA, p < 0.0001) significantly affected the magnitude of the complex shear modulus. Generally, the results illustrated that a higher density of reactive lysines was associated with more solid-like and stiffer gels, presumably because of a higher density of functional crosslinks with THPP (Supplemental Fig. S1, available online at www.liebertonline.com).
Metabolite concentrations
Both K-period (ANOVA, p < 0.01) and concentration (ANOVA, p < 0.0001) were found to have a significant effect on the concentration of all three measured metabolites. In general, cells encapsulated in ELPs of moderate K-period (9 or 12) and low concentration (100 mg/mL) consumed more glucose and pyruvate and produced more lactate than cells encapsulated in ELPs of all other K-periods and concentrations (Supplemental Fig. S2, available online at www.liebertonline.com).
Cell content, sGAG, and OHP accumulation
K-period (ANOVA, p < 0.0001), but not ELP concentration (ANOVA, p > 0.6), had a significant effect on the number of cells per sample at day 28, with formulations of lower crosslink densities (higher K-period) possessing environments that promoted cell viability and/or proliferation (Supplemental Fig. 3A, available online at www.liebertonline.com). Both ELP concentration and K-period had a significant effect on sGAG and OHP accumulation (ANOVA, p < 0.0001). Formulations prepared at low concentrations or those having a moderate crosslink density accumulated significantly more sGAG and OHP than other formulations (Supplemental Fig. 3B, C, available online at www.liebertonline.com).
Histological outcomes
Histological scoring categories were not considered to be additive (i.e., total histological score was not determined by simply summing scores for each category) because of assumed nonequal contributions of each category to the overall variability of the dataset. Therefore, scores were analyzed via principal component analysis. The results revealed that the first two factors explained greater than 80% of the variability in the data. Factor 1 was heavily weighted by the matrix score (weighting factor: 0.92) and secondarily by the Safranin-O score (weighting factor: 0.39), whereas Factor 2 was heavily weighted by the cell distribution score (weighting factor: −0.70) and secondarily by cell population (weighting factor: −0.62). These findings indicated that the majority of variability in the histological grading data is explained by scoring for extracellular matrix components with a small amount of additional information being explained by cellular categories. Factors 1 and 2 were used for ANN modeling.
SOM simulation
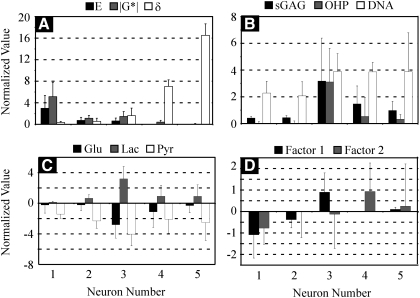
Mapping resulted in a significant effect of clustering on each ELP formulation parameter (p < 0.0001) and measured outcome (p < 0.0001). Mapping results revealed that the mechanical properties (in particular, loss angle and compressive modulus) showed the most significant mean separation amongst neurons (Fig. 2A). Formulations with significantly higher values for compressive and shear modulus were contained in Neuron 1 versus all other neurons (p < 0.0001). All pairwise comparisons revealed significant differences between two neurons, with the exception of Neurons 2 and 3 (E: p = 0.72; |G*|: p = 0.3), 4 and 5 (E: p > 0.99; |G*|: p = 0.08), or 3 and 5 (E only: p = 0.6) which were found to be similar. Loss angle expectedly followed the opposite trend, with highly elastic formulations (low loss angle) mapping to Neuron 1, corresponding to higher compressive and shear stiffness. All pairwise comparisons for loss angle revealed significant differences except that between Neurons 1 and 2 (p > 0.4).
FIG. 2.
Mean normalized values for (A) mechanical properties, (B) biochemical data, (C) metabolite data, and (D) histological outputs from artificial neural network modeling by neuron (mean ± standard deviation).
Formulations contained in Neuron 3 were associated with significantly higher sGAG and OHP accumulation (p < 0.0001) (Fig. 2B), and higher metabolic (Fig. 2C) outputs (p < 0.001), than formulations mapping to Neurons 1 or 2. Neurons 4 and 5 also contained higher values of biochemical composition and most metabolite outputs than Neurons 1 and 2. DNA/sample values in formulations associated with Neuron 3 were significantly higher than formulations associated with Neurons 1 and 2 (p < 0.0001), but not significantly different from values for formulations mapping to Neurons 4 (p = 0.93) or 5 (p = 0.98). Histological Factor 1, which was most heavily weighted by the matrix score and secondarily by the Safranin-O score, was highest in Neuron 3 (p < 0.05) (Fig. 2D), while the highest positive values of Factor 2 were contained in Neuron 4 (Fig. 2D). This is consistent with Factor 2 being heavily negatively weighted by cell population and distribution scores, but being positively weighted by the matrix score, given that formulations with the second highest levels of OHP accumulation were also contained in Neuron 4.
Mean values for ELP formulation parameters contained within each neuron are shown in Figure 3. Neurons containing formulations with high compressive and shear stiffnesses (Neurons 1 and 2) contained formulations with low to moderate MWs, moderate ELP concentrations, and low K-periods (Fig. 3). Formulations producing the highest values for biochemical, metabolic, and histological (Factor 1) outputs were contained in Neuron 3 and were characterized most notably by ELPs of low concentration and moderate K-period (Fig. 3), suggesting an interaction between these two parameters that lead to optimal cellular activity. Neurons 4 and 5 also contained formulations that supported significantly higher biochemical, metabolic, and histological outputs compared with Neurons 1 and 2, but were of significantly lower stiffness and are most notably different from formulations in Neurons 1 and 2 by their K-period. This suggests that K-period has strong power for predicting both mechanical properties and cellular activity for these crosslinked ELP gels. An increasing or decreasing trend was not observed for MW or concentration with neuron number, suggesting these parameters may not be as useful as predictors of outcomes as K-period. However, K-period decreased from Neurons 4 to 5 and ELP concentration steadily increased from Neurons 3 to 5, suggesting an interaction between K-period and concentration, and thus the knowledge of both these parameters may be necessary for accurately predicting the outcomes.
FIG. 3.
Elastin-like polypeptide formulation parameters by neuron (mean ± standard deviation).
The percentage of a formulation's samples located in each neuron as well as the number of mismatched samples for each formulation were also analyzed (Supplemental Table 1, available online at www.liebertonline.com). The results of this analysis revealed that only 15 of 160 samples, or a little more than 9% of samples, were mismatched as a result of this neural network training. In total, 81% of formulations (13/16) had greater than 90% of samples mapping to the same neuron.
Discussion
This study was designed to test the ability of an unsupervised neural network to recognize patterns in competing mechanical and biological outcomes from crosslinked ELP scaffolds for cartilage matrix regeneration. The unsupervised network was successfully used to reveal relationships between parameters of 16 different formulations of crosslinked ELP hydrogel scaffolds and 11 diverse and competing outcome measures relevant to cartilage tissue regeneration in vitro. The frequency of reactive lysine residues (K-period) in ELP was found to be the strongest predictor of both mechanical properties and biological outcomes of in vitro studies of cartilage matrix regeneration. Further, formulations prepared from low ELP concentrations (∼100–150 mg/mL) and intermediate K-periods (∼7–9) were found to result in hydrogels possessing favorable mechanical properties while still supporting abundant cartilage-like matrix synthesis, suggesting these ranges as optimal design criteria for engineering ELP-based cartilage scaffolds. The neural network was able to capture many of these observations, with results that led to mapping of formulations associated with the highest cellular bioactivities within one neuron, Neuron 3 (Formulations 4, 13, 14, and 15; Table 1, Fig. 2). Formulations within this neuron possessed intermediate mechanical properties, between those associated with stiff solids and liquid-like, viscous fluids. It is also noteworthy that Neuron 3 contained three of four formulations that metabolized glucose almost entirely via the anaerobic pathway (i.e., lactate production to glucose consumption ratio was near 2) and showed accumulation of extracellular matrix with collagen to sGAG ratios near those of native tissue (Formulations 4, 13, and 15; Table 1). Other neurons containing formulations with moderate to high cellular bioactivity (Neurons 4 and 5) corresponded to more viscous and less stiff ELP hydrogels, suggesting that favorable biological activity was also promoted in less solid-like hydrogels; in contrast, little to no evidence of biological activity was observed for those crosslinked ELP gels that exhibited solid-like behaviors with high compressive or complex shear moduli (i.e., >15 kPa). Taken together, these results demonstrate that formulations resulting in stiffer hydrogels, driven by higher crosslink densities, are not favorable for supporting optimal cellular bioactivity, pointing to K-period as the most important ELP parameter for predicting both mechanical properties (low K-periods) and favorable biochemical and metabolic outcomes (moderate K-periods).
The strong dependence of both mechanical and biological outcomes on K-period, or crosslink density, was somewhat surprising given the wide range of ELP MWs studied here. These findings suggest that the apparent MW between crosslinks may be a far stronger determinant of outcomes than starting MW for the uncrosslinked ELP. Despite this finding, it is noteworthy that higher MW ELP formulations were neither associated with favorable biological outcomes, nor stiff and solid-like gels, independent of their K-period. This observation suggests an interaction between K-period and MW that may relate to a dependence of crosslinker access to lysine residues on ELP MW, with easier access afforded by lower MW ELPs. Also, this observation suggests some flexibility in the design of ELPs, and possibly other polymers, to emphasize utility of low to intermediate MW polymers.
Interestingly, DNA levels for crosslinked ELPs mapping to Neurons 3–5 were not significantly different, despite ample evidence of differences in other biological outcomes such as histological score and biochemical composition. This may reflect an ability for ELP stiffness to regulate cellular phenotype and matrix production, as substrate stiffness is a well-known determinant of cellular phenotype in other model systems.67 It is also possible that the higher K-period (low crosslink densities) formulations associated with Neurons 4 and 5 allow for diffusion of synthesized matrix components from the gels. Regardless of the cause, knowledge that DNA content does not significantly contribute to the overall variability in this system could allow one to eliminate measurement of this variable in future studies, pointing to the utility of neural network modeling for identifying relevant outcome measures.
The idea of using advanced mathematical and statistical tools to study the effects of biomaterial formulations on functional outcomes has gained popularity for the purposes of accelerating biomaterial design in applications involving biological interfaces.68–70 With most techniques, however, challenges exist with the simultaneous study of multiple, diverse, and/or competing outcomes. In contrast, ANN modeling offers advantages over many deterministic techniques that have been used to predict tissue engineering processes such as matrix synthesis71 and metabolite consumption and evolution.72 Although some deterministic, mechanism-dependent models have the advantage of providing temporal and spatial dependencies of the modeled process, they generally do not allow more than one outcome for a given set of inputs. ANN modeling, as demonstrated here, is able to incorporate statistical variation in these processes and in such a way that allows the user to visualize multiple states of biomaterial parameters and outcomes simultaneously. Unsupervised ANN modeling, as used here, was also shown to be highly repeatable in its mapping of formulations, such that on average, >90% of all samples within a formulation mapped to the same neuron across all formulations. Further, it was noted that the ANN provided statistical separation of means of all parameters amongst neurons for this dataset of 10 samples. This observation suggests that the ANN will be useful for biological studies that are frequently resource-limited in terms of sample number. One limitation of using unsupervised ANN, however, is that this form of ANN is not capable of predicting outcomes for previously untested formulations. This capability is afforded by supervised forms of ANN and has been demonstrated for mechanical properties of a similar crosslinked ELP system73 as well as for predicting fibrinogen absorption to polymeric surfaces designed for use in stents.74
In an effort to minimize bias based on range differences amongst variables, each measured parameter was normalized using a pooled standard deviation for that variable across all formulations before the pseudoexperimental data set was created. One limitation of this normalization method is that the range represented by the loss angle variable is still greater than the range exhibited by all other variables, even after normalization. This could influence mapping according to this variable by range alone. Therefore, caution should be exercised in choosing a normalization method to minimize the potential of biasing mapping that could arise from large differences in perceived variability amongst measured parameters.
In summary, the work presented here was designed to test the ability of unsupervised ANNs to recognize patterns in outcomes of mechanical and biological properties for chondrocytes in crosslinked ELP gels. The ANN was able to successfully separate formulations based on these diverse measurement outcomes, as shown by significant differences in means of outcomes amongst neurons. The ANN was very useful for identifying an optimal range of ELP physical properties that promote scaffold integrity while supporting extracellular matrix synthesis. This optimal range of formulation parameters consists of moderate crosslink densities (K-period between 6 and 12), lower ELP MW (∼50 kDa), and moderate ELP concentrations (∼150 mg/mL), which provide the requisite mechanical stiffness while maximizing nutrient transport and retention of matrix molecules. Overall, unsupervised ANN modeling provided a method by which the effects of three ELP formulation parameters were able to be related to 11 diverse and competing outcome measures, and a method by which ELP formulations could be rationally identified for further investigation.
Acknowledgments
This work was funded by NIH Grant EB002263 (to L.A.S.), NIH Grant AG15768 (to M.A.H.), and NSF Grant DMS-0616597 (to M.A.H.). The authors thank Dr. Bruce Klitzman for support in metabolite analysis.
Disclosure Statement
No competing financial interests exist.
References
- 1.Betre H. Setton L.A. Meyer D.E. Chilkoti A. Characterization of a genetically engineered elastin-like polypeptide for cartilaginous tissue repair. Biomacromolecules. 2002;3:910. doi: 10.1021/bm0255037. [DOI] [PubMed] [Google Scholar]
- 2.Chenite A. Chaput C. Wang D. Combes C. Buschmann M.D. Hoemann C.D. Leroux J.C. Atkinson B.L. Binette F. Selmani A. Novel injectable neutral solutions of chitosan form biodegradable gels in situ. Biomaterials. 2000;21:2155. doi: 10.1016/s0142-9612(00)00116-2. [DOI] [PubMed] [Google Scholar]
- 3.Fisher J.P. Seongbong J. Mikos A.G. Reddi A.H. Thermoreversible hydrogel scaffolds for articular cartilage engineering. J Biomed Mater Res A. 2004;71A:268. doi: 10.1002/jbm.a.30148. [DOI] [PubMed] [Google Scholar]
- 4.Freed L.E. Marquis J.C. Nohria A. Emmanual J. Mikos A.G. Langer R. Neocartilage formation in vitro and in vivo using cells cultured on synthetic biodegradable polymers. J Biomed Mater Res. 1993;27:11. doi: 10.1002/jbm.820270104. [DOI] [PubMed] [Google Scholar]
- 5.Kang S.W. Jeon O. Kim B.S. Poly(lactic-co-glycolic acid) microspheres as an injectable scaffold for cartilage tissue engineering. Tissue Eng. 2005;11:438. doi: 10.1089/ten.2005.11.438. [DOI] [PubMed] [Google Scholar]
- 6.Li W.J. Tuli R. Okafor C. Derfoul A. Danielson K.G. Hall D.J. Tuan R.S. A three-dimensional nanofibrous scaffold for cartilage tissue engineering using human mesenchymal stem cells. Biomaterials. 2005;26:599. doi: 10.1016/j.biomaterials.2004.03.005. [DOI] [PubMed] [Google Scholar]
- 7.Meinel L. Hofmann S. Karageorgiou V. Zichner L. Langer R. Kaplan D. Vunjak-Novakovic G. Engineering cartilage-like tissue using human mesenchymal stem cells and silk protein scaffolds. Biotechnol Bioeng. 2004;88:379. doi: 10.1002/bit.20252. [DOI] [PubMed] [Google Scholar]
- 8.Nehrer S. Breinan H.A. Ramappa A. Young G. Shortkroff S. Louie L.K. Sledge C.B. Yannas I.V. Spector M. Matrix collagen type and pore size influence behaviour of seeded canine chondrocytes. Biomaterials. 1997;18:769. doi: 10.1016/s0142-9612(97)00001-x. [DOI] [PubMed] [Google Scholar]
- 9.Nettles D.L. Elder S.H. Gilbert J.A. Potential use of chitosan as a cell scaffold material for cartilage tissue engineering. Tissue Eng. 2002;8:1009. doi: 10.1089/107632702320934100. [DOI] [PubMed] [Google Scholar]
- 10.Nettles D.L. Vail T.P. Morgan M.T. Grinstaff M.W. Setton L.A. Photocrosslinkable hyaluronan as a scaffold for articular cartilage repair. Ann Biomed Eng. 2004;32:391. doi: 10.1023/b:abme.0000017552.65260.94. [DOI] [PubMed] [Google Scholar]
- 11.Paige K.T. Cima L.G. Yaremchuk M.J. Vacanti J.P. Vacanti C.A. Injectable Cartilage. Plast Reconstr Surg. 1995;96:1390. doi: 10.1097/00006534-199511000-00024. [DOI] [PubMed] [Google Scholar]
- 12.Passaretti D. Silverman R.P. Huang W. Kirchhoff C.H. Ashiku S. Randolph M.A. Yaremchuk M.J. Cultured chondrocytes produce injectable tissue-engineered cartilage in hydrogel polymer. Tissue Eng. 2001;7:805. doi: 10.1089/107632701753337744. [DOI] [PubMed] [Google Scholar]
- 13.Saim A.B. Cao Y.L. Weng Y.L. Chang C.N. Vacanti M.A. Vacanti C.A. Eavey R.D. Engineering autogenous cartilage in the shape of a helix using an injectable hydrogel scaffold. Laryngoscope. 2000;110:1694. doi: 10.1097/00005537-200010000-00023. [DOI] [PubMed] [Google Scholar]
- 14.Stile R.A. Burghardt W.R. Healy K.E. Synthesis and characterization of injectable poly(N-isopropylacrylamide)-based hydrogels that support tissue formation in vitro. Macromolecules. 1999;32:7370. [Google Scholar]
- 15.Ehlers E.M. Fuss M. Rohwedel J. Russlies M. Kuhnel W. Behrens P. Development of a biocomposite to fill out articular cartilage lesions. Light, scanning and transmission electron microscopy of sheep chondrocytes cultured on a collagen I/III sponge. Ann Anat. 1999;181:513. doi: 10.1016/S0940-9602(99)80055-7. [DOI] [PubMed] [Google Scholar]
- 16.Gao R.Z. Dennis J.E. Solchaga L.A. Goldberg V.M. Caplan A.I. Repair of osteochondral defect with tissue-engineered two-phase composite material of injectable calcium phosphate and hyaluronan sponge. Tissue Eng. 2002;8:827. doi: 10.1089/10763270260424187. [DOI] [PubMed] [Google Scholar]
- 17.Slivka M.A. Leatherbury N.C. Kieswetter K. Niederauer G.G. Porous, resorbable, fiber-reinforced scaffolds tailored for articular cartilage repair. Tissue Eng. 2001;7:767. doi: 10.1089/107632701753337717. [DOI] [PubMed] [Google Scholar]
- 18.Elisseeff J. Anseth K. Sims D. McIntosh W. Randolph M. Yaremchuk M. Langer R. Transdermal photopolymerization of poly(ethylene oxide)-based injectable hydrogels for tissue-engineered cartilage. Plast Reconstr Surg. 1999;104:1014. doi: 10.1097/00006534-199909040-00017. [DOI] [PubMed] [Google Scholar]
- 19.Hoemann C.D. Sun J. Legare A. McKee M.D. Buschmann M.D. Tissue engineering of cartilage using an injectable and adhesive chitosan-based cell-delivery vehicle. Osteoarthritis Cartilage. 2005;13:318. doi: 10.1016/j.joca.2004.12.001. [DOI] [PubMed] [Google Scholar]
- 20.Nettles D.L. Kitaoka K. Hanson N.A. Flahiff C. Mata B.A. Hsu E.W. Chilkoti A. Setton L.A. In situ crosslinking elastin-like polypeptide gels for articular cartilage regeneration in a goat osteochondral defect model. Tissue Eng. 2008;14:1133. doi: 10.1089/ten.tea.2007.0245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bryant S.J. Anseth K.S. Hydrogel properties influence ECM production by chondrocytes photoencapsulated in poly(ethylene glycol) hydrogels. J Biomed Mater Res. 2001;59:63. doi: 10.1002/jbm.1217. [DOI] [PubMed] [Google Scholar]
- 22.Bryant S.J. Bender R.J. Durand K.L. Anseth K.S. Encapsulating chondrocytes in degrading PEG hydrogels with high modulus: engineering gel structural changes to facilitate cartilaginous tissue production. Biotechnol Bioeng. 2004;86:747. doi: 10.1002/bit.20160. [DOI] [PubMed] [Google Scholar]
- 23.Bryant S.J. Chowdhury T.T. Lee D.A. Bader D.L. Anseth K.S. Crosslinking density influences chondrocyte metabolism in dynamically loaded photocrosslinked poly(ethylene glycol) hydrogels. Ann Biomed Eng. 2004;32:407. doi: 10.1023/b:abme.0000017535.00602.ca. [DOI] [PubMed] [Google Scholar]
- 24.Hubbell J.A. Materials as morphogenetic guides in tissue engineering. Curr Opin Biotechnol. 2003;14:551. doi: 10.1016/j.copbio.2003.09.004. [DOI] [PubMed] [Google Scholar]
- 25.Lee J. Macosko C.W. Urry D.W. Mechanical properties of cross-linked synthetic elastomeric polypentapeptides. Macromolecules. 2001;34:5968. doi: 10.1021/bm0000900. [DOI] [PubMed] [Google Scholar]
- 26.Lee J. Macosko C.W. Urry D.W. Swelling behavior of gamma-irradiation cross-linked elastomeric polypentapeptide-based hydrogels. Macromolecules. 2001;34:4114. [Google Scholar]
- 27.Martens P.J. Bryant S.J. Anseth K.S. Tailoring the degradation of hydrogels formed from multivinyl poly(ethylene glycol) and poly(vinyl alcohol) macromers for cartilage tissue engineering. Biomacromolecules. 2003;4:283. doi: 10.1021/bm025666v. [DOI] [PubMed] [Google Scholar]
- 28.Miot S. Woodfield T. Daniels A.U. Suetterlin R. Peterschmitt I. Heberer M. van Blitterswijk C.A. Riesle J. Martin I. Effects of scaffold composition and architecture on human nasal chondrocyte redifferentiation and cartilaginous matrix deposition. Biomaterials. 2005;26:2479. doi: 10.1016/j.biomaterials.2004.06.048. [DOI] [PubMed] [Google Scholar]
- 29.Sontjens S.H.M. Nettles D.L. Carnahan M.A. Setton L.A. Grinstaff M.W. Biodendrimer-based hydrogel scaffolds for cartilage tissue repair. Biomacromolecules. 2006;7:310. doi: 10.1021/bm050663e. [DOI] [PubMed] [Google Scholar]
- 30.Temenoff J.S. Athanasiou K.A. LeBaron R.G. Mikos A.G. Effect of poly(ethylene glycol) molecular weight on tensile and swelling properties of oligo(poly(ethylene glycol) fumarate) hydrogels for cartilage tissue engineering. J Biomed Mater Res. 2002;59:429. doi: 10.1002/jbm.1259. [DOI] [PubMed] [Google Scholar]
- 31.Urry D.W. Pattanaik A. Xu J. Woods T.C. McPherson D.T. Parker T.M. Elastic protein-based polymers in soft tissue augmentation and generation. J Biomater Sci Polym Ed. 1998;9:1015. doi: 10.1163/156856298x00316. [DOI] [PubMed] [Google Scholar]
- 32.Buckwalter J.A. Articular cartilage. Instr Course Lect. 1983;32:349. [PubMed] [Google Scholar]
- 33.Buckwalter J.A. Mankin H.J. Articular cartilage I. Tissue design and chondrocyte-matrix interactions. J Bone Joint Surg Am. 1997;79A:600. [PubMed] [Google Scholar]
- 34.Akizuki S. Mow V.C. Muller F. Pita J.C. Howell D.S. Manicourt D.H. Tensile properties of human knee joint cartilage: influence of ionic conditions, wieght bearing, and fibrillation on the tensile modulus. J Orthop Res. 1986;4:379. doi: 10.1002/jor.1100040401. [DOI] [PubMed] [Google Scholar]
- 35.Hayes W.C. Bodine A.J. Flow-independent viscoelastic properties of articular-cartilage matrix. J Biomech. 1978;11:407. doi: 10.1016/0021-9290(78)90075-1. [DOI] [PubMed] [Google Scholar]
- 36.Kempson G.E. Freeman M.A.R. Swanson S.A.V. Tensile properties of articular cartilage. Nature. 1968;220:1127. doi: 10.1038/2201127b0. [DOI] [PubMed] [Google Scholar]
- 37.Setton L.A. Elliot D.M. Mow V.C. Altered mechanics of cartilage with osteoarthritis: human osteoarthritis and an experimental model of joint degeneration. Osteoarthritis Cartilage. 1999;7:2. doi: 10.1053/joca.1998.0170. [DOI] [PubMed] [Google Scholar]
- 38.Setton L.A. Mow V.C. Howell D.S. Mechanical behavior of articular cartilage in shear is altered by transection of the anterior cruciate ligament. J Orthop Res. 1995;12:437. doi: 10.1002/jor.1100130402. [DOI] [PubMed] [Google Scholar]
- 39.Ateshian G.A. Hung C.T. Patellofemoral joint biomechanics and tissue engineering. Clin Orthop Relat Res. 2005;81 doi: 10.1097/01.blo.0000171542.53342.46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Guilak F. Functional tissue engineering: the role of biomechanics in reparative medicine. Ann N Y Acad Sci. 2002;961:193. doi: 10.1111/j.1749-6632.2002.tb03080.x. [DOI] [PubMed] [Google Scholar]
- 41.Guilak F. Setton L.A. Functional tissue engineering and the role of biomechanical signalling in articular cartilage repair. In: Guilak F., editor; Butler D.L., editor; Goldstein S.A., editor; Mooney D.J., editor. Functional Tissue Engineering. New York: Springer-Verlag; 2003. pp. 277–290. [Google Scholar]
- 42.Hutmacher D.W. Scaffolds in tissue engineering bone and cartilage. Biomaterials. 2000;21:2529. doi: 10.1016/s0142-9612(00)00121-6. [DOI] [PubMed] [Google Scholar]
- 43.Yang S.F. Leong K.F. Du Z.H. Chua C.K. The design of scaffolds for use in tissue engineering. Part 1: traditional factors. Tissue Eng. 2001;7:679. doi: 10.1089/107632701753337645. [DOI] [PubMed] [Google Scholar]
- 44.Sandberg L.B. Soskel N.T. Leslie J.G. Elastin structure, biosynthesis, and relation to disease states. N Engl J Med. 1981;304:566. doi: 10.1056/NEJM198103053041004. [DOI] [PubMed] [Google Scholar]
- 45.McHale M.K. Setton L.A. Chilkoti A. Synthesis and in vitro evaluation of enzymatically cross-linked elastin-like polypeptide gels for cartilaginous tissue repair. Tissue Eng. 2005;11:1768. doi: 10.1089/ten.2005.11.1768. [DOI] [PubMed] [Google Scholar]
- 46.Betre H. Ong S.R. Guilak F. Chilkoti A. Fermor B. Setton L.A. Chondrocytic differentiation of human adipose-derived adult stem cells in elastin-like polypeptide. Biomaterials. 2006;27:91. doi: 10.1016/j.biomaterials.2005.05.071. [DOI] [PubMed] [Google Scholar]
- 47.Urry D.W. Parker T.M. Reid M.C. Gowda D.C. Biocompatibility of the bioelastic materials, poly(GVGVP) and its gamma-irradiation cross-linked matrix—summary of generic biological test results. J Bioact Compat Polym. 1991;6:263. [Google Scholar]
- 48.Lim D.W. Nettles D.L. Setton L.A. Chilkoti A. Rapid crosslinking of elastin-like polypeptides with hydroxymethylphosphines in aqueous solution. Biomacromolecules. 2007;8:1463. doi: 10.1021/bm061059m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kohonen T. Self-Organization and Associative Memory. Berlin/Heidelberg: Springer-Verlag; 1988. [Google Scholar]
- 50.Nikkila J. Toronen P. Kaski S. Venna J. Castren E. Wong G. Analysis and visualization of gene expression data using self-organizing maps. Neural Netw. 2002;15:953. doi: 10.1016/s0893-6080(02)00070-9. [DOI] [PubMed] [Google Scholar]
- 51.Toronen P. Kolehmainen M. Wong C. Castren E. Analysis of gene expression data using self-organizing maps. FEBS Lett. 1999;451:142. doi: 10.1016/s0014-5793(99)00524-4. [DOI] [PubMed] [Google Scholar]
- 52.Bhadeshia H. Neural networks in materials science. Neural Netw Mater Sci. 1999;39:966. [Google Scholar]
- 53.Schneider G. Wrede P. Artificial neural networks for computer-based molecular design. Prog Biophys Mol Biol. 1998;70:175. doi: 10.1016/s0079-6107(98)00026-1. [DOI] [PubMed] [Google Scholar]
- 54.Darling E.M. Guilak F. A neural network model for cell classification based on single-cell biomechanical properties. Tissue Eng. 2008;14:1507. doi: 10.1089/ten.tea.2008.0180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lim D.W. Nettles D.L. Setton L.A. Chilkoti A. In-situ crosslinking of elastin-like polypeptide block copolymers for tissue repair. Biomacromolecules. 2008;9:222. doi: 10.1021/bm7007982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Trabbic-Carlson K. Setton L.A. Chilkoti A. Swelling and mechanical behaviors of chemically cross-linked hydrogels of elastin-like polypeptides. Biomacromolecules. 2003;4:572. doi: 10.1021/bm025671z. [DOI] [PubMed] [Google Scholar]
- 57.Nettles D.L. Chilkoti A. Setton L.A. Early metabolite levels predict long-term matrix synthesis for chondrocytes in elastin-like polypeptide biopolymer scaffolds. Tissue Eng. 2009;15:2113. doi: 10.1089/ten.tea.2008.0448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lim D.W. Trabbic-Carlson K. MacKay J.A. Chilkoti A. Improved non-chromatographic purification of a recombinant protein by cationic elastin-like polypeptides. Biomacromolecules. 2007;8:1417. doi: 10.1021/bm060849t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Meyer D.E. Chilkoti A. Purification of recombinant proteins by fusion with thermally responsive polypeptides. Nat Biotechnol. 1999;17:1112. doi: 10.1038/15100. [DOI] [PubMed] [Google Scholar]
- 60.LeRoux M.A. Guilak F. Setton L.A. Compressive and shear properties of alginate gel: effects of sodium ions and alginate concentration. J Biomed Mater Res. 1999;47:46. doi: 10.1002/(sici)1097-4636(199910)47:1<46::aid-jbm6>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 61.Farndale R.W. Buttle D.J. Barrett A.J. Improved quantitation and discrimination of sulfated glycosaminoglycans by use of dimethylmethylene blue. Biochim Biophys Acta. 1986;883:173. doi: 10.1016/0304-4165(86)90306-5. [DOI] [PubMed] [Google Scholar]
- 62.Neidert M.R. Lee E.S. Oegema T.R. Tranquillo R.T. Enhanced fibrin remodeling in vitro with TGF-beta 1, insulin and plasmin for improved tissue-equivalents. Biomaterials. 2002;23:3717. doi: 10.1016/s0142-9612(02)00106-0. [DOI] [PubMed] [Google Scholar]
- 63.Mainil-Varlet P. Aigner T. Brittberg M. Bullough P. Hollander A. Hunziker E. Kandel R. Nehrer S. Pritzker K. Roberts S. Stauffer E. Histological assessment of cartilage repair—a report by the histology endpoint committee of the international cartilage repair society (ICRS) J Bone Joint Surg Am. 2003;85A:45. [PubMed] [Google Scholar]
- 64.O'Driscoll S.W. Keeley F.W. Salter R.B. Durability of regenerated articular-cartilage produced by free autogenous periosteal grafts in major full-thickness defects in joint surfaces under the influence of continuous passive motion—a follow-up report at one year. J Bone Joint Surg Am. 1988;70A:595. [PubMed] [Google Scholar]
- 65.Jackson J.E. A User's Guide to Prinicpal Components. New York, NY: Wiley; 1991. [Google Scholar]
- 66.Smith J.R. Knight D. Kohn J. Rasheed K. Weber N. Kholodovych V. Welsh W.J. Using surrogate modeling in the prediciton of fibrinogen adsorption onto polymer surfaces. J Chem Inf Comput Sci. 2004;44:1088. doi: 10.1021/ci0499774. [DOI] [PubMed] [Google Scholar]
- 67.Engler A.J. Sen S. Sweeney H.L. Discher D.E. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 68.Abramson S.D. Alexe G. Hammer P.L. Kohn J. A computational approach to predicting cell growth on polymeric biomaterials. J Biomed Mater Res A. 2005;73A:116. doi: 10.1002/jbm.a.30266. [DOI] [PubMed] [Google Scholar]
- 69.Anselme K. Bigerelle M. Modelling approach in cell/material interactions studies. Biomaterials. 2006;27:1187. doi: 10.1016/j.biomaterials.2005.10.009. [DOI] [PubMed] [Google Scholar]
- 70.Chen Y.L. Chen H.C. Lee H.P. Chan H.Y. Hu Y.C. Rational development of GAG-augmented chitosan membranes by fractional factorial design methodology. Biomaterials. 2006;27:2222. doi: 10.1016/j.biomaterials.2005.10.029. [DOI] [PubMed] [Google Scholar]
- 71.Obradovic B. Meldon J.H. Freed L.E. Vunjak-Novakovic G. Glycosaminoglycan deposition in engineered cartilage: experiments and mathematical model. AIChE J. 2000;46:1860. [Google Scholar]
- 72.Sengers B.G. Heywood H.K. Lee D.A. Oomens C.W.J. Bader D.L. Nutrient utilization by bovine articular chondrocytes: a combined experimental and theoretical approach. J Biomech Eng Trans ASME. 2005;127:758. doi: 10.1115/1.1993664. [DOI] [PubMed] [Google Scholar]
- 73.Haider M.A. Nettlesr D.L. Trabbic-Carlsonr K. Chilkotir A. Settonr L.A. Proceedings of the Summer Bioengineering Conference. Vail; Colorado: 2005. Predictive modeling of polypeptide hydrogel mechanical properties for cartilage repair using artificial neurla networks. Paper no. 173514. [Google Scholar]
- 74.Smith J.R. Kholodovych V. Knight D. Kohn J. Welsh W.J. Predicting fibrinogen adsorption to polymeric surfaces in silico: a combined method approach. Polymer. 2005;46:4296. [Google Scholar]