Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2006 Oct;98(4):835–844. doi: 10.1093/aob/mcl164

Relative Extents of Preformation and Neoformation in Tree Shoots: Analysis by a Deconvolution Method

YANN GUÉDON 1, J G PUNTIERI 2,*, S SABATIER 1, D BARTHÉLÉMY 1
PMCID: PMC2806178  PMID: 16899472

Abstract

• Background and Aims Neoformation is the process by which organs not preformed in a bud are developed on a growing shoot, generally after preformation extension. The study of neoformation in trees has been hindered due to methodological reasons. The present report is aimed at assessing the relative importance of preformation and neoformation in the development of shoots of woody species.

• Methods A deconvolution method was applied to estimate the distribution of the number of neoformed organs for eight data sets corresponding to four Nothofagus species and a Juglans hybrid.

• Key Results The number of preformed organs was higher and less variable than the number of neoformed organs. Neoformation contributed more than preformation to explain full-size differences between shoots developed in different positions within the architecture of each tree species.

• Conclusions Differences between the distributions of the numbers of preformed and neoformed organs may be explained by alluding to the duration of differentiation and extension for each of these groups of organs. The deconvolution of distributions is a useful tool for the analysis of neoformation and shoot structure in trees.

Keywords: Preformation, neoformation, shoot, leaf primordia, deconvolution, Nothofagus, Juglans

INTRODUCTION

In many woody species from both temperate and tropical regions, foliated axes grow rhythmically (Hallé and Martin, 1968; Hallé et al., 1978; Bell, 1991). This implies that the extension of an axis portion or shoot is followed by the formation of a resting terminal bud consisting, very frequently, of a set of partially developed organs and one to several groups of undifferentiated cells (i.e. meristems). These primordial organs are called preformed organs and, usually, complete their development in the growth period following that of their inception. A shoot may also grow in length by developing neoformed organs, i.e. a shoot portion or set of organs, each of which differentiates and extends without ever integrating a resting bud. For these species, three types of shoots may, in theory, be distinguished based on the times of initiation and extension of their constituting organs: a shoot may be entirely preformed or entirely neoformed, or may be a mixed shoot, consisting of a proximal set of preformed organs and a distal set of neoformed organs (Caraglio and Barthélémy, 1997). Entirely preformed shoots have been reported for Ginkgo biloba (Critchfield, 1960), Fraxinus excelsior (Gill, 1971), Juglans regia (Sabatier et al., 1995), Fagus sylvatica (Roloff, 1987; Nicolini, 1998) and Nothofagus spp. (Puntieri et al., 2000, 2002a, b; Souza et al., 2000). Entirely neoformed shoots seem to be relatively uncommon, but have been described for some tropical trees (Borchert, 1969). Mixed shoots seem to be frequent in the vigorous axes of several tree species (Critchfield, 1960; Kozlowski, 1971; Nitta and Ohsawa, 1997; Puntieri et al., 2000; Souza et al., 2000; Gordon et al., 2006), although their existence in shorter axes has been proved at least once (Puntieri et al., 2002b).

Despite their importance for the understanding of tree architecture and physiology, relatively little information is available about the relevance of preformation and neoformation and their relative extent in the architecture of a tree species. There is evidence that preformed and neoformed leaves of the same shoot may differ in their developmental and functional attributes (Critchfield, 1960; Carles et al., 1964; Steeves and Sussex, 1989; Koike, 1990; Seleznyova and Greer, 2001). Such dissimilarities may be justified by the fact that these two kinds of leaves differentiate and/or extend at different times and, therefore, under different environmental conditions. The contribution of either type of leaves to the future development of the plant and the productivity of the population may indeed be different. A detailed and comparative description of preformation and neoformation and the analysis of their relative extent in trees would thus improve knowledge of plant growth and functioning.

Methodological restrictions have so far hindered scientific progress on the quantitative assessment of preformation and neoformation in woody plants. Whereas the study of preformation may be achieved through bud dissection during the resting period, that of neoformation poses methodological restrictions. The mean number of neoformed organs of a set of shoots may be estimated by subtracting the mean number of preformed organs in a sample of dissected buds from the mean number of organs of a sample of fully extended shoots derived from buds similar to those that were dissected (Puntieri et al., 2000; Souza et al., 2000). The result may be too coarse an estimation of neoformation, as the number of preformed organs in buds for a given species and architectural position is usually less disperse and asymmetric than that of the total number of organs of fully extended shoots derived from equivalent buds (de Reffye et al., 1991; Puntieri et al., 2000; Souza et al., 2000). No methods have so far allowed more detailed descriptions of neoformation. The aim of the present study was to apply a deconvolution method to estimate the neoformation distributions (rather than simply the mean number of neoformed organs) of shoots of five woody species known to develop both preformed and neoformed organs. For each of eight data sets, neoformation distributions were estimated from two independent distributions: that of the number of preformed organs and that of the total number of extended organs.

MATERIALS AND METHODS

In this study, eight published or unpublished data sets were used for which the development of neoformed organs was identified. Five of these data sets refer to South American species of Nothofagus (Nothofagaceae) and the other two to walnut interspecific hybrid Juglans major (Torr.) A. Heller 209 × Juglans regia L. (Juglandaceae). Each data set consisted of two samples taken in two successive years from randomly chosen trees within each population: sample I included buds and sample II consisted of fully extended shoots derived from buds equivalent, in terms of position in the trees, to those of sample I. Buds of sample I of each data set were dissected manually under a stereo-microscope, and the number of organs of each bud was counted. Shoots of sample II were observed in detail with magnifying glasses so as to identify the number of organs present. Buds and shoots with evident signs of damage were excluded. Depending on the data set, the sampled shoots were positioned at the distal end of the main vertical axis of the tree (trunk) and/or the largest horizontal branches (main branches) derived from the trunk. In the case of Nothofagus trees, shoot growth may be definite or, less frequently, indefinite. Nevertheless, it has been shown that trunk and main branch shoots derived from terminal buds and those derived from distal axillary buds are morphologically similar (Puntieri et al., 1998). Therefore, buds and shoots originating at terminal and distal axillary positions were taken as equivalent for the analysis of Nothofagus spp. data. On the contrary, the growth of the trunk of young Juglans spp. trees is indefinite and, since terminal and axillary buds in these trees produce shoots with different morphology (Sabatier and Barthélémy, 2000), only buds and shoots in terminal positions were sampled. The numbers of sampling units of each sample are indicated in Table 1. Data sets may be described as follows (whenever available, published reports for further information are indicated in parentheses).

Table 1.

Mean, standard deviation (s.d.) and coefficient of variation (CV) of the estimated probability mass functions of preformed and neoformed organs and index of dispersion (ID) for the estimated probability mass functions of neoformed organs for samples of tree shoots (see text for further details)

Preformation (X)
 Neoformation (Y)
Data set Position N1 N2 Mean s.d. CV Mean s.d. CV ID P(Y = 0) Data shift
Nal1 Trunk 176 37 6·24 1·26 0·20 3·70 1·79 0·48 0·87 0·068 –
Nal2 Trunk 20 21 13·00 0·95 0·07 10·55 5·54 0·52 2·91 0·045 4
Branch 20 20 12·70 2·41 0·19 1·60 2·51 1·57 3·94 0·330 2
Nd1 Trunk 1–4 53 24 13·48 4·22 0·31 8·50 4·02 0·47 1·90 0·000 –
Trunk 5–7 42 22 13·60 3·24 0·24 5·37 4·34 0·81 3·51 0·034 –
Trunk 8–9 47 26 12·67 3·07 0·24 5·24 4·89 0·93 4·55 0·067 –
Trunk 10 46 26 11·85 3·56 0·30 3·33 3·65 1·10 4·01 0·100 –
Branch 1 46 65 9·76 3·29 0·34 4·65 4·41 0·95 4·18 0·124 1
Branch 2 42 55 9·05 3·31 0·37 3·78 4·17 1·10 4·61 0·157 1
Branch 3 43 57 8·28 2·34 0·28 3·05 2·91 0·95 2·78 0·171 1
Branch 4 38 52 8·05 2·47 0·31 3·04 2·47 0·81 2·01 0·129 1
Branch 5 35 46 7·63 2·11 0·28 2·70 2·77 1·03 2·85 0·162 1
Nd2 Branch 1 101 217 13·66 3·33 0·24 5·29 3·59 0·68 2·44 0·048 –
Branch 2 105 216 13·87 2·90 0·21 3·32 2·59 0·78 2·02 0·104 –
Branch 3 103 217 13·84 2·73 0·20 2·50 2·07 0·83 1·72 0·113 –
Branch 4 95 218 13·81 2·73 0·20 1·75 1·14 0·65 0·73 0·148 –
Nan Branch 1 49 89 8·94 0·96 0·11 6·09 3·31 0·54 1·80 0·037 1
Branch 2 50 86 8·84 0·90 0·10 4·42 2·89 0·66 1·90 0·062 1
Branch 3 50 89 8·64 0·82 0·09 2·20 2·00 0·91 1·83 0·208 1
Branch 4 50 87 8·56 0·83 0·10 1·91 2·02 1·06 2·13 0·205 1
Branch 5 50 85 8·34 0·81 0·10 1·48 1·77 1·19 2·12 0·304 1
Np Trunk distal 47 71 19·96 1·84 0·09 7·35 4·95 0·67 3·33 0·059 4
Trunk proximal 43 47 14·91 3·01 0·20 6·19 3·06 0·49 1·51 0·057 4
JH1 Trunk 27 27 14·22 1·57 0·11 8·72 3·36 0·38 1·29 0·000 –
JH2 Trunk 55 29 16·98 1·53 0·09 12·30 4·64 0·38 1·75 0·000 –
Open in a new tab

The probability of a shoot consisting exclusively of preformed organs (i.e. neoformation, Y = 0) is indicated for each sample of each data set. Depending on the data set, Position refers to the position of the shoot on the tree (trunk or branch) and/or to the position of the shoot on its parent shoot counted from the parent shoot's distal end. N1 and N2 indicate, respectively, the number of disected buds of sample I or fully extended shoots of sample II of each data set. The data shift column indicates the number of scale units (organs) of shift applied to the total number of organs so as to account for the death of distal primordia.

Data set Nal1

Samples corresponded to the most distal trunk buds of 1-year-old shoots of 2-year-old seedlings of Nothofagus alpina (Poepp. et Endl.) Oerst. cultivated at the experimental nursery of the Instituto Nacional de Tecnología Agropecuaria (INTA) at Bariloche, Argentina (41 °04′S, 71 °10′W, 780 m altitude). These seedlings were growing under natural sunlight and were watered daily.

Data set Nal2

Data were collected concerning the composition of terminal buds and shoots of the trunk and main branches of 7- to 15-year-old saplings of N. alpina of a natural regeneration in a managed forest at Pucará, Parque Nacional Lanín, Argentina (41 °08′S, 71 °43′W, 1100 m altitude). These saplings derived from seeds and were growing under the thinned canopy of a mixed N. alpina–Nothofagus obliqua (Mirb.) Oerst. forest.

Data set Nd1

Data were collected concerning bud and shoot composition for the trunk (buds and shoots in positions 1–10 starting from the trunk's distal end) and the main branches (positions 1–5) of 10- to 15-year-old trees of Nothofagus dombeyi (Mirb.) Oerst. growing at Villa Mascardi, Argentina (41 °10′S, 71 °10′W and 850 m altitude; Puntieri et al., 2000). The selected trees correspond to the roadside regeneration cohort from seeds after the forest was cut down for road construction. In order to increase the numbers of buds or shoots for the estimation of distributions, buds or shoots of the trunk in different positions were pooled as follows: positions 1–4, 5–7, 8–9 and 10.

Data set Nd2

Data were collected from the four most distal buds and shoots of the main branches of 7- to 20-year-old N. dombeyi trees growing at Villa La Angostura, Argentina (41 °47′S, 71 °40′W and 770 m altitude; Puntieri et al., 2002a). These trees are growing at the margin of a road and derived from seeds after road construction.

Data set Nan

Data corresponded to the five most distal buds and shoots of the main branches of about 8- to 22-year-old Nothofagus antarctica (G. Forster) Oerst. trees growing at the Centro de Salmonicultura, Bariloche, Argentina (41 °10′S, 71 °25′W and 880 m altitude; Puntieri et al., 2002b). This population derived from stumps and represents the major woody cover of an area which was affected by an extensive fire.

Data set Np

Data were collected from the two most distal buds and shoots of main branches of 10- to 21-year-old trees of Nothofagus pumilio (Poepp. et Endl.) Krasser growing at Cerro Otto, Bariloche, Argentina (41 °09′S, 71 °10′W and 1350 m altitude; Souza et al., 2000). The sampled trees constitute the regeneration cohort among dispersed, older trees of N. pumilio.

Data set JH1

Data were collected concerning the composition of terminal buds and shoots of the trunk of 2-year-old hybrid walnut saplings freely growing in an open field plantation at Poët-Laval (44 °32′N, 5 °0′W, Drôme, France; Sabatier and Barthélémy, 2000).

Data set JH2

Data were collected concerning the composition of terminal buds and shoots of the trunk of 3-year-old hybrid walnut saplings freely growing in an open field plantation at Antagnac (44 °21′N, 0 °0′E, Lot et Garonne, France; Sabatier and Barthélémy, 2000). n = 29 for both samples.

Data analysis

The working model is of the form Z = X + Y where X represents the number of preformed organs and Y represents the number of neoformed organs. The aim was to estimate the distribution of the number of neoformed organs, PY, from two independent samples, one corresponding to the distribution of the total number of organs (in fully extended shoots of sample II), PZ, and the other to the distribution of the number of preformed organs, PX (in buds of sample I). If it is assumed that the random variables X and Y are independent, the distribution of the total number of organs is the convolution of two distributions (Feller, 1968): that of the number of preformed organs and that of the number of neoformed organs, expressed as:

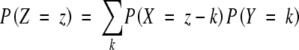graphic file with name M1.gif

with μZ = μX + μY and 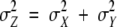Inline graphic (μ denotes the mean and σ the standard deviation of the corresponding random variable; the latter relationship is a consequence of the independence assumption).

This independence assumption is reasonable in cases where the dispersion of the number of preformed organs is small with respect to that of the number of extended organs, while it may be more questionable in other cases (for instance, if shoots with a higher number of preformed organs are assumed to produce a higher number of neoformed organs). The estimation problem is a deconvolution problem for discrete distributions. The deconvolution problem was extensively studied both in statistics and in signal processing; see Eggermont and LaRiccia (2001) and references therein. The deconvolution algorithm applied to the count data is summarized in the Appendix.

One output of the deconvolution method is the estimate of the probability P(Y = 0) of occurrence of shoots only composed of a preformed part. Because of the degree of incompleteness of the data, the individual probability masses py = P(Y = y) cannot be precisely estimated, while the estimates of the mean μY and the standard deviation σY (s.d.) and, consequently, of the coefficient of variation σY/μY (CV) are far more reliable (because of the strength of the convolution assumption). Hence, the estimates of P(Y = 0) should be interpreted with more caution than the estimates of μY and σY in Table 1. The deconvolution procedure is implemented in the AMAPmod software (Godin et al., 1997).

For each sample of each data set, the observed distribution for preformed organs and the estimated distribution for neoformed organs were described by means of the following descriptors: mean, s.d., skewness coefficient and CV. The index of dispersion (ID) defined as 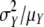Inline graphic (Johnson et al., 1993) was also computed for each neoformation distribution. 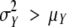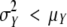This index, which equals 1 for a Poisson distribution, is widely used for counting distributions as a measure of data overdispersion (Inline graphic) or underdispersion (Inline graphic).

For data sets Nal2, Nd1 (branches), Nan and Np, some fully extended shoots had fewer organs than the buds with lowest preformation, which is explained by the spontaneous death of a number of preformed primordia, together with the apex of the shoot, before the extension of neoformed organs. Based on previous information concerning the number of preformed organs usually aborting with the apex of each species (Souza et al., 2000; Puntieri et al., 2002b; J. Puntieri, unpubl. res.), the distributions of the total number of organs for these data sets were shifted 1–4 units to the right (depending on the species and position concerned; Table 1).

RESULTS

For all data sets analysed, the mean number of preformed organs was higher than the mean number of neoformed organs. Within each data set, the s.d. tended to be either higher for neoformed organs than for preformed organs (Nal1, Nal2, Nan, trunk of Np, JH1 and JH2) or similar for both distributions (Nd1, Nd2, branch of Np; Table 1).

For data set Nal1, shoots had a low probability of consisting only of preformed organs. The mean number of preformed organs was similar for trunk and main branch shoots of Nal2, but the s.d. was higher for the latter (Table 1). For this data set, neoformation had a higher mean and s.d. for the trunk than for the branches. Trunk shoots had a much lower probability of not including neoformed organs than branch shoots. The mean number of preformed organs was about twice as high for saplings (Nal2) as for seedlings (Nal1) of N. alpina (Table 1).

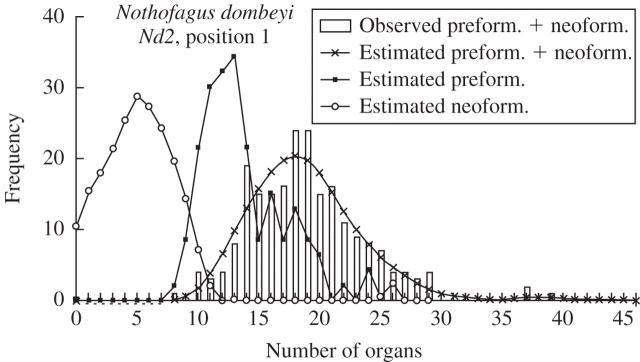
For position 1 of data set Nd2, the observed and estimated distributions for sample II as well as the estimated distributions for the numbers of preformed and neoformed organs are shown (Fig. 1). In this case, the mean number of preformed organs was higher than that of neoformed organs, whereas the s.d. was slightly higher for neoformed than preformed organs (Table 1). For these shoots, there was a low probability of shoots consisting exclusively of preformed organs.

Fig. 1.

Fig. 1.

Open in a new tab

Observed and estimated distributions of the numbers of preformed and preformed + neoformed organs and deconvolution-estimated distribution of the number of neoformed organs for distal branch shoots of Nothofagus dombeyi (Nd2 data set).

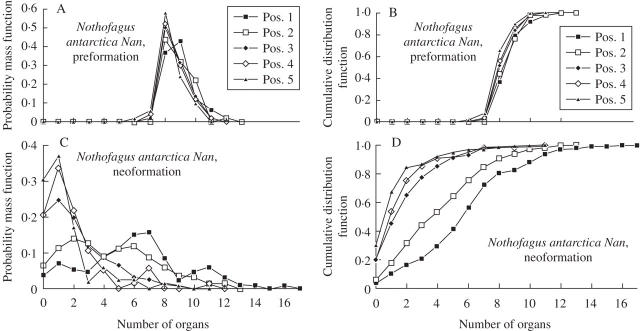
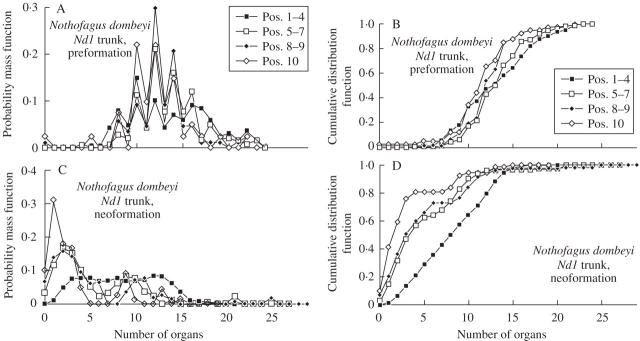
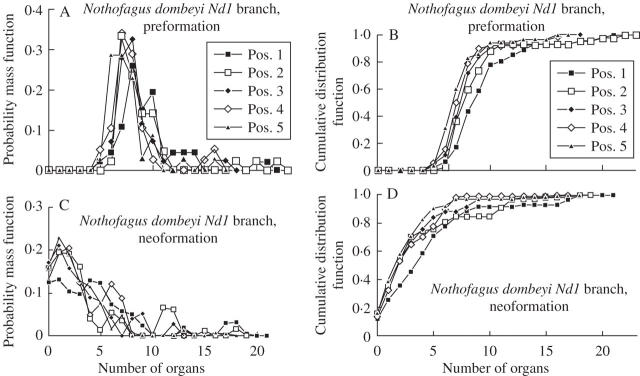
For data sets Nd1, Nd2 and Nan, the mean and s.d. of the number of preformed organs was similar for all positions on the same shoot type (i.e. trunk or branch; Table 1). The mean number of neoformed organs diminished from distal to proximal positions for all three data sets (Figs 2–5). The s.d. decreased in a similar way for Nd2, Nan and the branches of Nd1, but showed little variation for the trunk of Nd1 (Table 1). The CV of the number of neoformed organs was relatively constant (approx. 1) for all positions of trunk shoots and branch shoots of Nd1, except for the most distal trunk shoots (positions 1–4), for which it was lower. This coefficient also showed little variation among positions of Nd2. The CV of the number of neoformed organs increased from distal to proximal positions in Nan. The ID decreased from distal to proximal positions in branch shoots of Nd2. The ID was close to 2 for all positions of Nan. The probability of a shoot consisting exclusively of preformed organs increased as the position of the shoot approached the proximal end of its parent shoot (Table 1).

Fig. 5.

Fig. 5.

Open in a new tab

Preformation (A, B) and neoformation (C, D) of trunk shoots of Nothofagus antarctica (data set Nan) according to shoot position numbered from the distal node of the parent shoot. Estimated probability mass (left column) and cumulative distribution functions (right column) are shown.

Fig. 2.

Fig. 2.

Open in a new tab

Preformation (A, B) and neoformation (C, D) of trunk shoots of Nothofagus dombeyi (data set Nd1) according to shoot position numbered from the distal node of the parent shoot. Estimated probability mass (left column) and cumulative distribution functions (right column) are shown.

The probability mass functions of preformed organs for data sets Nd1, Nd2 and Nan were more bell-shaped and symmetrical than the corresponding probability mass functions for neoformed organs. In consonance, cumulative distribution functions had more sigmoid outlines for preformed than for neoformed organs. These differences were more notable as the shoot position approached the proximal end of a parent shoot (Figs 2–5).

For data set Np, the number of preformed organs had a higher mean and lower s.d. for the distal position compared with the proximal position (Table 1). Regarding neoformation, a higher mean and s.d. were found for the distal than for the proximal positions. The probability of a shoot consisting exclusively of preformed organs was low and similar for both positions (Table 1).

The mean numbers of preformed and neoformed organs were higher for data set JH2 than for JH1. In the case of preformed organs, little difference in s.d. was detected between both data sets. With regards to neoformation, the s.d. was higher for JH2 than for JH1, which rendered the CV similar between data sets (Table 1). The probability of shoots consisting exclusively of preformed organs was zero (Table 1).

DISCUSSION

Preformation and neoformation as components of shoot size

One of the outcomes of the present study is that, for the species under survey, preformation is more relevant than neoformation in the mean number of organs developed by shoots at a specific position within a tree's architecture. The number of preformed organs depends both on the individual tree and on the position of the bud on the tree (Figs 3 and 4). The present and several previous contributions indicate that the distribution of the number of preformed organs per bud, although basically unimodal, varies depending on the position of the bud on the tree as well as on tree age and growth conditions (Gill, 1971; Remphrey and Powell, 1984; Remphrey and Davidson, 1994; Puntieri et al., 2000, 2002a,b; Souza et al., 2000; Costes, 2003; Gordon et al., 2006). According to these results, preformation is the first determinant of axis differentiation and tree architecture. In contrast, other studies remarked on the relative constancy of the mean number of primordia per vegetative bud in each tree species (Ohlert, 1837 and Assaf, 1965, quoted in Rivals, 1965; Thorp et al., 1994). Two explanations may be proposed for this discrepancy. One of them is the criteria of tree and bud selection: buds in similar architectural positions and collected from trees at a similar growth stage and under similar conditions may have similar numbers of primordia. This could be the case for the studies on orchard trees cited above. The second explanation could be the number of axis types characterizing the architecture of a particular tree species: tree species with a low number of axis types could have less variation in terms of preformation. This justification may only be partially valid, since some of the species presented by Assaf (in Rivals, 1965) as exhibiting a constant mean number of primordia in buds, e.g. Carya olivaeformis, Castanea sativa and Juglans regia var. parisienne, resemble architecturally those included in the present study.

Fig. 3.

Fig. 3.

Open in a new tab

Preformation (A, B) and neoformation (C, D) of branch shoots of Nothofagus dombeyi (data set Nd1) according to shoot position numbered from the distal node of the parent shoot. Estimated probability mass (left column) and cumulative distribution functions (right column) are shown.

Fig. 4.

Fig. 4.

Open in a new tab

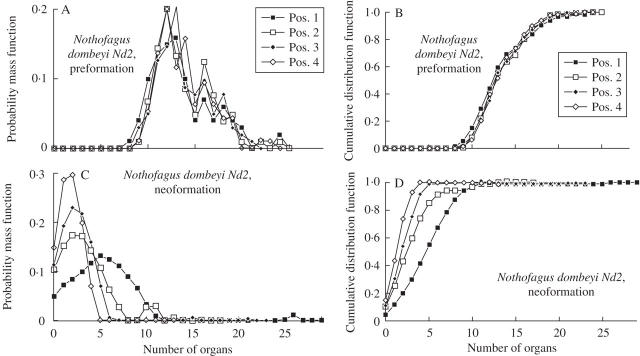
Preformation (A, B) and neoformation (C, D) of trunk shoots of Nothofagus dombeyi (data set Nd2) according to shoot position numbered from the distal node of the parent shoot. Estimated probability mass (left column) and cumulative distribution functions (right column) are shown.

For the species studied here, neoformation contributed less than preformation to the total number of organs of shoots, with the exception of trunk shoots of young N. alpina (data set Nal2) and Juglans (JH1 and JH2) trees for which almost as many neoformed organs as preformed organs developed. For long shoots of Prunus armeniaca (Costes, 1993), Actinidia spp. (Snowball, 1997) and Prunus persica (Gordon et al., 2006), neoformation has been shown to contribute to the total number of nodes per shoot to a larger extent than preformation. The results indicate that, although neoformation development was a likely event in all data sets analysed here, it may not occur in shoots of most data sets concerning Nothofagus species. In general terms, the probability of a shoot including only preformed organs is lower for distal than for proximal shoots of the same trees (data sets Nd1, Nd2 and Na; Table 1) and lower for the trunk than for the branches of the same tree (data set Nd1). At least under some conditions, the most distal shoots derived from the trunk of N. dombeyi trees (data set Nd1) have a very high probability of including preformed and neoformed organs (Table 1). This seems to be the case also for Juglans hybrids (data sets JH1 and JH2).

The differences in the number of neoformed organs among shoots in different positions on the same parent shoot are larger than those in the number of preformed organs. The more distal a shoot, the higher the number of neoformed organs it would be able to develop. This indicates that proximal-to-distal trends of increasing size among shoots derived from a common parent shoot would be linked to variations in both neoformation and preformation.

Distributions of preformed and neoformed organs

The present as well as previous information on several tree species support the view that the distribution of the number of preformed organs in a bud follows approximately symmetric frequency distributions with low dispersion around a mean value (e.g. Rivals, 1965; Champagnat, 1983; Puntieri et al., 2000, 2002a; Sabatier and Barthélémy, 2000; Souza et al., 2000; Seleznyova et al., 2002). Agreement among studies in this respect is more general whenever bud selection observes architectural criteria (e.g. position on the tree, tree age and developmental stage). On the contrary, distributions of the number of neoformed organs deviated from symmetric distributions for all data sets included in the present study.

Preformation and neoformation distributions for each data set and shoot position differed not only in their mean values, as discussed above, but also regarding their dispersion as measured by the s.d. The s.d. of the number of neoformed organs estimated through deconvolution was higher than that of the number of preformed organs, which may be partly explained by alluding to the time of differentiation of preformed and neoformed organs. All preformed organs of a bud would be initiated in a single event of cell differentiation from a shoot's apical meristem at the end of the period of shoot extension (Steeves and Sussex, 1989; Puntieri et al., 2002a). After bud-break, which tends to occur more or less simultaneously within a population (Kozlowski, 1971; Puntieri et al., 1998, 2000; Sabatier et al., 1998; Sabatier and Barthélémy, 1999; Stecconi et al., 2000), all preformed organs complete their development as shoots extend. The simultaneous extension of these organs corresponds to the spring peak in shoot growth (Kozlowski, 1971; Puntieri et al., 1998, 2002b). This implies that both initiation and extension of preformed organs take place, for each population, within narrow periods of time. After preformation extension, the shoot's apex may either cease growth (by aborting or entering a dormancy period, sensu Borchert, 1991) or produce neoformed organs. Both initiation and extension of neoformed organs would take place in a stepwise fashion during longer periods of time than those of preformed organs (Critchfield, 1960; Kozlowski, 1971). For N. dombeyi, neoformed organs start differentiating and extending in late spring and stop extending in mid- to late summer (depending on shoot position); from then until early autumn, primordia accumulate in the terminal bud (Puntieri et al., 2002a). The hypothesis could be proposed that the development of each neoformed organ would depend on the local conditions (both internal and external) affecting the shoot concerned, such as architectural position (including topology and geometry), radiation incidence, and water and nutrient supply to the shoot, rather than those affecting the whole tree, such as daylength and water availability in the soil. Whereas shoots in some architectural positions and facing favourable local conditions (e.g. with high incident radiation and nutrient supply) would continue adding neoformed organs to their structure after preformation extension, those in other positions and/or under less favourable conditions would stop growing. This would partly explain the large differences in growth cessation time among shoots in the same architectural positions on similar plants (Puntieri et al., 1998; Stecconi et al., 2000). By the time all shoots have entered dormancy, the number of neoformed organs per shoot would differ notably among shoots even within the same architectural position of similar trees. Since terminal buds of the studied species always include at least some leaf primordia, the differentiation of distal primordia would proceed further on than their extension. This uncoupling of differentiation and extension indicates the end of the neoformation and the beginning of next year's preformation.

Gradients of decreasing numbers of neoformed organs from distal to proximal branches on the same parent shoot (such as those shown here for data sets Nd1 and Nd2) have been explained in terms of endogenously determined gradients of meristem functioning (Barthélémy et al., 1997; Barthélémy, 2003). The variations in the number of neoformed organs within each position observed in the present study could be interpreted as resulting from different shoots being subject to different local conditions (as defined above; see Davidson and Remphrey, 1994; Souza et al., 2000) and would account for shoot plasticity as observed in other species (Gordon et al., 2006). The probability of development of exclusively preformed shoots indicates that the potentiality of a shoot to develop neoformed organs may not necessarily be expressed. This may be the case on most occasions for Juglans spp. and hybrids, where preformation seems to be the rule whereas neoformation occurs in particularly favourable conditions (e.g. cultivated trees such as those studied here and grafted scions in irrigated conditions; Sabatier et al., 1999).

Deconvolution as a method of neoformation analysis and characterization

The deconvolution method applied here allowed the estimation of the distribution of the number of neoformed organs per shoot from two observed distributions: that of the number of preformed organs in buds and that of the number of organs of fully extended shoots derived from equivalent buds. In the present study, this was achieved by defining data sets with two architectural criteria: the type of axis, often associated with functional roles; and the position of buds and shoots along their parent shoot, which allows size gradients within each axis to be dealt with (Barthélémy et al., 1997; Puntieri et al., 2003). Data set Nd1 is a good example of a case in which both preformation and neoformation differ in mean value between two axis types (trunk and main branches). Data sets Nd1, Nd2 and Nan exemplify within-axis gradients, especially in terms of the number of neoformed organs. After taking these sources of variation into account, the deconvolution technique proved a useful tool for the description of preformation and neoformation, even for data sets which, a priori, might be considered insufficient (e.g. data sets JH1 and JH2).

CONCLUSIONS

For each axis type of a tree species, there seems to be little variation in the number of leaf primordia of a bud and, thus, in the number of preformed leaves of the shoot originating from this bud. As a result, an accurate estimation of the distribution of these organs results from bud dissection following architectural criteria. According to the deconvolution method applied, distributions of neoformed organs would be more variable and less symmetric both within and between positions on trees of the same species. This indicates that neoformation responses within a specific position of a tree would be involved in the plastic response of trees to factors acting locally at the time of shoot extension. This hypothesis could be tested through the assessment of neoformation in shoots subject to known and controlled conditions.

Acknowledgments

We thank M. S. Souza, M. Stecconi, J. Grosfeld and C. Brion for their contributions in the sampling and analyses of Nothofagus buds and shoots, and the Administración de Parques Nacionales and the Instituto Nacional de Tecnología Agropecuaria (Argentina) for providing the permits and facilities to study Nothofagus populations.

APPENDIX

Deconvolution algorithm

Recall that the preformation distribution PX is supposed to be known. One may compute an estimate of the neoformation distribution PY = {py} by the following algorithm essentially due to Shepp and Vardi (1982). Let {py(0)} be an initial guess for the neoformation distribution and let θ(k) denote the current value of the parameters of the neoformation distribution at iteration k. The iteration of the non-parametric deconvolution algorithm is

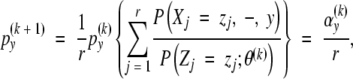graphic file with name M6.gif (A1)

where r is the sample size and αy(k) is the expected multiplicity of y neoformed organs given the total number of organs and the current parameters at iteration k. This is an example of the EM algorithm (Dempster et al., 1977; McLachlan and Krishnan, 1997) applied to solve a non-parametric maximum likelihood estimation problem. Unfortunately, direct application of the above-defined algorithm generally shows that fewer and fewer smooth distributions are obtained as the iteration progresses. The standard solution then consists of stating the deconvolution problem as a maximum penalized likelihood estimation problem; see Eggermont and LaRiccia (2001) and references therein. It should be noted that the count data context is far more simple that the general deconvolution problem (also referred to as the contamination problem) since, in this case, the distribution of interest is a discrete distribution defined on a finite support and not a continuous distribution.

For the regularization of the estimated neoformation distribution, a penalty term is thus incorporated in the likelihood. In the framework of the EM algorithm, the E-step is unchanged but for the M-step, the maximization of

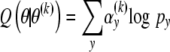graphic file with name M7.gif

is replaced by the maximization of

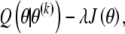graphic file with name M8.gif (A2)

where λ is a tuning constant that determines the relative importance of Q(θ|θ(k)) and J(θ), and J(θ) is a roughness penalty. In the present case, J(θ) will be the sum of squared second differences:

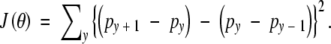graphic file with name M9.gif

Green (1990) demonstrated the computational economy and accelerated convergence yielded by employing the one-step-late (OSL) algorithm. The OSL algorithm solves

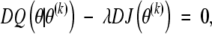graphic file with name M10.gif (A3)

where D denotes the derivative operator.

The only difference between equation (A3) and equating the derivatives of expression (A2) to 0 is that in equation (A3), the derivatives of the penalty are evaluated at the current value θ(k). Both expression (A2) and equation (A3) have the same fixed point so the OSL algorithm converges to a maximum penalized likelihood estimate.

Let

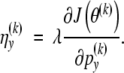graphic file with name M11.gif

The M-step (A1) is replaced by

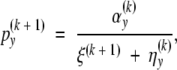graphic file with name M12.gif

where ξ(k+1) is the unique solution for ξ in the equation

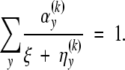graphic file with name M13.gif

LITERATURE CITED

  1. Barthélémy D. 2003. Botanical background for plant architecture analysis and modelling. In: Hu BG, Jaeger M, eds. International Symposium on Plant growth Modelling, Simulation, Visualization and their Applications. Beijing, China: Tsinghua University Press & Springer, 1–20.
  2. Barthélémy D, Caraglio Y, Costes E. 1997. Architecture, gradients morphogénétiques et age physiologique chez les végétaux. In: Bouchon J, de Reffye P, Barthélémy D, eds. Modélisation et simulation de l'architecture des végétaux. Paris, France: Institut National de la Recherche Agronomique, Science Update, 89–136.
  3. Bell A. 1991. Plant form, an illustrated guide to flowering plant morphology. Oxford, UK: Oxford University Press.
  4. Borchert R. 1969. Unusual shoot growth pattern in a tropical tree, Oreopanax (Araliaceae). American Journal of Botany 56: 1033–1041. [Google Scholar]
  5. Borchert R. 1991. Growth periodicity and dormancy. In: Raghavendra AS, ed. Physiology of trees. New York, USA: John Wiley & Sons, 221–239.
  6. Caraglio Y, Barthélémy D. 1997. Revue critique des termes relatifs à la croissance et à la ramification des tiges des végétaux vasculaires. In: Bouchon J, de Reffye P, Barthélémy D, eds. Modélisation et simulation de l'architecture des végétaux. Paris, France: Institut National de la Recherche Agronomique, Science Update, 11–87.
  7. Carles MMJ, Assaf R, Magny J, Rivals P. 1964. Différences physiologiques dans les rameaux entre la partie néoformée et la partie préformée dans le bourgeon. Comptes Rendus de l'Academie des Sciences de Paris 259: 3348–3351. [Google Scholar]
  8. Champagnat P. 1983. Quelques particularités biologiques des arbres. Bulletin de la Societé de Botanique Francaise 130: 11–20. [Google Scholar]
  9. Costes E. 1993. Architecture aérienne de l'abricotier en développement libre. Acta Botanica Gallica 140: 249–261. [Google Scholar]
  10. Costes E. 2003. Winter bud content according to position in 3-year-old branching systems of ‘granny Smith’ apple. Annals of Botany 92: 581–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Critchfield WD. 1960. Leaf dimorphism in Populus trichocarpa. American Journal of Botany 47: 699–711. [Google Scholar]
  12. Davidson CG, Remphrey WR. 1994. Shoot neoformation in clones of Fraxinus pennsylvanica in relation to genotype, site and prunning treatments. Trees 8: 205–212. [Google Scholar]
  13. Dempster AP, Laird NM, Rubin DB. 1977. Maximum likelihood from incomplete data via the EM algorithm (with discussion). Journal of the Royal Statistical Society Series B, 39: 1–38. [Google Scholar]
  14. Eggermont PPB, LaRiccia VN. 2001. Maximum penalized likelihood estimation, volume 1: density estimation. New York, USA: Springer.
  15. Feller W. 1968. An introduction to probability theory and its applications, Vol. 1, 3rd edn. New York, USA: Wiley.
  16. Gill AM. 1971. The formation, growth and fate of buds of Fraxinus americana L. in Central Massachusetts. Harvard Forestry Papers 20: 1–16. [Google Scholar]
  17. Godin C, Guédon Y, Costes E, Caraglio Y. 1997. Measuring and analysing plants with the AMAPmod software. In: Michalewicz MT, ed. Plants to ecosystems—advances in computational life sciences, Vol. 1. Victoria, Australia: CSIRO Publishing, 53–84.
  18. Gordon D, Damiano C, DeJong TM. 2006. Preformation in vegetative buds of Prunus persica: factors influencing number of leaf primordia in overwintering buds. Tree Physiology 26: 537–544. [DOI] [PubMed] [Google Scholar]
  19. Green PJ. 1990. On the use of the EM algorithm for penalized likelihood estimation. Journal of the Royal Statistical Society, Series B 52: 443–452. [Google Scholar]
  20. Hallé F, Martin R. 1968. Etude de la croissance rythmique chez l'Hévéa (Hevea brasiliensis Müll. Arg., Euphorbiacées—Crotonoïdées). Adansonia 8: 475–504. [Google Scholar]
  21. Hallé F, Oldeman RAA, Tomlinson P. 1978. Tropical trees and forests. An architectural analysis. Berlin, Germany: Springer-Verlag.
  22. Johnson NL, Kotz S, Kemp AW. 1993. Univariate discrete distributions, 2nd edn. New York, USA: Wiley.
  23. Koike T. 1990. Autumn coloring, photosynthetic performance and leaf development of deciduous broad-leaves trees in relation to forest succession. Tree Physiology 7: 21–32. [DOI] [PubMed] [Google Scholar]
  24. Kozlowski TT. 1971. Growth and development of trees. Vol. I. Seed germination, ontogeny and shoot growth. New York, USA: Academic Press.
  25. McLachlan GJ, Krishnan T. 1997. The EM algorithm and extensions. New York, USA: Wiley.
  26. Nicolini E. 1998. Architecture et gradients morphogénétiques chez de jeunes hêtres (Fagus sylvatica L. Fagaceae) en milieu forestier. Canadian Journal of Botany 76: 1232–1244. [Google Scholar]
  27. Nitta I, Ohsawa M. 1997. Leaf dynamics and shoot phenology of eleven warm-temperate evergreen broad-leaved trees near their northern limit in central Japan. Plant Ecology 130: 71–88. [Google Scholar]
  28. Puntieri JG, Barthélémy D, Martinez P, Raffaele E, Brion C. 1998. Annual shoot growth and branching patterns in Nothofagus dombeyi (Fagaceae). Canadian Journal of Botany 76: 673–685. [Google Scholar]
  29. Puntieri JG, Souza MS, Barthélémy D, Brion C, Núñez M, Mazzini C. 2000. Preformation, neoformation, and shoot structure in Nothofagus dombeyi (Nothofagaceae). Canadian Journal of Botany 78: 1044–1054. [Google Scholar]
  30. Puntieri JG, Barthélémy D, Mazzini C, Brion C. 2002a. Periods of organogenesis in shoots of Nothofagus dombeyi (Mirb.) Oersted (Nothofagaceae). Annals of Botany 89: 115–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Puntieri JG, Stecconi M, Barthélémy D. 2002b. Preformation and neoformation in shoots of Nothofagus antarctica (G. Forster) Oerst. (Nothofagaceae) shrubs from northern Patagonia. Annals of Botany 89: 665–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Puntieri JG, Souza MS, Brion C, Mazzini C, Barthélémy D. 2003. Axis differentiation in two South American Nothofagus species (Nothofagaceae). Annals of Botany 92: 589–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. de Reffye P, Elguero E, Costes E. 1991. Growth units construction in trees: a stochastic approach. Acta Biotheoretica 39: 325–342. [Google Scholar]
  34. Remphrey WR, Davidson CG. 1994. Shoot preformation in clones of Fraxinus pennsylvanica in relation to site and year of bud formation. Trees 8: 126–131. [Google Scholar]
  35. Remphrey WR, Powell GR. 1984. Crown architecture of Larix laricina saplings: shoot preformation and neoformation and relationship to shoot vigour. Canadian Journal of Botany 62: 2181–2192. [Google Scholar]
  36. Rivals P. 1965. Essai sur la croissance des arbres et sur leurs systèmes de floraison (application aux espéces fruitières). Journal d'Agriculture Tropicale et de Botanique Appliquée 12: 655–686. [Google Scholar]
  37. Roloff A. 1987. Morphologie der Kronenentwicklung von Fagus sylvatica L. (Rotbuche) unter besonderer Berücksichtigung neuartiger Veränderungen. I. Morphogenetischer Zyklus, Anomalien infolge Prolepsis und Blattfall. Flora 179: 355–378. [Google Scholar]
  38. Sabatier S, Barthélémy D. 1999. Growth dynamics and morphology of annual shoots, according to their architectural position, in young Cedrus atlantica (Endl.) Manetti ex Carrière (Pinaceae). Annals of Botany 84: 387–392. [Google Scholar]
  39. Sabatier S, Barthélémy D. 2000. Bud content in relation to shoot morphology and position on vegetative shoots of Juglans regia L. (Juglandaceae). Annals of Botany 87: 117–123. [Google Scholar]
  40. Sabatier S, Barthélémy D, Ducousso I., Germain E. 1995. Nature de la pousse annuelle chez le Noyer commun, Juglans regia L. var Lara (Juglandaceae): préformation hivernale et printanière. In: Bouchon J, ed. Architecture des arbres fruitiers et forestiers. Paris, France: INRA Editions, Les colloques, 109–124.
  41. Sabatier S, Barthélémy D, Ducousso I, Germain E. 1998. Modalités d'allongement et morphologie des pousses annuelles chez le noyer commun, Juglans regia L. ‘Lara’ (Juglandaceae). Canadian Journal of Botany 76: 1253–1264. [Google Scholar]
  42. Sabatier S, Barthélémy D, Ducousso I, Germain E. 1999. Allongement et morphologie de pousses annuelles issues de greffe chez le Noyer commun, Juglans regia L. cv. Lara (Juglandaceae). Canadian Journal of Botany 77: 1595–1603. [Google Scholar]
  43. Seleznyova AN, Greer DH. 2001. Effects of leaf position on leaf area expansion of kiwifruit (Actinidia deliciosa) shoots: development of a modelling framework. Annals of Botany 88: 605–615. [Google Scholar]
  44. Seleznyova AN, Thorp TG, Bartnett AM, Costes E. 2002. Quantitative analysis of shoot development and branching patterns in Actinidia. Annals of Botany 89: 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Shepp LA, Vardi Y. 1982. Maximum likelihood reconstruction in emission tomography. IEEE Transactions on Medical Imaging 1: 113–122. [DOI] [PubMed] [Google Scholar]
  46. Snowball AM. 1997. Seasonal cycle of shoot development in selected Actinidia species. New Zealand Journal of Crop and Horticultural Science 25: 221–231. [Google Scholar]
  47. Souza MS, Puntieri JG, Barthélémy D, Brion C. 2000. Bud content and its relation to shoot size and structure in Nothofagus pumilio (Poepp. et Endl.) Krasser (Nothofagaceae). Annals of Botany 85: 547–555. [Google Scholar]
  48. Stecconi M, Puntieri J, Barthélémy D. 2000. Annual shoot-growth in Nothofagus antarctica (G. Forster) Oersted (Fagaceae) from northern Patagonia. Trees 14: 289–296. [Google Scholar]
  49. Steeves TA, Sussex IM. 1989. Patterns in plant development, 2nd edn. Cambridge, UK: Cambridge University Press.
  50. Thorp TG, Aspinall D, Sedgley M. 1994. Preformation of node number in vegetative and reproductive proleptic shoot modules of Persea (Lauraceae). Annals of Botany 73: 13–22. [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES