Comparing Pairwise and Simultaneous Joint Registrations of Decorrelating Interval Exams using Entropic Graphs

Abstract

The interest in registering a set of images has quickly risen in the field of medical image analysis. Mutual information (MI) based methods are well-established for pairwise registration but their extension to higher dimensions (multiple images) has encountered practical implementation difficulties. We extend the use of alpha mutual information (αMI) as the similarity measure to simultaneously register multiple images. αMI of a set of images can be directly estimated using entropic graphs spanning feature vectors extracted from the images, which is demonstrated to be practically feasible for joint registration.

In this paper we are specifically interested in monitoring malignant tumor changes using simultaneous registration of multiple interval MR or CT scans. Tumor scans are typically a decorrelating sequence due to the cycles of heterogeneous cell death and growth. The accuracy of joint and pairwise registration using entropic graph methods is evaluated by registering several sets of interval exams. We show that for the parameters we investigated simultaneous joint registration method yields lower average registration errors compared to pairwise. Different degrees of decorrelation in the serial scans are studied and registration performance suggests that an appropriate scanning interval can be determined for efficiently monitoring lesion changes. Different levels of observation noise are added to the image sequences and the experimental results show that entropic graph based methods are robust and can be used reliably for multiple image registration.

1 Introduction

Most malignant tumors are rapidly changing structures that threaten the life of the patient. Interval MR or CT scanning is often performed to follow these changes. Quantification of such changes is important especially for early detection of response to therapy, or even more importantly as a means of validating mechanistic hypotheses regarding therapeutic action and cellular response.

While segmentation of the interval exams is one method of quantifying response to therapy, since segmentation can be quite noisy, it is quite possible that such an approach is not capable of reliably detecting small changes. Another approach to quantifying tumor change is nonlinear registration of the serial interval exams followed by regional integration of the resulting Jacobian determinants [1]. Here the boundaries of the regional analysis need to be identified in only one of the interval exams as the registration will propagate those boundaries in a consistent manner to the remainder of the registered interval exams. Over the duration of interval imaging the tumor may morph significantly in a background of acquisition system related noise. For example, growing tumors generate heterogeneous regions of increased hypoxia and cellular density, as well as apoptosis and necrosis; likewise cells responding regionally to therapy die and necrose as well. Over the total span of interval imaging the tumor typically decorrelates with its initial appearance even with perfect registration due to cycles of heterogeneous cell death and growth.

There are typically two approaches to detecting these geometric deformations in serial interval exams – pairwise and joint registration. The pairwise registration method is to repeatedly perform pairwise registration over all the images in the set and settle for a transformation of all the images with a fixed reference frame based on a series of compositions. But this would not guarantee jointly optimal or unique results. On the other hand, joint registration achieves a consistent correspondence of pixels across all images and thus aligns them to a common spatial frame by optimizing an objective function that is calculated using all the images in the group. Recently several papers have discussed the importance of registering multiple images simultaneously and have shown improved registration accuracy compared to pairwise methods.

Bhatia et al. [2] binned all pairs of intensities, comprising the voxel intensity in the reference and the corresponding intensity in each image into a single histogram and computed normalized mutual information (NMI). This was applied to an atlas construction problem where the maximization of NMI was subjected to the condition that the total deformation onto the common spatial frame summed to zero. A minimum description length based framework was proposed in [3]. Groupwise registration was achieved by minimizing the length of the encoded messages consisting of the reference image, the reference frame, the transformation model and its parameters, and discrepancy images. Learned-Miller [4] discussed joint registration in the context of bias removal where entropy was computed at the same voxel across the image stack and summed over all voxels. Its applicability to small image sets (too few samples) may be limited by noisy entropy estimates.

All the above methods targeted same modality applications. A method of group alignment minimizing the summation of pairwise dissimilarity while improving inverse consistency and transitivity was discussed in [5]. Studholme and Cardenas [6] estimated the joint density function of the image set and used a measure of self information to drive alignment. Zhang and Rangarajan [7] reported a study of several higher dimensional information theoretic measures for joint registration. In the last two methods joint densities are estimated and optimally stored. These methods are directly applicable to multi-modality registration.

Maximizing mutual information between images is one of the most broadly used methods for pairwise image registration [8,9,10]. Its primary advantage is the ability to accomplish reliable and accurate alignment between the image pairs although their intensities may be non-linearly related. Even when we monitor tumor changes using the same imaging modality, the intensities of corresponding locations may not be linearly related due to tumor cell growth or death. Therefore, mutual information based registration is the one of choice for our application. In this approach, probability densities are usually estimated using histogram or kernel techniques, which are well established for low-dimensional problems. While using histograms to compute mutual information for pairwise registration has been vastly studied and validated in registration literature, its extension to higher dimensions has encountered computational difficulties due to the sparse nature of the multi-dimensional histograms.

Neemuchwala et al. used alpha mutual information (αMI) – an extension of mutual information – as the similarity measure for image registration [11]. The introduction of entropic graphs enables the practical computation of the similarity measure in high dimensions. In this paper we extend the utilization of αMI to simultaneous registration of multiple images. With this unified similarity measure calculated based on all the images in the group we can maximize the joint correspondence through the optimization of a single objective function that measures the statistical dependency of all images simultaneously. Since this similarity measure is a mutual information it can be used for multi-modality registration. The alpha mutual information of a set of images is calculated through entropic graphs spanning the feature vectors extracted from the images. It eliminates the need to estimate joint densities of the feature vectors, which could become very computationally intensive for multiple image cases. Using k-nearest neighbor graphs we have demonstrated its computational feasibility by registering several images simultaneously.

While our effort is focused on following tumor shape change, clearly there are many other sources of serially decorrelating image sequences for which the following techniques and comparisons are applicable. In this paper we examine the relative registration accuracy of both pairwise and joint registration applied to 2D decorrelated image sequences; the 2D results can be generalized directly to 3D. Additionally entropic estimation of mutual information was implemented by extraction of wavelet feature vectors followed by entropic graph estimation of αMI [12]. Both joint and pairwise registration has been implemented and tested on the same data sets using the same initialization and geometric deformation model for performance comparison.

2 Methods

2.1 Alpha Mutual Information and Entropic Graphs

The alpha divergence between two densities f₁ and f₂ of fractional order α ∈ (0, 1) is given by [13,14]

$$D_{\alpha }(f_1||f_2)=\frac{1}{\alpha -1}log\int f_1^{\alpha }(z)f_2^{(1-\alpha )}(z)dz.$$ (1)

D_α(f₁||f₂) is a measure of dissimilarity between f₁ and f₂ and it converges to the Kullback-Liebler divergence $\int f_1(z)log\frac{f_1(z)}{f_2(z)}dz$ as α → 1[13].

Let Z₁ and Z₂ be two random variables with marginal densities f₁(z₁) and f₂(z₂) and joint density f_1,2(z₁, z₂). Similar to Shannon MI, the alpha mutual information between Z₁ and Z₂ is defined as the divergence between their joint density and the product of their marginal densities,

$$\begin{array}{l}\alpha MI(Z_1,Z_2)=D_{\alpha }(f_{1,2}(z_1,z_2)||f_1(z_1)f_2(z_2))\\ =\frac{1}{\alpha -1}log\iint f_{1,2}^{\alpha }(z_1,z_2){[f_1(z_1)f_2(z_2)]}^{1-\alpha }{dz}_1{dz}_2.\end{array}$$ (2)

If Z₁ and Z₂ are independent, we have f_1,2(z₁, z₂) = f₁(z₁)f₂(z₂) and thus αMI = 0, which means that the random variables do not provide any information about each other and thus agrees with their independence assumption. A limiting case of αMI when αapproaches 1 is Shannon MI given by

$$MI(Z_1,Z_2)=\iint f_{1,2}(z_1,z_2)log\frac{f_{1,2}(z_1,z_2)}{f_1(z_1)f_2(z_2)}{dz}_1{dz}_2.$$ (3)

The αMI among multiple random variables Z₁, Z₂, ···, Z_M is a generalization of (2)

$$\begin{array}{l}\alpha MI(Z_1,Z_2,\cdots ,Z_M)\\ =\frac{1}{\alpha -1}log\int \cdots \int f_{1,2,\cdots ,M}^{\alpha }(z_1,z_2,\cdots ,z_M)\\ ·{[f_1(z_1)f_2(z_2)\cdots f_M(z_M)]}^{1-\alpha }{dz}_1{dz}_2\cdots {dz}_M\end{array}$$ (4)

The computational advantage of αMI relies on its direct estimation using entropic graphs (see [12] for details). Examples of entropic graphs are minimal spanning trees, Steiner trees, traveling salesman problems, k-nearest neighbor graphs, etc. By circumventing the intermediate estimation of the marginal and joint densities, entropic graph approaches to estimating αMI are suitable in multiple image registration.

2.2 Alpha Mutual Information as Similarity Measure for Image Registration

Since alpha mutual information is capable of capturing the information content across the whole set of images and it can be directly estimated using entropic graphs, we choose it as the similarity measure in simultaneous registration of multiple images.

The basic framework for entropic graph image registration is as follows. Given multiple images I₁, I₂, ···, I_M, let 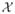represent the common coordinate space and x ∈ 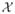is a spatial coordinate on which an image pixel is defined. To emphasize image dependence on the geometric space, we denote the images with explicit coordinates as I₁(x), I₂(x), ···, I_M (x). For a geometric transformation set T = {T₁, T₂, ···, T_M}∈ 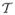, the transformed images after interpolation are I₁(T₁(x)), I₂(T₂(x)), ···, I_M (T_M (x)), respectively. Notice that we have applied a transformation for each image which is not always required. If a certain image is selected as the reference, the transformation posed on it will be identity. We specify each transformation to show that if a common spatial frame other than any of the images is chosen as the reference, each image can be transformed to that common coordinate space. In such a framework, simultaneous multiple image registration can be solved by finding the optimal transformation set T̂ ∈ 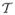such that the alpha mutual information is maximized:

$$\widehat{T}=arg\underset{T\in \mathcal{T}}{max}\alpha MI(I_1(T_1(x)),I_2(T_2(x)),\cdots ,I_M(T_M(x)))$$ (5)

2.3 Feature Extraction

The αMI between a set of images is estimated using the entropic graphs spanning the feature vectors extracted from these images. Examples of feature vectors include: the intensity and spatial location of representative samples; the position and orientation of a randomly chosen edge; a vector of samples in a textured region; or the output vector of a spatial prediction filter. The choice of feature vectors is typically application dependent. The desirable feature vectors should be capable of thoroughly representing the images while keeping the number of feature vectors small since the construction of entropic graphs becomes more computationally expensive with the increase of the number of vectors.

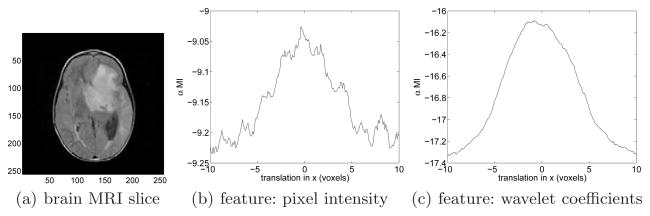
To study the effect of different types of feature vectors on the estimation of αMI, we examine the estimated αMI as a function of transformation parameters. An axial MR T1 weighted slice (shown in Fig. 1(a)) is selected as the reference image and it is affine transformed to generate the floating image. We limit the geometric transformation to affine only since here our objective is to get a basic idea of the profile of this similarity measure. αMI between the reference and floating images is estimated using two types of features: (a) pixel intensity scalar and (b) concatenated wavelet coefficient vector.

Fig. 1.

Profiles of αMI calculated based on different feature vectors: (a) An axial MR T1 weighted slice as the reference image; (b) intensity value of each pixel as the feature vector (scalar in this specific case); (c) concatenated wavelet coefficients except the high frequency component as the feature vector.

Intensity value of a representative pixel is a straightforward choice for feature vector. In this case, the feature vector is in fact a scalar. In Fig. 1(b), αMI values are plotted with respect to the translation in the horizontal direction. The general trend of estimated αMI is as expected, i.e., peak at the center and tapering off from the center, but it suffers many local extrema due to high frequency noise in the MRI scan.

An immediate solution to this noisy objective function is to remove high frequency noise before estimating αMI. Over the past several years wavelet transforms have gained widespread acceptance in signal processing and image compression in particular with the establishment of the JPEG2000 standard [15]. They are capable of well representing an image using relatively small number of wavelet coefficients. We have taken advantage of the efficiency of wavelet transforms and used concatenated wavelet coefficients as feature vectors. The Daubechies wavelet transform with 4 coefficients is applied to the images and all coefficients except the high-frequency components are used to form the feature vector. Fig. 1(c) illustrates the objective function profile using the wavelet feature vectors. Note that the αMI curve is much smoother than its pixel intensity counterpart (Fig. 1(b)). Although calculating wavelet coefficients introduces some computational overhead, the much less noisy objective function not only leads to faster convergence, but is also less likely for the optimizer to get trapped in local optima. We used wavelet feature vectors in our experiments.

3 Experimental Results

In this paper we jointly register a series of decorrelating images using the proposed algorithm. While our effort is focused on following tumor shape change, the proposed joint registration algorithm applies to general multiple image registration as well since the derivation of the registration algorithm does not make any assumptions on the nature of the images.

3.1 Synthetic Decorrelating Image Sequences

Since our primary goal is to quantitatively compare the performance of joint and pairwise registration methods, it is necessary to know the ground truth. One way is to work on real image sequences and consult experts to manually draw the ground truth based on landmark correspondences. This is very time-consuming, labor-intensive and costly because a reasonably large number of experts are needed to provide reliable ground truth due to human subjectivity. An alternative is to use synthetic data via Monte Carlo simulations to demonstrate the statistical performance. We take the latter approach and systematically generate image sequences that mimic lesion changes.

1. Image Deformation and Decorrelation

During chemotherapy the lesion usually changes in the following fashion: some malignant cells die as a result of drug and/or radiation therapy; in the mean time some benign cells turn malignant due to the propagation of pathological cells. For a given patient during the monitoring period the existing lesion may change its shape and new lesion structure may be introduced as well. The lesion change can be modeled as a low order Markov chain due to the short temporal dependence between scans – simply put, in a series of exams, the lesion at a certain time point relies heavily on the previous Q exams (Q is a small integer). In our simulations, we choose first-order Markov model to generate the test image sequences.

Let 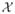represent the coordinate space of the region we are interested. For x ∈ 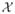, Y_i(x), i = 1, ···, N, is the scene at x at the i-th scanning time point. The scenes are generated using the following rule:

$$Y_i(x)=\beta Y_{i-1}(T(x))+(1-\beta )G_i(x),i=2,\cdots ,N$$ (6)

where Y₁(x) and G_i(x), i = 2, ···, N are Rayleigh random variables $\sqrt{v_1^2+v_2^2}$, where v₁ and v₂ are lowpass filtered Gaussian random variables. A Gaussian filter of kernel size 23 × 23 was used in our experiments. T is a geometric deformation and Y_i−1(T (x)) is the interpolated scene after applying the deformation T. Y₁(x) represents the structures that exist at the beginning of the imaging period while G_i(x) includes new structures introduced along the imaging period.

β ∈ (0, 1] is a constant which controls the correlation between adjacent image pairs assuming perfect registration. The smaller β is, the images are more decorrelated. In the trivial case of β = 1 the image sequence consists of deformations of existing structures only.

In the ideal noise-free case, the obtained images are exactly the scenes, i.e., I_i = Y_i. From the properties of first order Markov sequence, M I (I₁, I₂, …, I_N) = M I(I₁, I_N). Since the mutual information of the sequence is the same as the smallest mutual information between the image pairs, joint registration does not hold an advantage over pairwise.

However, during the image acquisition procedure random observation noise is inevitable and the images in the sequence are modeled as

$$I_i(x)=Y_i(x)+n_i(x),i=1,2,\cdots ,N$$ (7)

where n_i(x) is a Rayleigh noise of the same characteristic as described above except that the lowpass Gaussian filter is of a much smaller kernel size (5 × 5 in our experiments).

The images for the simulations were generated serially based on (6) and (7). Each new image was obtained by first applying a geometric deformation (T) to the previous scene in the series and then adding Rayleigh noise and finally adding a random acquisition noise.

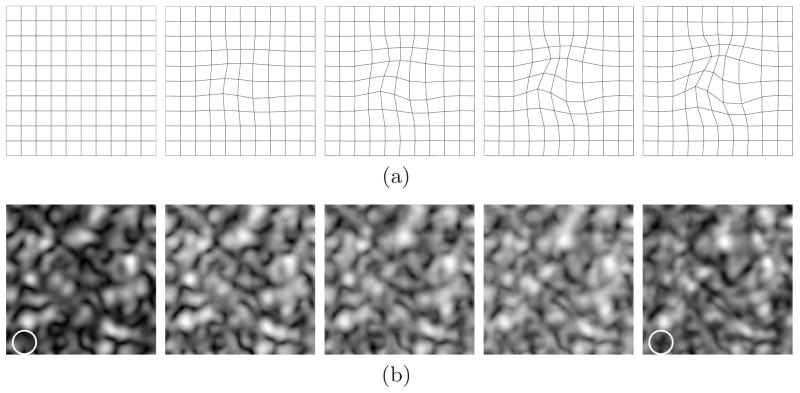
In our experiments, thin plate splines (TPS) model [16] is used as the geometric deformation T and thus the introduced deformation is a serially increasing TPS deformation shown in Fig. 2(a). An example of realizations of the Markov process for β = 0.8 is shown in Fig. 2(b), where both deformation of existing structures in the first image and introduction of new structures are included in the subsequent images. At the bottom left corner of the images (indicated by circles in white), there is a structure in the fifth image which has not shown in the first one. This is an example of new structures introduced during the Markov process since this area is out of the deformation field and thus the possibility that the structure is the result of geometric deformations is excluded.

Fig. 2.

Geometric deformations and generated images. (a) Consecutive TPS deformation; (b) An example of generated image sequence with β = 0.8.

2. Registration Results

To register a series of images, two approaches have been applied: sequentially pairwise registration and simultaneously joint registration of multiple images. In both approaches, αMI (5) is used as the similarity measure.

In all registration efforts TPS was employed as the deformation interpolant with 49 uniformly distributed control points placed on the nodes of a 7×7 rectangular grid spanning the deformed area in the image. k-nearest neighbor graphs were used to estimate αMI (α = 0.99) due to their computational advantage. Optimization was implemented using Nelder-Mead simplex minimization [17] by moving the control points in the floating images. On a Pentium 4, 3.06 GHz with 4 Gb memory, it took approximately 12 minutes to register a pair of images and 4–5 hours for joint registration of five images.

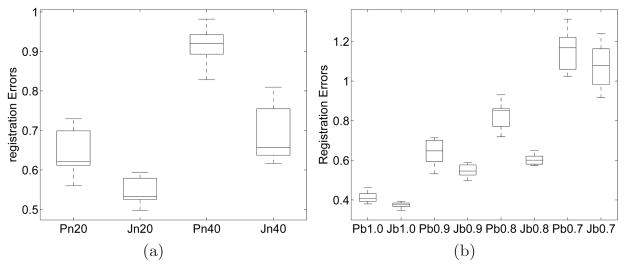
The registration errors are illustrated with boxplots. In each boxplot, the bottom, middle, and upper lines of the box represent the 25th percentile, median, and 75th percentile of the errors. The whisker shows the extent of the rest of the data and the outliers are shown as “+”. The performance comparison of pairwise and joint registration is shown in Fig. 3.

Fig. 3.

Registration errors for both joint and pairwise registrations. (a) Average registration errors for different acquisition noise levels (β = 0.9); (b) Average registration errors for different β values (the acquisition noise level is 20%). The labels in the horizontal axis: ‘P’ and ‘J’ indicate pairwise and joint registration, respectively; the number following ‘n’ indicates the observation noise level, e.g., ‘n20’ means the noise level is 20% of the signal power; the number after ‘b’ is the value of β.

Fig. 3(a) shows the average registration errors for image sequences generated with β = 0.9. Joint registration outperforms its pairwise counterpart yielding lower registration errors. One common cause for pairwise registration errors is the propagation of errors along image pairs. This is due to the composition used to map all the floating images to a common reference. In joint registration, since every floating image is registered to the reference image simultaneously under the constraints of one unified objective function, this error propagation does not occur. Another reason for joint registration’s better performance is that when all the images are registered simultaneously, they can provide additional information to other images. For example, with acquisition noise some structure is corrupted in an image, the other images may be able to provide supplemental information regarding the same structure and thus help the corrupted image to align with others.

Fig. 3(a) also shows the effects of additive acquisition noise on registration performance. Two noise levels have been tested: 20% and 40% of the signal power. At 40% noise level, the image quality is more deteriorated. As a result, the performance of both joint and pairwise registration methods is more adversely affected. For pairwise registration at such high noise levels, inaccurate registration is more likely to occur for some pair and the registration error will be carried over to the subsequent pairs. Therefore, although the observation noise is uncorrelated in each image, the noise in an image actually has affected the performance of registering the other images. On the other hand, for joint registration, even if every image in the sequence is severely corrupted, the uncorrelated observation noise will not affect the matching of other images. Therefore, the performance degradation is less severe for joint registration. So the higher the noise, the greater is the improvement observed for joint registration compared to pairwise.

β controls the weight of new structures in the whole signal component. The smaller the value of β, the more decorrelation and thus less mutual information between adjacent pairs of exams. For both joint and pairwise registration there must be adequate amount of mutual information between the images to achieve good registration ac curacy. Therefore, β plays a crucial role in registration performance. The average errors for different values of β are shown in Fig. 3(b). The registration errors for both pairwise and joint methods increase as β decreases. With preliminary experimental results we observe that joint registration produces significantly lower average registration errors than pairwise when β ≥ 0.8. When β is smaller than 0.8, the registration error increases significantly for both methods and there is no observable advantage of either method.

This study can be used to determine appropriate intervals for patient scanning to efficiently monitor lesion change. With small time interval between exams the adjacent exam pairs are highly correlated and registration results are expected to be excellent. However, imaging too frequently can be expensive and the difference between adjacent exams may be too trivial to track or analyze. On the other hand, long intervals render the registration problem intractable because of poorly correlated images with very different lesion structure. Clearly the sampling interval is an important consideration factor to monitor lesion change effiectively.

3.2 Artificial Lesion Changes

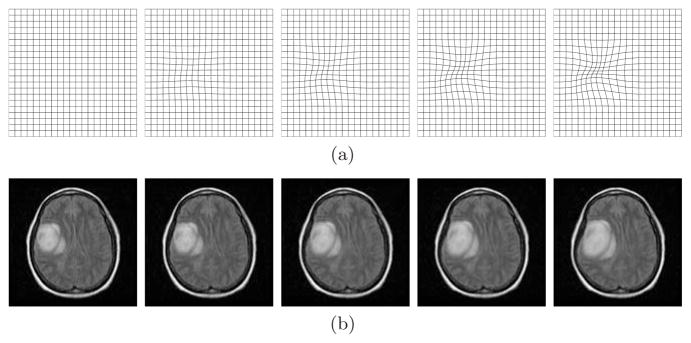
With the promising results we have obtained above, we proceed to track lesion change in brain MRI scans. We choose a 256 × 256 brain MRI scan (the lower left image in Fig. 4) as the base image and introduce consecutive B-spline deformation to simulate a series of lesion changes. The introduced B-spline deformation is shown in the upper row of Fig. 4. The lower row shows an example of the image sequence generated with known deformation plus a random Rayleigh observation noise.

Fig. 4.

Geometric deformations and corresponding brain images. (a) Consecutive B-spline geometric deformation; (b) Corresponding brain image sequence.

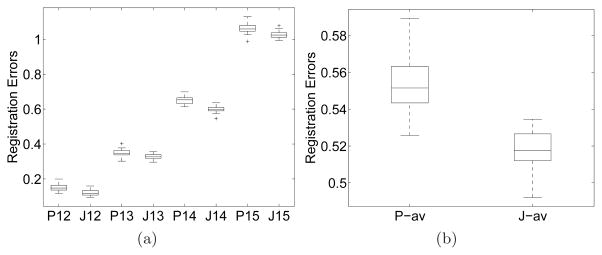
20 realizations of image sequences generated using the formula (6) and (7) with β = 1 underwent registration with both joint and pairwise approaches. Registration errors are calculated in the approximate area where the lesion is located. The registration errors plotted in Fig. 5 show that the joint method outperforms pairwise.

Fig. 5.

Registration errors for both joint and pairwise registration of the brain sequences. (a) Registration errors between image pairs; (b) Average registration errors across the image sequence. The labels in the horizontal axis: ‘P’ and ‘J’ mean pairwise and joint registration, respectively; the two digits following ‘P’ or ‘J’ are the indices for an image pair, e.g., ‘14’ means the alignment of I₄ to I₁; ‘-av’ after ‘P’ or ‘J’ means average.

4 Conclusion

We have developed a joint registration algorithm using αMI as the similarity measure. We have implemented and tested the joint registration algorithm for multiple image registration on several sets of image data. For comparison, we have also registered the same data sets using the pairwise approach. The experimental results have affirmed that the joint method outperforms pairwise in registering noisy image sequences by yielding lower average registration errors. The high registration accuracy of αMI based joint registration shows that it can be used as a reliable means to simultaneously register multiple images.

We have studied the performance change of joint registration as correlation (β) decreases. In conclusion joint registration works well for sufficiently large β values (> 0.8) and this observation can help us pick the optimal scanning interval to efficiently and effectively monitor lesions.