Prediction of supertype-specific HLA class I binding peptides using support vector machines

Abstract

Experimental approaches for identifying T-cell epitopes are time-consuming, costly and not applicable to the large scale screening. Computer modeling methods can help to minimize the number of experiments required, enable a systematic scanning for candidate major histocompatibility complex (MHC) binding peptides and thus speed up vaccine development. We developed a prediction system based on a novel data representation of peptide/MHC interaction and support vector machines (SVM) for prediction of peptides that promiscuously bind to multiple Human Leukocyte Antigen (HLA, human MHC) alleles belonging to a HLA supertype. Ten-fold cross-validation results showed that the overall performance of SVM models is improved in comparison to our previously published methods based on hidden Markov models (HMM) and artificial neural networks (ANN), also confirmed by blind testing. At specificity 0.90, sensitivity values of SVM models were 0.90 and 0.92 for HLA-A2 and -A3 dataset respectively. Average area under the receiver operating curve (A_ROC) of SVM models in blind testing are 0.89 and 0.92 for HLA-A2 and -A3 datasets. A_ROC of HLA-A2 and -A3 SVM models were 0.94 and 0.95, validated using a full overlapping study of 9-mer peptides from human papillomavirus type 16 E6 and E7 proteins. In addition, a large-scale experimental dataset has been used to validate HLA-A2 and -A3 SVM models. The SVM prediction models were integrated into a web-based computational system MULTIPRED1, accessible at antigen.i2r.a-star.edu.sg/multipred1/.

1. Introduction

Cellular immunity in vertebrates is mediated by T cells of the immune system which generate highly specific and lasting immune responses to pathogens (Fabbri et al., 2003). T-cell-based immune responses are mediated by antigenic peptides presented by major histocompatibility complex (MHC) molecules (Pamer and Cresswell, 1998; Yewdell and Bennink, 2001). Antigenic peptides bind MHC molecules and form peptide/MHC complexes. Peptide/MHC complexes shown to be recognized by T cells are called T-cell epitopes. Identifying promiscuous peptides that bind multiple Human Leukocyte Antigen (HLA, human MHC) alleles is a basis for T cell epitope mapping and epitope-based vaccine development (Berzofsky et al., 2001; Srinivasan et al., 2004a; De Groot, 2006). HLA genes are the most polymorphic human genes known (Williams, 2001), with more than 2400 allelic variants identified in the human population as of July 2006 (www.anthonynolan.org.uk/HIG/). Because of the high HLA polymorphism, identifying promiscuous peptides that bind more than one HLA allele is essential for the development of vaccines with a broad and unbiased coverage of the human population. HLA alleles that share sequence similarity and that bind largely overlapping sets of peptides define HLA supertypes (Sette and Sidney, 1999; Doytchinova et al., 2004; Lund et al., 2004). Promiscuous peptides have been reported in the context of HLA supertypes (Threlked et al., 1997; Wilson et al., 2003; Srinivasan et al., 2004b). Epitope-based vaccines show great potential in fighting infectious diseases (Sette et al., 2000; Ada, 2003; Wilson et al., 2003), and they are also investigated for control of cancers, allergy, autoimmunity, and even dementia (Alexander et al., 2002; Durrant and Ramage, 2005; Quintana and Cohen, 2005; Verhagen et al., 2005; Wisniewski and Frangione, 2005; De Groot, 2006).

Experimental validation of peptide binding to HLA molecules is time-consuming and costly, and thus not applicable to large scale screening across multiple HLA alleles. Computational methods are instrumental for systematic large-scale identification of MHC-binding peptides (Schirle et al., 2001; Brusic et al., 2004). One type of methods is structure-based approach that relies on structural conservation observed in 3D structure of peptide–MHC complexes (Schueler-Furman et al., 2000; Bui et al., 2006; Tong et al., 2006). These methods are computationally intensive, and have mainly been applied to MHC molecules with known crystal structures. Data-driven approaches include statistical methods based on experimental peptide binding measurements. These methods include binding motifs (Rammensee et al., 1993), quantitative matrices (Parker et al., 1994; Singh and Raghava, 2003; Reche and Reinherz, 2005; Peters and Sette, 2005), artificial neural networks (ANN) (Honeyman et al., 1998; Christensen et al., 2003), hidden Markov models (HMM) (Mamitsuka, 1998; Brusic et al., 2002), decision trees (Savoie et al., 1999; Segal et al., 2001), discriminant analysis (Mallios, 2001), multivariate regression (Lin et al., 2004), ensemble classifier (Xiao and Segal, 2005), support vector machines (SVM) (Donnes and Elofsson, 2002; Zhao et al., 2003; Bhasin and Raghava, 2004; Riedesel et al., 2004; Bozic et al., 2005; Liu et al., 2006; Cui et al., 2007), and biosupport vector machine which is modified from a conventional support vector machine by introducing a biobasis function so that the non-numerical attributes of amino acids can be recognized without a feature extraction process (Yang and Johnson, 2005). Recently a structure- and sequence-based method was reported, in which residue-based energy terms from the molecular dynamics simulations are used as features to train SVM prediction models for peptide/MHC class I binding (Antes et al., 2006).

SVM-based models showed higher accuracy than other prediction methods in studies of peptide binding to a single HLA molecule. We have employed SVM models with a novel data representation, which captures information of the interaction between a peptide and an HLA molecule and allows the use of a single model for prediction of peptide binding to a multiplicity of alleles that belong to a particular HLA supertype. Earlier we reported the application of HMM (Brusic et al., 2002) and ANN (Zhang et al., 2005b) for prediction of peptide binding to the HLA-A2 supertype. A web-based prediction system, MULTIPRED (Zhang et al., 2005a), was developed using HMM and ANN models. In this study we extended MULTIPRED by applying SVM models. The SVM-MULTIPRED was applied to prediction of HLA class I supertype-specific promiscuous binding peptides in the context of HLA-A2 and -A3. Extensive testing, including blind testing and 10-fold cross-validation, were performed to assess the performance of the prediction models. Validation of the models was conducted using experimental data from human papillomavirus (HPV) type 16 E6 and E7 proteins and a large-scale experimental dataset made available recently by Peters et al. (2006). The performance of the SVM models were compared with that of HMM and ANN models. MULTIPRED1 is the updated version of MULTIPRED (Zhang et al., 2005a). MULTIPRED1 is accessible at antigen.i2r.a-star.edu.sg/multipred1/.

2. Materials and methods

2.1. Data and data representation

Nine-mer peptide data were extracted from the MHCPEP database (Brusic et al., 1994), published articles, and a set of HLA non-binding peptides (Brusic, V. unpublished data). The HLA-A2 supertype dataset, named as Dataset1, has 3050 peptides (664 binders and 2386 non-binders) related to 15 alleles (Table 1) of HLA-A2 supertype and the HLA-A3 supertype dataset, named Dataset2, has 2216 peptides (680 binders and 1536 non-binders) related to eight alleles (Table 2) of HLA-A3 supertype. Nine-mer peptides were used in building models because the predominant length of peptides that bind HLA-A2 and -A3 (class I) alleles is nine-amino-acid long (Rammensee et al., 1993). The datasets are available for download at antigen.i2r.a-star.edu.sg/multipred1/data.

Table 1.

Number of 9-mer peptides related to 15 HLA alleles belonging to A2 supertype in Dataset1

HLA-A2 allele	Binders	Non-binders	Total
A*0201	440	1999	2439
A*0202	45	25	70
A*0203	46	7	53
A*0204	23	224	247
A*0205	16	40	56
A*0206	43	37	80
A*0207	4	11	15
A*0208	0	4	4
A*0209	5	1	6
A*0210	3	0	3
A*0211	4	0	4
A*0214	8	1	9
A*0217	2	4	6
A*6802	23	31	54
A*6901	2	2	4
Total	664	2386	3050

Table 2.

Number of 9-mer peptides related to eight HLA alleles belonging to A3 supertype in Dataset2

HLA-A3 allele	Binders	Non-binders	Total
A*0301	107	89	196
A*0302	146	259	405
A*1101	142	223	365
A*1102	142	211	353
A*3101	44	54	98
A*3301	35	62	97
A*3303	5	0	5
A*6801	59	638	697
Total	680	1536	2216

To model the interaction between a peptide and a HLA molecule, a peptide/HLA interaction is represented by a virtual peptide composed of peptide residues and HLA residues that come in contact with the peptide (Zhang et al., 2005b). The HLA protein sequences were extracted from the IMGT/HLA Sequence Database, release 2.4.0 (http://www.anthonynolan.org.uk/HIG/). To simplify the data representation and eliminate redundant information, we considered only those contact residues that vary across the HLA-A2/A3 alleles appearing in Dataset1/Dataset2, and discarded the residues that are conserved across those HLA-A2/A3 alleles. The contact residues conserve across the alleles will not provide any useful information to feature vectors, as they are same in all feature vectors. There are in total 48 peptide contact residues of which 29 are non-conserved across HLA-A variants (Chelvanayagam, 1996; Brusic et al., 2002). Of 29 non-conserved residues, 12 are non-conserved across the 15 HLA-A2 alleles, see Table 3. By combining the 9-mer peptide and the 12 non-conserved contact residues we defined a virtual peptide. The virtual peptide has 21 amino acids capturing the interaction information between a peptide and a HLA-A2 allele: P1-P2-P3-P4-P5-P6-P7-P8-P9-R9-R62-R63-R66-R70-R73-R74-R95-R97-R99-R152-R156. P denotes peptide residues and R denotes HLA-A contact residues. Of the 29 non-conserved residues, 12 are non-conserved across the eight HLA-A3 alleles, see Table 4. There are 20 amino acids and each of them can be encoded as a binary string of length 20 with a unique position set to “1” and other positions set to “0”. For example, the first two amino acids, alanine (A) and cysteine (C) are encoded by 10000000000000000000 and 01000000000000000000 respectively, and the last amino acid tyrosine (Y) is encoded by 00000000000000000001. A 21-amino-acid-long peptide can be represented as a binary string of length 420.

Table 3.

Non-conserved contact residues across the 15 HLA-A2 alleles appearing in Dataset1

Positions	9	62	63	66	70	73	74	95	97	99	152	156
A*0201	F	G	E	K	H	T	H	V	R	Y	V	L
A*0202	F	G	E	K	H	T	H	L	R	Y	V	W
A*0203	F	G	E	K	H	T	H	V	R	Y	E	W
A*0204	F	G	E	K	H	T	H	V	M	Y	V	L
A*0205	Y	G	E	K	H	T	H	L	R	Y	V	W
A*0206	Y	G	E	K	H	T	H	V	R	Y	V	L
A*0207	F	G	E	K	H	T	H	V	R	C	V	L
A*0208	Y	G	E	N	H	T	H	L	R	Y	V	W
A*0209	F	G	E	K	H	T	H	V	R	Y	V	L
A*0210	Y	G	E	K	H	T	H	V	R	F	V	L
A*0211	F	G	E	K	H	I	D	V	R	Y	V	L
A*0214	Y	G	E	K	H	T	H	L	R	Y	V	L
A*0217	F	G	E	K	H	T	H	L	M	F	V	L
A*6802	Y	R	N	N	Q	T	D	I	R	Y	V	W
A*6901	Y	R	N	N	Q	T	D	V	R	Y	V	L

Table 4.

Non-conserved contact residues across the eight HLA-A3 alleles appearing in Dataset2

Positions	9	62	63	70	73	97	114	142	152	156	163	171
A*0301	F	Q	E	Q	T	I	R	I	E	L	T	Y
A*0302	F	Q	E	Q	T	I	R	I	V	Q	T	Y
A*1101	Y	Q	E	Q	T	I	R	I	A	Q	R	Y
A*1102	Y	Q	E	Q	T	I	R	I	A	Q	R	Y
A*3101	T	Q	E	H	I	M	Q	I	V	L	T	Y
A*3301	T	R	N	H	I	M	Q	I	V	L	T	H
A*3303	T	R	N	H	I	M	Q	I	V	L	T	Y
A*6801	Y	R	N	Q	T	M	R	T	V	W	T	Y

2.2. Support vector machines

SVMs are popular due to attractive features and their promising performance. SVMs implement a simple idea: they map pattern vectors to a high-dimensional feature space where a best separating hyperplane can be constructed (Webb, 2002). It provides a linear separation in an augmented space, by means of defined kernels. A SVM is an implementation of the Structural Risk Minimization (SRM) principle, which minimizes the upper bound on the expected generalization error (Vapnik, 1998). The SRM principle was shown to be superior to traditional Empirical Risk Minimization (ERM) principle, employed by conventional neural networks. SRM minimizes an upper bound on the expected risk, as opposed to ERM that minimizes the error on the training data. This difference enables SVMs to generalize well, which is a statistical learning goal (Gunn, 1998).

Here we consider the binary classification task in which we have a set of training patterns {x_i, i= 1,…n} assigned to one of two classes, ω₁ and ω₂, with corresponding labels g(x)=0. In this study, x_i is a binary string representing a 9-mer peptide and class ω₁ and ω₂ correspond to HLA binders and non-binders. The linear discriminate function is:

$$g(x)=w^{T}x+w_0$$ (1)

with decision rule

$$w^{T}x+w_0\{\begin{array}{c}>0\hfill \\ <0\hfill \end{array}\Rightarrow x\in \{\begin{array}{c}{\omega }_1\text{with}\text{corresponding}\text{numeric}\text{value}{y}_i=+1\hfill \\ {\omega }_2\text{with}\text{corresponding}\text{numeric}\text{value}{y}_i=-1\hfill \end{array}$$ (2)

All training points are correctly classified if

$$y_i(w^T{x}_i+w_0)>0\text{for}\text{all}i$$

There may be more than one separating hyperplanes. The maximal margin classifier determines the hyperplane for which the margin – the distance to two parallel hyperplanes on each side of the separating hyperplane – is the largest. The assumption is that the larger the margin, the better the generalization error of the linear classifier defined by the separating hyperplane. To aid generalization, a margin, b>0, is introduced. Solution must satisfy the condition:

$$y_i(w^T{x}_i+w_0)\ge b$$ (3)

Without loss of generality, a value b=1 may be taken, defining canonical hyperplane:

$$\begin{array}{l}{\text{H}}_1:w^T{x}_i+w_0=+1\text{and}{\text{H}}_2:w^T{x}_i+w_0\\ =-1,\text{and}\text{have}\\ w^{T}x+w_0\{\begin{array}{c}\ge +1\\ \le -1\end{array}\Rightarrow x\in \{\begin{array}{c}{\omega }_1\text{with}\text{corresponding}\text{numeric}\text{value}{y}_i=+1\\ {\omega }_2\text{with}\text{corresponding}\text{numeric}\text{value}{y}_i=-1\end{array}\end{array}$$ (4)

The distance between each of these two hyperplanes and the separating hyperplane, g(x)=0, is 1/|w| and is termed margin. Maximizing the margin means that we seek a solution that minimize |w| subject to the constraints

$$y_i(w^T{x}_i+w_0)\ge 1i=1,\dots ,n$$ (5)

A standard approach to optimization problems that have equality and inequality constraints is the Lagrange formalism (Fletcher, 1987). This formalism leads to the primal form of the objective function, L_p, given by

$$L_{\text{p}}=\frac{1}{2}{w}^{T}w-\text{∑}_{i=1}^n{\alpha }_i(y_i(w^T{x}_i+w_0)-1)$$ (6)

where {α_i, i=1,…n;α_i ≥0} are the Lagrange multipliers. The solution to the problem of minimizing w^Tw subject to constraints (5) is equivalent to determining the saddle point of the function L_p, at which L_p is minimized with respect to w and w₀ and maximized with respect to the α_i. Differentiating L_p with respect to w and w₀ and equating to zero yields:

$$\begin{array}{cc}\text{∑}_{i=1}^n{\alpha }_i{y}_i=0& w=\text{∑}_{i=1}^n{\alpha }_i{y}_i{x}_i\end{array}$$

Substituting into Eq. (6) gives the dual form of the Lagrangian:

$$L_p=\text{∑}_{i=1}^n{\alpha }_i-\frac{1}{2}\text{∑}_{i=1}^n\text{∑}_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathit{\text{x}}}_i^T{x}_j$$

which is maximized with respect to the α_i subject to:

$${\alpha }_i\ge 0\text{∑}_{i=1}^n{\alpha }_i{y}_i=0$$

The support vector algorithm may be applied in a transformed feature space, φ(x), using a nonlinear function. The discriminate function shown in Eq. (1) now changes to:

$$g(x)=(w^T\mathit{\varphi }(x)+w_x)$$

Acceptable kernels must be expressible as an inner product in a feature space, or k(x,y) = φ^T(x) φ(y). Frequently used kernels are polynomial:

$$k(x,y)={(1+x^{T}y)}^d$$

and radial basis (Gaussian) kernel:

$$k(x,y)=\text{exp}(-||x-y||/(g^2))$$

Both polynomial and Gaussian kernels have been tried in our experiments.

2.3. Training, testing and validation

Training of support vector machines was carried out using SVMlight (Joachims, 1999). An input to this package is a binary vector indicating whether a particular amino acid is presented at a particular position and a label with value 1 or 0 indicating if the peptide is a HLA binder or non-binder. Three kernel functions were examined (linear, polynomial and radial basis), and three existing parameters were optimized (trade-off c, power d for polynomial kernel, and parameter g for radial kernel). SVM models with kernels and parameter settings were trained and evaluated for each of HLA-A2 and -A3 dataset. Parameter values used during this process were the following: c (trade-off between training error and margin) was varied from 0.01 to 20, d (degree in polynomial kernel) from 1 to 10 and g (as shown in Gaussian kernel) from 0.001 to 1. Models that showed the best performance (one for each supertype) were used for final testing and validation. Although by default threshold 0 represents the separating hyperplane, data available are often imbalanced and not randomly distributed. Moving the decision boundary, which is equivalent to choosing a different threshold, is often used for remedying the imbalanced training-data problem (Wu and Chang, 2003). In our experiments, the decision boundary (threshold) was chosen using the performance measures of the SVM models.

The predictive performance was assessed using sensitivity (SE) and specificity (SP), and receiver operating characteristic (ROC) analysis. TP is the number of true positives (experimental binders predicted as binders), FP the number of false positives (experimental non-binders predicted as binders), TN the number of true negatives (experimental non-binders predicted as non-binders) and FN the number of false negatives (experimental binders predicted as non-binders), SE=TP/(TP+FN) indicates the percentage of correctly predicted binders; SP = TN/(TN+FP) stands for the percentage of correctly predicted non-binders. The ROC curve is a plot of SE against (1-SP) at various classification thresholds (Swets, 1988). The area under the ROC curve (A_ROC) is a measure for the overall prediction performance. Values of A_ROC<0.7 represent poor predictions; A_ROC>0.8 represents good and A_ROC>0.9 represents excellent predictions, while A_ROC=0.5 represents random guessing (Swets, 1988). The statistical significance of the comparisons was assessed by t-test. The t-test assesses whether the means of two groups are statistically different from each other (Pagano and Gauvreau, 2000) and is suitable for evaluation of statistical differences for small number of measurements (30 or less in a sample).

Cross-validation is a method for error rate estimation. It implements a simple idea: the dataset of size n samples is partitioned into two parts, the model parameters are estimated using one set and the goodness-of-fit criterion evaluated on the second set. The cross-validation estimates the goodness-of-fit, which identifies how well a statistical model fits a set of observations. In our experiments, 10-fold cross-validation was performed to evaluate the performance of the classifiers. The dataset was randomly divided into 10 sets with approximately equal size. For each “fold”, the classifier is trained using all but one of the 10 groups and then tested on the remaining “unseen” group. This procedure is repeated for each of the 10 groups. The final A_ROC is calculated by micro-averaging the results obtained from the 10 runs (TP, TN, FP, and FN were summed up before the calculation of A_ROC).

In addition to cross-validation, we also performed blind testing for the assessment of the performance of SVM models for prediction of promiscuous HLA-A2 and -A3 binding peptides. For testing purposes, a model was built for each allele. The test set for each model included all peptides related to the allele, while the training set consisted of all peptides related to other HLA alleles from the same supertype. Thus prediction of peptides that bind one HLA allele was performed without any prior knowledge of the peptides binding or not binding to this allele. Because the actual prediction model incorporates all data, the testing results are likely to represent an underestimate of the actual performance. We trained five HLA-A2 and seven HLA-A3 models — the selected molecules are shown in Tables 5 and 6. Other alleles were not used for testing, as there was insufficient experimental data related to them for testing to be valid. The performance of SVM was compared to performances of existing methods, HMM and ANN models.

Table 5.

Blind testing on five HLA-A2 alleles: numbers of peptides in training and testing sets

HLA-A2 allele	Training data		Testing data
	Binders	Non-binders	Binders	Non-binders
A*0201	224	378	440	1999
A*0202	619	2361	45	25
A*0204	641	2162	23	224
A*0205	648	2346	16	40
A*0206	621	2349	43	37

Table 6.

Blind testing on seven HLA-A3 alleles: numbers of peptides in training and testing sets

HLA-A3 allele	Training data		Testing data
	Binders	Non-binders	Binders	Non-binders
A*0301	573	1447	107	89
A*0302	534	1277	146	259
A*1101	538	1313	142	223
A*1102	538	1325	142	211
A*3101	636	1482	44	54
A*3301	645	1474	35	62
A*6801	621	898	59	638

Stratified 10-fold cross-validation was performed on peptides related to A*0201 and A*0302 molecules. In stratified 10-fold cross-validation, the dataset is randomly divided into 10 sets with approximately equal size and class distributions. And the peptides in the training data that were similar (only one amino acid different) to any peptide from the test set were removed.

A set of 240 9-mer peptides of HPV type 16 E6 and E7 proteins with experimentally identified binding affinity were used for model validation (Kast et al., 1994). Experiments revealed that there are four 9-mer peptides, E6-7, E6-18, E6-26 and E6-52, bind to A*0201 in HPV E6 and seven A*0201 9-mer binders, E7-7, E7-11, E7-12, E7-66, E7-82, E7-85 and E7-86 in HPV E7. There are nine 9-mer peptides, E6-7, E6-33, E6-42, E6-59, E6-75, E6-89, E6-93, E6-125 and E6-143, that bind A*0301 in HPV E6 and one weak A*0301 binder, E7-89 in HPV E7. The training datasets were checked for the duplicate 9-mers peptides pertaining to E6 and E7 proteins and were removed. After removing duplicates, there were 3027 9-mer peptides (651 binders and 2376 non-binders) and 2164 9-mer peptides (653 binders and 1511 non-binders) in the training datasets for HLA-A2 and HLA-A3 models respectively. The comparative performance with other servers for prediction of promiscuous HLA class I peptides was not possible because of unmatched allelic variants that are covered by models in different servers.

A large experimental dataset of quantitative MHC– peptide binding data was recently made available (Peters et al., 2006). Using this dataset, they compared the performance of different bioinformatics approaches, including MULTIPRED ANN and HMM models, in predicting MHC binding peptides. The performance of these models has been reported in Tables 2 and 3 of the paper. We used the same dataset for evaluation of our HLA-A2/A3 SVM models. In the Peters dataset, the IC50 value used to separate binders and non-binders is 500 nM, whereas in the Dataset1 and Dataset2, the IC50 value used to separate binders and non-binders is 5000 nM. The difference in the threshold setting results in some discrepancy between our datasets and the Peters dataset. Some identical peptides between Dataset1, Dataset2 and the Peters dataset have been classified into different classes. The binding affinities of such peptides in Dataset1 and Dataset2 were modified to the binding affinities in the Peters dataset and these overlapping peptides were removed from the test sets. The number of 9-mer peptides in the Peters dataset related to HLA-A2/A3 alleles, the number of overlapping 9-mer peptides between Dataset1/Dataset2 and the Peters dataset and the number of non-overlapping peptides used for testing of the HLA-A2/A3 SVM models are shown in Tables 7 and 8 respectively. The testing datasets are available for download at antigen.i2r.a-star.edu.sg/multipred1/data.

Table 7.

Number of 9-mer peptides in the Peters dataset related to HLA-A2 alleles; number of overlapping peptides between Dataset1 and the Peters dataset; number of non-overlapping peptides (binders/non-binders) used for testing of the HLA-A2 SVM model

	A*0201	A*0202	A*0203	A*0206	A*6802	A*6901
The Peters dataset	3089	1447	1443	1437	1434	833
Overlapping	240	54	48	47	47	0
Non-overlapping	2849 (1024/1825)	1393 (611/782)	1395 (600/795)	1390 (480/910)	1387 (387/1000)	833 (86/747)

Table 8.

Number of 9-mer peptides in the Peters dataset related to HLA-A3 alleles; number of overlapping peptides between Dataset2 and the Peters dataset; number of non-overlapping peptides (binders/non-binders) used for testing of the HLA-A3 SVM model

	A*0301	A*1101	A*3101	A*3301	A*6801
The Peters dataset	2094	1985	1869	1140	1141
Overlapping	97	102	71	70	69
Non-overlapping	1997(452/1545)	1883(618/1265)	1798(399/1399)	1070(161/909)	1072(455/617)

2.4. Comparison of prediction methods

The performance of the SVM method was compared to the previously reported MULTIPRED models based on HMM (Brusic et al., 2002) and ANN (Zhang et al., 2005b). All models were retrained with the current dataset and assessed using the same train/test partitions.

3. Results

3.1. Cross-validation results

Ten-fold cross-validation was performed on all three methods. The A_ROC of ANN models is 0.93 for HLA-A2 dataset and 0.89 for HLA-A3 dataset. The A_ROCof HMM models are 0.77 for HLA-A2 dataset and 0.71 for HLA-A3 dataset. The A_ROC of SVM models are 0.95 for HLA-A2 dataset and 0.97 for HLA-A3 dataset. The sensitivities of the models were calculated at three levels: SP values of 0.8, 0.9 and 0.95 (Tables 9 and 10). For both HLA-A2 and HLA-A3 datasets, SVM models are of the highest sensitivity. Especially when specificity threshold is high (at 0.95), the sensitivity of SVM models is markedly higher that that of ANN and HMM models. The A_ROC values of the models in predicting peptides binding to HLA-A2/A3 alleles are listed in Tables 11 and 12. “Average” is the average of the A_ROC values for the individual tests and “Std. dev” is the standard deviation of the measurements. SVM models perform the best on all alleles with average A_ROC=0.914 for HLA-A2 alleles and A_ROC =0.951 for HLA-A3 alleles. Figs. 1 and 2 show the specificity and sensitivity relationship in 10-fold cross-validation.

Table 9.

Sensitivities and (prediction thresholds) for 10-fold cross-validation on Dataset1 using SVM, ANN and HMM models

Specificity	Sensitivity
	SVM	ANN	HMM
0.80	0.96 (−0.82)	0.95	0.69
0.90	0.90 (−0.52)	0.84	0.55
0.95	0.76 (−0.02)	0.55	0.42

The values are given for three levels of specificity, 0.8, 0.9 and 0.95.

Table 10.

Sensitivities and (prediction thresholds) for 10-fold cross-validation on Dataset2 using SVM, ANN and HMM models

Specificity	Sensitivity
	SVM	ANN	HMM
0.80	0.97 (−0.65)	0.86	0.56
0.90	0.92 (−0.30)	0.66	0.36
0.95	0.84 (−0.05)	0.41	0.24

The values are given for three levels of specificity, 0.8, 0.9 and 0.95.

Table 11.

A_ROC values for 10-fold cross-validation on Dataset1 using SVM, ANN and HMM models

HLA-A2 allele	SVM	ANN	HMM
A*0201	0.96	0.94	0.90
A*0202	0.83	0.65	0.80
A*0204	0.94	0.83	0.87
A*0205	0.96	0.91	0.82
A*0206	0.88	0.81	0.84
Average	0.914	0.828	0.846
Std. dev	0.057	0.113	0.039

Table 12.

A_ROC values for 10-fold cross-validation on Dataset2 using SVM, ANN and HMM models

HLA-A3 allele	SVM	ANN	HMM
A*0301	0.96	0.87	0.93
A*0302	0.92	0.84	0.84
A*1101	0.98	0.91	0.91
A*1102	0.96	0.89	0.85
A*3101	0.89	0.72	0.66
*3301	0.96	0.65	0.54
A*6801	0.99	0.95	0.93
Average	0.951	0.833	0.809
Std. dev	0.034	0.108	0.151

Fig. 1.

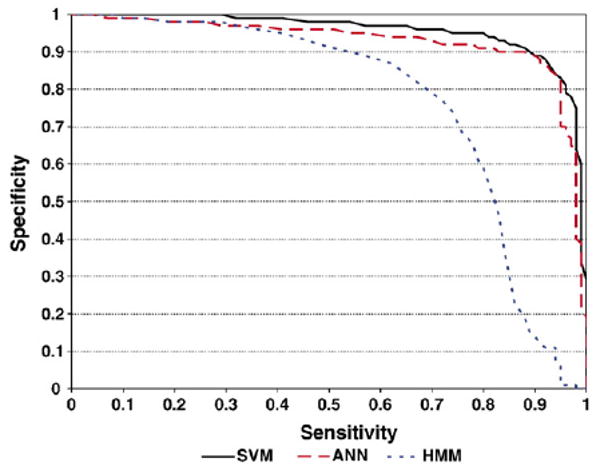
Sensitivity vs. specificity in 10-fold cross-validation on Dataset1 using SVM, ANN and HMM models.

Fig. 2.

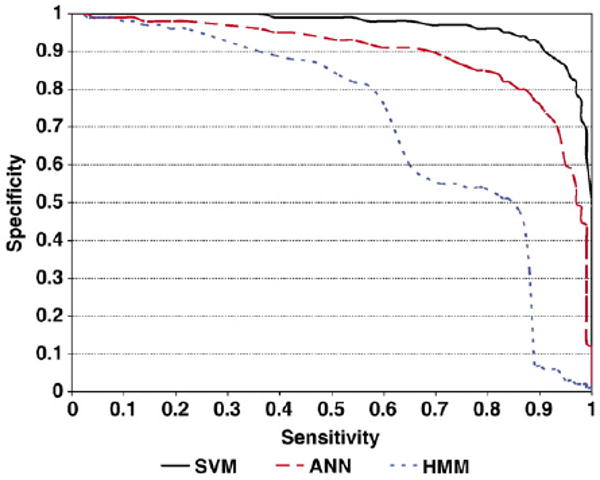
Sensitivity vs. specificity in 10-fold cross-validation on Dataset2 using SVM, ANN and HMM models.

3.2. Blind testing results

The A_ROC values of the prediction models in blind testing are shown in Tables 13 and 14. The A_ROC values of predictions for peptide binding to A*0201, A*0204, A*0205, A*0301, A*1101, A*1102, A*3301, A*6801 were equal to or higher than 0.90. Overall, predictions models performed well (A_roc=0.892 for HLA-A2 alleles and A_ROC=0.924 for HLA-A3 alleles). The significance of these results is that training sets in this particular assessment did not include any of the peptides from test sets which contain all the peptides related with an allele at one time. The results corroborate that this method can be used for prediction of good or excellent accuracy of peptide binding to complete supertypes, even for those alleles where no binding data are available.

Table 13.

A_ROC values for blind testing on HLA-A2 dataset using SVM, ANN and HMM models

HLA-A2 allele	SVM	ANN	HMM
A*0201	0.90	0.87	0.93
A*0202	0.81	0.76	0.73
A*0204	0.93	0.88	0.92
A*0205	0.97	0.93	0.94
A*0206	0.85	0.91	0.88
Average	0.892	0.87	0.88
Std.dev.	0.063	0.066	0.087

Table 14.

A_ROC values for blind testing on HLA-A3 dataset using SVM, ANN and HMM models

HLA-A3 allele	SVM	ANN	HMM
A*0301	0.93	0.89	0.94
A*0302	0.86	0.84	0.86
A*1101	0.96	0.91	0.91
A*1102	0.96	0.86	0.86
A*3101	0.87	0.69	0.66
A*3301	0.92	0.63	0.58
A*6801	0.97	0.96	0.95
Average	0.924	0.83	0.8229
Std.dev.	0.044	0.144	0.120

The A_ROC values for A*0202, A*1102, A*3101 and A*3301 prediction models were improved markedly using SVM models (Tables 13 and 14), This might be explained by the fact that sets of peptides related to these molecules are relatively small (less than 100 peptides). SVM are known to outperform other prediction methods on smaller datasets. HMM performed better on A*0201 and A*0301 (however, SVM still has reasonably high A_ROC values for these two molecules), and both HMM and ANN models of A*0206 molecule performed better then the corresponding SVM model.

T-test was applied to determine whether the difference in SVM, HMM and ANN predictive performance is statistically significant. The results showed that the performance of SVM is statistically better than the performances of other two methods on HLA-A3 alleles (P<0.05). However, the same conclusion could not be drawn for HLA-A2 alleles. This might be due either to similar performance of studied predictive models or to the imbalance in the HLA-A2 dataset. SVM often do not perform the best on imbalanced datasets (Wu and Chang, 2003), and HLA-A2 Dataset1 is imbalanced in two ways: binders/non-binders ratio is close to 1:4, and peptides related to A*0201 present 80% (2439 of 3050), while peptides related to all other alleles present only 20% of the total dataset. The HLA-A3 Dataset2 is more balanced in both aspects, and in this case we observed statistically better performance of SVM than other prediction methods.

3.3. Validation using HPV E6 and E7 proteins

The A_ROC values of SVM, HMM, and ANN predictions for HPV E6 and E7 proteins are shown in Table 15. Overall, SVM models show better performance on prediction of peptides derived as a full overlapping set from viral proteins E6 and E7 than ANN and HMM. SVM show the highest A_ROC for HLA-A3 supertype predictions, and SVM and ANN show the same excellent performance on predictions for HLA-A2 supertype.

Table 15.

A_ROC values for predictions on HPV E6 and E7 proteins using SVM, ANN and HMM models

	SVM	ANN	HMM
A2 AROC	0.94	0.94	0.88
A3 AROC	0.95	0.80	0.91

In summary, we report the improved overall performance of SVM models for prediction of peptide binding to multiple molecules of HLA-A3 supertype, and at least as good performance for HLA-A2 as supported it with exhaustive testing. We have shown that SVM models can predict peptide binding to HLA-A2 and HLA-A3 molecules with good performance, including those alleles for which no experimental binding data are currently available.

3.4. Validation using the Peters dataset

The A_ROC values of HLA-A2 SVM model for predictions of binding peptides for HLA-A2 supertype alleles (A*0201, A*0202, A*0203, A*0206, A*6802 and A*6901) using the Peters dataset (Table 16) show marked improvement for all studied alleles. We note that HLA-A2 SVM model performs well in predicting A*6901 binding peptides (A_ROC=0.81) although only four peptides related to A*6901 were used for model training. In addition, HLA-A2 SVM model showed better performance in predicting peptides binding to all HLA-A2 alleles than all the external tools evaluated in (Peters et al., 2006) and is equal or better for three of five studied HLA-A3 alleles than the best external tool. We note that only five A*3301-related peptides were in Dataset2 for training of HLA-A3 SVM model.

Table 16.

A_ROC values of SVM models for predictions of binding peptides for HLA-A2 and -A3 supertypes using the Peters dataset

HLA-A*	0201	0202	0203	0206	6802	6901
SVM AROC	0.91	0.83	0.82	0.79	0.74	0.81
ANN AROC	0.88	0.79	0.79	0.74	<0.64	–
HLA-A*	0301	1101	3101		3301	6801
SVM AROC	0.87	0.89	0.83		0.79	0.76
ANN AROC	0.85	0.87	<0.83		<0.81	<0.77

A_ROC values of ANN MULTIPRED are taken from Peters et al. (2006).

In Dataset2, there were 697 peptides related to A*6801 with 8.5% of them being binders and 91.5% being non-binders. To understand why HLA-A3 SVM model performed poorly in predicting peptide binding to A*6801, we performed additional analysis at the peptide sequence level. The poor performance of the HLA-A3 SVM model in predicting peptides binding to A*6801 was because the limited number of binders in training dataset do not represent the diverse pattern of A*6801 binding motif. For example, in the training data all binders had K or R at the anchor position 9, while Y, which is present in some binders in the Peters dataset was not represented in the training data. This emphasizes the need for use of representative datasets for development of MHC-binding prediction servers. While the accuracy of predictions will improve by adding new data to the training sets, it is important to note that about a quarter of MHC class I binding peptides lack canonical binding motifs (A. Sette, personal communication). These peptides are underrepresented in the current datasets, which are used both for training and testing, and therefore the values of accuracy of predictive methods are likely to be somewhat lower than reported, across all comparative studies.

3.5. MULTIPRED1 — an online computational system for prediction of promiscuous HLA binding peptides

Previously we developed MULTIPRED (Zhang et al., 2005a), a web-based computational system for prediction of peptide binding to multiple molecules belonging to HLA class I A2, A3 and class II DR supertypes. It uses HMM and ANN as predictive engines. With SVM models integrated, an updated version of the system – MULTIPRED1 – was developed.

In MULTIPRED1, the prediction scores produced by SVM models were rescaled to map them into the range from one to nine. The mapping of scores was done according to equation, Score_N=(Score − Score_min)/(Score_max−Score_min)×8+1, where Score_N denotes the normalized score, Score denotes the raw prediction score produced by SVM models, and Score_max and Score_min denote the possible minimum and maximum values of the raw scores respectively. The values for Score_max and Score_min were obtained through extensive testing. More than 650 randomly selected protein sequences from the NCBI protein database (contained more than 220,000 9-mer peptides) were used for prediction using the SVM models. Since the testing data contains huge number of 9-mer peptides, the highest and lowest predicted score from the testing data were taken as reasonable maximum and minimum scores for normalization.

4. Discussion and conclusion

Throughout training and testing, we examined different kernels (linear, radial basis and polynomial) and optimized SVM parameters (trade-off c, parameter g for radial basis kernel and degree d for polynomial kernel). The models that had the best performances (in terms of the highest average blind testing A_ROC value for molecules within a given supertype) were: Gaussian kernel with g=0.1 and c=0.5 for HLA-A2 and Gaussian kernel with g=0.1 and c=2 for HLA-A3 supertype.

We report that Gaussian kernel performs best on both HLA-A2 and -A3 molecules. This is in contrast to the report by (Zhao et al., 2003), where linear kernel showed the best performance for T-cell epitopes prediction. However, their model was trained only for a single allele (A*0201) and their dataset contained a smaller number of peptides (203). Our results also differ from those reported by Donnes and Elofsson (2002), who trained a different SVM model, including different selection of kernels and parameters, for each allele. These results indicate that future improvements of SVM performance will likely be driven by the increase of datasets, rather than optimization of kernel function and SVM parameters. The main difference between this work and other studies that employed SVM for prediction of HLA binders is that each SVM model built is for prediction of peptides that bind molecules from an entire supertype (HLA-A2 or -A3). In addition, our models can predict peptide binding to HLA-A2 and -A3 alleles for which no binding data are available. For example, HLA-A2 SVM model performs reasonably well in predicting A*6901 binding peptides (A_ROC =0.81) when validated using the Peters dataset in spite of only four A*6901-related peptides being used for training the model. However, the limited number of peptides in training dataset may affect the performance of the prediction models, as in the case of A*6801.

Development of epitope-based vaccines is progressing rapidly. Selection of peptides for candidate subunit vaccines is one of the greatest obstacles in the development of vaccines with broad and non-ethnically-biased coverage of the human population. Computational systems that can predict promiscuous peptides complement experimental approaches for overcoming this obstacle.