The Dynamics of Conditioning and Extinction

Abstract

Pigeons responded to intermittently reinforced classical conditioning trials with erratic bouts of responding to the CS. Responding depended on whether the prior trial contained a peck, food, or both. A linear-persistence/learning model moved animals into and out of a response state, and a Weibull distribution for number of within-trial responses governed in-state pecking. Variations of trial and inter-trial durations caused correlated changes in rate and probability of responding, and model parameters. A novel prediction—in the protracted absence of food, response rates can plateau above zero—was validated. The model predicted smooth acquisition functions when instantiated with the probability of food, but a more accurate jagged learning curve when instantiated with trial-to-trial records of reinforcement. The Skinnerian parameter was dominant only when food could be accelerated or delayed by pecking. These experiments provide a framework for trial-by-trial accounts of conditioning and extinction that increases the information available from the data, permitting them to comment more definitively on complex contemporary models of momentum and conditioning.

Estes’s stimulus sampling theory provided the first approximation to a general quantitative theory of learning; by adding a hypothetical attentional mechanism to conditioning, it carried analysis one step beyond extant linear learning models into the realm of theory (Atkinson & Estes, 1962; Bower, 1994; Estes, 1950, 1962; Healy, Kosslyn, & Shiffrin, 1992). Wagner and Rescorla (1972) added the important nuance that the asymptotic level of conditioning might be partitioned among stimuli that are associated with reinforcers, as a function of their reliability as predictors of reinforcement; that refinement has had tremendous and widespread impact (Siegel & Allan, 1996). The attempt to couch the theory in ways that account for increasing amounts of the variance in behavior has been one of the main engines driving modern learning theory. Models have been the agents of progress, the go-betweens that reshaped both our theoretical inferences about the conditioning processes, and our modes of analysis of the data. In this theoretical-empirical dialog, the Rescorla-Wagner (R-W) model has been paragon.

Despite the elegant mathematical form of their arguments, the predictions of recent learning models are almost always qualitative—a particular constellation of cues is predicted to block or enhance conditioning more than others, due to their differential associability, or their history of association, and those effects are measured by differences in speed of acquisition or extinction, or as response rate in test trials. Individual differences, and the brevity of learning and extinction processes, make convergence on meaningful parametric values difficult: There are nothing like the basic constants of physics and chemistry to be found in psychology. To this is the added difficulty of a general analytic solution of the R-W model (Danks, 2003; Yamaguchi, 2006). As Bitterman astutely noted, the residue of these difficulties leaves predictions which are at best ordinal, and dependent on simplifying assumptions concerning the map from reinforcers to associations, and from associations to responses:

The only thing we have now that begins to approximate a general theory of conditioning was introduced more than 30 years ago by Rescorla and Wagner (1972). … An especially attractive feature of the theory is its statement in equational form, the old linear equation of Bush and Mosteller (1951) in a different and now familiar notation, which opens the door to quantitative prediction. That door, unfortunately, remains unentered. Without values for the several parameters of the equation, associative strength cannot be computed, which means that predictions from the theory can be no more than ordinal, and even then those predictions are made on the naïve assumption of a one-to-one relation between associative strength and performance. (Bitterman, 2006, p. 367)

To pass through the doorway that these pioneers have opened requires techniques for estimating parameters in which we can have some confidence; and to achieve that requires a database of more than a few score learning and testing trials. But most regnant paradigms get only a few conditioning sessions out of an organism (see, e.g., Mackintosh, 1974), whereupon the subject is no longer naive. To reduce error variance, therefore, data must be averaged over many animals. This is inefficient in terms of data utilization, and also confounds the variability of learning parameters as a function of conditions with the variability of performance across subjects (Loftus & Masson, 1994). The pooled data may not yield parameters representative of individual animals; when functions are nonlinear, as are most learning models, the average of parameters of individual animals may deviate from the parameters of pooled data (Estes, 1956; Killeen, 2001). Averaging the output of “large N” studies is therefore an expensive and non-optimal way to narrow the confidence intervals on parameters (Ashby & O'Brien, 2008).

Most learning is not in any case the learning of novel responses to novel stimuli. It is refining, retuning, reinstating or remembering sequences of action that may have had a checkered history of association with reinforcement. In the present article, we make a virtue of the necessity to work with non-naïve animals, to explore ways to compile adequate data for convergence on parameters, and prediction of data on an instance-by-instance basis. Our strategy is to use voluminous data sets to choose among learning processes that permit both Pavlovian and Skinnerian associations. Our tactic is to develop and deploy general versions of the linear learning equation—an error-correction equation in modern parlance—to characterize repeated acquisition, extinction and reacquisition of conditioned responding.

Perhaps the most important problem with the traditional paradigm is its ecological validity: Conditioning and extinction acting in isolation may occur at different rates than when occurring in mélange (Rescorla, 2000a, 2000b). This limits the generalizability of acquisition-extinction analyses to newly acquired associations. A seldom-explored alternative approach consists of setting up reinforcement contingencies that engender continual sequences of acquisition and extinction. This would allow the estimation of within-subject learning parameters on the basis of large data sets, thus increasing the efficiency of data use and disentangling between-subject variability in parameter estimates from variability in performance. Against the possibility that animals will just stop learning at some point in extended probabilistic training, Colwill and Rescorla (1988; Colwill & Triola, 2002) have shown that, if anything, associations increase throughout such training.

One of Skinner’s many innovations was to examine the effects of mixtures of extinction and conditioning in a systematic manner. He originally studied Fixed-Interval schedules under the rubric “Periodic Reconditioning” (Skinner, 1938). But absent computers to aggregate the masses of data his operant techniques generated, he studied the temporal patterns drawn by cumulative recorders (Skinner, 1976). Cumulative records are artful and sometimes elegant; but difficult to translate into that common currency of science, numbers (Killeen, 1985). With a few notable exceptions (e.g., Davison & Baum, 2000; Shull, 1991; Shull, Gaynor, & Grimes, 2001), subsequent generations of operant conditioners tended to aggregate data and report summary statistics, even though computers had made a plethora of analyses possible. Limited implementations of conditional reconditioning have begun to provide critical insights on learning (e.g., Davison & Baum, 2006).

Recent contributions to the study of continual reconditioning are found in Kacelnik and Reboreda (1993), Killeen (2003), and Shull and Grimes (2006). The first two studies exploited the natural tendency of animals to approach signs of impending reinforcement, known as sign-tracking (Hearst & Jenkins, 1974; Janssen, Farley, & Hearst, 1995). Sign-tracking has been extensively studied as Pavlovian conditioned behavior (Hearst, 1975; Locurto, Terrace, & Gibbon, 1981; Vogel, Castro, & Saavedra, 2006). It is frequently elicited in birds using a positive automaintenance procedure (e.g., Perkins, Beavers, Hancock, Hemmendinger, & Ricci, 1975), in which the illumination of a response key is followed by food, regardless of the bird’s behavior. Kacelnik and Reboreda and Killeen recorded pecks to the illuminated key as indicators of an acquired key-food association. In both studies a negative contingency between key pecking and food, known as negative automaintenance (Williams & Williams, 1972), was imposed. In negative automaintenance an omission contingency is superimposed such that key pecks cancel forthcoming food deliveries, whereas absent key pecks, food follows key illuminations. Key-food pairing elicits key pecking (conditioning), which, in turn, eliminates the key-food pairings, reducing key pecking (extinction), which re-establishes key-food pairings (conditioning), and so on. This generates alternating epochs of responding and non-responding, in which responding eventually moves off key or lever (Myerson, 1974; Sanabria, Sitomer, & Killeen, 2006), and, to a naive recorder, “extinguishes”. Presenting food whether or not the animal responds provides a more enduring, but no less stochastic, record of conditioning (Perkins et al., 1975). The data look similar to those shown in Figure 2 below; a self-similar random walk ranging from epochs of non-responding to epochs of responding with high probabilities. Such data are paragons of what we wish to understand: How does one make scientific sense of such an unstable dynamic process? A simple average rate certainly won’t do. Killeen (2003) showed that data like these had fractal properties, with Hurst exponents in the “pink noise” range. But, other than alerting us to control over multiple time scales, this throws no new light on the data in terms of psychological processes.

Figure 2.

Moving averages of the number of responses per 5-s trial over 25 trials from one representative subject and condition (Pigeon 98, first condition, 40 s ITI).

To generate a data-base in which pecking is being continually conditioned and extinguished, we instituted probabilistic classical conditioning, with the unconditioned stimulus (US) generally presented independently of responding. Using this paradigm, we examined the effect of duration of inter-trial interval (ITI; Experiment 1), duration of conditioned stimulus (CS; Experiment 2), and peck-US contingency (Experiment 3) on the dynamics of key peck conditioning and extinction.

Experiment 1 –Effects of ITI Duration and US Probability

Method

Subjects

Six experienced adult homing pigeons (Columba livia) were housed in a room with a 12:12-hr day:night cycle, with dawn at 6:00 am. They had free access to water and grit in their home cages. Running weights were maintained just above their 80% ad libitum weight; a pigeon was excluded from a session if its weight exceeded its running weight by more than 7%. When required, supplementary feeding of ACE-HI pigeon pellets (Star Milling Co.) was given at the end of each day, no fewer than 12 hrs before experimental sessions were conducted. Supplementary feeding amounts were based equally on current deviation and on a moving average of supplements over the last 15 sessions.

Apparatus

Experimental sessions were conducted in three MED Associates test chambers (305 mm long, 241 mm wide, and 292 mm high), enclosed in sound and light-attenuating boxes equipped with a ventilating fan. The sidewalls and ceiling of the experimental chambers were clear plastic. The floor consisted of thin metal bars above a catch pan. A plastic translucent response key 25 mm in diameter was located 70 mm from the ceiling, centered horizontally on the front of the chamber. The key could be illuminated by green, white, or red light emitted from diodes behind the keys. A square opening 77 mm across was located 20 mm above the floor on the front panel, and could provide access to milo grain when the food hopper (Coulbourne Instruments, part H14-10R) was activated. A house light was mounted 12 mm from the ceiling on the back wall. The ventilation fan on the rear wall of the enclosing chamber provided masking noise of 60 dB. Experimental events were arranged and recorded via a Med-PC interface connected to a PC computer controlled by Med-PC IV software.

Procedure

Each session started with the illumination of the house light, which remained on for the duration of the session. Sessions started with a 40-s ITI, followed by a 5-s trial, for a total cycle duration of 45 s. During the ITI only the house light was lit; during the trial the center response key was illuminated white. After completing a cycle, the key light was turned off for 2.5 s, during which food could be delivered. Two and a half seconds after the end of a cycle, a new cycle started, or the session ended and the house light was turned off. Food was always provided at the end of the first trial of every session. Pecking the center key during a trial had no programmed effect.

Initially, food was accessible for 2.5 s with reinforcement p = .1 at the end of every trial after the first, regardless of the pigeon’s behavior. In subsequent conditions, the ITI was changed from 40 s to 20 s, and then to 80 s for 3 pigeons; for the other 3 pigeons, ITI was changed to 80 s first, and then to 20 s. Inter-trial intervals for all pigeons were then returned to 40 s. Each session lasted for 200 cycles when ITI = 20 s, 100 cycles when ITI = 40 s, and 50 cycles when ITI = 80 s. In the last condition, the probability of reinforcement was reduced to .05 at the 40s ITI. One pigeon (#113) had ceased responding by the end of the .1 series, and was not run in the .05 condition. Table 1 arrays these conditions and the number of sessions at each.

Table 1.

Conditions of Experiment 1

Order	ITIa	Pb	Sessions
1	40 s	.1	20–21
2	20 s, 80 s	.1	21–23
3	80 s, 20 s	.1	20–22
4	40 s	.1	21–23
5	40 s	.05	24–29

Note: Half the subjects experienced the extreme ITIs in the order 20 s 80 s, half in the other order.

^aITI is Inter-trial Interval

^bp is the probability of the trial ending with food.

Results

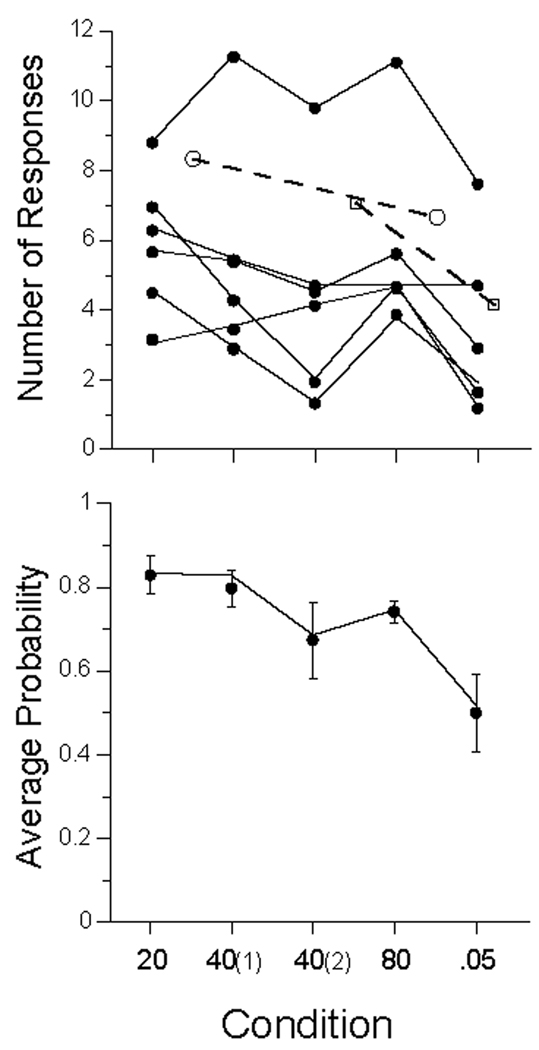
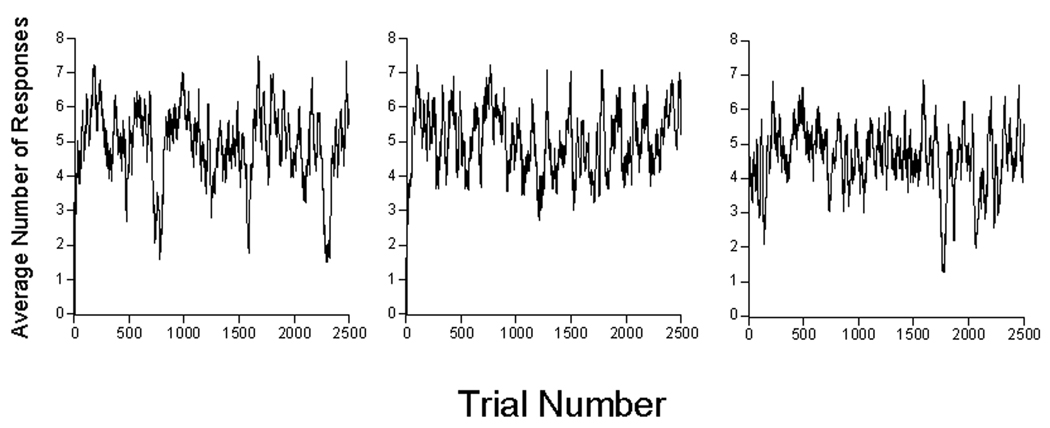
The first dozen trails of each condition were discarded, and the responses in the remaining trials, averaging 2500 per condition, are presented in the top panel of Figure 1 as mean number of responses per 5-s trial. The high-rate subject at the top of the graph is P106 (cf Figure 3 below). There appears a slight decrease in average response rates as the ITI increased, and a larger decrease when the probability of food decreased from .1 to .05. Rates in the second exposure to the 40 s condition were lower than the first. These changes are echoed in the lower panel, which gives the relative frequency of at least one response on a trial. The interposition of other ITIs between the first and second exposure to the 40-s ITI caused a slight decrease in rate and probability of responding in 5 of the 6 birds, although the spread in rates in the top panel and the error bars in the bottom, indicate that that trend would not achieve significance.

Figure 1.

Data from Experiment 1. Top Panel: average number of responses per trial (dots) for each subject., ranging from Pigeon 106 (top curve) to Pigeon 105 (bottom in condition 20). Open symbols represent data from Perkins and associates (1975). Bottom panel: Average probability of making at least one response on a trial averaged over pigeons; bars give standard errors. Unbroken lines in both panels are from the MP model, described later in the text.

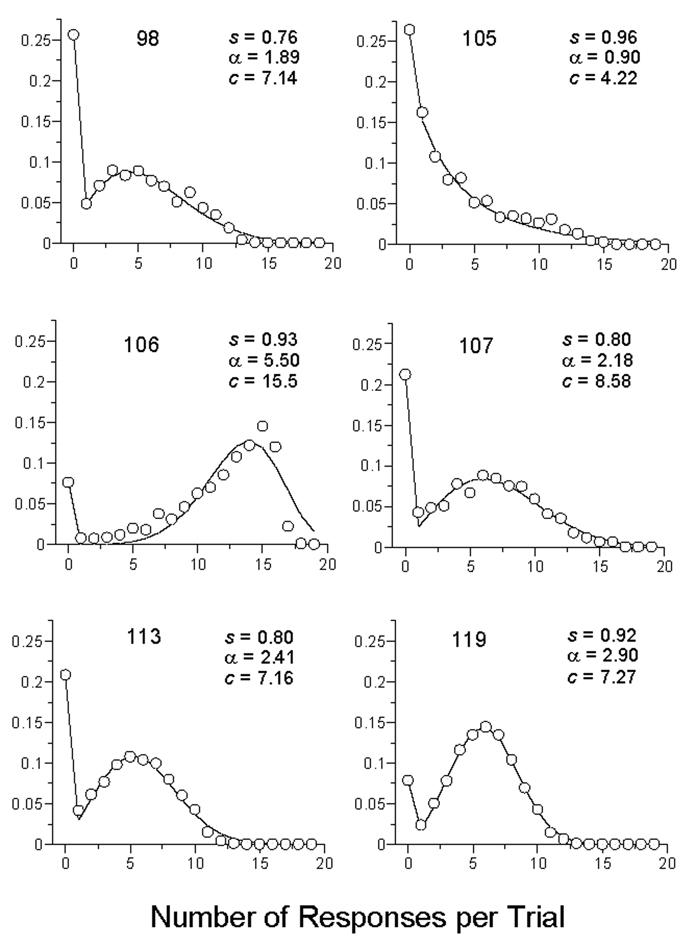
Figure 3.

The relative frequency of trials containing 0, 1, 2, … responses. The data are from all trials of the first condition of Experiment 1. The curves are drawn by the Weibull response rate model (Equation 1). The parameter s is the probability of being in the response state; the complement of this probability accounts for most of the variance in the first data point. The parameter α dictates the shape, from exponential (α = 1) to approximately normal (α ≈ 3) to increasingly peaked (α ≈ 5). The parameter c is proportional to the mean number of responses on trials in the response state, and gives the rank order of the curves in Figure 1 at condition 20.

These data seem inconsistent with the many studies that have shown faster acquisition of the key-peck response at longer ITIs. But the present data were probabilistically-maintained responses over the course of many sessions. Only one other report, that of Perkins and associates (1975), constitutes a relatively close prequel to this one. These authors maintained responding on schedules of non-contingent partial reinforcement after CSs associated with different delays, probabilities, and ITIs. They used 5 different key-colors associated with different conditions within each study. Those that come closest to those of the present experiment are shown as open symbols in Figure 1. The circles represents the average response rate of 4 pigeons on 4-s trials (converted to this 5-s base) receiving reinforcement on 1/6 (~16.7%) of the trials, at ITIs of 30 s (first circle) and 120 s (second circle). These data also indicate a slight decrease in rates with increasing ITIs. These investigators also reported a condition with 8-s trials and 60-s ITIs involving probabilistic reinforcement. The first square in Figure 1 shows the average rate (per 5 s) of 4 pigeons at a probability of 3/27 (~11.1%), and the second at a probability of 1/27 (~3.7%). Their subjects, like ours (and like a few other studies reported by these authors) showed a decrease in responding with a decrease in probability of reinforcement.

Any inferences one may wish to draw concerning these data are chastened by a glance at the inter-subject variability of Figure 1 and of Perkins and associates’ (1975) data. The effect size is small given that variability, and in fact some authors such as Gibbon, Baldock, Locurto, Gold, and Terrace (1977) report no effect of ITI on response rate in sustained automaintenance conditions; others (e.g., Terrace, Gibbon, Farrell, and Baldock, 1975) report some effect. Representing inter-trial variability visually is no simpler than characterizing inter-subject variability; Figure 2 gives an approximation for one subject (P98) under the first 40 s ITI condition, with data averaged in running windows of 25 trials. There is an early rise in rates to around 6 per trial, then slow drift down over the first thousand trials, with rates stabilizing thereafter at around 4 responses per trial. There may be within-session warm-up and cool down effects not obvious in this figure. We may proceed with similar displays and characterizations of them for each of the subjects in each of the conditions—all different. Or we may average performance over the whole of the experimental condition, as we did to generate the vanilla Figure 1. Or we may average data over the last 5 or 10 sessions as is the traditional modus operandi for such data. But such averages reduce a performance yielding thousands of bits of data to a report conveying only a few bits of information. As is apparent from the (smoothed) trace of Figure 2, the averages do not tell the whole story. How do we pick a path between the over-simplification of Figure 1, and the overwhelming complexity of Figures such as 2? And how do we tell a story of psychological processes, rather than of procedural results? Models help, assayed next.

Analysis: The Models

1. The Response Output Model

The goal of this research is to develop a procedure that can provide a more informative characterization of the dynamics of conditioning. To do this we begin analysis with the simplest and oldest of learning models, a linear learning model of associative strength. These analyses have been in play for over half a century (Bower, 1994; Burke & Estes, 1956; Bush & Mosteller, 1951; Couvillon & Bitterman, 1985; Levine & Burke, 1972), with the Rescorla-Wagner model a modern avatar (Miller, Barnet, & Grahame, 1995; Wasserman & Miller, 1997). Because associative strengths are asymptotically bounded by the unit interval, it is seductive to think that they can be directly mapped to probabilities of responding, or to the probabilities of being in a conditioned state. Probabilities can be estimated by taking the number of trials containing at least one response within some epoch, say, 25 trials, and dividing that by the number of trials in that epoch (cf. Figure 2). There are three problems with this approach:

1. Twenty-five trials is an arbitrary epoch which may or may not coincide with a meaningful theoretical/behavioral window.

2. Information about the contingencies that were operative within that epoch are lost, along with the blurring of responses to them.

3. Parsing trials into those with and without a response discards information. Response probability makes no distinction between trials containing one response and trials containing 10 responses, even though they may convey different information about response strength.

4. As Bitterman noted above, associative strengths are not necessarily isomorphic with probability (Rescorla, 2001).

The map between response rates and inferred strength must be the first problem attacked. The place to start is by looking at, and characterizing, the distribution of responses during a CS. Figure 3 displays the relative frequency of 0, 1, 2, … responses during a trial in the first condition of Experiment 1 for each of its participants.

The curves through the distributions are linear functions of Weibull densities:

$$\begin{array}{l}p\left(n=0\right)=s_i\cdot w\left(n,\alpha ,c\right)+1-s_i,\hfill \\ p\left(n>0\right)=s_i\cdot w\left(n,\alpha ,c\right).\hfill \end{array}$$ (1)

The variable s_i is the probability that the animal is in the response state on the i^th trial. For the data in Figure 3, this is averaged over all trials. The w-function is the Weibull density with index n for the actual number of responses during the CS, the shape parameter α, and the scale parameter c, which is proportional to the mean number of responses on a trial. The first line of (1) gives the probability of no responses on a trial: It is the probability that the animal is in the response state (s_i) and makes no responses (w(n, α, c)), plus the probability that it is out of the response state (1 − s_i). The second line gives the probabiilty all non-zero responses.

The Weibull distribution is a generalization of the Exponential/Poisson distribution that was recommended by Killeen, Hall, Reilly, and Kettle (2002) as a map from response rate to response probability. That recommendation was made for free operant responding during brief observational epochs. The Poisson also provides an approximate account of the response distributions shown in Figure 2. It is inferior to the Weibull, however, even when the additional shape parameter is taken into account using the Akaike Information Criterion (AIC). The Weibull distributionⁱ is:

$$W\left(n,\alpha ,c\right)=1-e^{-(n/c{)}^{\alpha }}$$ (2)

According to this model, when the animal is in a response state, it begins responding after trial onset and emits n responses during the course of that trial. It is obvious that when α = 1, the Weibull reduces to the exponential distribution recommended by Killeen and associates (2002). In that case, there is a constant probability 1/c of terminating the response state from one response to the next, and the cumulative distribution is the concave asymptotic form we might associate with learning curves. Pigeon 105 exemplifies such a shape parameter, as witnessed by the almost-exponential shape of its density shown in Figure 3. Just below him, Pigeon 107 has a more representative shape parameter, around 2. Whenever α > 1, as was generally found here, there is an increasing probability of terminating responding as the trial elapses—the hazard function increases. When α is slightly greater than 3, the function most closely approximates the normal distribution, as seen in the data for P119. Pigeon 106, familiar from the top of Figure 1, has the most extreme shape parameter seen anywhere in these experiments, α ≈ 5. The poor fit of the function to this animal is due to his “running through” many trials, which were not long enough for his distribution to come to their natural end.

It is the Weibull density, the derivative of Equation 2, that drew the curves through the data in Figure 3. The density is easily called as a function in Excel® as = Weibull(n, α, c, false). It is readily interpreted as an extreme value distribution, one complementary to that shown to hold for latencies (Killeen et al., 2002). In this paper the Weibull is not used as part of a theory of behavior, but rather as a convenient interface between response rates and the conditioning machinery. Conditioning is assumed to act on s, the probability of being in the response state, a mode of activation (Timberlake, 2000, 2003) that supports key-pecking.

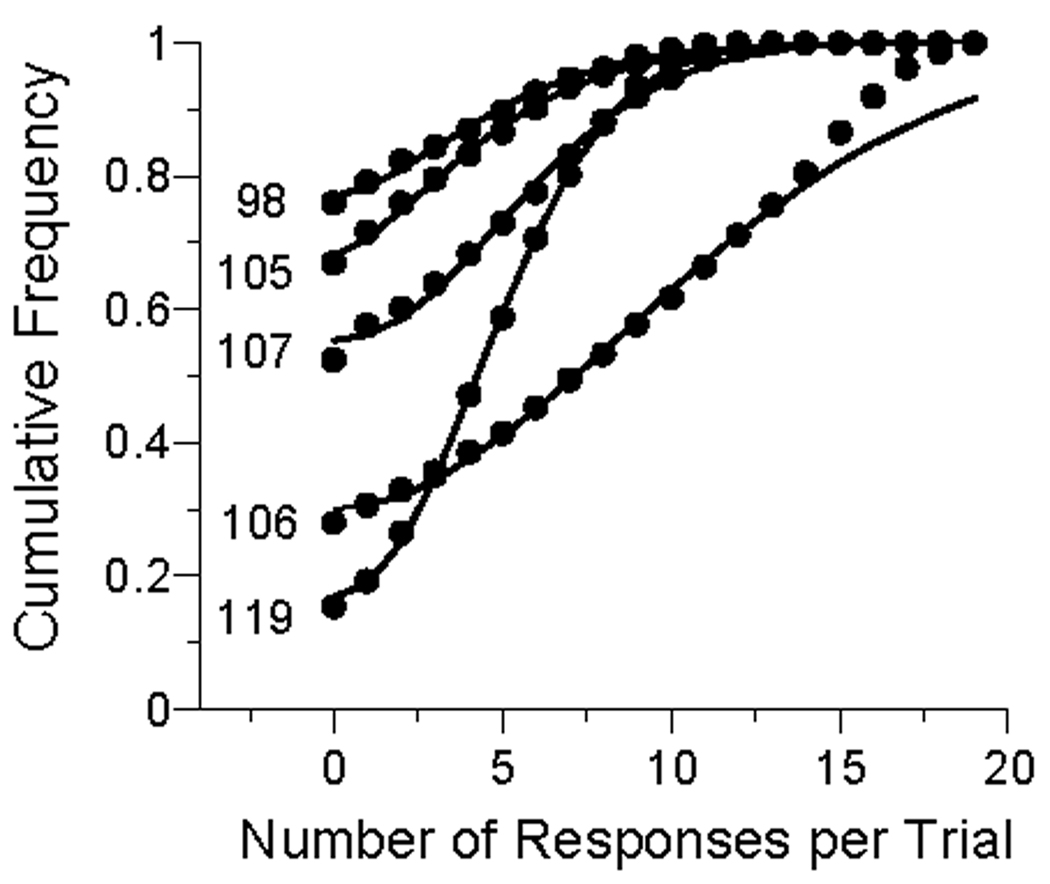
Does the Weibull continue to act as an adequate model of the response distribution after tens of thousands of trials? For a different, and more succinct, picture of the distributions, in Figure 4 we plot the cumulative probability of emitting n responses on a trial, along with the linear functions of the Weibull distribution. As before, the y-intercept of the distribution is the average probability of not making a response; the corresponding theoretical value is the probability of being out of the state, plus the (small) probability of being in the state but still not making a response. Thereafter, the probability of being in the state multiplies the cumulative Weibull distribution. The fits to the data are generally excellent, except, once again, for P106, who did not have time for a graceful wind-down. This subject continues to “run through” the end of the trial, a good fit requires the Weibull distribution to be “censored”, involving another parameter, which was not deemed worthwhile for its present purposes.

Figure 4.

The cumulative frequency of trials containing 0, 1, 2, … responses. The data are from all trials of the last condition of Experiment 1. The curves are drawn by the Weibull response rate model (Equation 1), using the distribution function, rather than the density.

2. Changes in response state probability: Momentum and Pavlovian conditioning

In his analysis of the dynamics of responding under negative automaintenance schedules, Killeen (2003) found that the best first-order predictor was the probability that the animal was in a response state, as given by a linear average of it’s probability of being in that state on the last trial, and the behavior on the last trial. In the case of a trial in which a response occurred, the probability of being in the response state is incremented toward its ceiling (θ = 1) using the classic (Killeen, 1981) linear average:

$$s_i^{\prime }=s_i+{\pi }_R\left(\theta -s_i\right)$$ (3)

where pi (π) is a rate parameter. Pi will take different values depending on the contingencies: π _R subscripts the Response, being instantiated as π_P on trials containing a peck, and π_Q on quiet trials. Theta (θ) is 1 on trials that predict future responding, and 0 on trials that predict quiescence. Thus, after a trial on which the animal responded, the probability of being in the response state on the next trial will increase as:

$$s_i^{\prime }=s_i+{\pi }_P\left(1-s_i\right),$$

whereas after a trial that contained no peck, it will decrease as:

$$s_i^{\prime }=s_i+{\pi }_Q\left(0-s_i\right).$$

After these intermediate values of strength are computed, they are perturbed by the delivery or non-delivery of food. For that we use a version of the same “exponentially-weighted moving average” of Equation 3:

$$s_{i+1}=s_i^{\prime }+{\pi }_O\left(\theta -s_i^{\prime }\right).$$ (4)

Now the learning parameter π_O subscripts the Outcome (Food or Empty). All of these pi parameters tell us how quickly probability approaches its ceiling or floor, and thus how quickly the state on the prior trial is washed out of control (Tonneau, 2005). For geometric progressions such as these, the mean distance back is (1-π)/π, whenever π > 0. One might say that this is the size of the window on the past when the window is half open. As before, theta (θ) is 1 on trials that strengthen responding, and 0 on trials that weaken it. Thus, after a trial on which food was delivered, we might expect to see the probability of being in the response state on the next trial (s_i+1) increase as:

$$s_{i+1}=s_i^{\prime }+{\pi }_F\left(1-s_i^{\prime }\right),$$

whereas after a trial that contained no food, it might decrease as:

$$s_{i+1}=s_i^{\prime }+{\pi }_E\left(0-s_i^{\prime }\right).$$

These steps may be combined in a single expression, as noted in the Appendix. Although shamefully simple compared to more recent theoretical treatments, such linear operator models can acquit themselves well in mapping performance (e. g. Grace, 2002).

There are four performance parameters in this model corresponding to the four operative contingencies, each with an associated ceiling or floor. We list them in Table 2, where parenthetical signs indicate whether behavior is being strengthened (positive entails that θ = 1) or weakened (negative entails that θ = 0).ⁱⁱ The values assumed by these parameters, as a function of the conditions of reinforcement, are the key objects of our study.

Table 2.

The Momentum/Pavlovian model with events mapped onto direction and rate parameters

Event	Representation
Peck	P: (+/−)πP
No Peck (Quiet)	Q: (+/−)πQ
Food	F: (+/−)πF
Empty/Ext.	E: (+/−)πE

Note: The parentheticals indicate whether the learning process is driving behavior up (positive entails that θ = 1) or down (negative entails that θ = 0); the rate parameters themselves are always positive.

Notice that this model makes no special provision for whether a response and food co-occurred on a trial. It is a model of persistence, or behavioral momentum, and Pavlovian conditioning of the CS. Since these factors may always be operative, it is presented first, and the role of Skinnerian response-outcome associations subsequently evaluated. The model also takes no account of warm-up or cool-down effects that may occur as each session progresses. Covarying these out could only help the fit of the models to the residuals; but it would also put one more layer of parameters between the data and the readers eye.

The matrix of Table 2 is referred to as the Momentum/Pavlov Model, or MP Model. By calling it a model of momentum, it is not meant that a new hypothetical construct is invoked to explain the data. It simply is a way of recognizing that response strength will not in general change maximally upon receipt of food or extinction. Just how quickly it will change is given by the parameters π_P and π_Q. If these are 1, there will be no lag in responsiveness and no need for the construct; if they equal 0, the animal will persist at the current probability indefinitely, and there will be no need for the construct of conditioning. In early models without momentum (that is, where these parameters were de facto 1), goodness of fit was at least e¹⁰ worse than in the model as developed here, and typically worse than the comparison model, to be described below.

3. Implementation

To fit the model to the data we use Equation 1 to calculate the probability of the observed data given the model. Two hypothetical cases illustrate the computation of this probability:

1. Assume the following: no key pecks on trial i, the predicted probability of being in the response state s_i = 2/3, and the Weibull parameters were α = 2, c = 6; then:

   The probability of the data (0 responses) given the model p(d_i | m) is the probability of being:

   1. Out of the response state, 1 − s_i, times the probability of no response when out of the state, 1.0: (1 − 2/3)·1 = 1/3. To that add the probability of being:
   2. In the state, times the probability of no responses in the state: 2/3w(n, 2, 6) = 2/3·0;
   3. the sum of which equals p(d_i = 0 | m)≈ .333 + 0 ≈ 0.333.

2. If four pecks were made on trial i, given the same model parameters, then:

   The probability would be p(d_i = 4 | m) = 0 + 2/3w(n, 4, 6), ≈ 0.142.

The natural logarithm of these conditional probabilities gives the index of merit of the model for this trial: that is, it gives the log-likelihood (LL_i) of the data (given the model) on trial i. These logarithms are summed over the thousands of trials in each condition to give a total index of merit LL (Myung, 2003). Case 1 above added ln(1/3) ≈ −1.1 to the index, whereas Case 2 added ln(.142) ≈ −1.9, its smaller value reflecting the poorer performance of the model in predicting the data on that trial. The parameters are adjusted iteratively to maximize this sum, and thus to maximize the likelihood of the data given the model. The LL is a sufficient statistic, so that it contains all information in the sample relevant to making any inference between the models in question (Cox & Hinkley, 1974).

A base (comparison) model

Log likelihoods are less familiar to this audience than are coefficients of determination—the proportion of variance accounted for by the model. The coefficient of determination compares the residual error (the mean square error) with that available from a simple default model, the mean (whose error term is the variance); if a candidate model can do no better than the mean, it is said to account for zero percent of the variance around the mean. In like manner, the maximum likelihood analysis becomes more interpretable if it is compared to a default, or Base model. The Base model we adopt has a similar structure to our candidate model: It uses Equation 1, and updates the probability of being in the response state as a moving average of the recent probability of a response on a trial:

$$s_{i+1}=\gamma P_i+\left(1-\gamma \right)s_i,0<\gamma <1.$$ (5)

where gamma (γ) is the weight given to the most recent event, and P takes a value of 1 if there was a response on the prior trial and 0 otherwise. Equation 5 is a linear average, also called an exponentially weighted moving average. It can also be written as s_i+1 = s_i + γ(P_i − s_i), which reveals its similarity to the Momentum/Pavlovian model, with the one parameter γ replacing the four contingency parameters of that model. The base model attempts to do the best possible job of predicting future behavior from past behavior, with its handicap being ignorance as to whether food or extinction occurred on a trial. It is a model of perseveration, or momentum, pure and simple. It invokes 3 explicit parameters: γ, α, and c. Other details are covered in the Appendix.

4. An Index of Merit for the Models

The log-likelihood does not take into account the number of free parameters utilized in the model. Therefore we employ a transformation of the log-likelihood that takes model parsimony into account. The Akaike Information Criterion, or AIC, (Burnham & Anderson, 2002) corrects the log likelihood of the model for the number of free parameters in the model, in order to provide an unbiased estimate of the information theoretic distance between model and data:

$$\mathit{\text{AIC}}=2\left(n_P-\mathit{\text{LL}}\right)$$ (6)

where n_P is the number of free parameters, and LL is the total log-likelihood of the data given the model. (We do not require the secondary correction for small sample size, AIC_C).

We compare the models under analysis with the simple perseveration model, the Base model, characterized by Equations 1 and 5. This comparison is done by subtraction of their AICs. The smaller the AIC, the better the adjusted fit to the data. There are n_P = 3 parameters in the base model (hereinafter Base), and 6 parameters (or 8 in later versions) in the candidate model (hereinafter Model), so the relative AIC is:

$$\begin{array}{ll}\mathit{\text{Merit}}\hfill & =\mathit{\text{ Relative AIC}}=\mathit{\text{AIC}}(\mathit{\text{Base}})-\mathit{\text{AIC}}(\mathit{\text{Model}})\hfill \\ \hfill & =2\left(3-{\mathit{\text{LL}}}_B\right)-2\left(6-{\mathit{\text{LL}}}_M\right)\hfill \\ \hfill & =2\left({\mathit{\text{LL}}}_M-{\mathit{\text{LL}}}_B\right)-6\hfill \end{array}$$ (7)

Because logarithms of probabilities are negative, the actual log likelihoods are negative. However, our index of merit subtracts the model AIC from the base AIC, so that it is generally positive, and is larger as the model under purview is better than the Base model. The relative AIC is a linear function of the log-likelihood ratio of Model to Base (LLR = log[(likelihood of Model)/(likelihood of Base)]). Because of the additional free parameters of the Model, it must account for e³ as much variance as the Base model just to break even. An index of merit of 4 for a model means that, under that model, the data are e⁴—approximately 50 times—as probable as under the Base model, after taking into account the difference in number of free parameters. A net merit of 4 is our criterion for claiming strong support for one model over another. If the prior probabilities of the model under consideration and the Base (or other comparison) model are deemed equal, Bayes theorem tells us that when the index of merit is greater than 4 (after handicapping for excess parameters) then the posterior odds of the candidate model compared to the comparison is at least 50/1.

The Base model is nested in the Pavlovian/Momentum model: Setting π_Q = −π_P = γ, and π_F = π_E = 0 reduces it to the Base model. For summary data we also display the Bayesian Information Criterion (BIC; Schwarz, 1978), which sets a higher standard for the admission of free parameters in large data sets such as ours; BIC ≈ −2LL + kln(n). This modeling framework is now applied to the results of the first experiment.

The index of merit is relative to the default Base model, just as the “proportion of variance accounted for” in quotidian use is relative to a default model (the mean). If the default model is very bad, the candidate model looks very good by comparison. If for instance we had use the mean response rate or probability over all sessions in a condition as the default model, the candidate would be on the order of e⁴⁰⁰ better in most of the experiments. A tougher test would be to contrast the present linear operator model with the more sophisticated models in the literature, but that is not, per reviewers’ advice, included here.

Applying the Models

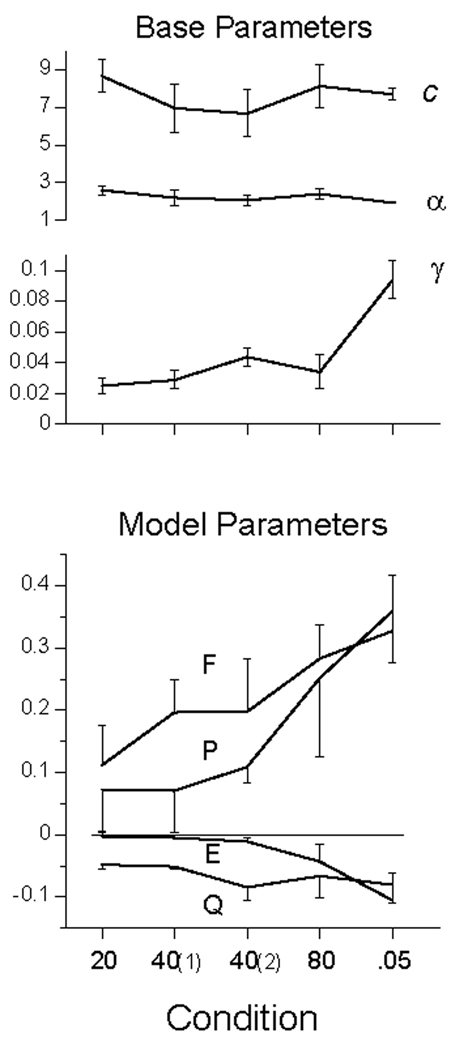
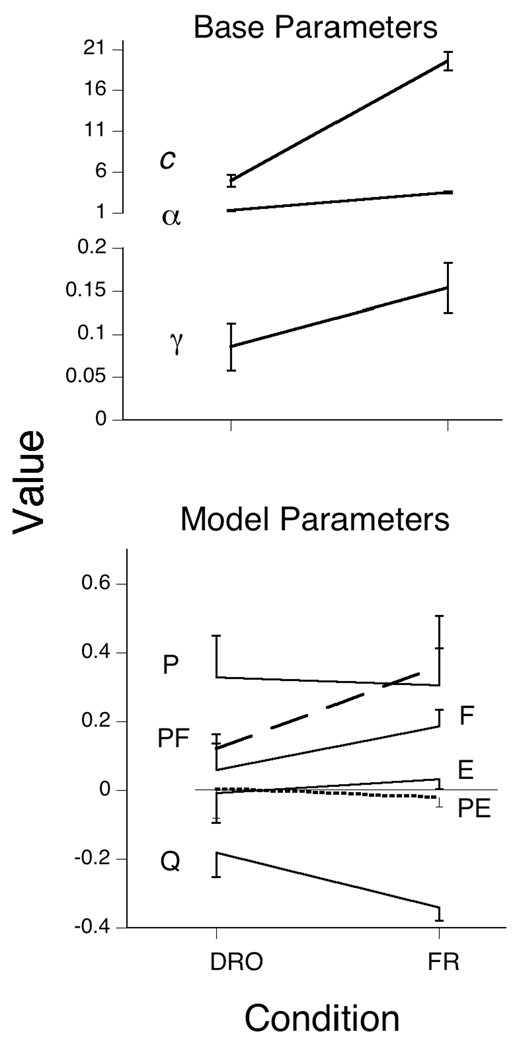
The AIC advantage of the Pavlovian model over the Base model averaged 43 AIC points for the first four conditions, in which only 2 of the 24 subject by condition comparisons did not exceed our criterion for strong evidence (improvement over the Base by 4 points). For the last, p = .05, condition the average merit jumped to 183 points. Figure 5 shows that the Weibull response rate parameters were little affected by the varied conditions. The average value of c, 8.2, corresponded to a mean of 7.3 responses per trial on trials where a response was made (the mean is primarily a function of c, but also of α). The average value of the shape parameter α was 2.4: The modal response distribution looked like that of Pigeon 113 in Figure 3. The values of these Weibull parameters were always essentially identical for the Base and MP models, and were therefore shared by them.

Figure 5.

The average parameters of the Base and MP models for Experiment 1. The first four conditions are identified by their ITI, with the first and second exposure to the 40s ITI noted parenthetically. The same Weibull parameters, c and α, were used for both models. In the last condition, the probability of hopper activation on a trial was reduced from .1 to .05, with ITI = 40. The error bars delimit the SEM.

The values of gamma, γ, the perseveration constant in the Base model, averaged .038 in the first four conditions, and increased to .100 in the p = .05 condition. This indicates that there was a greater amount of character—more local variance—in this last condition for the moving average to take advantage of; a feature which was also exploited by the MP model. There was no change in the rate of responding—given that the animal is in a response state—as indicated by the constancy of c. All of the decrease seen in Figure 1 was due to changes in the probability of entering a response state, as given by the model and seen in the model’s predictions, traced by the lines in the bottom panel of Figure 1. Parameter values for each animal are listed in Table 3, and indices of merit in Table 4.

Table 3.

Parameter values of the Base and MP models for the data of Experiment 1, and of the MPS model for the p = .05 condition.

B#a	Parb	20	401	402	80	.05	B#	Par	20	401	402	80	.05
98	γ	.02	.03	.05	.02	.08	107	γ	.02	.05	.05	.01	.04
	c	8.78	6.93	5.31	7.77	5.90		c	8.56	8.20	7.47	8.69	8.00
	α	3.00	2.08	1.55	2.30	1.76		α	2.57	2.20	2.11	2.22	2.00
	P	.00	.02	.04	−.01	.27		P	.06	.00	.04	.00	.06
	Q	−.02	−.03	−.05	−.01	−.19		Q	−.03	−.04	−.06	−.01	−.05
	F	.00	.05	.03	.22	.00		F	.29	.27	.12	.30	.30
	E	.00	.00	.00	.00	.01		E	−.02	.00	.00	−.01	.00
	PF	.20	.00	.13	.00	.00		PF	.00	.00	.00	.00	.00
	PE	.00	.00	.00	.00	−.08		PE	.00	.00	.00	.00	−.04
105	γ	.05	.04	.11	.10	.12	113	γ	.02	.05	.04	.03
	c	5.69	5.12	7.18	7.49	5.74		c	6.90	5.45	4.79	6.45
	α	1.56	1.31	2.13	2.33	1.62		α	2.51	2.22	1.76	2.46
	P	.04	.05	.19	.61	.32		P	.02	.06	.06	.68
	Q	−.04	−.04	−.24	−.15	.02		Q	−.02	−.06	−.04	.12
	F	.03	.00	.56	.33	.34		F	.00	.14	.00	−.06
	E	.00	.00	.03	−.10	−.30		E	.00	−.01	.00	−.16
	PF	.14	.04	.34	.00	.00		PF	.05	.00	.00	.00
	PE	.00	.02	−.04	.00	.28		PE	.00	.00	−.01	.00
106	γ	.05	.02	.07	.02	.12	119	γ	.01	.01	.03	.02	.06
	c	12.71	13.88	13.29	14.35	12.40		c	8.12	7.17	6.41	7.78	6.76
	α	3.54	4.49	3.55	4.25	2.36		α	3.17	2.92	2.49	2.30	2.44
	P	.05	.10	.18	.17	.30		P	.21	.28	.04	−.01	.48
	Q	−.06	−.07	−.14	−.07	−.16		Q	−.05	−.07	−.04	−.01	−.17
	F	.00	.00	.27	.27	.54		F	.90	.65	.31	.23	.50
	E	.01	.03	.00	−.02	−.03		E	−.02	−.03	.00	.00	.00
	PF	.19	.43	.16	.10	.00		PF	−.02	.00	−.01	.00	.00
	PE	.00	−.01	−.01	.00	−.01		PE	.09	.17	.00	.00	−.04

^aB# is Bird number.

^bPar is parameter: γ the rate constant for the comparison Base model; c the Weibull rate constant; α the Weibull shape constant; and the remaining letters indicate the rate constants brought into play on trials with (P) or without (Q) a response; with (F) or without (E) food; and the Skinnerian interaction terms PF and PE.

Table 4.

Indices of merit for the model comparison of Experiment 1

B#	Metrica	20	401	402	80	.05
98	CD	0.03	0.06	0.17	0.06	0.19
	AIC	9	−1	32	29	115
	BIC	−17	−18	15	20	97
105	CD	0.07	0.02	0.17	0.13	0.16
	AIC	57	72	162	105	375
	BIC	38	55	134	91	352
106	CD	0.17	0.03	0.18	0.05	0.19
	AIC	47	40	69	5	217
	BIC	22	17	46	−14	193
107	CD	0.04	0.09	0.14	0.05	0.11
	AIC	101	40	13	18	88
	BIC	82	34	2	8	70
113	CD	0.04	0.07	0.30	0.03
	AIC	12	27	38	24
	BIC	−7	10	19	9
119	CD	0.02	0.01	0.02	0.07	0.07
	AIC	57	40	8	29	87
	BIC	25	17	−14	19	69
Grp	CD	0.06	0.05	0.16	0.06	0.14
	AIC	47	36	54	35	176
	BIC	24	19	34	22	156

^aThe metrics of goodness of fit for the models are the coefficient of determination, the Akaike information criterion, and the Bayesian information criterion. Values of the last two greater than 4 constitute strong evidence for the MPS model.

The weighted average parameters of the MP model are shown in the bottom panel of Figure 5 (the values for each subject were weighted by the variance accounted for by the model for that subject). Just as autoshaping is fastest with longer ITIs, the impact of the π_F and π_P parameters increases markedly with ITI. The increase in π_F indicates that at long ITIs, the delivery of food, independent of pigeons’ behavior, increases the probability of a response on the next trial. It increases 11% of its distance towards 1.0 in the ITI 20s condition, up to 28% in the ITI 80s condition. Also notice that π_F is everywhere of greater absolute magnitude than π_E, a finding consistent with that of Rescorla (2002a, 2002b).

The increase in π_P indicates that pecking acquires more behavioral momentum as the ITI is increased. The parameter π_Q remains around −7% over conditions (although a drop from −5% to −10% in the first and second replication of the 40 s conditions accounts for the decrease in probability of responding in the second exposure). A trial without a response decreases the probability of a response on the next by 7%. The parameter π_E hovers at zero for the short and intermediate ITIs: Extinction trials add no new information about the animals’ state on the next trial, and do not change behavior from the status quo ante. Under these conditions extinction does not discourage responding. The law of disuse, rather than extinction, is operative: If an animal does not respond, momentum in not responding (measured by π_Q) carries response probability lower and lower. At the longest ITI and in the p = .05 condition, E trials decrease the probability of being in a response state on the next by 4% and 10% respectively. When reinforcement is scarce, both food and extinction matter more, as indicated by increased values of π_F and π_E; but the somewhat surprising effect on π_E is modest compared to the former. The importance of food when it is scarce is substantial—with π_F increasing to over 30% in the p = .05 condition. The fall toward extinction of responding, driven by π_Q and π_E, is arrested only by delivery of food, a strong tonic to responding (π_F), or an increasingly improbable peck, which, as reflected in π_P, is associated with substantially enhanced response probabilities on the next trial.

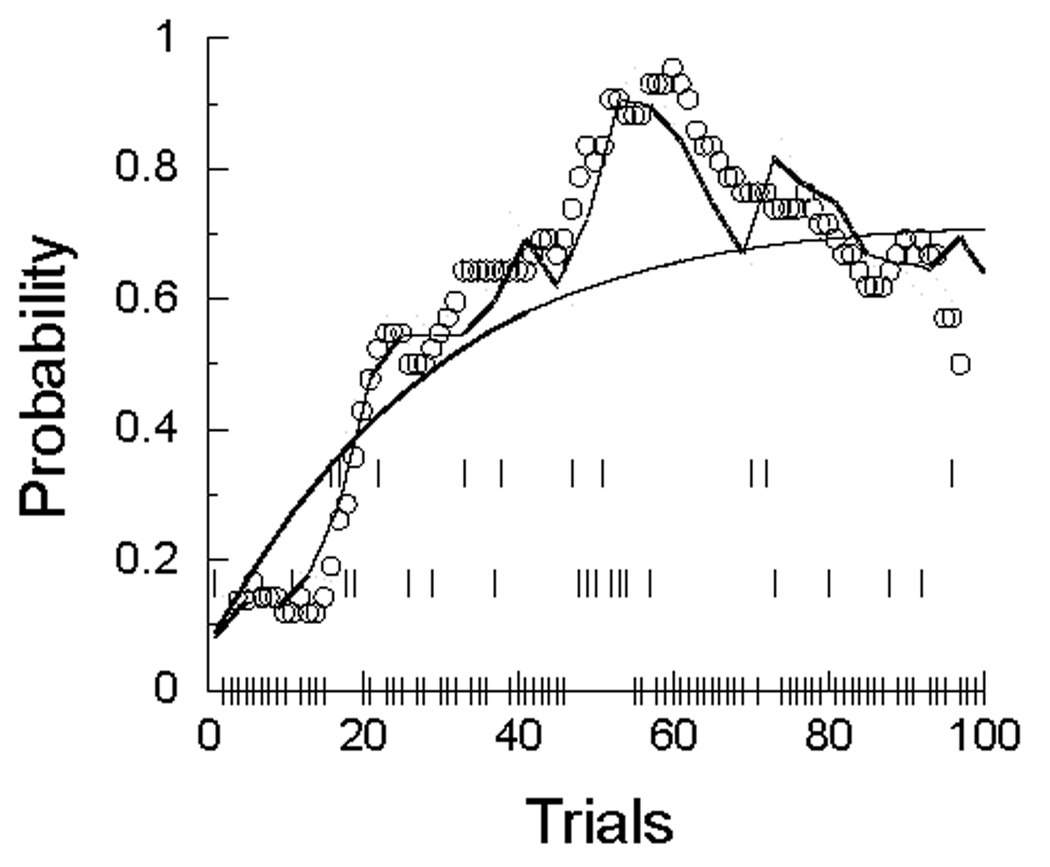
We may see how close the simulations look to the real performance, such as that shown in Figure 2. We did this by replacing the pigeon with a random number generator, using the average parameters from the first condition, shown in Figure 5. The probability of the generator’s entering a response state was adjusted using the MP model, and when in the response state, it emitted responses according to a Weibull distribution with the parameters shown in the top of Figure 5. Figure 6 plots the resulting data in a fashion similar to that shown in Figure 2 (a running average of 25 trials). Comparison of the three panels cautions how different a profile can result from a system operating according to the same fixed parameters once a random element enters. Analyses are wonted that can deal with such vagaries without recourse to averaging over a dozen animals. By analysis on a trial by trial basis, the present models attempt to take a step in that direction.

Figure 6.

Moving averages of the number of responses per 5-s trial over 25 trials from three representative “statrats”, characterized by the average parameters of real pigeons in the first condition, 40 s ITI. The only difference among these three panels is the random number seed for Trial 1. Compare with Figure 2.

These graphs have a similar character to those generated by the pigeons (although they lack the change in levels shown by P98 in Figure 2; a change not clearly shown by most of the other subjects). The challenge is how to measure “similar” in a fashion other than impressionistically. Killeen (2003) showed that responding had a fractal structure, and given the self-similar aspect of these curves, that is likely to be the case here. However, the indices yielded by fractal analysis throw little new light on the psychological processes. The AIC values returned by the model provide another guide for those comfortable with likelihood analyses; they tell us how good the candidate model is relative to a plausible contender.

The variance accounted for in the probability of responding will look pathetic to those used to fitting averaged data: It averages around 10% in Experiment 1, and around 15% in the remaining experiments. But even when the probability of a response on the next trial is known exactly, there is probabilistic variance associate with Bernoulli processes such as these: in particular, a variance of p(1-p). The parameters were not selected to maximize variance accounted for, and in aggregates of data, much of the sampling error that is inevitable in single-trial predictions is averaged out. When the average rate over the next ten trials, rather than the single next trial, are the prediction, the variance accounted for by the matrix models doubles. At the same time, the ability to speak to the trial-by-trial adjustment of the parameters is blunted. Other analyses, educing predictions from the model and testing them against the data, follow.

Hazard functions

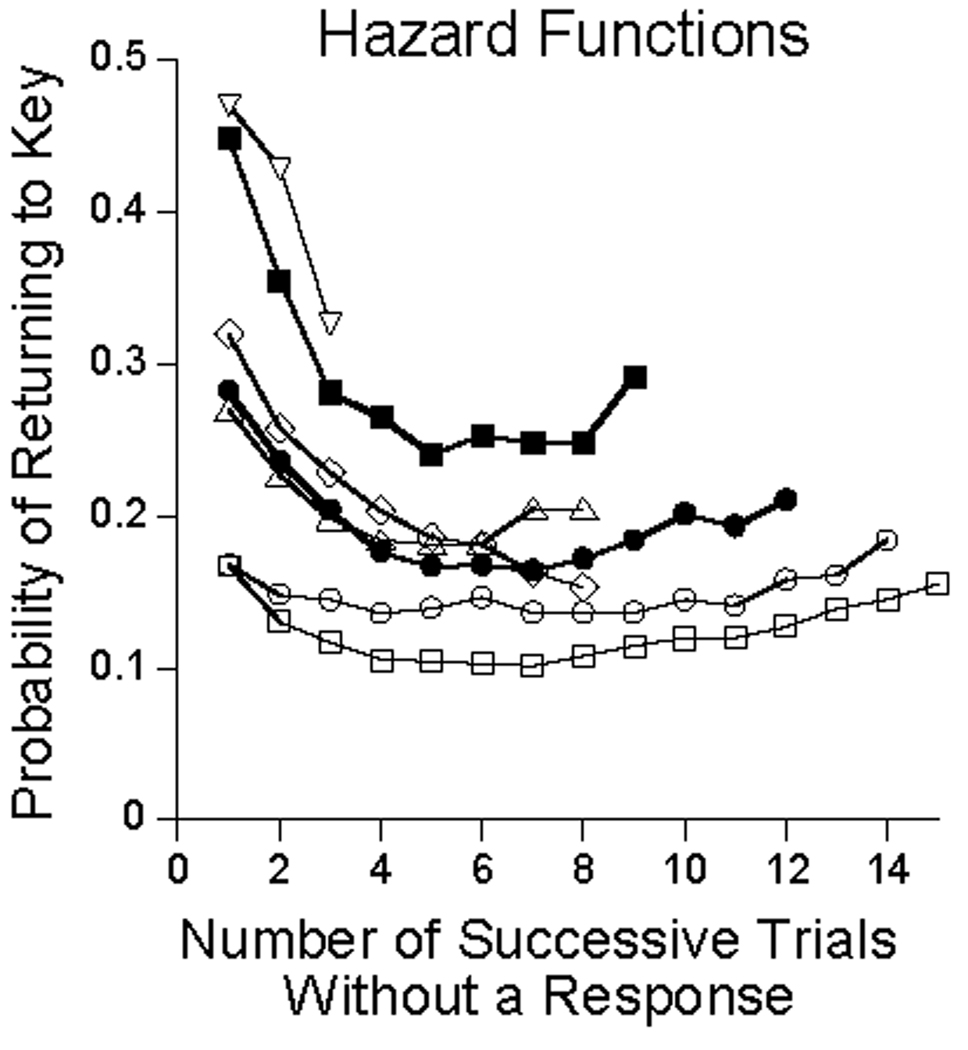
That π_Q and π_E are negative in the p = .05 condition makes a strong prediction about sojourns away from the key: When an animal does not respond on a trial, there is a greater likelihood that he will not respond on the next, and yet greater on the next, and so on. Only free food (or the unlikely peck despite the odds) saves him. The probability of food is 5%, but the cumulative probability is continually increasing, reaching 50% after 15 trials since the first non-response. The probability of returning to the key should decrease at first, flatten and then eventually increase. A simple test of this prediction is possible: plot the probability of returning to the key after various numbers of quiet trials. In making these plots, each point has to be corrected for the number of opportunities left for the next quiet trial. Such plots of marginal probabilities are called hazard functions. If there is a constant probability of returning to the key, as would be the case if returns were at random, the hazard function would be flat. The above analysis predicts hazard functions that decrease under the pressure of the negative parameters, and eventually increase as the cumulative probability of the arrival of food increases.

Figure 7 shows the functions for individual animals (truncated when the residual response probabilities fell to 1%). They show the predicted form. The filled squares shows the averaged results from of running three “statrats” in the program, with parameters taken from the .05 condition of Figure 5. If the model controls behavior the way it is claimed, the output of the statrats should resemble that of the pigeons. There is indeed a family resemblance, although the statrats’ hazard function was more elevated than the average of the pigeons, indicating a greater eagerness to return to the operandum than was the case for the birds. Note also that the predicted decrease—first 8% of the distance to 0 from π_Q and then another 11% from π_E —predicts a decrease to 82% of the initial value after the first quiet. That is, from about 0.45 to 0.37 for the statrats, and from about .28 to about .23 for the average pigeon. These are right in line with the functions of Figure 7. The eventual flattening and slow rise in the functions is due to the cumulative effects of π_F.

Figure 7.

The marginal probability of ending a run of quiet trials. The unfilled symbols are for individual animals, and the filled circles represents their average performance. The hazard function represented by filled squares comes from simulations of the model.

Is momentum necessary?

In the parameters π_P and π_Q the MP model invokes a trait of persistence or momentum, which may appear supererogatory to some readers. However, the base model, the linear average of the recent probability of responding, actually proves a strong contender to the MP model. It embodies the adage “The best predictor of what you will do tomorrow is what you did today”. It is the simplest model of persistence, or momentum. We may contrast it with a MP-minus-M model: that is, adjust the probability of responding on the next trial as a function of food or extinction on the current trial, while holding the momentum parameters at zero. Even though the base model has one fewer parameter, it easily trumps the MP-M model. For example, for P98, the median advantage of the MP model over the base model was 14 AIC points in the .1 condition, and 58 points in the .05 condition. But without the momentum aspect, the MP-M model tumbles to a median of 106 points below the base model in the .1 conditions, and 540 points below in the .05 condition. However one characterizes the action of the π_P and π_Q parameters, their presence in the model is absolutely necessary. This analysis carries the within-session measurement of resistance to change reported by Tonneau, Ríos, and Cabrera (2006) to the next level of contact with data.

Operant conditioning

What is the role of response-reinforcer pairing in controlling this performance? The first analysis of these data (unreported here) consisted of a model involving all interaction terms, and those alone: PF, PE, QF, QE. Although this interaction model was substantially better than the Base model (18 AIC units over all conditions, 73 in the p = .05 condition), it was always trumped by the Momentum/Pavlov model (51 AIC units over all conditions, 183 in the p = .05 condition).

In search of evidence of Skinnerian conditioning, we asked whether there was a correlation between the number of responses on a trial and the probability of responding on the next trial. Any simple correlation could be just due to persistence; but if response-reinforcer contiguity is a factor in strengthening responding, then that correlation should be larger for trials that end with food (r_F) than for trials that end without food (r_E). When many responses occur on a reinforced trial, there are: (a) more responses in close contiguity with the reinforcer, and (b) the last of them is likely to be closer in time to the reinforcer than the case on trials with only a few responses. Therefore there should be a positive correlation between number of responses on trials ending with food, and number of responses on the next trial. It is different for trials that end without food: When many responses occur on a non-reinforced trial, there are many more instances of the response subject to extinction; this should not only undermine a positive correlation, it could drive it negative. We can therefore test for Skinnerian conditioning by correlating the number of responses on F and E trials that had at least one response (the predictors) with the presence or absence of a response on the next trial (the criterion). If contiguity of multiple responses with food strengthens behavior more than contiguity of one response to food, the correlation with subsequent responding should be larger when the trial was followed by food than when it wasn’t. That is, we would expect r_F > r_E. We restrict the analysis to trials with at least one response, so that the correlation isn’t simply driven by the information that the animal is in a response state, which we know from π_P has good predictive value.

We analyzed the data for all subjects from all conditions, and found no evidence for value added by multiple response-reinforcer contiguity. For no animal was the average correlation between predictor and criterion greater when the predictor was followed by food than when it was not. The averages over all subjects and conditions were r_F = 0.035 and r_E = 0.081. With an average n of 150 for r_F and 1470 for r_E for each of the 29 pairs of correlations, the conclusion is unavoidable: Reinforcement on trials with multiple responses did not increase the probability of a response on the next trial any more than did extinction on trials with multiple responses.

Perhaps fitting a delay of reinforcement model from each response to an eventual reinforcer would show evidence of operant conditioning? This was our first model of these data, not reported here. We found no value added by the extra parameter (the slope of the delay-of-reinforcement gradient).

Convinced that there must be some way to adduce evidence of (adventitious) operant conditioning, we turned to the next analysis. It remains possible that reinforcement increases the probability of staying in the response state on the next trial: Possibly the commitment to a behavioral module (Timberlake, 1994), rather than the details of actions within the module, is what gets strengthened by reinforcement. To test this hypothesis, an conditioning factors, π_PF and π_PE, were added to the model. If response-reinforcer contiguity added strengthening/ prediction beyond that afforded by the independent actions of persistence and of food delivery, one or both of these parameters should take values above zero; and should add significantly to predictive accuracy when it does. We measure accuracy with the AIC score; any increase (after handicapping for the added parameter) lends credibility, while increases by at least 4 constitute strong evidence.

The average value of π_PF across the 29 cases was 0.064: that is, the probability of a response on the next trial increased by 6% beyond that predicted by momentum and mere delivery of food (independent of the presence or absence of a peck). For two birds, 107 and 119, there was no advantage, and π_PF remained close to zero, as often negative as positive. Of the 19 remaining pigeon by condition cases, 11 showed an AIC advantage for the added parameter, five of them meeting our criterion for strong evidence. Of these four birds that showed evidence of Skinnerian conditioning, the average value of π_PF was 8%, which may be compared to 16% for π_P and 14% for π_F. Examining the data on a condition-by-condition basis, all four of these pigeons showed evidence of Skinnerian conditioning in the ITI 20 condition (three of them strong evidence), and in all cases but one π_PF was larger than either π_P or π_F. Across all six animals, the advantage of adding the contiguity parameter was 2.6 AIC points at ITI 20, 0.8 at ITI 40, and −1.5 at ITI 80. (The negative value indicates that the cost of the extra parameter in Equation 7 is not repaid by increased predictive ability.) In the p = .05 condition the total advantage conferred by the π_PF parameter increased to 6.4. (When the Skinnerian parameter comes into play, there is typically a readjustment of the other parameters that had been tasked with picking up the slack.) The Skinnerian extinction parameter π_PE was almost never called into play, and exerted negligible improvement in the predictions.

These results indicate that Skinnerian conditioning was strongest where Pavlovian conditioning was weakest—whether that weakness was due to a small ITI-to-trial ratio (ITI 20) or to a less reliable CS (p = .05). This is consistent with the findings of Woodruff, Conner, Gamzu, and Williams (1977). π_PF and π_PE will be retained in subsequent analyses, where the full model will be called the MPS (Momentum/Pavlovian/Skinnerian) model.

Implications for Acquisition and Extinction

Based on Equation 4 and the parameters shown in Figure 5, we may predict the courses of acquisition and extinction in similar contexts—it is given by Equation A5 in the appendix. For the parameters in Figure 5, the MPS model predicts faster acquisition at longer ITIs—the trial spacing effect, along with an increasing dependence on the original starting strength (derived from hopper training) as trial spacing decreases. Pretraining plays a critical role in determining the speed of acquisition (Davol, Steinhauer, & Lee, 2002; Downing & Neuringer, 2003); the current analysis suggests that this is in part due to elevation of the initial probability of a response, s₀, possibly through generalization of hopper stimuli and key stimuli (Sperling, Perkins, & Duncan, 1977; Steinhauer, 1982). Conditioning of the context proceeds rapidly, however, so that more than a few pretraining trials in the same context will slow the speed of subsequent key-conditioning (Balsam & Schwartz, 2004).

The predicted number of trials to criterion show an approximate power-law relation between trials-to acquisition and the inter-trial interval (Gibbon et al., 1977). Those researchers, along with Terrace, Gibbon, Farrell, and Baldock (1975), found that both acquisition, and response probability in steady-state performance after acquisition, co-varied with the ratio of trial duration to ITI. The permutation Gibbon, Farrell, Locurto, Duncan, and Terrace (1980) found that partial reinforcement during acquisition had no effect on trials to acquisition, when those were measured as reinforced trials to acquisition. This is consistent with the acquisition equations in the appendix. Despite these tantalizing similarities, however, the obvious difference in the parameters for the p = .1 and .05 conditions seen in Figure 5 undermines confidence in extrapolations to typical acquisition, where p = 1.0.

It is possible to test the predictions for extinction within the context of the present experiments, where parameter change is not so central an issue, for there were long stretches (especially in the p = .05 condition) without food. The relevant equation, transplanted from the appendix (Equation A6), is:

$$s_{i+1}=s_i\left(1-{\pi }_E\right)\left(1+{\pi }_{P-Q}\left(1-s_i\right)\right),$$ (8)

where the strength s_i+1 gives the probability of entering a response state on that trial. All parameters are positive, with asymptotes of 0 or 1 used as appropriate to the signs shown in Figure 5. Neither π_F nor π_PF appear because there are no food trials in a series of extinction trials, and π_PE is typically small, and its work can be adequately handled by π_E. The probability of responding on a trial decreases with π_E as expected (note the element −π_Es_i)—substantially when s_i is large, not much at all when s_i is small. Only the difference in the two momentum parameters, π_P − π_Q affects the prediction; for parsimony we collapse those into a single parameter representing their difference π_P−Q = π_P − π_Q. Equation 8 makes an apparently counterfactual prediction.

A surprising prediction

Inspection of Figure 5 shows that π_P−Q is generally positive. Because it multiplies the probability of not responding (Equation 8 contains the element π_P−Q(1 − s_i)), on the average π_P−Q increases the probability of responding on each trial, and does so more as s_i gets small. Depending on the specific value of the parameters, this restorative force may be sufficient to forestall extinction. To show this more clearly, we solve Equation 8 for its fixed point, or steady state, which occurs when s_i+1 = s_i:

$$s_{\infty }=1-\frac{{\pi }_E}{{\pi }_{P-Q}\left(1-{\pi }_E\right)},\text{\hspace{1em}where}0<{\pi }_{P-Q}\left(1-{\pi }_E\right)\le {\pi }_E;$$ (9)

this is the level at which responding is predicted to stabilize after a long string of extinction trials.

If response probability fluctuates below the level of s_i, the next response (if and when it occurs, which it does with probability s_i) will drive probability up; and if it fluctuates above this level, the next trial will drive it down. For responding to extinguish, it is necessary that the force of extinction be greater than the restoring force:

$${\pi }_E\ge \frac{{\pi }_{P-Q}}{1+{\pi }_{P-Q}}.$$ (10)

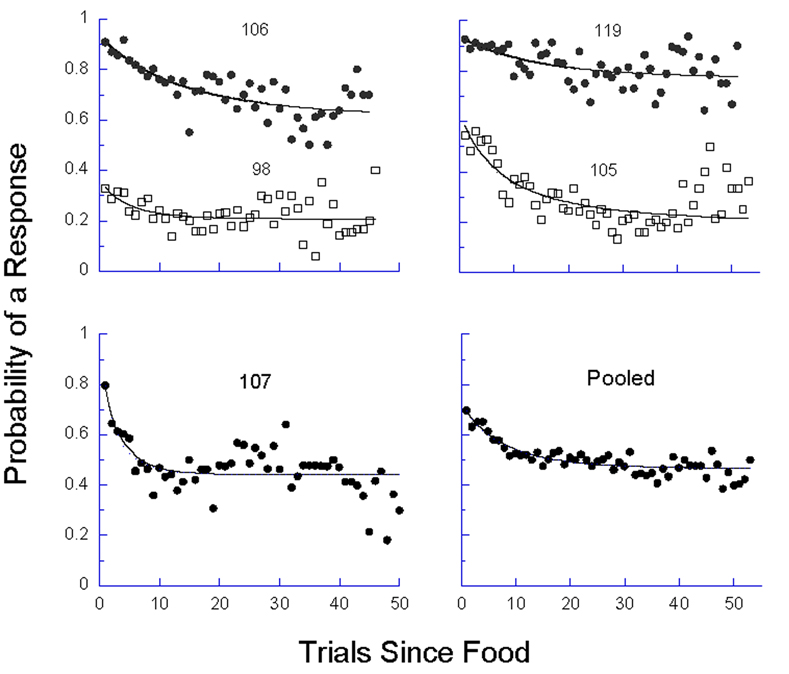
This is automatically satisfied whenever momentum in quiescence, π_Q, is greater than momentum in pecking π_P--whenever π_P−Q is negative. That is especially likely to be the case in rich contexts where quiescence on the target key may be associated with foraging in another patch or responding on a concurrent schedule. For the parameters in Figure 5 under p = .05, however, this is never the case; indeed, the more general inequality of Equation 10 is never satisfied. Therefore Equations 8 and 9 make the egregious prediction that the probability of responding will fall (with a speed dictated by π_E) to a non-zero equilibrium dictated by Equation 9. We may directly test this derivation by plotting the course of extinction within the context of dynamic reconditioning of these experiments. The best data come from the p = .05 condition, which contained long strings of non-reinforced responding. The courses of extinction, along with the locus of Equation 8, is shown in Figure 8.

Figure 8.

The average probability of responding as a function of the number of trials since reinforcement, from the p = .05 condition. The number of observations decrease by 5% from one trial to the next, from hundreds for the first points to 10 for the last displayed. The curve comes from Equation 8, using parameters π_P−Q and π_E fit to these data.

Do Equations 8–10 condemn the birds to an endless Sisyphean repetition of unreinforced responding? If not, what then saves them? Those equations are continuous approximations of a finitary process. Because the right-hand side of Equation 8 is multiplied by s_i, if that probability ever does get close enough to 0 through a low-probability series of quiescent trials, it may never recover. It is also likely that after hundreds of extinction trials, the governing parameters would change, as they did change across the conditions of this experiment, releasing the animals to seek more profitable employment. The maximum number of consecutive trials without food in this condition averaged around 120. Surely over unreinforced strings of length 95 through 120, the probability of responding would be decreasing toward zero. Such was the case for two animals, 98 and 107, whose response probability decreased significantly (using a binomial test) to around 5% (the drift for 107 is already visible in Figure 8). The predicted fixed points and obtained probabilities for another two, 105 and 119, were invariant: .20→.19; .77→.78; pigeon 106 showed a decrease in probability, .61→.54, that was not significant by the binomial test. The substantial momentum shown in Figure 8, and extended in some cases by the binomial analysis, resonates with the data of Killeen (2003; cf. Sanabria, Sitomer & Killeen, 2006), where some pigeons persisted in responding over many thousands of trials of negative automaintenance.

The validation of this unlikely prediction should, by some accounts of how science works, lend credence to the model. But it certainly could also be viewed as a fault of the model, in that it predicts the flatlines of Figure 8, when few animals, except perhaps those subjected to learned helplessness training, will persist in unreinforced responding indefinitely. On that basis we could reject the MPS model, as it does not specify when the animals will abandon a response mode (as reflected in changes in the persistence parameters). Conversely, the data of Figure 8 indict models that do not predict the plateaus that are clearly manifest there. On that same basis we could therefore reject all of the remaining models. Clean slate. But perhaps the most profitable path is to reject Popper in favor of MPS, which permits tracking of parameters over an indefinite number of trials, to see when, under extended dashing of expectations, those begin to change.

Equation 8 contains the element s_i(1 − s_i): The product of the probability of a response and its complement enters the prediction of response probability on the next trial. This element is the core of the “logistic map”. Depending on the coefficient of this term, the pattern of behavior it governs is complex, and may become chaotic. This, along with the multiple timescales associated with the rate parameters, is the origin of the chaos that Killeen (2003) found in the signatures of pigeons responding over many trials of automaintenance, and the factor that gives the displays in Figure 2 and Figure 6 their self-similar character.

Experiment 2: Trial Duration

The trial-spacing effect depends on both the duration of the ITI, and on the trial duration; arrangements that keep that ratio constant often yield about the same speed of acquisition of responding. Therefore, to test both the generalizability of the response rate model, and the MPS model, in this experiment the trial duration is systematically varied.

Method

Subjects and Apparatus

Six experienced adult homing pigeons (Columba livia), housed in similar conditions as before, served. Pigeons 105, 106, 107, 113, and 119, who had participated in Experiment 1, were joined by 108, who replaced 98. The apparatus remained the same.

Procedure

Seven sessions of extinction were conducted before beginning this experiment. In extinction stimulus conditions were similar to those of Experiment 1, but the ITI was 35 s and trial duration 10 s; no food was delivered (p = 0). In experimental conditions, food was delivered with p = .05, ITI remained 35 s, and trial duration varied, starting at 10 s for 13 sessions. Then half the subjects went to condition CS 5s, half to CS 20 s. Finally CS 10 s was recovered. All sessions lasted 150 trials; Table 5 reports the number of sessions per condition.

Table 5.

Conditions of Experiment 2

Order	Trial Duration	Sessions
1	10 s	13
2	5 s, 20 s	13
3	20 s, 5 s	13
4	10 s	14

Note: Half the subjects experienced the extreme trial durations in the order 5 s 20 s, half in the other order.

Results

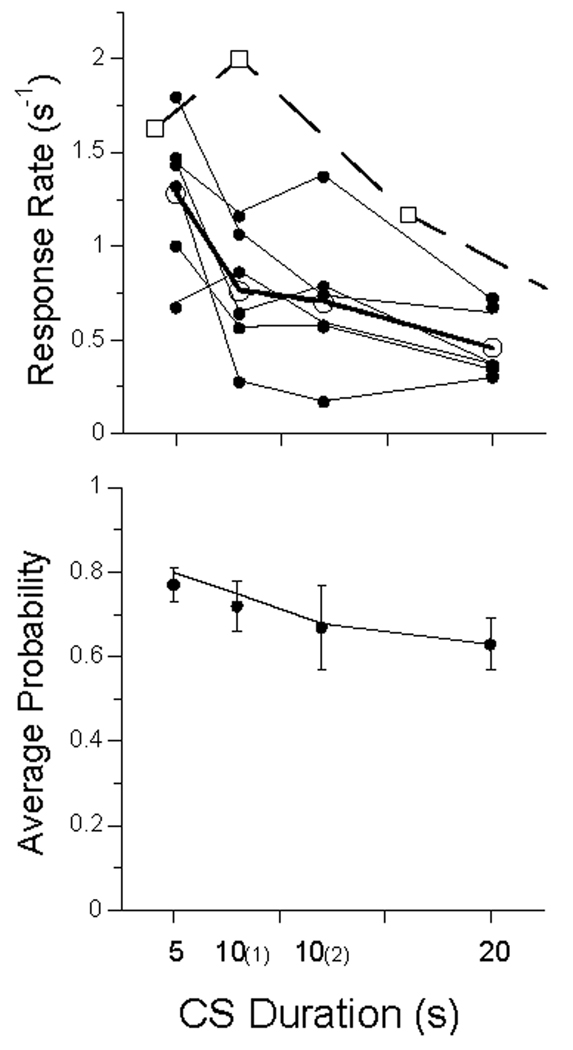
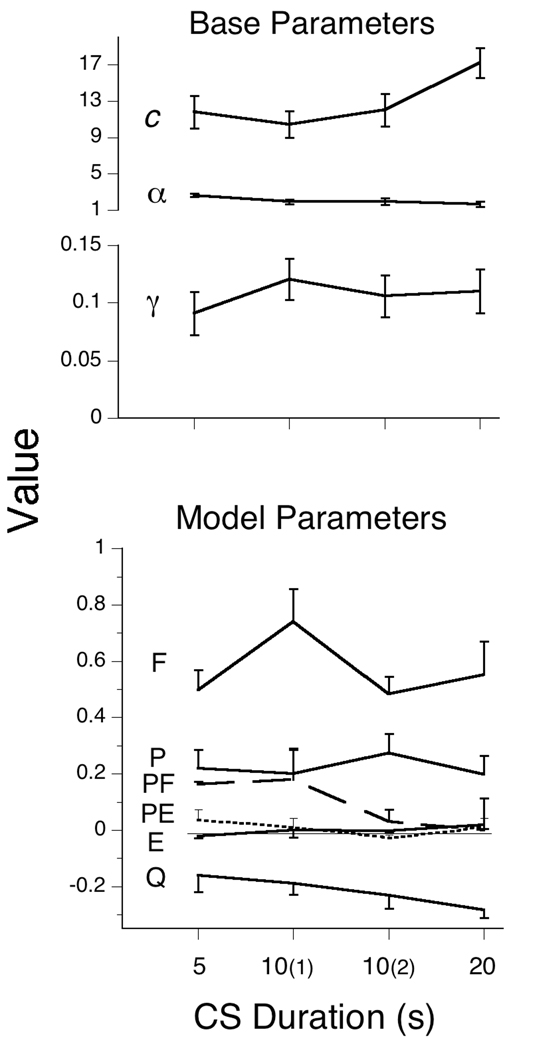
In the last session of extinction the typical pigeon pecked on 3% of the trials. This is a lower percentage than shown in Figure 8, because it follows 6 sessions of extinction. Extinction happens. Upon moving to the first experimental condition, this proportion increased to an average of 75%. The average response rates and probabilities of responding are shown in Figure 9. Both rates and probabilities decreased as CS duration increased. Also shown are averages rate from 4 pigeons studied by Perkins and associates (1975) for CS durations of 4, 8, 16, and 32 s for pigeons maintained on probabilistic (p = 1/6) Pavlovian conditioning schedules, with an ITI of 30 s. (The average rate at 32 s was 0.2 responses per second). The higher rates for Perkins’s subjects are probably due to their higher rates of reinforcement (1/6 trials compared to our 1/20). The decrease in response rate with CS duration is consistent with the data of Gibbon, Baldock, Locurto, Gold, and Terrace (1977), who found that rate decreased as a power function of trial duration, with exponent −0.75. A power function also described rates in the present experiments, accounting for 99% of the variance in the average data, with exponent −0.74.

Figure 9.

Data from Experiment 2. Top Panel: average response rate (dots) for each subject. Open circles gives average rate, and squares represent data from Perkins and associates (1975). Bottom panel: Average probability of making at least one response on a trial averaged over pigeons; bars give standard errors. Unbroken lines in both panels are from the MPS model.

The MPS model continued to outperform the Base momentum model, with an average advantage of 130 AIC units, giving it an advantage in likelihood of e¹³⁰. The parameters were larger than those found in the last condition of Experiment 1 (see Figure 10 and Table 6 and Table 7), and on the average did not show major changes among conditions, although the impact of a trial with food was greatest in the first condition studied, 10(1), and there were slight decreases in π_PF and π_Q as a function of trial duration. There was a moderate increase in the average number of responses emitted (c, top panel of Figure 10) as trial duration increased from 5 to 20; the birds adjusted to having longer to peck before the chance of reinforcement carried them to the hopper.

Figure 10.

The average parameters of the Base and MPS models for Experiment 2. The conditions are identified by their trial duration, with the first and second exposure to the 10s ITI noted parenthetically. The same Weibull parameters, c and α, were used for both models. The error bars delimit the SEMs. π_PF is traced by a dashed line, and π_PE by a dotted line.

Table 6.

Indices of merit for the model comparison of Experiment 2

B#	Metrica	5	101	102	20
105	CD	0.01	0.32	0.26	0.29
	AIC	5	347	365	360
	BIC	0	319	342	338
106	CD	0.27	0.07	0.26	0.15
	AIC	169	106	285	163
	BIC	152	79	262	141
107	CD	0.25	0.12	0.22	0.11
	AIC	193	141	172	119
	BIC	170	118	155	97
108	CD	0.10	0.14	0.08	0.05
	AIC	79	127	49	37
	BIC	62	104	32	20
113	CD	0.23	0.15	0.04	0.05
	AIC	183	214	40	34
	BIC	155	197	12	17
119	CD	0.12	0.11	0.12	0.10
	AIC	75	56	81	54
	BIC	53	45	53	32
Group	CD	0.18	0.12	0.22	0.10
	AIC	124	134	127	87
	BIC	107	111	104	64

^aThe metrics of goodness of fit for the models are the coefficient of determination, the Akaike information criterion, and the Bayesian information criterion. Values of the last two greater than 4 constitute strong evidence for the MPS model.

Table 7.

Parameter values of the Base and MPS models for the data of Experiment 2

B#	Par	5	101	102	20	B#	Par	5	101	102	20
105	γ	0.01	0.17	0.13	0.14	108	γ	0.11	0.14	0.08	0.05
	c	8.47	7.07	6.45	15.67		c	5.70	119.00	41.00	29.00
	α	3.03	1.53	1.58	1.73		α	1.45	0.15	0.06	0.08
	P	0.00	0.16	0.21	0.34		P	0.10	0.29	0.02	0.00
	Q	−0.01	−0.27	−0.33	−0.45		Q	−0.15	−0.24	−0.03	−0.08
	F	0.13	0.83	0.55	0.71		F	0.55	1.00	0.20	0.30
	E	0.00	0.02	0.01	0.04		E	0.04	0.03	0.00	−0.01
	PF	0.00	0.39	0.00	0.00		PF	0.00	0.00	0.00	0.00
	PE	0.00	−0.02	−0.03	−0.07		PE	0.00	−0.02	0.00	0.10
106	γ	0.12	0.09	0.15	0.18	113	γ	0.13	0.12	0.07	0.08
	c	12.87	16.53	16.87	22.21		c	17.22	10.77	10.08	11.40
	α	3.32	2.00	1.78	1.30		α	2.01	2.12	2.60	1.21
	P	0.31	0.08	0.45	0.30		P	0.39	0.54	0.12	0.06
	Q	−0.19	−0.21	−0.30	−0.29		Q	−0.19	−0.10	−0.11	−0.09
	F	0.68	0.35	0.44	0.60		F	0.34	0.87	0.39	0.27
	E	0.00	0.10	−0.14	0.02		E	−0.06	−0.10	0.02	0.02
	PF	0.00	0.62	0.00	0.00		PF	0.34	0.00	0.02	0.00
	PE	−0.03	−0.02	−0.08	−0.03		PE	0.00	0.00	0.00	0.00
107	γ	0.14	0.14	0.15	0.11	119	γ	0.08	0.05	0.08	0.06
	c	8.95	9.26	11.73	17.65		c	10.04	15.25	16.99	19.68
	α	2.68	1.60	1.73	1.42		α	2.96	3.18	3.61	2.35
	P	0.00	0.00	0.19	−0.04		P	0.26	0.00	0.41	0.05
	Q	−0.14	−0.14	−0.16	−0.19		Q	−0.10	−0.02	−0.15	−0.09
	F	0.69	0.69	0.48	0.38		F	0.00	0.32	0.64	0.46
	E	−0.03	−0.02	−0.02	0.01		E	−0.02	0.00	−0.02	−0.01
	PF	0.00	0.00	0.00	0.00		PF	0.67	0.00	0.25	0.00
	PE	0.17	0.18	0.00	0.15		PE	0.00	0.00	0.00	0.12

Despite the importance of trial duration for acquisition of autoshaped responding, the changes in the conditioning parameters as a function of that variable were modest. They did, however, work in unison to decrease response rates as the CS duration increased. The only-moderate changes may be due to the very short ITI in this series. The biggest effect was the transition into the first condition of the experiment, the first 10 s CS, after several sessions of extinction, where the Pavlovian and Skinnerian learning parameters π_F and π_PF were as large or larger than in any other conditions. Empty trials, although common, had little effect on behavior, as π_E was generally very close to 0. In general, the dominance of π_F over π_PF (and the other parameters), especially at the longest CS duration, may have been due to the extended opportunity for nonreinforced pecking in that long CS condition.

In interpreting these parameters, and those of Figure 5, it is important to keep in mind that π_E was in play on 95% on the trials; either π_P or π_Q on every trial; π_F on 5% of the trials; and π_PF on fewer than 5% of the trials. Thus, a trial with food in this experiment would move response strength a very substantial 60% of the way to maximum—but this happened only rarely.

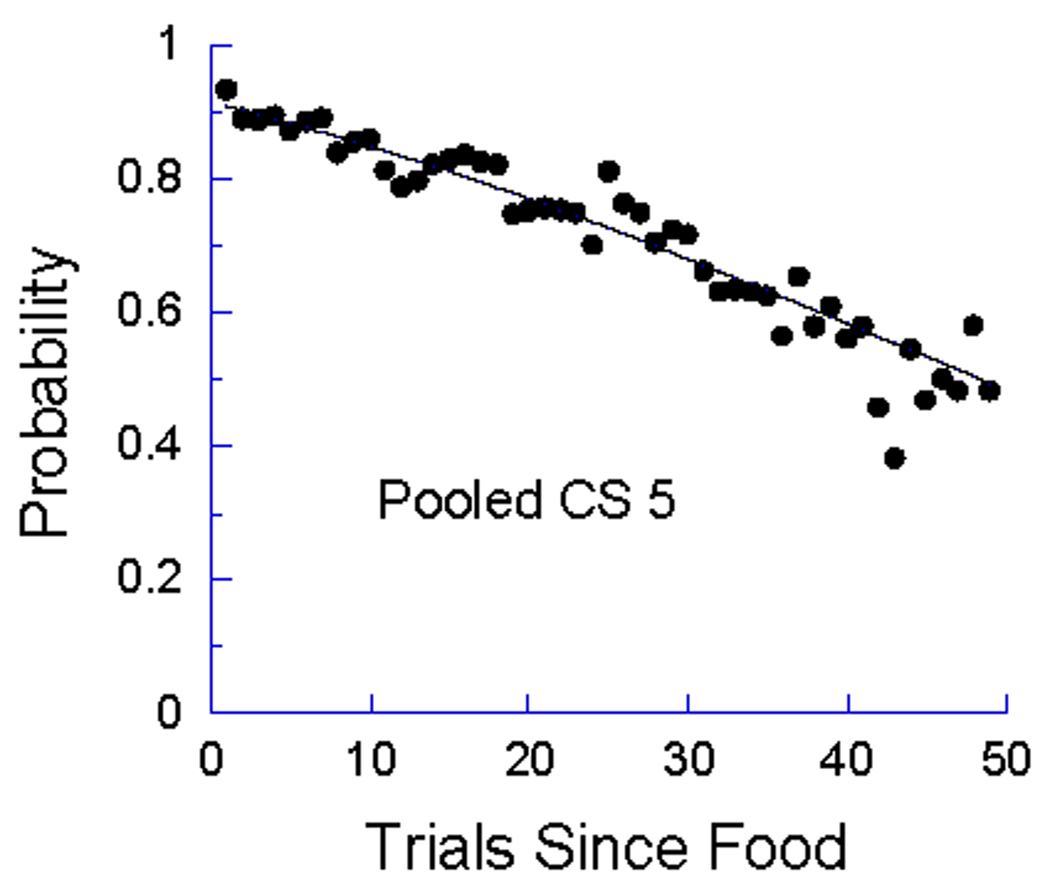
Once again the quiescence parameter π_Q was the primary force driving the probability of entry into the response state toward 0, having a mean value of −.215. This value, so close to that for π_P (.222), indicates that the momenta of pecking and quiescence were, on the average, essentially identical. This situation, π_P−Q ≈ 0, will not sustain asymptotic responding above zero (see Equation 10); with so short an ITI, that is perhaps not surprising. The success of this prediction is illustrated in Figure 11 for the 5 s CS condition, which showed no evidence of a plateau. The slight negative acceleration is due to the dominance in the pooled data of profiles from animals whose π_P−Q was negative. This analysis may throw additional light on within-session partial reinforcement extinction effects (Rescorla, 1999), as different animals or paradigms may have quite different values of π_P−Q.

Figure 11.

The average probability of responding as a function of the number of trials since reinforcement, from the CS 5 s condition of Experiment 2, pooled over subjects. The number of observations decrease by 5% from one trial to the next, from 485 for the first point to 29 for the last displayed. The curve comes from Equation 8, using parameters π_P−Q and π_E fit to these data.

Because these conditions were preceded by seven sessions of extinction, the opportunity arises to trace the course of re-acquisition for these birds, and compare with the model’s profiles. The probability of a response on each of the first 100 trials, averaged over all pigeons, and over a 7-trial moving window, is drawn as circles in Figure 12. The MPS model provides a closed form solution to the acquisition curve. The equation is shown in the appendix; the smooth acquisition curve is shown in Figure 12. The curve provides—at best—an idealized picture of the process, because it assumes that response probability is dependent on the programmed probability of food, p, which is uniform over trials. MPS can do better than that by using the real thing—whether food was delivered or not—to inform its predictions. Replacing p with the trial-to-trial relative frequency across animals, represented by the hatch marks in the figure, and keeping all parameters otherwise the same, gives the jagged curve, a better characterization of the process. Figure 12 draws a graphic reminder of a point made by Benedict and Ayres (1972): Nonlinear dynamic processes, such as the course of learning, can be extremely sensitive to the particulars of stochastic processes. Generic models with asymptotic parameters, such as limiting values for p or even for s, will provide at best an idealization; the dynamics is in the details. The text-book smooth curve shown in Figure 12 does not represent the character of the data. Over the full course of the experimental conditions, MPS easily supports its burden of parameters, as attested by its AICs, and carries us from milk-toast descriptions to the jagged profiles of Figure 12; to predictions with teeth.

Figure 12.

The average probability of responding as a function of the number of trials since the start of the CS 10 s condition of Experiment 2, pooled over subjects, and represented as a 7-trial moving average (circles). The hatch marks indicate trials on which one (plotted at p = 1/6) or two (plotted at p = 2/6) pigeons happened to have received food. In no cases did the same trial end with food for more than two pigeons. The smooth curve comes from MPS, setting p = .06, with all other parameters fit to these data. The jagged curve comes from the same equation with the same parameters, but uses the obtained relative frequency of food as given by the hatch marks.

All of the manipulations so far have been classic Pavlovian kinds, varying experimental parameters that did not interact with behavior, and those only modestly (see, e. g., Schachtman, 2004, for some modern developments). Although non-contingent food presentation can leave response-outcome associations intact (Colwill, 2001; Rescorla, 1992), all of the response-outcome associations up to this point were adventitious. We conducted the last series of experiments in order to complement those open-loop Pavlovian operations with closed-loop instrumental operations having more consistent contingencies.

Experiment 3: FR and DRO Contingencies of Reinforcement

Method

Subjects and Apparatus

Eight experienced adult homing pigeons (Columba livia), half having served in other experiments reported in this paper, were employed. They were maintained under the same conditions as the prior experiments. The apparatus was the same as used before.

Procedure

Before the experiment proper, 6–7 sessions of extinction were conducted with a 35-s ITI and 10 s trial duration; the probability of food delivery was zero (p = 0). A preliminary series of experiments was conducted with p = .05. In these conditions, which we call FR 3 and DRO, reinforcement contingencies were intended to vary response-reinforcement contiguity in opposite directions. However, the low probability of exposure to those contingencies—5% of the trials at most, usually less—gave animals insufficient exposure to the Skinnerian contingencies: In a number of cases there was no change consistent with the direction in which the contingencies were pushing. The probability of food was increased to p = .1, and the series replicated.

DRO

A differential reinforcement of other behavior (DRO) schedule was operative concurrently with baseline automaintenance contingencies, but only when food was programmed, which happened with a probability of p = .10. If an animal pecked during the 2 s preceding the delivery of food in a DRO trial, the trial was extended for an additional 2 s from the peck, until the pigeon had not pecked for 2 s, when food was finally delivered. All pigeons received 18 sessions of baseline training before being moved to the experimental conditions.

FR

A fixed ratio (FR) 3 schedule of reinforcement was operative concurrently with baseline automaintenance contingencies, but only when food was programmed. Thus, a trial in the FR 3 condition in which food was programmed (10% of the trials) would be terminated immediately by food delivery as soon as 3 key pecks were emitted. If 3 pecks were not emitted, the trial ended with non-contingent food presentation.

The order of experimental conditions was determined by the mean response rate during the last 5 sessions of baseline: Low responders were assigned first to DRO, and high responders to FR 3. Table 8 shows the order of presentation of conditions and the number of sessions in each condition. In analyzing the data, all trials with a reinforcer were excluded from measurement of goodness of fit. This is because responding could have extended or shortened the trial duration, undermining comparison. This reduced the data-base by 10%.

Table 8.

Order (number of sessions) in each condition of Experiment 3

Condition/ Bird	P43	P86	P87	P89	P90	P105	P106	P107
Training	1 (18)	1 (18)	1 (18)	1 (18)	1 (18)	1 (18)	1 (18)	1 (18)
FR 3	2 (17)	3 (7)	3 (7)	2 (17)	2 (17)	3 (17)	2 (17)	3 (7)
DRO 2 s	3 (7)	2 (17)	2 (17)	3 (7)	3 (7)	2 (7)	3 (7)	2 (17)

Results

The contingencies, even though present on only 10% of the trials (DRO) or fewer (FR, which would end with food after 10 seconds if the FR contingency had not been met), were effective with most of the animals. This is consistent with the results of Locurto, Duncan, Terrace, and Gibbon (1980). The requirements were satisfied on 79% of the trials (median, with inter-quartile range from 68 to 81 percent). The effects of the contingencies on response rates and probabilities are displayed in Figure 13. Reinforcement contingencies clearly matter, by both affecting the probability of entering a response state, and number of responses emitted in that state.

Figure 13.

Data from Experiment 3. Top Panel: average response rate (dots) for each subject. Bottom panel: Average probability of making at least one response on a trial averaged over pigeons; bars give standard errors. Lines in both panels are from the MPS model.

Of the 24 subject by condition analyses, in 18 the MPS model exceeded our criterion for strong evidence (see Table 9). Averaged over all subjects, the AIC advantage for the MPS model over the Base model was 38 points. Figure 13 displays the weighted average parameters for the Base model (simple persistence), and for the MPS model for the key DRO-FR comparisons. Table 9 lists the individual parameters. Note that as the contingencies went from DRO to FR, all parameters in the top panel increased in value. The increase in α indicates that the distribution of number of responses moved from one that looked like a gamma distribution (α = 1.46) to one that looked like a skewed normal distribution (α = 2.23; see Figure 3). The doubling of c reflects a large increase in the mean number of responses emitted in the response state in the FR condition. The increase in γ indicates that pecking tended to occur more often in alternative strings of responding or quiescence, making it advantageous for the simple moving average of the base model to place more weight on the recent history of responding in the FR conditions.

Table 9.

Indices of merit, and parameter values of the Base and MPS models for the data of Experiment 3

B# Sched.	43		86		87		89
	FR	DRO	FR	DRO	FR	DRO	FR	DRO
CD	0.11	0.16	0.21	0.07	0.09	0.05	0.12	0.02
AIC	77	19	−5	84	−2	−2	63	19
BIC	59	4	−19	66	−14	−17	39	−1
--------	---------------		---------------		---------------		---------------
γ	0.15	0.08	0.12	0.08	0.02	0.06	0.08	0.04
α	11.66	3.62	16.95	6.93	12.90	10.75	7.99	4.39
c	2.45	1.57	2.36	1.01	1.49	1.84	1.85	1.69
P	0.31	0.16	0.09	0.22	0.04	0.02	0.11	0.83
Q	−0.20	−0.10	−0.26	−0.12	−0.03	−0.03	−0.33	0.41
F	0.31	0.10	0.14	−0.13	0.01	0.00	0.18	−0.47
E	−0.01	0.00	0.07	0.02	0.00	0.00	0.09	−0.74
PF	0.00	0.42	0.00	0.00	0.00	0.07	0.00	0.00
PE	0.00	0.00	0.00	0.00	0.00	0.00	−0.03	0.13

B# Sched.	90		105		106		107
	FR	DRO	FR	DRO	FR	DRO	FR	DRO
CD	0.53	0.31	0.13	0.06	0.20	0.07	0.18	0.42
AIC	435	176	10	17	2	84	71	9
BIC	406	151	0	5	−8	66	54	−2
--------	---------------		---------------		---------------		---------------
γ	0.31	0.26	0.22	0.03	0.11	0.08	0.18	0.09
α	12.64	4.64	15.76	10.15	16.52	6.93	14.31	5.82
c	2.53	1.42	2.11	1.52	2.34	1.01	2.00	1.39
P	0.66	0.82	0.24	0.02	0.00	0.22	0.12	0.14
Q	−0.55	−0.46	−0.18	−0.03	−0.27	−0.12	−0.25	−0.10
F	0.18	0.16	0.07	0.13	0.01	−0.13	0.52	0.03
E	0.02	0.01	0.00	0.00	0.15	0.02	0.00	0.00
PF	1.00	0.57	0.00	0.00	0.00	0.00	0.14	0.00
PE	−0.05	−0.09	0.00	0.00	0.00	0.00	0.00	0.00

The main purpose of this experiment was to test the sensitivity of the MPS model to changes in behavior brought about by the manipulation of contingencies of reinforcement, and in particular to monitor changes in the instrumental learning parameter, π_PF. Figure 13 shows that there was a large increase in π_PF under the FR contingencies, and smaller changes in some of the other parameters (see Table 9). Trials without a reinforcer had, on the average, no effect, as π_E was very close to zero for most animals in most conditions, as was π_PE. The momentum parameter for the Base model (γ) was larger under the FR condition, suggesting greater movement into and out of response states, while those for the MPS model (π_P, and π_Q) were in line with those found in Experiment 2. The decrease in the latter under FR suggests a kind of ratio strain: absence from the key on one trial became a better predictor of absence on the next.

The smaller value of π_PF under DRO should not be taken as an indication that the animals were learning less; they were learning to do other things than key pecking. A smaller value of π_PF indicates that they were less likely to peck on an ensuing trial. If they received food on a trial with a peck, the peck was removed from the reinforcer by at least 2 s, and was followed by non-key-peck behavior. This latter was successfully reinforced, yielding the smaller tendency to peck on the next trial than found under the FR contingency.

The impression from the first two experiments, that the power of instrumental contingencies was weak compared to Pavlovian contingencies, now stands corrected. Where there is no instrumental contingency, but only adventitious pairing of responding as in the first two experiments, control by that pairing can be weak or nil. This may be due to the many instances of pecking without presentation of food, causing the animal to place little weight on pecking as a predictor of food. In the present experiment, FR contingencies trebled the Skinnerian parameter π_PF to from .12 to .36. Under the FR contingencies, each contingent presentation of food moved the typical animal a third of the way to certain responding on the next trial, with the persistence and Pavlovian parameters together halving the remaining distance. The increase in response rates seen in the top panel of Figure 13 for FR thus arises from two factors: An increased probability of entering a response state in that condition due to the action of the above parameters; and a higher rate of responding once in that state, reflected by the increase in c. The first set of conditioning factors are substantial, and consistent with the theoretical position of Donahoe, Palmer, and Burgos (1997a); yet they are inadequate to completely explain the large differences in rate. Differential proximity between responses and reinforcement in these two conditions is further affecting the behavior within the response state, much as it does in free operant schedules (e. g., Killeen, 1969). The parameter c reflects the operation of instrumental conditioning in the response state moving more of the conditioned behavior onto the key.

The joint role of respondent and operant conditioning demonstrated here was presaged by Wasserman, Hunter, Gutowski, and Bader (1975) in their study of automaintained responding in chicks, with warmth as the US/S^R. Locurto, Duncan, Terrace, and Gibbon (1980) found similar interactions, and suggested adopting "an 'interactivist' position wherein Pavlovian and instrumental relations are seen as independent variables which conjointly determine the outcome of any conditioning procedure" (p. 42). It was manifest in an experiment by Osborne and Killeen (1977), who superimposed CSs ranging from 7.5 s to 120 s on a VI schedule that only reinforced responses spaced by 3 s (TAND[VT60, DRL3]). Even though the CS signaled non-contingent food, it enhanced median response rates from a baseline of 25/min to 170/min at the shortest CS, decreasing monotonically to 45/min at the longest. They successfully analyzed within the CS with an extreme value function in the same family as the Weibull used here. Such within-CS analysis begins to fill one of the silences of the Rescorla Wagner model (Hanson, 1977; Miller & Barnet, 1993).

General Discussion

Momentum

The analysis of momentum, or durability of responding, has a long history marked by two changes of paradigm. The first was the discovery of the Partial Reinforcement Extinction Effect (PREE) by Humphreys (1939)—the paradoxical result that probabilistic reinforcement generates more responses in extinction than does continuous reinforcement. It generated a tremendous and continuing amount of research (Mackintosh, 1974). The second was the renewed call of attention to momentum by Nevin and his students (Nevin & Grace, 2001; Nevin, Mandell, & Atak, 1983; Nevin, Tota, Torquato, & Shull, 1990), under the rubric behavioral momentum. As the case for the PREE, which it helps to explicate (Nevin, 1988), the study of behavioral momentum has applications well beyond the animal behavior laboratory (Nevin, 1996; Plaud & Gaither, 1996). It is most closely associated with the opposing forces of π_P and π_Q, and, in extinction, with their simple difference π_P−Q.

Nevin and associates’ work has shown that behavioral momentum is most closely associated with Pavlovian forces, such as the relative densities of food in CS and background, and less so with instrumental contingencies and rates of responding. Consistent with their results, Figure 5 shows that when ITI was varied, persistence in both pecking π_P and quiescence π_Q, and their difference, π_P−Q, increased with the Pavlovian variable of ITI-to-Trial (ITI/T) ratio; Figure 1 and Figure 9 show that when trial duration was varied, persistence in both pecking and quiescence decreased with decreases in ITI/T; and Figure 13 shows that despite radically different responding under DRO and FR contingencies, π_P−Q was about the same in those experimental conditions, indicating that momentum would also be about the same, echoing Nevin’s conclusions. The influence of prior behavior on current behavior has been demonstrated in a different paradigm by de la Piedad, Field, and Rachlin (2006), who underscored the importance of the persistence they demonstrated for issues of rationality and self-control, a theme most beautifully introduced to our field by James (1890a, 1890b). The current paradigm and analysis provides a new set of operations for testing and developing behavioral momentum theory, and other more general theories of momentum and choice (e.g., Killeen, 1992; Roe, Busemeyer, & Townsend, 2001).

Conditioning

“Today, most contemporary theories of acquired behavior are predicated on observations initially made to assess the Rescorla-Wagner model” (Miller et al., 1995, p. 381). The Momentum-Pavlov-Skinner (MPS) model developed here is in that tradition; it is an “error-correction” model, like the Rescorla-Wagner (R-W) model and its linear-learning model forbears. Deviation from complete momentum or quiescence, and deviation from complete conditioning or extinction, both proceed as a function of distance from asymptote. This aperçu, however, may reflect more a limitation of imagination on our part than on the organisms’. Only a few of the infinite number of possible models of conditioning have been evaluated.

Does the MPS model capture learning or performance effects? It predicts response strength, s, the probability that the animal will be in a response state, with the rate of responding in that state given by the Weibull distribution. What the animal learns in this context relative frequencies of food given key light, and food given both light and peck. The scheduled probabilities of these is constant (at .1 or .05 or 0) in all these experiments; but the random sampling of trials by responses makes the observed frequencies a continually varying estimator of those probabilities. The strengths of the context, key, and peck state could be continuously varying, each in their own way, with our reduction to a net strength (s, probability of entering the response state) a synopsis of more nuanced 3-way tugs of war among these factors. Models that keep separate accounts of these components of learning might easily trump MPS in rich data sets such as these, despite their extra parameters, or in others where the forces are put into strong opposition. By treating instrumental responses as stimuli to be approached in the same manner as a lit key (Bindra, 1978), SOCR (Stout & Miller, 2007), attentional models (Frey & Sears, 1978; Mackintosh, 1975), RET (Gallistel & Gibbon, 2000) and its refinement by Kakade and Dayan (2002), SOP (Brandon, Vogel, & Wagner, 2003), WILL (Dayan, Niv, Seymour, & Daw, 2006), and the artificial neural net genre (e. g., Burgos, 1997; Donahoe, Palmer, & Dorsel, 1994) may be evaluated against these data. This paradigm also provides an ideal environment to analyze the potential progression of “learned irrelevance” (Baker, Murphy, & Mehta, 2003).

A limitation of the current analysis is its focus on one well-prepared response, appetitive key-pecking in the pigeon. The relative importance of operant and respondent control will vary substantially depending on the response system studied (Donahoe, Palmer, & Burgos, 1997b; Jenkins, 1977; Timberlake, 1999). Another is that we have fit only a limited number of models to the data--albeit more than mentioned here, including versions of SOCR (Stout & Miller, 2007), attentional models (Frey & Sears, 1978; Mackintosh, 1975), RET (Gallistel & Gibbon, 2000) and its improvement by Kakade and Dayan (2002). The models we presented in this paper were the best of the lot. But other models might have done better; in particular ones with attention (Mackintosh, 1975), or memory (Bouton, 1993; Wagner, 1981) as latent states. All theories, successful and otherwise, are at best sufficient accounts of the phenomena that they cover (Mazur, 2006), as Poincare (1905/1952) noted long ago.

The dependent variable was a standard operant response. Holland (1979) has shown that omission contingencies have differential effects on various components of Pavlovian conditioned responding in rats. It may be that the difference is merely greater associability of different responses (Killeen, Hanson, & Osborne, 1978; Seligman, 1970), manifested as differences in the pi parameters. Indeed, it maybe that in some configurations the Pavlovian parameter goes negative, with delivery of food increasing goal approach (Timberlake, 1994) on the next trial, competing with the measured operant. Such possibilities have yet to be demonstrated.

Another limitation is that MPS does not address the key contribution of the R-W model and its successors, cue competition and the partitioning of attention in the conditioning process. It did not need to here because changes in the predictive value of key or peck change the probability of entering the response state in the same direction: The conditionals coordinate, rather than compete. Independent book-keeping for cue, context, and peck conditioning were assayed in preliminary evaluation of the above models, but the experimental paradigm did not generate enough leverage where those models might contribute in their strong suites. The partitioning out of momentum that the MPS model permits may, for the right experimental paradigm, provide a much clearer signal for how the Pavlovian and Skinnerian factors—or Pavlovian and Pavlovian factors—compete; or where one differentially sets the occasion for the other (Colwill & Rescorla, 1986; Nadel & Willner, 1980; Schmajuk, Lamoureux, & Holland, 1998). Such qualitative tests work hand-in-hand with quantitative ones (Roberts & Pashler, 2000) to converge on models that are powerful, parsimonious, and in register with the complexity of evolved processes such as learning. Although we strive for a unified theory of behavior, the best way to achieve it may be by perfecting modules that can account for their domain, while exchanging information with modules of other domains (Guilhardi, Yi, & Church, 2007).

In their penetrating assessment of the R-W model, Miller, Barnet and Grahame (1995) noted 18 theoretical successes, and about as many failures. They go on to observe that newer models are “highly complex or have their own list of failures at least as extensive as the R-W model.” (p. 381); but that each of the new models has its strengths in fixing some of the failures of R-W. It is our hope that by embedding contemporary models in the present framework, which permits variance due to momentum to be partitioned out, and which permits ad libitum degrees of freedom in the data to counterpoise those required for modern complex models of conditioning (see, e.g., Hall, 2002 for an overview), that the models themselves may compete on a higher playing field. Dynamic analysis may also permit the refinement of experiments, and permit reduction of the number of subjects required to answer behavioral or pharmacological questions (Corrado, Sugrue, Seung, & Newsome, 2005; Smith et al., 2004). The MPS model is but a second step through the door opened by Bush and Mosteller so many years ago.

Figure 14.

The average parameters of the Base and MPS models for the DRO and FR contingencies of Experiment 3. The same Weibull parameters, c and α, were used for the response distributions of both models. The error bars delimit the SEMs.

Appendix

Framing the Model

There are 8 explicit parameters in the MPS model: The response parameters α and c, the two momentum parameters, the two Pavlovian parameters, and the Skinnerian parameters. (The Skinnerian parameters are partially redundant with the persistence parameter, but no attempt was made to enforce further parsimony in these already overworked data.) There are also implicit parameters. These involve the structure of the model and how that interacts with the parameters and data (Myung & Pitt, 1997). The directions of conditioning (the nominal signs of the learning parameters specifying their asymptotes θ, here fixed at 0 or 1), are such considerations. Another is the starting value of s, s₀, which is estimated as the average probability of a response over the first dozen trials of each condition, with those trials then excluded from all indices of merit. Because the logarithmic transformation penalizes errors exponentially as they approach maximum (e.g., predicting a response probability close to zero and having a response occur), a floor (of probability of data given model) of 0.00001 was placed under both the candidate and default models; it was rare for them to step on that floor except during the iterative process of parameter estimation. All analyses were conducted in Excel® using the Solver add-in.

Looking Ahead

In general, the linear learning model was unquestionably better than the base model of momentum—the AIC index of merit advantage for the learning model was typically close to 100 units. What does this mean in terms of ability to predict behavior? Most readers unfamiliar with AIC and log likelihood analysis will appreciate some other indices of merit, such as variance accounted for by the model. However we are predicting response rates on a trial by trial basis, not the typical averages over the last 10 sessions each consisting of scores of observations. There is no opportunity to average out noise in the present dynamical analysis. In light of this, predictions were not so bad: the MPS model accounted for over 10% of the variance in response rates on the next trial in Experiment 1, even though the analysis did not optimize goodness of fit for this variable. In the p = .05 condition, accuracy increased to 16%.

Whereas these might not seem impressive figures, nor might the advantage of the MPS model seem impressive in that metric, most considerations of variance accounted for –coefficients of determination—are calculated on average data, where noise has been minimized by averaging. None, to our knowledge, reflect accuracy on a moment-to-moment, or at least trial-by-trial, basis. Because conditions are always changing as a function of the behavior of the animal in this closed-loop system, there is no obvious larger unit over which we could aggregate data to improve accuracy. But there is a less-than-obvious one, described next.

The conditioning predicated by the learning model has a longer provenance than over just the next trial; a measure of accuracy that is both more informative, and more consistent with traditional reports of coefficients of determination, can be derived by asking how well the imputed strength, s_i, predicts behavior over the next few trials. Because the learning model posits geometric changes in performance as a function of contingencies, accuracy of prediction should also decrease geometrically with distance into the future. Accuracy decreases because the stochastic processes that might carry the animal over a response threshold on a trial or not, throw a multiplicative shadow into the future. Therefore accuracy should decrease approximately as (1-γ)ⁿ, as vicissitudes of responding and reinforcement carry the conditioning process along an increasingly random walk. We may take advantage of this by averaging measured responding over the next score trials, giving greatest weight to the next trial, less to the trial after that, and so on, and using events on the current trial to project those temporally discounted future response rates. This was accomplished by weighting the accuracy of prediction on the next trial by 20%; adding to that accuracy on the trial after that weighted by 16%; on the trial after that by .2(.8)², then by .2(.8)³, etc. This “forward” exponentially-weighted moving average places half the predictive weight on the 3 trials subsequent to the prediction, trailing off geometrically into the future. Accuracy at predicting this discounted future in the p = .05 condition doubled, to 28% of the variance in response rates accounted for by the MPS model. A similar doubling of the coefficient of determination was seen in spot checks of the other conditions.

Asymptotic Responding

In this paper the conditioning process is characterized from trial to trial by a difference equation—the strength on the prior trial, plus the probability of a response times π_P and a non-response by π_Q; that is then adjusted by the probability of food times π_F and no food by π_E; and finally the probability of both a response and food times π_PF, or of a response and no food by π_PE. This permits continuous idealizations of acquisition and extinction.

Representation of a stochastic process by its probabilities gives a domesticated version of an intrinsically wild process. For instance, performance is vulnerable to a “gambler’s ruin”—a series of non-reinforced trials that leads to extinction. The probabilistic solutions do not take this sudden-death into account, and do not allow for the recuperative strength provided by spontaneous recovery at the start of new sessions. Nonetheless, they provide some insights to the process. We begin by analysis of the momentum factor, and then blend it with the conditioning factors. Here the direction toward ceiling or floor is assumed, in the conventional manner. Conditioning enters after momentum, rather than before, as in the analysis programs. The order of entry makes some difference in accuracy of fit.

1. Momentum

Letting p(P_i) represent the probability of responding on the i^th trial, the momentum of responding is carried forward from the last trial as:

$$s_i^{\prime }=s_i+p\left(P_i\right){\pi }_P\left(1-s_i\right)+\left(1-p\left(P_i\right)\right){\pi }_Q\left(0-s_i\right);$$

that is, as the strength coming out of the prior trial, s_i, plus probability of a response, p(P_i), times π_P (the momentum-of-pecking rate parameter), times the distance to the ceiling strength (1 − s_i); plus the probability of not pecking times the momentum-in-quiescence parameter π_Q times the distance to the floor of strength. The probability of pecking is approximately equal to the strength, s_i, so substitute for p(P_i) and simplify to:

$$s_i^{\prime }=s_i\left(1+\left(1-s_i\right)\left({\pi }_P-{\pi }_Q\right)\right).$$ (A1)

The difference in momentum parameters is gated by the distance of strength to its ceiling, to increment response probability. This is slightly off, because there is a finite probability of being in the response state and not pecking; but that is negligible. The variable $s_i^{\prime }$ is the momentum of responding that is carried forward to the next trial.

2. Pavlovian conditioning

Food occurs with probability p, so:

$$s_i^{″}=s_i^{\prime }+p{\pi }_F\left(1-s_i^{\prime }\right)+\left(1-p\right){\pi }_E\left(0-s_i^{\prime }\right);$$

that is, as the status quo ante ($s_i^{\prime }$), plus the probability of food times the Pavlovian parameter π_F times the distance to ceiling; plus the probability of no food times the Pavlovian extinction parameter π_E times the distance to floor. Collecting terms yields:

$$s_i^{″}=s_i^{\prime }(1+p({\pi }_E-{\pi }_F)-{\pi }_E)+p{\pi }_F.$$ (A2)

When the probability of food is p = 1, the influence of π_E drops out, leaving strength on a march toward 1; and conversely where p = 0, strength decreases geometrically from one trial to the next by the factor (1 − π_E).

To predict responding on the next trial, the intervening variable $s_i^{\prime }$ is removed by substituting from A2 into A1. Because the parameters π_P and π_Q always enter as a difference, some parsimony is achieved by writing π_P − π_Q as π_P−Q. Then Equations A1 and A2 give:

$$s_i^{″}=s_i\left(1+{\pi }_{P-Q}\left(1-s_i\right)\right)\left(1+p\left({\pi }_E-{\pi }_F\right)-{\pi }_E\right)+p{\pi }_F$$ (A3)

3. Skinnerian conditioning

Remembering that food occurs with probability p, and a peck with probability s”, the increment to strength conferred by operant conditioning is:

$$s_{i+1}=s_i^{″}+s_i^{″}\left(p{\pi }_{PF}\left(1-s″\right)+\left(1-p\right){\pi }_{PE}\left(1-s″\right)\left(0-s″\right)\right);$$

Strength after Pavlovian updating, plus the probability of a response times the large parenthetical. Inside the parenthetical is the probability of food times its rate parameter times the distance to the ceiling; plus the probability of no food times its rate parameter times the probability of no peck times its distance to the floor. This may be simplified to:

$$s_{i+1}=s_i^{″}\left(1+\left(1-s_i^{″}\right)\left(p{\pi }_{PF}-\left(1-p\right)s_i^{″}{\pi }_{PE}\right)\right)$$ (A4)

Inserting A3 into this gives the final equation of prediction, too unenlightening to be written out here—even though it is less complicated than the full solution to the R-W model (Yamaguchi, 2006). It is simpler to evaluate A3, and then insert it into A4. A spreadsheet for analyzing data with the present theory on a trial-by-trial basis is available from the authors.

Special Cases

Acquisition

In the case of acquisition, where few or no responses have yet occurred, A3 provides a good equation of prediction. Since the probability of food p is typically 1.0, it can be further simplified to the acquisition function:

$$s_{i+1}=s_i\left(1+{\pi }_{P-Q}\left(1-s_i\right)\right)\left(1-{\pi }_F\right)+{\pi }_F.$$ (A5)

Equation A5 can range from a classic exponential-integral learning curve (when π_P−Q is of small magnitude), through approximately linear, to an S-shaped ogive, depending on the two parameters, the net rate of persistence (π_P−Q) and the rate of acquisition (π_F).

Extinction

In extinction p = 0, and A3 simplifies to:

$$s_{i+1}=s_i\left(1-{\pi }_E\right)\left(1+{\pi }_{P-Q}\left(1-s_i\right)\right),$$ (A6)

which appears as Equation 8 in the text. Equation A6 assumes that π_PE is smaller, and extinction decrements can be handled by π_E; this has been the case for all of the data analyzed here, and setting π_PE to zero is a parsimonious way to simplify the Equation.