Carbonic acid buffer changes during complete brain ischemia

Abstract

Simultaneous measurements of tissue PCO₂ (Pt_CO2), interstitial H⁺ concentration ([H⁺]_o), and tissue lactate content were used to examine changes in interstitial ${\text{HCO}}_3^{-}$ concentration ( ${[{\text{HCO}}_3^{-}]}_{\text{o}}$) during complete ischemia. In normoglycemic rats (blood glucose of 6–8 mM; neocortical ischemic-induced lactate content 8–12 mmol/kg) [H⁺]_o increased from 7.22 ± 0.02 to 6.79 ± 0.02 pH (n = 3). By contrast, in hyperglycemic rats (blood glucose 18–75 mM; ischemic-induced lactate content 19–31 mmol/kg) [H⁺]_o rose by a significantly larger amount to 6.19 ± 0.02 pH (n = 7), Given that ${\text{HCO}}_3^{-}$ is the predominant interstitial H⁺ buffer, changes in peak Pt_CO2 show why peak [H⁺]_o were bimodally distributed compared with lactate content. Between 8 and 12 mmol/kg lactate, when peak Pt_CO2 rose from 99 to 186 Torr but [H⁺]_o, was constant at 6.79 pH, calculated ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ increased from 11.9 to 21.9 mM. Then after transitional changes, peak Pt_CO2 and [H⁺]_o remained constant at 389 ± 9 Torr (n = 7) and 6.19 pH despite the fact that tissue lactate ranged from 19 to 31 mmol/kg lactate, respectively; ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ must have remained constant at 12.3 ± 0.7 mM (n = 7). Since ischemic brain continued to produce another 12 more mmol/kg of lactic acid above 19 mmol/kg lactate without further changes in Pt_CO2 or [H⁺]_o, H⁺ and ${\text{HCO}}_3^{-}$ must have been heterogeneously compartmented. The continued lactic acid production occurred in a compartment that occupied 36% of neocortical space. This compartment is likely to represent glial cells.

Excessive Brain Acidosis is thought to worsen the outcome from stroke in humans (29) and animals (23, 30), but the specific cellular mechanisms by which such putative injury occurs remain undefined. Indeed, the absolute magnitude of H⁺ accumulation that could lead to ischemic brain necrosis in any cell compartment has not been measured. This lack, in part, stems from the complexity of the dynamic and interactive mechanisms by which H⁺ concentrations are regulated in a multicompartmented system such as the brain.

Both systemic and cellular processes influence H⁺ regulation in brain. Systemic processes include modifying the flux of volatile H⁺ buffers (CO₂ and NH₃) as well as H⁺-related ionic species across the blood-brain barrier by changes in pulmonary ventilation and cerebral blood flow. Cellular mechanisms include at least three physiological and chemical processes: 1) metabolic production and consumption of acids and bases; 2) cell physicochemical H⁺ buffers; and 3) ion transport across cell membranes (38). The last-mentioned mechanism has not been studied in ischemic brain. This omission undoubtedly stems from the tendency to regard ischemic brain tissue as a homogenous proteinaceous ionic milieu without compartmentation by intact plasma membranes (37).

We recently provided evidence implying that at least one population of brain cell plasma membranes remains intact during complete ischemia (19). Even under conditions of ischemic brain lactic acidosis that ultimately evolve to brain necrosis (i.e., lactate accumulation to >19 mmol/kg in neocortex; see Ref. 23), membranes appear to remain impermeable to H⁺ and H⁺-related ionic species so long as complete ischemia lasts. The finding suggests, therefore, an understanding of the mechanisms by which brain cell plasma membranes regulate H⁺ under normal and ischemic conditions may reveal important mechanisms through which excessive acidosis destroys brain tissue.

We have proposed that two factors may account for the brain’s ionic impermeability toward H⁺ during hyperglycemic and complete ischemia. The first factor consists of regulation of brain [H⁺] via antiports for Na⁺-H⁺ and ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ (31, 42) that are arrested during ischemia by the degradation of transmembrane gradients for Na⁺ and Cl⁻ and sufficient loss of brain ${\text{HCO}}_3^{-}$ stores. The second factor involves a decline in the diffusional permeability of the intact plasma membranes to H⁺, perhaps because of titration of surface proteins by excess H⁺. If these postulates are correct, worsening brain acidosis would be confined to the intracellular space bounded by such intact plasma membranes during hyperglycemia ischemia.

In the present study we report simultaneous measurements of interstitial [H⁺] and tissue PCO₂ as well as peak neocortical lactate content during complete brain ischemia in anesthetized rats. The results provide further evidence of continued compartmentation of [H⁺] during hyperglycemic brain ischemia. In addition, we report a new technique to assess brain total ${\text{HCO}}_3^{-}$ content. As will be shown, the measurements indicate that, during severe ischemia, ${\text{HCO}}_3^{-}$ stores are exhausted from some intact population of brain cells and that the exhaustion occurs at or near a degree of lactate accumulation that previously has been associated with necrosis of all brain cells. Indirect evidence suggests that this unknown population of intact cells represents glia. If correct, the findings imply that brain infarction can be correlated to a loss of plasma membrane H⁺ regulatory mechanisms as well as intracellular ${\text{HCO}}_3^{-}$ stores in glia, a cell population increasingly recognized as contributing to H⁺ regulatory mechanisms of brain (13, 26). A preliminary report of some aspects of this work has appeared (16,18, 20)

METHODS

Animal preparation and recording

Male Wistar rats (250–400 g) were anesthetized with halothane (5% induction; 3% maintenance during surgery; 1.5–2.0% during recordings) and spontaneously ventilated with a 30% O₂-N₂ mixture via an inhalation mask. A tail artery and femoral vein were cannulated, and a 4- to 5-mm diameter craniotomy was made over parietal cortex, 1 mm lateral to the sagittal suture. Then animals were mounted in a standard head holder and warmed to 37°C. Normal (15) Ringer solution at 37°C flowed through a superfusion cup, placed around the craniotomy site, that was fastened in place with 3.5% agar and 150 mM NaCl. H⁺ ion-selective micropipettes (ISMs) and a tissue PCO₂ (Pt_CO2) semimicroelectrode (Microelectrodes, Londonberry, NH MI-720) were mounted on a Narishige MT-5 micromanipulator, the H⁺ ISM being placed immediately adjacent but 500 μm deeper than the active surface of the CO₂ electrode.

The assembled electrode array was advanced toward the brain so that the Pt_CO2 electrode recorded from the parietal pial surface while the H⁺ ISM penetrated 500 μm below in the interstitial space. After calibrations (see below) the superfusion cup was filled with light mineral oil to prevent loss of CO₂ from the pial surface. Arterial pH, PO₂ (Pa_O2), and PCO₂ (Pa_CO2) were stabilized and monitored with a Corning 158 blood gas analyzer. Brain carbohydrate stores were adjusted by intraperitoneal injections of 0.93 M D-glucose (8.35 g/kg) or intravenous injection of regular insulin (2.0–6.0 U/kg of U-100 Iletin). Blood glucose was measured with a Glucometer (Miles Laboratories, Naperville, IL). After animals attained the desired blood glucose level, complete ischemia was induced by cardiac arrest from intravenous injection of 0.5 ml of 1 M KCl. When interstitial [H⁺] ([H⁺]_o) and Pt_CO2 reached plateaus, animals were quickly decapitated and their heads dropped into liquid N₂ for subsequent measurements of lactate content via enzyme fluorometric techniques (43).

Electrode preparation and calibration

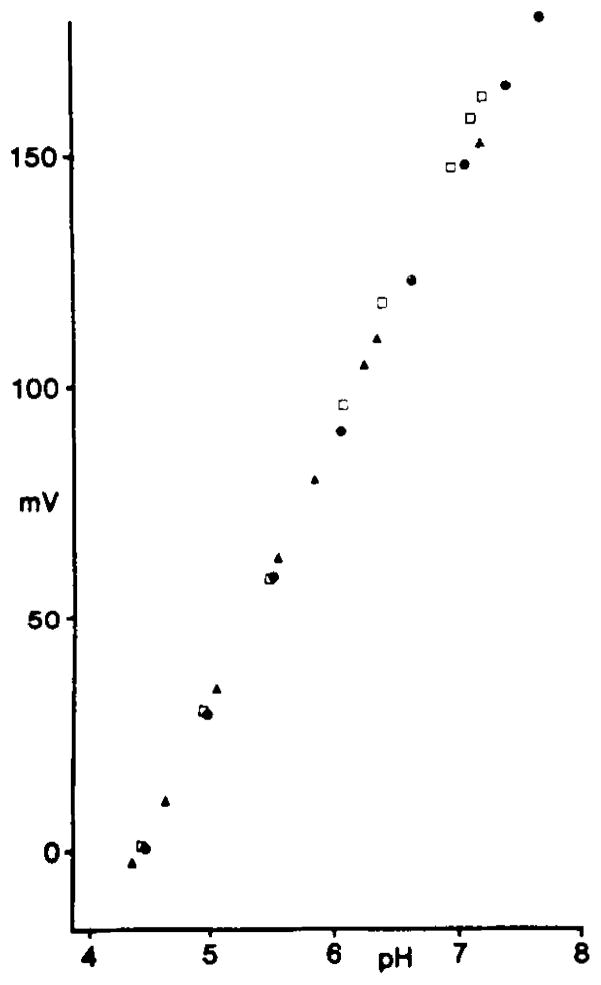
H⁺ ISMs based on tridodecylamine (1) were constructed, calibrated, and used as previously described (15, 19). We previously mentioned (15) that exposure of the neutral ionophore ligand, tridodecylamine, to CO₂ did not appear to influence the behavior of H⁺ ISMs to changes in [H⁺], although such CO₂ exposure was described in the original construction of these H⁺ ISMs (1). Here we report this finding in more detail. Potassium phosphate solutions were buffered to different [H⁺] with sodium hydroxide and then exposed to different PCO₂’s to determine if CO₂ influenced the linearity of H⁺ ISM output (Fig. 1). Figure 1 shows 5% or 100% CO₂ minimally influenced the H⁺ electrode output slope compared with solutions equilibrated with room air containing an approximate PCO₂ of 0.1 Torr.

FIG. 1.

Response of ion-selective micropipette (ISM) to changes in [H⁺] at different PCO₂’s. Potassium phosphate solutions were buffered to different [H⁺] with sodium hydroxide and then equilibrated with CO₂ at different partial pressures. Solid dots, linearity (correlation coefficient 0.999) and sensitivity (58 mV/decade change in [H⁺]) of liquid membrane H⁺ ISMs equilibrated at 25°C with room air (PCO₂ ~0.1 Torr); open squares, H⁺ ISM response after same solutions were equilibrated with 5% CO₂-95% O₂ (correlation coefficient 0.999; 61 mV/decade change in [H⁺]); solid triangles, H⁺ ISM response after solutions were equilibrated with 100% CO₂ (correlation coefficient 0.999; 61 mV/decade change in [H⁺]). These results show that H⁺ ISMs based on neutral ionophore tridodecylamine are not influenced by PCO₂’s that exceed those found in brain in vivo. However, H⁺ ISMs do show a minor reduction in slope to changes in [H⁺] when PCO₂ is nearly zero.

Pt_CO2 electrodes (MI-720) were used as supplied from the manufacturer (Microelectrodes). We are unaware of published reports describing this electrode and therefore outline its use and characteristics. The active surface consisted of a thin Teflon membrane. The electrode was filled with 5 mM NaHCO₃ and 20 mM NaCl and connected to unity gain, high-performance buffer amplifiers (15). Pt_CO2 electrodes were calibrated at a place remote from the animal in humidified gas streams of 5% CO₂-95% O₂ and 100% CO₂. For in situ electrode calibration the Pt_CO2 electrode was placed in the superfusion cup while normal Ringer solution equilibrated with either 5% CO₂-95% O₂ (7.35 pH at 25°C) or 100% CO₂ (6.11 pH at 25°C) flowed through the cup. The PCO₂ of the calibration gases (Torr) is described by

$${\text{Pco}}_2=({\text{P}}_{\text{B}}-{\text{P}}_{\text{W}})\%{\text{CO}}_2/100$$ (1)

where P_B is the barometric pressure (Torr), and P_w is the water vapor pressure (Torr) at the specified temperature. Output of the Pt_CO2 electrode is described by

$$\text{mV}=Alog[{\text{Pco}}_2(100\%{\text{CO}}_2)/{\text{Pco}}_2(5\%{\text{CO}}_2)]+C$$ (2)

where C is a constant dependent on the complete electrical system, and A is the slope of the electrode output in millivolts per decade change in PCO₂. A is equal to RT/F where R is the gas constant, T is the temperature, and F the Faraday constant. At room temperature the Pt_CO2 electrode slope (A) was 52 ± 3 (n = 12) mV per decade change in PCO₂. Pt_CO2 response time was defined as the time required for the output of the electrode to reach 95% (t₉₅) of its final value after a step change in P_CO2. t₉₅ for the Pt_CO2 electrode was measured in the following manner. The electrode was placed in a loose-fitting plastic tube (5 cm long and 0.4 cm ID) connected to one port of a three-way stopcock. The other two ports received either humidified 5% CO₂-95% O₂ or 100% CO₂. In this way, gas streams that passed the active surface of the CO₂ electrode could be rapidly switched from one concentration to another. Figure 2 shows a typical recording from such measurements. t₉₅ for the MI-720 CO₂ electrode lay between 30 and 40 s.

FIG. 2.

Response time of CO₂ electrode. CO₂ electrode was exposed to low flow stream of humidified 5% CO₂-95% O₂. This gas was then switched to humidified 100% CO₂ (downgoing arrow) and then back to 5% CO₂-95% O₂ (upgoing arrow) via 3-way stopcock. Time for electrode response to reach 95% of its maximal change was 30–40 s.

Interstitial ${\text{HCO}}_3^{-}$

[ ${\text{HCO}}_3^{-}$] is derived from simultaneous measurements of test solution pH and PCO₂. Henderson first described the dissociation of carbonic acid in biological solutions as

$${}^1[{\text{H}}^{+}]=K_{1}S{\text{Pco}}_2/[{\text{HCO}}_3^{-}]$$ (3)

which is based on the law of chemical equilibrium and the isohydric principle (5). In 1916, Hasselbalch transformed Eq. 3 into the well-recognized Henderson-Hasselbalch equation (5)

$${}^1\text{p}\text{H}=\text{p}{K}_1+log([{\text{HCO}}_3^{-}]/S{\text{Pco}}_2)$$ (4)

where [ ${\text{HCO}}_3^{-}$] is expressed in millimolars, S is a solubility constant for CO₂ (mM/mmHg), and K₁ is the first ionization constant for carbonic acid. Both S and K₁ vary with temperature and osmolality (22, 39) and when corrected for these two physical variables are represented as S′ and $K_1^{\prime }$, respectively. $K_1^{\prime }$ also varies with pH (22, 39). This, of course, is not characteristic of a true thermodynamic constant but stems from the use of S′PCO₂ as a quantity that approximates the sum of aqueous CO₂ plus carbonic acid (39). This can be seen more clearly from Eq. 5, a–f. Exposure of a salt solution to CO₂ gas [(CO₂)_g] results in solvation of CO₂ according to

$${({\text{CO}}_2)}_{\text{g}}\rightleftharpoons {[{\text{CO}}_2]}_{\text{aq}}+[{\text{H}}_2\text{O}]$$ (5a)

The amount of dissolved CO₂ ([CO₂]_aq) in the solution is given by Henry’s law

$$S^{\prime }{\text{Pco}}_2={[{\text{CO}}_2]}_{\text{aq}}$$ (5b)

Dissolved CO₂ then reacts with water to form carbonic acid

$${[{\text{CO}}_2]}_{\text{aq}}+[{\text{H}}_2\text{O}]\rightleftharpoons [{\text{H}}_2{\text{CO}}_3]$$ (5c)

Carbonic acid goes through a first ionization to form ${\text{HCO}}_3^{-}$

$$[{\text{H}}_2{\text{CO}}_3]\rightleftharpoons [{\text{H}}^{+}]+[{\text{HCO}}_3^{-}]$$ (5d)

In biological systems, PCO₂ is commonly used to estimate dissolved [CO₂] so that

$${[{\text{CO}}_2]}_{\text{aq}}+[{\text{H}}_2{\text{CO}}_3]\approx S^{\prime }{\text{Pco}}_2$$ (5e)

Since the carbonic acid concentration is pH dependent, $K_1^{\prime }$, the apparent first ionization constant, is also pH dependent

$$\begin{array}{l}([{\text{H}}^{+}][{\text{HCO}}_3^{-}]/{[{\text{CO}}_2]}_{\text{aq}}[{\text{H}}_2{\text{CO}}_3])\\ \approx ([{\text{H}}^{+}][{\text{HCO}}_3]/S^{\prime }{\text{Pco}}_2)=K_1^{\prime }\end{array}$$ (5f)

Notice that the second ionization constant, $K_2^{\prime }$, defined as

$$[{\text{H}}^{+}][{\text{CO}}_3^{2-}]/[{\text{HCO}}_3^{-}]=K_2^{\prime }$$ (5g)

is not pH dependent because no S′PCO₂ term is involved in the equation.

Mitchell et al. (22) determined S′ and $K_1^{\prime }$ for human cerebrospinal fluid at different temperatures and pH values. Their values are in close agreement with those given for S′ (34) and $K_1^{\prime }$ (35) of brain homogenates at comparable temperature and pH. However, since the spectrum of these experimental values for S′ and $K_1^{\prime }$ were insufficient for use in total CO₂ measurements (see below), which were done at room temperature (20°C), or for in vivo calculations under ischemic conditions (pH ~6), we fitted the experimental data of Mitchell et al. (22) to the following curves in order to extrapolate their data to our experimental conditions

$$S^{\prime }=0.4650·{\text{t}}^{-0.7426}$$ (6)

where t is in degrees Celsius (correction coefficient is >0.999).

$$K_1^{\prime }=(ln[{\text{H}}^{+}]/16.0381)/-2.6481\times {10}^7$$ (7)

with a correlation coefficient of 0.963. Changes in $K_1^{\prime }$ due to temperature fluctuations are small and can be predicted from the effect of temperature on the standard free-energy equation for $K_1^{\prime }$ (6). S′ and $K_1^{\prime }$ were not corrected for osmolality because no information is available as to how brain interstitial osmolality might vary under ischemic conditions.

Total CO₂ and total ${\text{HCO}}_3^{-}$ calculations

Determination of brain total CO₂ (tCO₂) has traditionally been performed using the Van Slyke technique (44). According to this method, frozen samples of brain are placed in a closed container after which excess strong acid is added to liberate all carbonic acid buffer species as CO₂ gas. The latter is absorbed onto some material that is then weighed to reflect the amount of trapped CO₂. This procedure has two serious drawbacks. First, it requires hours to trap all the liberated CO₂. Second, the technique for handling brain samples is very sensitive to error because CO₂ or water vapor from the environment can deposit onto brain samples frozen with liquid N₂ and handled near −79°C temperature. For this reason, an elaborate and expensive cold box system with a controlled atmospheric environment has been used (14).

We report here an inexpensive and rapid method for determination of tCO₂ that is reproducible (±0.2 mM determined from 10 consecutive measurements of a standard ${\text{HCO}}_3^{-}$-based Ringer solution), sensitive (>±0.1 mM as estimated from equivalent voltage sensitivity of recording system), and accurate (see Fig. 4). The method used the MI-720 CO₂ electrode (Microelectrodes). Rats were anesthetized with halothane and ventilated spontaneously. Arterial blood gases were stabilized, and after 60–70 min at a specific Pa_CO2, heads were frozen with liquid N₂ by the method of Pontén and Siesjö (27). Animals were then decapitated and their heads stored at −80°C. Small pieces (10–20 mg) of cerebral cortex were dissected from whole brain at −25°C. Total brain samples (20–100 mg) were placed in individual 10-ml closed plastic containers for 2–5 h of equilibration at −25°C. If samples were used before this period of equilibration, tCO₂ values were consistently elevated from those obtained by Kjällquist et al. (14). This may have resulted because of deposition of environmental CO₂ onto frozen samples whose temperatures were still below −79°C (freezing point for CO₂) during initial freezing and handling. There was no detectable difference (i.e., <0.1 mM) in comparable tCO₂ values measured after 2–5 h at −25°C. Therefore, this delay did not allow time for significant loss of endogenous tCO₂ stores to occur from the samples. The experimenter wore a surgical mask at all times to prevent condensation of water vapor onto the frozen brain samples.

FIG. 4.

Comparison of rat neocortical total CO₂ (tCO₂) content to arterial PCO₂ (Pa_CO2). Rats were anesthetized with halothane and spontaneously ventilated. Pa_CO2 levels were stabilized by varying halothane from 1.5 to 2.5% while arterial pH and Pa_O2 were within normal limits. After 1 h at desired Pa_CO2 level, rat brains were frozen by method of Pontén and Siesjö (27) and processed for tCO₂ measurements (see text and Fig. 3). Open squares, new data determined by method described here; solid dots, data of Kjällquist et al. (14) determined by traditional Van Slyke technique. Both sets of data fit line described by equation shown, with correlation coefficient of 0.988. Individually, data show correlation coefficients of 0.989 (solid dots) and 0.948 (open squares) to similar lines.

To measure tCO₂, 300 μl of 150 mM sodium fluoride (previously adjusted to pH 7 with sodium hydroxide) was placed in a 10-ml test tube. A brain sample (20–100 mg) was then added to the tube immediately followed by 2 ml of light mineral oil. Next, 100 μl of 1 M HCl was gently added to the aqueous layer. Finally, the active surface of the CO₂ electrode was carefully lowered into the aqueous phase. Then, as the entire system warmed back to room temperature and HCl penetrated the sample to liberate CO₂ gas, electrode output rose to a peak over 15–30 min (Fig. 3). Immediately before each tCO₂ measurement the CO₂ electrode was calibrated as shown in Fig. 3. Figure 4 shows the relation of tCO₂ to Pa_CO2 and illustrates the similarity of our results compared with those of Kjällquist et al. (14) who used the traditional Van Slyke technique. When both sets of data are combined, tCO₂ can be related to Pa_CO2 by

FIG. 3.

Response of CO₂ electrode during total CO₂ (tCO₂) measurement. Three hundred microliters of 150 mM sodium fluoride was placed in a test tube. Approximately 100 mg of frozen (−25°C) rat neocortex was then added to tube and immediately covered by 2 ml of light mineral oil. Then 100 μl of 1 M HCl was injected into aqueous phase. Next CO₂ electrode was calibrated in a humidified 5% and 100% CO₂ gas stream and subsequently placed into aqueous phase of sample (indicated by “sample” above). PCO₂ dropped initially and then slowly reached a peak value over 15–25 min as brain ${\text{HCO}}_3^{-}$ was titrated to CO₂ and sample returned to room temperature. Here a 110-mg sample of neocortex (from animal with arterial PCO₂ of 90 Torr) produced a final PCO₂ of 95 Torr. This is consistent with tCO₂ of 19.9 mmol/kg neocortex (see text for details of calculations and Fig. 4 for tCO₂ comparison to arterial PCO₂).

$${\text{tCO}}_2=2.2146e^{1.1245(log{\text{Pa}}_{{\text{CO}}_2})}$$ (8)

with a correlation coefficient of 0.988. tCO₂ (mmol/kg) can be used to estimate neocortical total ${\text{HCO}}_3^{-}{[{\text{HCO}}_3^{-})}_{\text{t}}]$ content (mmol/kg) as previously described (38)

$${({\text{HCO}}_3^{-})}_{\text{t}}={\text{tCO}}_2-(S^{\prime }{\text{Pt}}_{{\text{CO}}_2}-{[{\text{HCO}}_3^{-}]}_{\text{a}}0.03)0.8$$ (9)

where S′Pt_CO2 represents dissolved CO₂ and arterial ${[\text{HCO}}_3^{-}]({[{\text{HCO}}_3^{-}]}_{\text{a}})$ is calculated by the Henderson-Hasselbalch equation from arterial pH and Pa_CO2. Brain blood volume is estimated to be 0.03 of the total brain volume, and 0.8 is a conversion factor to change liters to kilogram of brain (38).

RESULTS

Rats were divided into two groups, one with a blood glucose of 6–8 mM (normoglycemic) and the other with a blood glucose of 18–75 mM (hyperglycemic). Preischemic blood (Table 1) and brain (Table 2) physiological variables were similar in all animals. Table 1 shows that animals were normoxic and normothermic and had normal hematocrits; the mild respiratory acidosis and slightly low systolic blood pressure level reflect that animals had adequate levels of halothane anesthesia.

TABLE 1.

Blood physiological variables

	Preischemia
	Normoglycemia	Hyperglycemia
n	3	7
pH	7.29±0.03	7.23±0.02
PaCO2, Torr	64±9	67±3
PaO2, Torr	98±5	111±6
Glucose, mM	6–8	18–75
Hematocrit, %	40±1	44±1
Systolic blood pressure, mmHg	102±1	99±1
Rectal temperature, °C	37±0.5	37±0.5

Values are means ± SE. Pa_O2, arterial PO₂; Pa_CO2, arterial PCO₂.

TABLE 2.

Brain physiological variables

	Normoglycemia (n = 3)		Hyperglycemia (n = 7)
	Preischemia	Ischemia	Preischemia	Ischemia
pHo	7.22±0.02	6.79±0.02	7.22±0.02	6.19±0.02
[H+]o, nM	60±2	164±8	61±2	657±3
PtCO2, Torr	74±9	99–186	80±3	389±9
Lactate, mmol/kg brain		7.54–12.12		19.31–30.89
${{[\text{HCO}}_3^{-}]}_{\text{o}}$, mM	28.5±2.7	11.9–21.9	31.3±1.6	12.3±0.7
${{\text{(HCO}}_3^{-})}_{\text{t}}$, mmol/kg brain	14.2±0.3	13.2–11.8	14.2±0.3	6.3±0.2
tCO2, mmol/kg brain	16.8±1.4		17.2±0.3

Values are means ± SE. Pt_CO2, tissue PCO₂; tCO₂, total CO₂; subscript o, interstitial; subscript t, total.

Preischemic rat brain Pt_CO2 levels (Table 2) were slightly higher (6–7 Torr) than expected from predictions based on arteriovenous PCO₂ values (7) or a recent Pt_CO2 microelectrode study (11). On the other hand, the differences between Pt_CO2 and Pa_CO2 reported here are in close agreement to those where brain Pt_CO2 was measured with a mass spectrometer-based electrode (33). The higher Pt_CO2 values found with our surface electrode (Table 2) or by means of mass spectroscopy (33) may have occurred because of tissue compression (and resultant diminished blood flow and CO₂ accumulation) from the relatively large electrodes that were used. Should actual preischemic Pt_CO2 be 6–7 Torr lower than reported here, potential error in peak Pt_CO2 levels would be <20 Torr because the millivolt change in Pt_CO2 electrode output would be unaffected (Eq. 2; Fig. 6). Similarly, such an error in Pt_CO2 would mean a concomitant error of <1 mM in peak ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ values (Eq. 4; Fig. 8). The resolution of both the [H⁺]_o and Pt_CO2 measurements is better than 1 mV or 0.02 pH and 2 Torr, respectively.

FIG. 6.

Comparison of peak changes in interstitial [H⁺] ([H⁺]_o) and tissue PCO₂ (Pt_CO2,) with lactate production during complete ischemia. Top graph: peak change in [H⁺]_o measured with ion-selective micropipette compared with lactate assessed by enzyme fluorometric techniques from neocortex frozen at peak change in [H⁺]_o. Brain lactate content was modulated by preischemic systemic treatment with insulin or glucose. Peak [H⁺]_o was bimodally distributed. A: in normoglycemia, when blood glucose ranged from 6 to 8 mM and lactate ranged from 7.54 to 12.12 mol/kg, [H⁺]_o rose to constant peak of 6.79 ± 0.02 (n = 3). B and C: transition zone shaded by diagonal lines to reflect variability of peak [H⁺]_o levels there. Black dots, simultaneous [H⁺]_o and Pt_CO2 measurements; triangles, [H⁺]_o data from analogous experiments in Ref. 19. D: under hyperglycemic conditions, when blood glucose ranged from 18 to 75 mM and lactate ranged from 19.81 to 30.89 mmol/kg, peak [H⁺]_o rose by constant but larger amount to reach peak level of 6.19 ± 0.02 pH (n = 7). These results indicate that [H⁺]_o was at steady state but not equilibrium with some acid-producing brain cell compartment between 8 and 13 and 19 and 31 mmol/kg lactate. Bottom graph: simultaneous peak Pt_CO2, measurements. During normoglycemia (A) and mild hyperglycemia (B), peak Pt_CO2, values rose linearly with peak lactate content. However, between 17 and 19 mmol/kg lactate, peak Pt_CO2 rose abruptly and reached peak of 389 ± 9 Torr that persisted through 31 mmol/kg lactate. Constancy of peak value of Pt_CO2 after 19 mmol/kg lactate indicates that ${\text{HCO}}_3^{-}$ was probably exhausted from some ischemic brain cell pool, even though this pool continued to generate another 12 mM of lactic acid.

FIG. 8.

Interstitial ${[\text{HCO}}_3^{-}]({{[\text{HCO}}_3^{-}]}_{\text{o}})$ peak changes after complete ischemia. Black dots, direct calculations from peak values of [H⁺]_o and total PCO₂ (Pt_CO2 shown by black dots in Fig. 6. A: during normoglycemic ischemia, peak ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ rose from 11.9 to 21.9 rnM between-8 and 13 mmol/kg lactate when [H⁺]_o was constant at 6.79 ± 0.02 pH and peak Pt_CO2, was linearly rising. B and C: peak ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ began to fall when peak [H⁺]_o and Pt_CO2 changed abruptly. D: ${{[\text{HCO}}_3^{-}]}_{\text{o}}$, then remained constant at 12.3 ± 0.7 mM between 19 and 31 mmol/kg lactate when [H⁺]_o and P_PtCO2, were also constant.

Ischemic changes in [H⁺]_o and Pt_CO2

[H⁺]_o and Pt_CO2 rose as soon as blood pressure fell in all animals (Fig. 5). No correlative change in Pt_CO2 was seen when the [H⁺]_o showed a characteristic alkaline-going transient (15) that occurs at the time of anoxic depolarization (8). This means that, as previously speculated, fluctuations in Pt_CO2 are unlikely to contribute to this calcium-sensitive alkaline spike (15). Peak levels of [H⁺]_o were bimodally distributed in relation to lactate content (Fig. 6). In spite of the fact that preischemic blood glucoses ranged from 6 to 8 mM and ischemic brain lactate contents ranged from 8 to 12 mmol/kg in normoglycemic animals, [H⁺]_o always rose from 7.22 ± 0.02 pH by a constant amount to 6.79 ± 0.02 pH (n = 3) (Table 2). Similarly, although preischemic blood glucoses ranged from 18 to 75 mM and ischemic brain lactates ranged from 19 to 31 mmol/kg in hyperglycemic animals, [H⁺]_o rose from 7.22 ± 0.02 pH by a constant but larger amount to 6.19 ± 0.02 pH (n = 7) (Table 2). Peak changes in Pt&, followed a somewhat different pattern. Initially, peak Pt_CO2 rose linearly with lactate content until the latter reached 17 mmol/kg (Fig. 6). Peak Pt_CO2 then rose abruptly to 389 ± 9 Torr (n = 7) by 19 mmol/kg lactate and remained constant through 31 mmol/kg lactate.

FIG. 5.

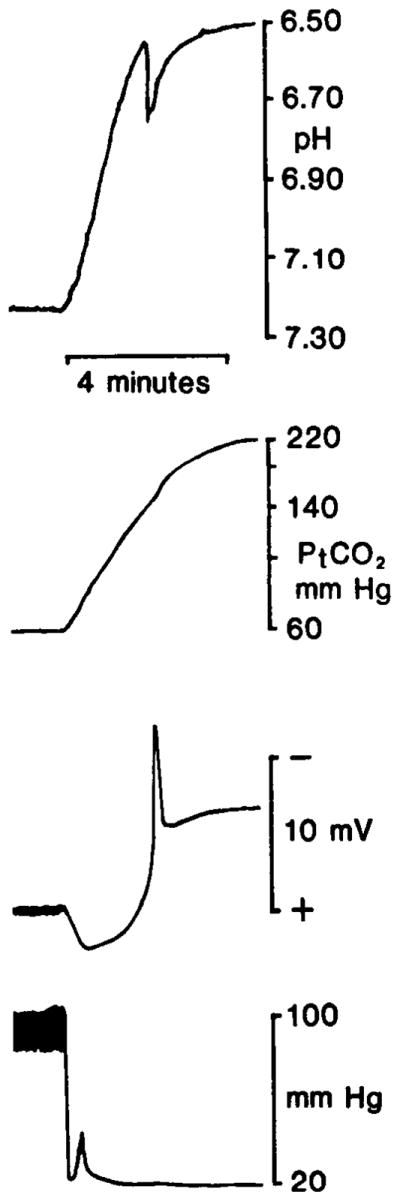
Interstitial [H⁺] ([H⁺]_o) and tissue PCO₂ (Pt_CO2) changes recorded simultaneously during complete ischemia. Typical recording of [H⁺]_o (top trace) and accompanying DC signal (3rd trace from top) is shown from double-barreled H⁺ ISM positioned 500 μm down in parietal cortex. Pt_CO2, (2nd truce from top) was recorded from overlying pial surface. Animals were pretreated with systemic insulin or glucose to modulate brain preischemic carbohydrate stores and ischemic brain lactate content. In this case, preischemic blood glucose was 20 mM. After cardiac arrest, brain lactate content reached a peak of 16.95 mol/kg neocortex. Both [H⁺]_o and Pt_CO2 rose as soon as blood pressure fell from cardiac arrest (bottom trace). In this case, [H⁺]_o began at 7.25 pH and reached a peak of 6.47 pH after ~5 min of ischemia while Pt_CO2 began at 63 Torr and reached a peak of 220 Torr over same period. Characteristic alkaline-going transient in [H⁺]_o that occurs after cardiac arrest shows no relation to Pt_CO2 record but is precisely correlated with large negative DC shift of anoxic depolarization (3rd trace from top). Latter is known to occur when massive amounts of Na⁺ leave interstitial space.

Titration of brain H⁺ buffers is generally thought to occur simultaneously in response to an acid load (37). Comparison of changes in Pt_CO2 to lactate generated during brain ischemia suggests that this may not always be true. If the change in Pt_CO2 is plotted against lactate content, a graph as shown in Fig. 7 is seen. The linearly rising portion of this graph can be described by a straight line [ΔPt_CO2 = 11.9 (lactate) − 42.33] with a correlation coefficient of 0.976. This line can then be extrapolated to zero change in Pt_CO2 to suggest that 3.6 mmol/kg lactate accumulated before a change in Pt_CO2 was seen. Preischemic lactate content is ~1 mmol/kg in anesthetized and spontaneously breathing animals (19). Hence, ~2.6 mmol/kg lactic acid was generated before a change in Pt_CO2 occurred. This means that 2.6 mmol/kg of some other H⁺ buffer was first exhausted before brain ${\text{HCO}}_3^{-}$ was titrated. Phosphocreatine (PCr) is a storage form of ATP that phosphorylates ADP via creatine kinase (Crk) according to

FIG. 7.

Changes in tissue PCO₂ (Pt_CO2) compared with lactate content during complete ischemia. Amount of lactate generated in complete ischemia before brain ${\text{HCO}}_3^{-}$ stores began to be titrated can be estimated by extrapolating above data to zero change in Pt_CO2. Five data points (black dots) between 8 and 17 mmol/kg lactate fit straight line (correlation coefficient 0.976) that is described by: Pt_CO2 = 11.9 (lactate) −42.3. This equation describes a line that intercepts Y-axis at 3.6 mmol/kg lactate. However, since normal preischemic lactate content is ~1 mmol/kg neocortex (see Ref. l9), this equation predicts that 2.6 mmol/kg lactate were generated in complete ischemia before ${\text{HCO}}_3^{-}$ began to be titrated to CO₂. Therefore, at least at start of accumulation of excess H⁺ during ischemia, physicochemical H⁺ buffers can be used in succession rather than simultaneously as is most often assumed to occur. Identity of this initial H⁺ physicochemical buffer remains unknown, However, depletion of high-energy phosphates (PCr/ATP) would account for H⁺ buffering of ~2 mmol/kg lactic acid, and therefore PCr/ATP H⁺ buffering seems a likely source to account for first 2.6 mmol/kg of lactic acid generated.

$$\text{PCr}+\text{ADP}+{\text{H}}^{+}\stackrel{\text{Crk}}{\rightleftharpoons }\text{Cr}+\text{ATP}$$ (10)

This reaction has a free energy of zero, and therefore a rise in ADP or [H⁺] will promote formation of ATP and creatine (Cr) (36). However, since ATP hydrolysis is associated with release of H⁺ on a mole for mole basis, net H⁺ titration via PCr stores should be equivalent to PCr content minus ATP content. PCr stores are ~5 mmol/kg and ATP stores are ~3 mmol/kg in rat brain (19, 36). Hence, PCr should buffer ~2 mM of excess lactic acid. The considerations suggest that PCr first buffers excess lactic acid before ${\text{HCO}}_3^{-}$ begins to do the same after an accumulation of ~2–3 mmol/kg lactate.

Changes in brain ${\text{HCO}}_3^{-}$

CO₂ is a highly diffusible gas in tissues and crosses intact membranes rapidly (21). Therefore, Pt_CO2 will rise when ${\text{HCO}}_3^{-}$ stores are titrated in any isolated compartment of a closed system, such as the brain during complete ischemia. Pt_CO2, measurements when combined with simultaneous measurements of [H⁺]_o during complete ischemia allow one to predict remaining ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ (according to Eq. 3 or 4). In addition, the amount of ${{\text{(HCO}}_3^{-})}_{\text{t}}$ neutralized by lactic acidosis can be predicted from changes in Pt_CO2, (where [ ${\text{HCO}}_3^{-}$] lost is equal to the change in Pt_CO2, times S′). We will deal with these two ${\text{HCO}}_3^{-}$ variables separately.

Changes in Pt_CO2, suggest how [H⁺]_o could remain constant between 8 and 12 and 19 and 31 mmol/kg lactate (Fig. 6). Between 8 and 12 mmol/kg lactate, when Pt_CO2, rose linearly but [H⁺]_o remained constant, calculated ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ (Eq. 3 or 4) must have increased from 11.9 to 21.9 mM (Fig. 8). Then, after transitional changes (between 12 and 19 mmol/kg lactate), [H⁺]_o and Pt_CO2, remained constant; at that point, ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ must have remained constant at 12.3 ± 0.7 mM (Fig. 8; n = 7; Table 2). Above 19 mmol/kg lactate, ${\text{HCO}}_3^{-}$ must have been exhausted in any cells that continued to produce lactic acid if additional intracellular H⁺ buffers in such cells were less plentiful than ${\text{HCO}}_3^{-}$ and if such additional buffers possessed ionization equilibrium constants less than or near that of the ${\text{CO}}_2-{\text{HCO}}_3^{-}$ system. These considerations imply that H⁺ and H⁺-related ionic species (such as ${\text{HCO}}_3^{-}$) may remain heterogeneously distributed between acid- and nonacid-producing compartments during hyperglycemic and complete ischemia.

Pt_CO2 (Fig. 6) and ${{\text{(HCO}}_3^{-})}_{\text{t}}$, measurements can be used to estimate the pH and size of the unknown compartment, respectively. If ${\text{HCO}}_3^{-}$ stores in the unknown compartment were exhausted to <l mM (as discussed above) while Pt_CO2, was 389 Torr, pH can be predicted from Eq. 3 or 4 to be <5.2 in the compartment that continued to generate lactic acid >19 mmol/kg lactate. Also, the amount of ${{\text{(HCO}}_3^{-})}_{\text{t}}$ lost during complete ischemia is equal to the measured change in Pt_CO2, multiplied by S′ and 0.8 (a multiplication factor to convert mM to mmol/kg) (Fig. 9). Accordingly, since 6.3 mmol/kg ${{\text{(HCO}}_3^{-})}_{\text{t}}$, remained in brain tissue at lactate values >19 mmol/kg lactate (Fig. 9; Table 2), the size of the unknown compartment can be estimated. If remaining ${\text{HCO}}_3^{-}$ was distributed homogeneously, the size of the unknown compartment lacking ${\text{HCO}}_3^{-}$ would be ~36% of neocortical space; e.g., 6.3 mmol/kg brain is equivalent to 7.9 mM and 7.9 mM/12.3 mM is equal to 64%, representing the size of the space containing the remaining ${\text{HCO}}_3^{-}$ where the [ ${\text{HCO}}_3^{-}$] is 12.3 mM.

FIG. 9.

Changes in neocortical total ${\text{HCO}}_3^{-}[{({\text{HCO}}_3^{-})}_{\text{t}}]$ content compared with lactate content during complete ischemia. Dashed lines, preischemic neocortical ${{\text{(HCO}}_3^{-})}_{\text{t}}$, content of 14.2 ± 0.3 mmol/kg (n = 12) that is characteristic for rats anesthetized and spontaneously breathing with arterial PCO₂’s as shown in Table 1. Graph shows result of subtracting calculated ${\text{HCO}}_3^{-}$ lost from conversion to CO₂ during ischemia from preischemic level of 14.2 mmol/kg. Such calculations show that, above 19 mmol/kg lactate, 6.3 ± 0.2 mmol/kg of ${{\text{(HCO}}_3^{-})}_{\text{t}}$, were left in ischemic neocortices in spite of continued accumulation of lactate to 31 mmol/kg.

DISCUSSION

Previously, studies of brain during complete ischemia (37) considered the organ to behave as a homogeneous proteinaceous ionic milieu, but this no longer seems likely. In this study we used simultaneous measurements of Pt_CO2, and [H⁺]_o as well as measurements of ${{\text{(HCO}}_3^{-})}_{\text{t}}$ to illustrate peak changes in the behavior of carbonic acid buffer species during brain ischemia. Our results suggest that both ${\text{HCO}}_3^{-}$ and H⁺ remain heterogeneously distributed within brain during (hyperglycemic) complete ischemia with lactate accumulation >19 mmol/kg. Such a distribution for these ions must exist between ischemic interstitial space and some population of intact cells that continue to generate lactic acid.

Heterogeneous distribution of H⁺ and ${\text{HCO}}_3^{-}$ in ishernia

The finding of an ischemic-bimodal distribution for [H+]_o in comparison to a progressively climbing tissue lactate content (Fig. 6) led us to propose a model for ischemic brain H⁺ homeostasis (19). This model emphasizes for the first time the possible activity of plasma membranes during ischemia. Briefly stated, the model has four components under normal conditions. First, excess H⁺ ultimately leaves neurons via Na⁺-H⁺ or ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ antiports (31, 42) or as CO₂. Second, glial cells handle excess H⁺ similarly except that Na⁺-H⁺ and ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ antiport systems are segiegated to different sides of the glial cells, the first facing capillaries and the second facing the neurons (13). In this way, the acceleration of CO₂ hydration by carbonic anhydrase (32) will promote loss of H⁺ to blood via Na⁺-H⁺ antiport and return of ${\text{HCO}}_3^{-}$ to the interstitial space and neurons via ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ antiport (13). Third, ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ antiport can be directed inward or outward, as in erythrocytes (4), in order to neutralize excess H⁺ to CO₂ on either side of the glial cell membrane. Fourth, power to complete Na⁺-H⁺ exchange (and perhaps ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ exchange; see Refs. 31,42) comes from the Na⁺ gradient, which is maintained by Na⁺-K⁺-ATPase and a selective plasma membrane impermeability to Na⁺.

During complete ischemia with the absence of blood flow, the model can be conceptualized as a three-compartment system, consisting of neurons, glia, and the interstitial space, where each compartment is bounded by plasma membranes as described above. [Na⁺]_o drops by ~106 mM during complete ischemia (9), and neurons (and probably glia) are depolarized (8). Thus the combination of a diminished transmembrane Na⁺ gradient and the absence of membrane polarization may prevent egress of excess H⁺ from acidotic brain cells via Na⁺-H⁺ antiport (19). Instead, only ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ antiport would be expected to shuttle H⁺ across compartment boundaries, although there is also known to be a drop in [Cl⁻]_o to ~72 mM (9). Finally, when ${{\text{(HCO}}_3^{-})}_{\text{t}}$, stores are sufficiently exhausted in hyperglycemic ischemia, excess H⁺ would have no means of leaving intact brain cells, thus leaving only intracellular physicochemical H⁺ buffers to lessen rising [H⁺]. The Pt_CO2,-[H⁺]_o results reported here support this model with one refinement.

Measurements of tCO₂, and estimated loss of ${{\text{(HCO}}_3^{-})}_{\text{t}}$ compared with the amount of lactic acid generated (Fig. 9) allow us to propose that the remaining ${{\text{(HCO}}_3^{-})}_{\text{t}}$ in brain, if distributed homogeneously, would be confined to 64% of the neocortical space under hyperglycemic conditions. Estimates of the relative volumes of neurons, glia, and the interstitial space in rat neocortex suggest that the three compartments account, respectively, for 52.5, 32.5, and 15% of the whole (10). Since some ${\text{HCO}}_3^{-}$ remains in the interstitial space at and above 19 mmol/kg lactate (i.e., [H⁺]_o is 6.18–6.19 pH while Pt_CO2 is 389 Torr), the interstitial space would have to equilibrate with a compartment the size of intraneuronal space to account for an ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ of 12.3 mM, if remaining ${{\text{(HCO}}_3^{-})}_{\text{t}}$ were homogeneously distributed. A homogeneous ${{\text{(HCO}}_3^{-})}_{\text{t}}$ distribution is the most economical assumption, and if true, would mean that [H⁺] would be the same in both interstitial and intraneuronal space (i.e., 6.18–6.19 pH) at 19–31 mmol/kg lactate because Pt_CO2 should also be equivalent in both compartments. [H⁺] in the unknown compartment, which may be glia, is likely to be significantly more acidic than interstitial space. The latter conclusion stems from the observation that lactic acid was generated above a level of 19 mmol/kg lactate in a brain space in which ${\text{HCO}}_3^{-}$ stores were exhausted and Pt_CO2 was 389 Torr. Therefore, [H⁺] in this compartment was >5.2 pH while intraneuronal [H⁺]_o was presumably 6.18–6.19 pH (i.e., identical to [H⁺]_o,). Note that at this point considerable ${{\text{(HCO}}_3^{-})}_{\text{t}}$ remained in the neocortex. In fact, if all ${{\text{(HCO}}_3^{-})}_{\text{t}}$ stores were neutralized to CO₂, Pt_CO2, would have risen to ~636 Torr (Pt_CO2 = tCO₂/0.8 S′, where tCO₂ is 17.2 mmol/kg at Pa_CO2 of 67 Torr).

The unchanging level of [H⁺]_o at 6.18–6.19 pH during hyperglycemic and complete ischemia originally led us to assume that all brain cells might be impermeable either to excess H⁺ or their ionic determinants (40) >19 mmol/kg lactate (19). In light of the plateau of peak Pt_CO2 at 389 Torr (Fig. 6), we must now refine this assumption to suggest that excess H⁺ is likely to be confined to 36% of total neocortical space, a volume that is close to that of glial space. We speculate that acid accumulation of glia exceeds a pH of 5.2 when lactate exceeds 19 mmol/kg. This level of lactate accumulation previously has been correlated with infarction of brain after nearly complete ischemia (29). Recently, astrocytes in culture were shown to be irreversibly injured when exposed to solutions of 5.2 pH for 10 min (25), a value consistent with our calculations.

Implications toward glial function

Restriction of excess H⁺ to glial space above 19 mmol/kg lactate has important implications toward the physiological and biochemical behavior of ischemic brain. Such a restriction implies that anaerobic glycolysis ceases above 19 mmol/kg lactate in neurons. This follows because no further fall in ${{[\text{HCO}}_3^{-}]}_{\text{o}}$ or rise in Pt_CO2 occurred after this level of lactate accumulation, although ${\text{HCO}}_3^{-}$ remained in 64% of neocortical space. Cessation of neuronal lactic acid production might result from exhaustion of neuronal glucoses stores or a lack of glucose transport out of glia or into neurons. The mechanism of glucose transport across glial and neuron to membranes, although thought to occur via facilitated diffusion, remains speculative (2). In addition, why should such transport stop at 19 mmol/kg lactate? Alternatively, glucose utilization could stop because acidosis inhibited glycolytic enzymes (36). Such an interpretation would require postulating a different [H⁺] sensitivity of glycolytic enzymes in neurons compared with glial cells.

The potential importance of glia toward maintaining brain acid-base homeostasis under normal and ischemic conditions has been recognized in the past (13, 36). However, H⁺-related changes in glial plasma membrane function during ischemia have not been stressed and could account for the Pt_CO2 and [H⁺]_o results reported here. Under normoglycemic conditions (Figs. 6A and 8A) [H⁺]_o remained constant in the face of rising Pt_CO2 and ${{[\text{HCO}}_3^{-}]}_{\text{o}}$. We believe that this resulted from net secretion of ${\text{HCO}}_3^{-}$ to the interstitial space from astroglia. Net secretion of ${\text{HCO}}_3^{-}$ changed to net absorption (Figs. 6, B and C, and 8, B and C), perhaps as glial lactic acid production became predominant. Finally, net absorption and titration of ${\text{HCO}}_3^{-}$ stopped at 19 mmol/kg lactate. Why ${\text{HCO}}_3^{-}$ absorption should stop before all ${{\text{(HCO}}_3^{-})}_{\text{t}}$ is neutralized to CO₂, in spite of continued lactic acid production, remains unclear. However, evidence indicates that acid extrusion from barnacle muscle is reduced from 2.5 to <0.05 nM/min when [H+10 is raised from 8.6 to 6.8 pH (3). If a similar phenomenon occurs in glia, acid extrusion might stop completely when [H⁺]_o rose from its preischemic level of 7.22 to 6.18–6.19 pH.

Several pieces of evidence support these postulated aspects of glial cell function during hyperglycemic ischemia. First, astrocytes maintain impermeable plasma membranes to diffusion of Na⁺ and Cl⁻ when exposed to [K⁺]₀ of 54 mM in tissue culture and might also maintain an impermeability to Na⁺ and Cl⁻ in vivo during ischemia when [K⁺]₀ is known to rise to similar levels (45). Second, membrane electrical resistance of glia does not change during spreading depression (41) in spite of interstitial ion concentration changes (24) similar to those that occur during ischemia (9). Therefore, although probably depolarized during ischemia, glia may also maintain membrane electrical resistance (and concurrently, impermeability to ionic diffusion) during ischemia (19). Finally, we speculate that intraglial pH can fall to <5.2 pH. We previously provided evidence that ischemic brain can generate an interstitial pH (pH_o) as low as 5.4 (17). Under severely hyperglycemic conditions (blood glucose 17–75 mM) pH_o fell to 6.1–6.2 after 30 min of near complete ischemia. With recirculation, pH_o then fell abruptly to as low as 5.4. Brain is known to swell with reperfusion from severe incomplete ischemia (l2), and membrane permeability of edematous acid-producing cells may rise. If so, increased plasma membrane permeability to H⁺ or its ionic determinants (15, 19,40) could cause the second fall in pH_o to 5.4. Finally, since pH_o did not fall below ~6.1–6.2 during 30 min of incomplete ischemia, membrane impermeability to H⁺ or its ionic determinants either in glial cells or some other less likely compartment must persist for this time period.

Deterioration of the cooperative interaction between glial cells and neurons with respect to glucose utilization and waste (i.e., H⁺ and CO₂) removal via membrane transport mechanisms may be a fundamental step in the pathogenesis of irreversible injury of brain from ischemia (23). The present results show an abrupt deterioration in acid-base homeostasis at a range of lactate accumulation (13–19 mmol/kg) that previously has been correlated with the transition from a selective loss of vulnerable neurons (28) to brain infarction (30). Furthermore, our results implicate glia as both the final site of continued acid production and the repository of its lethal accumulation in ischemic brain.

FIG. 10.

Schematic of heterogeneous distribution of H⁺ and ${\text{HCO}}_3^{-}$ during hyperglycemic and complete ischemia. In complete ischemia, absence of blood flow prevents egress of excess CO₂ and H⁺-related ionic species from brain to blood. Thus brain can be regarded as 3-compartment system consisting of neurons, glia, and interstitial space (ISS) where each compartment is bounded by plasma membranes. Movement of excess H⁺ across such membranes is likely to occur via some combination of electroneutral Na⁺-H⁺ (1 and 3) and ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ (2 and 4) exchange transport. Both transport systems may be powered by transmembrane Na⁺ gradient under normal conditions. In ischemia, large drop in interstitial [Na⁺] and [Cl⁻] occurs, probably through entry of Na⁺ and Cl⁻ into neurons. Diminished interstitial [Na⁺] may prevent egress of excess H⁺ via Na⁺-H⁺ antiport in neurons (1) and glia (3). Furthermore, loss of membrane potential and fall in membrane resistence in neurons (shown by dashed line to neuronal membrane) during ischemia may indicate that small ions (such as ${\text{HCO}}_3^{-}$) equilibrate between neuronal and interstitial space. If so, [H⁺] would be same in both compartments because highly permeable CO₂ can be expected to be similar throughout all brain compartments. Support for this latter assumption comes from total ${\text{HCO}}_3^{-}[{({\text{HCO}}_3^{-})}_{\text{t}}]$ measurements, which show that ${{\text{(HCO}}_3^{-})}_{\text{t}}$, after hyperglycemic and complete ischemia is distributed in 64% of neocortical space, if it is distributed homogeneously (shown by diagonal lines). This volume is nearly equivalent to ISS plus neuronal space. ${{\text{(HCO}}_3^{-})}_{\text{t}}$, measurements further suggest that, above 19 mmol/kg lactate, continued anaerobic glycolysis occurred in compartment that occupied 36% of neocortical space, had exhausted its ${\text{HCO}}_3^{-}$ stores, and therefore may have had an internal pH of <5.2 and was surrounded by membranes that were impermeable to H⁺ and H⁺-related ionic species. This compartment is likely to be glia. Why glial ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ antiport (4) should stop before all ${{\text{(HCO}}_3^{-})}_{\text{t}}$ is titrated to CO₂ is unknown but may be related to [H⁺] sensitivity of ${\text{Cl}}^{-}-{\text{HCO}}_3^{-}$ antiport as well as continued integrity of glial plasma membranes.