Skip to main content
PMC home page
Malaria Journal logoLink to Malaria Journal
. 2009 Dec 16;8:296. doi: 10.1186/1475-2875-8-296

Modeling the risk of malaria for travelers to areas with stable malaria transmission

Eduardo Massad 1,2,✉, Ronald H Behrens 2, Marcelo N Burattini 1, Francisco AB Coutinho 1
PMCID: PMC2806379  PMID: 20015392

Abstract

Background

Malaria is an important threat to travelers visiting endemic regions. The risk of acquiring malaria is complex and a number of factors including transmission intensity, duration of exposure, season of the year and use of chemoprophylaxis have to be taken into account estimating risk.

Materials and methods

A mathematical model was developed to estimate the risk of non-immune individual acquiring falciparum malaria when traveling to the Amazon region of Brazil. The risk of malaria infection to travelers was calculated as a function of duration of exposure and season of arrival.

Results

The results suggest significant variation of risk for non-immune travelers depending on arrival season, duration of the visit and transmission intensity. The calculated risk for visitors staying longer than 4 months during peak transmission was 0.5% per visit.

Conclusions

Risk estimates based on mathematical modeling based on accurate data can be a valuable tool in assessing risk/benefits and cost/benefits when deciding on the value of interventions for travelers to malaria endemic regions.

Introduction

The risk of malaria for visitors to the nine Brazilian states of the Legal Amazon region - Acre, Amapá, Amazonas, Maranhão (western part), Mato Grosso (northern part), Pará (except Belém City), Rondônia, Roraima and Tocantins (western part) - is predominantly P. vivax (75%) with P. falciparum making up the remainder one quarter of surveillance reports. In addition, it should be noted that multidrug-resistant P. falciparum has been reported [1] in the same region. Transmission occurs in most forested areas below 900 m though there is some urban transmission around settlements and small cities in the region. Transmission intensity varies according to the season and municipality. It is higher in jungle areas where recent (<5 years) mining, lumbering and agricultural settlements than in urban areas, such as larger cities like Boa Vista, Macapá, Manaus, Maraba, Pôrto Velho, Rio Branco and Santarém, where transmission occurs on their outskirts. However, in the central areas of these cities transmission is negligible or non-existent.

In 2007 Brazil reported approximately 50% of the total number of the malaria cases in the Americas. Ninety-nine percent of those cases were from the Legal Amazon, where 10% to 15% of the population of Brazil population live [2]. Case numbers fell between 1992 to 2002 from 572,000 to 349,873, with around 16.5% of all the slides examined resulted positive for malaria. A rebound occurred between 2003 to 2007 with number of cases peaking at 607,000 in 2005 and 458,041 cases in 2007. All reported malaria cases were confirmed by laboratory analysis, and 19% in 2007 were P. falciparum. Theses cases were predominantly associated with population movement to the periphery of large cities in the Legal Amazon Region [2]. Therefore, the average burden of malaria over the last decade has been approximately 600,000 cases per year, with the proportion of falciparum around 20% ot total [3]. WHO estimated the total numbers of malaria cases in 2006 as approximately 1.4 million [2]. The difference between the two figures reflects either an underestimation (Brazilian official data) or an overestimation of the actual number of cases (WHO estimates). The true values probably lies between the two.

Brazil has the second largest number of foreign visitors in Latin America after Mexico [4]. In 2005 Brazil recorded 5.4 million international arrivals with 57% of these traveling coming from North America and Europe [5]. Of the total, 44% were leisure tourists. Preliminary analysis of tourism arrivals for 2004/2005 by Embratur [5], reveal that 39% of tourists cite Brazil's natural beauty as their reason for travel. However, 7% of leisure tourists ((3% of total tourists) state they visited the Brazilian Amazon. Therefore, estimated visits to the malaria endemic areas of Brazil are of the order of 160,000 per year. Embratur [5] identifies that tourists from the domestic market is much larger. The latest study indicates that of the annual 11 million domestic Brazilian travelers, around 300,000 visit the Amazon region. Therefore an estimated half a million non-resident visitors are exposed to malaria per year in this region [4].

Malaria prevention in non-immune travelers is based on chemoprophylaxis, recommended for all visitors to the region where there is active malaria transmission. However, all regimens have well recognized and not infrequent side effects, including severe events that interfere with routine daily activity. Therefore risk-management requires the balance of risk of infection and risk of toxicity when prescribing chemoprophylaxis. This balance is particularly important when the risk of malaria is low and the numbers exposed are significant [6].

This study was designed to use a mathematical model to estimate the risk of acquiring falciparum malaria for travelers to the endemic regions of Brazil.

The Model

The model assumes that the population of humans is subdivided into three classes and the population of mosquitoes is similarly divided into three compartments summarized in table S1, Additional file 1. It was separated from the human general population (individuals that are in the area) a cohort [7], denoted by primes and named "probe", which represent a cohort of travelers, followed through their entire exposure in the region, to calculate the risk of malaria acquisition.

The model's dynamics is described by the set of equations shown in the appendix.

A deterministic version (precisely determined through a known relationship) of the model was used to describe the malaria dynamics in the resident population level and a stochastic version (using a ranges of variable values providing a probability). On the equations analyzing the probes to describe the risk (probability of contracting malaria) of a single individual traveler visiting the region. This is based on the assumption that, since the probe is a small number of individuals, the biting rate will randomly fluctuate and the probability of infection is unpredictable.

The model's parameters are: a is the mosquitoes daily biting rate; a' is the mosquitoes daily biting rate in the probe; b is the proportion of infected bites that are actually infective to humans; b' is the proportion of infected bites that are infective to humans in the probe; c is the proportion of bites that are infective for mosquitoes; μH is the humans mortality rate; γH is the humans recovery rate from parasitaemia; rH is the humans birth rate; αH is the malaria-induced mortality rate of humans; σH is the lost of immunity due to malaria; μM is the mosquitoes daily mortality rate, τ is the extrinsic incubation period; rM is the mosquitoes fertility rate; κH is the humans carrying capacity and κM is the mosquitoes carrying capacity. We introduced the term [cS-dSsin(2πft)] in the susceptible mosquitoes population in order to simulate seasonality in the mosquitoes population [8,9]. The parameters cS and dS (cS >dS) vary the intensity by seasonality, mimicking severe or mild winters, through adjusting these parameters' values. The model parameters are shown in table S2, Additional file 2.

The seasonality parameters cS and dS where chosen to represent the observed seasonal variation in the Amazon region described by Tadei [10], who described a 30 fold difference in mosquito number between summer and winter.

Using the parameters in table S1, Additional file 1 the model calculates that around 250,000, falciparum malaria cases will occur annually, a number similar to WHO estimates for Brazil in 2006 [2].

Estimating the risk of malaria

In order to calculate the probability of an individual acquiring malaria infection, πmal after the introduction of a single case in an entirely susceptible population it was considered the probe (travelers within the region) followed through an entire outbreak. The probability of infection in this self-limiting outbreak is then given by the following expression:

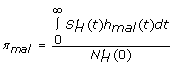graphic file with name 1475-2875-8-296-i1.gif (1)

In the above equation, S'H(t) and N'H(t) are respectively the number of susceptible hosts and the total population of the cohort used as a probe, and hmal(t) is the force of infection of malaria, defined as the per capita number of new cases per time unit [7] and expressed as

graphic file with name 1475-2875-8-296-i2.gif (2)

where IM(t) is the number of infected mosquitoes.

One can also calculate the average risk (probability) of infection for a traveler who arrives in the affected region at week Ω after the outbreak is triggered and remains there for ω weeks, Inline graphic. This is done by setting the limits of integration in equation (1) as:

graphic file with name 1475-2875-8-296-i4.gif (3)

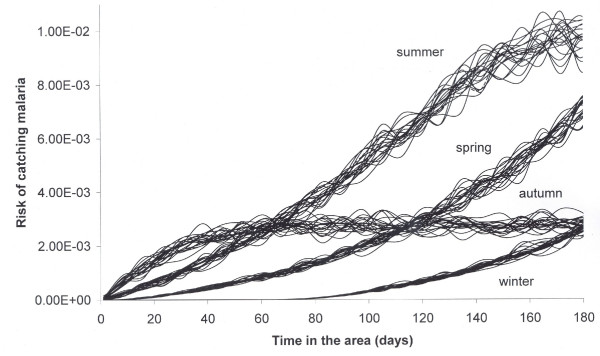
The average risk for a traveler who arrived in the Amazonian region at four different time periods was calculated, namely, in the dry season (winter) in the spring, in the wet season (summer) and in the fall. The model produces a result of 250,000 cases falciparum malaria per year. This number is very dependent on a number of other variables and parameters. In the sensitivity analysis below all the parameters are varied and as a consequence the yearly number of cases varies. The result for the risk calculation is shown in figure 1.

Figure 1.

Figure 1

Open in a new tab

Stochastic risk of catching falciparum malaria for travelers as a function of the period of the year they arrive and the time remaining in the area (the figure shows 20 iterations of the 1000 simulated).

Sensitivity analysis

In this section we analyze the sensitivity of the model to the parameters. This is done in two steps: a deterministic analysis at the populational level, which describes the sensitivity of the model to measurement variance in the parameters; and a stochastic analysis at the individual level, which determines the variation in the model's outcomes due to intrinsic stochasticity in some of the parameters.

Sensitivity of the model to variance in the parameters measures

The risk of malaria acquisition π as given by equation (3) is a function of a number of parameters collectively denoted by Pari. For a small variation of Pari, ΔPari, the variation in the risk π, Δπ, is given by the well-known error-propagation formula [11]:

graphic file with name 1475-2875-8-296-i5.gif (4)

The relative variation in the risk π, Δπ/π, as a function of the relative variation in the parameters ΔPari/Pari, is therefore:

graphic file with name 1475-2875-8-296-i6.gif (5)

The result of this analysis is given in table S3, Additional file 3.

The sensitivity of the model is significantly influenced by with the season of the year. The two parameters that are most influential in the model i are the biting rate a and the mosquitoes mortality rate μM. Biting rate and mosquito mortality are well recognized by entomologists as important parameters as they describe vectorial capacity (a quadratic component) and mortality expressed exponentially in the equation.

Variation in the model's outcomes due to intrinsic stochasticity in some of the parameters

Of all the parameters described in table S1, Additional file 1 the biting rate a single individual is subject, a', and the probability that an infectious biting is infective to the individual, b', for an occasional traveler are obviously stochastic variables. As mentioned above, it was assumed a Poisson distribution for the parameter a' and a Gamma distribution for the parameter b' with a small variance. The result is shown in table S4, Additional file 4 which shows the risk of malaria acquisition for a traveler who arrives at different moments of the year and remains 30 days in the area.

The highest risk of malaria acquisition occurs for individuals arriving in autumn (around one case for every 500 visitors) as the infected mosquitoes population is close to its peak and the proportion infected high (see figure 2).

Figure 2.

Figure 2

Open in a new tab

In the figure we show in the x-axis time in days. It starts arbitrarily at day 500 and illustrates seasonal variation of a mosquito population (susceptible and infected). The arrows define the relative season and seasonal impact on the susceptible mosquitoes populations (thin line) over the year. The figure also shows the infected mosquitoes (thick line) amplified 20 times.

Where an individual remains for a 1 year their risk is approximately 1.10 × 10-2 ± 2.75 × 10-5, that is, a relative error of ± 0.25%. This rate closely correlates with the incidence observed in Amazon residents of 1.16 × 10-2 per person-year. PAHO [12] estimates that this incidence, a maximum of 75 malaria cases per 1000 inhabitants annually will occur. We are estimating only the cases of falciparum malaria, which represent about one third of the total malaria cases, hereby total predicted P falciaprum malaria cases for this region is of the order of 33 cases per 1000 inhabitants per year.

Discussion

Mathematical models for estimating risks, as described in this paper, should be considered as auxiliary tools for decision-makers. Some caveats, however, are necessary; the model's outcomes are determined by assumptions in the dynamics of the system modeled and on the values given to the parameters. In our model, the most critical assumptions relate to homogeneity. For example, the Amazon region is very large and therefore, it is likely that some parameters will vary from region to region, such as the densities of vectors and human hosts (determined by the respective carrying capacities). The seasonal variations assumed in the model are simple and are only an approximation of the actual climatic variations that occur in the Amazon region. Notwithstanding the oversimplifications of our model, we believe that our results are a good approximation in the sense that the actual risk of malaria lies within the estimated confidence intervals calculated by the model.

Previous studies have attempted to determine the cumulative risk of acquiring malaria in travelers [6,13,14], but the estimated incidence rates were not generalizable to all travelers at all times, as malaria incidence varies greatly from year to year [15].

Mathematical modeling is well suited to adjust for seasonality and annual variations. In a previous analysis we modeled the risk of dengue and yellow fever, with similar approach to the one described here [16-18]. This is the first time that travelers' malaria risk estimates have been calculated using mathematical modeling. Our models are robust and have been tested extensively on Amazonian data [19]. Risk for malaria risk for endemic populations has also been estimated using modeling by Okell et.al [20].

The analysis presented quantifies the risk for non-immune travelers visiting the Amazonian region, adjusting by season and/or epidemic cycle.

A traveler arriving in summer (Dec-Feb) exposed for 120 days has at least a ten-fold higher risk of infection than a traveler who arrives in the winter (June-Aug) for a visit of similar duration. It is shown that the risk increases nonlinearly with time, but this again varies by season of exposure.

National and international recommendations for long term travelers; particularly those traveling through regions of varying transmission and with different malaria species have been very crude (all or nothing) and have a very limited evidence base [21].

The model can be used for highlighting the malaria risk in a way that many advisors and their clients can interpret. An individual arriving during the summer (Jan-Mar), that is, rainy season, has a probability of 0.00015 (1:6666) of being infected within a week of arrival if totally unprotected whilst it takes approximately 3 months for a traveler arriving during the winter months (Jun-Aug), that is, dry season, to be infected with the same likelihood, with intermediary values for arrivals during other seasons. In fact, Behrens et al. [22] estimated the incidence of malaria in UK travelers to Brazil as 1 case per 3000 person-years exposed over the years 2000-2005. During this period there were 394,559 visits with average visit duration of 22.5 days resulting in 9 vivax cases and no P falciparum cases in UK travelers. Running the model with this data the model produced a result of 1 case of falciparum malaria. Assuming that travel was predominantly during the winter months, this single case is a similar incidence (0) as observed in UK travelers, affirming the reliability of our current assumptions and values used in the model.

The model does not take account of pre-existing malaria immunity although for most naïve travelers this is not important. Another aspect that was not considered in this paper is chemoprophylaxis, which is about 95% efficient against falciparum malaria. Therefore, if only 50% of the travelers are compliant, then the number of expected cases is reduced by approximately 48%, although the risk for a non-treated individual does not change.

It is important to stress what is gained in terms of risk estimation with our model. It is known that the annual incidence of malaria among Amazon residents is of the order of 50 cases per 1000 inhabitants. This figure can be used as a proxy for the risk to travelers staying for at least one year in the region. However, the model provides estimations of the risk for travels of shorter durations and, since the risk for these short visits is dependent on the season of the year travelers arrive in the area, the model is essential for those estimations.

The model for the resident population is a modification of the classical Macdonald model [23]. The sensitivity of the model's outcome for errors in the measurements of the parameters was calculated. With exceptions of Macdonald [23] and Burattini et al. [8] who analyzed the sensitivity of the basic reproduction number to variation on the parameters, it seems to us that this is the first time the sensitivity of other Macdonald's model outcomes is analyzed. The results of this analysis point to a model that is very sensitive to the mosquitoes biting rate, a, and natural mortality rate, μM. A 1% error in the measurement of these parameters assumed but perhaps this can be improved. The travelers' population was approximately treated stochastically. By this we mean that we considered the bites received by a single individual are Poisson distributed with average equals to the deterministic value of mosquitoes biting rate, a, suffered by the resident population. In fact, the number of bites suffered by each individual is the product of the mosquitoes biting rate a times the number of infected mosquitoes in a certain area corresponding to the mosquitoes flying range, which was considered to be approximately constant. We also considered that the probability of infection to humans, b, as Gamma distributed around the average value used for the resident population and with a small variance.

The basic model could be applied to other regions where local information on force of transmission, parasite rates or similar malariometric data are available. Such risk estimates would help the travel medicine provider with a better starting point in their risk assessment and provide travelers with a feel for what their malaria risk is and balance this with the appropriateness of chemoprophylaxis.

Appendix 1

The equations describing the model are given below. The symbols describing the populations involved, the parameters and their values are described in the main text.

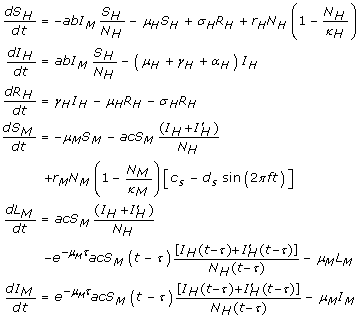graphic file with name 1475-2875-8-296-i7.gif (A1)

The evolution equations for the probe cohort are:

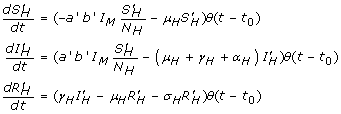graphic file with name 1475-2875-8-296-i8.gif (A2)

for

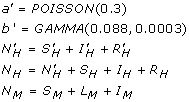graphic file with name 1475-2875-8-296-i9.gif (A3)

and θ(t - t0) is the Heaviside function.

Competing interests

The authors declare that they have no competing interests.

Authors' contributions

EM and FABC designed the study and the model and prepared the first draft.

EM, RHB, FABC and MNB analyzed the results. All authors contributed to the interpretation of the results and agreed the final draft.

Supplementary Material

Additional file 1

Table S1. Models' variables.

Click here for file (33.5KB, DOC)
Additional file 2

Table S2. Model's parameters.

Click here for file (131KB, DOC)
Additional file 3

Table S3. Sensitivity of the model to each of the parameters (Par) in different periods of the year. The analysis assumes a 1% variation in the value of each parameter and the risk was calculated for 30 days of permanence. The values of the parameters are given in table S2.

Click here for file (73.5KB, DOC)
Additional file 4

Table S4. Average risk of malaria acquisition (with confidence intervals) for travelers who remain 30 days in the area.

Click here for file (20.5KB, DOC)

Contributor Information

Eduardo Massad, Email: edmassad@dim.fm.usp.br.

Ronald H Behrens, Email: Ron.Behrens@lshtm.ac.uk.

Marcelo N Burattini, Email: mnburatt@usp.br.

Francisco AB Coutinho, Email: coutinho@dim.fm.usp.br.

Acknowledgements

This work was partially supported by FAPESP, CNPq and LIM01-HCFMUSP.

It was in part undertaken at UCLH/UCL who receive a proportion of funding from the Department of Health's NIHR Biomedical Research Centres funding scheme.

References

  1. WHO. http://www.who.int/ith/countries/bra/en/ Accessed in 29 May 2009.
  2. WHO. http://www.who.int/malaria/wmr2008/malaria.pdf Accessed in 29 May 2009.
  3. Ladislaw JLB. Situação da Malária na Amazônia Legal. Ministário da Saúde. Secretaria de Vigilância em Saúde; 2006. [Google Scholar]
  4. Ecobrasil. 2008. http://www.ecobrasil.org.br Accessed in 29 May 2009.
  5. Embratur. 2006. http://www.ecoviagem.com.br/ Accessed in 29 May 2009.
  6. Behrens RH, Bisoffi Z, Björkman A, Gascon J, Hatz C, Jelinek T, Legros F, Mühlberger N. TropNetEurop. Voltersvik P. Malaria prophylaxis policy for travellers from Europe to the Indian Sub Continent. Malaria Journal. 2006;5:7. doi: 10.1186/1475-2875-5-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Massad E, Ma S, Burattini MN, Tun Y, Coutinho FA, Ang LW. The risk of chikungunya fever in a dengue-endemic area. J Travel Med. 2008;15(3):147–55. doi: 10.1111/j.1708-8305.2008.00186.x. [DOI] [PubMed] [Google Scholar]
  8. Burattini MN, Chen M, Chow A, Coutinho FA, Goh KT, Lopez LF, Ma S, Massad E. Modelling the control strategies against dengue in Singapore. Epidemiology and Infection. 2008;136(3):309–319. doi: 10.1017/S0950268807008667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Forattini OP, Kakitani I, Massad E, Marucci D. Studies on mosquitoes(Diptera:Culicidae) and anthropic environment 4- Survey of resisting adults and synanthropic behaviour in South-Eastern Brazil. Revista de Saúde Pública. 1993;27:398–411. doi: 10.1590/s0034-89101993000600002. [DOI] [PubMed] [Google Scholar]
  10. Tadei W. Entomologia da malária em áreas de colonização da Amazônia. Chapter 4. MCT, pPD-Programa de Pesquisa Dirigida; 1997. pp. 157–168. [Google Scholar]
  11. Taylor JR. Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. 2. University Science Books, Mill Valley; 2001. p. 126. [Google Scholar]
  12. PAHO. http://www.paho.org/English/AD/DPC/CD/mal-day-08.htm Accessed in 29 May.
  13. Askling HH, Nilsson J, Tegnell A, Janzon R, Ekdahl K. Malaria Risk in Travelers. Emerging Infectious Diseases. 2005;11:463–441. doi: 10.3201/eid1103.040677. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Tada Y, Okabe N, Kimura M. Travelers' risk of malaria by destination country: A study from Japan. Travel Medicine and Infectious Diseases. 2008;6:368–372. doi: 10.1016/j.tmaid.2008.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. House HR, Ehlers JP. Travel-Related Infections. Emergency Medicine Clinics of North America. 2008;26:499–516. doi: 10.1016/j.emc.2008.01.008. [DOI] [PubMed] [Google Scholar]
  16. Massad E, Coutinho FA, Burattini MN, Lopez LF. The risk of yellow fever in a dengue-infested area. Trans R Soc Trop Med Hyg. 2001;95:370–4. doi: 10.1016/S0035-9203(01)90184-1. [DOI] [PubMed] [Google Scholar]
  17. Massad E, Burattini MN, Coutinho FA, Lopez LF. Dengue and the risk of urban yellow fever reintroduction in São Paulo State, Brazil. Rev Saude Publica. 2003;37:477–84. doi: 10.1590/S0034-89102003000400013. [DOI] [PubMed] [Google Scholar]
  18. Massad E, Coutinho FA, Burattini MN, Lopez LF, Struchiner CJ. Yellow fever vaccination: how much is enough? Vaccine. 2005;23:3908–14. doi: 10.1016/j.vaccine.2005.03.002. [DOI] [PubMed] [Google Scholar]
  19. Wyse APP. PhD thesis. Laboratório Nacional de Computação Científica, Brazil; 2007. Controle ótimo do vetor da malária para o modelo matemático sazonal. [Google Scholar]
  20. Okell LC, Drakeley CJ, Bousema T, Whitty CJM, Ghani AC. Modelling the Impact of Artemisinin Combination Therapy and Long-Acting Treatments on Malaria Transmission Intensity. PloS Med. 2008. p. e226. [DOI] [PMC free article] [PubMed]
  21. Chen LH, Wilson ME, Schlagenhauf P. Prevention of malaria in long-term travelers. JAMA. 2006;296:2234–2244. doi: 10.1001/jama.296.18.2234. [DOI] [PubMed] [Google Scholar]
  22. Behrens RH, Carroll B, Beran J, Bouchaud O, Hellgren U, Hatz C, Jelinek T, Legros F, Mühlberger N, Myrvang B, Siikamäki H, Visser L. The low and declining risk of malaria in travellers to Latin America: is there still an indication for chemoprophylaxis? Malaria Journal. 2007;6:114. doi: 10.1186/1475-2875-6-114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Macdonald G. The analysis of equilibrium in malaria. Trop Dis Bull. 1952;49:813–828. [PubMed] [Google Scholar]
  24. Santos RLC, Forattini OP, Burattini MN. Laboratory and field observations on duration of gonotrophic cycle of Anopheles albitarsis s.l. (Diptera: Culicidae) in southeastern Brazil. Journal of Medical Entomology. 2002;39(6):926–930. doi: 10.1603/0022-2585-39.6.926. [DOI] [PubMed] [Google Scholar]
  25. Molineaux L, Gramiccia G. The Garki Project: Research on the Epidemiology and Control of Malaria in the Sudan Savanna of West Africa. World Health Organization. Geneva; 1980. [Google Scholar]
  26. IBGE. 2007. http://www.ibge.gov.br/english/estatistica/populacao/contagem2007/default.shtm Accessed in 29 May.
  27. Molineaux L. In: Malaria: Principles and Practice of Malariology. Wernsdorfer WH, McGregor I, editor. Chap 35. Churchill Livingstone. Edinburgh; 1988. The Epidemiology of Human Malaria as an Explanation of its Distribution, Including Some Implications for its Control. 1988; pp. 913–998. [Google Scholar]
  28. Burattini MN, Massad E, Coutinho FAB. Malaria transmission rates estimated from serological data. Epidemiology an Infection. 1993;111:503–523. doi: 10.1017/S0950268800057241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Noronha E, Alecrim MDGC, Romero GAS, Macedo V. Clinical study of falciparum malaria in children in Manaus, AM, Brazil. Rev Soc Bras Med Trop. 2000;33(2):185–190. [PubMed] [Google Scholar]
  30. Santos RLC, Forattini OP, Burattini MN. Anopheles albitarsis s.l. (Diptera: Culicidae) survivorship and density in a rice irrigation area of the State of São Paulo, Brazil. Journal of Medical Entomology. 2004;41(5):997–1000. doi: 10.1603/0022-2585-41.5.997. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Additional file 1

Table S1. Models' variables.

Click here for file (33.5KB, DOC)
Additional file 2

Table S2. Model's parameters.

Click here for file (131KB, DOC)
Additional file 3

Table S3. Sensitivity of the model to each of the parameters (Par) in different periods of the year. The analysis assumes a 1% variation in the value of each parameter and the risk was calculated for 30 days of permanence. The values of the parameters are given in table S2.

Click here for file (73.5KB, DOC)
Additional file 4

Table S4. Average risk of malaria acquisition (with confidence intervals) for travelers who remain 30 days in the area.

Click here for file (20.5KB, DOC)

Articles from Malaria Journal are provided here courtesy of BMC

RESOURCES