Flux regulation of cardiac ryanodine receptor channels

Abstract

The cardiac type 2 ryanodine receptor (RYR2) is activated by Ca²⁺-induced Ca²⁺ release (CICR). The inherent positive feedback of CICR is well controlled in cells, but the nature of this control is debated. Here, we explore how the Ca²⁺ flux (lumen-to-cytosol) carried by an open RYR2 channel influences its own cytosolic Ca²⁺ regulatory sites as well as those on a neighboring channel. Both flux-dependent activation and inhibition of single channels were detected when there were super-physiological Ca²⁺ fluxes (>3 pA). Single-channel results indicate a pore inhibition site distance of 1.2 ± 0.16 nm and that the activation site on an open channel is shielded/protected from its own flux. Our results indicate that the Ca²⁺ flux mediated by an open RYR2 channel in cells (∼0.5 pA) is too small to substantially regulate (activate or inhibit) the channel carrying it, even though it is sufficient to activate a neighboring RYR2 channel.

INTRODUCTION

In cardiac muscle, surface membrane depolarization activates surface membrane Ca²⁺ channels (dihydropyridine receptor), which mediate a small Ca²⁺ influx into a cell. This small Ca²⁺ influx triggers the opening of type 2 RYR (RYR2) Ca²⁺ release channels that are located on the membrane of the SR. The opening of RYR2 channels results in a large SR Ca²⁺ flux that ultimately drives cardiac contractility. The RYR2 activation process is called Ca²⁺-induced Ca²⁺ release, or CICR (Fabiato, 1985; Bers, 2001; Fill and Copello, 2002), and represents a positive feedback process that is well controlled in cells. This positive feedback process consists of Ca²⁺ evoking Ca²⁺ release that can in turn evoke further Ca²⁺ release. How this positive feedback is controlled is not well understood. To gain understanding, it is important to define the extent to which the Ca²⁺ flux carried by an open RYR2 channel can act at its own cytosolic Ca²⁺ regulatory sites as well as those on neighboring channels.

In cardiac muscle cells, RYR2 channels exist and operate in tightly packed orthogonal arrays with an RYR2-RYR2 center spacing of ∼30 nm (Franzini-Armstrong et al., 1999). The cytoplasmic domain of the RYR2 channel extends ∼12 nm from the SR and has a center-corner distance of ∼14 nm (Samsó et al., 2005; Serysheva et al., 2005). The unit Ca²⁺ current carried by a single RYR2 channels in cells is thought to be ∼0.5 pA (Mejía-Alvarez et al., 1999; Kettlun et al., 2003; Gillespie and Fill, 2008). This 0.5 pA will elevate (when no buffering is present) local free Ca²⁺ levels to >15 µM within 25 nm from the open pore (Stern, 1992). The cytosolic Ca²⁺ EC₅₀ (half-maximal activation) of the RYR2 channel is 1–15 µM depending on the experimental conditions (Meissner, 1994; Sitsapesan and Williams, 1994; Saftenku et al., 2001; Copello et al., 2002; Fill and Copello, 2002). Thus, the physiological Ca²⁺ flux could substantially influence RYR2 Ca²⁺ activation status and likely activate neighboring RYR2 channels as well. Self-flux activation is the most fundamental form of Ca²⁺-induced Ca²⁺ release and would be the most difficult to control.

Flux regulation of single RYR2 channels has been reported in planar bilayer studies (Sitsapesan and Williams, 1994; Xu and Meissner, 1998; Laver, 2007). Sitsapesan and Williams (1994) reported that sulmazole-activated, not Ca²⁺-activated, RYR2 channels were sensitive to luminal Ca²⁺ concentration (consequently, lumen-to-cytosol Ca²⁺ flux) changes. Xu and Meissner (1998) showed that the Ca²⁺ flux mediated by caffeine-activated and Ca²⁺-activated single RYR2 channels can act at both cytosolic Ca²⁺ activation and/or inhibitory sites. They reported that fluxes ≥0.25 pA can activate and that fluxes ≥8 pA can inhibit. The inhibition is explained by a site ≤3 nm from the open pore. More recently, Laver (2007) proposed that Ca²⁺ passing through ATP-activated RYR2 channels acts on the cytosolic Ca²⁺ activation site, but also on a novel high affinity (IC₅₀, 1.2 µM) cytosolic Ca²⁺ inhibition site. Laver suggests that every pA of Ca²⁺ current through the channel elevates local Ca²⁺ 15 µM at the cytosolic activation site (which is 11 nm from the pore) and 0.35 µM at the inhibition site (which is 26 nm from the pore). It is clear that there is no consensus about how the Ca²⁺ flux carried by an RYR2 channel influences the channel’s function.

Here, we define the flux-dependent regulation of single Ca²⁺-activated RYR2 channels. The channels tested do not have their function and/or cytosolic Ca²⁺ sensitivity altered by caffeine, sulmazole, or ATP (without Mg²⁺ present). We find that channels can indeed be regulated by the Ca²⁺ flux they carry, but only when the flux is substantially larger than the physiological norm. We also more accurately specify the pore-to-inhibition site distance and show that the channel’s cytosolic activation machinery is somehow shielded or protected from its own flux.

MATERIALS AND METHODS

Microsome preparation

Heavy SR microsomes enriched in RYR2 channels were isolated from ventricles of adult rat hearts using established procedures (Tate et al., 1985). In brief, tissue was rinsed in saline solution (154 mM NaCl and 10 mM Tris-maleate, pH 6.8) at 4°C and then diced before being homogenized. A heavy SR microsome fraction was then separated from the homogenate by differential centrifugation. Microsomes were resuspended in a saline solution containing 300 mM sucrose before being flash frozen and stored at −80°C. Small aliquots of microsomes were thawed as needed and kept on ice until used.

Single-channel recording

Planar lipid bilayers were formed across a 100-µm hole in a thin (∼12 µm) Teflon partition separating two aqueous compartments. The bilayer was formed from a mixture of phosphatidylethanolamine, phosphatidylserine, and phosphatidylcholine in a 5:4:1 ratio. One compartment (cytosolic) was virtually grounded, and the cytosolic side of the RYR2 channel was eventually in this compartment (Tu et al., 1994; Fill and Copello, 2002). Initially, the cytosolic compartment was filled with a Tris-HEPES solution (120/250 mM; pH 7.4) and the other compartment (luminal) with Ca-HEPES (50/250 mM; pH 7.4). Microsomes and ∼400 mM CsCH₃SO₃ were then added to the cytosolic compartment while stirring. After channel incorporation, cytosolic and luminal solutions were changed (10× volume wash) to different test solutions. The composition of these test solutions is specified in the figure legends. Generally, solutions designed to explore the prospect of Ca²⁺ flux activation have cytosolic free Ca²⁺ concentrations less than the cytosolic Ca²⁺ EC₅₀ of the RYR2 channel. Solutions designed to explore Ca²⁺ flux inactivation have cytosolic Ca²⁺ levels more than the cytosolic Ca²⁺ activation EC₅₀ (i.e., activation sites largely occupied). In some cases, the cytosolic solutions contained 1 mM EGTA. The composition of Ca²⁺ buffer solutions was calculated using the MAXC program (WinMaxC; Stanford University, Palo Alto, CA) and verified using a Ca²⁺ electrode. All salts and chemicals (unless otherwise specified) were obtained from Sigma-Aldrich or EMD. Lipids were obtained from Avanti Polar Lipids, Inc. All experiments were performed at room temperature (21°C).

The membrane potential across the bilayer was controlled using an Axopatch 200B (MDS Analytical Technologies). Sample rate (unless otherwise specified) was 10 kHz, and recordings were filtered with a Bessel filter at 2 kHz for analysis. Data acquisition and analysis were performed using pClamp 9.0 (MDS Analytical Technologies). Summary results are presented as mean ± SEM, with statistical significance determined using the Student’s t test (P < 0.05 or as specified).

In a multi-RYR2 channel cluster, where openings are stochastic, there is always some possibility that all the channels will close simultaneously. This process is often referred to as stochastic attrition. To roughly estimate the time constant of stochastic attrition (τ_A) within an RYR2 cluster, we used the following equation (Stern and Cheng, 2004):

$${\tau }_A=\frac{\left[1-{(1-P_O)}^N\right]·MOT}{N·{(1-P_O)}^{N-1}·P_O}$$ (1)

In Eq. 1, P_o is open probability, N is number of channels present, and MOT is mean open time of individual independently gating RYR2 channels.

Flash photolysis

In some experiments, the cytosolic solution contained 4 mM DM-nitrophen and 50 µM Rhod-2. Rhod-2 excitation light from a Nd:YAG laser (532 nm; 4 mW) was pulsed (1 ns long at 10 kHz) and focused into a 400-µm diameter multimode optic fiber (n.a. 0.2). Rhod-2 emission was collected through the same fiber and projected onto an avalanche photodiode. High intensity UV flashes (5 ns long) for photolysis from another Nd:YAG laser (355 nm; 2 MW) were applied through the same optic fiber. Intensity of the photolytic flash was controlled by Q-switch triggering and monitored by a joule meter. Instrumentation was synchronized, and single-channel recording done using pClamp software/hardware (MDS Analytical Technologies). The optic fiber was micropositioned 500 µm directly in front of and centered on the bilayer. Thus, DM-nitrophen was photolyzed in the small volume (∼63 nl) between the optic fiber and bilayer. Solution in the photolyzed volume was then exchanged with unphotolyzed solution from the bath (1 ml) by stirring the bath. Rhod-2 emission was used to monitor local Ca²⁺ levels in the photolyzed volume. Photolysis liberated Ca²⁺ from DM-nitrophen. This increased the free Ca²⁺ in the photolyzed volume, and solution exchange (via rapid stirring) reduced it to basal levels with a time constant of 15–19 ms. Note that photolysis can generate a fast (<150 µs), large (>25 µM) transient Ca²⁺ overshoot that was not detected by our recording system. Identical photolytic Ca²⁺ stimuli were always applied, regardless of whether such an overshoot was present or not.

Diffusion analysis

To calculate the amplitude and spatial profile of the Ca²⁺ microdomain around an open RYR2 pore (Stern, 1992), a freeware application (PORE) developed by J. Kenyon (University of Nevada, Reno, NV) was used. PORE is a Visual Basic program that can be run in an Excel spreadsheet.

The Hill equation (Eq. 2) was used to fit (via nonlinear least squares) some results.

$$Po=\frac{PoMax·{\left[Ca\right]}^{H_C}}{K_D+{\left[Ca\right]}^{H_C}}$$ (2)

Here, [Ca] is Ca²⁺ concentration, PoMAX is the maximum Po, K_D is the dissociation constant, and H_c is the Hill coefficient.

The equation relating local [Ca], unit Ca²⁺ current, and distance from an open pore is well known (Eq. 3).

$$\begin{array}{l}\left[Ca\right]={\left[Ca\right]}_{\mathrm{\infty }}+\frac{i}{4\pi FDr}\exp \left(-r/\lambda \right)\text{,}\\ \text{where}\hspace{0.17em}\lambda =\sqrt{\frac{D}{k_{ON}·\left[B\right]}}\hspace{0.17em}\text{and}\hspace{0.17em}\left[B\right]=\frac{{\left[B\right]}_{TOT}·K_D}{K_D+{\left[Ca\right]}_{\mathrm{\infty }}}\end{array}$$ (3)

Here, [Ca] refers to the local free Ca²⁺ concentration as a function of distance (r) from the pore, [Ca]_∞ is the bath free Ca²⁺ concentration far from the pore, (i) is unit current, and F is the Faraday constant. The diffusion coefficient (D) used for Ca²⁺ and Mg²⁺ was 10⁻⁹ m²s⁻¹. In Eq. 3, the k_ON is the on rate for Ca²⁺ binding to the buffer, [B] is the free buffer concentration, [B]_TOT is the total buffer concentration, and K_D is the dissociation constant of the Ca buffer complex. The only Ca²⁺ buffer present in our experiments here was EGTA. The EGTA k_ON and K_D used here were 1.5 × 10⁻⁶ M⁻¹s⁻¹ and 1.58 × 10⁻⁷ M, respectively.

A function relating Po and Ca²⁺ current amplitude was generated using the equations above. The logic is that the RYR2 channel has cytosolic Ca²⁺ regulatory sites that are some distance from the pore. If Ca²⁺ coming through the pore can act on these sites, Po must be some function of unit current amplitude. In the absence of Ca²⁺ flux through the pore, Ca²⁺ action on these cytosolic sites is well described by the Hill function (Eq. 2). Local free Ca²⁺ concentration as a function of distance and unit current is described by Eq. 3. Thus, Eq. 4 can be generated by substituting [Ca] terms of Eq. 2 with local [Ca] from Eq. 3.

$$Po=\frac{PoMax·{\left({\left[Ca\right]}_{\infty }+\frac{i}{4\pi FDr}\exp \left(-r/\sqrt{\frac{D}{k_{ON}·\frac{{\left[B\right]}_{TOT}·K_D}{K_D+{\left[Ca\right]}_{\mathrm{\infty }}}}}\right)\right)}^{H_C}}{K_D+{\left({\left[Ca\right]}_{\mathrm{\infty }}+\frac{i}{4\pi FDr}\exp \left(-r/\sqrt{\frac{D}{k_{ON}·\frac{{\left[B\right]}_{TOT}·K_D}{K_D+{\left[Ca\right]}_{\mathrm{\infty }}}}}\right)\right)}^{H_C}}$$ (4)

Eq. 4 was used to fit (via nonlinear least squares) Po versus pA results to specify pore site distances when EGTA was present. The exponential terms are unnecessary in the absence of cytosolic buffer.

RESULTS

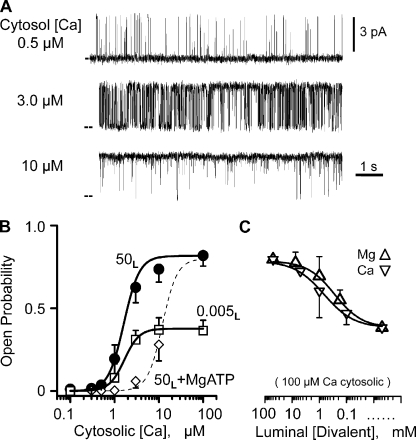
Ryanodine, caffeine, and ATP sensitivity (not depicted) were used to positively identify the channels studied here as RYR2 channels. To define how (or if) an RYR2 channel’s Ca²⁺ flux feeds back and regulates the channel, the characteristics of its cytosolic Ca²⁺ regulatory sites need to be defined first. To this end, sample single-channel recordings at three different cytosolic Ca²⁺ concentrations are shown in Fig. 1 A. The only charge carrier present was Ca²⁺ (50 mM luminal), and the typical unit current was 3.58 ± 0.03 pA (n = 44) moving in the lumen-to-cytosol direction. These recordings show that the Po increased with cytosolic Ca²⁺ concentration. Fig. 1 B shows summary Po results (mean ± SEM) collected in three different experimental conditions. Filled circles represent RYR2 cytosolic Ca²⁺ sensitivity when 50 mM of luminal Ca²⁺ (50_L) is present without cytosolic Mg²⁺ or ATP. Open squares represent RYR2 cytosolic Ca²⁺ sensitivity when 5 µM of luminal Ca²⁺ (0.005_L) is present also without cytosolic Mg²⁺ or ATP. At this lower luminal Ca²⁺ level, the lumen-to-cytosol current was carried by Cs⁺ (see legend to Fig. 1). The EC₅₀’s for these two datasets are 1.6 ± 0.41 µM (filled circles; Hc = 2.2) and 1.61 ± 0.34 µM (open squares; Hc = 2.7). Open diamonds are mean Po values with 50 mM of luminal Ca²⁺ (50_L), but now with cytosolic Mg-ATP present (see legend to Fig. 1). The thin dashed line is a complete dose–response curve (EC₅₀, 12 ± 2 µM; Hc = 2.6) generated by our group previously in similar experimental conditions (Zoghbi et al., 2004). This latter relationship is likely close to the RYR2’s cytosolic Ca²⁺ EC₅₀ in cells. Because cytosolic Mg²⁺ inhibits channels by multiple mechanisms (Meissner et al., 1986; Laver et al., 1997) and the RYR2 channel conducts Mg²⁺ (Fill and Copello, 2002), our RYR2 flux regulation studies described below were done without Mg-ATP present.

Figure 1.

Cytosolic calcium sensitivity. (A) Sample single-channel recordings made at three different cytosolic free Ca²⁺ levels. All recordings were made at 0 mV, and the closed (zero current) level is marked at left margin. Recordings were made with 50 mM of luminal Ca²⁺ present. The cytosolic solution also contained Tris-HEPES (120/250 mM; pH 7.4). The luminal solution contained Ca-HEPES (50/250 mM; pH 7.4). (B) Cytosolic Ca²⁺ dependence of Po. All Po measurements were made from >3-min recordings (0 mV) from 8–10 different channels at different steady-state cytosolic free Ca²⁺ concentrations. Lines are Hill equation fits. Filled circles represent the cytosolic Ca²⁺ sensitivity of the channel when 50 mM of luminal Ca²⁺ (50_L) is present. Open squares show when 0.005 mM of luminal Ca²⁺ is present. Open diamonds indicate 50 mM of luminal Ca²⁺ when cytosolic Mg-ATP is present, and the corresponding dose–response curve (thin dashed line) was reproduced from Zoghbi et al. (2004). In all cases, the cytosolic solution also contained 1 mM EGTA and Tris-HEPES (as above). Mg-ATP refers to 1 mM of free Mg²⁺ and 5 mM of total ATP. The luminal 0.005 Ca²⁺ solution contained 100 mM Cs-HEPES, pH 7.4. Thus, Cs⁺ was the primary charge carrier. (C) Luminal Ca²⁺ and Mg²⁺ dependence of Po at 0 mV. Channels were activated by 100 µM of cytosolic free Ca²⁺. Any endogenous CSQ that was attached to the channel was dissociated from the channel by a high ionic strength wash (see Results). Luminal Mg²⁺ (triangles) or Ca²⁺ (inverted triangles) was changed from 50 mM to 5 µM. An analogous luminal Ca²⁺/Mg²⁺ sensitivity result was presented previously by Qin et al. (2008). Again, the cytosolic solution also contained Tris-HEPES (as above). The luminal solution contained either Ca-HEPES or Mg-HEPES. When luminal free Ca²⁺ or Mg²⁺ was <10 mM, 100 mM Cs-HEPES, pH 7.4, was added to the luminal solution to assure ample charge carrier was always present.

Fig. 1 C shows the luminal Ca²⁺ and Mg²⁺ dependence of single RYR2 channels in the presence of 100 µM of cytosolic Ca²⁺ (no Mg-ATP). In these studies, 100 mM of luminal Cs⁺ was present when necessary to provide an additional charge carrier. High concentrations of luminal Ca²⁺ (>5 mM) are known to dissociate calsequestrin (CSQ) from channels in planar bilayers (Beard et al., 2004; Györke et al., 2004; Qin et al., 2008). Because all tested channels here were exposed to >5 mM before recording began, these channels are not likely to have CSQ associated with them. When luminal Ca²⁺ (Fig. 1 C, inverted triangle) or Mg²⁺ (triangle) concentration was decreased from 50 mM to 5 µM, the Po also decreased with an IC₅₀ (half-maximal inhibition) of ∼500 µM. This luminal titration explains the different maximum Po’s between the 50_L and 0.005_L curves in Fig. 1 B. This luminal action of Ca²⁺ and Mg²⁺ is likely not due to flux feeding through the channel because the cytosolic Ca²⁺ activation site was essentially saturated (because there was 100 µM of cytosolic Ca²⁺), and these two ions have opposite action when applied to the cytosolic side of the channel.

We do not believe this CSQ-independent luminal regulation mechanism is of major physiological consequence because it lacks Ca-Mg selectivity. The free Mg²⁺ inside the SR is very likely equal to that in the cytosol (∼1 mM) because there is no source of energy to hold it out of equilibrium (Somlyo et al., 1985). The process of SR Ca²⁺ release is thought to lower intra-SR free Ca²⁺ from ∼1 to ∼0.5 mM (Shannon and Bers, 1997). If so, then the combined intra-SR free Ca²⁺ and Mg²⁺ level upon release decreases from ∼2 to ∼1.5 mM. Fig. 1 C indicates that this magnitude change in intra-SR free divalent cation concentration will have very little effect on RYR2 Po via this CSQ-independent luminal regulatory mechanism.

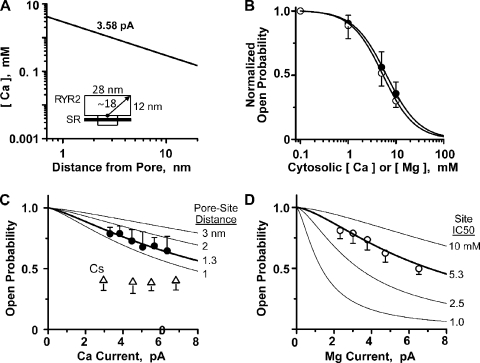
To learn more about the Ca²⁺ flux dependence of RYR2 gating, we began by calculating the free cytosolic Ca²⁺ concentration profile around an open RYR2 pore. In Fig. 2 A, the line is the calculated concentration (as a function of distance) when the channel is carrying a 3.58-pA Ca²⁺ current with no diffusible buffer present. The approximate dimensions of the cytosolic domain of the RYR2 channel (Samsó et al., 2005; Serysheva et al., 2005) are indicated in the inset to help place the distances on the abscissa in context. Note that the free Ca²⁺ concentrations over the entire cytoplasmic domain of the channel are >100 µM, and the free Ca²⁺ concentrations within 3 nm of the open pore reach levels >1 mM.

Figure 2.

Flux-dependent inhibition of single RYR2 channel activity. (A) Local diffusion from a point source here was calculated with cytosolic Ca²⁺ of 100 nM in the presence of different unit Ca²⁺ currents. The thick line is for 3.58 pA, reflecting the typical unit current we measure when there is 50 mM of luminal Ca²⁺ present. (Inset) A cartoon depicting the approximate dimensions of a single RYR2 channel. (B) Cytosolic Ca²⁺ (filled circles) or Mg²⁺ (open circles) inhibition of single RYR2 channels activated by 100 µM of cytosolic free Ca²⁺. Experiments here were done at 0 mV. Cytosolic Ca²⁺ or Mg²⁺ was changed from 100 µM to 10 mM. Lines are Hill equation fits. The Ca²⁺ and Mg²⁺ IC₅₀’s were 6.2 ± 0.34 mM (Hc = −1.3) and 5.3 ± 0.69 mM (Hc = −1.5), respectively. Results represent data collected from five to eight different channels. The cytosolic solution also contained Tris-HEPES (120/250 mM; pH 7.4). The luminal solution contained 5 µM of added Ca²⁺ and 100 mM Cs-HEPES, pH 7.4. (C) Luminal-to-cytosolic Ca²⁺ flux dependence of Po. These results represent data collected from six to nine RYR2 different channels. The cytosolic free Ca²⁺ was 7 µM, and unit Ca²⁺ current was varied by changing the membrane potential. Filled circles are Po values with Ca²⁺ as sole charge carrier. The thick line is a fit using Eq. 4 (described in Materials and methods) to the filled circles revealing a pore site distance of 1.3 nm. This fit assumes the cytosolic Ca²⁺ inhibition site properties defined in B, and the pore site distance sensitivity of this relationship is illustrated by the labeled thin lines. Open triangles are Po values when Cs⁺ (instead of Ca²⁺) was charge carrier. The cytosolic solution contained 1 mM EGTA and Tris-HEPES (as above). When Ca²⁺ was charge carrier, the luminal solution contained Ca-HEPES (50/250 mM; pH 7.4). When Cs⁺ was charge carrier, the luminal solution contained 5 µM of added Ca²⁺ and 100 mM Cs-HEPES, pH 7.4. (D) Luminal-to-cytosolic Mg²⁺ flux dependence of Po. These results represent data collected from seven to eight RYR2 channels. Again, cytosolic free Ca²⁺ was 7 µM, and unit Mg²⁺ current was varied by changing the membrane potential. The thick line is fit using Eq. 4 and indicates a pore site distance of 1.1 nm. This fit assumes the cytosolic Mg²⁺ inhibition site properties defined in B, and the IC₅₀ sensitivity of this relationship is illustrated by the labeled thin lines. The cytosolic solution also contained 1 mM EGTA and Tris-HEPES (as above), and the luminal solution contained Mg-HEPES.

Fig. 2 B shows that high concentrations (≥1 mM) of cytosolic Ca²⁺ (filled circles) or Mg²⁺ (open circles) inhibit the RYR2 channel. These experiments were done starting with 100 µM of cytosolic Ca²⁺, and then 1–10 mM Ca²⁺ or Mg²⁺ was added to the cytosolic bath. The Ca²⁺ and Mg²⁺ IC₅₀’s are 6.2 ± 0.34 mM (PoMax = 0.81; Hc = −1.3) and 5.3 ± 0.69 mM (PoMax = 0.81; Hc = −1.5), respectively. These values were not significantly different. In Fig. 2 C, Po was measured as a function of Ca²⁺ current amplitude when there was 7 µM of cytosolic free Ca²⁺ present. Current amplitude was modulated by changing membrane potential. Single RYR2 Po decreased as Ca²⁺ flux amplitude increased (Fig. 2 C, circles). To establish that this Po decrease with unit current amplitude was due to Ca²⁺ feed-through, we changed the charge carrier to Cs⁺ (Fig. 2 C, triangles). When Cs⁺ was charge carrier, the Po did not change with unit current amplitude. The reduced Po associated with the charge carrier change is explained by the applied change in luminal Ca²⁺ concentration (50 mM for the circles, 5 µM for the triangles; see Fig. 1 B). Fig. 2 D shows an analogous study, but with a lumen-to-cytosol Mg²⁺ current instead of a Ca²⁺ current. The Po also decreased as a function of current amplitude. Results in Fig. 2 (C and D) were fit (thick lines) using Eq. 4 (see Materials and methods) and the Hill parameters defined in Fig. 2 B. The fit in Fig. 2 C indicates that the responsible cytosolic inhibition site would need to be 1.3 nm from the pore. The fit in Fig. 2 D indicates that the site would need to be 1.1 nm from the pore.

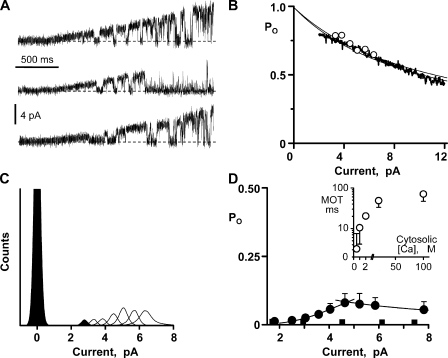
In our hands, prolonged periods at large nonzero membrane potential reduce bilayer stability, making long steady-state recordings at large membrane potentials impractical. Thus, we used voltage ramps to explore flux inhibition by larger Ca²⁺ currents. Fig. 3 A shows sample single-channel recordings where the charge carrier was provided by 50 mM of luminal Ca²⁺. A general decrease in Po is visible as current amplitude increases. In Fig. 3 B, the relationship between Ca²⁺ current amplitude and Po was determined from ensemble recordings, and one such recording is shown (thick line). This ensemble was generated from 200 single-channel voltage ramp sweeps collected from four different channels. The downward slope of the ensemble recording indicates that Po decreased as Ca²⁺ current increased. Eq. 4 was used to fit (thin line) the ensemble trace and indicated a pore inhibition site distance of 1.4 nm. The open circles in Fig. 3 B are the flux inhibition points from Fig. 2 C. The second thin line is the fit to another ensemble dataset (not depicted) generated with 10 mM of luminal Ca²⁺ present. This pore site distance determined from this other dataset was 1.5 nm.

Figure 3.

Flux sensitivity of single RYR2 channel activity. (A) Sample single-channel recordings are shown as membrane potential was ramped between −50 and +50 mV. Charge carrier was Ca²⁺ (50 mM luminal), the cytosolic free Ca²⁺ was 50 µM, and unit current was in the lumen-to-cytosolic direction. Zero current level is marked by a dotted line. The cytosolic solution also contained Tris-HEPES (120/250 mM; pH 7.4). The luminal solution contained Ca-HEPES (50/250 mM; pH 7.4). (B) Ensemble traces were generated by averaging 200 single-channel sweeps from four different channels with either 50 or 10 mM of Ca²⁺ luminal solution present. Solutions as above, but the 10-mM Ca²⁺ luminal solution contained 10 mM Ca-HEPES. Lines are the fits to these ensembles traces (only the 50-mM Ca²⁺ ensemble trace is shown). The best fit distances were 1.4 and 1.5 nm, respectively. These fits were made assuming a cytosolic Ca²⁺ inhibition site with IC₅₀ = 6.2 mM (Hc = −1.3). Open circles are data points reproduced from C. (C) Representative all-points histograms when cytosolic free Ca²⁺ was 0.5 µM. Histograms made at seven different membrane potentials are superimposed (one filled and all others open). Zero current level is centered at 0 pA. Here, the cytosolic solution also contained 1 mM EGTA and Tris-HEPES (as above). The luminal solution contained Ca-HEPES (50/250 mM; pH 7.4). (D) Flux activation of single RYR2 channel activity. Gaussian fitting of all-points histograms compiled from four to six different channels (cytosolic free Ca²⁺, 0.5 µM) was used to determine how Po varies with Ca²⁺ current amplitude. Filled circles correspond to when all current was due to lumen-to-cytosol Ca²⁺ flux (solutions as those described for C). Increasing Ca²⁺ current from 2 to 5 pA elevated Po. Increasing it further slightly reduced Po. This flux activation and inhibition was fit as described in Materials and methods. Filled squares correspond to when most current was carried by Cs⁺, instead of Ca²⁺. To accomplish this, the luminal solution was changed to one containing 50 µM of added Ca²⁺ and 200 mM Cs-HEPES, pH 7.4. The Po did not change with increasing Cs⁺ current. (Inset) The cytosolic Ca²⁺ dependency of MOT of single RYR2 channels (solutions like those described for C).

Calcium flux activation of a single RYR2 channel is demonstrated in Fig. 3 C. Again, the charge carrier was Ca²⁺ (50 mM luminal), but now the cytosolic bath Ca²⁺ was 0.5 µM, which is below the cytosolic Ca²⁺ EC₅₀. This means that the cytosolic activation site is available to respond to local Ca²⁺ fluctuations. Long recordings were made at different membrane potentials. Sample all-points histograms generated from these recordings are superimposed in Fig. 3 C. The area of the open current peaks (those between 2 and 8 pA) changed as unit current amplitude increased. The Po for each histogram was calculated as the relative area of the open and closed peaks and then plotted as a function of unit Ca²⁺ current in Fig. 3 D (filled circles). With Ca²⁺ as charge carrier, the Po increased as unit Ca²⁺ current changed from 2 to ∼5 pA. It then slightly decreased as current increased further. Fig. 3 D also shows a parallel study done with Cs⁺ as charge carrier. The current-dependent changes in Po when Ca²⁺ was the charge carrier (filled circles) were not evident when Cs⁺ was charge carrier (filled squares). This indicates that the Ca²⁺ current–dependent Po changes were not a consequence of the membrane potential change.

Eq. 4 was used to fit the rising and falling phases of the Po versus pA data in Fig. 3 D (filled circles). The fit to the falling phase indicated a pore site distance of 0.5 nm. The fit to the activation (rising phase) requires more explanation. Assuming that the responsible activation site operates like the traditional steady-state Ca²⁺ activation site (EC₅₀ = 1.6 µM; Hc = 2.2), the fit (Fig. 3 D) to the rising phase indicates a pore-activation site distance of 1,700 nm. This is clearly not possible because the cytosolic activation site must be somewhere within ∼18 nm of the pore (Samsó et al., 2005; Serysheva et al., 2005). The local Ca²⁺ concentration at a distance of 18 nm from this open RYR2 pore, which is carrying a 3.58-pA Ca²⁺ flux, is 165 µM (Fig. 2 A). This level of cytosolic Ca²⁺ might be expected to either prolong the opening or immediately reactivate the channel once it closes (Fig. 1 B). If so, the flux would be expected to substantially elevate Po. However, the observed Po change generated by the flux was quite modest. This implies that the RYR2’s cytosolic Ca²⁺ activation machinery may be somehow “shielded” from the channel’s own Ca²⁺ flux. To have some gauge of the extent of this shielding, the pore-activation site distance was fixed at 18 nm and the rising phase (or flux activation) was refit. This refitting indicated that a cytosolic activation site 18 nm from the pore would need to have a Ca²⁺ EC₅₀ of 440 µM (Hc = 2.97) to explain the results if it were free to respond to the fluxed Ca²⁺ (Fig. 3 D).

As suggested above, Ca²⁺ flux could influence activation if the fluxed Ca²⁺ prolongs channel opening (i.e., extend mean open time [MOT]) and/or if it increases the likelihood of channel reopening. RYR2 MOT and open event frequency were measured when the Ca²⁺ flux was 1.81 or 3.58 pA. The MOTs (n = 6) were 2.9 ± 2.1 and 12 ± 9 ms, and the frequencies were 3.6 ± 5.4 and 3.4 ± 4.3 Hz, respectively. Although these numbers suggest that the flux activates RYR2 by increasing its MOT (not event frequency), these MOTs were not significantly different. We measured the MOTs of single RYR2 channels exposed to different levels of cytosolic bath Ca²⁺, and these are plotted in Fig. 3 D (inset, open circles). Note that the MOT here was 71 ± 24 ms at a cytosolic bath Ca²⁺ of 100 µM. This is significantly larger than the MOT when a 3.58-pA Ca²⁺ flux elevates local cytosolic Ca²⁺ to >100 µM (P < 0.05; 71 ± 24 vs. 12 ± 9 ms; n = 6). This supports the idea that the RYR2’s cytosolic Ca²⁺ activation machinery is somehow “shielded” from the channel’s own Ca²⁺ flux.

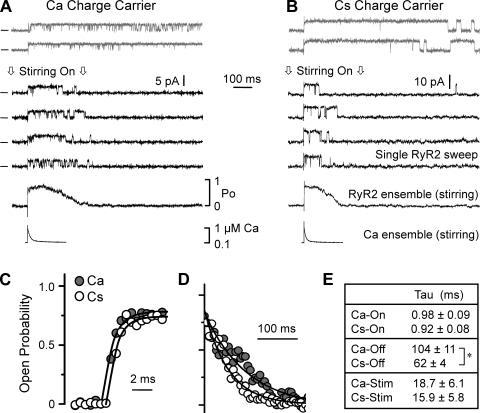
The local Ca²⁺ concentration profile near an open Ca²⁺-conducting pore is established/dissipated quickly (<1 ms) when the channel opens/closes (Stern, 1992). Such fast cytosolic Ca²⁺ changes (<1 ms) are known to robustly activate RYR2 channels in bilayers (Györke and Fill, 1993; Schiefer et al., 1995; Sitsapesan et al., 1995; Valdivia et al., 1995; Laver and Curtis, 1996). Fig. 4 shows how single RYR2 channels conducting either Cs⁺ or Ca²⁺ respond to fast cytosolic Ca²⁺ changes. Flash photolysis of cytosolic caged Ca²⁺ was used to rapidly elevate the free Ca²⁺ level near the channel (see Materials and methods). The steady-state cytosolic free Ca²⁺ was ∼100 nM, and the resting Po was near zero. Fig. 4 A shows six sample single-channel sweeps when the channel was mediating a Ca²⁺ flux (3.58 pA; lumen-to-cytosol). The top two recordings (gray) were made when the cytosolic bath solution was not being stirred. This is important because stirring of the cytosolic bath removes local Ca²⁺ and thus local Ca²⁺ remained elevated (above basal levels) for several seconds. The channel rapidly activated and remained active for the duration of the recording period. The lower four recordings (black) were made during continuous rapid stirring of the cytosolic bath, and thus the applied local Ca²⁺ stimuli was transient (rise time, ∼100 µs; decay time constant, ∼15–19 ms). Again, the channel rapidly activated, but this time its activity ceased before the end of the recording period. Shown below the single-channel recordings is an ensemble trace that was generated by averaging >40 single-channel sweeps. Below this ensemble is a recording of the applied Ca²⁺ stimulus, which was measured via Rhod-2 fluorescence. Fig. 4 B shows a similar experiment, but in this case the channel was mediating a Cs⁺ flux, not a Ca²⁺ flux. Again, the channel activated rapidly upon the abrupt Ca²⁺ elevation and deactivated as the stimulating Ca²⁺ was washed away.

Figure 4.

Kinetics of single RYR2 channel Ca²⁺ activation and deactivation. Local cytosolic free Ca²⁺ increases around a channel were generated by flash photolysis of caged Ca²⁺. Single RYR2 channels were repeatedly activated by photolytic Ca²⁺ stimuli (>5-s interval). Cytosolic solution contained Tris-HEPES (120/250 mM; pH 7.4), 100 nM of free Ca²⁺, 4 mM DM-nitrophen, 50 µM Rhod-2, and 2 mM glutathione. (A) Six single RYR2 channel sweeps when the lumen-to-cytosol current (3.58 pA) was carried by Ca²⁺ are shown at top. The cytosolic solution was as described above, and the luminal solution contained Ca-HEPES (50/250 mM; pH 7.4). Recordings were made at 0 mV. Open events are upward, and zero current level is marked at left. The top two recordings (gray) were made when the cytosolic bath solution was not being stirred. The lower four recordings were made during continuous, vigorous stirring of the cytosolic bath. This stirring efficiently exchanged the local photolyzed solution near the channel with unphotolyzed (basal free Ca²⁺) solution from the bath, generating transient Ca²⁺ stimuli (rise time, ∼100 µs; decay time constant, ∼15–19 ms). An ensemble trace generated from >40 single-channel sweeps (while stirring) is shown just below the single-channel recordings. Below the ensemble trace is the corresponding recording of the applied local stimulus (while stirring). (B) Like A, but the lumen-to-cytosol current (7.9 pA) was carried by Cs⁺. This channel was not the same as shown in A. The cytosolic solution was as described above, and the luminal solution contained 5 µM of added Ca²⁺ and 250 mM Cs-HEPES, pH 7.4. (C) Calcium activation kinetics. Four ensemble RYR2 activity traces from different RYR2 channels with either Ca²⁺ (filled circles) or Cs⁺ (open circles) as charge carrier were averaged and then fit (lines) by a single-exponential function. (D) Calcium deactivation kinetics. The decay phase and exponential fits of the same averaged ensemble traces described in C are shown. Only a small subset of the points fit is actually shown. (E) Time constants of Ca²⁺ activation and deactivation in response to the applied transient Ca²⁺ stimulus. Ca-On and Cs-On refer to the activation time constants when Ca²⁺ or Cs⁺ was charge carrier, respectively. Ca-Off and Cs-Off refer to the inhibition time constants. Ca-Stim and Cs-Stim refer to Ca²⁺ stimulus decay time constant when Cs⁺ or Cs⁺ was charge carrier, respectively. The asterisk indicates a significant difference (P < 0.02).

Fig. 4 (C and D) show the time courses of RYR2 activation and deactivation on an expanded time scale. Filled circles indicate when the RYR2 was conducting Ca²⁺, and the open circles are when the RYR2 was conducting Cs⁺. In Fig. 4 C, the Cs⁺ rise time points are shifted to avoid overlap. In Fig. 4 D, only a subset of the Po decay points are shown (80 to 5% peak Po). Single exponentials were fit to the Po rise and fall. Fig. 4 E lists the salient time constants. The Ca²⁺ stimulus decay time constants (Ca-Stim and Cs-Stim) when Ca²⁺ or Cs⁺ was charge carrier were not significantly different. The Ca²⁺ activation time constants (Ca-On and Cs-On) were also not different. However, the Ca²⁺ deactivation time constants (Ca-Off and Cs-Off) were significantly different. This slower Po decay when Ca²⁺ was charge carrier may be due to a luminal Ca²⁺ action (see Fig. 1 C), a feed-through Ca²⁺ action (see Fig. 3 D), or some combination of both. Note that there was 50 mM of luminal Ca²⁺ present when Ca²⁺ was charge carrier and just 5 µM when Cs⁺ was charge carrier.

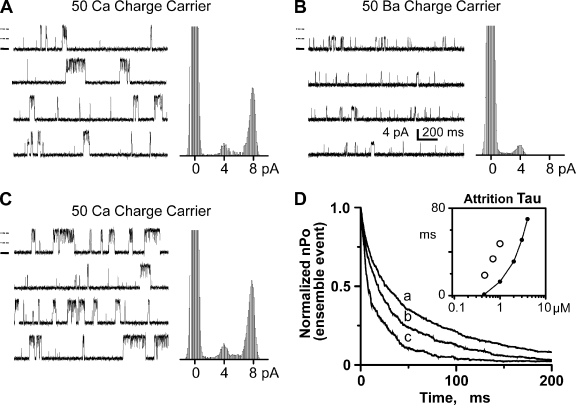
Multiple RYR2 channels are frequently incorporated into the bilayer. Occasionally, these channels will open and close in a concerted fashion, as has been reported by others (Marx et al., 2001; Laver, 2007). Fig. 5 shows sample recordings from one such occurrence. All recordings shown here are from the same incorporation, which deposited two channels into the bilayer. Fig. 5 A shows the channel activity when the channels were carrying a lumen-to-cytosol Ca²⁺ current. The two channels frequently open at the same time, resulting in events with double the usual single-channel current amplitude. Fig. 5 B shows what happens when the charge carrier was changed from Ca²⁺ to Ba²⁺. The frequent double amplitude events are no longer evident. Fig. 5 C shows that the double amplitude events return when the charge carrier was changed back to Ca²⁺. Because cytosolic Ba²⁺ does not activate the RYR2 channel (Fill and Copello, 2002), these results suggest that Ca²⁺ passing through the open pore of one channel is activating the second neighboring RYR2 channel. We call this coordinated gating to distinguish it from the flux-independent FK-506 binding protein–mediated coupled gating reported by Marx et al. (2001).

Figure 5.

Flux-dependent coordinated RYR2 channel activity. (A) Sample coordinated channel recordings (two channels present) and all-points histogram. The cytosolic solution contained 1 mM EGTA (0.45 µM of free Ca²⁺) and Tris-HEPES (120/250 mM; pH 7.4). The luminal solution contained Ca-HEPES (50/250 mM; pH 7.4). Recordings (left) were made at 0 mV. Open events are upward, and zero current level is marked for the top recording by a thick solid line. The thin dashed lines (above zero current mark) indicate normal current level for one or two open channels. All-points histograms (right) were made from a long recording from which these sample recordings were taken. (B) Same channel and conditions as in A, but the 50 mM Ca²⁺ in the luminal solution was exchanged for Ba²⁺. (C) Same channel and conditions as in B, but the 50 mM Ba²⁺ in the luminal solution was changed back to Ca²⁺. (D) Ensemble traces were generated by aligning and summing many individual coordinated events (two channel events). Only the decay phase is shown here. Solutions are those described for A, except that the cytosolic free Ca²⁺ level was varied as indicated below. Trace marked “a” has a time constant of 47.49 ms and was generated from 2,308 events collected with 1 µM of cytosolic free Ca²⁺ present. Trace marked “b” has a time constant of 33.65 ms and was generated from 1,252 events collected with 0.7 µM of cytosolic free Ca²⁺ present. Trace marked “c” has a time constant of 18.62 ms and was generated from 792 events collected with 0.45 µM of cytosolic free Ca²⁺ present. The inset plots attrition time constants (ms) as a function of cytosolic free Ca²⁺ concentration (µM). Open circles are the time constants determined by single-exponential fits to the ensemble traces. The connected filled points are the predicted stochastic attrition calculated using Eq. 1, assuming two channels are present. This calculation assumes the single-channel Po’s as shown in Fig. 1 B and single-channel MOTs as shown in Fig. 3 D (inset). For example, single-channel Po’s were 0.03, 0.09, and 0.19 for 0.45, 0.7, and 1 µM of cytosolic free Ca²⁺, respectively. Single-channel MOTs for these same Ca²⁺ levels were 1.04, 6.86, and 11.46 ms, respectively.

The two channels would need to be within ∼1.8 µm of each other for the neighboring channels to “see” each other’s fluxed Ca²⁺ at a level equal to their cytosolic Ca²⁺ EC₅₀. Peng et al. (2004) showed that single RYR channels in bilayers randomly diffuse an average of 5 µm every 3 s. Thus, it would be very unlikely that two independently diffusing channels would remain within ∼1.8 µm of each other for more than a few seconds. Because we observed consistent Ca²⁺ flux coordinated gating of neighboring channels for extended periods of time (>1 h), the neighboring channels do not likely diffuse independently of each other. We believe that the neighboring channels are probably physically linked together, perhaps at their normal cellular spacing. If so, then the center spacing between the neighboring channels in the bilayer would be ∼30 nm (Franzini-Armstrong et al., 1999).

Many coordinated RYR2 openings were aligned (to t = 0) to generate ensemble events. The on-time constant of these ensemble coordinated events was always ≤0.75 ms, consistent with the cytosolic Ca²⁺ activation rate measured earlier. Fig. 5 D compares the decay phase of ensemble coordinated events (normalized to peak intra-event nPo) collected at three different resting cytosolic Ca²⁺ concentrations (a = 1, b = 0.7, and c = 0.45 µM). The decay time constants of coordinated events increased with resting cytosolic Ca²⁺ concentration. These decay time constants are plotted as a function of cytosolic Ca²⁺ in the inset in Fig. 5 D (open circles). Also plotted is the predicted stochastic attrition for a cluster of two independently gating channels (line). This stochastic attrition prediction was generated using single RYR2 Po and MOTs results. The decay times of the coordinated events were slower than that predicted for a simple stochastic attrition termination mechanism.

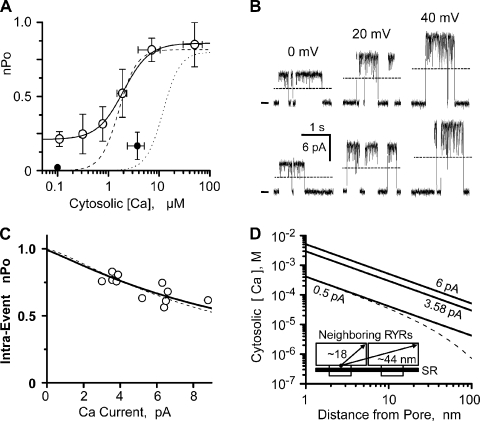
In multichannel studies, the parameter nPo is typically used to describe the probability of channels being open. Fig. 6 A shows how overall (not intra-event) nPo varies with resting cytosolic Ca²⁺ concentration. Open and filled circles represent nPo without and with cytosolic Mg-ATP present, respectively. The cytosolic EC₅₀ of coordinated events was 1.98 µM (PoMax = 0.86, PoMin = 0.26, and Hc = 1.7). The dotted and dashed lines reflect the Ca²⁺ sensitivity of individual RYR2 channels with and without cytosolic Mg²⁺-ATP present (also see Fig. 1 B). In the absence of Mg²⁺-ATP, the coordinated channels have substantial stationary nPo at low cytosolic Ca²⁺ levels (0.1 µM). This is most likely due to inter-RYR2 Ca²⁺ flux activation prolonging activity within the RYR2 cluster. The low nPo with Mg²⁺-ATP present at 0.1 µM is also consistent with this possibility because Mg²⁺-ATP reduces the cytosolic RYR2 Ca²⁺ sensitivity.

Figure 6.

Flux inhibition of coordinated RYR2 channel activity. (A) Cytosolic Ca²⁺ sensitivity of coordinated RYR2 channel activity (nPo). Overall nPo was defined from coordinated channel recordings at 0 mV. The cytosolic solution contained 1 mM EGTA and Tris-HEPES (120/250 mM; pH 7.4). The luminal solution contained Ca-HEPES (50/250 mM; pH 7.4). Open circles summarize the nPo (mean ± SEM; n = 7 different experiments). The solid line is a Hill equation fit to open circles (EC₅₀ = 1.98 µM, PoMax = 0.86, PoMin = 0.26, and Hc = 1.7). Small filled circles are after cytosolic Mg-ATP was added (1 mM of free Mg²⁺ and 5 mM of total ATP; n = 5 different experiments). Thin dashed and dotted lines are the single RYR2 50L and 50L plus Mg-ATP curves from Fig. 1 B. (B) Sample recording of coordinated events (two channels present). Solutions here are like those described for A (0.1 µM of cytosolic free Ca²⁺). Sample events at 0, 20, and 40 mV are shown. Open events are upward, zero current level is marked at left, and one open-channel current level is indicated by the dashed lines. All recordings shown are from the same channel incorporation. (C) Inhibition of intra-event nPo by increasing Ca²⁺ flux. Results collected from five different coordinated channels where only two channels were present. Solutions like those described for A (0.1 or 0.3 µM of cytosolic free Ca²⁺). Unit current was varied by changing membrane potential. Open circles are individual determinations. Dashed line is reproduced from Fig. 3 C. Thick solid line is a fit to the open circles and indicates a site distance from the pore of 1.5 nm (IC₅₀ = 6.2 mM and Hc = −1.3). The free bath Ca²⁺ used for this fitting was 134 µM, which is the average predicted free [Ca²⁺] (for 3.58 and 6.20 pA) at 30 nm from an open pore. This distance (30 nm) is approximately the inter-pore distance of two adjacent RYR2 pores in cells. (D) Calcium diffusion from a point source was calculated with cytosolic Ca²⁺ of 100 nM and no buffer present (thick lines) for unit Ca²⁺ currents of 6, 3.58, and 0.5 pA. The dashed line is for 0.5 pA current with 244 µM of cytosolic Ca²⁺ buffer (Km = 673 nM) present (Bers, 2001). It was assumed that the k_ON of this buffer was diffusion limited. (Inset) A cartoon depicting salient dimensions of neighboring RYR2 channels.

Fig. 6 B shows selected coordinated events collected at three different membrane potentials. The flicker between the double and single open state (dotted line) increases as unit Ca²⁺ current gets larger. This increased flicker reflects changing intra-event nPo. Fig. 6 C plots intra-event nPo as a function of unit Ca²⁺ current and represents results collected from five different channel incorporations. Eq. 4 fit (thick line), assuming the usual cytosolic inhibition site (EC₅₀, 6.2 µM; Hc = −1.3), indicates a pore inhibition site distance of 1.5 nm. This is consistent with our previous single-channel pore inhibition site distance determinations. Fig. 6 D shows predicted local free Ca²⁺ profiles over a distance covering two neighboring RYR2 channels. Profiles are shown for three different unit currents (6, 3.58, and 0.5 pA). The dotted line is for a 0.5-pA current in the presence of physiological Ca²⁺ buffering (Bers, 2001).

DISCUSSION

Our results suggest that single Ca²⁺-activated RYR2 channels can be modulated by the Ca²⁺ flux they carry if that flux is large enough (>3 pA). A large lumen-to-cytosol Ca²⁺ flux can act at both cytosolic activation and inhibition sites. However, the RYR2 carries a Ca²⁺ flux of <0.5 pA in cells (Mejía-Alvarez et al., 1999; Kettlun et al., 2003; Gillespie and Fill, 2008). Thus, an RYR2 channel is not likely to be regulated by its own flux in cells. Our results also suggest that the single RYR2 cytosolic Ca²⁺ activation mechanism is much more sensitive to cytosolic bath Ca²⁺ than to fluxed Ca²⁺. This leads to the suggestion that the RYR2 cytosolic Ca²⁺ activation machinery is somehow protected/shielded from its own Ca²⁺ flux.

Cytosolic pore inhibition site distance

Flux-dependent inhibition was measured six ways, and each time the results were fit using Eq. 4 to determine a pore site distance. This fitting assumed the responsible site was the same that operates under steady-state conditions (IC₅₀ = 6.2 mM; Hc = −1.3). The six individual pore site determinations were 1.3, 1.1, 1.4, 1.5, 0.5, and 1.5 nm, yielding an average pore inhibition site distance of 1.2 ± 0.16 nm. This is consistent with Xu and Meissner (1998), who predicted an RYR2 pore inhibition site distance of <3 nm assuming steady-state parameters similar to those we used. For the RYR1 channel, a pore inhibition site distance of 3–6 nm was reported, also assuming traditional steady-state inhibition parameters (Tripathy and Meissner, 1996). Laver (2007) more recently suggested that the RYR2 channel is regulated by a cytosolic inhibition site with an IC₅₀ of 1.2 µM with a pore inhibition site distance of 26 nm. Because the maximum cytosolic pore site distance is ∼20 nm, Laver (2007) suggests that this site may be on the very periphery of the channel or possibly on an adjacent, closely associated regulatory protein. The difference between our pore inhibition site determination and that of Laver (2007) could be explained if our channels, and those of Xu and Meissner (1998), did not have this adjacent, closely associated regulatory protein.

Xu and Meissner (1998) also reported that RYR2 Ca²⁺ fluxes ≥0.25 pA can act at cytosolic activation sites, and those ≥8 pA can act on inhibitory sites. Our results are generally consistent with this, except that we found detectable Ca²⁺ flux activation and inhibition only when Ca²⁺ fluxes were >3 pA. Our lower flux sensitivity may be explained by the absence of caffeine in our studies. Xu and Meissner (1998) also reported a paradoxical RYR2 activation upon 20 mM BAPTA application and proposed that RYR2 has “BAPTA-inaccessible” activation and “BAPTA-accessible” inhibition sites. In other words, they suggested that the cytosolic Ca²⁺ activation site is protected somehow. We make a similar prediction here, but ours is not based on BAPTA buffering.

Cytosolic pore-activation site distance

Flux-dependent RYR2 activation was observed here (Fig. 3, C and D). It was observed when the cytosolic resting free Ca²⁺ was low (0.5 µM). It increased Po from near zero to ∼0.08 as Ca²⁺ flux amplitude increased from 2 to ∼5 pA. This level of Ca²⁺ current will elevate local Ca²⁺ concentration over the entire cytosolic domain of the RYR2, carrying it to levels >100 µM. When free Ca²⁺ in the cytosolic bath is elevated to 100 µM (see Fig. 1 B), the Po of the RYR2 channels is ∼0.8 (i.e., 10 times greater than the maximal Ca²⁺ flux activation observed). Thus, the relatively small degree of RYR2 Ca²⁺ flux activation suggests that the channel’s cytosolic Ca²⁺ activation mechanism is somehow shielded from its own Ca²⁺ flux.

Our results also show that the function of two neighboring RYR2 channels can be coordinated when the channels were carrying a lumen-to-cytosol Ca²⁺ flux, consistent with the findings of Laver (2007). Like Laver (2007), our results indicate that this coordinated function is due to inter-RYR2 Ca²⁺ flux activation. Thus, single RYR2 channels are not very sensitive to their own Ca²⁺ flux, but that very same flux is sufficient to robustly/consistently activate a neighboring channel. Why might a single RYR2 channel be insensitive to its own flux? Some possible flux “protection” mechanisms might include: (1) Ca²⁺ occupancy rendering cytosolic activation site(s) flux insensitive, and/or (2) a protein conformational-dependent mechanism where channel opening physically alters the activation machinery somehow.

The Ca²⁺ occupancy possibility can be explained as follows. The channel opens when cytosolic bath Ca²⁺ binds to the activation site(s). Once open, Ca²⁺ flux through the channel elevates the local Ca²⁺ concentration. The fluxed Ca²⁺, however, cannot bind to the activation site(s) if the initial activating Ca²⁺ is already bound. The bound Ca²⁺ provides some inherent “protection” of the activation site(s). If the initial activating Ca²⁺ remains bound after the channel closes, this protection would last until the Ca²⁺ unbinds. Standard Ca²⁺-binding kinetics is consistent with this possibility because local fluxed Ca²⁺ levels theoretically dissipate faster than the channels close (Schiefer et al., 1995; Vélez et al., 1997; Soeller and Cannell, 2002). If the channel does indeed close with Ca²⁺ still bound, however, then open event duration (MOT) would be independent of cytosolic Ca²⁺ concentration, and this is clearly not the case. Fig. 3 D (inset) as well as Xu and Meissner (1998) show that RYR2 MOT varies with steady-state cytosolic Ca²⁺ levels. This implies that Ca²⁺ unbinds before the channel closes, giving Ca²⁺ a chance to rebind and prolong opening. Thus, a Ca²⁺ occupation protection mechanism may be kinetically possible but is not consistent with experimental observation. The conformational-dependent mechanism can be explained as follows. Protein movements associated with channel activation may determine (fatefully link) opening with channel closing. This type of mechanism was first proposed by Stern et al. (1997), and they called it fateful inactivation. In this case, the cytosolic Ca²⁺ sensitivity of MOT would not be generated by Ca²⁺ rebinding to the open channel but, instead, would be a consequence of how the channel was activated. This could explain our MOT results.

Role of cytosolic co-agonists

There is a prevalent contention that the effects of luminal Ca²⁺ (including flux-dependent regulation) require the presence of a cytosolic RYR2 agonist like ATP or caffeine. Consequently, some previous studies of Ca²⁺ flux regulation have been done in the presence of such agonists (Tripathy and Meissner, 1996; Xu and Meissner, 1998; Laver, 2007). The use of ATP is occasionally justified by arguing that ATP is a “physiological” agonist. This is certainly true, but the agonistic action of ATP in cells is normally offset by the antagonistic action of Mg²⁺. Applying ATP alone shifts RYR2 cytosolic Ca²⁺ sensitivity, making the channel more sensitive to Ca²⁺ flux regulation. For example, Laver (2007) reports an EC₅₀ of 5.4 µM if RYR2 channels are activated by Ca²⁺ alone and an EC₅₀ of 0.5 µM when they are coactivated by Ca²⁺ and ATP (no Mg²⁺). When ATP and Mg²⁺ are added together, the cytosolic Ca²⁺ sensitivity (EC₅₀) of the RYR2 channel shifts from ∼2 to ∼12 µM (Fig. 1 B), making the channels less prone to Ca²⁺ flux activation. Here, studies of RYR2 flux regulation were done with Ca²⁺-activated channels.

Cellular consequences

In cells, the RYR2 channel carries a unit Ca²⁺ current of ∼0.5 pA (Mejía-Alvarez et al., 1999; Kettlun et al., 2003; Gillespie and Fill, 2008). The cytosol is thought to contain ∼244 µM of Ca²⁺ buffer (average Km = 673 nM) (Bers, 2001). Using these values and the known dimensions of a single RYR2 channel (Samsó et al., 2005; Serysheva et al., 2005), some predictions about Ca²⁺ flux regulation of RYR2 channels in cells can be made.

Fig. 6 D shows the Ca²⁺ profile around an open pore conducting a 0.5-pA Ca²⁺ current with and without physiological buffers present. We assume here that the cytosolic buffer has a diffusion-limited k_ON. Because there are clearly some slow and fixed buffers in cells, the Ca²⁺ profile with the buffer present likely overestimates the action of the buffer. Our results indicate that the cytosolic Ca²⁺ inhibition site sits at a point 1.2 nm from the pore and has an IC₅₀ of 6.2 mM. Fig. 6 D suggests that there will be ∼0.4 mM Ca²⁺ at this site when the channel opens in cells, and thus little (if any) Ca²⁺ flux–dependent inhibition should occur. Because cytosolic Ca²⁺ and Mg²⁺ inhibit the RYR2 channel with similar IC₅₀’s (Fig. 2 B), the action of fluxed Ca²⁺ may well depend on how much Mg²⁺ is present. Assuming the cytosol contains ∼1 mM of free Mg²⁺, the combined free Ca²⁺ and Mg²⁺ concentration at the cytosolic inhibition site would increase from 1 and 1.4 mM when the channel opens. Our results indicate that this would only minimally reduce Po (0.73 to 0.69) or generate a relatively minor degree of flux-dependent inhibition.

The cytosolic Ca²⁺ activation site must be somewhere within 18 nm of the pore. The RYR2 Ca²⁺ EC₅₀ in cells (with Mg-ATP present) is 12 µM (Fig. 1 B) (Zoghbi et al., 2004). With a physiological Ca²⁺ current (0.5 pA), the entire cytoplasmic domain around an open single RYR2 would “see” local Ca²⁺ levels >20 µM. Thus, it is possible for the Ca²⁺ flux to feedback and influence the activation status of the channel carrying it. Our results, however, suggest that channels are largely insensitive to their own Ca²⁺ flux, even when that flux is >2 pA. Thus, the flux carried by an RYR2 channel in cells is unlikely to influence its own activation status.

The RYR2-RYR2 center spacing in cells is ∼30 nm (Franzini-Armstrong et al., 1999). Fig. 6 D indicates that local Ca²⁺ will be 7–15 µM at a distance of 30 nm from an open RYR2 pore conducting a 0.5-pA Ca²⁺ current. Thus, the opening of an RYR channel in a cell will elevate local Ca²⁺ levels around neighboring channels to about the RYR2 Ca²⁺ activation EC₅₀ (∼12 µM). This likely explains the highly concerted channel activation within an RYR2 cluster that underlies the Ca²⁺ spark in cells. Release sites (i.e., RYR2 clusters) in cells are separated by ∼760 nm radially and by ∼1,800 nm longitudinally (Parker et al., 1996). With normal physiological Ca²⁺ buffering, the local Ca²⁺ level falls to basal levels (100 nM) at a distance of ∼300 nm from an open RYR2 channel conducting a 0.5-pA Ca²⁺ current. Thus, RYR2 Ca²⁺ release at one cluster would not be likely to activate RYR2 channels in a neighboring cluster, consistent with sparks being localized at non-propagating events in cells.