A topology-preserving approach to the segmentation of brain images with multiple sclerosis lesions

Abstract

We describe a new fully automatic method for the segmentation of brain images that contain multiple sclerosis white matter lesions. Multichannel magnetic resonance images are used to delineate multiple sclerosis lesions while segmenting the brain into its major structures. The method is an atlas-based segmentation technique employing a topological atlas as well as a statistical atlas. An advantage of this approach is that all segmented structures are topologically constrained, thereby allowing subsequent processing such as cortical unfolding or diffeomorphic shape analysis techniques. Evaluation with both simulated and real data sets demonstrates that the method has an accuracy competitive with state-of-the-art MS lesion segmentation methods, while simultaneously segmenting the whole brain.

Introduction

Multiple sclerosis (MS) is a demyelinating disease of the central nervous system that commonly leads to inflammatory and atrophic pathology, and is often associated with cognitive impairment (Benedict and Bobholz, 2007; Calabresi, 2005). MS pathology is primarily expressed as focal lesions in the white matter (WM) of the brain, but the state and progression of the disease is also correlated with cerebral atrophy (Fisher et al., 2008; Benedict and Bobholz, 2007; Ge, 2006). Because of its superior contrast, magnetic resonance (MR) imaging is the modality of choice for clinical evaluation of MS. Quantitative analysis of MR images to measure and monitor lesion load and tissue volumes has become invaluable for patient follow-up and evaluation of therapies. Manual delineation of MS lesions, however, is both challenging and time-consuming as three-dimensional information from several MR contrasts must be integrated.

Techniques for automated MS lesion segmentation generally employ intensity-based classifiers. A common approach for performing unsupervised lesion segmentation involves modeling the distribution of intensities in healthy brain MR images as a Gaussian Mixture Model (GMM) and then segmenting the lesions as outliers of this model. In their work, Leemput et al. (2001) introduced typicality weights for each voxel and class as well as intensity and contextual constraints to segment MS lesions as outliers. Aït-Ali et al. (2005) used a trimmed likelihood estimator (TLE) to estimate a GMM from different time points. A Mahalanobis distance was used to distinguish the lesions from healthy tissue, and intensity constraints were imposed after this step to reduce the false positives. More recent methods further combined a TLE with a mean shift algorithm (García-Lorenzo et al., 2008) or a Hidden Markov chain (Bricq et al., 2008). These methods also segment lesions as outliers of the normal brain distribution.

Instead of modeling lesions as outliers of a distribution, some methods model lesions as a separate class. Harmouche et al. (2006) introduced an unsupervised Bayesian lesion classifier with different intensity distributions for different regions of the brain. Lesions are segmented based on posterior probabilities and entropy values. Freifeld et al. (2007) used a constrained GMM to model the image and active contours to delineate lesions.

Supervised classifiers that model lesions as distinct classes have also been used. Warfield et al. (2000) combined a k-nearest neighbor (kNN) classifier with an elastic template registration to segment the MS brains. In addition to intensity features provided by the input images, the classifier also used features from a distance map generated from a digital template. The method iterates between kNN classification and elastic registration of the digital template to the hard segmentation of the MS brain generated by the classifier to refine the segmentation of structures and lesions. A similar approach is introduced by Warfield et al. (1995) where a GMM is used to classify the major brain tissues and an elastically registered template is used to distinguish the healthy gray matter (GM) from WM combined with MS lesions. Lesions are then separated from WM using a minimum distance classifier. Zijdenbos et al. (2002) used a back propagation artificial neural network (ANN) to segment MS lesions. T1, T2, and proton density (PD) weighted MR images as well as probabilistic atlases of cerebrospinal fluid (CSF), WM, and GM were used as input nodes. Wu et al. (2006) performed an intensity-based kNN classification followed by a template-driven segmentation and partial volume artifact correction technique to improve the classification.

Segmentation methods assuming models of healthy brain tissues (without adapting for lesions) have also been reported in the literature, utilizing a post-processing step to find lesions. Souplet et al. (2008) used a TLE to segment the healthy tissue from T1 and T2 sequences, and derived a threshold from parameters of the healthy brain to delineate the lesions on an enhanced FLuid-Attennuated Inversion Recovery (FLAIR) sequence. Younis et al. (2007) used a grouping artificial immune network to segment the brain from T1 and T2 sequences, extracted CSF from the T1 image, and segmented the lesions on the T2 image with masked CSF. Similar methods have been proposed for the detection of white matter signal abnormalities that frequently occur in Alzheimer's disease and older populations (Anbeek et al., 2004; Admiraal-Behloul et al., 2005; Lao et al., 2008).

All of the aforementioned techniques suffer from one or more drawbacks. First, many methods focus solely on segmenting lesions, even though volumetric analysis of other brain structures in MS is becoming an active area of research (Ramasamy et al., 2009). The approaches that do consider other structures typically require post-processing steps to enhance the lesion segmentation, affecting the consistency of the overall segmentation. None of these methods segments the sub-cortical structures of the brain, and cortical surface analysis (Thompson et al., 2004; Tosun et al., 2004) would require specificalized adaptation as the topology of the brain is altered by the lesions. Second, the extent and location of brain atrophy, important for monitoring the progression of the disease, is either not computed or is not subject to validation. Standard processing techniques for measuring these quantities (Smith et al., 2002) often require modification before being applied to data that possess lesions (Sdika and Pelletier, 2009). Third, many lesion segmentation algorithms employ lesion intensity profiles, which are dependent on a specific acquisition pulse sequence and may need to be modified or retrained to process data acquired using alternative pulse sequences. Methods modeling lesions as outliers are highly dependent on the choice of a threshold to characterize the outliers, which often requires some manually segmented data.

In this paper, we propose a new technique for segmenting white matter lesions in MS that provides a detailed and topologically consistent segmentation of the brain into its main cortical and sub-cortical components. The method incorporates both spatial and intensity information to segment multichannel MR images without post-processing. Although it utilizes multichannel acquisitions, training data are not required to model the intensity distributions, making the algorithm flexible enough to be applied to data originating from a variety of pulse sequences. A novel scheme has been introduced to use the information from different input sequences in an efficient way. Moreover, this method enforces topological constraints in such a way that the segmented images maintain topological equivalence with those of healthy subjects, allowing the direct use of techniques for performing cortical reconstruction and unfolding (Tosun et al., 2004), as well as diffeomorphic shape analysis (Beg et al., 2005). The former is a topic of substantial interest since specific patterns of cortical thinning have been found to be associated with specific impairments in MS patients (Benedict et al., 2002; Sailer et al., 2003). Because our topology-preserving framework may be readily applied to cortical reconstruction methods, studies involving associations between cortical geometry and clinical measures in MS will be greatly facilitated. As shown in our previous work, topology preservation also leads to more robust representations of anatomy because configurations such as a pixel of gray matter appearing in the middle of white matter are prohibited.

The work of Warfield et al. (2000) bears several similarities to our approach in its use of templates and distance maps. Distance maps from the boundaries of structures may be used to inform an algorithm about the typical location of MS lesions. This limits the number of false positives often caused by the intensity similarities of lesions to other healthy structures, a common challenge for intensity-based classification of lesions. Although Warfield et al. (2000) also used such distance maps, their work is not concerned with preserving topology, the template that is used to compute the distance maps is generated with a different approach, and a supervised classifier is employed as opposed to the unsupervised classifier used in our work.

The method builds upon our previous work on TOpology-preserving Anatomical Segmentation (TOADS) (Bazin and Pham, 2008) by introducing several essential new concepts to effectively model the lesions while maintaining the constraints provided by topological and statistical atlases. A key observation from which the new approach is formulated is that topological outliers, such as lesions, can be addressed in a topology-preserving framework when they are grouped together with the underlying tissues. We evaluate this new approach with both simulated and real images, demonstrating good performance compared to other recent lesion segmentation methods. Preliminary versions of the proposed method have been previously presented at conference workshops (Shiee et al., 2008a,b). The version presented herein is a new implementation with new validation results.

Method

In this section, we first review TOADS, which is designed to segment healthy brain images. We then introduce several new elements to generalize the model for brain images with MS. These elements include a lesion class that shares its spatial distribution prior with healthy white matter and modified relationship functions for reducing lesion false positives in unlikely locations. Also, a new intensity weighting scheme is introduced for efficient utilization of the intensity information from multichannel inputs. The resulting algorithm, Lesion-TOADS, simultaneously segments major brain structures as well as lesions. We have released the algorithm as a user-friendly plug-in to MIPAV (McAuliffe et al., 2001) which is a freely available software developed at the National Institutes of Health for the analysis and visualization of medical images.

Statistical and topological atlas-based segmentation in healthy anatomy

Lesion-TOADS segments the brain into its major structures (sulcal CSF, ventricular CSF, cortical gray matter, cerebral white matter, cerebellar gray matter, cerebellar white matter, putamen, thalamus, caudate, and brainstem) while delineating MS white matter lesions. It is based on TOADS, which incorporates information from statistical and topological atlases into an intensity-based classification technique to yield a topologically consistent segmentation of healthy brain anatomy. A brief overview of this method is provided in the following, with additional details available in (Bazin and Pham, 2008).

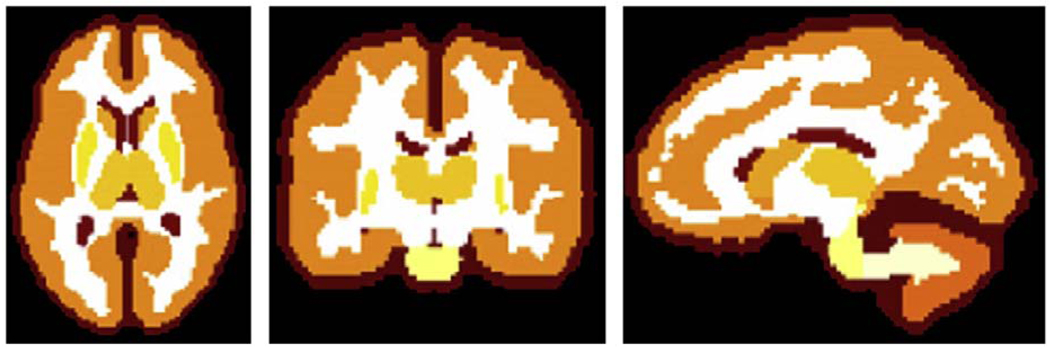
TOADS utilizes a statistical atlas as well as a topological atlas. The statistical atlas is built from a set of 18 manual delineations of the structures of interest, based on the IBSR data set (Worth, 1996). The boundary of each structure was blurred to make a smooth probability map and to account for anatomical variations beyond those present within the training set. The statistical atlas affects the segmentation of adjacent structures having similar intensity. The topological atlas is a parcellation of the brain edited to encode a specific topology for each structure and group of structures, based on statistical atlases and anatomy textbooks (see Fig. 1). The topologically consistent hard segmentation of the brain is initialized from this topological atlas as will be explained later in this section. It is also used for lowering the influence of competing intensity clusters in regions that are spatially non-contiguous. Prior to the segmentation, the atlases are rigidly registered to the studied MR image, and the registration is further updated at each iteration of the segmentation algorithm.

Fig. 1.

Topological atlas in axial, coronal, and sagittal views.

Given a D-channel MR image, I, TOADS performs two interleaved processes consisting of (1) performing a fuzzy segmentation, and (2) defining topologically consistent regions using fast marching. The fuzzy segmentation is obtained by minimizing the following energy function:

$$E={\displaystyle \sum _{\mathit{\text{jk}}}\frac{u_{\mathit{\text{jk}}}^q}{r_{\mathit{\text{jk}}}}}\parallel g_j·I_j-c_k{\parallel }^2+\frac{\beta }{2}{\displaystyle \sum _{l\in N_j,m\ne k}\frac{u_{\mathit{\text{jk}}}^q}{r_{\mathit{\text{jk}}}}}{u}_{\mathit{\text{lm}}}^q+\frac{\gamma }{2}{\displaystyle \sum _{m\ne k}{w}_{km}\frac{u_{\mathit{\text{jk}}}^q}{r_{\mathit{\text{jk}}}}{p}_{\mathit{\text{jm}}}^q}$$ (1)

with respect to fuzzy membership functions u_jk for each pixel j and structure k, a gain field vector g_j that models intensity inhomogeneities for each channel, and the vector of intensity centroids c_k for each structure. Note that the (·) operator in Eq. (1) represents an element by element multiplication. The first term in Eq. (1) is data driven, the second term enforces smoothness on the memberships (Pham, 2001), and the third term controls the influence of the statistical atlas. The parameters β and γ control the relative weighting of each term and are set empirically (we set β = γ = 0.1 in all the reported experiments). The exponent q is a parameter controlling the “hardness” of the membership functions and is typically set to 2. The gain field is a smoothly varying function modeled as a low degree polynomial (we used a polynomial of degree three, see Pham and Bazin (2006) for details). The variables p_jk are probabilities derived from the statistical atlas that represent the prior probability of pixel j being inside structure k. The variables w_km and r_jk weight the impact of the atlas and the structure relationships as described in the following.

The atlas weight w_km between two classes is a function of distance between their centroids:

$$w_{\mathit{\text{km}}}=\frac{1}{1+\frac{1-s_w}{s_w}{\displaystyle {\sum }_i\frac{{(c_k^i-c_m^i)}^2}{({\sigma }_k^i+{\sigma }_m^i{)}^2}}}$$ (2)

where s_w is a divergence parameter and ${\sigma }_k^d$ is the estimated standard deviation of the intensities within class k on channel i. The atlas weight is one when c_k = c_m but goes to zero when (c_k − c_m)² » (σ_k + σ_m)² (the divergence parameter enforces w_km = s_w if (c_k − c_m)² = (σ_k + σ_m)², we set s_w = 0.1 in our experiments). With this definition of w_km, the atlas prior influences the segmentation only where the intensity contrast between structures is low. We have found that the method is able to segment a large variety of MR images successfully by this set of parameter values.

The relationship weights r_jk take into account global and local relationships between the structures, and are defined by

$$r_{\mathit{\text{jk}}}=\{\begin{array}{cc}1\hfill & \text{for}j\text{in}k\text{or}\mathrm{a}\text{structure}\text{bordering}k,\hfill \\ p_{\mathit{\text{jk}}}\hfill & \text{otherwise}.\hfill \end{array}$$ (3)

The relationship weights penalize against membership configurations that are inconsistent with the topology atlas.

The energy function (1) is used to compute membership functions for each structure in a coordinate descent fashion, similar to the fuzzy C-means clustering algorithm and its derivative FANTASM (Fuzzy And Noise Tolerant Adaptive Segmentation Method) (Pham, 2001). In addition, we compute a topologically consistent “hard” segmentation that is derived from the memberships. To this end, we initialize the hard segmentation of the brain from the topology atlas and update it homeomorphically at the next iterations of the algorithm. This is accomplished by a fast marching method, which is a technique for modeling a front propagation problem that moves according to a pre-defined speed function (Sethian, 1999). The hard segmentation is updated by two successive iterations of thinning and growing, which are fast marching procedures where the speed function is modulated by the memberships and the topology is preserved. The first step starts from the current hard segmentation and thins the structures into a skeleton-like object with a speed function $f_{\mathit{\text{jk}}}^{-}=\frac{u_{\mathit{\text{jk}}}}{{\text{max}}_m{u}_{\mathit{\text{jm}}}}$ and then the second step grows the structures back to find the optimal boundary by the speed function $f_{\mathit{\text{jk}}}^{+}=\frac{{\mathit{\text{max}}}_m{u}_{\mathit{\text{jm}}}}{u_{\mathit{\text{jk}}}}$, using a minimal path strategy (Bazin and Pham, 2008; Li et al., 2006). Thinning removes the errors due to the mis-alignment of the atlas to the image, as only the voxels with high membership are kept inside the structures during this process. Conversely, the growing step starts from the boundaries of thinned structures and expands them simultaneously until they reach to the boundary of other structures based on the membership values. This way, the hard segmentation captures more details of the structure boundaries at each iteration while remaining topologically equivalent to the topological atlas. Also, this updated hard segmentation plays the role of the topological atlas in the computation of relations and distances in subsequent steps of the algorithm.

The centroids of the classes associated with the smaller structures may be less stable than the ones associated with the larger structures. This is due to the fact that fewer intensity samples are effectively used in computing the centroid of these classes. To make these centroids more stable, we introduced the concept of linked centroids computation. The linked centroids approach is based on the fact that different classes modeling structures with the same underlying brain tissue type also have similar intensity profiles. Consequently, it is reasonable to use the intensity information of all of these classes in the computation of the intensity centroid of each. In this way, the larger structures stabilize the centroids of the smaller ones, yielding a better segmentation of the smaller structures. We compute the linked centroids as follows:

$$c_k=\frac{{\displaystyle {\sum }_j{u}_{\mathit{\text{jk}}}^2{g}_j{I}_j+\alpha {\displaystyle {\sum }_{l\in T(k)}{\displaystyle {\sum }_j{u}_{\mathit{\text{jl}}}^2{g}_j{I}_j}}}}{{\displaystyle {\sum }_j{u}_{\mathit{\text{jk}}}^2+{\displaystyle {\sum }_{l\in T(k)}{\displaystyle {\sum }_j{u}_{\mathit{\text{jl}}}^2}}}},$$ (4)

in which α controls the influence of other structures on computation of c_k and is set to 0.1 in this work. T(k) is the set of the structures having the same underlying tissue type as k. For instance, T(caudate) = {cortical GM, putamen, thalamus, cerebellum GM}.

The complete TOADS algorithm is composed of the following steps:

1. Align atlases to image and set initial segmentation to the topological atlas.

2. Compute r_jk from current hard segmentation.

3. Compute the memberships u_jk, centroids c_k, and the inhomogeneity field g_j.

4. Thin structures using the fast marching algorithm.

5. Grow back the structures and update the segmentation.

6. Refine the alignment of the atlases.

7. Loop to step 2 until convergence.

The convergence criterion is the relative amount of change in the energy E with each iteration. We choose a threshold of 10⁻⁴ or a maximum of 100 iterations. In our experiments on more than 500 cases, the algorithm converged in less than 40 iterations for most cases and less than 100 iterations for all others.

Lesions in topology-preserving segmentation

TOADS is based on anatomical priors, which seems to conflict with the globally distributed nature of MS lesions. Since lesions can occur anywhere in the WM, we cannot systematically associate them with a specific topological or statistical model, unlike other structures. Similarly, the topology of the WM is modified arbitrarily by the appearance of lesions. However, if we make the observation that the MS lesions must appear inside the WM region, we can then assume that the structures made of WM grouped with the lesions have the same shape and topology as healthy WM. Thus, for anatomical purposes, WM and lesions are treated as a single structure. This allows our previously generated topological and statistical atlases to be directly applicable to the segmentation of brain images possessing lesions, even though they were created from images of healthy subjects.

To address lesions in TOADS, we first add an additional lesion class to our model, with a corresponding lesion membership function and intensity centroid. We also need to modify the definitions of the atlas weights w_km and the relationship weights r_jk to reflect the new model, as described later in this section. The values of the statistical atlas prior p_j,lesion are set to the WM value. The speed function for evolving the hard segmentation of the grouped WM and lesions uses the sum of membership functions for WM and lesions, i.e., $f_{j,\mathit{\text{WM}}}^{-}=\frac{u_{j,\mathit{\text{WM}}}+u_{j,\mathit{\text{lesion}}}}{{\mathit{\text{max}}}_m{u}_{\mathit{\text{jm}}}}$ and $f_{j,k}^{+}=\frac{{\mathit{\text{max}}}_m{u}_{\mathit{\text{jm}}}}{u_{j,\mathit{\text{WM}}}+u_{j,\mathit{\text{lesion}}}}$. The lesions and WM are then separated by selecting, inside the grouped region, whichever has the higher membership value. With these alterations, we preserve the topology of brain structures while computing a competitive process between WM, lesions, and neighboring structures.

The atlas weights should be large when the centroids of two nearby structures are close to each other. For the lesion atlas weight, we use the lesion centroid to compute w_lesion,m in Eq. (2). When comparing lesions and WM, however, the atlas priors should have no influence, so we set w_lesion,wm = 0. Similarly, the relationship function r_j,lesion can be replaced by the function of the underlying region, i.e., r_j,lesion = r_j,wm. However, in some regions we further modify this function to reduce the potential for false positives.

Limiting false positives

With the adaptations described in the previous section, MS lesions now can be modeled as a separate cluster in the TOADS intensity atlas-based segmentation algorithm with the desirable topological properties. However, classifying lesions using a tissue classification or clustering technique often suffers from a large amount of false positives. This is due to the fact that lesions can have intensity profiles close to those of other structures in the brain. For example in T1 images, MS lesions appear as hypointense WM voxels whose intensity is close to GM intensity (see Fig. 2). Because we compute a hard segmentation of brain structures at each step of our algorithm, we can use our knowledge about areas where false positives commonly occur to define an appropriate relationship function.

Fig. 2.

MS lesions contrasts in MR images: hypointense WM on T1 looks similar to GM, hyperintense WM on T2 and PD looks similar to CSF. Lesions are brighter than other tissues on FLAIR, but the boundary of the ventricles is also hyperintense (see areas pointed by red arrow). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Because the intensity centroid of the lesion class lies between centroids of GM and WM, their boundaries are common areas for false positives (although true lesions can also occur in this zone). Similarly, the boundary between WM and ventricles may appear bright in T2, PD, and FLAIR images and yet not contain any lesion. To address this problem, we update the relationship function between lesions and these structures as a function of the distance from the boundary of GM and ventricles:

$$r_{\mathrm{j},\text{lesion}}=\mathbf{\{}\begin{array}{cc}\left(\frac{d_{\text{min}}}{d_{\text{max,VENT}}}\right)r_{\mathrm{j},\text{wm}}\hfill & d_{\mathrm{j},\text{VENT}}\le d_{\text{min}},\hfill \\ \left(\frac{d_{\text{min}}}{d_{\text{max},\text{GM}}}\right)r_{\mathrm{j},\text{wm}}\hfill & d_{\mathrm{j},\text{GM}}\le d_{\text{min}},\hfill \\ \left(\frac{d_{\mathrm{j},\text{VEN}}}{d_{\text{max},\text{VEN}}}\right)r_{\mathrm{j},\text{wm}}\hfill & d_{j,\text{VEN}}\le d_{\text{max},\text{VEN}},\hfill \\ \left(\frac{d_{j,\text{GM}}}{d_{\text{max},\text{GM}}}\right)r_{\mathrm{j},\text{wm}}\hfill & d_{\mathrm{j},\text{GM}}\le d_{\text{max},\text{GM}},\hfill \\ \hfill r_{\mathrm{j},\text{wm}}\hfill & \text{otherwise}.\hfill \end{array}$$ (5)

where d_j,VEN and d_j,GM are the distance to ventricles and GM structures, respectively.

In addition, the relationship function for the cortical GM is also modified in the region where d_j,VEN<d_max,VEN, to preserve the boundary between WM and CSF:

$${\tilde{r}}_{\mathrm{j},\text{gm}}=\mathbf{\{}\begin{array}{cc}\hfill \left(\frac{d_{\mathrm{j},\text{VEN}}}{d_{\text{max},\text{VEN}}}\right)r_{\mathrm{j},\text{gm}}\hfill & \hfill d_{\mathrm{j},\text{VEN}}\le d_{\text{max},\text{VEN}},\hfill \\ \hfill r_{\mathrm{j},\text{gm}}\hfill & \hfill \text{otherwise}.\hfill \end{array}$$ (6)

The relationship function for sub-cortical structures is unchanged, as these structures legitimately share a boundary with the ventricles.

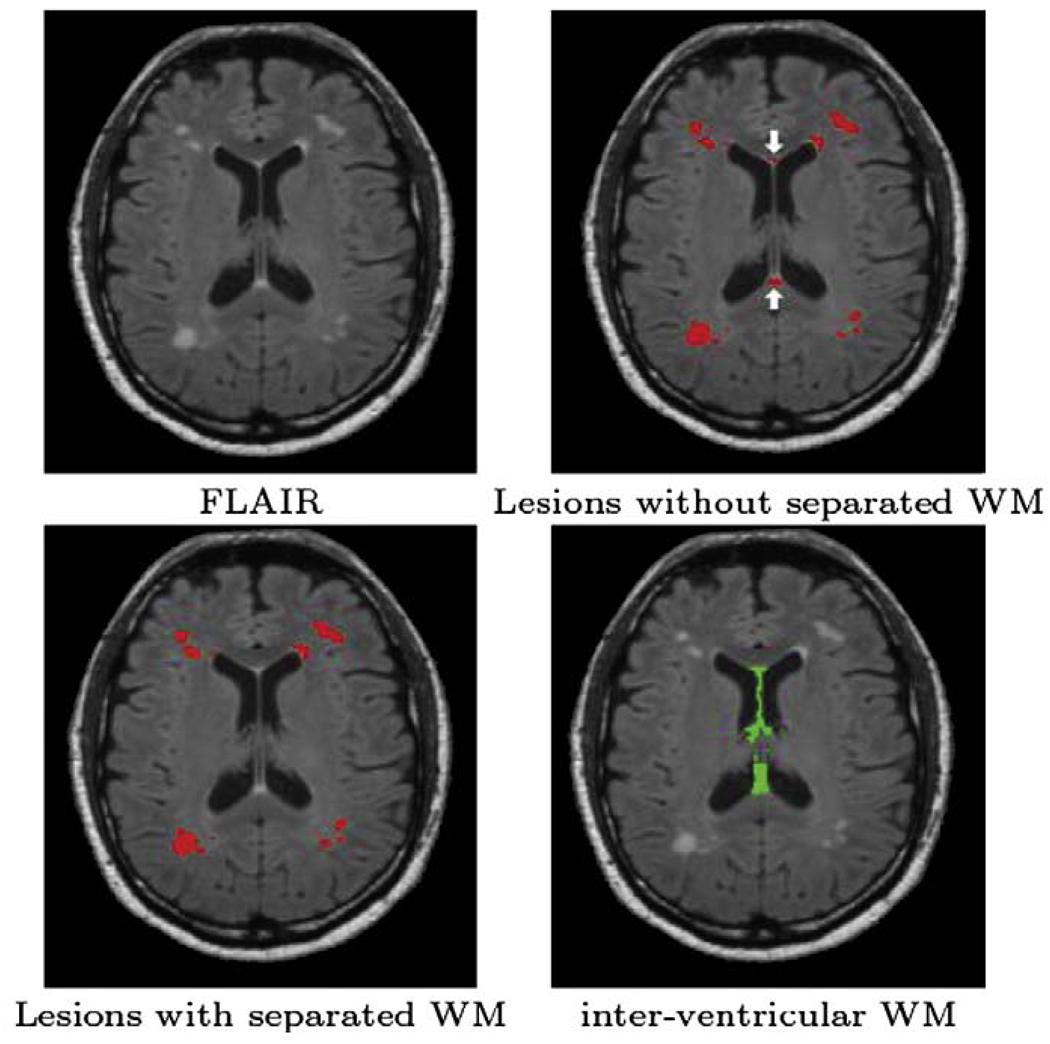
Another area where false positives commonly occur is between the ventricles and in the subarachnoid space. This is due to high signal intensity artifacts within CSF in FLAIR images, that are most pronounced in the posterior fossa. These artifacts are considered to be the result of an inflow of CSF that was originally outside the region affected by the inversion pulse, as well as the result of irregularities in the amplitude of the initial inversion pulse (Kallmes et al., 2001; Bakshi et al., 2000; Hajnala et al., 2001). By modifying the statistical atlas to treat this region as a separate class, we can add an option to the algorithm so users may suppress the lesions in these areas and reduce the false positives due to these common artifacts (see Fig. 3). We call this new class interventricular WM. We also modify the relationship function for lesions with respect to distance from inter ventricular WM:

$${\tilde{r}}_{\mathrm{j},\text{lesion}}=\mathbf{\{}\begin{array}{cc}\left(\frac{d_{\text{min}}}{d_{\text{max},{\text{WM}}_{\text{int}}}}\right)r_{\mathrm{j},\text{lesion}}\hfill & d_{\mathrm{j},{\text{WM}}_{\text{int}}}\le d_{\text{min}},\hfill \\ \left(\frac{d_{\mathrm{j},{\text{WM}}_{\text{int}}}}{d_{\text{max},{\text{WM}}_{\text{int}}}}\right)r_{\mathrm{j},\text{lesion}}\hfill & d_{\mathrm{j},{\text{WM}}_{\text{int}}}\le d_{\text{max},{\text{WM}}_{\text{int}},}\hfill \\ \hfill r_{\mathrm{j},\text{lesion}}\hfill & \text{otherwise}.\hfill \end{array}$$ (7)

where d_j,WMint is the distance from the boundary of interventricular WM.

Fig. 3.

Example of removing false positives using an interventricular WM class. White arrows show the common false positives (caused by hyperintensities between ventricles) which have been removed by adding the extra class.

The value of d_{max,structure} should be chosen small enough such that the lesion membership of a real lesion voxel near a healthy structure boundary is not affected to an extent that it gets segmented as a healthy tissue. On the other hand d_{max,structure} should be large enough to eliminate the false positives. We set d_max,VEN = d_max,GM = 5 voxels, large enough to limit occurrence of false positives without hindering the detection of lesions near the boundary. These values assume that the images are typically 1 mm isotropic volumes.

As previously mentioned, FLAIR artifacts can occur in the subarachnoid space. This area is not necessarily in contact with interventricular WM, but if we choose d_j,WMint large enough, the false positives can be removed. Noting that lesions should not appear in the vicinity of interventricular WM, having a large d_j,WMint is also favorable for lesion segmentation because it penalizes more in distances very close to the boundary. We chose d_j,WMint = 20 voxels.

We also associate the voxels inside the structures to a non-zero distance value d_min to improve the algorithm performance in the detection of lesions near the boundary of WM with other structures (e.g., GM in the case of juxtacortical lesions and ventricles in the case of periventricular lesions). In the initialization of the algorithm, it is likely that a lesion close to the boundary of WM with another structure overlaps with that structure in the aligned topological atlas. Setting the distance function to zero inside that structure will force the lesion membership in the overlapped areas to zero, resulting in mis-segmentation of the lesion as a healthy structure. Different values of d_min are needed based on the input images of the algorithm. For T2/PD, because of the similarity of the lesion intensity to that of GM/CSF, we set d_min = 1, while in FLAIR the distinct contrast of lesions works well with d_min = 0.5.

Multichannel weighting

Although FLAIR images provide excellent contrast for lesions, they do not possess good contrast for non-lesion brain structures, especially at the boundary of the cortex and CSF. Also, we observed a large variability of the lesion intensity on T1 sequence, from values close to the CSF intensity to values near the GM intensity. These contrast variabilities on different MR pulse sequences cause inaccuracy in the segmentation of both lesions and brain structures, revealing the need for a more effective use of the intensity information from each of the input channels. To address this issue, we incorporated a class-dependent weighting scheme in which channel and class-dependent weights ${\omega }_k^i$ tune the effect of each channel i on the segmentation of each class k. The ${\omega }_k^i\text{'}\mathrm{s}$ are constrained to add up to one for each class. For simultaneous lesion and tissue classification, we set ${\mathrm{\omega }}_{\text{sulcal\hspace{1em}CSF}}^{\text{FLAIR}}=0,{\mathrm{\omega }}_{\text{sulcal\hspace{1em}CSF}}^{\mathrm{T}1}=1,{\mathrm{\omega }}_{\text{lesion}}^{\mathrm{T}1}=0,{{\mathrm{\omega }-}_{\text{lesion}}}^{\text{FLAIR}}=1$ and put all other weights equal to 0.5. By this choice of ${\omega }_k^i\text{'}\mathrm{s}$, the segmentation of sulcal CSF is only affected by the T1-weighted image, the variability of lesion intensity on T1-weighted image does not deteriorate the segmentation of lesions, and, finally, other tissues are segmented properly by equally weighting the intensity information of all the input channels.

In addition to this multichannel weighting scheme, we further enhance the clustering model using the approach described by Roy et al. (2008) to particularly improve accuracy on Magnetization Prepared RApid Gradient Echo (MPRAGE) T1-weighted images. In this model, a new pre-determined variable for each class called compactness $p_k^i$ is incorporated to control the variability of cluster k on channel i. It possesses large values for classes with small variance and small values for classes with large variance. We set $p_{\text{CSF}}^{\text{MPRAGE}}=1.25$ and all other compactness parameters equal to 1. So the energy function for Lesion-TOADS becomes

$$\begin{array}{cc}E=\hfill & {\displaystyle \sum _{\mathit{\text{jk}}}\frac{u_{\mathit{\text{jk}}}^q}{r_{\mathit{\text{jk}}}}{\displaystyle \sum _i{\mathrm{\omega }}_k^i\Vert g_j^i{I}_j^i}-c_k^i{\Vert }^{2p_k^i}+\frac{\beta }{2}{\displaystyle \sum _{l\in N_j,m\ne k}\frac{u_{\mathit{\text{jk}}}^q}{r_{\mathit{\text{jk}}}}{u}_{lm}^q}}\hfill \\ \hfill & +\frac{\gamma }{2}{\displaystyle \sum _{m\ne k}{w}_{km}\frac{u_{\mathit{\text{jk}}}^q}{r_{\mathit{\text{jk}}}}{p}_{jm}^q,}\hfill \end{array}$$ (8)

where i denotes the input channels. Fig. 4 shows a comparison between the results of Lesion-TOADS before and after incorporating the introduced intensity weighting scheme and the compactness variable. It can be seen from the second row of this figure that the segmentation of both MS lesions and sulcal CSF has been significantly improved.

Fig. 4.

A slice from T1-MPRAGE and FLAIR images of a MS subject with high intensity variability on T1-MPRAGE (first row) and comparison of its maximum membership classification by regular and enhanced methods (second row). CSF, GM, WM, and lesions are shown in dark red, orange, white, and light red, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Finally, an initialization for the intensity centroids of the different structures is necessary. We employ a simplistic intensity template of the expected centroids for each channel (T1-weighted, T2-weighted, proton density weighted, and FLAIR). When processing a multichannel image, we first estimate the robust minimum and maximum of the intensity in each channel (the intensity values at 5% and 95% of the histogram, respectively), and normalize the profiles such that 0 corresponds to the minimum and 1 to the maximum. We initialize the centroids to empirically determined values stemming from the expected intensities of the three major tissue classes and lesions. After the centroids are initialized, however, they are allowed to evolve freely to minimize the energy of Eq. (8).

Software

We have implemented Lesion-TOADS as a software plug-in to the Medical Image Processing, Analysis and Visualization (MIPAV) software package developed by the National Institutes of Health (McAuliffe et al., 2001). The MIPAV package allows reading of nearly all common file formats, including DICOM, Analyze, and NIFTI, and is available on Linux, Windows, and Mac platforms. The plug-in provides a user-friendly graphical user interface to execute the algorithm on a loaded data set or to easily change the default parameters. The plug-in is also scriptable, making it suitable for studies involving a large number of patients. We have also implemented Lesion-TOADS as a module in the Medic Automated Pipeline Scheduler (MAPS) (Lucas et al., 2008), which is an extension to the MIPAV plug-in framework that allows the user to graphically create and execute pipelines for multi-stage processing tasks. Lesion-TOADS takes about 45 min to run on a modern Linux workstation. Fig. 5 shows the user interface of the software.

Fig. 5.

The user interface of the lesion segmentation software.

Experimental Results

We evaluated the performance of Lesion-TOADS on both simulated and real images.

Simulated images

We first applied Lesion-TOADS to the Brainweb MS phantom with variable levels of noise and field inhomogeneity (Collins et al., 1998). This data set contains T1, T2, and PD weighted images but no FLAIR image. We applied our topologically constrained segmentation algorithm to segment the brain and lesions. To compute a hard segmentation for lesions at voxel j inside the cerebral WM class, u_WM and u_lesion were compared and if u_lesion(j) > u_WM(j), voxel j is classified as a lesion. We computed the Dice similarity coefficient $\left(\mathit{\text{DSC}}=\frac{2|\mathit{\text{Seg}}\cap \mathit{\text{Ref}}|}{|\mathit{\text{Seg}}|+|\mathit{\text{Ref}}|}\right)$ (Dice, 1945) between our segmentation (Seg) and the Brainweb ground truth (Ref) to evaluate Lesion-TOADS segmentation. Here, |A| is the volume of A. DSC reflects differences in locations more strongly than differences in size (Zidjenbos et al., 1994). It ranges from 0 to 1, where 0 indicates no spatial overlap between two delineations and 1 indicates perfect agreement. DSC values of 0.7 and higher suggests good agreement between two delineations (Bartko, 1991).

Because the original Brainweb ground truth is only concerned with the three major tissue classes (GM, WM, and CSF), we performed a manual segmentation to separate cerebellum, brainstem, cerebrum, and sub-cortical structures. Table 1 and Fig. 14 show the DSC values between Lesion-TOADS segmentation and the Brainweb ground truth for both lesions and structures. Fig. 6 also investigates the effect of changing the inhomogeneity on the performance of the method.

Table 1.

Dice similarity coefficients for Brainweb data set with variable noise (20% inhomogeneity).

Noise	Tissues			Structures*
	WM	GM	CSF	WM-CR	GM-CR	CBS	GM-CB	Sub-cortical	Vent	Lesion
1%	0.934	0.917	0.899	0.944	0.919	0.764	0.879	0.756	0.885	0.823
3%	0.927	0.912	0.900	0.937	0.913	0.758	0.877	0.743	0.887	0.812
5%	0.918	0.901	0.898	0.928	0.904	0.746	0.861	0.736	0.885	0.792
7%	0.905	0.889	0.893	0.915	0.891	0.735	0.861	0.720	0.883	0.729
Mean	0.921	0.905	0.898	0.931	0.907	0.751	0.870	0.739	0.885	0.789
Std. Dev.	0.012	0.012	0.003	0.013	0.012	0.013	0.007	0.015	0.002	0.042
Healthy brain	0.919	0.906	0.903	0.936	0.902	0.705	0.842	0.809	0.851	-

^*Cerebrum-GM, cerebellum-GM, cerebrum-WM, and ventricles are denoted as GM-CR, GM-CL, WM-CR, and Vent, respectively. Brainstem grouped with cerebellum-WM is denoted by CBS and putamen, and thalamus and caudate are presented as Sub-cortical.

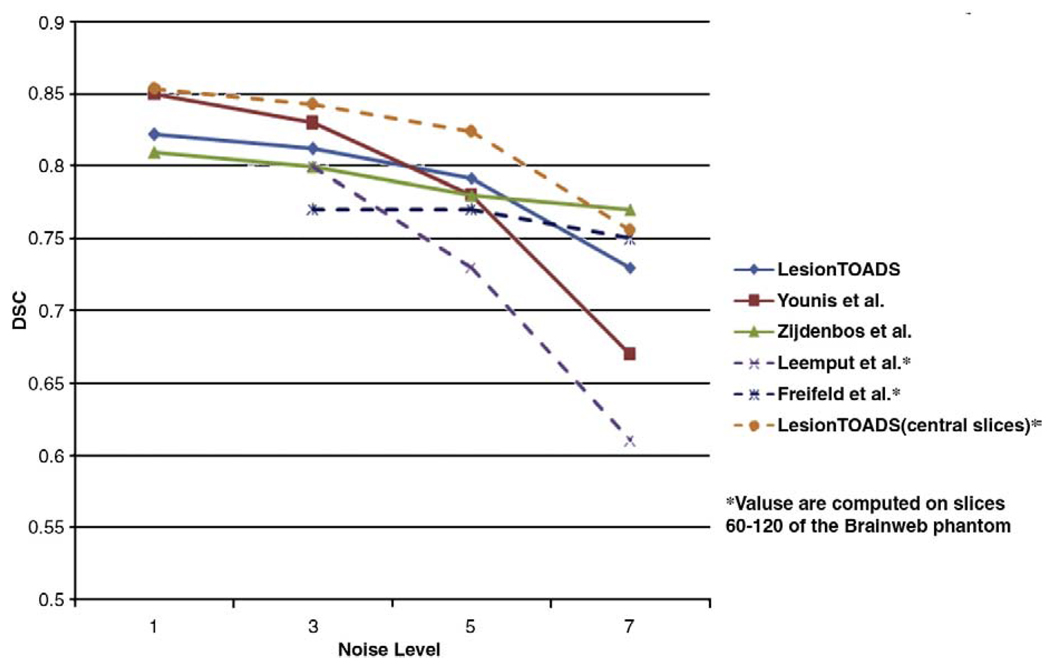
Fig. 14.

Dice similarity coefficients for lesion segmentation of different methods on the Brainweb phantom with 3% noise.

Fig. 6.

Dice similarity coefficient for CSF, WM, GM, and lesions in different levels of noise and inhomogeneity.

To evaluate the performance of Lesion-TOADS with respect to lesion segmentation, we also computed three other measures for lesions: the false positive ratio $\left(\mathit{\text{FP}}=\frac{|\mathit{\text{Seg}}|-|\mathit{\text{Seg}}\cap \mathit{\text{Ref}}|}{|\mathit{\text{Ref}}|}\right)$, the true positive ratio $\left(\mathit{\text{TP}}=\frac{|\mathit{\text{Seg}}\cap \mathit{\text{Ref}}|}{|\mathit{\text{Ref}}|}\right)$, and the volume difference $(\mathit{\text{VD}}=|1-\frac{|\mathit{\text{Seg}}|}{|\mathit{\text{Ref}}|}|)$, as reported in Table 2.

Table 2.

Dice similarity coefficient, false positive ratio, true positive ratio, and volume difference for lesions.

Noise	DSC	FP	TP	VD
1%	0.822	0.241	0.867	0.109
3%	0.812	0.256	0.859	0.115
5%	0.792	0.265	0.830	0.095
7%	0.729	0.421	0.816	0.236
Average	0.789	0.296	0.843	0.139
Std. Dev.	0.042	0.084	0.024	0.065

Fig. 7 and fig 8 show the membership functions for different structures as well as the hard segmentation of a phantom with 3% level of noise which is the default noise level of the Brainweb phantom and is considered representative of the noise level in most anatomical MR images. The former shows a slice without any lesions while the latter shows a slice possessing lesions.

Fig. 7.

Segmentation example for the Brainweb phantom with 3% noise and 20% inhomogeneity (this particular slice does not contain lesions). From left to right, top to bottom: T1, T2, true segmentation, computed segmentation, membership functions for ventricles, caudate, putamen, thalamus, cerebral GM, and cerebral WM.

Fig. 8.

Segmentation example for the Brainweb phantom with 3% noise and 20% inhomogeneity. From left to right, top to bottom: T1, T2, true segmentation, computed segmentation, true segmentation of lesions, computed segmentation of lesions, membership function for CSF, ventricles, cerebral GM, and cerebral WM.

To measure the capability of Lesion-TOADS on the segmentation of healthy brains, we used Lesion-TOADS to segment the same data set from the phantom without lesions (3% noise, 20% inhomogeneity). A very small fraction of voxels were falsely classified as lesions (0.038% of the total brain volume) while the segmentation of other structures still had high overlap values (see last row of Table 1). These results show the ability of Lesion-TOADS to simultaneously segment MS lesions and other tissues and its robustness to noise and field inhomogeneity on both brains with MS lesions and healthy brains.

Real images

We also applied Lesion-TOADS to a data set of 10 real MR images acquired from MS patients. T1-MPRAGE images (TR = 10 ms; TE = 6 ms; flipping angle α = 8°; in-plane resolution=0.828 mm × 0.828 mm; slice thickness = 1.1 mm) and FLAIR images (TR = 11000 ms; TE = 68 ms; TI = 2800 ms; in-plane resolution = 0.83 mm × 0.83 mm; slice thickness = 2.2 mm) were acquired on a 3 Tesla MRI scanner (Philips Medical Systems, Best, The Netherlands). The imaging protocols were approved by local institutional review boards.

A delineation from a semi-automated, expert-guided segmentation technique was used as the reference standard. In this method, an expert selected the region that contains lesions, then a region growing technique using a local thresholding procedure was applied. The threshold for the region growing was adjusted to the satisfaction of the expert based on the FLAIR image.

Before applying Lesion-TOADS to this data set, we registered the T1 image to the FLAIR image using a mutual information registration algorithm within the MIPAV software package. The brain was then extracted using an automated skull stripping algorithm (Carass et al., 2007) applied to the T1 image, and the resulting mask was applied to the FLAIR image.

We evaluated the performance of Lesion-TOADS on real MR images in terms of both spatial and volumetric agreement. To measure the spatial accuracy of the method, we computed the DSC and TP for all subjects resulting in an average of 0.633 and 0.712, respectively, showing good spatial agreement between Lesion-TOADS results and the reference standard. We also performed a correlation analysis between the total lesion volume segmented automatically and the reference standard lesion volume. A Pearson correlation coefficient of 0.93 (p<0.0001) was achieved, demonstrating very good volumetric agreement between the segmentation of Lesion-TOADS and the reference standard. Fig. 9 shows the plot of the total lesion volume segmented by lesion-TOADS versus the reference standard lesion volume for these subjects.

Fig. 9.

Plot of total lesion volume segmented by Lesion-TOADS versus the reference standard (r = 0.93). Volumes are in mm³.

Fig. 10 shows the result of the lesion segmentation and hard classification of structures on one of the subjects by Lesion-TOADS. This figure demonstrates the ability of the method to segment the lesions while segmenting the other brain tissues as well. Fig. 11 shows a 3D surface representation of sub-cortical structures and lesions, generated from the results of our method. Note how the 3D rendering outlines the global structure of the lesions.

Fig. 10.

Result of Lesion-TOADS segmentation on one of the MS subjects.

Fig. 11.

Lesion-TOADS segmentation results. A 3D surface reconstruction of different structures. Lesions are shown in yellow, ventricles are shown in blue, and sub-cortical structures are shown in red, green, and purple. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Application to cortical reconstruction

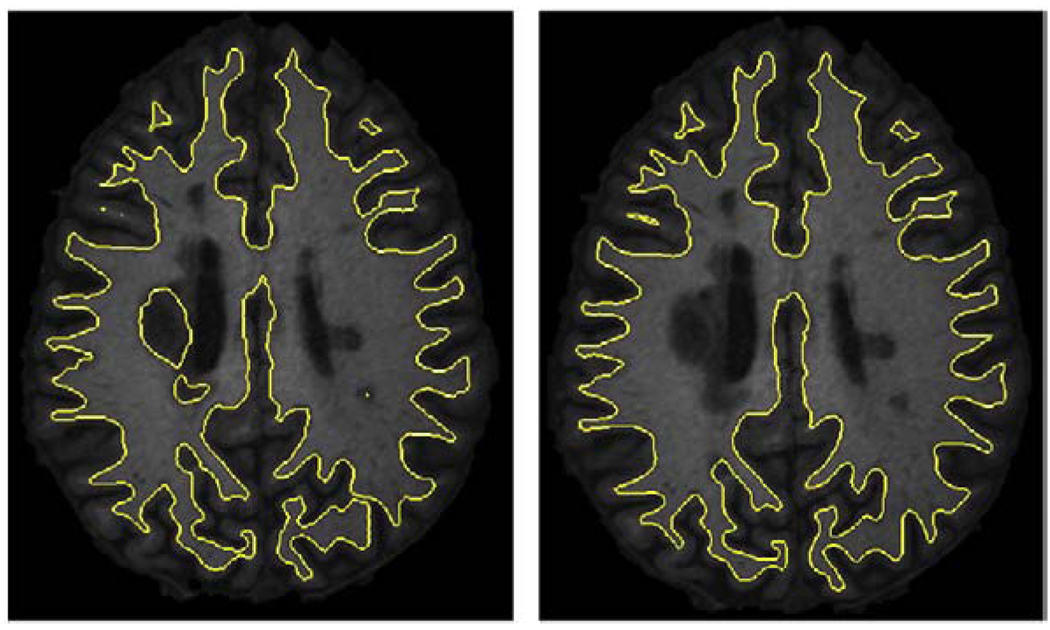
Cortical reconstruction plays an important role in measuring thickness and other morphometric analyses. However, most reconstruction methods assume a healthy brain, and the presence of the WM lesions can lead to inaccurate representation of the cortex. As lesions and WM are grouped together in our method, it can be readily incorporated into cortical reconstruction methods. Our group has been involved in the development of a cortical reconstruction approach known as Cortical Reconstruction Using Implicit Surface Evolution (CRUISE) (Han et al., 2004). CRUISE is composed of three major steps. First, the brain volume is extracted from the MR image. Next, TOADS segments the brain into its structures. Third, the inner, central, and pial surfaces are generated by the means of a topology-preserving geometric deformable model (TGDM). Lesion-TOADS may be directly used to replace the TOADS segmentation step in this pipeline. In Fig. 12, a comparison between the result of CRUISE with TOADS and those of CRUISE with integration of Lesion-TOADS is shown. This figure shows an axial cut from the inner surface superimposed on the corresponding slice from the T1 image. The method based on Lesion-TOADS avoids the wrong representation of the cortex near the lesions, while it shows the same performance on the other areas. Fig. 13 shows the thickness analysis of the cortex of a MS patient's brain with an average thickness of 3.1 mm.

Fig. 12.

Comparison of inner surfaces from CRUISE: left image shows the surface constructed with TOADS while right one shows the result of CRUISE by means of Lesion-TOADS.

Fig. 13.

The cortical thickness of a MS patient. The thickness value is mapped on the pial surface and represented in millimeters.

Discussion

Four different measures were employed to evaluate the algorithm's performance on the Brainweb simulated data. In volumetric applications, a low VD is desirable; however, it can not be interpreted by itself as it does not contain any information about the spatial correspondence of different segmentations. The DSC takes into account both volume and spatial correspondence. The low percentage of VD combined with high value of DSC suggests that the method would be a reliable method for lesion load studies. Moreover, high values of TP and reasonably low values of FP reflect a reasonably high accuracy of the method. Note that in subjects with a very small lesion load, FP is very sensitive and changes substantially for a small number of voxels.

We compared the results of Lesion-TOADS on the Brainweb phantom against several methods on both lesion segmentation (Fig. 14) and tissue classification (Table 3). As can be seen, Lesion-TOADS is comparable to these methods with the benefit of obtaining separate sub-cortical structures and preserving topology all in one algorithm. Moreover, none of these techniques except (Leemput et al., 2001) simultaneously compensates for RF field inhomogeneities. Although the method by Younis et al. (2007) achieves better lesion delineation in low noise levels, it is not as robust as Lesion-TOADS to noise. Also, this method was trained using the 0% noise data set, which is usually not available for real data sets. Note also that in our algorithm, the detection of lesions would be improved if a FLAIR acquisition had been available, but the results highlight the relative insensitivity of Lesion-TOADS to input sequences.

Table 3.

Comparison of Dice similarity coefficients for the tissue classification between different methods on the Brainweb phantom with 3% noise.

Method	CSF	WM	GM
Lesion-TOADS	0.90	0.93	0.91
Younis et al. (2007)	0.94	0.91	0.89
Leemput et al. (2001)*	0.89	0.94	0.95
Freifeld et al. (2007)**	0.91	0.93	0.95
Aït-Ali et al. (2005)	0.58	0.90	0.95

^*Values reported in a diagram, so these are approximate values.

^**Overlap values for Van Leemput method are not reported by Leemput et al. (2001), but Freifeld et al. reported overlap values based on the implementation of this method in EMS software package (www.medicalimagecomputing.com).

Our method is less robust to noise for the segmentation of lesions in comparison to that of other structures, because of two main factors. First, the parameters were tuned for lower noise cases that are more common in real MR images. For high levels of noise a different set of parameters would be required, but we chose to fix all parameters in our experiments so as to study the algorithm performance without any retuning. Second, lesions are grouped with white matter in the topological framework and are not considered as a separate object, which limits the ability of the topology constraints to reduce the effects of noise. Note also that the DSC is more sensitive for structures with smaller volumes. This is also evident in Fig. 6, as more variability is seen in the DSC versus inhomogeneity for lesions in comparison to other structures. Note, however, that the lesion segmentation is still more robust to noise than some other competing methods, as shown in Fig. 14. The performance of the lesion segmentation is slightly reduced in the absence of field inhomogeneities, as the method still estimates a small but non-zero field.

These problems have little impact on the performance of Lesion-TOADS on real data sets, where the noise levels are often more reasonable. As shown in Table 4, the segmentation of lesions with Lesion-TOADS on real data is comparable to that of other recently reported methods. The methods presented by Wu et al. (2006) and Zijdenbos et al. (2002) are supervised methods, which make them dependent on the particular input pulse sequences by which the classifier is trained while as shown in Section 3, Lesion-TOADS performs well on both T1/T2 and T1/FLAIR combination of input images. The intensity profile of lesions may vary based on the acquisition parameters, and supervised methods may need to be retrained. In addition, the other methods listed neither segment the sub-cortical structures nor preserve the topology of the brain. Fig. 9 shows that Lesion-TOADS tends to underestimate the lesion volume when compared against the semi-automated approach. Lesion boundaries are rarely clearly defined and the final decision of what is lesion and what is not is highly subjective. It is therefore not uncommon to encounter some bias when comparing two different approaches. In a visual comparison of the two results by neuroradiologists, the Lesion-TOADS results were considered to be just as acceptable when compared to the semi-automated results.

Table 4.

Comparison of Dice similarity coefficients for the lesion segmentation between different methods on different real data sets.

Method	DSC
Lesion-TOADS	0.63
Wu et al. (2006)	0.70
Harmouche et al. (2006)	0.609
Zijdenbos et al. (2002)*	0.60
García-Lorenzo et al. (2008)	0.55
Aït-Ali et al. (2005)	0.52
Leemput et al. (2001)	0.51

^*This is the average of the reported DSCs computed between the result of this method and seven manual segmentations.

The comparison between different segmentation methods on the real data sets always suffers from the fact that unlike the simulated phantoms, there is no global real data set and ground truth for comparison. However, at the recent 2008 Medical Imaging Computing and Computer Assisted Intervention (MICCAI 08) segmentation challenge (Styner et al., 2008), a thorough comparison between different lesion segmentation methods was performed on the same MS data sets manually segmented by two raters. The challenge included data sets from two different studies, one provided by the University of North Carolina with 10 patients and the other provided by the Children's Hospital of Boston with 14 cases. In both studies, T1, T2, and FLAIR acquisitions with 0.5 mm isotropic resolution were available. The methods were evaluated based on four metrics: VD (as described in Experimental Results), average distance (AD) which is a symmetric average surface distance to the expert rater segmentation, TP (as described in Experimental Results), and the false negative ratio $\left(\mathit{\text{FN}}=\frac{|\mathit{\text{Seg}}|-|\mathit{\text{Seg}}|\cap |\mathit{\text{Ref}}|}{|\mathit{\text{Seg}}|}\right)$. All metrics were scored in relation to how the expert raters compare to one another. A score of 90 for any of the metric would equal performance akin an expert rater. In addition to 24 subjects provided before the workshop, seven subjects were provided on the workshop day for an onsite competition. The average score on all metrics and all data sets were used to compare the performance of the different methods. An earlier development version of Lesion-TOADS (Shiee et al., 2008b) ranked third among nine methods with an overall score of 75, which was very close to the scores of the first and second ranked methods (77 and 76, respectively). Among all methods, only Lesion-TOADS provided an anatomically consistent segmentation that includes sub-cortical structures in addition to a lesion segmentation.

Conclusions and future work

In this paper, we presented a new fully automatic segmentation technique for detecting WM MS lesions. The performance of the method has been evaluated on both simulated and real data and showed favorable performance with current lesion segmentation techniques. Preserving topology, which is a unique feature of Lesion-TOADS in comparison with the other techniques, has been of central interest in neuroimaging for applications ranging from computational anatomy to cortical reconstruction and mapping. Until now, these methods have focused on brains devoid of lesions and other structures that would alter the overall topology. In MS, brain atrophy has been observed in addition to the appearance of lesions. Lesion-TOADS will enable volumetric analysis, cortical thickness analysis, and diffeomorphic shape analysis in MS populations, potentially leading to new insights on the disease. We are conducting this technique in a joint study of MS lesions, cortical and sub-cortical volumes, and cortical thickness in MS patients. Although we only study WM MS lesions, this is a general framework to incorporate pathology embedded inside a specific tissue class into a topology-preserving framework. However, studying lesions that involve more than one structure in a topology-preserving framework remains an open problem. The method can also be used in aging and other studies in which WM lesions are present.

Several areas require further research. Black holes are a MS lesion sub-type that appear extremely hypointense on T1 images. This subtype is associated histopathologically with severe tissue destruction, including axonal loss in post-mortem studies (van Walderveen et al., 1998), showing the importance of its delineation in MS studies. Hyperintense areas on T2 and FLAIR images may correspond to all or only a portion of a black hole (Neema et al., 2007). This different intensity profile hinders complete segmentation of black holes as a separate lesion type with our current method.

In addition to more commonly described WM locations, MS lesions can also involve GM, and their occurrence in different regions of the GM has been reported in the literature (Trapp and Nave, 2008). However, GM lesions are less visible on conventional MRI sequences such as T2 (Kidd et al., 1999). FLAIR and double inversion recovery protocols improve the visibility of these type of MS lesions to some extent, but imaging protocols that reliably define such lesions are not yet established except perhaps in high field scanners (7T or higher). Currently, Lesion-TOADS is only capable of segmenting the juxtacortical lesions that are inside WM. Upon development of the imaging sequences that make the MS lesions inside the cortex visible, the introduced topology-preserving framework for WM MS lesions can be readily adapted and used for GM MS lesion segmentation. In our future work, we will seek to demonstrate the ability of Lesion-TOADS in the segmentation of MS lesions that are inside GM.