Covariance-regularized regression and classification for high-dimensional problems

Summary

In recent years, many methods have been developed for regression in high-dimensional settings. We propose covariance-regularized regression, a family of methods that use a shrunken estimate of the inverse covariance matrix of the features in order to achieve superior prediction. An estimate of the inverse covariance matrix is obtained by maximizing its log likelihood, under a multivariate normal model, subject to a constraint on its elements; this estimate is then used to estimate coefficients for the regression of the response onto the features. We show that ridge regression, the lasso, and the elastic net are special cases of covariance-regularized regression, and we demonstrate that certain previously unexplored forms of covariance-regularized regression can outperform existing methods in a range of situations. The covariance-regularized regression framework is extended to generalized linear models and linear discriminant analysis, and is used to analyze gene expression data sets with multiple class and survival outcomes.

1. Introduction

In high-dimensional regression problems, where p, the number of features, is nearly as large as, or larger than, n, the number of observations, ordinary least squares regression does not provide a satisfactory solution. A remedy for the shortcomings of least squares is to modify the sum of squared errors criterion used to estimate the regression coefficients, using penalties that are based on the magnitudes of the coefficients:

$$\widehat{\beta }=arg\underset{\beta }{min}\mid \mid \mathbf{y}-\mathbf{X}\beta \mid {\mid }^2+{\lambda }_1\mid \mid \beta \mid {\mid }^{p_1}+{\lambda }_2\mid \mid \beta \mid {\mid }^{p_2}$$ (1)

(Here, the notation ||β||^s is used to indicate ${\sum }_{i=1}^p\mid {\beta }_i{\mid }^s$.) Many popular regularization methods fall into this framework. For instance, when λ₂ = 0, p₁ = 0 gives best subset selection, p₁ = 2 gives ridge regression (Hoerl & Kennard 1970), and p₁ = 1 gives the lasso (Tibshirani 1996). More generally, for λ₂ = 0 and p₁ ≥ 0, the above equation defines the bridge estimators (Frank & Friedman 1993). Equation 1 defines the elastic net (up to a scaling) in the case that p₁ = 1 and p₂ = 2 (Zou & Hastie 2005). In this paper, we present a new approach to regularizing linear regression that involves applying a penalty not to the sum of squared errors, but rather to the log likelihood of the inverse covariance matrix under a multivariate normal model.

The least squares solution is β̂ = (X^TX)⁻¹X^Ty. In multivariate normal theory, the entries of (X^TX)⁻¹ that equal zero correspond to pairs of variables that have no partial correlation; in other words, pairs of variables that are conditionally independent, given all of the other features in the data. Non-zero entries of (X^TX)⁻¹ correspond to nonzero partial correlations. One way to perform regularization of least squares regression is to shrink the matrix (X^TX)⁻¹; in fact, this is done by ridge regression, since the ridge solution can be written as β̂_ridge = (X^TX + λI)⁻¹X^Ty. Here, we propose a more general approach to shrinkage of the inverse covariance matrix. Our method involves estimating a regularized inverse covariance matrix by maximizing its log likelihood under a multivariate normal model, subject to a constraint on its elements. In doing this, we attempt to distinguish between variables that truly are partially correlated with each other and variables that in fact have zero partial correlation. We then use this regularized inverse covariance matrix in order to obtain regularized regression coefficients. We call the class of regression methods defined by this procedure the scout.

In Section 2, we present the scout criteria and explain the method in greater detail. We also discuss connections between the scout and pre-existing regression methods. In particular, we show that ridge regression, the lasso, and the elastic net are special cases of the scout. In addition, we present some specific members of the scout class that perform well relative to pre-existing methods in a variety of situations. In Sections 3, 4, and 5, we demonstrate the use of these methods in regression, classification, and generalized linear model settings on simulated data and on a number of gene expression data sets.

2. The Scout Method

2.1. The General Scout Family

Let X = (x₁,…, x_p) denote an n × p matrix of data, where n is the number of observations and p the number of features. Let y denote a vector of length n, containing a response value for each observation. Assume that the columns of X are standardized, and that y is centered. We can create a matrix X̃ = (X y), which has dimension n × (p+1). If we assume that X̃ is generated from the model N(0, Σ), then we can find the maximum likelihood estimator of the population inverse covariance matrix Σ⁻¹ by maximizing

$$log(det{\mathbf{\sum }}^{-1})-\text{tr}(\mathbf{S}{\mathbf{\sum }}^{-1})$$ (2)

where $\mathbf{S}=\left(\begin{array}{cc}{\mathbf{S}}_{\mathbf{xx}}& {\mathbf{S}}_{\mathbf{xy}}\\ {{\mathbf{S}}_{\mathbf{xy}}}^T& S_{yy}\end{array}\right)$ is the empirical covariance matrix of X̃. Assume for a moment that S is invertible. Then, the maximum likelihood estimator for Σ⁻¹ is S⁻¹ (we use the fact that $\frac{d}{d\mathbf{W}}$ log det W = W^-1 for a symmetric positive definite matrix W). Let $\mathbf{\Theta }=\left(\begin{array}{cc}{\mathbf{\Theta }}_{\mathbf{xx}}& {\mathbf{\Theta }}_{\mathbf{xy}}\\ {{\mathbf{\Theta }}_{\mathbf{xy}}}^T& {\mathrm{\Theta }}_{yy}\end{array}\right)$ denote a symmetric estimate of Σ⁻¹. The problem of regressing y onto X is closely related to the problem of estimating Σ⁻¹, since the least squares coefficients for the regression equal $-\frac{{\mathbf{\Theta }}_{\mathbf{xy}}}{{\mathrm{\Theta }}_{yy}}$ for Θ = S⁻¹ (this follows from the partitioned inverse formula). If p > n, then some type of regularization is needed in order to estimate the regression coefficients, since S is not invertible. Even if p < n, we may want to shrink the least squares coefficients in some way in order to achieve superior prediction. The connection between estimation of Θ and estimation of the least squares coefficients suggests the possibility that rather than shrinking the coefficients β by applying a penalty to the sum of squared errors for the regression of y onto X, as is done in e.g. ridge regression or the lasso, we can obtain shrunken β estimates through maximization of the penalized log likelihood of the inverse covariance matrix Σ⁻¹.

To do this, one could estimate Σ⁻¹ as Θ that maximizes

$$log(det\mathbf{\Theta })-\text{tr}(\mathbf{S}\mathbf{\Theta })-J(\mathbf{\Theta })$$ (3)

where J(Θ) is a penalty function. For example, J(Θ) = ||Θ||^p denotes the sum of absolute values of the elements of Θ if p = 1, and it denotes the sum of squared elements of Θ if p = 2. Our regression coefficients would then be given by the formula $\beta =-\frac{{\mathbf{\Theta }}_{\mathbf{xy}}}{{\mathrm{\Theta }}_{yy}}$. However, recall that if X̃ ~ N (0, Σ), then the ij element of Θ gives the correlation of x̃_i with x̃_j, conditional on all of the other variables in X̃. Note that y is included in X̃. So it does not make sense to regularize the elements of Θ as presented above, because we really care about the partial correlations of pairs of variables given the other variables, as opposed to the partial correlations of pairs of variables given the other variables and the response.

For these reasons, rather than obtaining an estimate of Σ⁻¹ by maximizing the penalized log likelihood in Equation 3, we estimate it via a two-stage maximization, given in the following algorithm:

The Scout Procedure for General Penalty Functions

1. Compute Θ̂_xx, which maximizes

   $$log(det{\mathbf{\Theta }}_{\mathbf{xx}})-\text{tr}({\mathbf{S}}_{\mathbf{xx}}{\mathbf{\Theta }}_{\mathbf{xx}})-J_1({\mathbf{\Theta }}_{\mathbf{xx}})$$ (4)

2. Compute Θ̂, which maximizes

   $$log(det\mathbf{\Theta })-\text{tr}(\mathbf{S}\mathbf{\Theta })-J_2(\mathbf{\Theta })$$ (5)

   where the top left p × p submatrix of Θ̂ is constrained to equal Θ̂_xx, the solution to Step 1.

3. Compute β̂, defined by $\widehat{\beta }=-\frac{{\widehat{\mathbf{\Theta }}}_{\mathbf{xy}}}{{\widehat{\mathrm{\Theta }}}_{yy}}$.

4. Compute β̂* = cβ̂, where c is the coefficient for the regression of y onto Xβ̂.

β̂* denotes the regularized coefficients obtained using this new method. Step 1 of the Scout Procedure involves obtaining shrunken estimates of (Σ_xx)⁻¹ in order to smooth our estimates of which variables are conditionally independent. Step 2 involves obtaining shrunken estimates of Σ⁻¹, conditional on (Σ⁻¹)_xx = Θ̂_xx, the estimate obtained in Step 1. Thus, we obtain regularized estimates of which predictors are dependent on y, given all of the other predictors. The scaling in the last step is performed because it has been found, empirically, to improve performance.

By penalizing the entries of the inverse covariance matrix of the predictors in Step 1 of the Scout Procedure, we are attempting to distinguish between pairs of variables that truly are conditionally dependent, and pairs of variables that appear to be conditionally dependent due only to chance. We are searching, or scouting, for variables that truly are correlated with each other, conditional on all of the other variables. Our hope is that sets of variables that truly are conditionally dependent will also be related to the response. In the context of a microarray experiment, where the variables are genes and the response is some clinical outcome, this assumption is reasonable: we seek genes that are part of a pathway related to the response. One expects that such genes will also be conditionally dependent. In Step 2, we shrink our estimates of the partial correlation between each predictor and the response, given the shrunken partial correlations between the predictors that we estimated in Step 1. In contrast to ordinary least squares regression, which uses the inverse of the empirical covariance matrix to compute regression coefficients, we jointly model the relationship that the p predictors have with each other and with the response in order to obtain shrunken regression coefficients.

We define the scout family of estimated coefficients for the regression of y onto X as the solutions β̂* obtained in Step 4 of the Scout Procedure. We refer to the penalized log likelihoods in Steps 1 and 2 of the Scout Procedure as the first and second scout criteria.

In the rest of the paper, when we discuss properties of the scout, for ease of notation we will ignore the scale factor in Step 4 of the Scout Procedure. For instance, if we claim that two procedures yield the same regression coefficients, we more specifically mean that the regression coefficients are the same up to scaling by a constant factor.

Least squares, the elastic net, the lasso, and ridge regression result from the scout procedure with appropriate choices of J₁ and J₂ (up to a scaling by a constant). Details are in Table 1. The first two results can be shown directly by differentiating the scout criteria, and the others follow from Equation 11 in Section 2.4.

Table 1.

Special cases of the scout.

J1(Θxx)	J2(Θ)	Method
0	0	Least Squares
tr(Θxx)	0	Ridge Regression
tr(Θxx)	||Θ||1	Elastic Net
0	||Θ||1	Lasso
0	||Θ||2	Ridge Regression

2.2. L_p Penalties

Throughout the remainder of this paper, we will exclusively be interested in the case that J₁(Θ) = λ₁||Θ||^p₁ and $J_2(\mathbf{\Theta })=\frac{{\lambda }_2}{2}\mid \mid \mathbf{\Theta }\mid {\mid }^{p_2}$, where the norm is taken elementwise over the entries of Θ, and where λ₁, λ₂ ≥ 0. For ease of notation, Scout(p₁, p₂) will refer to the solution to the scout criterion with J₁ and J₂ as just mentioned. If λ₂ = 0, then this will be indicated by Scout(p₁, ·), and if λ₁ = 0, then this will be indicated by Scout(·, p₂). Therefore, in the rest of this paper, the Scout Procedure will be as follows:

The Scout Procedure with L_p Penalties

1. Compute Θ̂_xx, which maximizes

   $$log(det{\mathbf{\Theta }}_{\mathbf{xx}})-\text{tr}({\mathbf{S}}_{\mathbf{xx}}{\mathbf{\Theta }}_{\mathbf{xx}})-{\lambda }_1\mid \mid {\mathbf{\Theta }}_{\mathbf{xx}}\mid {\mid }^{p_1}$$ (6)

2. Compute Θ̂, which maximizes

   $$log(det\mathbf{\Theta })-\text{tr}(\mathbf{S}\mathbf{\Theta })-\frac{{\lambda }_2}{2}\mid \mid \mathbf{\Theta }\mid {\mid }^{p_2}$$ (7)

   where the top left p × p submatrix of Θ̂ is constrained to equal Θ̂_xx, the solution to Step 1. Note that because of this constraint, the penalty really is only being applied to the last row and column of Θ̂.

3. Compute β̂, defined by $\widehat{\beta }=-\frac{{\widehat{\mathbf{\Theta }}}_{\mathbf{xy}}}{{\widehat{\mathrm{\Theta }}}_{yy}}$.

4. Compute β̂* = cβ̂, where c is the coefficient for the regression of y onto Xβ̂.

(Note that in Step 2, because the top left p × p submatrix of Θ̂ is fixed, the penalty on the top left p × p elements has no effect).

2.3. Simple Example

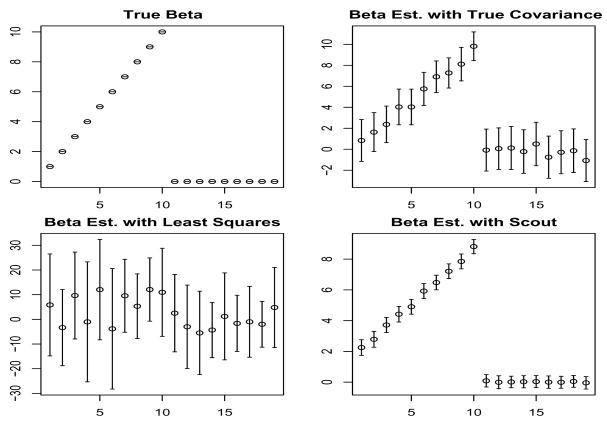
Here, we present a toy example in which n = 20 observations on p = 19 variables are generated under the model y = Xβ + ε, where β_j = j for j ≤ 10 and β_j = 0 for j > 10, and where ε ~ N (0, 25). In addition, the first 10 variables have correlation 0.5 with each other; the rest are uncorrelated.

Figure 1 shows the average over 500 simulations of the following four quantities: the true value of β, the least squares regression coefficients, the estimate Σ⁻¹Cov(X, y) where Σ is the true covariance matrix of X in the underlying model, and the Scout(1, ·) regression estimate. It is not surprising that least squares performs poorly in this situation, since N is barely larger than p. Scout(1, ·) performs extremely well; though it results in coefficient estimates that are slightly biased, they have much less variance than the estimates obtained using the true covariance matrix. This simple example demonstrates that benefits can result from the use of a shrunken estimate of the inverse covariance matrix.

Fig. 1.

Data were generated under a simple model; results shown are averaged over 500 simulations. Standard error bars and coefficient estimates are shown. Clockwise from the top left, panels show the true value of β, Σ⁻¹Cov(X, y), (X^TX)⁻¹X^Ty, and Scout (1,·).

2.4. Minimization of the Scout Criteria with L_p Penalties

If λ₁ = 0, then the minimum of the first scout criterion is given by (S_xx)⁻¹ (if S_xx is invertible). In the case that λ₁ > 0 and p₁ = 1, minimization of the first scout criterion has been studied extensively; see e.g. Meinshausen & Bühlmann (2006). The solution can be found via the “graphical lasso”, an efficient algorithm given by Banerjee et al. (2008) and Friedman et al. (2008b) that involves iteratively regressing one row of the estimated covariance matrix onto the others, subject to an L₁ constraint, in order to update the estimate for that row.

If λ₁ > 0 and p₁ = 2, the solution to Step 1 of the Scout Procedure is even easier. We want to find θ_xx that maximizes

$$log(det{\mathbf{\Theta }}_{\mathbf{xx}})-\text{tr}({\mathbf{S}}_{\mathbf{xx}}{\mathbf{\Theta }}_{\mathbf{xx}})-\lambda \mid \mid {\mathbf{\Theta }}_{\mathbf{xx}}\mid {\mid }^2$$ (8)

Differentiating with respect to θ_xx, we see that the maximum solves

$${{\mathbf{\Theta }}_{\mathbf{xx}}}^{-1}-2\lambda {\mathbf{\Theta }}_{\mathbf{xx}}={\mathbf{S}}_{\mathbf{xx}}$$ (9)

This equation implies that θ_xx and S_xx share the same eigenvectors. Letting λ_i denote the i^th eigenvalue of θ_xx and letting s_i denote the i^th eigenvalue of S_xx, it is clear that

$$\frac{1}{{\theta }_i}-2\lambda {\theta }_i=s_i$$ (10)

We can easily solve for λ_i, and can therefore solve the first scout criterion exactly in the case p₁ = 2, in essentially just the computational cost of obtaining the eigenvalues of S_xx.

It turns out that if p₂ = 1 or p₂ = 2, then it is not necessary to minimize the second scout criterion directly, as there is an easier alternative:

Claim 1

For p₂ ∈ {1, 2}, the solution to Step 3 of the Scout Procedure is equal to the solution to the following, up to scaling by a constant:

$$\widehat{\beta }=arg\underset{\beta }{min}\{{\beta }^T{\widehat{\mathbf{\sum }}}_{\mathbf{xx}}\beta -2{{\mathbf{S}}_{\mathbf{xy}}}^T\beta +{\lambda }_2\mid \mid \beta \mid {\mid }^{p_2}\}$$ (11)

where Σ̂_xx is the inverse of the solution to Step 1 of the Scout Procedure.

(The proof of Claim 1 is in Section 8.1.1 in the Appendix.) Therefore, we can replace Steps 2 and 3 of the Scout Procedure with an L_p2 regression. It is trivial to show that if λ₂ = 0 in the Scout Procedure, then the scout solution is given by β̂ = (Σ̂_xx)⁻¹S_xy. It also follows that if λ₁ = 0, then the cases λ₂ = 0, p₂ = 1, and p₂ = 2 correspond to ordinary least squares regression (if the empirical covariance matrix is invertible), the lasso, and ridge regression, respectively.

In addition, we will show in Section 2.5.1 that if p₁ = 2 and p₂ = 1, then the scout can be re-written as an elastic net problem with slightly different data; therefore, fast algorithms for solving the elastic net (Friedman et al. 2008a) can be used to solve Scout(2, 1). The methods for minimizing the scout criteria are summarized in Table 2.

Table 2.

Minimization of the scout criteria: special cases. The scout criteria can be easily minimized if λ₁ = 0 or p₁ ∈ {1, 2}, and if λ₂ = 0 or p₂ ∈ {1, 2}.

	λ2 = 0	p2 = 1	p2 = 2
λ1 = 0	Least Squares	L1 Regression	L2 Regression
p1 = 1	Graphical Lasso	Graphical Lasso + L1 Reg.	Graphical Lasso + L2 Reg.
p1 = 2	Eigenvalue Problem	Elastic Net	Eigenvalue Problem + L2 Reg.

We compared computation times for Scout(2, ·), Scout(1, ·), Scout(2, 1), and Scout(1, 1) on an example with n = 100, λ₂ = λ₁ = 0.2, and X dense. All timings were carried out on a Intel Xeon 2.80 GHz processor. Table 3 shows the number of CPU seconds required for each of these methods for a range of values of p. For all methods, after the scout coefficients have been estimated for a given set of parameter values, estimation for different parameter values is faster due to a warm start (when p₁ = 1) or because the eigen decomposition has already been computed (when p₁ = 2).

Table 3.

Timing comparisons for minimization of the scout criteria. The numbers of CPU seconds required to run four versions of the scout are shown, for λ₁ = λ₂ = 0.2, n = 100, X dense, and various values of p.

p	Scout(1, ·)	Scout(1, 1)	Scout(2, ·)	Scout(2, 1)
500	1.685	1.700	0.034	0.072
1000	22.432	22.504	0.083	0.239
2000	241.289	241.483	0.260	0.466

2.5. Properties of the Scout

In this section, for ease of notation, we will consider an equivalent form of the Scout Procedure obtained by replacing S_xx with X^T X and S_xy with X^T y.

2.5.1. Similarities between Scout, Ridge Regression, and the Elastic Net

Let ${\mathbf{U}}_{n\times p}{\mathbf{D}}_{p\times p}{\mathbf{V}}_{p\times p}^T$ denote the singular value decomposition of X with d_i the i^th diagonal element of D and d₁ ≥ d₂ ≥ … ≥ d_r > d_r+1 = … = d_p = 0, where r = rank(X) ≤ min(n, p). Consider Scout(2, p₂). As previously discussed, the first step in the Scout Procedure corresponds to finding θ that solves

$${\mathbf{\Theta }}^{-1}-2{\lambda }_1\mathbf{\Theta }={\mathbf{X}}^T\mathbf{X}$$ (12)

Since θ and X^TX therefore share the same eigenvectors, it follows that θ⁻¹ = V(D² + D̃²)V^T where D̃² is a p×p diagonal matrix with i^th diagonal entry equal to $\frac{1}{2}(-{d_i}^2+\sqrt{{d_i}^4+8{\lambda }_1})$. It is not difficult to see that ridge regression, Scout(2, ·), and Scout(2, 2) result in similar regression coefficients:

$$\begin{array}{l}{\widehat{\beta }}_{rr}={(\mathbf{V}({\mathbf{D}}^2+c\mathbf{I}){\mathbf{V}}^T)}^{-1}{\mathbf{X}}^T\mathbf{y}\\ {\widehat{\beta }}_{\mathit{scout}(2,·)}={(\mathbf{V}({\mathbf{D}}^2+{\stackrel{\sim }{\mathbf{D}}}^2){\mathbf{V}}^T)}^{-1}{\mathbf{X}}^T\mathbf{y}\\ {\widehat{\beta }}_{\mathit{scout}(2,2)}={(\mathbf{V}({\mathbf{D}}^2+{\stackrel{\sim }{\mathbf{D}}}^2+{\lambda }_2\mathbf{I}){\mathbf{V}}^T)}^{-1}{\mathbf{X}}^T\mathbf{y}\end{array}$$ (13)

Therefore, while ridge regression simply adds a constant to the diagonal elements of D in the least squares solution, Scout(2, ·) instead adds a function that is monotone decreasing in the value of the diagonal element. (The consequences of this alternative shrinkage are explored under a latent variable model in Section 2.6). Scout(2, 2) is a compromise between Scout(2, ·) and ridge regression.

In addition, we note that the solutions to the naive elastic net and Scout(2, 1) are quite similar:

$$\begin{array}{l}{\widehat{\beta }}_{\mathit{enet}}=arg\underset{\beta }{min}{\beta }^T\mathbf{V}({\mathbf{D}}^2+c\mathbf{I}){\mathbf{V}}^T\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+{\lambda }_2\mid \mid \beta \mid {\mid }^1\\ {\widehat{\beta }}_{\mathit{scout}(2,1)}=arg\underset{\beta }{min}{\beta }^T\mathbf{V}({\mathbf{D}}^2+{\stackrel{\sim }{\mathbf{D}}}^2){\mathbf{V}}^T\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+{\lambda }_2\mid \mid \beta \mid {\mid }^1\end{array}$$ (14)

In fact, both solutions can be re-written:

$$\begin{array}{l}{\widehat{\beta }}_{\mathit{enet}}=arg\underset{\beta }{min}{\beta }^T{\mathbf{X}}^T\mathbf{X}\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+c\mid \mid \beta \mid {\mid }^2+{\lambda }_2\mid \mid \beta \mid {\mid }^1\\ {\widehat{\beta }}_{\mathit{scout}(2,1)}=arg\underset{\beta }{min}{\beta }^T\mathbf{V}({\widehat{\mathbf{D}}}^2+\sqrt{2{\lambda }_1}\mathbf{I}){\mathbf{V}}^T\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+{\lambda }_2\mid \mid \beta \mid {\mid }^1\\ =arg\underset{\beta }{min}{\beta }^T\mathbf{V}{\widehat{\mathbf{D}}}^2{\mathbf{V}}^T\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+\sqrt{2{\lambda }_1}\mid \mid \beta \mid {\mid }^2+{\lambda }_2\mid \mid \beta \mid {\mid }^1\\ =arg\underset{\beta }{min}{\beta }^T{\mathbf{X}}^{\ast T}{\mathbf{X}}^{\ast }\beta -2{\beta }^T{\mathbf{X}}^{\ast T}{\mathbf{y}}^{\ast }+\sqrt{2{\lambda }_1}\mid \mid \beta \mid {\mid }^2+{\lambda }_2\mid \mid \beta \mid {\mid }^1\end{array}$$ (15)

where D̂ is a diagonal matrix with diagonal elements $\frac{1}{2}(d_i^2+\sqrt{d_i^4+8{\lambda }_1})-\sqrt{2{\lambda }_1}$, X*= D̂_(r)V_(r)^T, ${\mathbf{y}}^{\ast }={\widehat{\mathbf{D}}}_{(\mathbf{r})}^{-1}{\mathbf{D}}_{(\mathbf{r})}{{\mathbf{U}}_{(\mathbf{r})}}^T\mathbf{y}$. D_(r) and D̂_(r) are the r × r submatrices of D and D̂ corresponding to non-zero diagonal elements, and U_(r) and V_(r) correspond to the first r columns of U and V. From Equation 15, it is clear that Scout(2, 1) solutions can be obtained using software for the elastic net on data X* (which has dimension no greater than the original data X) and y*. In addition, given the similarity between the elastic net and Scout(2, 1) solutions, it is not surprising that Scout(2, 1) shares some of the elastic net’s desirable properties, as is shown in Section 2.5.2.

2.5.2. Variable Grouping Effect

Zou & Hastie (2005) show that unlike the lasso, the elastic net and ridge regression have a variable grouping effect: correlated variables result in similar coefficients. The same is true of Scout(2, 1):

Claim 2

Assume that the predictors are standardized and that y is centered. Let ρ denote the correlation between x_i and x_j, and let β̂ denote the solution to Scout(2, 1). If sgn(β̂_i) = sgn(β̂_j), then the following holds:

$$\mid {\widehat{\beta }}_i-{\widehat{\beta }}_j\mid \le \sqrt{\frac{2(1-\rho )}{{\lambda }_1}}\mid \mid \mathbf{y}\mid \mid$$ (16)

The proof of Claim 2 is in Section 8.1.2 in the Appendix. Similar results hold for Scout(2, ·) and Scout(2, 2), without the assumptions about the signs of β̂_i and β̂_j.

2.5.3. Connections to Regression with Orthogonal Features

Assume that the features are standardized, and consider the scout criterion with p₁ = 1. For λ₁ sufficiently large, the solution θ̂_xx to the first scout criterion (Equation 6) is a diagonal matrix with diagonal elements $\frac{1}{{\lambda }_1+{\mathbf{x}}_i^T{\mathbf{x}}_i}$. (More specifically, if ${\lambda }_1\ge \mid {\mathbf{x}}_i^T{\mathbf{x}}_j\mid$ for all i ≠ j, then then the scout criterion with p₁ = 1 results in a diagonal matrix; see Banerjee et al. (2008) Theorem 4). Thus, if ${\widehat{\beta }}_i^{\ast }$ is the i^th component of the Scout(1, ·) solution, then ${\widehat{\beta }}_i^{\ast }=\frac{{\mathbf{x}}_i^T\mathbf{y}}{{\lambda }_1+1}$. If λ₂ > 0, then the resulting scout solutions with p₂ = 1 are given by a variation of the univariate soft thresholding formula for L₁ regression:

$${\widehat{\beta }}_i^{\ast }=\frac{1}{{\lambda }_1+1}sgn({\mathbf{x}}_i^T\mathbf{y})max(0,\mid {\mathbf{x}}_i^T\mathbf{y}\mid -\frac{{\lambda }_2}{2})$$ (17)

Similarly, if p₂ = 2, the resulting scout solutions are given by the following formula:

$${\widehat{\beta }}^{\ast }={(1+{\lambda }_1+{\lambda }_2)}^{-1}{\mathbf{X}}^T\mathbf{y}$$ (18)

Therefore, as the parameter λ₁ is increased, the solutions that are obtained range (up to a scaling) from the ordinary L_p2 multivariate regression solution to the regularized regression solution for orthonormal features.

2.6. An Underlying Latent Variable Model

Let X be a n × p matrix of n observations on p variables, and y a n × 1 vector of response values. Suppose that X and y are generated under the following latent variable model:

$$\begin{array}{l}\mathbf{X}=d_1{\mathbf{u}}_1{\mathbf{v}}_1^T+d_2{\mathbf{u}}_2{\mathbf{v}}_2^T\\ d_1,d_2>0\\ \mathbf{y}={\mathbf{u}}_1+\epsilon \end{array}$$ (19)

where u_i and v_j are the singular vectors of X, and ε is a n × 1 vector of noise.

Claim 3

Under this model, if d₁ > d₂, then Scout(2, ·) results in estimates of the regression coefficients that have lower variance than those obtained via ridge regression.

A more technical explanation of Claim 3, as well as a proof, are given in Section 8.1.3 of the Appendix. Note that a simple example of the above model would be the case of a block diagonal covariance matrix with two blocks, where one of the blocks of correlated features is associated with the outcome. In the case of gene expression data, these blocks could represent gene pathways, one of which is responsible for, and has expression that is correlated with, the outcome. Claim 3 shows that if the signal associated with the relevant gene pathway is sufficiently large, then Scout(2, ·) will provide a benefit over ridge.

3. Numerical Studies: Regression via the Scout

3.1. Simulated Data

We compare the performance of ordinary least squares, the lasso, the elastic net, Scout(2, 1), and Scout(1, 1) on a suite of five simulated examples. The first four simulations are based on those used in the original elastic net paper (Zou & Hastie 2005) and the original lasso paper (Tibshirani 1996). The fifth is of our own invention. All five simulations are based on the model y = Xβ + σε where ε ~ N(0, 1). For each simulation, each data set consists of a small training set, a small validation set (used to select the values of the various parameters) and a large test set. We indicate the size of the training, validation, and test sets using the notation ·/·/·. The five simulations are as follows:

1. Each data set consists of 20/20/200 observations, 8 predictors with coefficients β = (3, 1.5, 0, 0, 2, 0, 0, 0), and σ = 3. The pairwise correlation between x_i and x_j is 0.5^{| i − j |}.

2. This simulation is as in Simulation 1, except that β_i = 0.85 for all i.

3. Each data set consists of 100/100/400 observations and 40 predictors. β_i = 0 for i ∈ 1, …, 10 and for i ∈ 21, …, 30; for all other i, β_i = 2. We also set σ = 15 and the correlation between all pairs of predictors was 0.5.

4. Each data set consists of 50/50/400 observations and 40 predictors. β_i = 3 for i ∈ 1, …, 15 and β_i = 0 for i ∈ 16, …, 40, and σ = 15. The predictors are generated as follows:

   $$\begin{array}{l}{\mathbf{x}}_i={\mathbf{z}}_1+{\epsilon }_i^x,{\mathbf{z}}_1\sim N(0,1),i=1,\dots ,5\\ {\mathbf{x}}_i={\mathbf{z}}_2+{\epsilon }_i^x,{\mathbf{z}}_2\sim N(0,1),i=6,\dots ,10\\ {\mathbf{x}}_i={\mathbf{z}}_3+{\epsilon }_i^x,{\mathbf{z}}_3\sim N(0,1),i=11,\dots ,15\end{array}$$ (20)

   Also, x_i ~ N (0, 1) are independent and identically distributed for i = 16, …, 40, and ${\epsilon }_i^x\sim N(0,0.01)$ are independent and identically distributed for i = 1, …, 15.

5. Each data set consists of 50/50/400 observations and 50 predictors; β_i = 2 for i < 9 and β_i = 0 for i ≥ 9. σ = 2 and Cor(x_i, x_j) = .5 · 1_{i,j ≤ 9}.

For each simulation, 200 data sets were generated, and the median mean squared errors (with standard errors given in parentheses) are given in Table 4. For each simulation, the two methods resulting in lowest median mean squared error are shown in bold. The scout provides an improvement over the lasso in all simulations. Both scout methods result in lower mean squared error than the elastic net in Simulations 2, 3, and 5; in Simulations 1 and 4, the scout methods are quite competitive. Table 5 shows median L₂ distances between the true and estimated coefficients for each of the five models.

Table 4.

Median mean squared error over 200 simulated data sets is shown for each simulation. Standard errors are given in parentheses. For each simulation, the two methods with lowest median mean squared errors are shown in bold. Least squares was not performed for Simulation 5, because p = n.

Simulation	Least Squares	Lasso	ENet	Scout(1, 1)	Scout(2, 1)
Sim 1	5.83(0.43)	2.30(0.16)	1.77(0.20)	1.71(0.13)	1.85(0.14)
Sim 2	5.83(0.43)	2.84(0.10)	1.90(0.10)	0.89(0.08)	1.15(0.10)
Sim 3	147.14(3.63)	42.03(0.91)	30.79(0.61)	20.11(0.16)	18.22(0.27)
Sim 4	961.57(42.82)	46.44(2.14)	20.49(1.97)	23.15(1.62)	23.70(1.89)
Sim 5	NA	1.32(0.06)	0.55(0.02)	0.27(0.02)	0.52(0.04)

Table 5.

Median L₂ distance over 200 simulated data sets is shown for each simulation; details are as in Table 4.

Simulation	Least Squares	Lasso	ENet	Scout(1, 1)	Scout(2, 1)
Sim 1	3.05(0.10)	1.74(0.05)	1.65(0.08)	1.58(0.05)	1.62(0.06)
Sim 2	3.05(0.10)	1.95(0.02)	1.62(0.03)	0.90(0.03)	1.04(0.04)
Sim 3	17.03(0.22)	8.91(0.09)	7.70(0.06)	6.15(0.01)	5.83(0.03)
Sim 4	168.40(5.13)	17.40(0.16)	3.85(0.13)	5.19(2.3)	3.80(0.14)
Sim 5	NA	1.23(0.04)	1.03(0.03)	0.62(0.03)	0.89(0.02)

3.2. Making Use of Observations without Response Values

In Step 1 of the Scout Procedure, we estimate the inverse covariance matrix based on the training set X data, and in Steps 2–4, we compute a penalized least squares solution based on that estimated inverse covariance matrix and Cov(X, y). Step 1 of this procedure does not involve the response y at all.

Now, consider a situation in which one has access to a large amount of X data, but responses are known for only some of the observations. (For instance, this could be the case for a medical researcher who has clinical measurements on hundreds of cancer patients, but survival times for only dozens of patients.) More specifically, let X₁ denote the observations for which there is an associated response y, and let X₂ denote the observations for which no response data is available. Then, one could estimate the inverse covariance matrix in Step 1 of the Scout Procedure using both X₁ and X₂, and perform Step 2 using Cov(X₁, y). By also using X₂ in Step 1, we achieve a more accurate estimate of the inverse covariance matrix than would have been possible using only X₁.

Such an approach will not provide an improvement in all cases. For instance, consider the trivial case in which the response is a linear function of the predictors, p < n, and there is no noise: y = X₁β. Then, the least squares solution, using only X₁ and not X₂, is β̂ = (X₁^TX₁)⁻¹X₁^Ty = (X₁^TX₁)⁻¹X₁^TX₁β = β. In this case, it clearly is best to only use X₁ in estimating the inverse covariance matrix. However, one can imagine situations in which one can use X₂ to obtain a more accurate estimate of the inverse covariance matrix.

Consider a model in which a latent variable has generated some of the features, as well as the response. In particular, suppose that the data are generated as follows:

$$\begin{array}{l}{x}_{ij}=2u_i+{\epsilon }_{ij},j=1,\dots ,5,i=1,\dots ,n\\ x_{ij}={\epsilon }_{ij},j=6,\dots ,10,i=1,\dots ,n\\ y_i=8u_i+4{\epsilon }_i^{\prime },i=1,\dots ,n\end{array}$$ (21)

In addition, we let ε_ij, ${\epsilon }_i^{\prime }$, u_i ~ N (0, 1) i.i.d. The first five variables are “signal” variables, and the rest are “noise” variables. Suppose that we have three sets of observations: a training set of size n = 12, for which the y values are known, a test set of size n = 200, for which we wish to predict the y values, and an additional set of size n = 36 observations for which we do not know the y values and do not wish to predict them. This layout is shown in Table 6.

Table 6.

Making use of observations w/o response values: Set-up. The training set consists of 12 observations and associated responses. We wish to predict responses on a test set of 200 observations. We have access to 36 observations for which responses are not available and not of interest.

	Sample Size	Response Description
Training Set	12	Available
Test Set	200	Unavailable - Must be predicted
Additional Obs.	36	Unavailable - Not of interest

We compare the performances of the scout and other regression methods. The scout method is applied in two ways: using only the training set X values to estimate the inverse covariance matrix, and using also the observations without response values. All tuning parameter values are chosen by 5-fold cross-validation. The results in Table 7 are the average mean squared prediction errors obtained over 500 simulations. From the table, it is clear that both versions of scout outperform all of the other methods. In addition, using observations that do not have response values does result in a significant improvement.

Table 7.

Making use of observations w/o response values: Results. Mean squared prediction errors are averaged over 500 simulations; standard errors are shown in parentheses.

Method	Mean Squared Prediction Error
Scout(1, ·) w/Additional Obs.	25.65 (0.38)
Scout(1, ·) w/o Additional Obs.	29.92 (0.62)
ENet	32.38 (1.04)
Lasso	47.24 (3.58)
Σ−1Cov(X, y)	86.66 (2.07)
Least Squares	1104.9 (428.84)
Null Model	79.24 (0.3)

In this example, twelve labeled observations on ten variables do not suffice to reliably estimate the inverse covariance matrix. The scout can make use of the observations that lack response values in order to improve the estimate of the inverse covariance matrix, thereby yielding superior predictions. It is worth noting that in this exaple, the formula β̂ = Σ⁻¹Cov(X₁, y) (where Σ is the true covariance matrix) yields an average prediction error that is higher than that of the null model. Therefore, it is clear that in this example, shrinkage is necessary to achieve good predictions.

4. Classification via the Scout

In classification problems, linear discriminant analysis (LDA) can be used if n > p, but when p > n, regularization of the within-class covariance matrix is necessary. Regularized linear discriminant analysis is discussed in Friedman (1989) and Guo et al. (2007). In Guo et al. (2007), the within-class covariance matrix is shrunken, as in ridge regression, by adding a multiple of the identity matrix to the empirical covariance matrix. Here, we instead estimate a shrunken within-class inverse covariance matrix by maximizing its log likelihood, under a multivariate normal model, subject to an L_p penalty on its elements.

4.1. Details of Extension of Scout to Classification

Consider a classification problem with K classes; each observation belongs to some class k ∈ 1, …, K. Let C(i) denote the class of training set observation i, which is denoted X_i. Our goal is to classify observations in an independent test set.

Let μ̂_k denote the p × 1 vector that contains the mean of observations in class k, and let ${\mathbf{S}}_{\mathbf{wc}}=\frac{1}{n-K}{\sum }_{k=1}^K{\sum }_{i:C(i)=k}(X_i-{\widehat{\mu }}_k){(X_i-{\widehat{\mu }}_k)}^T$ denote the estimated within-class covariance matrix (based on the training set) that is used for ordinary LDA. Then, the scout procedure for clasification is as follows:

The Scout Procedure for Classification

1. Compute the shrunken within-class inverse covariance matrix ${\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}$ as follows:

   $${\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}=arg\underset{{\mathbf{\sum }}^{-1}}{max}\{logdet{\mathbf{\sum }}^{-1}-\text{tr}({\mathbf{S}}_{\mathbf{wc}}{\mathbf{\sum }}^{-1})-\lambda \mid \mid {\mathbf{\sum }}^{-1}\mid {\mid }^s\}$$ (22)

   where λ is a shrinkage parameter.

2. Classify test set observation X to class k′ if $k^{\prime }=arg{max}_k{\delta }_k^{\lambda }(X)$, where

   $${\delta }_k^{\lambda }(X)=X^T{\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}{\widehat{\mu }}_k-\frac{1}{2}{\widehat{\mu }}_k^T{\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}{\widehat{\mu }}_k+log{\pi }_k$$ (23)

   and π_k is the frequency of class k in the training set.

This procedure is analogous to LDA, but we have replaced S_wc with a shrunken estimate.

This classification rule performs quite well on real microarray data (as is shown below), but has the drawback that it results in a classification rule that makes use of all of the genes. We can remedy this in one of two ways. We can apply the method described above to only the genes with highest univariate rankings on the training data; this is done in the next section. Alternatively, we can apply an L₁ penalty in estimating the quantity ${\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}{\widehat{\mu }}_k$; note (from Equation 23) that sparsity in this quantity will result in a classification rule that is sparse in the features. Details of this second method, which is not implemented here, are given in Section 8.2 of the Appendix. We will refer to the method detailed in Equation 23 as Scout(s, ·) because the penalized log likelihood that is maximized in Equation 22 is analogous to the first scout criterion in the regression case. The tuning parameter λ in Equations 22 and 23 can be chosen via cross-validation.

4.2. Ramaswamy Data

We assess the performance of this method on the Ramaswamy microarray data set, which is discussed in detail in Ramaswamy et al. (2002) and explored further in Zhu & Hastie (2004) and Guo et al. (2007). It consists of a training set of 144 samples and a test set of 54 samples, each of which contains measurements on 16063 genes. The samples are classified into 14 distinct cancer types. We compare the performance of Scout(2, ·) to nearest shrunken centroids (NSC) (Tibshirani et al. (2002) and Tibshirani et al. (2003)), L₂ penalized multinomial (Zhu & Hastie 2004), the support vector machine (SVM) with one-versus-all classification (Ramaswamy et al. 2002), and regularized discriminant analysis (RDA) (Guo et al. 2007). For each method, tuning parameter values were chosen by cross-validation. In addition to running Scout(2, ·) on all 16063 genes, we also ran it on only the genes with highest univariate t-statistics (Tibshirani et al. 2002) in the training set. In the latter case, cross-validation was performed in order to select the number of genes to include in the model. (The model with 4000 genes had lowest cross-validation error). Note that the selection of genes with highest t-statistics was performed separately in each training fold during cross-validation.

The results can be seen in Table 8. Scout(2, ·) performed on the 4000 genes with highest training set t-statistics had the lowest test error rate out of all of the methods that we considered.

Table 8.

Cross-validation and test set errors for the following methods are compared on the Ramaswamy Data: Scout(2, ·), Scout(2, ·) using the genes with highest t-statistics on the training set, regularized discriminant analysis, nearest shrunken centroids, support vector machine using one-versus-all classification, and the L₂ penalized multinomial. With the exception of RDA, all methods were performed after cube roots of the data were taken and the patients were standardized. RDA was run on the standardized patients, without taking cube roots, as this led to much better performance.

Method	CV Err. (of 144)	Test Err. (of 54)	No. Genes
NSC	35	17	5217
L2 Penalized Mult.	29	15	16063
SVM	33	14	16063
RDA	34	10	16063
Scout(2, ·)	38	11	16063
Scout(2, ·) High T-stat.	21	8	4000

5. Extension to Generalized Linear Models and the Cox Model

We have discussed the application of the scout to classification and regression problems, and we have shown examples in which these methods perform well. In fact, the scout can also be used in fitting generalized linear models, by replacing the iteratively reweighted least squares step with a covariance-regularized regression. In particular, we discuss the use of the scout in the context of fitting a Cox proportional hazards model for survival data. We present an example involving four lymphoma microarray datasets in which the scout results in improved performance relative to other methods.

5.1. Details of Extension of Scout to the Cox Model

Consider survival data of the form (y_i, xⁱ, δ_i) for i ∈ 1, …, n, where δ_i is an indicator variable that equals 1 if observation i is complete and 0 if censored, and xⁱ is a vector of predictors ( $x_1^i,\dots ,x_p^i$) for individual i. Failure times are t₁ < t₂ < … < t_k; there are d_i failures at time t_i. We wish to estimate the parameter β = (β₁, …, β_p)^T in the proportional hazards model λ(t|x) = λ_o(t)exp(Σ_j x_jβ_j). We assume that censoring is noninformative. Letting η = Xβ, D the set of indices of the failures, R_r the set of indices of the individuals at risk at time t_r, and D_r the set of indices of the failures at t_r, the partial likelihood is given as follows (see e.g. Kalbfleisch & Prentice (1980)):

$$L(\beta )={\mathrm{\Pi }}_{r\in D}\frac{exp({\sum }_{j\in D_r}{\eta }_j)}{{({\sum }_{j\in R_r}exp({\eta }_j))}^{d_r}}$$ (24)

In order to fit the proportional hazards model, we must find the β that maximizes the likelihood above. Note that $\frac{\partial l}{\partial \beta }={(\frac{\partial \eta }{\partial \beta })}^T\frac{\partial l}{\partial \eta }={\mathbf{X}}^T\frac{\partial l}{\partial \eta }$ and $\frac{{\partial }^{2}l}{\partial \beta {\beta }^T}\approx {\mathbf{X}}^T\frac{{\partial }^{2}l}{\partial \eta {\eta }^T}\mathbf{X}$. Let $\mathbf{u}=\frac{\partial l}{\partial \eta }$ and $\mathbf{A}=-\frac{{\partial }^{2}l}{\partial \eta {\eta }^T}$. The iteratively reweighted least squares algorithm that implements the Newton-Raphson method, for β₀ the value of β from the previous step, involves finding β that solves

$${\mathbf{X}}^T\mathbf{AX}(\beta -{\beta }_0)={\mathbf{X}}^T\mathbf{u}$$ (25)

This is equivalent to finding β that minimizes

$$\mid \mid {\mathbf{y}}^{\ast }-{\mathbf{X}}^{\ast }{\beta }^{\ast }\mid {\mid }^2$$ (26)

where X^* = A^1/2X, y^* = A^−1/2u, β^* = β − β_o (Green 1984).

The traditional iterative reweighted least squares algorithm involves solving the above least squares problem repeatedly, recomputing y^* and X^* at each step and setting β₀ equal to the solution β attained at the previous iteration. We propose to solve the above equation using the scout, rather than by a simple linear regression. We have found empirically that good results are obtained if we initially set β₀ = 0, and then perform just one Newton-Raphson step (using the scout). This is convenient, since for data sets with many features, solving a scout regression can be time-consuming. Therefore, our implementation of the scout method for survival data involves simply performing one Newton-Raphson step, beginning with β₀ = 0.

Using the notation $\mathrm{\Theta }=\left(\begin{array}{cc}{\mathbf{\Theta }}_{\mathbf{xx}}& {\mathbf{\Theta }}_{\mathbf{xy}}\\ {{\mathbf{\Theta }}_{\mathbf{xy}}}^T& {\mathrm{\Theta }}_{yy}\end{array}\right)$ and $\mathbf{S}=\left(\begin{array}{cc}{\mathbf{X}}^T\mathbf{AX}& {\mathbf{X}}^T\mathbf{u}\\ {\mathbf{u}}^T\mathbf{X}& {\mathbf{u}}^T{\mathbf{A}}^{-1}\mathbf{u}\end{array}\right)$, the Scout Procedure for survival data is almost identical to the regression case, as follows:

The Scout Procedure for the Cox Model

1. Let Θ̂_xx maximize

   $$logdet{\mathbf{\Theta }}_{\mathbf{xx}}-\text{tr}({\mathbf{S}}_{\mathbf{xx}}{\mathbf{\Theta }}_{\mathbf{xx}})-{\lambda }_1\mid \mid {\mathbf{\Theta }}_{\mathbf{xx}}\mid {\mid }^{p_1}$$ (27)

2. Let Θ̂ maximize

   $$logdet\mathbf{\Theta }-\text{tr}(\mathbf{S}\mathbf{\Theta })-{\lambda }_2\mid \mid \mathbf{\Theta }\mid {\mid }^{p_2}$$ (28)

   where the top p × p submatrix of Θ is constrained to equal Θ̂_xx, obtained in the previous step.

3. Compute $\widehat{\beta }=-\frac{{\widehat{\mathbf{\Theta }}}_{\mathbf{xy}}}{{\widehat{\mathrm{\Theta }}}_{yy}}$.

4. Let β̂^* = cβ̂, where c is the coefficient of a Cox proportional hazards model fit to y using Xβ as a predictor.

β̂^* obtained in Step 4 is the vector of estimated coefficients for the Cox proportional hazards model. In the procedure above, λ₁, λ₂ > 0 are tuning parameters. In keeping with the notation of previous sections, we will refer to the resulting coefficient estimates as Scout(p₁, p₂).

5.2. Lymphoma Data

We illustrate the effectiveness of the scout method on survival data using four different data sets, all involving survival times and gene expression measurements for patients with diffuse large B-cell lymphoma. The four data sets are as follows: Rosenwald et al. (2002) (“Rosenwald”), which consists of 240 patients, Shipp et al. (2002) (“Shipp”), which consists of 58 patients, Hummel et al. (2006) (“Hummel”), which consists of 81 patients, and Monti et al. (2005) (“Monti”), which consists of 129 patients. For consistency and ease of comparison, we considered only a subset of around 1482 genes that were present in all four data sets.

We randomly split each of the data sets into a training set, a validation set, and a test set of equal sizes. For each data set, we fit four models to the training set: the L₁ penalized Cox proportional hazards (“L₁ Cox”) method of Park & Hastie (2007), the supervised principal components (SPC) method of Bair & Tibshirani (2004), Scout(2, 1), and Scout(1, 1). For each data set, we chose the tuning parameter values that resulted in the predictor that gave the highest log likelihood when used to fit a Cox proportional hazards model on the validation set (this predictor was X_valβ_train for L₁ Cox and scout, and it was the first supervised principal component for SPC). We tested the resulting models on the test set. The mean value of 2(log(L) − log(L_o)) over ten separate training/test/validation set splits is given in Table 9, where L denotes the likelihood of the Cox proportional hazards model fit on the test set using the predictor obtained from the training set (for L₁ Cox and scout, this was X_testβ_train, and for SPC, this was the first supervised principal component), and L_o denotes the likelihood of the null model. From Tables 9 and 10, it is clear that the scout results in predictors that are quite competitive with, if not better than, the competing methods on all four data sets.

Table 9.

Mean of 2(log(L) − log(L_o)) on Survival Data. L₁ Cox, supervised principal components, Scout(1, 1), and Scout(2, 1) are compared on the Hummel, Monti, Rosenwald, and Shipp data sets over ten random training/validation/test set splits. The predictor obtained from the training set is fit on the test set using a Cox proportional hazards model, and the median value of 2(log(L) − log(L_o)) over the ten repetitions is reported. For each data set, the two highest mean values of 2(log(L) − log(L_o)) are shown in bold.

Data Set	L1 Cox	SPC	Scout(1, 1)	Scout(2, 1)
Hummel	2.640	3.823	4.245	3.293
Monti	1.647	1.231	2.149	2.606
Rosenwald	4.129	3.542	3.987	4.930
Shipp	1.903	1.004	2.807	2.627

Table 10.

Median Number of Genes Used for Survival Data. L₁ Cox, supervised principal components, Scout(1, 1) and Scout(2, 1) are compared on the Hummel, Monti, Rosenwald, and Shipp data sets over ten random training/validation/test set splits; the median number of genes used in each of the resulting models is reported.

Data Set	L1Cox	SPC	Scout(1, 1)	Scout(2, 1)
Hummel	14	33	78	13
Monti	18.5	17	801.5	144.5
Rosenwald	37.5	32	294	85
Shipp	5.5	10	4.5	5

6. Discussion

We have presented covariance-regularized regression, a class of regression procedures (the “scout” family) obtained by maximizing the log likelihood of the inverse covariance matrix of the data, rather than by minimizing the sum of squared errors, subject to a penalty. We have shown that three well-known regression methods - ridge, the lasso, and the elastic net - fall into the covariance-regularized regression framework. In addition, we have explored some new methods within this framework. We have extended the covariance-regularized regression framework to classification and generalized linear model settings, and we have demonstrated the performance of the resulting methods on a number of gene expression data sets.

A drawback of the scout method is that when p₁ = 1 and the number of features is large, then minimizing the first scout criterion can be quite slow. When more than a few thousand features are present, the scout with p₁ = 1 is not a viable option at present. However, scout with p₁ = 2 is very fast, and we are confident that computational and algorithmic improvements will lead to increases in the number of features for which the scout criteria can be minimized with p₁ = 1.

Covariance-regularized regression represents a new way to understand existing regularization methods for regression, as well as an approach to develop new regularization methods that appear to perform better in practice in many examples.

8. Appendix

8.1. Proofs of Claims

8.1.1. Proof of Claim 1

First, suppose that p₂ = 1. Consider the penalized log-likelihood

$$logdet\mathbf{\Theta }-\text{tr}(\mathbf{S}\mathbf{\Theta })-\frac{{\lambda }_2}{2}\mid \mid \mathbf{\Theta }\mid {\mid }^1$$ (29)

with Θ_xx, the top left p × p submatrix of Θ, fixed to equal the matrix that maximizes the log likelihood in Step 1 of the Scout Procedure. It is clear that if Θ̂ maximizes the log likelihood, then ${({\widehat{\mathbf{\Theta }}}^{-1})}_{yy}=S_{yy}+\frac{{\lambda }_2}{2}$. The subgradient equation for maximization of the remaining portion of the log-likelihood is

$$0={({\mathbf{\Theta }}^{-1})}_{\mathbf{xy}}-{\mathbf{S}}_{\mathbf{xy}}-\frac{{\lambda }_2}{2}\mathrm{\Gamma }$$ (30)

where Γ_i = 1 if the i^th element of Θ_xy is positive, Γ_i = −1 if the i^th element of Θ_xy is negative, and otherwise Γ_i is between −1 and 1.

Let β = Θ_xx(Θ⁻¹)_xy. Therefore, we equivalently wish to find β that solves

$$0=2{({\mathbf{\Theta }}_{\mathbf{xx}})}^{-1}\beta -2{\mathbf{S}}_{\mathbf{xy}}-{\lambda }_2\mathrm{\Gamma }$$ (31)

From the partitioned inverse formula, it is clear that sgn(β) = −sgn(Θ_xy). Therefore, our task is equivalent to finding β which minimizes

$${\beta }^T{({\mathbf{\Theta }}_{\mathbf{xx}})}^{-1}\beta -2{\mathbf{S}}_{\mathbf{xy}}\beta +{\lambda }_2\mid \mid \beta \mid {\mid }^1$$ (32)

Of course, this is Equation 11. It is an L₁-penalized regression of y onto X, using only the inner products, with S_xx replaced with (Θ_xx) ⁻¹. In other words, β̂ that solves Equation 11 is given by Θ_xx(Θ⁻¹)_xy, where Θ solves Step 2 of the Scout Procedure.

Now, the solution to Step 3 of the Scout Procedure is $-\frac{{\mathbf{\Theta }}_{\mathbf{xy}}}{{\mathbf{\Theta }}_{\mathbf{yy}}}$. By the partitioned inverse formula, Θ_xx(Θ⁻¹)_xy + Θ_xy(Θ⁻¹)_yy = 0, so $-\frac{{\mathbf{\Theta }}_{\mathbf{xy}}}{{\mathrm{\Theta }}_{yy}}=\frac{{\mathbf{\Theta }}_{\mathbf{xx}}{({\mathbf{\Theta }}^{-1})}_{\mathbf{xy}}}{{({\mathbf{\Theta }}^{-1})}_{yy}{\mathrm{\Theta }}_{yy}}=\frac{\beta }{{({\mathbf{\Theta }}^{-1})}_{yy}{\mathrm{\Theta }}_{yy}}$. In other words, the solution to Step 3 of the Scout Procedure and the solution to Equation 11 differ by a factor of (Θ⁻¹)_yyΘ_yy. Since Step 4 of the Scout Procedure involves scaling the solution to Step 3 by a constant, it is clear that one can replace Step 3 of the Scout Procedure with the solution to Equation 11.

Now, suppose p₂ = 2. To find Θ_xy that maximizes this penalized log-likelihood, we take the gradient and set it to zero:

$$0={({\mathbf{\Theta }}^{-1})}_{\mathbf{xy}}-{\mathbf{S}}_{\mathbf{xy}}-\frac{{\lambda }_2}{2}{\mathbf{\Theta }}_{\mathbf{xy}}$$ (33)

Again, let β = Θ_xx(Θ⁻¹)_xy. Therefore, we equivalently wish to find β that solves

$$0=2{({\mathbf{\Theta }}_{\mathbf{xx}})}^{-1}\beta -2{\mathbf{S}}_{\mathbf{xy}}+2{\lambda }_3\beta$$ (34)

for some new constant λ₃, using the fact, from the partitioned inverse formula, that $-\frac{\beta }{{({\mathbf{\Theta }}^{-1})}_{yy}}={\mathbf{\Theta }}_{\mathbf{xy}}$. The solution β minimizes

$${\beta }^T{({\mathbf{\Theta }}_{\mathbf{xx}})}^{-1}\beta -{{\mathbf{S}}_{\mathbf{xy}}}^T\beta +{\lambda }_3{\beta }^T\beta$$

Of course, this is again Equation 11. Therefore, β̂ that solves Equation 11 is given (up to scaling by a constant) by Θ_xx(Θ⁻¹)_xy, where Θ solves Step 2 of the Scout Procedure. As before, by the partitioned inverse formula, and since Step 4 of the Scout Procedure involves scaling the solution to Step 3 by a constant, it is clear that one can replace Step 3 of the Scout Procedure with the solution to Equation 11.

8.1.2. Proof of Claim 2

Recall that the solution to Scout(2, 1) minimizes the following:

$${\beta }^T(\mathbf{V}({\mathbf{D}}^2+{\stackrel{\sim }{\mathbf{D}}}^2){\mathbf{V}}^T)\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+{\lambda }_2\mid \mid \beta \mid {\mid }^1$$ (35)

where D̃² is a p × p diagonal matrix with i^th diagonal entry equal to $\frac{1}{2}(-{d_i}^2+\sqrt{{d_i}^4+8{\lambda }_1})$ and X = UDV^T. Equivalently, the solution minimizes

$$\begin{array}{c}{\beta }^T(\mathbf{V}(\frac{1}{2}{\mathbf{D}}^2+\frac{1}{2}{\overline{\mathbf{D}}}^2+\sqrt{2{\lambda }_1}){\mathbf{V}}^T)\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+{\lambda }_2\mid \mid \beta \mid {\mid }^1\\ ={\beta }^T(\mathbf{V}(\frac{1}{2}{\mathbf{D}}^2+\frac{1}{2}{\overline{\mathbf{D}}}^2){\mathbf{V}}^T)\beta -2{\beta }^T{\mathbf{X}}^T\mathbf{y}+{\lambda }_2\mid \mid \beta \mid {\mid }^1+\sqrt{2{\lambda }_1}\mid \mid \beta \mid {\mid }^2\end{array}$$ (36)

where D̄² is the diagonal matrix with elements $\sqrt{{d_i}^4+8{\lambda }_1}-\sqrt{8{\lambda }_1}$, because V is p × p orthogonal. It is easy to see that the solution also minimizes the following:

$$\mid \mid {\mathbf{y}}^{\ast }-{\mathbf{X}}^{\ast }\beta \mid {\mid }^2+{\lambda }_2\mid \mid \beta \mid {\mid }^1+\sqrt{2{\lambda }_1}\mid \mid \beta \mid {\mid }^2$$ (37)

where ${\mathbf{X}}^{\ast }=\frac{1}{\sqrt{2}}\left(\begin{array}{c}\mathbf{X}\\ \overline{\mathbf{D}}{\mathbf{V}}^T\end{array}\right),{\mathbf{y}}^{\ast }=\left(\begin{array}{c}\sqrt{2}\mathbf{y}\\ 0\end{array}\right)$. If β̂ minimizes Equation 37, and if we assume that sgn(β̂_i) = sgn(β̂_j), then it follows that

$$\sqrt{2{\lambda }_1}\mid {\widehat{\beta }}_i-{\widehat{\beta }}_j\mid =\mid {({\mathbf{x}}_i^{\ast }-{\mathbf{x}}_j^{\ast })}^T({\mathbf{y}}^{\ast }-{\mathbf{X}}^{\ast }\widehat{\beta })\mid$$ (38)

Note that

$$\mid \mid {\mathbf{y}}^{\ast }-{\mathbf{X}}^{\ast }\widehat{\beta }\mid {\mid }^2\le \mid \mid {\mathbf{y}}^{\ast }-{\mathbf{X}}^{\ast }\widehat{\beta }\mid {\mid }^2+{\lambda }_2\mid \mid \widehat{\beta }\mid {\mid }^1+\sqrt{2{\lambda }_1}\mid \mid \widehat{\beta }\mid {\mid }^2\le \mid \mid {\mathbf{y}}^{\ast }\mid {\mid }^2=2\mid \mid \mathbf{y}\mid {\mid }^2$$ (39)

Therefore,

$$\mid {\widehat{\beta }}_i-{\widehat{\beta }}_j\mid \le \sqrt{\frac{1}{2{\lambda }_1}}\mid \mid {\mathbf{x}}_i^{\ast }-{\mathbf{x}}_j^{\ast }\mid \mid \mid \mid \mathbf{y}\mid \mid \sqrt{2}$$ (40)

Now, $\mid \mid {\mathbf{x}}_i^{\ast }-{\mathbf{x}}_j^{\ast }\mid {\mid }^2=\frac{1}{2}\mid \mid {\mathbf{x}}_i-{\mathbf{x}}_j\mid {\mid }^2+\frac{1}{2}\mid \mid {(\overline{\mathbf{D}}{\mathbf{V}}^T)}_i-{(\overline{\mathbf{D}}{\mathbf{V}}^T)}_j\mid {\mid }^2$. Since we assumed that the features are standardized, it follows that $\mid \mid {\mathbf{x}}_i^{\ast }-{\mathbf{x}}_j^{\ast }\mid {\mid }^2=1-\rho +\frac{1}{2}\mid \mid {(\overline{\mathbf{D}}{\mathbf{V}}^T)}_i-{(\overline{\mathbf{D}}{\mathbf{V}}^T)}_j\mid {\mid }^2$ where ρ is the correlation between x_i and x_j. It also is easy to see that ||(D̄V^T)_i − (D̄V^T)_j||² ≤ 1 − ρ. Therefore, it follows that

$$\mid {\widehat{\beta }}_i-{\widehat{\beta }}_j\mid \le \sqrt{\frac{2(1-\rho )}{{\lambda }_1}}\mid \mid \mathbf{y}\mid \mid$$ (41)

8.1.3. Proof of Claim 3

Consider data generated under the latent variable model given in Section 2.6. Note that it follows that

$${\mathbf{X}}^T\mathbf{X}=d_1^2{\mathbf{v}}_1{\mathbf{v}}_1^T+d_2^2{\mathbf{v}}_2{\mathbf{v}}_2^T=\sum _{j=1}^p{d}_j^2{\mathbf{v}}_j{\mathbf{v}}_j^T$$ (42)

where d₃ = … = d_p = 0. We consider two options for the regression of y onto X: ridge regression and Scout(2, ·). Let β̂^rr and β̂^sc denote the resulting estimates, and let λ^rr and λ^sc be the tuning parameters of the two methods, respectively.

$$\begin{array}{l}{\widehat{\beta }}^{rr}={({\mathbf{X}}^T\mathbf{X}+{\lambda }^{rr}\mathbf{I})}^{-1}{\mathbf{X}}^T\mathbf{y}\\ =(\sum _{j=1}^p\frac{1}{d_j^2+{\lambda }^{rr}}{\mathbf{v}}_j{\mathbf{v}}_j^T)(d_1{\mathbf{v}}_1{\mathbf{u}}_1^T+d_2{\mathbf{v}}_2{\mathbf{u}}_2^T)({\mathbf{u}}_1+\epsilon )\\ =\frac{d_1}{d_1^2+{\lambda }^{rr}}{\mathbf{v}}_1+(\frac{d_1}{d_1^2+{\lambda }^{rr}}{\mathbf{v}}_1{\mathbf{u}}_1^T+\frac{d_2}{d_2^2+{\lambda }^{rr}}{\mathbf{v}}_2{\mathbf{u}}_2^T)\epsilon \end{array}$$ (43)

Similarly, using the fact that Scout(2, ·) results in replacing $d_j^2$ with $\frac{1}{2}(d_j^2+\sqrt{d_j^4+8{\lambda }^{sc}})$:

$$\begin{array}{l}{\widehat{\beta }}^{sc}=(\sum _{j=1}^p\frac{2}{d_j^2+\sqrt{d_j^4+8{\lambda }^{sc}}}{\mathbf{v}}_j{\mathbf{v}}_j^T)(d_1{\mathbf{v}}_1{\mathbf{u}}_1^T+d_2{\mathbf{v}}_2{\mathbf{u}}_2^T)({\mathbf{u}}_1+\epsilon )\\ =\frac{2d_1}{d_1^2+\sqrt{d_1^4+8{\lambda }^{sc}}}{\mathbf{v}}_1+(\frac{2d_1}{d_1^2+\sqrt{d_1^4+8{\lambda }^{sc}}}{\mathbf{v}}_1{\mathbf{u}}_1^T+\frac{2d_2}{d_2^2+\sqrt{d_2^4+8{\lambda }^{sc}}}{\mathbf{v}}_2{\mathbf{u}}_2^T)\epsilon \end{array}$$ (44)

It is clear that the signal part of β̂^rr is $\frac{d_1}{d_1^2+{\lambda }^{rr}}{\mathbf{v}}_1$, and that the signal part of β̂^sc is $\frac{2d_1}{d_1^2+\sqrt{d_1^4+8{\lambda }^{sc}}}{\mathbf{v}}_1$. The following relationship between λ^rr and λ^sc results in signals that are equal:

$${\lambda }^{rr}=\frac{-d_1^2+\sqrt{d_1^4+8{\lambda }^{sc}}}{2}$$ (45)

From now on, we assume that Equation 45 holds. It is clear that the noise parts of β̂^rr and β̂^sc are $(\frac{d_1}{d_1^2+{\lambda }^{rr}}{\mathbf{v}}_1{\mathbf{u}}_1^T+\frac{d_2}{d_2^2+{\lambda }^{rr}}{\mathbf{v}}_2{\mathbf{u}}_2^T)\epsilon$ and $(\frac{2d_1}{d_1^2+\sqrt{d_1^4+8{\lambda }^{sc}}}{\mathbf{v}}_1{\mathbf{u}}_1^T+\frac{2d_2}{d_2^2+\sqrt{d_2^4+8{\lambda }^{sc}}}{\mathbf{v}}_2{\mathbf{u}}_2^T)\epsilon$. Using Equation 45, we know that $\frac{d_1}{d_1^2+{\lambda }^{rr}}{\mathbf{v}}_1{\mathbf{u}}_1^T=\frac{2d_1}{d_1^2+\sqrt{d_1^4+8{\lambda }^{sc}}}{\mathbf{v}}_1{\mathbf{u}}_1^T$. So it suffces to compare $\frac{d_2}{d_2^2+{\lambda }^{rr}}$ and $\frac{2d_2}{d_2^2+\sqrt{d_2^4+8{\lambda }^{sc}}}$. Recall that d₂ > 0. So,

$$\begin{array}{l}(d_2^2+{\lambda }^{rr})-(\frac{d_2^2+\sqrt{d_2^4+8{\lambda }^{sc}}}{2})=(d_2^2+\frac{-d_1^2+\sqrt{d_1^4+8{\lambda }^{sc}}}{2})-(\frac{d_2^2+\sqrt{d_2^4+8{\lambda }^{sc}}}{2})\\ =\frac{1}{2}\{(\sqrt{d_1^4+8{\lambda }^{sc}}-d_1^2)-(\sqrt{d_2^4+8{\lambda }^{sc}}-d_2^2)\}\end{array}$$ (46)

If d₁ > d₂, then the above quantity is negative; if d₁ < d₂, then it is positive. Therefore, the scout solution has a smaller noise term than the ridge solution if and only if d₁ > d₂. In other words, if the portion of X that is correlated with y has a stronger signal than the portion that is orthogonal to y, then Scout(2, ·) will perform better than ridge, because it will shrink the parts of the inverse covariance matrix that correspond to variables that are uncorrelated with the response.

8.2. Feature Selection for Scout LDA

The method that we propose in Section 4.1 can be easily modified in order to perform built-in feature selection. Using the notation in Section 4.1, we observe that

$${\widehat{\mu }}_k=arg\underset{{\mu }_k}{min}\{\sum _{i:C(i)=k}{(X_i-{\mu }_k)}^T{\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}(X_i-{\mu }_k)\}$$ (47)

and so we replace μ̂_k in Equation 23 with

$${\widehat{\mu }}_k^{\lambda ,\rho }=arg\underset{{\mu }_k}{min}\{\sum _{i:C(i)=k}{(X_i-{\mu }_k)}^T{\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}(X_i-{\mu }_k)+\rho \mid \mid {\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}{\mu }_k\mid {\mid }^1\}$$ (48)

The above can be solved via an L₁ regression, and it gives the following classification rule for a test observation X:

$${\delta }_k^{\lambda ,\rho }(X)=X^T{\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}{\widehat{\mu }}_k^{\lambda ,\rho }-\frac{1}{2}{({\widehat{\mu }}_k^{\lambda ,\rho })}^T{\widehat{\mathbf{\sum }}}_{\mathbf{wc},\lambda }^{-1}{\widehat{\mu }}_k^{\lambda ,\rho }+log{\pi }_k$$ (49)