Kindergarten Predictors of Math Learning Disability

Abstract

The aim of the present study was to address how to effectively predict mathematics learning disability (MLD). Specifically, we addressed whether cognitive data obtained during kindergarten can effectively predict which children will have MLD in third grade, whether an abbreviated test battery could be as effective as a standard psychoeducational assessment at predicting MLD, and whether the abbreviated battery corresponded to the literature on MLD characteristics. Participants were 226 children who enrolled in a 4-year prospective longitudinal study during kindergarten. We administered measures of mathematics achievement, formal and informal mathematics ability, visual-spatial reasoning, and rapid automatized naming and examined which test scores and test items from kindergarten best predicted MLD at grades 2 and 3. Statistical models using standardized scores from the entire test battery correctly classified ~80–83 percent of the participants as having, or not having, MLD. Regression models using scores from only individual test items were less predictive than models containing the standard scores, except for models using a specific subset of test items that dealt with reading numerals, number constancy, magnitude judgments of one-digit numbers, or mental addition of one-digit numbers. These models were as accurate in predicting MLD as was the model including the entire set of standard scores from the battery of tests examined. Our findings indicate that it is possible to effectively predict which kindergartners are at risk for MLD, and thus the findings have implications for early screening of MLD.

The primary aim of the present study was to examine whether cognitive data obtained from psychoeducational or neuropsychological assessments of kindergarteners can effectively predict math achievement outcome in third grade. Although this study of predictors was not a screening study per se, the findings from the present study may have direct implications for early screening of risk for math learning disability (MLD). The findings may also contribute toward efforts to identify core deficits that underlie MLD. Relative to knowledge about reading disability (RD), there is less known about the core deficit(s) of mathematics disability, and there are few evidence-based screening tools available for detecting risk for poor achievement in mathematics. The proposed project was designed to help address these gaps in research-based practice.

The Need for Early Identification of MLD

It is important to identify risk for MLD, because—like poor reading achievement—poor math achievement is a risk factor for negative outcomes in both childhood and adulthood. Education level achieved in adulthood is associated with math performance level (Delazer, Girelli, Grana, & Domahs, 2003). Math literacy in adulthood increases the likelihood of full-time employment, and differences in math literacy rates contribute to the disparity of employment between Caucasians and African Americans in the United States (Rivera-Batiz, 1992). Successful math achievement is necessary not only for the increasingly more technological occupations of the 21st century, but also for a wide range of occupations and daily activities not traditionally considered to be mathematical, ranging from carpet laying (Masingila, 1994) to nursing (Pozzi, Noss, & Hoyles, 1998). Thus, efforts to enhance math achievement serve society and its individuals at many levels. For these reasons, it is important to identify obstacles to successful math achievement early in a child’s school experience.

Efforts to Define MLD

Historically, specific learning disability (LD) has been identified through IQ testing, either alone or in conjunction with an achievement test discrepancy. On the one hand, reliance on IQ testing is not surprising, because IQ tests were developed to predict which children would succeed in school (Ceci, 1991). Indeed, performance on intelligence tests predicts a wide variety of outcomes, even indices of health and longevity (Gottfredson & Deary, 2004). However, despite federally mandated guidelines to define LD based on an IQ–Achievement discrepancy, the discrepancy model has received little if any empirical support; in fact, there is empirical support against the use of a discrepancy-based definition for LD in general, and for RD specifically (Francis et al., 2005). It is therefore not surprising that the discrepancy model alone also does not help us to define MLD (e.g., Mazzocco & Myers, 2003).

In pursuing a definition of MLD, it is useful to examine the evolution of the recently published consensus definition of RD (Dyslexia Working Group, 2002). This consensus definition was based on approximately 30 years of research on the core cognitive features underlying RD (NICHD Reading Panel, 2000). Comparable work to identify core deficits of MLD is in progress (Geary, 1993, 2004; Hanich, Jordan, Kaplan, & Dick, 2001; Jordan, Hanich, & Kaplan, 2003; Landerl, Bevan, & Butterworth, 2004; Mazzocco & Myers, 2003). In the absence of a consensus definition of MLD, it is necessary to rely on proxy definitions. Low math achievement scores are most often used for this purpose (e.g., Geary, 2004; Jordan et al., 2003; Jordan & Montani, 1997; Mazzocco & Myers, 2003), although the definition of “low” varies across studies, from the bottom 10 to 35 percent. Unfortunately, group characteristics of children with MLD may vary as a function of which percentile cutoff is used, as suggested by recent findings (Murphy, Mazzocco, Hanich, & Early, 2005).

In the present study, we considered poor math achievement as an indicator of MLD, acknowledging that these are separate albeit overlapping categories. Each term is used to describe a group of children performing below age and/or grade expectations in math accuracy, strategy use, or both. We recognize that reliance on a “poor achievement” based definition of MLD leads to excluding some children who “overachieve” despite having MLD (false negatives), and who thus score in or above the average range on tests of math achievement. We also acknowledge the possible inclusion of children whose poor math achievement results from factors other than MLD (false positives), such as a primary diagnosis of attention deficit hyperactivity disorder (Badian, 1983), poor instruction (Stevenson, Parker, Wilkinson, Bonnevaux, & Gonzalez, 1978), or low socioeconomic status (SES; Leventhal & Brooks-Gunn, 2003)—domains that are not necessarily mutually exclusive.

There are several reasons for our focus on poor math achievement as a definition of MLD. First and foremost is the lack of a consensus definition of MLD independent of math achievement level. Second, in order to minimize the number of false positives included in our MLD group, it is necessary to increase (hopefully very slightly) our rate of false negatives, which we do by relying on a conservative criterion of unequivocally poor math achievement (children in the bottom 10th percentile). This is in contrast with other studies, where higher cutoffs (e.g., at the 25th to 35th percentiles) lead to more children with MLD (fewer false negatives), but also include children whose poor math performance is likely to result from causes other than MLD (more false positives). Determining prediction accuracy requires a careful balance of these and other accuracy measures, as we discuss later (in the Method section). Finally, although our interest primarily concerns MLD, if we establish a means by which to identify children at risk for very poor math achievement—more broadly defined, but unequivocal—this may inform us about MLD more specifically.

Characterizing MLD

For the last several decades MLD has received relatively little research attention. The overall number of research studies on MLD has been low, although this number has been increasing gradually. In contrast, research on RD has increased more rapidly during this same time period, despite the fact that both RD and MLD have comparable frequency rates of ~6 percent (Badian, 1983; NICHD Reading Panel, 2000). Currently, the topics of MLD and math achievement are of interest to researchers and educators worldwide (e.g., Montague, Woodward, & Bryant, 2004), as reflected in national and international assessments geared toward informing mathematics education reform, and as reflected by funding priorities established at the national level. For instance, the National Council of Teachers of Mathematics (NCTM) has published standards for math education that are now used as curriculum standards throughout much of the United States. The National Institutes of Health, the National Science Foundation, and the Institute for Education Sciences have all developed programs or research initiatives for the study of mathematics, including the study of MLD. This recent surge in math research activity hardly reaches the existing level of research on RD, but it has moved the field of MLD from its infancy.

From this recent body of research, there are several investigator-initiated definitions of MLD, and emerging evidence that MLD is heritable in at least some cases (Alarcon, DeFries, Light, & Pennington, 1997; Oliver et al., 2004). More importantly, there is evidence of specific cognitive characteristics of MLD. Children with MLD perform more poorly than their peers on verbal short-term memory (Geary, Hamson, & Hoard, 2000), on phonological memory (Cirino, Carlson, Francis, & Fletcher, 2004; Hecht, Torgesen, Wagner, & Rashotte, 2001), and on math fact retrieval skills (Geary & Hoard, 2001; Jordan et al., 2003). Difficulty with both math fact retrieval and calculation skills has been reported regardless of co-occurring RD (Geary & Hoard, 2001; Jordan et al., 2003; Russell & Ginsburg, 1984; Shalev & Gross-Tsur, 2001). Executive functions are related to both math fact retrieval (Kaufmann, 2002) and math calculation procedures (Bull & Scerif, 2001), and working memory deficits in children with MLD have been described both broadly, in terms of weak verbal short-term memory (Geary, Hoard, & Hamson, 1999), and more specifically, as related to numeric processing (Landerl et al., 2004; Siegel & Ryan, 1989). Rapid automatized naming (Temple & Sherwood, 2002) and visual-spatial reasoning tasks (Casey, Pezaris, & Nuttall, 1992) are correlates of concurrent and later math performance (Mazzocco & Myers, 2003), although it is not necessarily the case that these skills underlie MLD per se (Jordan et al., 2003; Landerl et al., 2004). In view of the wide-ranging cognitive correlates of MLD and the complications in defining math per se, it is not surprising that we are, at this point, without a consensus definition of MLD.

In the present study, we wished to examine what combination of measures was most effective at predicting poor math achievement. It was important to include measures reflecting skills that, as described above, characterize children with MLD. Although we did not develop test items to capture these skills, we deliberately selected standardized tests used to measure skills from one or more of the domains described in the paragraph above (e.g., rapid automatized naming, fact retrieval, number sense skills, visual-spatial reasoning, counting principles), or measures like those from the Test of Early Math Ability—Second Edition and Key Math—Revised, which include separate items tapping skills from each of several such domains. We hypothesized that it would be possible to predict poor math achievement using an abbreviated assessment, provided that the assessment included items from the principle areas of deficiency—spatial skills, number sense, and fact retrieval—observed in children with MLD.

Predicting Poor Math Achievement

Although there have been studies of relatively short-term prediction of MLD, such as over two consecutive grades (e.g., Teisl, Mazzocco, & Myers, 2001), our aim was to address prediction of poor math achievement several years after kindergarten. The relation between early, overall cognitive performance (at or before kindergarten) and later school achievement is stronger for reading skills than it is for math skills (Stevenson & Newman, 1986); so assessments of broad skills alone, such as IQ testing, are not useful for identifying children with specific MLD. The pattern or scatter of IQ subtest scores is also not predictive of math (or reading) achievement (Watkins & Glutting, 2000), despite use of sub-test scores to define specific syndromes in clinical and school settings (as reviewed by Watkins, Kush, & Glutting, 1997). Thus, to identify MLD, it is necessary to identify behavioral criteria that are not captured by broad-level achievement or intellectual testing.

Alternative approaches to cognitive assessment include neuropsychological or psychoeducational testing. The latter is time intensive, so it is not efficient for schoolwide individualized testing or screening purposes. However, Fayol, Barrouillet, and Marinthe (1998) demonstrated that neuropsychological testing is effective for predicting MLD even in preschoolers. These researchers reported that neuropsychological testing performance at age 5 years was correlated with arithmetic problem-solving ability both concurrently and at age 6 years. Skills were differentially predictive at different ages, even when comparing ages 5 versus 6 years. For instance, the ability to read numerals at age 6 years was more strongly correlated with performance on a draw-a-person task than with the neuropsychological screen, although correlations with both measures were statistically significant. Looking at long-term predictors, Clarren, Martin, and Townes (1993) reported that kindergarten performance can successfully predict academic achievement outcome 10 years later, and that prediction accuracy is enhanced by a comprehensive IQ-neuropsychological testing combination approach. Although their findings support the notion that early prediction of MLD is possible, the question that remains is how to make early prediction feasible. In the present study, we examined how well small subsets of scores obtained at kindergarten predicted math achievement level in third grade. This research was part of an ongoing prospective, longitudinal study of math ability and disability during the elementary school years.

METHOD

Participants

Participants were recruited from one of seven participating schools from one suburban public school district. The criteria used to target participating schools were ones believed to enhance long-term retention in the longitudinal study, and to diminish potential influences on poor math achievement that occur with high mobility or lower SES. Additional demographic characteristics of these samples are described elsewhere in more detail (Mazzocco & Myers, 2002). Initial enrollment in the study was open to all English-speaking students attending regular half-day kindergarten in one of the participating schools. Recruitment efforts, described elsewhere in greater detail (Mazzocco & Myers, 2002), resulted in an initial sample of 249 children enrolled. A total of 226 children were tested at least three times between kindergarten and third grade; 210 were in the study for all 4 years. One child from this latter group was identified as having a known neurological condition associated with risk for poor academic achievement, and was thus omitted from the final sample. The present report is based primarily on the 209 participants who participated in all 4 years of the study through third grade (including 103 boys and 106 girls), although some data presented are drawn from the group of 226 with partial data. During the course of their study participation, 9 children subsequently repeated either kindergarten (n = 2), first grade (n = 6), or second grade (n = 1). Thus, during the fourth year of the longitudinal study, these nine children were actually in second grade. Demographic characteristics of the study participants did not differ for the total group of 226 versus the subgroup of 209.

Procedures

Children were enrolled when informed consent was received from the child’s parent. Thereafter, each child was tested individually during two to three sessions per year. Each testing session began with completion of a child assent form. Children did not receive remuneration for participating, but they did receive a colorful pencil and a ruler or bookmark following completion of a testing session.

Materials

During each year of the study, the assessment battery included standardized measures of basic math, reading-related, and visual-spatial skills. In the present study, we examined how performance on these measures during kindergarten was associated with math achievement during second and third grade. Thus, the predictor variables examined were from measures administered during kindergarten (listed in Table 1), and outcome variables were from math achievement measures administered during second and third grades.

TABLE 1.

Predictor Variables, Including Standardized Composite Scores and Individual Test Item Data, Obtained During Kindergarten

Predictor Variable	Number of Items Included in Item Analyses
Standardized measures
Test of Early Math Ability–Second Edition (TEMA-2)	33
KeyMath–Revised (KM-R): subtests
Numeration	5
Addition	3
Measurement	9
Geometry	10
Developmental Test of Visual Perception–Second	–
Edition (DTVP-2) Position in Space, Figure
Ground, Form Constancy, and Visual Closure subtests
Rapid Automatized Naming (RAN)–Response Times	–
Colors, Objects, Numbers subtests examined separately
Stanford Binet–Fourth Edition Verbal score	–
Stanford Binet Quantitative Reasoning subtest score	11
Stanford Binet Visual/Abstract Reasoning Area score	–
Demographic variables
Child’s sex	–
Handedness	–
Socioeconomic status	–
Child knows own birthday	–
Mother’s education level	–

Math Measures for Predictor and Outcome Variables

Math performance and achievement were assessed with the age-appropriate subtests of the KeyMath–Revised (KM-R) achievement test (Connolly, 1988), the Test of Early Mathematics Ability-2 (TEMA-2) (Ginsburg & Baroody, 1990), and the Woodcock Johnson–Revised (WJ-R) Math Calculations subtest (Woodcock & Johnson, 1989). These were current versions of each test at the time the study began. The KM-R is used as a diagnostic assessment of children’s math concepts and skills, and of the ability to apply these concepts and skills. It is normed for grades K through 9, and is based on three areas—Basic Concepts, Operations, and Applications. The test–retest reliability indices for KM-R age-referenced total scores exceed 0.90. The TEMA-2, normed for children age 2–8 years, is used to assess formal and informal mastery of mathematics-related concepts. The test–retest reliability for the TEMA-2 is 0.94. The WJ-R Calculation subtest involves paper and pencil math calculations (as does a portion of the Operations section of the KM-R). The reliability coefficient for the Calculation subtest, reported for the primary school age group, is 0.93. In addition to the core battery, the Stanford Binet Fourth Edition (SB-IV; Thorndike, Hagen, & Sattler, 1986) intelligence test was administered during kindergarten or early first grade. The SB-IV provided an overall full-scale IQ score, and a subtest score on quantitative reasoning, which was included as a math measure. Age-referenced standard scores were derived from each of these measures. Note that the Stanford Binet Fifth Edition was not available at the onset of the study, and that scores from the SB-IV are based on a mean of 100 and standard deviation of 16. Also, scores obtained from a test 13 years after it was normed are subject to the Flynn effect (Flynn, 1987), and are thus inflated relative to current IQ test scores.

Kindergarten Reading Skills

To measure reading-related skills, we administered the WJ-R Letter Word Identification (LWID) subtest as a measure of single-letter or single-word recognition. An age-referenced standard score was derived from this measure. The reliability coefficient for the LWID subtest for primary school-age children is 0.96. Nonstandardized reaction time scores were obtained from a measure of rapid automatized naming (RAN; Denckla & Rudel, 1976), which was administered annually. The WJ-R Word Attack subtest is more indicative of RD than is performance on the LWID subtest, because it is used to measure phonological decoding—a skill described throughout the literature on RD as essential to successful reading. However, the Word Attack subtest is developmentally inappropriate for use with kindergartners, so it was excluded from the kindergarten testing battery.

Kindergarten Visual-Spatial Skills

The four motor-reduced subtests of the Developmental Test of Visual Perception–Second Edition (DTVP-2; Hammill, Pearson, & Voress, 1993) were administered. The DTVP-2 subtests involve matching figures on the basis of direction (Position in Space), identifying shapes in embedded designs (Figure Ground), Visual Closure skills, and matching shapes (Form Constancy). Age-referenced standard scores were derived from each of these measures. The test–retest reliability indices for these four DTVP-2 subtests range from 0.80 to 0.85.

Demographic Variables

Although cognitive variables were of primary interest in this study, we collected information on a limited number of potentially important influences on our outcome variables. First, immediately prior to testing, the examiner recorded handedness when the child “signed” the assent form that preceded testing. After testing, parents completed a brief questionnaire that included information regarding highest level of education completed for each parent with whom the child resided. We also recorded which of seven schools the child attended, and SES variables linked for each school’s individual zoning district, based on ZIP code.

Variables

Predictor Variables

From each of the standardized measures, a standardized, age-referenced score was derived. Predictor variables from the kindergarten data included the composite (overall) scores representing performance on math, reading, and visual-spatial performance tests or subtests (see Table 1); the vocabulary and quantitative subtest scores from the SB-IV; the four motor-reduced subtests of the DTVP-2; and reaction time for each of the three RAN subtests, which were Colors, Numbers, and Objects.

In addition to the standardized composite scores, we also examined performance on individual test items as predictors of poor math achievement. The inclusion of individual items was of primary interest in this study, because our question concerned how to effectively predict poor math achievement without an extensive test battery. We examined performance on individual items from the TEMA-2; the four age-appropriate subtests of the KM-R, which were Numeration, Geometry, Measurement, and Addition subtests; and SB-IV quantitative subtest. Dichotomous pass/fail scores were assigned to each item administered. Individual items were categorized as either formal or informal skills, and further categorized as items measuring a specific mathematics skill, such as counting aloud (further categorized by counting with or without sets, skip counting, large or small numbers); counting rules: cardinality, constancy; enumeration of object sets: magnitude judgment/number line (with one- or two-digit numbers), reading/writing numerals; concrete addition (with manipulatives); or recognizing shapes/patterns. We omitted test items that all children passed (or failed) from a given test or subtest. Thus all items that were given to nearly all children, but that were neither passed nor failed by all participants, were included in the initial item analyses.

Preliminary Analyses to Establish the Outcome Variable

In order to determine how accurately our predictor variables classified children as having MLD, it was necessary to establish a definition of MLD. In an earlier study, we explored alternative criteria for poor math achievement and math disability, as reported elsewhere in detail (Mazzocco & Myers, 2003), including children in the bottom 10th percentile of their sample, children in the bottom quartile of their sample, and children with standard scores below 85. Based on findings from earlier studies, we selected to use a cutoff score (vs. a discrepancy score), and to use the 10 percent criteria for our definition of MLD. We relied on TEMA-2 and WJ-R Calculation scores. We initially sought to identify children with (1) MLD in third grade; (2) MLD in second grade, and (3) MLD in both grades. A total of 226 children were considered in the overall set of analyses. Forty-two children were classified as MLD in grade 3. Although 40 children met criteria for MLD during grade 2, only 23 children met MLD criteria in both grades. Of the 40 children with MLD in grade 2, 14 moved to a non-MLD classification by the next academic year, and 3 had missing grade-3 data. Of the 42 children with MLD in grade 3, 17 were not classified as math disabled the year before, and two had no grade-2 MLD data.

In view of the instability associated with meeting LD criteria at a single point in time, we determined that the most meaningful criteria for MLD in this study was persistent, unequivocally low math achievement during both second and third grades. Of our original sample of 226 children with data from kindergarten to grade 3, 209 had data for both second and third grade. Of these, 23 had persistent poor math achievement. This made up our group with MLD, and all others were classified as not having math disability. Note that this rate of approximately 10 percent is comparable to reports of MLD in the literature, which range from 6 to 10 percent (Badian, 1983; Ramaa & Gowramma, 2002; Shalev, Auerbach, Manor, & Gross-Tsur, 2000).

Statistical Analyses

All statistical analyses were performed using the statistical software package STATA 7.0. As an initial step, univariate analyses were performed on all the independent variables of interest in order to determine which set of variables were statistically associated with investigator-defined MLD. The continuous test score variables were assessed using the parametric t test for independent samples, while all categorical or dichotomous variables were assessed using the χ² goodness-of-fit test. Those variables that were found to be highly associated with MLD were then used in the set of multivariable logistic regression analyses. The variables were further assessed for colinearity, to minimize the number of covariates entered in each regression model.

RESULTS

Preliminary Analyses

Although demographic variables were not of primary interest in this study, we wished to consider whether any such variables needed to be controlled for in the primary analyses. No statistical differences were found between MLD status groups (MLD vs. non-MLD) for gender or handedness, whether focusing on MLD outcome in grade 2, grade 3, or both grades. Therefore, these variables were excluded from all subsequent analyses. Similarly, whether a child changed schools was not statistically associated with MLD in both grades. Although moving schools between grades 1 and 2 was associated with grade 2 MLD, this did not reach statistical significance, p = 0.081. Although there were only seven students who moved between grades 1 and 2, those who did change schools during the study period were over twice as likely to be classified as having MLD in grade 2 as were children who did not change schools (42.9 vs. 17.1 percent, respectively). SES as measured by child’s school was not statistically associated with risk for MLD, because the percentage of children with MLD in the five “lowest” SES schools (~14 percent) was statistically comparable to the percentage in the two “highest” schools (~9 percent). Finally, among the variables that measured the academic history of the parents, the mother’s highest level of education completed was associated with MLD status, χ²(4, n = 202) = 9.85, p < 0.05. Children whose mothers completed college were less likely to have MLD than children whose mothers did not complete college (< 3 vs. ~15 percent, respectively). Although each of these and other variables are important, none significantly contributed to the final models described below, and thus are not discussed further.

Primary Analyses

We first examined the predication accuracy of multivariate logistic regression analyses based on standardized test scores for individual tests or subtests. When using logistic regression analyses, we regressed the binary outcome variable, MLD or not MLD, on both continuous independent variables (the test scores) and dichotomous independent variables (pass or fail scores for test items). These models allowed us to calculate the predicted odds ratio (OR) of MLD for a given test score or test item, while statistically controlling for all other covariates in the model. In addition, these models provided predicted probabilities of MLD for a given set of test scores and/or test items answered correctly.

In Table 2, we present results from three of these models. Note that the KM-R Addition subtest raw score was used in place of a standard score, because the latter was not available. The Addition subtest is standardized for children at or above $5\frac{1}{2}$ years of age, and many of our participants were younger than $5\frac{1}{2}$ years. In addition to reported accuracy measures, Table 2 includes the p values from the Hosmer–Lemeshow (H-L) goodness-of-fit test, and the area under the curve obtained from ROC (receiver operator characteristic) analysis. Several “good” models are presented to avoid the impression that there is only one “best” model. The presented models are examples of our strongest models, and not a complete summary of all possible models that were explored.

TABLE 2.

Measures of Accuracy for Three Statistical Models Predicting MLD, Using Composite Scores as Predictors, and MLD in Grades 2 and 3 as the Outcome Variable

	Scores Included in Model
	Model 1: KM-R Geometry and Measurement Subtests n = 207	Model 2: KM-R (4 Subtests) and TEMA-2 n = 206	Model 3: KM-R, TEMA-2, DTVP-2, and RAN n = 182*
Sensitivity	77.3%	77.3%	91.7%
Specificity	78.9%	84.2%	78.2%
Positive PV	30.4%	37.0%	22.9%
Negative PV	96.7%	96.9%	99.3%
Correctly classified	78.7%	83.5%	79.1%
ROC	0.860	0.908	0.915
H-L p-value	0.877	0.811	0.972

Note. H-L = Hosmer–Lemeshow goodness-of-fit test, PV = predictive value.

^*Any child missing one of the 12 test scores (four KM-R, TEMA-2, four DTVP-2 subtests, and three RAN scores) was excluded from the analysis.

The ORs and corresponding 95 percent confidence intervals (CIs) are given in Table 3 for each variable of the most inclusive model (Model 3). In the case of the standardized test scores, the OR represents the odds of MLD for each unit increase in scores, whereas for test items, the OR represents the odds of MLD for a passing grade on the question as compared to a failing grade. The fact that the ORs are less than 1 indicates that a higher score, or passing a question, results in a decreased risk of MLD, as compared to a lower score, or failing a given question.

TABLE 3.

Data for Individual Predictor Variables in the Model Using Maximum Number of Math, Reading, and Visual-Spatial Standard Scores (Model 3 from Table 2), n = 182

	Odds Ratio	Standard Error	95% Conf. Interval
TEMA-2	0.844	0.056	0.737–0.967
RAN numbers RT	0.977	0.019	0.939–1.015
KM-R
Numeration	1.046	0.351	0.542–2.019
Geometry	1.005	0.1621	0.732–1.380
Addition/raw	1.038	0.392	0.495–2.178
Measurement	0.731	0.187	0.443–1.208
DTVP-2
Position in space	0.798	0.166	0.531–1.120
Figure ground	0.842	0.119	0.638–1.113
Visual closure	1.091	0.245	0.702–1.696
Form constancy	1.135	0.309	0.666–1.935

Note. Variables are composite standard scores unless otherwise noted. RT = response time, Raw = raw score.

Model Building

The deviance of the regression model is a measure of the model fidelity to the data. Ideally, we seek models that have a high fidelity (e.g., low deviance), but that are also parsimonious (e.g., have as few independent variables as possible). In general, increasing the number of parameters in a model decreases the deviance. A model can be “penalized” for having more parameters, and the Akaike’s Information Criterion (AIC) is a statistic that incorporates this fidelity/parsimony trade-off. As seen in Table 2, adding more predictors does not necessarily maximize classification accuracy of a model. The H-L test is a goodness-of-fit test that compares the model predictions to the data. The null hypothesis is that the model fits the data, so a nonsignificant p value for this test suggests that we cannot reject the hypothesis that the model fits the data. Finally, the ROC statistic is a measure of the predictive power of the model, and is obtained from the graph of the true positive rate against the false positive rate. An ROC of 0.5 means that the model has no predictive power, while an ROC of 1.0 is perfect prediction. In general, the criterion used to state that one model is better than another is somewhat subjective. We used the statistics listed above to help us assess which models were most useful in predicting MLD, and we report on the most predictive.

First, we considered the model likely to be maximally predictive of MLD. We initially ran 34 models, with resulting ROC values ranging from 0.710 to 0.915. Sixteen models had ROC values <0.80, and were not considered further. Seven models had ROC values >0.860, and were examined more closely. They included models based only on standard scores and models including individual test items. Table 2 is a summary of the sensitivity, specificity, and positive (PPV) and negative predictive values (NPV) for three different models chosen from the “better” (more accurately predictive) models based on low AIC criteria and high ROC values. These three models were based on only standard scores. Assuming that more information would yield more accurate prediction, we found that the statistical models that included the standardized total test scores for the TEMA-2 and the KM-R subtests had ROC values of approximately 0.90. We then examined whether some of the models based on subsets of individual items either significantly improved the predictive accuracy of any models based on only standard scores, or were at least as predictive as the latter despite using fewer measures. Before reporting on these models, we review the importance of considering different measures of accuracy when determining a model’s predictive “worth.”

Measures of Prediction Accuracy: Sensitivity/Specificity Analysis

Once parameters for a given logistic model have been estimated, we can use the predicted probabilities to classify an individual as either having MLD or not having MLD, based on the particular values of the independent variables for that individual. The results of this classification can then be compared to actual MLD status to obtain the estimated sensitivity and specificity of this classification scheme. These were our primary analyses of interest. Sensitivity is defined as the ability of a test to accurately identify those who are positive for a condition, whereas specificity is the ability to accurately identify those who are negative. Our results are divided into true positives (those correctly predicted as developing math difficulty), false positives (those who have average math achievement and who are identified as positive), true negatives (those who are correctly identified as not having math difficulty), and false negatives (those who have math difficulty but are “missed” by the predictive test). PPV reflects, of those who “test” positive, the percentage who are indeed positive by some gold standard. In our case, our gold standard is our investigator-established definition of MLD, low TEMA-2 or WJ-R Calculation performance in grades 2 and 3. NPV reflects the number of true negatives as a percentage of all those who test negative. All four of these values were derived for each statistical model. They were then compared across models to determine the most beneficial combination of predictor variables for assessing the outcome variable of interest in this study.

In Table 4 we illustrate how accuracy based on one index can be deceiving if all four indices of accuracy are not considered simultaneously. Only for the purpose of illustration, we demonstrate how well children’s knowledge of their own birthday predicts risk for MLD. Using our definition of MLD as the gold standard, we then chart how many children who test positive (i.e., who do not know their own birth date, month, and day) meet our MLD criteria; and how many who test negative for MLD (i.e., who correctly report their birth date, month, and day) do not have MLD. Parts 2 and 3 of Table 4 illustrate that although specificity increases when using first grade self-reports versus kindergarten self-reports, the overall accuracy of predicting which children have MLD is very low for either grade, because prediction accuracy is a function of all four indices. In kindergarten, both sensitivity and specificity are only moderately accurate, and so there is a large number of false positives. Specificity increases in first grade, but sensitivity drops and results in a higher number of false negatives. Thus, when examining the statistical models using composite or item scores, we considered all four accuracy measures to determine the most beneficial combination of predictor variables. Ideally, we would like to maximize both sensitivity and specificity, while also maintaining high PPVs and NPVs.

TABLE 4.

Illustration of the Association Between the Four Indices of Prediction Accuracy, Using Grade K or 1 Data and Grade 2 and 3 MLD Status as the Gold Standard for Presence of MLD

	Test Results = Positive (MLD)	Test Results = Negative (Not MLD)
Part 1: Definitions of Accuracy Indices
MLD	True positive	False negative	Sensitivity: P(test+|MLD+)
Not MLD	False positive	True negative	Specificity: P(test−|MLD−)
	Positive predictive value P(MLD+| test+)*	Negative predictive value P(MLD−| test−)
MLD Status at Grade 3	Test Positive (MLD)	Test Negative (Not MLD)
Part 2: Accuracy Based on Kindergarten Predictor Variables
MLD	26	15	Sensitivity: 0.63
Not MLD	61	104	Specificity: = 0.63
	Positive predictive value = 0.30	Negative predictive value = 0.87
MLD Status at Grade 3	Test Positive (MLD)	Test Negative (Not MLD)	Based on First Grade Data
Part 3: Accuracy Based on First-Grade Predictor Variables
MLD	12	29	Sensitivity: 0.29
Not MLD	11	159	Specificity: 0.94
	Positive predictive value = 0.52	Negative predictive value = 0.85

^*P(MLD+|test+) refers to the probability that a child is truly positive for MLD given that the test result for MLD is positive.

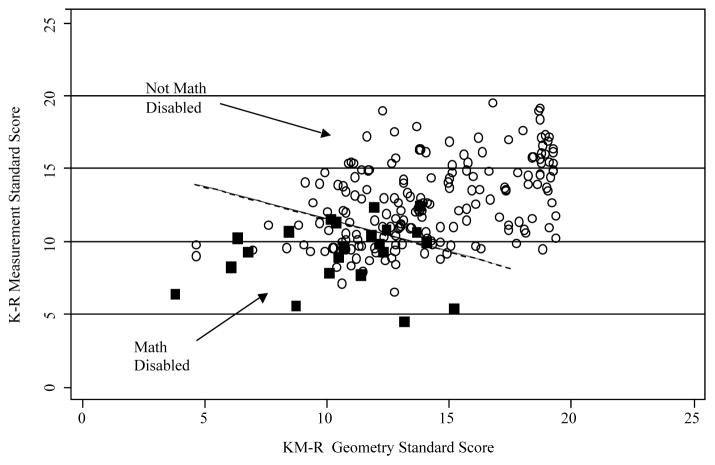
Figure 1 graphically illustrates this procedure for one of the statistical models. Our sensitivity analysis for this model determined that a predicted probability of 15 percent is the best classification scheme in terms of optimizing accuracy of classifying children as having MLD or as not having MLD, in both grades 2 and 3. That is, individuals with a predicted probability of 15 percent or greater are classified as MLD, and those with probabilities less than 15 percent of having MLD are classified as non-MLD. The line on the graph corresponds to standardized scores that give a predicted probability of 15 percent, and coordinates below the line represent probabilities greater than 15 percent.

FIGURE 1.

Plot of third grade KeyMath-Revised Measurement standardized score against KeyMath-Revised Geometry standardized score, for children with MLD (solid squares) and children without MLD (open circles). The line represents the classification criteria according to Model 1 in Table 2, which in this case is based on a criterion of 15 percent chance of having MLD. The combination of test scores corresponding to the 15 percent chance would fall on the line. The open circles below the line (less than a 15 percent chance) represent false positives, and the solid squares above the line (more than a 15 percent chance) are false negatives.

When we consider the logistic models using individual test items only, it is difficult to estimate the sensitivity and specificity of the model because the predicted probabilities are no longer continuous, but discrete. A better way to illustrate predicted MLD from these models is to plot the probability of MLD for either side of a cutoff score that is derived from one of our models. Scores from this procedure are adjusted to reflect the mean for each group. Using these weighted averages for each item that was included in a given model, we plotted the number of children who do or do not meet criteria for MLD. From Figure 1, it is evident that those who score above the cutoff (and thus below the line) have a much higher probability of MLD than those who scored below the cutoff, although errors in classification do still occur.

To maximize prediction accuracy efficiency, we wished to combine items in statistical models, as an alternative to using the full test battery that was included in the initial models. From the initial univariate analysis of all 71 individual test items, we had found that 15 items were not significantly associated with MLD. Among the remaining 57 items, significant colinearity emerged among different subsets of items, as expected. It was only necessary to include representative items from each set of correlated items, enabling us to reduce the final number of individual items to 18, and thus to avoid the redundancy that would naturally evolve from including all variables in the model-building exercise described below. Note that test items omitted because of their close association with other test items may be equally as effective at predicting MLD as are those items included in our final models. For this reason, items are identified by task, rather than by name or item number. The final models included six or more items from the TEMA-2, the KM-R subtests, and/or the SB-IV Quantitative Reasoning subtest.

Among the initial models that had ROC values >0.86, classification accuracy ranged from 83 to 89 percent, with errors including both false positives and false negatives, as reported in Table 5. What was interesting, however, is that each of these most accurate models included a specific subset of the same four test items. Because these four test items were also representative of sets of items with high colinearity, it is more appropriate to identify them by task than by item number. These items involved: number constancy when observing the counting of object sets, with sets totaling fewer than six items; reading one-digit numerals; concrete addition of one-digit numbers, using manipulatives; and magnitude judgments (number line concepts) comparing two one-digit numbers.

TABLE 5.

Measures of Accuracy for Four Final Statistical Models Predicting MLD, Using Item Scores as Predictors, and MLD in Grades 2 and 3 as the Outcome Variable, n = 207

	Model 4	Model 5	Model 6	Model 7
Items in model	8	6	4	17
Sensitivity	79.0%	81.8%	82.6%	71.4%
Specificity	88.0%	90.3%	83.9%	84.5%
PPV	40.5%	50.0%	38.8%	26.3%
NPV	97.6%	97.7%	97.5%	97.5%
Correctly classified	87.1%	89.4%	83.7%	83.6%
ROC	0.89	0.87	0.88	0.88

Note. PPV = postive predictive value; NPV = negative predictive value; ROC = receiver operating curve.

Item scores included the four commonly occurring TEMA-2 items that appeared in the most accurate of our first set of analyses, and which appear in Table 7. Models 4 and 5 included two additional items from either the TEMA-2 or the KeyMath-R, respectively; whereas Model 6 included only the four core TEMA-2 items. Model 7 included 13 more items from the TEMA-2 and KeyMath-R.

Using these four items that continued to reappear in the most accurate statistical models, we continued to build additional models until ROC values reached a plateau, which occurred with ROC values ~0.89. Four of these models appear in Table 5. Note that the ROC value for these models is comparable to the ROC reported for the model using all standardized composite scores from the kindergarten test battery (see Table 6). Table 6 summarizes the OR for each item in Model 6, which was based on only the four core test items. Table 7 is a summary of the predictive value of each of these four test items and of additional test items, when considered individually. (Table 7 also includes some of the items that were not as predictive of MLD.) Table 5 illustrates how adding items to the models does not necessarily improve the classification accuracy. Classification accuracy was also unchanged when adding scores from the RAN, DTVP-2, or IQ tests.

TABLE 6.

Odds Ratios for Individual Variables in the Model Using Four Individual Item Scores (Model 6 from Table 6), n = 209

	Odds Ratio	Standard Error	95% Conf. Interval
Constancy	0.227	0.164	0.055–0.936
Magnitude judgment	0.108	0.062	0.035–0.332
Reading numerals	0.144	0.112	0.031–0.665
Adding numbers	0.220	0.142	0.062–0.777

Note. Variables are raw scores from single items assessing the named principle.

TABLE 7.

Percentage of Children Failing Individual Test Items, Including the Four Test Items from Model 6, Table 6; n = 209

	MLD	Not MLD	χ2*	p Value
Items from Model 6
Number constancy	34.8	7.5	16.15	<0.0001
Magnitude judgments	69.6	12.4	44.12	<0.0001
Reading numerals	34.8	2.7	36.15	<0.0001
Adding with manipulatives	82.6	30.7	23.88	<0.0001
Additional items that differentiate MLD vs. non-MLD
Counting 5 items correctly	17.4	2.7	10.74	0.001
Count 10 items correctly	4.4	0.0	8.13	=0.004
Count backward from 10	65.2	19.9	22.50	<0.0001
Cardinality (up to 5 items)	21.7	3.2	14.07	<0.0001
Counting 10 from a set of 25	17.4	0.005	24.89	<0.0001
Number line concepts (one-digit numbers)	61.1	23.0	12.29	<0.0001
Additional items that do not differentiate MLD vs. non-MLD
Counting items aloud, ≤5	0.0	0.01	0.12	0.72
Understands “more”	0.0	1.6	0.38	0.54

Note. MLD = math learning disability.

DISCUSSION

In this study, we examined which standard test scores and individual test items obtained at kindergarten were most predictive of MLD at grades 2 and 3. We first considered models likely to be maximally predictive of MLD. Assuming that more information would yield a more accurate prediction, we found that the statistical models that included the standardized total test scores from the entire test battery had ROC values of approximately 0.90. We then examined whether possible models based on select subsets of individual items could be used to either significantly improve the initial model’s predictive accuracy, or to provide a model as predictive as the initial model while using fewer measures.

When we considered individual test items, the logistic regression models were generally less predictive than those containing the standard scores, giving ROC values in the range of 0.70–0.89. Nevertheless, we found that the statistical models with the “best” accuracy ratings each included the same core subset of four test items. These models were highly predictive, with ROC values greater than 0.80; they provided sensitivity and specificity values close to 80 percent, with NPVs in excess of 90 percent. However, the PPVs from these models were low, resulting in a high number of false positives. This is due–at least in part—to the fact that the prevalence of MLD is small, confined to roughly 10 percent of the participant sample.

The test items were consistently associated with several of the MLD outcome measures, and included TEMA-2 questions that dealt with reading numerals, number constancy, magnitude judgments of one-digit numbers, and mental addition of one-digit numbers. Four such models that were based on these specific test items had ROC values approaching 0.90. These models, including the examples in Tables 5 and 6, were as accurate in predicting MLD as was the model including multiple standard composite scores seen in Table 2. Thus, although we could not significantly improve the ROC of ~0.90 obtained when using all composite scores, we were able to find models including six to eight items that also had ROC values of ~0.90.

These findings offer some support for the notion that MLD results primarily from deficits in numeric processing (e.g., Landerl et al., 2004), as measured by skills in reading numerals, counting principles (Geary et al., 1999), number line concepts, and mental addition. In their study, Landerl and colleagues examined numeric-specific and numeric-irrelevant skills, such as numeral naming versus general naming skills, respectively. They found that the former, but not the latter, differentiated children with or without MLD, regardless of whether RD was also present. Our findings suggest that similar numeric skills are predictive of later poor math achievement and that the addition of RAN or spatial test scores did not improve prediction accuracy of our statistical models. However, some numeric test items were also not predictive of MLD in the initial univariate analyses. For instance, items that involved counting sets of items fewer than six or more than 13, and response time on RAN numbers failed to differentiate MLD groups. (Table 7 includes numeric items that failed to effectively predict MLD, as well as items that did predict MLD.) Considered together, our findings illustrate that a simple distinction between numeric versus nonnumeric skills is insufficient for determining effective predictors of MLD.

One interpretation of these findings is that skills in all areas tapped by these predictive test items are necessary for successful math achievement. An alternative but noncompeting interpretation is that different subtypes of MLD lead to deficits in a unique subset of skills associated with MLD, and that skills for each subset need to be assessed to screen for all subtypes of poor math achievement. We believe that the evidence from this research supports the first of these contentions, and that the second contention is neither clearly supported nor refuted by the current findings. Most important is that our findings support the notion that kindergartners can be effectively screened for MLD risk status, regardless of whether subtypes exist or can be identified as early as kindergarten. Future research efforts will be devoted to testing an empirically driven screening battery, with the aim of testing intervention models. Toward that goal, evidence for subtypes also needs to be explored further.

Contributions of this Study to Defining and Assessing MLD

The incidence of MLD varies as a function of defining criteria, evident in the wide-ranging criteria reported in research and practice. This variability illustrates the importance of considering consistency in performance—both at a point in time and over time—as an indicator of MLD. Historically, traditional definitions of LD have been based on an IQ–achievement discrepancy, but we (Mazzocco & Myers, 2003) and others (e.g., Francis et al., 2005) have argued that these definitions are insufficient at best. Similarly, use of a single test score can be misleading, and reliance on one score leads to great instability of group membership when differentiating children with MLD from children without MLD. Thus, we avoided using either a discrepancy formula or a single score to define MLD in this study. Restricting our definition of MLD to the 10th percentile cutoff score diminished the rate of false positives, and helped us maximize PPV. Moreover, there is evidence that using the 10th versus 25th percentile as a criterion results in qualitative group differences, and that the former is more consistent with current conceptualizations of MLD (Murphy, Mazzocco, Hanich, & Early, 2005). Finally, we further limited the false positive rate (from ~40 to 23 children) by requiring poor math performance at two consecutive grade levels versus at one point in time.

Although we used two time points to define MLD for the present study, we are not proposing that meeting criteria twice consecutively is necessarily sufficient for the purpose of identifying children with MLD in applied settings. It is unknown whether persistent MLD for 2 years is likely to result in persistent MLD throughout the school-age years, or whether meeting MLD criteria in grades 2 and 3 is as indicative of future MLD as is meeting these criteria in other grades. These are among the questions we are addressing through continued work with our longitudinal study participants. However, the advantage to using two time periods over one is clear, and there is evidence from studies of children with disease-related poor math achievement that children with poor math achievement show declines over time, whereas children in nonaffected comparison groups show steady, age-appropriate levels on the WJ-R Math Calculations subtest (Carey, Moore, Pasvogel, Hutter, & Kaemingk, 2004). In our study, it remains to be seen whether poor achievement at each grade level is likely to persist over time, and whether subgroups of normally achieving children begin to show poor math achievement in or after grade 4.

Advocates of alternative testing for LD argue that test scores should be linked to specific behavioral criteria (Francis et al., 2005). The findings from the present study implicate behavioral criteria that may be predictive of future poor math achievement, when these behavioral criteria are measured in kindergarten. The subset of test items present in each of the most predictive models are not to be misused as a simple four-item screening battery, but instead the constructive validity of skills represented by each measure should be further investigated so that each behavioral criterion can be measured with maximum accuracy. Note that the skills to emerge in our most predictive statistical models included formal skills (e.g., reading numerals) and informal skills (e.g., number constancy, magnitude judgments). Also note that adding reading or spatial scores did not significantly improve the predictive accuracy of our statistical models.

Finally, additional sources of information used to fine-tune prediction criteria may be drawn from behavioral measures. For instance, cognitive and behavioral indices—including teacher rating forms—predict risk for LD in school-age children (Glascoe, 2001; Teisl et al., 2001), and both cognitive skills and self-report study attitudes predict risk for LD in college students (Murray & Wren, 2003). It is unclear whether or to what degree these additions will enhance the prediction of MLD, or whether they may assist in identifying MLD subtypes.

Identifying Subtypes of MLD

Although MLD and RD can co-occur, many children with MLD do not have RD, and the majority of children with RD do not have MLD (Lewis, Hitch, & Walker, 1994; Mazzocco & Myers, 2003). Landerl et al. (2004) propose that the cognitive underpinnings of MLD are the same in children with or without co-occurring RD; their notion is supported by findings that deficits in numeric processing and math fact retrieval skills do not differ across these two subgroups (Hanich et al., 2001). On the one hand, our findings also support this notion, because including reading-related scores or visual-spatial performance scores did not improve the accuracy of the most predictive statistical models. However, it is difficult to tease apart numerically ‘pure’ items from tasks that underlie academic performance in both mathematics and reading, such as reading numerals. It is also unclear whether colinearity masked our findings. Thus, the question regarding MLD subtypes remains an important issue for future research.

Limitations of the Study

Definitions of MLD

We recognize that the outcome of this study was contingent on our investigator-defined criterion for MLD. We used a cutoff of 10 percent, whereas others have reported on MLD using cutoffs of 25 or 35 percent. In studies designed to identify cognitive characteristics of children with MLD, using a higher cutoff maximized sample size for statistical comparisons, and diminished false negatives (e.g., Geary, 2004). In the present study, it was important to maximize PPV, so we used a more conservative criterion (10 percent). This cutoff yields rates of MLD consistent with reported prevalence rates of 6–10 percent.

Sample Characteristics

The findings from the present study are also limited by some of the characteristics of our overall participant group. At the onset of our study, kindergarten participants were all enrolled in a single public school district that was using the McGraw-Hill curriculum for mathematics education. It is possible that our findings are limited by this variable, and that predictors of MLD in the present study would be less (or more) predictive of MLD among children exposed to a different curriculum.

Age-Dependent Criteria

The present study is limited to predictor variables obtained during kindergarten. It is unknown how well these items will differentiate older children with or without MLD. Different key items may emerge if predictor models are based on performance by preschoolers, or by older school-age children (e.g., grades 1–3). For instance, Fayol et al. (1998) found that a measure of sensory and visual-motor integration was more strongly correlated with arithmetic during kindergarten than was performance on a draw-a-person task during first grade. Similarly, although poor fact retrieval is a hallmark characteristic of MLD (Geary, 2004; Jordan et al., 2003; Russell & Ginsburg, 1984), math fact performance is unlikely to differentiate kindergartners with or without MLD, because few kindergartners demonstrate consistent mastery of many math facts, as based on norms from the TEMA-2 (Ginsburg & Baroody, 1990).

Implications for Screening for MLD

The findings from the present study have implications for early screening of MLD. Specifically, the findings suggest that screening at kindergarten is possible, and that performance across several specific measures may be particularly informative of an underlying MLD. The extent to which these findings are informative for screening purposes is limited by the same factors limiting generalization of the findings to predicting MLD, as described above. For example, whether to include a task in a screening test for MLD depends on normative and MLD performance ceilings on that task at different ages. In one of the few normative studies of number processing skills in adults, the majority (>90 percent) of adults age 18–70 years (n = 282) demonstrated performance ceilings on counting tasks and on selected number comprehension, processing, and calculations tasks (Delazer et al., 2003), but some tasks were not subject to performance ceilings. Approximation and estimation tasks were difficult for adults, but some estimation tasks, such as number line estimation, are appropriate for children. Performance on number line estimation is positively correlated with math achievement during the early primary school-age years (Siegler & Booth, 2004). Thus data from normative and MLD research can help inform us of the most effective items to include in screening measures.

Factors Influencing Prediction Accuracy

Although we significantly improved upon the common practice of using a single score to “define” our group of children with MLD, we recognize that our definition could be further improved by factors that were not within the scope of the present research. For instance, intervention efforts as well as the characteristics of specific curricula may interact with the manifestation of MLD. One strength of the study is the fact that all children at kindergarten (and most of the children in second and third grades) were in the same school district, and were therefore exposed to the same math curriculum, albeit with variations naturally occurring at the levels of individual schools, classrooms, and teachers.

It is also possible that prediction accuracy differs between boys and girls, such that the inclusion (or exclusion) of any of the above-mentioned factors may differentially affect accuracy for boys versus girls. Casey, Pezaris, & Nuttall (1992) found that performance on spatial skills was more predictive of math achievement in boys than it was in girls, despite the fact that the eighth-grade girls and boys in their study had comparable overall levels of math achievement. Moreover, this gender difference interacted with handedness, because prediction accuracy was comparable for boys and left-handed girls, with spatial skill accounting for approximately 33 percent of the variance in math achievement in these groups—but did not account for any of the variance among right-handed girls whose relatives were all right-handed. Aside from the neuropsychological implications for variation in math processing, these findings further illustrate the complexities involved in predicting which children are at risk for poor math achievement.

CONCLUSION AND FUTURE DIRECTIONS

Prediction accuracy ultimately depends on the gold standard definition for the group to be identified, which brings us back to the math LD/poor math achievement distinction. To the extent that these categories overlap, predicting for one group should help us identify children in the other, and will identify those children in both. If the objective is to identify potential candidate skills for early intervention, then inclusion of false positives—children without MLD—meets the objective, because children may have poor math achievement for other reasons, and their risk would be ameliorated by educational support. If the objective is to differentiate the two groups, it is necessary to identify the core deficits of MLD. Although the findings from the present study implicate some areas of core deficits for MLD, it is unclear what primary deficit(s) are responsible for participants’ poor performance on either the specific core subset of four items to emerge as most predictive, or for their meeting MLD criteria in second and third grades.

These findings do provide a foundation for empirical work on early screening and intervention in mathematics, and contribute to our goal of defining MLD and its cognitive underpinnings. If we use the final model in Table 6 as a starting point, we can seek to delineate the cognitive domains represented by the core test items, and develop additional items that can reliably evaluate the presence, absence, or developmental trajectory of specific behavioral criteria. Some researchers believe that reliance on numeric skills alone is most effective for understanding MLD (Landerl et al., 2004). Alternatively, we can use numeric and correlated items, such as working memory, to predict math ability or achievement. For instance, inhibition, task switching, and working memory have been implicated as predictive of concurrent math ability in primary school-age children (Bull & Scerif, 2001); and working memory is deficient in children with MLD (Geary, 2004; Kaufmann, 2002; McLean & Hitch, 1999). Phonological working memory and phonological awareness have been shown to be predictive of concurrent math achievement levels in primary school-age children (Cirino et al., 2004). Although the addition of RAN did not improve the predictive accuracy of the statistical models developed in our study, this may have resulted from the restricted range of performance on the RAN during kindergarten, relative to the range observed in a K–3 sample such as that included in Cirino et al.’s study. Even young children do show an association between reading and math skills, in terms of brain activation patterns (Key et al., 2004), and as seen in correlations between RAN and TEMA-2 composite scores (Mazzocco & Myers, 2003) and phonological processing and mathematical computation (Hecht et al., 2001). It is unclear to what extent cognitive correlates will inform us of the deficits that underlie MLD, but we believe that it is important to pursue this line of work in view of the replication of these findings across studies with different criteria for MLD and different study populations.

Clarren, Martin, and Townes (1993) demonstrated that different combinations of items from a neuropsychological battery were accurate at predicting math versus reading achievement over the longer term. It remains to be seen how well our identified skills predict math achievement in middle school or beyond. Nevertheless, our study supports the notion that kindergarten performance on a specific combination of math items can predict math learning disability. Some of the questions that remain concern which items are optimal for efficiently screening poor math achievement at different grades, what additional items can further enhance prediction accuracy, and whether subsets of these and other scores can eventually reflect a particular MLD subtype for which a child is at risk. We are investigating each of these questions through our continuation of the longitudinal study described in this report.

Biographies

Michèle M. M. Mazzocco is a developmental psychologist with research interests in cognitive development. She is Associate Professor of Psychiatry at the Johns Hopkins School of Medicine, and Associate Professor of Population and Family Health Sciences at the Johns Hopkins Bloomberg School of Public Health. In 1997, she initiated an ongoing longitudinal research program focusing on math abilities, running parallel studies of math skills in typically developing children, children with math learning disability, and children with fragile X, Turner, or Barth syndrome.

Richard E. Thompson is an Assistant Scientist in Biostatistics at the Johns Hopkins Bloomberg School of Public Health. He received his Ph.D. in biometry from Medical University of South Carolina. His primary field of research is in the area of environmental statistics. Dr. Thompson is Associate Director of the Johns Hopkins Biostatistics Center. He has coauthored articles in a variety of medical fields including cardiology, radiology, neurology, gastroenterology, psychology, and medical genetics.