Abstract
Background
In many randomized and non-randomized comparative trials, researchers measure a continuous endpoint repeatedly in order to decrease intra-patient variability and thus increase statistical power. There has been little guidance in the literature as to selecting the optimal number of repeated measures.
Methods
The degree to which adding a further measure increases statistical power can be derived from simple formulae. This "marginal benefit" can be used to inform the optimal number of repeat assessments.
Results
Although repeating assessments can have dramatic effects on power, marginal benefit of an additional measure rapidly decreases as the number of measures rises. There is little value in increasing the number of either baseline or post-treatment assessments beyond four, or seven where baseline assessments are taken. An exception is when correlations between measures are low, for instance, episodic conditions such as headache.
Conclusions
The proposed method offers a rational basis for determining the number of repeat measures in repeat measures designs.
Background
Many studies measure a continuous endpoint repeatedly over time. In some cases, this is because researchers wish to judge the time course of a symptom or to evaluate how the effect of a treatment changes over time. For example, in a study of thoracic surgery, patients were evaluated every three months after thoracic surgery to determine the incidence and duration of chronic postoperative pain. The researchers found that the incidence of pain at one year was high and only slightly lower than at three months, showing that post-thoracotomy pain is common and persistent[1]. In such studies, the number and timing of repeated measures needs to be decided on a study-by-study basis depending on the scientific interests of the investigators.
Measures may also be repeated in order obtain a more precise estimate of an endpoint. In simple terms, measure a patient once and they may be having a particularly good or bad day; measure them several times and you are more likely to get a fair picture of how they are doing in general. Repeat assessment reduces intra-patient variability and thus increases study power. This is of particular relevance to comparative studies. For instance, in a randomized trial of soy and placebo for cancer-related hot flashes, patients recorded the number of hot flashes they experienced each day during a baseline assessment period and then during treatment. In this case, the researchers were interested in the change between baseline and follow-up in each group so as to determine drug effect. The time course of symptoms was not at issue. The researchers therefore took a mean of each patient's hot flash score during the baseline period and subtracted the mean of the final four treatment weeks to create a change score. Change scores were compared between groups using a t-test [2]. In addition to using means, post-randomization measures may also be summarized by area-under-the-curve [3] or slope scores,[4] which are particularly relevant if treatment effects diverge over time.
There has been little guidance in the methodologic literature as to how researchers should select the number of repeated measures for repeated measures designs. In the few papers that have discussed power and repeat measurement (for example, Frison and Pocock[5]), the number of measures is seen as a fixed design characteristic, with sample size derived accordingly. Perhaps as a corollary, randomized and other comparative trials involving repeated measures almost invariably lack a statistical rationale for the number of measures taken. Measures are most commonly taken at particular temporal "landmarks", such as the beginning of each chemotherapy cycle, or each day during treatment. Apparently little consideration is given to how increasing or reducing the number of measures affects power.
Consequently, it is not difficult to find studies that appear to have either too few or too many repeat assessments. In a trial of acupuncture for back pain, for example, pain was measured on a visual analog scale (VAS) once at baseline and once following treatment [6]. The standard deviations were very high: mean post-treatment score was 38 mm with a standard deviation of 28 mm (recalculated using raw data from the authors). Part of this variability in pain scores reflects intra-patient variability that would have been reduced had the VAS been repeated several times. This would surely have been feasible in this population. There are also numerous studies where extremely large number of measures were taken, far beyond the point where additional measures would have improved precision to an important degree. For example, in a trial of a topical treatment for HIV-related peripheral neuropathy, patients were required to record pain four times a day for four weeks at baseline and at follow-up, a total of 224 data points [7]. No rationale was provided for such extensive data collection and there was clearly a cost: 46% of patients dropped-out before the end of the trial. In the hot flashes example given above, symptoms were measured every day for four weeks at baseline and for 12 weeks following randomization, a total of 102 data points [2]. The authors do not explain why such extensive data collection was required to answer the study question.
In this paper I argue that the number of repeat measures should not be seen as a fixed design characteristic, rather it is a design choice that can be informed by statistical considerations. I then outline a method for guiding decisions concerning the number of repeat measures and deduce several rules of thumb that can be applied in trial design.
Methods
To determine an optimal number of repeat measures, I use the premise that the ideal number from a statistical viewpoint is infinity, as this would maximally reduce intra-patient variance. However, it would be best in terms of researcher and patient time and effort if only a single assessment was made. Increasing the number of repeat assessments thus has a benefit in statistical terms that is offset by cost. Whereas cost can be estimated only in general terms by researchers (would patients put up with another questionnaire? how much time would it take for an additional range of motion assessment?) statistical efficiency benefits can be quantified. In the following, I describe the formulae for determining the relative benefit of additional repeat assessments for statistical power and deduce some general design principles.
The key question is the degree to which adding a further measure – for example, assessing pain five times rather than four times – increases statistical power. This is known as the "marginal benefit" of repeat measurement. We will start with the situation where data are recorded only after intervention. This is typical in trials of acute sequelae of a predictable event, for example, post-operative pain, chemotherapy nausea or muscle soreness following exercise. It can be shown (see Figure 1) that required sample size (n) patients per group is proportional to the number of measurements (r) and the mean correlation between measurements (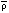 ).
).
Figure 1.
Derivation of statistical formula
![]()
Marginal change in sample size for r + 1 compared to r assessments is therefore:
![]()
This equation does not require that measurements be equally spaced or that correlations between measurements be constant.
It is common that trials investigate an endpoint that can be informatively measured before treatment. In trials of back pain, hypertension or obesity, for example, researchers want to test whether an intervention reduces patients' pain scores, blood pressure or weight from a baseline value. Typically the endpoint in such trials is measured one or more times at baseline and again following treatment. Baseline and post-treatment scores are summarized separately and change analyzed.
Analysis of covariance (ANCOVA) has been repeatedly demonstrated to be the most powerful method of analysis for this type of trial[5,8,9]. The following discussion will thus only include reference to ANCOVA (rather than say, t-test of change between baseline and follow-up). Frison and Pocock[5] have derived a generalized sample size equation that can be used to assess power for ANCOVA where baseline measures are taken before treatment: p is the number of baseline measures; subscripts pre, post and mix refer, respectively, to the mean correlations within baseline measurements, within follow-up measurements and between baseline and follow-up measures (Figure 2).
Figure 2.
Derivation of statistical formula
![]()
As is the case for trials without baseline measures, there is no requirement that correlations be equal or that assessments be equally spaced.
Frison and Pocock report that typical figures for pre, post and mix are 0.7, 0.7, and 0.5. [5] Some figures from my own studies are given in table 1. In general, these data support Frison and Pocock's generalization. Exceptions include episodic conditions, such as headache, in which case correlations are lower, and where the study outcome is measured immediately before and after a single treatment session, in which case correlations are higher. The correlations in table 1 can be used to determine the marginal benefit of additional measures for typical trials.
Table 1.
Empirical estimates of correlations from a variety of studies
| Endpoint | When assessed | Pre* | Post** | Mix*** |
| Profile of Mood States[10] | Immediately before and after a single treatment | 0.83 | ||
| Profile of Mood States[10] | Every three days during hospitalization | 0.56 | 0.54 | |
| Cancer pain+ | 2, 24 and 48 hrs after single treatment | 0.67 | ||
| Daily scores of migraine headache+ | Four weeks at baseline and at one year later | 0.53 | 0.59 | 0.48 |
| Brief Fatigue Inventory+ | Weeks -1, 0, 5 and 6 | 0.76 | 0.94 | 0.65 |
| Hot flashes+ | Daily for one week at baseline and six weeks later | 0.40 | 0.8 | 0.54 |
| Shortness of breath+ | Daily for seven days | 0.82 | ||
| Muscle soreness after running [11] | Twice daily for five days | 0.58 | ||
| Chronic neck pain [12] | Baseline and three weeks later | 0.39 | ||
| Neck range of motion [13] | Before and after a single treatment | 0.88 | ||
| Neck pain [13] | Before and after a single treatment | 0.9 | ||
| Constant Murley score of shoulder pain and dysfunction [14] | Baseline and four weeks later | 0.57 | ||
| Back pain by visual analog score [6] | Baseline and four weeks later | 0.56 | ||
| In chronic headache patients+: | ||||
| SF36 Physical functioning | Baseline and one year later | 0.75 | ||
| SF36 Role limitation physical | Baseline and one year later | 0.47 | ||
| SF36 Role limitation emotional | Baseline and one year later | 0.36 | ||
| SF36 social functioning | Baseline and one year later | 0.45 | ||
| SF36 bodily pain | Baseline and one year later | 0.52 | ||
| SF36 general health | Baseline and one year later | 0.74 | ||
| SF36 health change | Baseline and one year later | 0.24 | ||
| SF36 energy fatigue | Baseline and one year later | 0.66 | ||
| Tumor size in mice [15] | Every three days | 0.89 | ||
| Prostate specific antigen [16] | Four times over 8 to 16 months | 0.58 |
+ unpublished data * Mean correlation between baseline measures **Mean correlation between follow-up measures *** Mean correlation between baseline and follow-up measures
Results
Trials without baseline measures
Table 2 shows the marginal relative decreases in sample size given various numbers of assessments and correlations. For example, if correlation between measures is 0.65, increasing the number of measures from two to three decreases sample size requirements by about 6%. As correlation is reciprocally related to intra-patient variability, additional measures are of greatest value when correlation is low. It is also clear that repeating measurements more than a few times has little effect on power. For example, for a correlation of 0.65, taking four repeated measures only improves power by 3% compared to three assessments, a negligible value in the context of power calculation.
Table 2.
Marginal decrease in sample size for increasing the number of measures given various correlations between measures. The table refers to the case where no baseline measures are taken.
| Correlation | |||||||
| Measures | 0 | 0.15 | 0.35 | 0.5 | 0.65 | 0.85 | 1 |
| 2 | -50.0% | -42.5% | -32.5% | -25.0% | -17.5% | -7.5% | 0% |
| 3 | -16.7% | -14.2% | -10.8% | -8.3% | -5.8% | -2.5% | 0% |
| 4 | -8.3% | -7.1% | -5.4% | -4.2% | -2.9% | -1.3% | 0% |
| 5 | -5.0% | -4.3% | -3.3% | -2.5% | -1.8% | -0.8% | 0% |
| 6 | -3.3% | -2.8% | -2.2% | -1.7% | -1.2% | -0.5% | 0% |
| 7 | -2.4% | -2.0% | -1.5% | -1.2% | -0.8% | -0.4% | 0% |
| 8 | -1.8% | -1.5% | -1.2% | -0.9% | -0.6% | -0.3% | 0% |
| 9 | -1.4% | -1.2% | -0.9% | -0.7% | -0.5% | -0.2% | 0% |
| 10 | -1.1% | -0.9% | -0.7% | -0.6% | -0.4% | -0.2% | 0% |
| 11 | -0.9% | -0.8% | -0.6% | -0.5% | -0.3% | -0.1% | 0% |
| 15 | -0.5% | -0.4% | -0.3% | -0.2% | -0.2% | -0.1% | 0% |
Trials with baseline measures
Tables 3,4,5 show the effect on sample size of increasing the number of follow-up assessments and baseline assessments given different correlations for pre, post and mix. It is assumed for tables 1, 2, 3, 4, 5 that neither the mean of the measures nor the mean correlation between measures depends on the number of measures. This will generally be the case where, for example, a decision needs to be made whether to measure the severity of a chronic condition for one or two weeks at baseline. However, care should be taken with possible exceptions. An example might be if an endpoint was measured twice a day instead of just once. In this case, correlations between measurements 12 hours apart might be higher than those taken 24 hours apart. A second possible exception is acute conditions of limited duration: measuring pain after surgery for seven days rather than four days after surgery will not improve precision if few or no patients are in pain after day four.
Table 3.
Sample sizes for various combinations of baseline (p) and follow-up (r) measures. Correlations for pre, post and mix are 0.7, 0.7 and 0.5. Results given relative to a trial with a single baseline and follow-up measure.
| Number of baseline measures (p) | ||||||||||||
| No. of follow-up measures (r) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 |
| 1 | 100% | 94% | 92% | 90% | 89% | 89% | 88% | 88% | 88% | 88% | 87% | 87% |
| 2 | 80% | 74% | 72% | 70% | 69% | 69% | 68% | 68% | 68% | 68% | 67% | 67% |
| 3 | 73% | 67% | 65% | 64% | 63% | 62% | 62% | 61% | 61% | 61% | 61% | 60% |
| 4 | 70% | 64% | 62% | 60% | 59% | 59% | 58% | 58% | 58% | 58% | 57% | 57% |
| 5 | 68% | 62% | 60% | 58% | 57% | 57% | 56% | 56% | 56% | 56% | 55% | 55% |
| 6 | 67% | 61% | 58% | 57% | 56% | 56% | 55% | 55% | 55% | 54% | 54% | 54% |
| 7 | 66% | 60% | 57% | 56% | 55% | 55% | 54% | 54% | 54% | 53% | 53% | 53% |
| 8 | 65% | 59% | 57% | 55% | 54% | 54% | 53% | 53% | 53% | 53% | 52% | 52% |
| 9 | 64% | 59% | 56% | 55% | 54% | 53% | 53% | 53% | 52% | 52% | 52% | 51% |
| 10 | 64% | 58% | 56% | 54% | 53% | 53% | 52% | 52% | 52% | 52% | 51% | 51% |
| 12 | 63% | 57% | 55% | 54% | 53% | 52% | 52% | 51% | 51% | 51% | 51% | 50% |
| 15 | 63% | 57% | 54% | 53% | 52% | 52% | 51% | 51% | 51% | 50% | 50% | 50% |
Table 4.
Sample sizes for various combinations of baseline (p) and follow-up (r) measures. Correlations for pre, post and mix are 0.5, 0.5 and 0.5. Results given relative to a trial with a single baseline and follow-up measure.
| Number of baseline measures (p) | ||||||||||||
| No. of follow-up measures (r) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 |
| 1 | 100% | 89% | 83% | 80% | 78% | 76% | 75% | 74% | 73% | 73% | 72% | 71% |
| 2 | 67% | 56% | 50% | 47% | 44% | 43% | 42% | 41% | 40% | 39% | 38% | 38% |
| 3 | 56% | 44% | 39% | 36% | 33% | 32% | 31% | 30% | 29% | 28% | 27% | 26% |
| 4 | 50% | 39% | 33% | 30% | 28% | 26% | 25% | 24% | 23% | 23% | 22% | 21% |
| 5 | 47% | 36% | 30% | 27% | 24% | 23% | 22% | 21% | 20% | 19% | 18% | 18% |
| 6 | 44% | 33% | 28% | 24% | 22% | 21% | 19% | 19% | 18% | 17% | 16% | 15% |
| 7 | 43% | 32% | 26% | 23% | 21% | 19% | 18% | 17% | 16% | 16% | 15% | 14% |
| 8 | 42% | 31% | 25% | 22% | 19% | 18% | 17% | 16% | 15% | 14% | 13% | 13% |
| 9 | 41% | 30% | 24% | 21% | 19% | 17% | 16% | 15% | 14% | 13% | 13% | 12% |
| 10 | 40% | 29% | 23% | 20% | 18% | 16% | 15% | 14% | 13% | 13% | 12% | 11% |
| 12 | 39% | 28% | 22% | 19% | 17% | 15% | 14% | 13% | 12% | 12% | 11% | 10% |
| 15 | 38% | 27% | 21% | 18% | 16% | 14% | 13% | 12% | 11% | 11% | 10% | 9% |
Table 5.
Sample sizes for various combinations of baseline (p) and follow-up (r) measures. Correlations for pre, post and mix are 0.9, 0.9 and 0.8. Results given relative to a trial with a single baseline and follow-up measure.
| Number of baseline measures (p) | ||||||||||||
| No. of follow-up measures (r) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 |
| 1 | 100% | 91% | 87% | 86% | 85% | 84% | 83% | 83% | 83% | 82% | 82% | 82% |
| 2 | 86% | 77% | 73% | 72% | 71% | 70% | 69% | 69% | 69% | 69% | 68% | 68% |
| 3 | 81% | 72% | 69% | 67% | 66% | 65% | 65% | 64% | 64% | 64% | 64% | 63% |
| 4 | 79% | 70% | 66% | 65% | 64% | 63% | 63% | 62% | 62% | 62% | 61% | 61% |
| 5 | 78% | 68% | 65% | 63% | 62% | 62% | 61% | 61% | 60% | 60% | 60% | 59% |
| 6 | 77% | 67% | 64% | 62% | 61% | 61% | 60% | 60% | 60% | 59% | 59% | 59% |
| 7 | 76% | 67% | 63% | 62% | 61% | 60% | 60% | 59% | 59% | 59% | 58% | 58% |
| 8 | 76% | 66% | 63% | 61% | 60% | 60% | 59% | 59% | 58% | 58% | 58% | 57% |
| 9 | 75% | 66% | 63% | 61% | 60% | 59% | 59% | 58% | 58% | 58% | 57% | 57% |
| 10 | 75% | 66% | 62% | 61% | 60% | 59% | 58% | 58% | 58% | 57% | 57% | 57% |
| 12 | 75% | 65% | 62% | 60% | 59% | 58% | 58% | 57% | 57% | 57% | 57% | 56% |
| 15 | 74% | 65% | 61% | 60% | 59% | 58% | 57% | 57% | 57% | 56% | 56% | 56% |
Table 3 gives the most common situation of moderate correlation between baseline and follow-up measures and high correlation within measures. Table 4 shows moderate correlation for within and between measures, typical in an episodic condition. Table 5 shows very high correlations for studies where assessments are taken close together, or in the case of measures with low intra-patient variability such as laboratory data.
As an example, given the most common case of pre, post and mix at 0.7, 0.7, and 0.5, a trial with four baseline and four follow-up measurements would require 60% of the number of patients of a trial with just one baseline and follow-up; a trial with seven assessments at baseline and follow-up would require 54% as many patients. The same figures are shown in a different format in table 6, which gives the relative decrease in sample size for a number of different combinations of follow-up and or baseline assessments. For example, a trial with seven baseline and follow-up measures would require 10% fewer patients than a trial with four of each type of measure where pre, post and mix are 0.7, 0.7, and 0.5.
Table 6.
Relative decrease in sample size given various scenarios for increasing the number of baseline (p) or follow-up (r) measures.
| pre | post | mix | Change from | Change to | Sample size reduction | ||
| No. of baseline measures (p) | No. of follow-up measures (r) | No. of baseline measures (p) | No. of follow-up measures (r) | ||||
| 0.7 | 0.7 | 0.5 | 1 | 1 | 1 | 4 | 30% |
| 4 | 1 | 10% | |||||
| 4 | 4 | 40% | |||||
| 4 | 4 | 4 | 7 | 7% | |||
| 7 | 4 | 3% | |||||
| 7 | 7 | 10% | |||||
| 7 | 7 | 7 | 14 | 5% | |||
| 14 | 7 | 2% | |||||
| 14 | 14 | 8% | |||||
| 14 | 14 | 28 | 28 | 4% | |||
| 0.5 | 0.5 | 0.5 | 1 | 1 | 1 | 4 | 50% |
| 4 | 1 | 20% | |||||
| 4 | 4 | 70% | |||||
| 4 | 4 | 4 | 7 | 24% | |||
| 7 | 4 | 17% | |||||
| 7 | 7 | 40% | |||||
| 7 | 7 | 7 | 14 | 27% | |||
| 14 | 7 | 22% | |||||
| 14 | 14 | 48% | |||||
| 14 | 14 | 28 | 28 | 49% | |||
| 0.9 | 0.9 | 0.8 | 1 | 1 | 1 | 4 | 21% |
| 4 | 1 | 14% | |||||
| 4 | 4 | 35% | |||||
| 4 | 4 | 4 | 7 | 5% | |||
| 7 | 4 | 3% | |||||
| 7 | 7 | 8% | |||||
| 7 | 7 | 7 | 14 | 3% | |||
| 14 | 7 | 3% | |||||
| 14 | 14 | 6% | |||||
| 14 | 14 | 28 | 28 | 3% | |||
Some general patterns emerge:
1. Repeating measures can have dramatic effects on power. Increasing the number of follow-up and / or baseline measures from a single one to three or four can reduce sample sizes by 35 – 70%. However, the increases in power for each additional measure rapidly decreases with increasing number of assessments.
2. Under the assumption that pre and post are similar, it is more valuable to increase the number of follow-up than baseline assessments. This makes intuitive sense: we should be more concerned about the precision of an endpoint than a covariate.
3. The marginal value of additional follow-up assessments is higher where baseline measurements are taken. Take the case where pre and post are 0.7 and mix is 0.5. For a trial without baseline measures, increasing the number of post-treatment assessments from four to seven decreases sample size by about 4%. The corresponding figures for trials with one or four baseline measures are 6% and 7%. Nonetheless, with the exception of the scenario described in point 4 below, there is little value increasing the number of either baseline or post treatment assessments beyond six or seven.
4. The only situation where it is worthwhile to make more than six or seven assessments is when correlation is moderate and similar between all time periods. This is most likely to be the case for episodic conditions such as headache, where scores at any one time will be poorly correlated with scores at any other time.
Conclusion
Investigators may measure a continuous endpoint repeatedly because they wish to judge the time course of a symptom. In such cases, the number of repeat measures will depend upon the scientific interests of the investigators. Alternatively, investigators may use repeat measurement to increase the precision of an estimate. Though this is a particular concern for randomized or non-randomized comparative studies, it is also pertinent to a variety of other research designs: for example, epidemiologic cohort studies may take a measure such as blood pressure, prostate specific antigen or serum micronutrient levels at baseline and then determine whether this predicts development of disease; repeating baselines will improve the precision of such predictions.
Where measures are repeated to improve precision, decisions about the number of repeated measures, that is, the number of within-patient observations, mirror those of standard power calculation, which concerns observations of separate patients. In both cases, statistical concerns to minimize variance are balanced by logistical concerns to minimize number of assessments. Whilst an extensive literature has developed on various methods for selecting a particular number of patients to study, the number of assessments per patient has received little attention, perhaps because this has tended to be seen as a fixed characteristic of any particular trial design. Here I have shown that simple statistical considerations can be used to guide the number of repeated measures in repeated measures designs. Given the most common correlation structure, taking four baselines and seven follow-up measures dramatically improves power compared to a single baseline and follow-up; where no baseline is taken, four follow-up measures importantly improves power; however, the marginal value of including additional measures rapidly diminishes.
Competing interests
None declared
Pre-publication history
The pre-publication history for this paper can be accessed here:
References
- Perttunen K, Tasmuth T, Kalso E. Chronic pain after thoracic surgery: a follow-up study. Acta Anaesthesiol Scand. 1999;43:563–567. doi: 10.1034/j.1399-6576.1999.430513.x. [DOI] [PubMed] [Google Scholar]
- Van Patten CL, Olivotto IA, Chambers GK, Gelmon KA, Hislop TG, Templeton E, Wattie A, Prior JC. Effect of Soy Phytoestrogens on Hot Flashes in Postmenopausal Women With Breast Cancer: A Randomized, Controlled Clinical Trial. Journal of Clinical Oncology. 2002;20:1449–1455. doi: 10.1200/JCO.20.6.1449. [DOI] [PubMed] [Google Scholar]
- Matthews JNS, Altman DG, Campbell MJ, Royston P. Analysis of serial measurements in medical research. BMJ. 1990;300:230–235. doi: 10.1136/bmj.300.6719.230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frison LJ, Pocock SJ. Linearly divergent treatment effects in clinical trials with repeated measures: efficient analysis using summary statistics. Stat Med. 1997;16:2855–2872. doi: 10.1002/(SICI)1097-0258(19971230)16:24<2855::AID-SIM749>3.3.CO;2-P. [DOI] [PubMed] [Google Scholar]
- Frison L, Pocock SJ. Repeated measures in clinical trials: analysis using mean summary statistics and its implications for design. Stat Med. 1992;11:1685–1704. doi: 10.1002/sim.4780111304. [DOI] [PubMed] [Google Scholar]
- Grant DJ, Bishop-Miller J, Winchester DM, Anderson M, Faulkner S. A randomized comparative trial of acupuncture versus transcutaneous electrical nerve stimulation for chronic back pain in the elderly. Pain. 1999;82:9–13. doi: 10.1016/S0304-3959(99)00027-5. [DOI] [PubMed] [Google Scholar]
- Paice JA, Ferrans CE, Lashley FR, Shott S, Vizgirda V, Pitrak D. Topical Capsaicin in the Management of HIV-Associated Peripheral Neuropathy. Journal of Pain and Symptom Management. 2000;19:45–52. doi: 10.1016/S0885-3924(99)00139-6. [DOI] [PubMed] [Google Scholar]
- Senn S. Repeated measures in clinical trials: analysis using mean summary statistics and its implications for design. Stat Med. 1994;13:197–198. doi: 10.1002/sim.4780130210. [DOI] [PubMed] [Google Scholar]
- Vickers AJ. The use of percentage change from baseline as an outcome in a controlled trial is statistically inefficient: a simulation study. BMC Med Res Methodol. 2001;1:6. doi: 10.1186/1471-2288-1-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassileth BR, Vickers AJ, Magill LA. Music therapy for mood disturbance during hospitalization for autologous stem cell transplantation: a randomized controlled trial. Cancer. 2003. [DOI] [PubMed]
- Vickers AJ, Fisher P, Smith C, Wyllie SE, Rees R. Homeopathic Arnica 30x is ineffective for muscle soreness after long-distance running: a randomized, double-blind, placebo-controlled trial. Clin J Pain. 1998;14:227–231. doi: 10.1097/00002508-199809000-00009. [DOI] [PubMed] [Google Scholar]
- Irnich D, Behrens N, Molzen H, Konig A, Gleditsch J, Krauss M, Natalis M, Senn E, Beyer A, Schops P. Randomised trial of acupuncture compared with conventional massage and "sham" laser acupuncture for treatment of chronic neck pain. BMJ. 2001;322:1574–1578. doi: 10.1136/bmj.322.7302.1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irnich D, Behrens N, Gleditsch J, Stor W, Schreiber MA, Schops P, Vickers AJ, Beyer A. Immediate effects of dry needling and acupuncture at distant points in chronic neck pain: results of a randomized, double-blind, sham-controlled crossover trial. Pain. 2002;99:83–89. doi: 10.1016/S0304-3959(02)00062-3. [DOI] [PubMed] [Google Scholar]
- Kleinhenz J, Streitberger K, Windeler J, Gussbacher A, Mavridis G, Martin E. Randomised clinical trial comparing the effects of acupuncture and a newly designed placebo needle in rotator cuff tendinitis. Pain. 1999;83:235–241. doi: 10.1016/S0304-3959(99)00107-4. [DOI] [PubMed] [Google Scholar]
- Cheung NK, Modak S, Vickers A, Knuckles B. Orally administered beta-glucans enhance anti-tumor effects of monoclonal antibodies. Cancer Immunol Immunother. 2002;51:557–564. doi: 10.1007/s00262-002-0321-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kattan MW, Wheeler TM, Scardino PT. Postoperative nomogram for disease recurrence after radical prostatectomy for prostate cancer. J Clin Oncol. 1999;17:1499–1507. doi: 10.1200/JCO.1999.17.5.1499. [DOI] [PubMed] [Google Scholar]




