Scaffold Topologies II: Analysis of Chemical Databases

Abstract

We have systematically enumerated graph representations of scaffold topologies for up to 8-ring molecules and 4-valence atoms, thus providing coverage of the lower portion of the chemical space of small molecules (Pollock et al.¹). Here, we examine scaffold topology distributions for several databases: ChemNavigator and PubChem for commercially available chemicals, the Dictionary of Natural Products, a set of 2,742 launched drugs, WOMBAT, a database of medicinal chemistry compounds, and two subsets of PubChem, “actives” and DSSTox comprising toxic substances. We also examined a virtual database of exhaustively enumerated small organic molecules, GDB,² and contrast the scaffold topology distribution from these collections to the complete coverage of up to 8-ring molecules. For reasons related, perhaps, to synthetic accessibility and complexity, scaffolds exhibiting 6 rings or more are poorly represented. Among all collections examined, PubChem has the greatest scaffold topological diversity, whereas GDB is the most limited. More than 50% of all entries (13,000,000+ actual and 13,000,000+ virtual compounds) exhibit only 8 distinct topologies, one of which is the non-scaffold topology that represents all treelike structures. However, most of the topologies are represented by a single or very small number of examples. Within topologies, we found that 3-way scaffold connections (3-nodes) are much more frequent compared to 4-way (4-node) connections. Fused rings have a slightly higher frequency in biologically oriented databases. Scaffold topologies can be the first step toward an efficient coarse-grained classification scheme of the molecules found in chemical databases.

1 Introduction

Drugs are the cornerstone of allopathic medicine, and the vast majority have emerged from the private sector (pharmaceutical industry). Drug discovery is almost uniquely supported by the ability of the inventors to obtain patent rights regarding the usability and/or chemical structures of drugs. Pharmaceutical R&D, and more recently the National Institutes of Health (NIH) and other agencies, have become more and more interested in tools and means to query the therapeutically relevant chemical space of small molecules (CSSM),^3–5 also known as ‘drug-like’ chemical space.⁶ To this end, the question of how vast this chemical space is has been addressed in several ways— most of them related to in silico technologies, such as virtual chemical library enumeration starting from known lists of reagents. Such methods, however, explore only the limited space covered by (a) known chemical reactions and (b) available/known chemical reagents. The question of how large is the chemical space received recent attention with the launch of the NIH Roadmap molecular libraries initiative.⁷ As the NIH is embarking in the selection and biological screening of 300,000 chemicals in search of novel chemical probes, the issue of which chemicals to acquire (from over 10,000,000 commercial structures) is not a trivial one.

Previous enumerations of the CSSM include: Kappler,^8–11 who generated all single-bonded carbon-only structures up through r = 8 rings and 21 – r atoms; Kerber et al.,¹² who produced all valid non-ionic molecular formulae composed of C, N, O, H using standard valences up to a molecular weight of 150 daltons and then generated all possible structures corresponding to each formula; and Fink et al.,^2,13 who completely enumerated all C, N, O, F structures up to 11 atoms and 160 daltons and then filtered them for simple valency, synthetic feasibility and stability. Each of these studies created a fine-grained coverage of a lower portion of the CSSM in which potentially feasible organic molecules were produced.

Here, we compare the results of a coarser grained classification, scaffold topologies, which themselves are not potential molecules but represent the elemental ring structures of organic molecules, against a variety of generic and biologically oriented chemical databases as well as the collection generated by Fink et al. This provides a high level view of the fundamental topological character of these databases and a unique insight into a large class of known and possible new chemicals.

2 Methods

The details of the mathematical methods we used are described in Pollock et al.¹ Here, we will summarize the definitions and algorithms that were needed for the analyses presented here.

2.1 Scaffold Topologies

A scaffold is the common portion of a series of related compounds from which it is possible to hang active groups or spacers to form more complex compounds (a well-known example of a scaffold is the peptide backbone). Here, we provide an operational definition:

Definition 1

We consider a scaffold to be a chemical graph composed solely of rings and optional linking linear structures. All branches of a scaffold terminate in a ring.

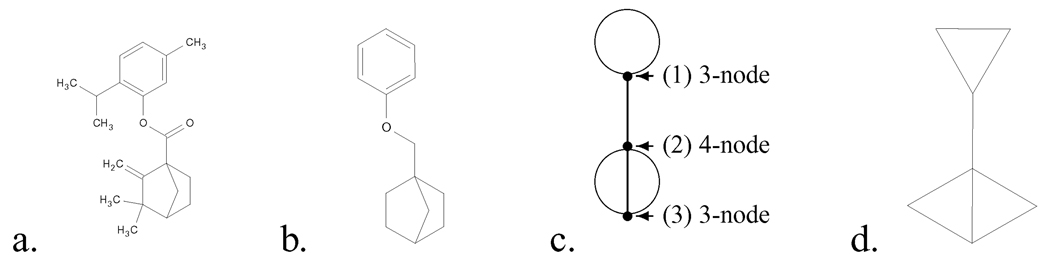
Scaffolds can also admit atoms double-bonded to ring atoms,¹⁴ but we do not include these special atoms in our description of scaffold topologies. Figure 1a,b shows a sample molecule and its corresponding scaffold.

Figure 1.

a. (5-methyl-2-propan-2-yl-phenyl) 3,3-dimethyl-2-methylidene-bicyclo[2.2.1]heptane-1-carboxylate [SMILES: CC(C)c1ccc(C)cc1OC(=O)C2(CCC3C2)C(=C)C3(C)C]. b. The scaffold corresponding to this molecule [C1CC2CCC1(C2)COc3ccccc3]. c. The topology corresponding to this scaffold (nodes are numbered as shown). d. A minimal representive of this topology [C1CC1C23CC2C3].

To simplify matters, in the discussion that follows, we will disregard the distinction between single, double and triple bonds as well as between different atom types (e.g., C, N, O, etc.); note that by the nature of scaffolds, hydrogen atoms will be omitted from the molecular descriptions. We will use the graph theory terminology of nodes and edges to indicate atoms and bonds, respectively.

A k-node is defined to be a node of degree k, where the degree indicates the number of edge segments incident to the node (see Figure 1c). The valence of the atom represented by the node determines the maximum value of k, so, for example, carbon atoms in a dehydrogenated molecule exist as 1, 2, 3 or 4-nodes. An ℓ-edge consists of ℓ edges connecting two distinct nodes. A loop is an edge that connects a node to itself. In Figure 1c, node 1 has a loop, nodes 1 and 2 are connected by a 1-edge, and nodes 2 and 3 are connected by a 3-edge.

The topology of a molecule’s scaffold is constructed from a molecule by recursively removing all of its 1-nodes (all branches that do not ultimately terminate in a ring on both ends), and by eliminating all of its 2-nodes (which simply divide an edge into two segments). The remaining nodes, which will be of degree three or greater, generate branching, initiating rings or ring connectors, and so establish the scaffold’s topology. Scaffold topologies may contain multiple edges and loops, both features that are not found in molecular graphs. Nodes of degree five or more are rare in the databases that we examined (see Section 3), so we will only consider scaffold topologies consisting of 3-nodes and 4-nodes,¹⁵ which correspond to carbon-based molecules.

Definition 2

A scaffold topology is constructed from a scaffold by

1. disregarding differences in atom type so nodes only differ by their connectivity,

2. treating multiple bonds as single edges, and

3. eliminating all 2-nodes from the resulting graph (except in the situation of a single ring in which case one 2-node is retained), 1-nodes having already been removed to produce the scaffold.

Since the recursive process of extracting a scaffold from a molecule involves in the worst case eliminating one atom (node) per step, where each step may require examining the entire adjacency matrix (i.e., $n_M^2$ entries, n_M counting the number of atoms in the original molecule), the time complexity of this process cannot exceed $n_M^3$. Hereafter, for simplicity, we will often shorten the term scaffold topology to topology, but we will always mean a graph as constructed above unless indicated otherwise.

Let r and N_k count the number of independent rings and k-nodes, respectively, then for topologies,¹

$$r=N_4+\frac{N_3}{2}+1.$$ (1)

For a fixed value of r, N₃ and N₄ will thus take on the integer values

$$\begin{array}{ccc}{N}_3& =& 2(r-1)\\ N_4& =& 0\end{array}|\begin{array}{c}2(r-2)\\ 1\end{array}|\begin{array}{c}2(r-3)\\ 2\end{array}|\begin{array}{c}\cdots \\ \cdots \end{array}|\begin{array}{c}2(r-i-1)\\ i\end{array}|\begin{array}{c}\cdots \\ \cdots \end{array}|\begin{array}{c}0\\ r-1\end{array},$$

and hence, for a topology, the total number of nodes (n) and edges (e) satisfy

$$r-1\le n\le 2(r-1)\text{\hspace{1em}and\hspace{1em}}2(r-1)\le e\le 3(r-1).$$

2.2 Comparing Topologies

Several schemes for uniquely characterizing molecular graphs have appeared (Trinajstíc et al.¹⁶ describes a number of methods; see also 17–19). This has been a difficult task as complex graphs can have sophisticated symmetries that defy easy classification (see Berger et al.²⁰ for some remarkable counterexamples in ring perception).

We represent both molecular graphs and their topologies by adjacency matrices, A. Since we are only interested in the connectivity of atoms in molecules and scaffolds, and not whether a bond is single, double or triple, all the molecular adjacency matrices will only have entries of zero or one. Topology adjacency matrices, however, can have nodes that are multiply connected with other nodes or with themselves (loops). From A, we compute the ordered return-index, an n × n matrix, as discussed in the companion paper.¹

We have exhaustively verified that after sorting with respect to the number of rings and the number of 3- or 4-nodes, the ordered return-index is sufficient to distinguish topologies with up through 8 rings for molecules with atoms of valence up to 4.¹ Therefore, this set of values under the conditions given establishes a unique characterization of scaffold topologies. For r = 11, we know of examples of topologies that have the same ordered return-indices, yet are distinct.¹ The ordered return-index is not sufficient to distinguish between graphs containing nodes of degree greater than four. Scaffolds with nodes of degree five or more are, however, rare as noted earlier.

Moreover, we have found that the diagonal of the ordered return-index is an excellent discriminator of topologies, which we use to speed database searches. We need only compare n diagonal entries rather than perform full comparisons of n × n matrices in nearly all cases. Out of a total of 1,547,689 topologies containing 8 rings or less, there are 2, 9 and 185 examples, respectively, in which groups of 4, 3 and 2 ordered return-indices, respectively, share a common diagonal but the full matrices differ, resulting in a total of 405 ambiguous cases when the diagonal is used for discrimination. In such events, we fall back to full matrix comparisons within the small groups of 4, 3 or 2 ordered return-indices.

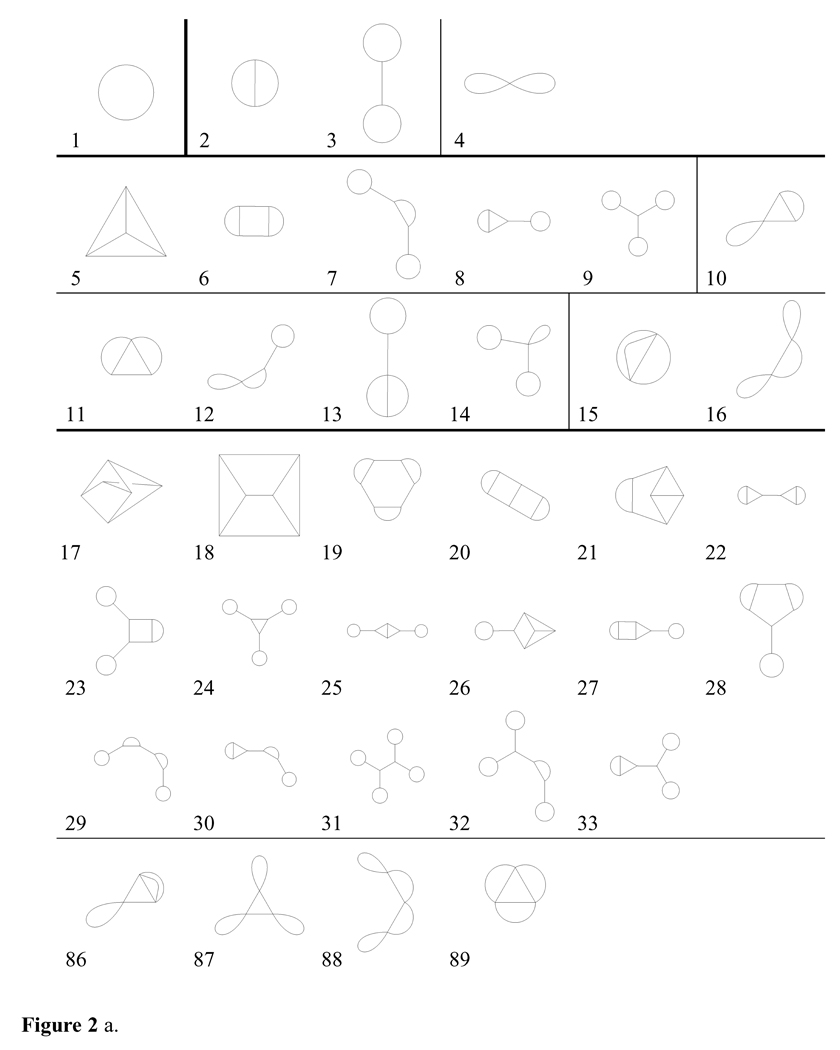
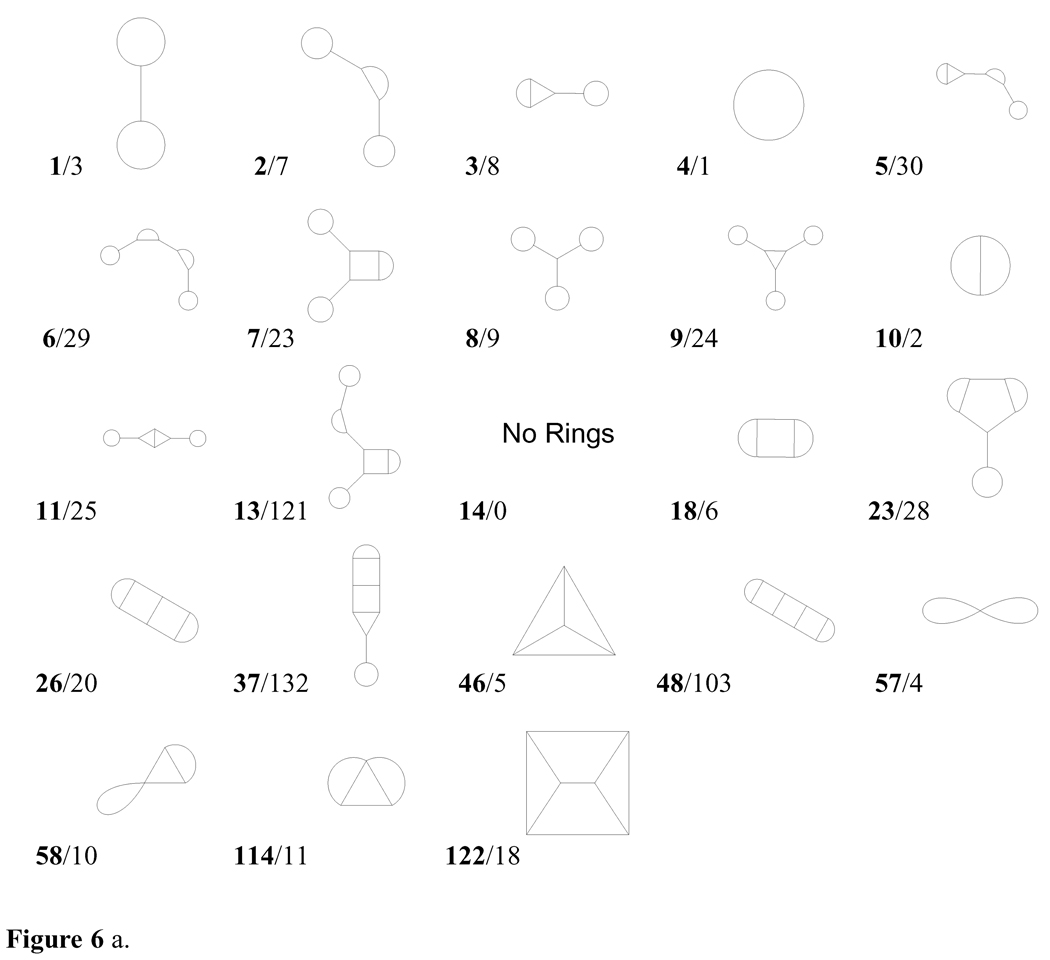
Table 1 shows the results of enumerating all possible topologies up through 8 rings. In Figure 2a, all scaffold topologies with 1–3 rings are presented as well as the 3-node only and 4-node only 4-ring topologies. 52 mixed 3/4-node 4-ring topologies are not shown. See Table 2 for further identifications. The corresponding minimal scaffolds require 3, 4–6, 4–10 and 5–14 nodes, respectively, for r = 1, 2, 3, 4. Figure 2b exhibits examples of all the topologies shown in Figure 2a, except for number 17, which was not present in any of the databases examined.

Table 1.

The total number of distinct scaffold topologies for 1 through 8 rings (top), and categorized by the number of 3-nodes, N₃, and 4-nodes, N₄ (bottom). The diagonal colors indicate the number of rings (r). Note that the (0, 0) topology is a loop with a 2-node.

Figure 2.

Figure 2 a. All 1–3-ring scaffold topologies and all 4-ring topologies possessing only 3-nodes or only 4-nodes. See Table 2 for further identification

Figure 2 b. Examples²¹ from the databases examined of molecules that exhibit each 1–3-ring topology and each 4-ring topology possessing only 3-nodes or 4-nodes, corresponding to the topologies in Figure 2. Note that none of the databases examined possessed an example of topology number 17. See Table 2 for further identification.

Table 2.

Descriptors for the scaffold topologies in Figure 2a.

r	1	2		3			4
N4	0	0	1	0	1	2	0	3
N3	0	2	0	4	2	0	6	0
topologies	1	2–3	4	5–9	10–14	15–16	17–33	86–89

2.3 Spiro Atoms

A spiro atom is the unique common member of two or more otherwise disjoint ring systems.²² As the topology fully describes the ring systems of a scaffold, the number of spiro atoms is an invariant for all scaffolds corresponding to a given topology. A scaffold’s topology is in general a smaller graph than the scaffold itself, and so is a convenient tool for the analysis of spiro atoms. A spiro atom by its definition requires a node of degree at least four. We implement an exhaustive breadth-first search technique to determine if any node in the topology corresponds to a spiro atom. In a search of chemical libraries, we may encounter atoms of degrees greater than four (e.g., sulfur), and so we can apply the concept of spiro degree to count the number of otherwise disjoint ring-systems of which an atom is the unique common member. If the degree of a spiro is not specified, it is assumed to be two. In Figure 2a, the only topologies that have spiro atoms are 4, 10, 12 and 86 with one, 16 with two, and 87 and 88 with three.

2.4 Database Measures

Let N_ik count the number of k-nodes in the i^th molecule of a chemical database containing M molecules from which molecules lacking a scaffold (i.e., possessing no rings) have been excluded. Let $N_{ik}^{(s)}$ count the number of k-nodes in the scaffold corresponding to the i^th molecule. The average fraction of atoms per molecule that make up the scaffold is then

$$\frac{{\displaystyle {\sum }_{i=1}^M{\displaystyle {\sum }_{k\ge 2}{N}_{ik}^{(s)}}}}{{\displaystyle {\sum }_{i=1}^M{\displaystyle {\sum }_{k\ge 1}{N}_{ik}}}},$$

where the maximum value of k in the databases we examined was 6. The average fraction of branch points (≥3-nodes) per scaffold is

$$\frac{{\displaystyle {\sum }_{i=1,r\ge 2}^M{\displaystyle {\sum }_{k\ge 3}{N}_{ik}^{(s)}}}}{{\displaystyle {\sum }_{i=1,r\ge 2}^M{\displaystyle {\sum }_{k\ge 2}{N}_{ik}^{(s)}}}},$$

which excludes single-ring (r = 1) structures. The average scaffold connectivity (node degree) is

$$\frac{{\displaystyle {\sum }_{i=1}^M{\displaystyle {\sum }_{k\ge 2}k{N}_{ik}^{(s)}}}}{{\displaystyle {\sum }_{i=1}^M{\displaystyle {\sum }_{k\ge 2}{N}_{ik}^{(s)}}}}.$$

The average number of independent rings per scaffold is

$$\frac{{\displaystyle {\sum }_{i=1}^M\left(\frac{1}{2}\left[{\displaystyle {\sum }_{k\ge 3}(k-2)N_{ik}^{(s)}}\right]+1\right)}}{M}=1+\frac{{\displaystyle {\sum }_{i=1}^M{\displaystyle {\sum }_{k\ge 3}(k-2)N_{ik}^{(s)}}}}{2M}.$$

This last quantity is derived from a generalization of Equation 1.

3 Analysis of Some Existing Databases

We computed scaffold topologies for the molecules found in several databases, as follows: Chem-Navigator,²³ which collects commercially available chemicals; the Dictionary of Natural Products (DNP);²⁴ an in-house compilation of 2,742 unique small molecules that are, or have been, launched drugs (Drugs); PubChem,²⁵ a public repository of small molecules which have been characterized for biological activity; PC “actives”, which is the PubChem subset labeled as “active”; the Distributed Structure-Searchable Toxicity (DSSTox)²⁶ database, also a subset of PubChem; and WOMBAT,²⁷ a collection of small molecules with known biological activity from medicinal chemistry literature (see Table 3). For each database, we processed SMILES^28,29 for all the molecules, removed salts, hydration information and counter-ions, then eliminated non-unique entries. We converted each SMILES to an adjacency matrix using OEChem,³⁰ stripped each molecule down to its simplified scaffold (see Section 2), then extracted the distinct topologies and cataloged their frequencies. Furthermore, we carried out the same procedure on the non-redundant union of all databases,³¹ which was used to compare the topological coverage of the individual databases. We note that 10,153 (42.8%) of the distinct topologies found in the merged database had a single representative and 17,634 (74.3%) had 5 or less representatives. We also examined the Generated Database of Chemical Space of Small Molecules (GDB),³² in which all organic molecules with 11 or less main atoms and molecular weight less than 160 daltons have been algorithmically generated, then filtered down for simple valency, synthetic feasibility and stability²

Table 3.

Databases examined, including a merged one constructed from all the others, their sizes, the number of distinct scaffolds produced, and the number of distinct topologies discovered. GDB, a generated database, was analyzed separately. a. Since the ordered return-index is not guaranteed to completely distinguish scaffold topologies for r> 8, the numbers presented in this table generally are lower bounds, however, we do believe them to be good estimates as we employed additional strategies for >8-ring structures to help provide further resolution, such as computing multiple ordered return-indices using different values in the adjacency matrix to represent loops. In addition, the total number of topologies for each database with r> 8 were small: < 0.62% except for DNP (3.68%) and PC actives (1.33%), both small databases. b. PubChem substances were used as at the time the analyses were performed, substances but not compounds could be identified as active.

Database	Version	Unique SMILES	Distinct scaffolds	Distinct topologiesa
ChemNavigator	October 2006	14,041,970	1,313,911	3,880
DNP	April 2006	132,434	31,819	3,199
Drugs	2006	2,742	1,312	155
PubChemb	November 7, 2006	11,595,690	1,210,092	22,612
PC actives	November 7, 2006	38,881	17,200	1,052
DSSTox	November 7, 2006	3,915	1,067	115
WOMBAT	December 2006	149,451	44,038	1,333
merged		25,029,900	2,056,025	23,737
GDB	2005	26,434,571	1,076,051	76

In Table 4, the scaffolds and topologies for each database are compared with the merged totals (columns 2 and 3), and then with the number of SMILES (molecules) in the database (columns 4 and 5). Relative to the merged database, of the two largest chemical databases, PubChem produced 5% fewer distinct scaffolds but nearly 6 times more topologies than ChemNavigator. DNP made a small (1.5%) relative contribution of scaffolds, but a good-sized (13.5%) contribution of topologies. Nearly 99% of GDB’s scaffolds did not overlap with the merged database, however, all of its topologies did.

Table 4.

For each database examined, the percentage the number of distinct scaffolds (topologies) makes with respect to the total number of distinct scaffolds (topologies) in the merged database, and the percentage ratio of scaffolds and topologies to unique SMILES (molecules) present in the database.

Database	% scaf. / merged scaf.	% top. / merged top.	% scaf. / SMILES	% top. / SMILES
ChemNavigator	63.905	16.346	9.357	0.0276
DNP	1.548	13.477	24.026	2.4155
Drugs	0.134	0.653	47.848	5.6528
PubChem	58.856	95.261	10.436	0.1950
PC actives	1.891	4.432	44.238	2.7057
DSSTox	0.190	0.484	27.254	2.9374
WOMBAT	7.269	5.616	29.467	0.8919
merged	100.000	100.000	8.214	0.0948
GDB	—	0.320	4.071	0.0003

The last two columns of Table 4 provide an indication of the databases’ scaffold and scaffold topological diversities. The smaller, biologically oriented databases (especially Drugs) have the greatest diversities, while GDB, with only 76 unique topologies but over 26,000,000 SMILES, has a very low topology to SMILES ratio, although its scaffold to SMILES ratio is much more in line with the other, especially the two large, databases. Thus, collections of very small molecules (< 160 Daltons) may have many scaffolds, but their underlying scaffold topologies remain quite limited. We note that the topology to SMILES ratio appears to be inversely correlated with the size of the databases (the larger the database, the smaller the ratio) and the scaffold to SMILES ratios are partially so, which suggests that a larger database typically contains more examples of a topology or a scaffold.

Xue and Bajorath³³ found that the scaffold to compound percentage was 44.53% for the Optiverse screening library based on diversity design (117,976 chemicals) and 26.94% for the May-bridge collection of compounds and intermediates used in medicinal chemistry (58,239 chemicals). For the biologically oriented databases here, the numbers (and database sizes) are comparable, ranging between 47.85% for Drugs to 24.03% for DNP.

As can be seen in Table 5, nearly all the molecules contain rings and can be stripped down into scaffolds (these findings are similar to those of Lewell et al.³⁴ and Koch et al.³⁵). Note, however, that 8.6% of the DNP structures, 6.5% of the Drugs and 3.9% of the PC actives, all biologically oriented, do not contain rings, as does 25.1% of DSSTox, by far the largest database percentage. 15.4% of the generated structures in GDB also lack rings. Note also that the larger databases of known chemicals contain, in general, larger structures. The most rings found in a single scaffold topology is a PubChem copper tetracarboranylphenylporphyrin with r = 165 (N₆ = 8,N₅ = 88, N₃ = 32). The next largest, a protein HIV inhibitor also from PubChem, has 107 rings (N₃ = 212). In general, the largest examples in each database possess no 4-nodes, only 3-nodes and possibly 5- or 6-nodes.

Table 5.

For each database, the percentage of molecules that do not contain rings, the maximum number of rings found in a single compound, and the population of molecules that possess at least one 5- or 6-node.

Database	% no rings	Maximum rings	> 4-nodes population
ChemNavigator	0.245	62	95
DNP	8.633	32	61
Drugs	6.492	18	0
PubChem	2.466	165	6488
PC actives	3.837	23	198
DSSTox	25.057	11	0
WOMBAT	1.641	34	0
merged	1.225	165	6593
GDB	15.414	6	0

Scaffold topologies containing a 5- or 6-node are rare; only 0.5% of the entries in the PC actives database (the most extreme case) contain nodes of such high degree. PubChem with 0.06% had the next greatest percentage of molecules possessing a scaffold with a 5- or 6-node, while Drugs, DSSTox, WOMBAT and GDB contain no such structures at all. We found no scaffolds that had nodes with degrees > 6. Therefore, we ignored such higher degree nodes and concentrated on topologies that contained nodes of at most degree 4. A major reason why there are so few nodes of degree > 4 is that those atoms with high valence (e.g., P and S) are typically not ring members, so are commonly stripped off when scaffolds are created.

A variety of chemical, geometrical and topological criteria have been used to describe molecules and to map out chemical space. Here, we concentrate on measures based on topological properties to characterize the databases of interest, as illustrated in Table 6. One such measure is the average fraction of atoms per molecule that make up the scaffold (see the first data column). In the biologically oriented databases (DNP, Drugs, PC actives, DSSTox and WOMBAT), this fraction averages 0.61–0.71, while in the other known chemical databases, that average is higher, ranging 0.72–0.74. Thus, biologically oriented molecules tend to exhibit a higher fraction of the molecule that is represented by chemical substituents to the scaffold, rather than as part of it. This is likely to increase chemical and pharmacophore diversity at a scaffold, which is a traditional way of exploring biological activity around a given scaffold. The lowest fraction of scaffold atoms (0.60) is in GDB, which indicates that these molecules contain a considerable fraction of non-scaffold structure. This is not surprising, since the goal of GDB is to exhaustively map chemical space and is, in a way, equivalent to the manner in which patents enumerate substituents for chemical completeness, a situation that only occasionally leads to synthesized compounds.

Table 6.

Basic database measures: average fraction of atoms per molecule that make up the scaffold, average fraction of branch points (≥ 3-nodes) per scaffold, average scaffold connectivity (node degree), average number of independent rings per scaffold. S

Database	Fraction scaffold	Fraction ≥ 3-nodes	Node degree	Number of rings
ChemNavigator	0.745	0.211	2.208	3.278
DNP	0.610	0.283	2.269	3.778
Drugs	0.636	0.236	2.202	2.854
PubChem	0.717	0.223	2.211	3.148
PC actives	0.714	0.249	2.232	3.311
DSSTox	0.649	0.239	2.133	2.225
WOMBAT	0.671	0.226	2.218	3.481
merged	0.733	0.217	2.210	3.235
GDB	0.605	0.307	2.049	1.653

Others³⁴ have computed the scaffold molecular weight fraction, a related measure. The atoms that are stripped to produce the scaffold include all hydrogens; in general, the scaffold tends to retain a majority of the molecular mass. In a collection of approximately 10,000 preclinical and clinical phase candidates, including some marketed drugs, 56% of the molecular weight of the compounds was present in the scaffolds³⁴ (as we define them here).

Another topological measure is the fraction of scaffold atoms that are essential for defining the scaffold topology of multi-ring systems. This is the fraction of branching (≥ 3)-nodes found within the scaffold. The second data column in the table lists the average fractions of scaffold atoms that define the scaffold topologies. These numbers tend to be around 0.22 for known chemicals, with somewhat higher values for the biologically oriented databases and GDB. GDB and DNP have by far the greatest branching structure within their scaffolds.

Bone and Villar³⁶ looked at the average connectivity (average node degree) of molecular structures as an indicator of diversity. The average node degree taken over all scaffolds is given in the third data column of Table 6. This measure is quite similar among databases of known chemicals, averaging around 2.21, with DNP having a marginally higher value and DSSTox a somewhat lower value. GDB scaffolds, averaging 2.05, are, on average, less connected.

Another such measure is the average number of independent rings per scaffold. Three-ring scaffolds are the most common in the version of DNP that Koch et al. examined, with the counts of two and four ringed-systems lying within one standard deviation.³⁵ Natural products have the highest average number of rings and marketed drugs the least, with natural product derivatives and combinatorially synthesized chemicals inbetween.³⁷ Our results show generally similar trends, but much less pronounced, since we examine larger collections (except for the drugs). DSSTox is an exception, with a lower average number of rings than any of the other databases of known chemicals. GDB has a much lower average ring count than the other databases, which is merely indicative of the artificial limits imposed by enumeration (160 daltons, 11 atoms).

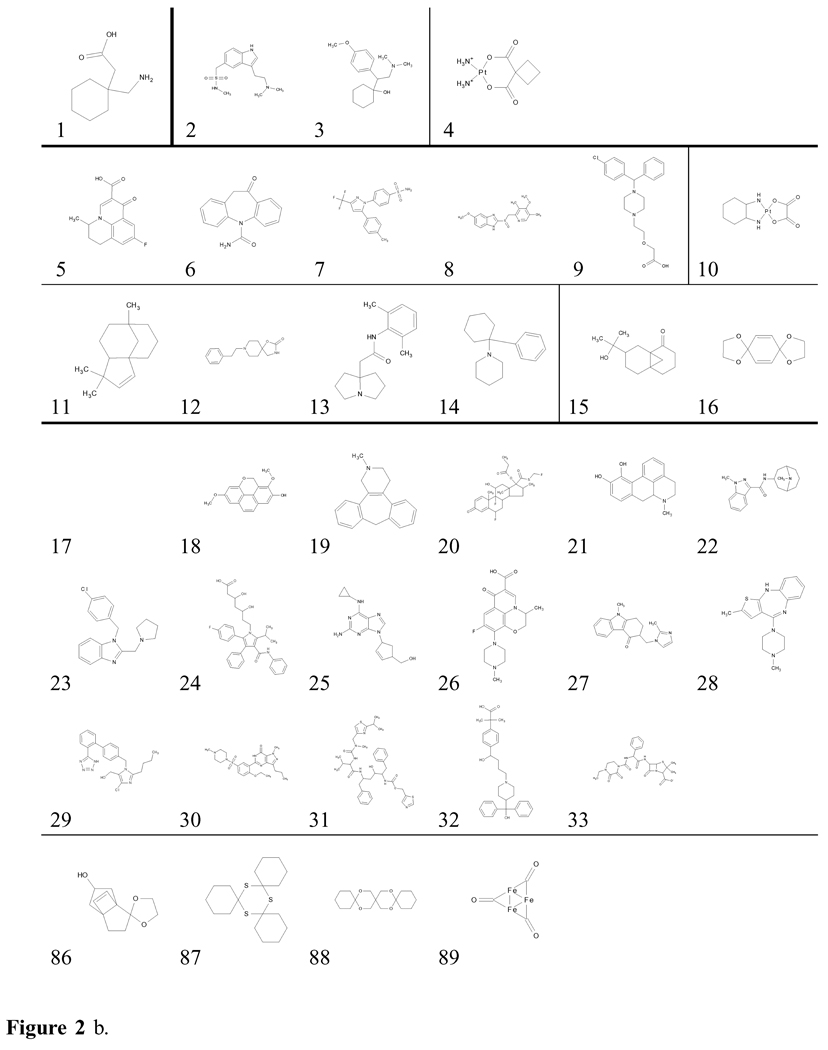
Figure 3 shows how the database population percentages correspond to the number of rings in more detail. All databases of known chemicals except DSSTox show fairly similar trends, peaking at three rings (except for Drugs which has 1.4% more two-ring than three-ring structures), with the majority of each database consisting of 2–4 ring molecules. DNP has the broadest peak, indicating that the number of rings in natural products are more evenly spread out than in other classes of chemicals. GDB has a different character than the above databases, peaking at one ring and then dropping sharply, nearly reaching zero at five rings. This is, of course, consistent with the limitations imposed on the database by the upper bound of 11 heavy atoms. DSSTox also peaks at one ring, however, its tail drops gradually, more like the other known chemical databases. Nearly $\frac{3}{4}$ of the scaffolds of toxic substances have two or less rings.

Figure 3.

The population percentages in the indicated databases with respect to the total database population for the number of rings per scaffold.

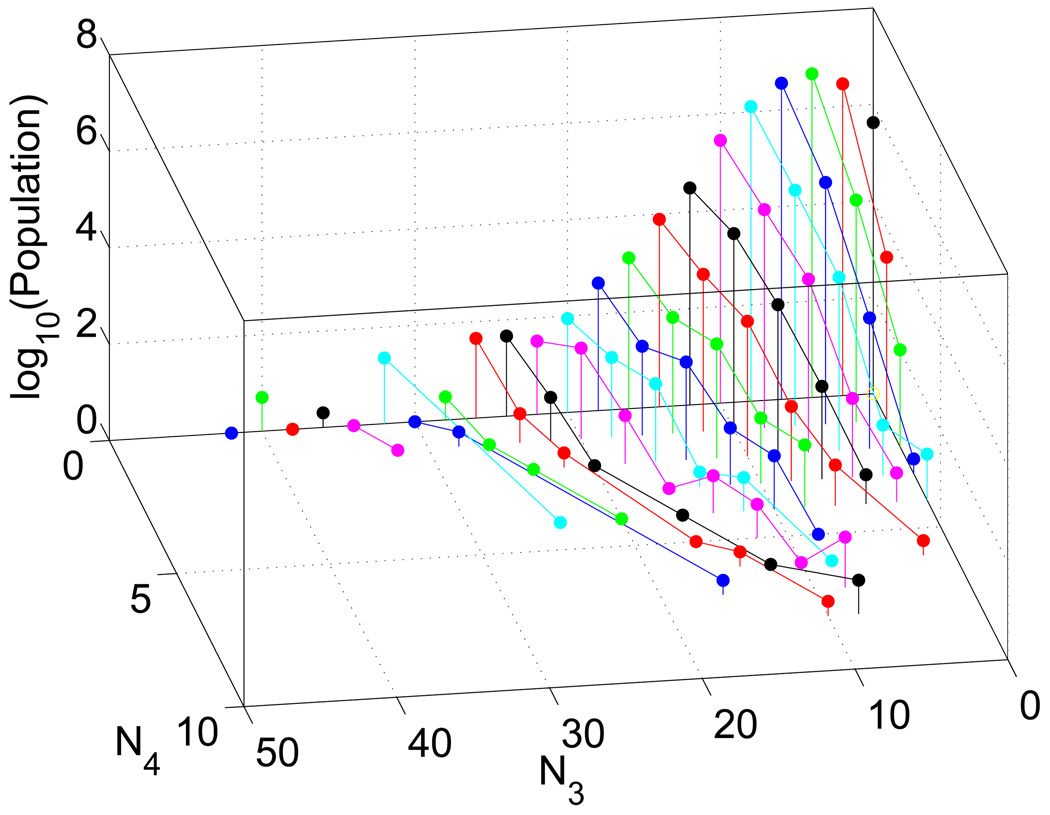
In Figure 4, the populations of scaffolds in the ChemNavigator database are displayed as a function of N₃, N₄ and r. (All of the individual databases showed similar trends.) The populations drop sharply as the number of rings increases. In addition, in this three-dimensional representation, we can see that the currently explored portion of chemical space is strongly biased against scaffolds with 4-nodes and hence 4-node scaffold topologies.

Figure 4.

Populations of scaffolds in the ChemNavigator database as a function of the number of 3- and 4-nodes, N₃ and N₄, and ordered, using connected stems of the same color, by the number of independent rings r. 5 outliers (scaffolds with N₃ > 50) have been excluded to make the main population trends of the graph easier to see.

The above trends are again evident when the numbers of topologies in the various databases are compared with the theoretical maxima that we have computed in Table 1. In Table 7, the fractions of the topologies present versus the theoretical possibilities are tabulated as a function of the number of rings, while in Table 8, the fractions for r = 1–6, categorized by N₃ and N₄, are displayed. Note that a blank entry means no topologies of the indicated class were present in the specified database, while 0.000 means that there were some examples present, but the number is zero to three decimal places. The fractions for r = 1 and 2 were 1.0 for all databases except DSSTox and were generally 1.0 for r = 3, the exceptions being Drugs, DSSTox and WOMBAT, all smaller databases. For r ≥ 4, the tendency towards structures with mostly 3-nodes starts to show up and becomes increasingly pronounced for higher values of r. This trend is especially notable in the Drugs and DSSTox collections.

Table 7.

The fractions of scaffold topologies in the indicated databases with respect to the theoretical maxima per number of rings r.

r =	1	2	3	4	5	6	7	8
ChemNavigator	1.000	1.000	1.000	0.91	0.542	0.134	0.013	0.001
DNP	1.000	1.000	1.000	0.795	0.425	0.082	0.007	0.000
Drugs	1.000	1.000	0.750	0.411	0.078	0.005	0.000	0.000
PubChem	1.000	1.000	1.000	0.986	0.854	0.299	0.036	0.002
PC actives	1.000	1.000	1.000	0.712	0.280	0.039	0.002	0.000
DSSTox	1.000	0.667	0.667	0.315	0.061	0.002	0.000	0.000
WOMBAT	1.000	1.000	0.917	0.658	0.278	0.052	0.004	0.000
merged	1.000	1.000	1.000	0.986	0.859	0.310	0.039	0.002
GDB	1.000	1.000	1.000	0.425	0.041	0.001	0.000	0.000

Table 8.

The fractions of scaffold topologies in the indicated databases with respect to the theoretical maxima per numbers of 3- and 4-nodes, N₃ and N₄, for structures with r = 1–6 rings. Blank entries indicate that no representatives of that class of topologies were found in the specified database.

r	N4	N3	Chem Nav.	DNP	Drugs	Pub Chem	PC actives	DSSTox	WOM BAT	merged	GDB
1	0	0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
2	0	2	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	1	0	1.000	1.000	1.000	1.000	1.000		1.000	1.000	1.000
3	0	4	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	1	2	1.000	1.000	0.800	1.000	1.000	0.600	1.000	1.000	1.000
	2	0	1.000	1.000		1.000	1.000		0.500	1.000	1.000
4	0	6	0.941	0.941	0.882	0.941	0.941	0.824	0.941	0.941	0.412
	1	4	1.000	0.900	0.467	1.000	0.900	0.300	0.933	1.000	0.433
	2	2	0.909	0.636	0.045	1.000	0.364		0.182	1.000	0.409
	3	0	0.250	0.250		1.000	0.250			1.000	0.500
5	0	8	0.930	0.887	0.479	0.944	0.831	0.394	0.831	0.944	0.127
	1	6	0.845	0.554	0.057	0.974	0.399	0.036	0.482	0.974	0.052
	2	4	0.364	0.303	0.004	0.868	0.127	0.004	0.053	0.873	0.022
	3	2	0.057	0.136		0.534				0.557
	4	0	0.300			0.400				0.400
6	0	10	0.642	0.451	0.054	0.851	0.345	0.031	0.482	0.851	0.008
	1	8	0.303	0.122	0.006	0.596	0.057	0.003	0.084	0.611	0.001
	2	6	0.059	0.053	0.000	0.228	0.011		0.009	0.241
	34	4	0.009	0.022		0.071	0.002		0.001	0.080
	4	2	0.007	0.007		0.060				0.060
	5	0				0.214				0.214

Considering the 4-ring scaffolds in detail, in most of the databases examined, 16 out of the 17 possible topologies are present for the scaffolds consisting only of 3-nodes. The missing structure is the molecule labeled by 17 in Figure 2a which resembles a Möbius strip and is the only topology of the group that does not have a planar representation. Molecules with nonplanar graphs are extremely rare; the first known example of a molecule with this topology was synthesized by Walba.³⁸ On the other extreme, most or all of the four 4-node only topologies are missing from the databases, except for PubChem which does have them all. For the mixed 3/4-node topologies, PubChem has examples of all and ChemNavigator nearly all, while the other databases contain some fraction of the possibilities. The generated structures of GDB enumerate only 40–50% of the various 4-ring topologies. All of the minimal scaffolds of the 4-node only topologies and 13 out of 17 of the 3-node only topologies can be represented with 11 carbons or less, for example (see Figure 2a), so the filtering of chemically unstable and synthetically infeasible compounds (including nonplanar graphs and all 3- and 4-member rings²) has removed a substantial fraction of topology types from this database.

The fraction of topologies compared to what is possible categorized by number of rings, or rings and 3- or 4-nodes, are indicators of the diversity of a database. Another is the population fraction of each distinct topology within the database. Table 9 displays the population percentages (with respect to the database’s total population) of classes of topologies categorized by N₃ and N₄ for r = 0–6. Here, the bias against scaffolds containing 4-nodes is very strong. Moreover, while the distributions peak for 3-ring scaffolds containing only 3-nodes, there are significant percentages of structures containing 1–5 rings, and zero rings in some cases such as for DNP, Drugs and DSSTox.

Table 9.

The population percentages in the indicated databases with respect to the total database population for topologies with the given numbers of 3- and 4-nodes, N₃ and N₄, for structures with r = 0–6 rings. Blank entries indicate that no representatives of that class of topologies were found in the specified database. r = 0 values represent structures that contain no rings.

r	N4	N3	Chem Nav.	DNP	Drugs	Pub Chem	PC actives	DSSTox	WOM BAT	merged	GDB
0	0	0	0.245	8.633	6.492	2.466	3.837	25.057	1.641	1.225	15.414
1	0	0	2.979	11.831	16.630	8.212	10.771	29.808	6.588	5.248	41.721
2	0	2	20.808	15.390	25.492	24.094	18.384	19.515	16.680	21.981	29.521
	1	0	0.017	0.285	0.109	0.112	0.273	0.060		0.061	2.425
3	0	4	36.792	19.126	23.669	30.813	26.067	12.746	28.190	34.064	7.299
	1	2	0.287	1.172	0.547	0.523	0.664	0.179	0.659	0.399	2.090
	2	0	0.001	0.023		0.015	0.036	0.001		0.007	0.110
4	0	6	25.694	13.106	16.156	20.376	20.370	7.612	25.496	23.463	1.008
	1	4	0.729	2.829	1.349	0.931	2.132	0.664	1.184	0.838	0.300
	2	2	0.004	0.215	0.036	0.031	0.051	0.005		0.016	0.041
	3	0	0.000	0.006		0.002	0.013			0.001	0.001
5	0	8	9.178	8.721	4.413	7.382	8.652	2.095	11.800	8.492	0.057
	1	6	0.554	2.115	0.839	0.682	1.103	0.383	0.971	0.630	0.010
	2	4	0.028	1.097	0.036	0.064	0.180	0.026	0.073	0.047	0.002
	3	2	0.000	0.022		0.002				0.001
	4	0	0.000			0.001				0.000
6	0	10	2.004	3.517	1.714	2.044	3.001	0.741	3.524	2.071	0.001
	1	8	0.238	1.808	0.511	0.356	0.651	0.128	0.472	0.301	0.000
	2	6	0.028	0.657	0.036	0.063	0.219		0.106	0.046
	3	4	0.000	0.137		0.006	0.013		0.010	0.003
	4	2	0.000	0.0005		0.0001				0.000
	5	0				0.000				0.000

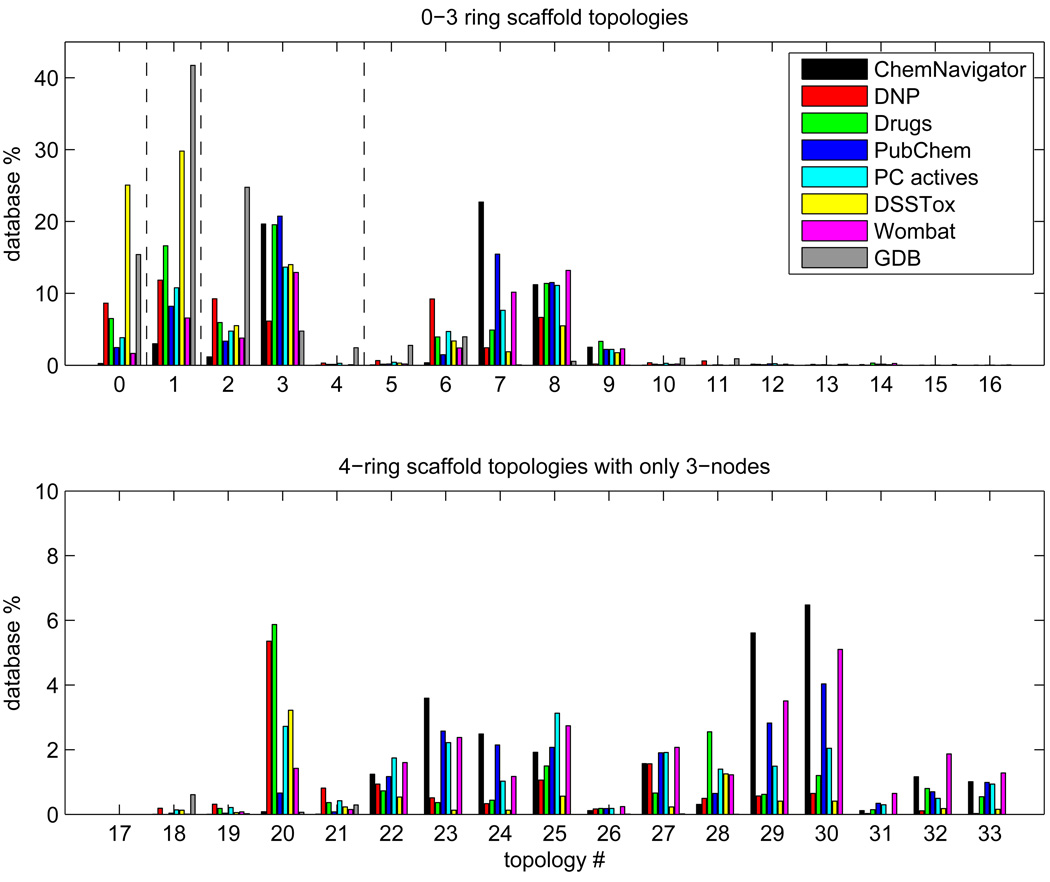
Figure 5 displays for each database the population percentages of the scaffold topologies 1– 33 shown in Figure 2a along with the situation when there are no rings present. Consider the seven databases of known chemicals first. Several competing trends are evident. The fraction of topologies possessing even one 4-node (numbers 10–16) is very small. 3-node only topologies that contain a nonlinear cluster of three or more fused rings are also rare (i.e., topology numbers 5, 17–19, 21 and 26, as opposed to 6, 20, 27 and 28, which are well populated linear clusters). Among the remaining topology types, those that consist of three or more rings emanating from a central vertex or vertices (i.e., 9 and 31–33) are the least common. In addition, it can be seen that the ChemNavigator and PubChem values show the same general qualitative trends compared to the other databases. ChemNavigator does, however, have fewer no-ring and single-ring structures than PubChem. Also, DNP topologies show a distinctive trend, having a higher proportion of linear fused ring assemblies than other databases (e.g., 6 and 20), but very few topologies involving multiple rings emanating from a central vertex or vertices. DNP (and Drugs) also have a considerable percentage of structures with no rings. DSSTox, as noted earlier, has a preponderance of no-ring and single-ring structures, and no examples at all of any 4-node only topologies and very few with any 4-nodes at all.

Figure 5.

The percentage frequencies of the first 33 scaffold topologies of Figure 2 in the indicated databases. The entry labeled zero indicates the database percentages of structures that do not contain rings. The dashed lines in the top graph divide the results into sets of topologies possessing 0, 1, 2 or 3 rings, respectively. The bottom graph displays the frequencies for 4-ring topologies containing only 3-nodes. Note that the vertical scales in the two graphs are different.

GDB also has a considerable percentage of structures with no rings. The other trends are also similar, except that unlike the other databases, topologies possessing a 4-node are not quite as rare. In addition, GDB favors the maximally fused 2- and 3-ring topologies, numbers 3 and 5, respectively, more than the other databases.

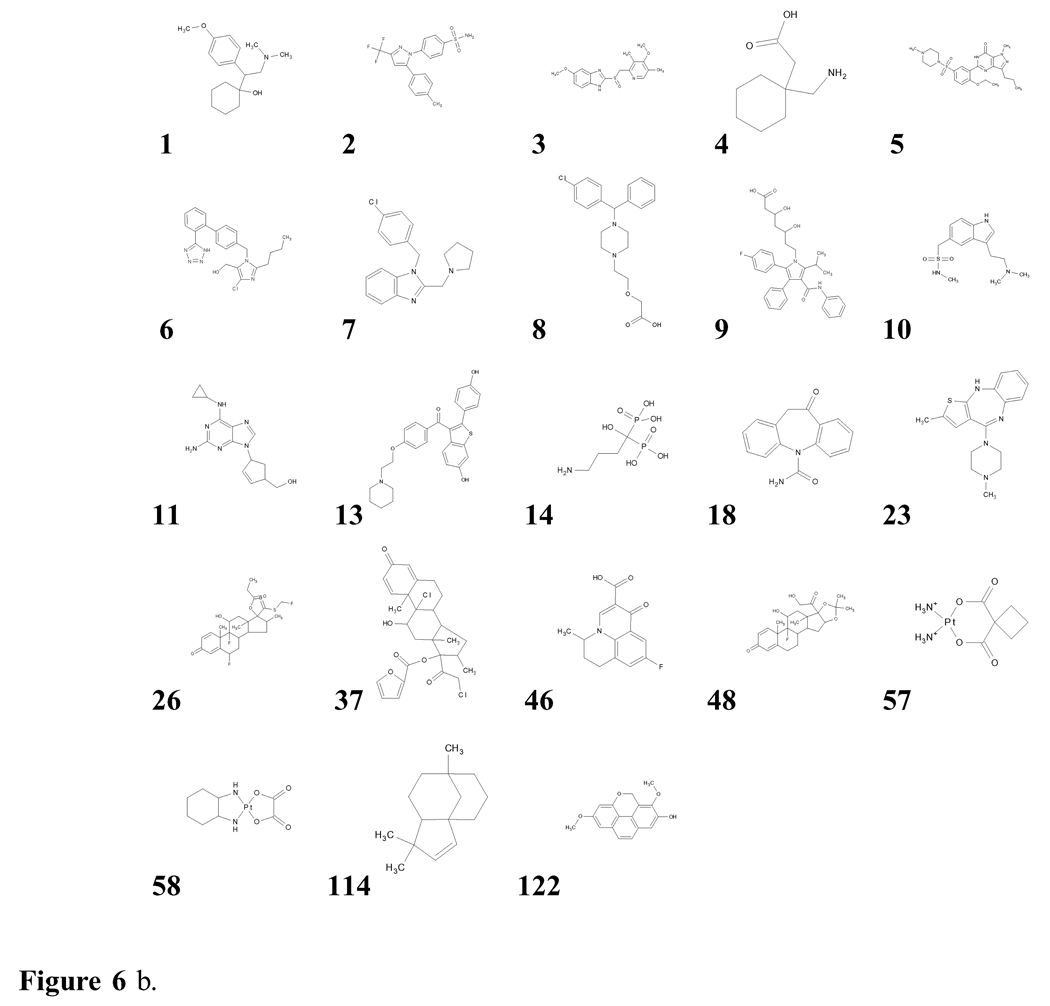
Table 10 presents the population percentages of the 10 most frequent topologies in each of the databases. These topologies are identified by their rank in the merged database; they are displayed in Figure 6a and examples of actual molecules are provided in Figure 6b.

Table 10.

The percentages of the 10 most frequent topologies present in each of the databases examined. The numbers in boldface refer to the rank in the merged database; the corresponding scaffold topologies are displayed in Figure 6a. The numbers at the bottom are the sum of the 10 percentages above. At least half the population of each database lies above the horizontal line segment dividing the corresponding column.

Chem Navigator		DNP		Drugs		PubChem		PC actives		DSSTox		WOMBAT		GDB
2.	22.694	4.	11.831	1.	19.548	1.	20.740	1.	13.642	4.	29.808	3.	13.200	10.	41.721
1.	19.646	10.	9.249	4.	16.630	2.	15.457	3.	11.101	14.	25.057	1.	12.901	14.	24.765
3.	11.196	18.	9.226	3.	11.379	3.	11.509	4.	10.771	1.	13.997	2.	10.160	1.	15.414
5.	6.474	14.	8.633	14.	6.492	4.	8.212	2.	7.652	10.	5.517	4.	6.588	4.	4.755
6.	5.609	3.	6.643	10.	5.945	5.	4.033	10.	4.743	3.	5.492	5.	5.101	18.	3.953
7.	3.590	1.	6.140	26.	5.872	10.	3.354	18.	4.681	18.	3.372	10.	3.779	46.	2.765
4.	2.979	26.	5.356	2.	4.887	6.	2.824	14.	3.837	26.	3.218	6.	3.510	57.	2.425
8.	2.505	48.	2.872	18.	3.939	7.	2.573	11.	3.130	2.	1.865	11.	2.741	58.	0.977
9.	2.486	2.	2.437	8.	3.319	14.	2.466	26.	2.721	8.	1.737	18.	2.399	114.	0.910
13.	2.094	37.	1.625	23.	2.553	8.	2.204	7.	2.220	23.	1.252	7.	2.375	122.	0.610
79.273		64.012		80.564		73.372		64.498		91.315		62.754		98.295

Figure 6.

Figure 6 a. The most frequent topologies present in the databases examined, numbered (in boldface) by their rank in the merged database. The second value for each entry is the topology number, 1–33 and 86–89 of which are shown in Figure 2a

Figure 6 b. Examples³⁹ from the databases examined of the most frequent topologies present, numbered by their rank in the merged database (compare with Figure 6a).

Only 18 distinct topologies are found in the collection of the 10 most common topologies from each of the seven databases of known chemicals, making up from 62.8–91.3% of the total populations. None of these topologies possess 4-nodes. There is some tendency for DNP to have more and DSSTox to have fewer scaffolds with linear assemblies of fused rings than the other databases (see Table 10 and Table 11). In general, the biologically oriented databases, except DSSTox, have greater percentages within their top 10 topologies exhibiting linear fused ring assemblies than the more general databases (i.e., ChemNavigator and PubChem). For GDB, five additional topologies not included in the above 18 define its second five most frequent topologies (7.7% of the population; note that 90.6% of the population is included in the top five topologies). Three of these contain 4-nodes, two of which are spiro. There is also a tendency toward linear assemblies of fused rings in this database (mostly due to the topology in Figure 6a ranked ¹⁰), however, note that two of GDB’s most frequent scaffold topologies (ranked 46 and 122 in Figure 6a) are nonlinear clusters of fused rings, which are rare in the other databases.

Table 11.

The number of rings (first number in each column pair) and the size of the largest fused ring system (second number) in each of the 10 most frequent topologies in the indicated databases. Nonlinear assemblies of fused rings are marked by an asterisk.

Chem Navigator		DNP		Drugs		PubChem		PC actives		DSSTox		WOMBAT		merged		GDB
3	1	1	1	2	1	2	1	2	1	1	1	3	2	2	1	2	2
2	1	2	2	1	1	3	1	3	2	0	0	2	1	3	1	0	0
3	2	3	3	3	2	3	2	1	1	2	1	3	1	3	2	2	1
4	2	0	0	0	0	1	1	3	1	2	2	1	1	1	1	1	1
4	1	3	2	2	2	4	2	2	2	3	2	4	2	4	2	3	3
4	2	2	1	4	4	2	2	3	3	3	3	2	2	4	1	3	3*
1	1	4	4	3	1	4	1	0	0	4	4	4	1	4	2	2	1
3	1	5	5	3	3	4	2	4	2	3	1	4	2	3	1	3	2
4	1	3	1	3	1	0	0	4	4	3	1	3	3	4	1	3	3
5	2	5	4	4	3	3	1	4	2	4	3	4	2	2	2	4	4*

If the 32 most frequent scaffolds and the acyclic compounds found in Bemis and Murcko’s analysis of the Comprehensive Medicinal Chemistry database⁴⁰ are converted to topologies, we find the following frequencies > 1%, where the boldfaced numbers indicate the rank in our merged database:

     1. 16.582     4. 14.355     14. 5.977     10. 5.527     26. 4.824     3. 4.336     18. 2.812

These values are remarkably similar to the results for Drugs in Table 10. Note that a substantial fraction (44.26%) of Bemis and Murcko’s data (of less frequent scaffolds) was not published. Only topology ³ has a significantly different placement in the two orderings.

The total number of scaffold topologies containing 8 rings or less is 1,547,689 (see Table 1). Of these, 850,878 (54.98%) contain spiro nodes, and 164,375 (10.62%) are nonplanar as determined by nauty.⁴¹ There are 9,474 topologies in the merged database with 8 or less rings, so 99.39% of the possible scaffold topologies are not found in any of the databases examined. Of those missing, 51.58% are planar and have spiro nodes, 3.60% are nonplanar with spiro nodes, and 7.09% are nonplanar and lack spiro nodes. Only 12 nonplanar and 2,099 spiro node topologies (all of which are planar) are present in the merged database. 9 of the nonplanar topologies are found only in PubChem and the total number of molecules represented by such topologies in the merged database is a mere 44, agreeing with Walba’s assessment³⁸ concerning the rarity of chemicals with nonplanar graphs. Of the databases that have topologies unique to them for r ≤ 8, the only biologically oriented ones are DNP and WOMBAT with just a few examples (372 and 49 molecules, respectively, representing about half as many topologies), while 55.48% of PubChem’s r ≤ 8 topologies (4959 / 8939) are present only there.

We computed the scaffold to SMILES ratios of the various known chemical databases for the 17 scaffold topologies that are common to the corresponding 10 most frequent topology collections in Table 10 (topologies ranked 1–11, 13, 18, 23, 26, 37 and 48 in Figure 6a), comprising at least 55% of the population of each of the databases. The average numerical rank (1–8) of the ratios taken from highest to lowest:

     Drugs     DSSTox     PC actives     DNP     WOMBAT     PubChem     ChemNavigator     merged     1.412     1.765        2.882       4.412    4.706       6.706          6.824          7.294

follow exactly the order of the database sizes from smallest to largest, reinforcing the observation for Table 4 that the size of the database has a significant influence on the observed ratio.

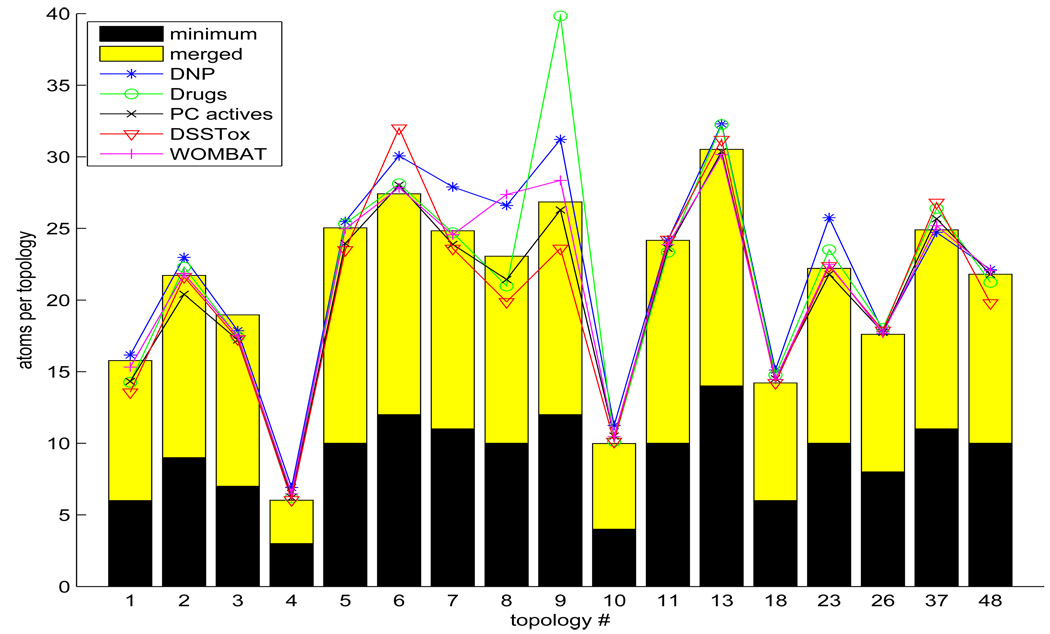
For the same set of databases and scaffold topologies, the average number of atoms per scaffold that make up each topology class are graphed in Figure 7. The two general databases, ChemNavigator and PubChem, have been omitted as they follow very similar trends to the merged database. The black bars indicate the number of atoms necessary to produce minimal scaffolds (a minimal loop is defined by 3 atoms), and the ratio of the merged averages to these is nearly constant, approximately 2.33, due in large part to the wealth of 6-membered rings throughout chemistry (note topology ⁴). (We note that the minimal scaffold is achieved in the merged database for 8 of the topologies, typically the smaller ones.) The anomalous jump at ⁹ for Drugs is derived from only 12 examples, one of which is the 128 atom scaffold of nesiritide. Omitting this outlier brings the mean down to 31.82. Topologies ranked ^6–9 and ²³ exhibit the most variability (3- and 4-ring structures with 1–3 dangling rings). Generally, DNP scaffolds have the most and DSSTox scaffolds the fewest atoms per topology class, although there are some exceptions.

Figure 7.

The average number of atoms comprising the scaffolds in the indicated databases that are members of the given ranked topologies (see Figure 6a). Minimum refers to the number of nodes needed to produce a minimal representative of the topology (see Figure 1d). The values for the merged database are the total bar heights.

4 Conclusions

We report the scaffold distribution and topological properties for seven databases of existing chemicals: ChemNavigator, DNP, Drugs, PubChem, PubChem “actives”, DSSTox and WOMBAT, to which we include a comparison with GDB, a collection of virtual small organic molecules. The greatest topological diversity is observed in PubChem. This is not surprising, since this is a public repository where information providers routinely upload a large variety of chemical structures.

The databases analyzed in this paper are already dated, but updating the values will not change the qualitative aspect of our results. We will provide semi-annual updates for some of these tables on our UNM Biocomputing website. For 6-ring scaffolds, PubChem molecules cover less than a third of the possible theoretical topological space (limited to ≤ 4-nodes), and this fraction declines rapidly for greater numbers of rings.

The least topologically diverse set is GDB, which is not surprising either. GDB has been developed using a “bottom-up” strategy for chemical space enumeration, where changes occur incrementally, one atom or one bond at a time algorithmically added to a list. By contrast, we regard this work on exhaustive enumeration as a “top-down” strategy, where the landscape of possibilities is mapped out to completeness. Our earlier, unpublished work, modifying one SMILES atom at a time, produced over 1.45 billion unique SMILES—all C.sp3 based, and all single bonds, up to 8 rings and 20 atoms.^8–11 We abandoned that strategy because this approach would quickly reach the asymptotic wall of combinatorial explosion: consider that, corresponding to the 1.45 billion alkanes, there are probably one billion mono-alkenes, mono-amines and mono-alcohols, to name a few possibilities while approximating for symmetry-related redundancy. The GENSMI algorithm became increasingly tedious to use at higher levels of complexity. Using the “top-down” strategy, one can drill down and achieve completeness using a divide and conquer approach. Completeness tests would be limited to only one topological subset, without having to compare all newly generated molecules to all others having the same number of rings and nodes. Thus, the GDB approach continues to be useful in exploring all possibilities of the low-molecular-weight chemical space, but topological landscaping brings a distinct perspective to the same problem.

Fine-grained enumerations of the CSSM do provide potential organic molecules from which a variety of chemical, geometrical and topological properties can be extracted, as well as possible drug leads, etc. Coarse-grained approaches like ours sacrifice details such as atom and bond types in the interests of restraining the inevitable combinatorial explosion, allowing for a much broader but shallower perspective which restricts itself to topological properties. Even coarser-grained explorations can be performed, such as the one by Lipkus,⁴² which classified the CSSM with a trio of topological descriptors. This work was performed before complete enumerations were available, so comparisons with the theoretical possibilities were limited.

The granularity of scaffold topological enumeration has an important feature when applied to real chemical databases. Lightly populated regions of structures rich in complexity, where the combinatorics make it infeasible to perform fine-grained enumeration, are well broken apart by our classification. Alternatively, heavily populated regions of simple topologies, where the combinatorics are much easier, are well suited for complete fine-grained subclassifications, and so the two levels of granularity are actually complementary. Scaffold topologies can be viewed as a low-resolution atlas of the major topological classes of organic ring systems (r ≤ 8), while fine-grained enumerations act as detailed roadmaps of particular regions.

In our analyses, we found a strong bias in all collections of existing chemical compounds (especially DSSTox, which is nearly devoid of 4-nodes) toward 3-node topologies, i.e., vertices branching out in three different directions (see Table 8 and Table 9). Other topological classes, such as those containing a nonlinear cluster of three or more fused rings (topology numbers 5, 17–19, 21 and 26 in Figure 2a) or three or more rings linked to a central vertex or vertices (topology numbers 9, 31–33), are relatively uncommon (the latter especially in the case of DNP) as was seen in Figure 5. Indeed, we see a modest tendency toward more linear fused ring assemblies in the biologically oriented databases (especially DNP), except for DSSTox, which is underrepresented by these structures. There is also a tendency toward fewer overall rings in DNP, Drugs and especially DSSTox, all of which also have significant fractions of molecules that do not contain any rings at all. Finally, we note compounds possessing nonplanar graphs are quite rare.

The average fraction of atoms that make up the scaffold tends to be lower for biologically active molecules, indicating that they have on average a higher number of chemical moieties substituted to the central scaffold, presumably to enhance pharmacophore diversity, thus contributing to biological activity. The scaffolds of natural products generally have more atoms than average, however.

Looking at the 10 most frequent topologies for each database, we find that a small number of topologies characterize most of the molecules. Only 8 topologies (1–5, 10, 14 and 18 in Figure 6) are needed to characterize half the population of the each of the eight databases. 62.8–91.3% of the database populations are characterized by 18 topologies. On the other hand, most of the topologies encountered are represented by a single or very small number of examples. This is consistent with the findings of other researchers in the context of scaffolds.^33,40 Only 0.61% of the possible scaffold topologies containing 8 rings or less have actual chemical representatives. As has also been seen by others,^10,12,13 the CSSM is vast and almost completely unexplored. The various databases examined, especially the biologically oriented ones, occupy very restricted regions.

We have developed a website⁴³ interfaced to a MySQL database, where one can enter a SMILES and get back a page displaying data relevant to the molecule’s scaffold topology. The output includes 2D diagrams of the original molecule and a minimal representative of the scaffold topology, some numerical details related to the topology, the number of matches of this topology in the public database PubChem, and some examples of this topology from PubChem. The SMILES of all molecules possessing this topology can also be extracted from the database.⁴⁴ In addition, the user can access theoretical results from our enumeration of all possible scaffold topologies. Depictions of all minimal representatives of scaffold topologies up through 4 rings are available. We will continue to extend the capabilities of this site, and provide updates of scaffold topology distributions for a number of databases.

To generate a scaffold topology, we effectively collapse a molecular structure to its essential ring and connecting linear structure. In the paired paper of Pollock et al.,¹ scaffold topologies are systematically built up from the most basic topologies of one and two rings, and then are uniquely characterized. Once a topology is available, a minimal or more complicated scaffold can be produced. The two papers, therefore, look at the problem of CSSM exploration from the opposing points of view of what is possible and what actually occurs.

The unique characterization of scaffold topologies makes it possible to create an efficient, searchable database that allows for rapid coarse-grained classification of organic molecules. For example, to analyze the scaffold topologies for the approximately 25 million unique SMILES in the merged database required less than 4 CPU-hours on a 2.2 GHz Linux system with 32 Gb of RAM. Such population-based topological analyses can easily be performed using this categorization technique, so this methodology complements existing techniques for CSSM mapping.