Abstract
Background and purpose:
Microemulsion propofol was developed to eliminate lipid solvent-related adverse events of long-chain triglyceride emulsion (LCT) propofol. We compared dose proportionality, pharmacokinetic and pharmacodynamic characteristics of both formulations.
Experimental approach:
The study was a randomized, two-period and crossover design with 7-day wash-out period. Microemulsion and LCT propofol were administered by zero-order infusion (0.75, 1.00 and 1.25 mg·kg−1·min−1) for 20 min in 30 beagle dogs (male/female = 5/5 for each rate). Arterial samples were collected at preset intervals. The electroencephalographic approximate entropy (ApEn) was used as a measure of propofol effect. Dose proportionality, pharmacokinetic and pharmacodynamic bioequivalence were evaluated by non-compartmental analyses. Population analysis was performed using nonlinear mixed effects modelling.
Key results:
Both formulations showed dose proportionality at the applied dose range. The ratios of geometric means of AUClast and AUCinf between both formulations were acceptable for bioequivalence, whereas that of Cmax was not. The pharmacodynamic bioequivalence was indicated by the arithmetic means of AAC (areas above the ApEn time curves) and E0 (baseline ApEn)–Emax (maximally decreased ApEn) between both formulations. The pharmacokinetics of both formulations were best described by three compartment models. Body weight was a significant covariate for V1 of both formulations and sex for k21 of microemulsion propofol. The blood-brain equilibration rate constants (ke0, min−1) were 0.476 and 0.696 for microemulsion and LCT propofol respectively.
Conclusions and implications:
Microemulsion propofol was pharmacodynamically bioequivalent to LCT propofol although pharmacokinetic bioequivalence was incomplete, and demonstrated linear pharmacokinetics at the applied dose ranges.
Keywords: pharmacokinetics, pharmacodynamics, propofol, dog, EEG, microemulsion
Introduction
We have developed a microemulsion formulation of propofol (Aquafol™, Daewon Pharmaceutical Co., Ltd., Seoul, Korea) to eliminate lipid solvent-related adverse events of the standard long-chain triglyceride emulsion (LCT) form of propofol (Diprivan®, AstraZeneca, London, UK) such as fat embolism, hypertriglyceridemia and pancreatitis (Park et al., 2003; Devlin et al., 2005; Yamakage et al., 2005). The original formulation of Aquafol™ was composed of 1% propofol, 8% polyethylene glycol 660 hydroxystearate (Solutol HS 15; BASF Company Ltd., Seoul, Korea) as a nonionic surfactant and 5% tetrahydrofurfuryl alcohol polyethylene glycol ether (Glycofurol; Roche, Basle, Switzerland) as a cosurfactant (Kim et al., 2007). This formulation was recently reconstituted with 10% purified poloxamer 188 (PP188) as a nonionic block copolymer surfactant and 0.7% polyethylene glycol 660 hydroxystearate as a nonionic surfactant (Lee et al., 2008), due to dose-limiting toxicities of the polymeric vehicles, such as skin rash (CTCAE v3.0 grade 2) (CTEP, 2006), pain, tenderness and redness at injection sites, urticaria, fever and dizziness, increases of total bilirubin and lactate dehydrogenase, vomiting, chest discomfort or pain (CTCAE v3.0 grade 1 for all) (CTEP, 2006).
Long-chain triglyceride emulsion propofol has a fast, potent and concentration-dependent effect on the central nervous system (CNS) with linear pharmacokinetics over a clinically relevant dose range, for which it has gained wide use in anaesthesia. Dose proportionality is a desirable property as it makes predicting the effects of dose adjustments easier (Hummel et al., 2008). It may be mainly affected by dose range, but not by species or size (Takizawa et al., 2004). In our previous study, reformulated microemulsion propofol showed nonlinear pharmacokinetics over the dose range of 0.5–1.5 mg·kg−1·min−1 in rats (Lee et al., 2008). LCT propofol shows linear pharmacokinetics over the dose range of 1.5–12 mg·kg−1·h−1 in humans (Schnider et al., 1998).
Pharmacokinetic and pharmacodynamic analyses of intravenous anesthetics provide us with insight into the factors affecting the onset and offset of drug effects. In particular, the comparison of pharmacodynamic characteristics between formulations may provide us with practical knowledge for drug effectiveness (Minto and Schnider, 2008). Modifications of propofol formulation may result in altered pharmacokinetic and pharmacodynamic characteristics (Dutta and Ebling, 1997; 1998;). PP188 in reformulated microemulsion propofol is a highly water-soluble nonionic polymer and is preferentially distributed to the extracellular fluid with minimal uptake into tissues (Grindel et al., 2002a). This may result in altered pharmacokinetic characteristics of reformulated microemulsion propofol, particularly, distribution, and hence, may affect the onset and offset of drug effect (Kim et al., 2007).
In the field of anesthesia, the target-controlled infusion system (TCI system, computer-controlled infusion pump) for propofol is frequently used for the induction and maintenance of anesthesia (Schuttler et al., 1988). Pharmacokinetic parameters to control plasma concentration of propofol (target plasma concentration-controlled infusion) and ke0 value to control effect-site concentration of propofol (target effect-site concentration-controlled infusion) are incorporated into the TCI system. The main purpose of population pharmacokinetic-pharmacodynamic analysis for propofol formulations is to obtain accurate and formulation-specific pharmacokinetic parameters and ke0 value for computer-controlled infusion of propofol formulations.
The aims of this study were to evaluate dose proportionality, formulation-specific disposition of propofol, pharmacokinetic and pharmacodynamic bioequivalence between microemulsion and LCT propofol in beagle dogs. In addition, the pharmacokinetics and pharmacodynamics of microemulsion propofol were also characterized by population analysis using nonlinear mixed-effects modelling.
Methods
Animals
This study was reviewed and approved (No. 2007-11-174) by the Institutional Animal Care and Use Committee of Asan Institute for Life Sciences, Asan Medical Center (Seoul, Korea) and complied with the Institute of Laboratory Animal Resources guide. Thirty three healthy beagle dogs (Central Lab. Animal Inc., Seoul, Korea) were included in the study. Three male dogs were used in a preliminary study and 30 dogs were used in the main pharmacokinetic and pharmacodynamic study (male/female = 15/15). The dogs were housed with controlled light/dark cycle (light on between 6:00 a.m. and 6:00 p.m.), an ambient temperature of 21–22°C and unlimited access to standard laboratory dog diet and water. Except for ad libitum water, the animals were fasted for 12 h prior to the induction of anesthesia.
Study preparations
Anesthesia was induced with the inhalation of isoflurane. After the animals were recumbent, they were intubated and mechanically ventilated with isoflurane (2.5%) in oxygen (100%), maintaining the end-tidal carbon dioxide partial pressure 30 and 35 mmHg. Capnography was instrumented and monitored between tracheal tube and circuits. Oxygen saturation was monitored with a pulse oximeter placed on the tongue. A urinary catheter was put in place. A femoral artery was cannulated using a cut-down tube (C3-350 mm, Korea Medical Supply Co., Ltd., Seoul, Korea) to obtain blood samples for the assay of plasma propofol concentrations and to measure arterial blood pressure (Solar 8000M, GE Medical Systems, Milwaukee, WI, USA). Body temperature was measured in the rectum and was maintained between 36.5 and 38°C using a warming pad (BLAKETROL®II, CSZ Products, Inc., Cincinnati, OH, USA). Lead II of the electrocardiogram was used to measure heart rate and to assess cardiac rhythm (QECG-3, Laxtha Inc., Daejeon, Korea). An intravenous catheter was placed in a cephalic vein and normal saline was infused at a rate of 20 mL·h−1. Vecuronium (0.1 mg·kg−1) was administered intravenously as needed for muscle relaxation. Needle-type electroencephalograph electrodes (Laxtha Inc., Daejeon, Korea) were placed over the frontal and occipital regions, which were similar to Modified Combinatorial Nomenclature in human medicine (F3, F4, O1 and O2) (Pellegrino and Sica, 2004).
After completion of preparation, the inspired concentration of isoflurane was reduced by 0.5% every 7–8 min to 0.5%. The baseline data were gathered at 0.5% inspired concentration of isoflurane. The electroencephalogram, electrocardiogram, mean arterial pressure (MAP), body temperature, end-tidal carbon dioxide partial pressure and peripheral oxygen saturation were recorded.
Drug administration
According to a previous study (Beths et al., 2001), canine anesthesia of adequate depth and satisfactory quality was achieved with plasma propofol concentrations of 2.5–4.7 µg·mL−1. On the basis of computer simulations (ASAN Pump, version 1.5, Bionet Co., Ltd., Seoul, Korea) with pharmacokinetic parameters obtained from various sources (Cockshott et al., 1992; Nolan and Reid, 1993; Beths et al., 2001), a minimal infusion rate to obtain 3 µg·mL−1 or higher of plasma propofol concentration following constant infusion for 10 min was determined to be 0.75 mg·kg−1·min−1. In a preliminary animal study, maximal electroencephalographic effect was observed following constant infusion at a rate of 0.75 mg·kg−1·min−1 for 20 min. As the infusion rate increased stepwise by 0.25 mg·kg−1·min−1, times to reach maximal electroencephalographic effect and to recover to baseline effect were faster and prolonged respectively. Pharmacokinetics and pharmacodynamics of microemulsion and LCT propofol were, therefore, determined upon zero-order infusion at the rates of 0.75, 1.00 and 1.25 mg·kg−1·min−1 (male/female = 5/5 per each infusion rate) for 20 min. The two propofol formulations were administered using an infusion pump (Perfusor® Compact, B.Braun Melsungen Ag, Melsungen, Germany). Each animal received both propofol formulations in a crossover fashion separated by a 7-day washout period, and the order of the drug administration was randomized.
Blood sample acquisition and drug assay
Arterial blood samples (3 mL) were collected immediately before (0 min) and at 2, 5, 7, 10, 15, 20, 30, 45, 60, 90, 120, 180, 240, 300 and 360 min after the start of infusion. Samples were collected in EDTA tubes and centrifuged for 30 min at 252×g. The plasma was stored at −70°C until assay.
Propofol in plasma was measured as follows. A 100 µL aliquot of plasma was mixed with 200 µL of acetonitrile, containing thymol as internal standard (100 ng·mL−1), at room temperature to deproteinize the sample. After vortex-mixing for 2 min and centrifugation (16 800×g for 5 min at 4°C), 20 µL aliquots of the supernatants were analysed by high-performance liquid chromatography using a Capcell Pak C18 UG120 column (Shiseido Fine Chemicals, Tokyo, Japan) and a mixture of acetonitrile and water (70:30, v/v, pH 4.0) as a mobile phase. The components of the column effluent were monitored by a fluorometric detector with excitation and emission wavelengths set at 276 nm and 310 nm respectively.
The lower limit of quantification of propofol was 20 ng·mL−1. The calibration curve was linear over the range of 20–10 000 ng·mL−1, with the coefficients of determination (R2) greater than 0.999. Intra-assay precision values were 0.8–2.2%. Inter-assay within-day and between-day precision values were less than 2.2% and 5.2% respectively. Intra-assay accuracy values were 94.2–105.4% of the nominal value. Inter-assay accuracy values were 95.2–105.5% of the nominal value.
Electroencephalographic analysis
The electroencephalographic activities of the four channels were continuously recorded by QEEG-8 (Laxtha Inc., Daejeon, Korea). The sampling frequency was 256 Hz. Baseline electroencephalographic activity was recorded for 5 min prior to the administration of both propofol formulations.
According to Pellegrino and Sica (2004), the amplitude of the electroencephalographic signal might be higher at the occipital area (O1 and O2) than at frontal area (F3 and F4) in dogs. Therefore, the signals from O1 and O2 were selected to analyse electroencephalography for population pharmacodynamic analysis.
The raw electroencephalographic signal was filtered between 0.5 and 50 Hz for online calculation of the electroencephalographic approximate entropy (ApEn, Telescan version 2.89 and Complexity version 2.83, Laxtha Inc.), which quantifies the regularity of the data time series and shows better baseline stability as a measure of the arousal state of the CNS than other univariate descriptors (Bruhn et al., 2002; Noh et al., 2006). To calculate ApEn, the length of the epoch (N) was 2560, the number of previous values (m) used to predict the subsequent values were 2 and a filtering level (r) was 15% of the SD of the amplitude values. Smoothing by means of a simple moving average was applied to the calculation of ApEn. The number of neighboring points utilized was seven. Serious artifacts, induced by movements of body or eyeballs, were excluded by checking the maximum amplitude for each epoch; if the amplitude was greater than 200 µV, the epoch was excluded. The appropriateness of artefact rejection was manually confirmed. Artefact rejection and analysis of each electroencephalographic parameter were performed by a single, experienced analyst, without knowledge of the treatments.
Non-compartmental analyses of pharmacokinetics and pharmacodynamics
Pharmacokinetic parameters were calculated by non-compartmental methods (WinNonlin Professional 5.2, Pharsight Corporation, Mountain View, CA, USA). The area under the curve from the time of administration to the last measured concentration (AUClast) was estimated by linear trapezoidal integration (linear interpolation). The area under the curve from administration to infinity (AUCinf) was calculated as the sum of AUClast+ Clast/λZ, in which Clast is the last measured concentration and λZ is the apparent terminal rate constant estimated by unweighted linear regression for the linear portion of the terminal log concentration-time curve. The maximal concentration (Cmax) and the time to reach Cmax (tmax) following a constant infusion of microemulsion and LCT propofol were determined from the observed data. Summary statistics were determined for each parameter.
To evaluate dose proportionality, dose-normalized AUCinf values of each dose groups were compared using one-way analysis of variance (Hummel et al., 2008). If the differences among three groups are statistically insignificant, we are able to conclude that pharmacokinetics showed dose proportionality. In addition, we used a power model and confidence interval (CI) criteria approach as follows (Hummel et al., 2008).
| (1) |
where dose proportionality implies that β1= 1 in equation (1) and PK denotes a pharmacokinetic variable (AUCinf in this study).
Analysis of variance was performed with a model that contained effects for sequence, subject nested within sequence, period and formulation for logarithmically transformed data. The effect of subject was treated as random effect, and all other effects were treated as fixed effects. In addition, P values were provided using F statistics (P < 0.05 indicated statistical significance). 90% CIs were constructed for the ratio of geometric means of Cmax, AUClast and AUCinf between microemulsion and LCT propofol. It can be concluded that the two formulations are bioequivalent if the 90% CI falls within the limits of 80% to 125% (FDA, 2001; EMEA, 2008).
Pharmacodynamic bioequivalence between both formulations was determined from the observed response of the CNS over time rather than on the estimates of pharmacodynamic model parameters. The inhibitory response of the CNS to propofol was characterized as follows: ApEn values were expressed as a percentage of a baseline (%ApEn). The areas above the %ApEn time curves (AAC) were calculated using linear trapezoidal integration with linear interpolation (Figure 1). Uniform weighting was used to calculate slopes. Differences between E0 (baseline ApEn) and Emax (maximally decreased ApEn) values (E0–Emax) were also calculated. Summary statistics were determined for both parameters. Also, we calculated 90% CIs for the ratio of the arithmetic means of AAC and E0–Emax between both formulations, based on an analysis of variance with a linear mixed effects model (WinNonlin Professional 5.2).
Figure 1.
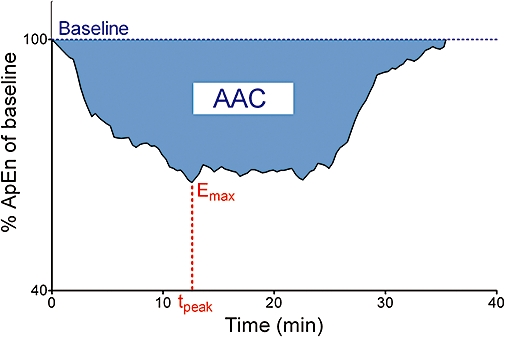
Schematic diagram of the area above the per cent approximate entropy time curves (AAC) in subject 17 (infusion rate, 0.75 mg·kg−1·min−1). The per cent approximate entropy (ApEn) of baseline is the electroencephalographic ApEn expressed as a percentage of the baseline ApEn. Emax, maximally decreased ApEn; tpeak, time to reach Emax.
To evaluate the dose-dependent inhibitory response of the CNS by both formulations, AAC and E0–Emax values for three infusion rates were tested using one way anova and multiple comparisons versus control (Holm-Sidak method), in which 0.75 mg·kg−1·min−1 was used as the control.
Population pharmacokinetic and pharmacodynamic analyses
Population pharmacokinetic and pharmacodynamic analyses were sequentially performed using NONMEM® VI (GloboMax LLC, Ellicott City, MD, USA) (Sheiner et al., 1979). One-, two- and three-compartment models with linear pharmacokinetics were fitted using an ADVAN1, 3 and 11 subroutines and the first-order conditional estimation (FOCE) with interaction procedure. The pharmacodynamics were described using an effect compartment model in which ke0, a first-order elimination rate constant characterizing effect site equilibration, was used to estimate the apparent effect site concentrations. For pharmacodynamic modelling, 3293 and 2806 points ApEn were selected for microemulsion and LCT formulation respectively. The selection criteria of ApEn data were similar to the previous work (Kang et al., 2007), which were as follows: (i) every 20–30 s during the 20 min after the beginning of propofol infusion; and (ii) every 30–40 s during the first 20 min, every 1–3 min during the second 20 min after the termination of propofol infusion. For each animal, the relation of ApEn with effect site concentration of propofol was analysed using a sigmoid Emax model (Holford and Sheiner, 1981):
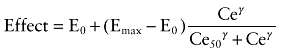 |
(2) |
where effect is ApEn, E0 is the baseline ApEn when no drug is present, Emax is ApEn value for maximum possible drug effect, Ce is the calculated effect-site concentration of propofol, Ce50 is the effect-site concentration associated with 50% maximal drug effect and γ is the steepness of the concentration-versus-response relation [equation (2)]. Pharmacodynamic models were fitted using an ADVAN6 subroutine and the FOCE with interaction procedure.
A diagonal matrix was estimated for the different distributions of ηs, where η is inter-individual random variability with mean zero and variance ω2. Inter-individual random variability on each of the pharmacokinetic parameters was modelled using a log-normal model. A constant coefficient of variation model was used for the residual random variability of pharmacokinetic models. Inter-individual random variabilities of Emax and E0 were modelled using an additive model and those of Ce50, γ and ke0 were modelled using a log-normal model. Residual random variability of pharmacodynamic models was modelled using an additive error model. Empirical Bayes estimates of pharmacokinetic and pharmacodynamic parameters of each individual were calculated.
The models were evaluated using statistical and graphical methods, which were facilitated by Xpose (version 4.0) run on the R statistical software package (version 2.7.2, the R Foundation for Statistical Computing, Vienna, Austria) (Jonsson and Karlsson, 1999) and PDxPop (version 3.1, ICON Development Solutions, Ellicott City, MD, USA). The potential covariates affecting parameters were explored for body weight, age, body surface area and sex. A stepwise, generalized additive modelling procedure was used to select covariates that could further explain inter-individual variability. The minimal value of the objective function (equal to minus twice the log likelihood) was used as the goodness-of-fit characteristic to discriminate between hierarchical models using the log likelihood ratio test (Beal and Sheiner, 1992). A P value of 0.05, representing a decrease in objective function value of 3.84 points was considered statistically significant (chi-squared distribution, degrees of freedom = 1).
Based on an analysis of variance with a linear mixed effects model, 90% CIs were constructed for the ratio of arithmetic means of empirical Bayes estimates of pharmacokinetic and pharmacodynamic parameters between microemulsion and LCT propofol (WinNonlin Professional 5.2).
Model diagnosis and validation
The prediction error was calculated as (measured – predicted)/predicted. The median prediction error (MDPE) and median absolute prediction error (MDAPE), which indicate bias and inaccuracy, respectively, were calculated to examine the quality of the prediction of the pharmacokinetic and pharmacodynamic models for the population.
The conditional weighted residuals (CWRES) of pharmacokinetic and pharmacodynamic models, a diagnostic tool to test for model misspecification, were calculated to reduce model misspecification that may result from utilizing weighted residuals with the FOCE method (Hooker et al., 2007).
For the final pharmacokinetic and pharmcodynamic models, a non-parametric bootstrap analysis was performed as an internal model validation (Parke et al., 1999), using Perl-speaks-NONMEM (PsN) tool-kit (Version 2.3.1) (Lindbom et al., 2005). Briefly, 2000 bootstrap replicates were generated by random sampling from the original data set with replacement. The final model parameter estimates were compared with both the median parameter values and the 2.5–97.5 percentiles of the nonparametric bootstrap replicates of the final model.
For each dose group, 2000 datasets were simulated from the final pharmacokinetic and pharmacodynamic models, respectively and the 95% prediction intervals were compared numerically and visually with actual plasma propofol concentration and ApEn data (Karlsson and Savic, 2007). Based on the final pharmacokinetic and pharmacodynamic models of microemulsion and LCT propofol, target effect-site concentration-controlled infusions of 3 µg·mL−1 for 10 min in a beagle dog weighed 10 kg were simulated to calculate the total amount of each formulation infused during 10-min period (ASAN Pump).
Statistics
The statistical analyses were performed with SigmaStat 3.5 for Windows (Systat Software, Inc., Chicago, IL, USA) and the R statistical software package. The baseline EEG and MAP data within an animal between arms of the crossover; the rate of rejected EEG fraction and selected number of ApEn data between microemulsion and LCT propofol were tested using paired t-test. The effects of formulation and infusion rate on MAP were simultaneously tested using anova with a nested design, in which each animal was nested in one of three infusion rates (Hicks and Turner, 1999). The time to reach Emax (tpeak) between both formulations was compared using Wilcoxon signed rank test. Data were summarized as mean ± SD unless stated otherwise. A P value less than 0.05 was considered statistically significant.
Materials
Propofol potentiates GABAA (γ-aminobutyric acid) receptor-mediated responses (Franks, 2006). The following is the basic formula of the microemulsion propofol (Aquafol™) used in this study: a mixture of 1% propofol, 10% PP188 (Daebong LS Co., LTD, Seoul, Korea), 0.7% polyethylene glycol 660 hydroxystearate (BASF Company Ltd., Seoul, Korea), 1% glycerin, 0.0008% disodium EDTA and 0.01% sodium ascorbate (Lee et al., 2008). The comparator formulation, LCT propofol, used was 1% Diprivan®.
Results
The mean age of animals was 11.5 ± 1.1 months (range: 11–16 months) and body weight was 10.2 ± 1.3 kg (range: 8.3–13.5 kg). The plasma concentrations of propofol obtained after infusions of propofol in either formulation over the 6h experimental period are shown in Figure 2.
Figure 2.
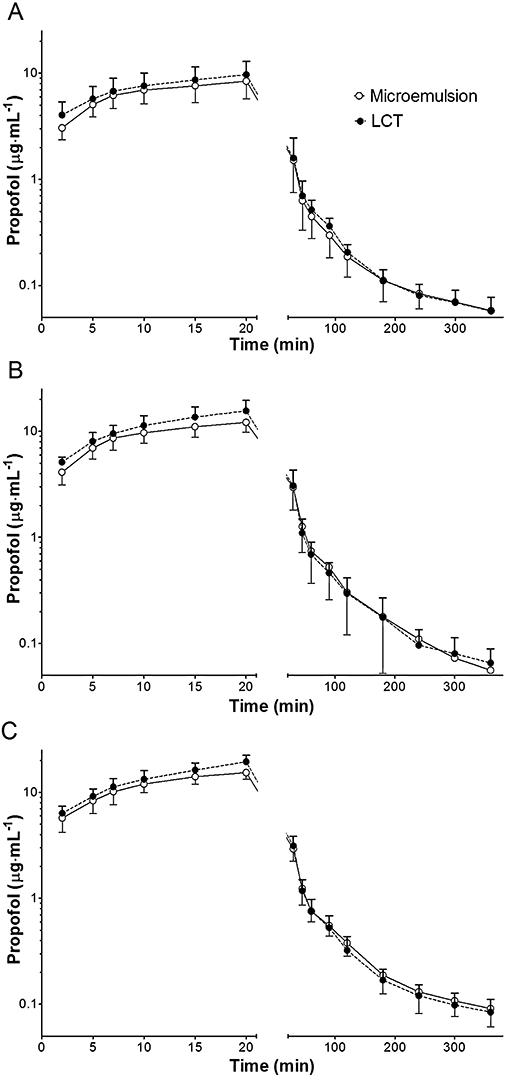
Time course of plasma propofol concentrations in dogs. Microemulsion and long-chain triglyceride emulsion (LCT) propofol were infused at a rate of 0.75 mg·kg−1·min−1 (A), 1.00 mg·kg−1·min−1 (B) and 1.25 mg·kg−1·min−1 (C) in a crossover fashion. Data are presented as mean ± SD (n= 10, each infusion rate).
There were no statistically significant sequence effects on the baseline electroencephalographic activity (P= 0.426) and MAP (P= 0.763). The changes of MAP over time for all animals are shown in Figure 3. Compared with baseline, MAP was decreased at all infusion rates of both formulations, which was recovered to baseline values approximately 25–30 min after discontinuation of infusion. However, the effects of formulation (P= 0.257) and infusion rate (P= 0.697) on MAP were not significant, and the interaction between the formulation and infusion rate on MAP was also not significant (P= 0.894).
Figure 3.
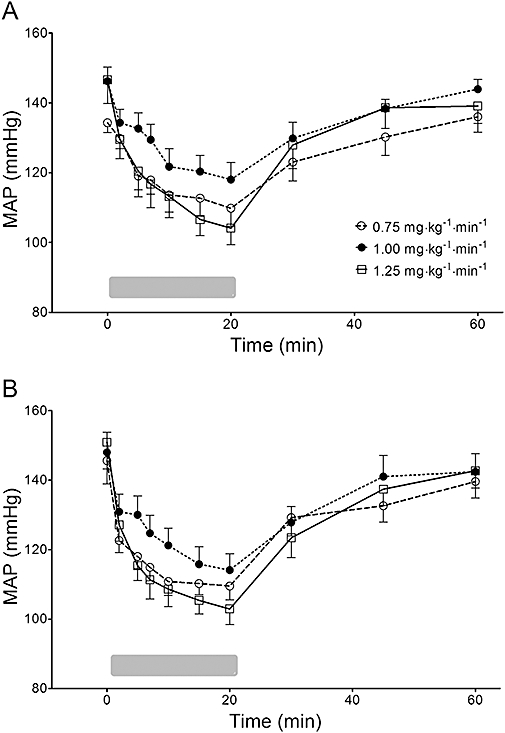
Changes of mean arterial pressure (MAP) over time following zero-order infusion of microemulsion (A) and LCT propofol (B) for 20 min in beagle dogs. The gray bar at the bottom indicates infusion of propofol. Data are presented as mean ± SD (n= 10, each infusion rate). LCT, long-chain triglyceride emulsion.
Non-compartmental pharmacokinetic and pharmacodynamic analyses
Table 1 shows the pharmacokinetic parameters of both propofol formulations that were calculated by non-compartmental methods. In all animals, at least 80% of the total area under the curve was covered by measured concentrations.
Table 1.
Noncompartmental pharmacokinetic parameters of microemulsion and long-chain triglyceride emulsion (LCT) propofol following zero-order infusion in beagle dogs
| Parameter |
Microemulsion propofol |
LCT propofol |
||||
|---|---|---|---|---|---|---|
| 0.75 mg·kg−1·min−1 | 1.00 mg·kg−1·min−1 | 1.25 mg·kg−1·min−1 | 0.75 mg·kg−1·min−1 | 1.00 mg·kg−1·min−1 | 1.25 mg·kg−1·min−1 | |
| λZ (min−1) | 0.00377 ± 0.00175 | 0.00662 ± 0.00275 | 0.00603 ± 0.00221 | 0.00383 ± 0.00277 | 0.00615 ± 0.00295 | 0.00433 ± 0.00203 |
| tmax (min) | 20.0 ± 0 | 20.0 ± 0 | 20.0 ± 0 | 20.0 ± 0 | 20.0 ± 0 | 20.0 ± 0 |
| Cmax ((g·mL−1) | 8.4 ± 2.7 | 12.1 ± 2.4 | 15.4 ± 2.0 | 9.7 ± 3.2 | 15.6 ± 4.0 | 19.4 ± 2.9 |
| AUClast ((g·mL−1·min) | 238.1 ± 64.2 | 358.1 ± 84.2 | 427.6 ± 61.8 | 267.2 ± 64.5 | 407.7 ± 88.5 | 476.6 ± 69.8 |
| AUCinf ((g·mL−1·min) | 258.3 ± 59.8 | 367.9 ± 84.4 | 450.9 ± 72.4 | 296.3 ± 65.9 | 422.3 ± 95.1 | 503.2 ± 75.3 |
| AUC%Extrap (%) | 8.3 ± 5.4 | 2.8 ± 1.5 | 4.8 ± 5.4 | 9.5 ± 9.6 | 3.3 ± 2.0 | 5.2 ± 3.5 |
| Vz (L·kg−1) | 21.1 ± 12.6 | 10.8 ± 6.8 | 12.9 ± 11.6 | 21.8 ± 17.9 | 10.2 ± 6.5 | 14.6 ± 7.6 |
| Cl (mL·min−1·kg−1) | 60.5 ± 12.1 | 56.7 ± 11.9 | 57.0 ± 10.8 | 52.7 ± 10.8 | 49.1 ± 8.7 | 50.6 ± 7.0 |
| MRTlast (min) | 32.9 ± 7.7 | 30.1 ± 6.6 | 30.8 ± 4.4 | 31.4 ± 6.8 | 27.6 ± 6.0 | 26.5 ± 5.2 |
| Vss (L·kg−1) | 6.0 ± 3.7 | 2.6 ± 0.9 | 3.7 ± 3.4 | 6.8 ± 7.8 | 2.3 ± 0.8 | 3.1 ± 1.6 |
Data are expressed as mean ± SD (n= 10, each infusion rate).
λZ, terminal elimination rate constant; tmax, time at maximal concentration; Cmax, maximal concentration; AUClast, area under the curve from administration to the last measured concentration; AUCinf, area under the curve from administration to infinity; AUC%Extrap, percentage of the extrapolated area under the curve at the total area under the curve; Vz, volume of distribution; MRTlast, Mean residence time to the last measured concentration; Vss, volume of distribution at steady state.
In the linear regression between log transformed total dose and AUCinf, the slope was 1.114 (95% CI = 0.860, 1.368) for microemulsion propofol and 0.968 (95% CI = 0.705, 1.231) for LCT propofol respectively. The 95% CIs of the slopes contained 1, which suggests dose proportionality. These linear pharmacokinetics were also demonstrated by the finding that the areas under the plasma concentration-time curve from time 0 to infinity normalized by dose (AUCinf/dose) for the infusion rates of 0.75, 1.00 and 1.25 mg·kg−1·min−1 were 1.7 ± 0.3, 1.7 ± 0.3 and 1.8 ± 0.3 min·µg·mg−1, respectively (microemulsion propofol, P= 0.571), and were 2.0 ± 0.5, 2.0 ± 0.3 and 2.1 ± 0.3 µg·mg−1·min respectively (LCT propofol, P= 0.913).
The 90% CIs for the ratio of geometric means of AUClast and AUCinf between microemulsion and LCT propofol are included in the acceptance range for bioequivalence (80–125%), whereas that of Cmax is not (Table 2). These findings indicated that microemulsion propofol in this study showed incomplete pharmacokinetic bioequivalence to LCT propoofol. The inter-subject variability was similar for both formulations. The analysis of variance did not indicate any differences between formulations for either sequence or period effects.
Table 2.
AUClast, AUCinf and Cmax of microemulsion (n= 30) propofol following zero-order infusion in beagle dogs
| Microemulsion propofol | LCT propofol | Ratio*(%) | 90% CI* | |
|---|---|---|---|---|
| AUClast (µg·mL−1·min) | 341.3 ± 104.9 | 407.3 ± 115.8 | 88.5 | 82.6–94.8 |
| AUCinf (µg·mL−1·min) | 359.0 ± 106.7 | 383.8 ± 114.4 | 87.8 | 82.3–93.6 |
| Cmax (µg·mL−1) | 12.0 ± 3.7 | 14.9 ± 5.2 | 81.4 | 75.2–88.1 |
Based on an analysis of variance with a linear mixed effects model that contained effects for sequence, subject nested within sequence, period and formulation for logarithmically transformed data.
Data are expressed as mean ± SD.
CI, confidence interval; AUCinf, area under the curve from administration to infinity; AUClast, area under the curve from administration to the last measured concentration; Cmax, maximal concentration.
AAC and E0–Emax for both formulations are shown in Table 3. The 90% CIs of arithmetic means of both parameters between the two formulations include 100%, which indicates pharmacodynamic bioequivalence. In addition, AAC (P < 0.001 for microemulsion propofol and P= 0.003 for LCT propofol) and E0–Emax (P < 0.001 for microemulsion propofol and P= 0.026 for LCT propofol) of both formulations increased consistently in a dose-dependent manner. There was no significant difference in tpeak between microemulsion (13.2 ± 6.1 min) and LCT propofol (11.2 ± 4.5 min) (P= 0.222).
Table 3.
Comparison of empirical Bayes estimates of pharmacodynamic parameters between microemulsion and long-chain triglyceride emulsion (LCT) propofol following constant infusion in beagle dogs
| Parameter | Infusion rates (mg·kg−1·min−1) | Microemulsion propofol | LCT propofol | Ratio*(%) | 90% CI* |
|---|---|---|---|---|---|
| AAC | 0.75 | 8.48 ± 4.11 | 8.58 ± 4.36 | 98.86 | 67.12–130.60 |
| 1.00 | 12.31 ± 3.46 | 13.15 ± 4.79 | 93.57 | 67.67–119.47 | |
| 1.25 | 21.45 ± 5.29† | 17.59 ± 6.49† | 121.94 | 97.25–146.63 | |
| E0–Emax | 0.75 | 0.397 ± 0.105 | 0.395 ± 0.108 | 100.55 | 82.36–118.75 |
| 1.00 | 0.431 ± 0.084 | 0.452 ± 0.102 | 95.32 | 79.16–111.48 | |
| 1.25 | 0.586 ± 0.103† | 0.548 ± 0.143† | 107.18 | 89.18–125.18 |
Based on an analysis of variance with a linear mixed effects model that contained effects for sequence, subject nested within sequence, period and formulation.
Significantly different (P < 0.05) from 0.75 mg·kg−1·min−1.
Data are expressed as mean ± SD (n= 10, each infusion rate).
CI, confidence interval; AAC, the area above the per cent approximate entropy (ApEn) time curves; E0, baseline ApEn; Emax, maximally decreased ApEn; E0–Emax, difference between E0 and Emax.
Population pharmacokinetic and pharmacodynamic analyses
The pharmacokinetics of both formulations were best described by a three compartment model. The results of the final pharmacokinetic models are summarized in Table 4. The final model of microemulsion propofol included body weight and sex as a significant covariate for V1 and k21 respectively. The typical values of k21 were 0.0314 for females and 0.0249 for males. The equation (3) describes V1 in the final model for microemulsion propofol:
Table 4.
Population pharmacokinetic parameter estimates, inter-individual variability (%CV) and median parameter values (2.5–97.5%) of the nonparametric bootstrap replicates of the final pharmacokinetic model of microemulsion (n= 30) and long-chain triglyceride emulsion (LCT) (n= 30) propofol
| Model | Parameter |
Microemulsion propofol |
LCT propofol |
||
|---|---|---|---|---|---|
| Estimate (RSE, %CV) | Median (2.5–97.5%) | Estimate (RSE, %CV) | Median (2.5–97.5%) | ||
| Basic | V1 (L) | 4.43 (4.51, 20.0) | – | 3.66 (4.73, 22.2) | – |
| k10 (min−1) | 0.135 (4.39, 17.2) | – | 0.146 (3.60, 14.1) | – | |
| k12 (min−1) | 0.0448 (5.96, 17.9) | – | 0.0447 (6.58, 29.4) | – | |
| k21 (min−1) | 0.0281 (5.77, 18.8) | – | 0.0269 (5.39, 18.2) | – | |
| k13 (min−1) | 0.0293 (10.6, 50.2) | – | 0.0286 (9.76, 43.2) | – | |
| k31 (min−1) | 0.00322 (14.5, 54.4) | – | 0.00281 (13.5, 54.1) | – | |
| σ2 | 0.125 (8.16, –) | – | 0.134 (8.96, –) | – | |
| Final | V1 (L) |
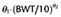 (–, 18.9) (–, 18.9) |
– |
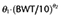 (–, 19.0) (–, 19.0) |
– |
| θ1= 4.40 (4.30, –) | 4.39 (4.06–4.79) | θ1= 3.64 (4.34, –) | 3.65 (3.34–3.95) | ||
| θ2= 0.408 (6.08, –) | – | θ2= 0.831 (48.5, –) | 0.848 (0.197–1.892) | ||
| k10 (min−1) | 0.135 (4.27, 16.6) | – | 0.135 (4.27, 16.6) | 0.144 (0.131–0.157) | |
| k12 (min−1) | 0.0456 (6.80, 20.9) | 0.0456 (0.0407–0.0518) | 0.0447 (7.58, 30.0) | 0.045 (0.0388–0.0526) | |
| k21 (min−1) |
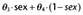 (–, 17.1) (–, 17.1) |
– | 0.0269 (5.43, 17.9) | 0.0265 (0.024–0.0301) | |
| (sex: male = 0, female = 1) | – | – | – | ||
| θ3= 0.0314 (8.06, –) | 0.0308 (0.0246–0.0375) | – | – | ||
| θ4= 0.0249 (9.00, –) | 0.0249 (0.0202–0.0297) | – | – | ||
| k13 (min−1) | 0.0290 (9,00, 48.8) | 0.0298 (0.0238–0.0580) | 0.0287 (9,90, 43.7) | 0.0293 (0.239–0.0387) | |
| k31 (min−1) | 0.00316 (14.9, 53.1) | 0.00303 (0.00069–0.00417) | 0.00281 (14.1, 54.2) | 0.00264 (0.00144–0.0037) | |
| σ2 | 0.125 (8.24, –) | 0.124 (0.106–0.144) | 0.134 (8.88, –) | 0.132 (0.197–1.892) | |
Inter-individual random variability and residual random variability were modelled using log-normal model and constant coefficient of variation model respectively. Nonparametric bootstrap analysis was repeated 2000 times.
CV, coefficient of variation; RSE, relative standard error; BWT, body weight; σ2, variance of residual random variability.
| (3) |
The model which included sex as a significant covariate for k21 resulted in an improvement in the objective function (4.864, P= 0.027 with degrees of freedom = 1) compared with the basic model. The final model, which included sex and body weight as a significant covariate for V1 and k21, resulted in an improvement in the objective function (8.912, P= 0.0116 with degrees of freedom = 2) compared with the basic model. All of the η's except η for k31 of the final pharmacokinetic model were normally distributed. Body weight was a significant covariate for V1 in the final pharmacokinetic model of LCT propofol [equation (4)].
| (4) |
The final model resulted in an improvement in the objective function (7.934, P= 0.00485 with degrees of freedom = 1) compared with the basic model. All of the η's except η for V1 and k31 of the final pharmacokinetic model were normally distributed.
The ApEn derived from left occipital area was chosen for pharmacodynamic modelling as the difference between E0 and Emax values of the left occipital area tended to increase more consistently in a dose-dependent manner than those of the right occipital area (data not shown). The fraction of EEG rejected as artifact in microemulsion and LCT propofol were 0.58 ± 0.88% and 0.33 ± 0.73% respectively (P= 0.348). The numbers of ApEn data per individual for microemulsion and LCT formulation were 109.8 ± 29.0 and 93.5 ± 27.7 respectively (P= 0.008). LCT propofol showed more unstable fluctuation of ApEn values over time after the termination of infusion, although we could not identify the exact causes for these observations. Therefore, we removed more ApEn data of LCT propofol for smoothing the response over time curves. Estimates of the population parameters of the final pharmacodynamic model for microemulsion and LCT propofol are summarized in Table 5. The blood-brain equilibration half-life (t1/2ke0) of microemulsion and LCT propofol was 1.5 and 1.0 min respectively. The η values of Ce50 and γ in the final pharmacodynamic model of microemulsion propofol were normally distributed and those of E0, Ce50, γ and ke0 in the final pharmacodynamic model of LCT propofol were normally distributed.
Table 5.
Population pharmacodynamic parameter estimates and inter-individual variability (%CV) and median parameter values (2.5–97.5%) of the nonparametric bootstrap replicates of the final pharmacodynamic model of microemulsion (n= 30) and long-chain triglyceride emulsion (LCT) (n= 30) propofol
| Parameter |
Microemulsion propofol |
LCT propofol |
||
|---|---|---|---|---|
| Estimate (RSE, %CV) | Median (2.5–97.5%) | Estimate (RSE, %CV) | Median (2.5–97.5%) | |
| E0 | 1.06 (1.62, –) | 1.06 (1.01–1.09) | 1.01 (2.22, 12.8) | 1.02 (0.971–1.06) |
| Emax | 0.609 (0.32, –) | 0.610 (0.594–0.622) | 0.601 (1.42, –) | 0.601 (0.580–0.615) |
| Ce50 (µg·mL−1) | 2.06 (7.48, 38.6) | 2.07 (1.79–2.45) | 2.50 (7.96, 36.9) | 2.50 (2.19–2.89) |
| γ | 3.27 (12.1, 48.6) | 3.45 (2.76–4.38) | 2.95 (9.86, 53.7) | 2.96 (2.44–3.58) |
| ke0 (min−1) | 0.476 (19.7, 85.8) | 0.475 (0.357–0.736) | 0.696 (17.4, 80.9) | 0.684 (0.515–1.02) |
| σ2 | 0.00167 (9.9, –) | 0.00162 (0.00132–0.00195) | 0.00124 (10.3, –) | 0.00123 (0.000977–0.00147) |
Inter-individual random variability and residual random variability were modelled using log-normal model and additive error model respectively. Nonparametric bootstrap analysis was repeated 2000 times.
Ce50, effect site concentration of propofol that produces 50% of maximal effect on approximate entropy; CV, coefficient of variation; RSE, relative standard error; E0, baseline value of electroencephalographic approximate entropy; Emax, maximally decreased value of approximate entropy; γ, steepness of the concentration-response relation; σ2, variance of residual random variability.
The inaccuracy (MDAPE) and bias (MDPE) of the final pharmacokinetic models were 17.50% and −0.99% for microemulsion propofol, and 17.71% and −3.56% for LCT propofol respectively. The inaccuracy and bias of the final pharmacodynamic models were 5.72% and 0.88% for microemulsion propofol, and 6.23% and 2.70% for LCT propofol respectively.
The CWRES of the final pharmacokinetic and pharmacodynamic models for microemulsion and LCT propofol were plotted against time for each individual (Figure 4). The CWRES are randomly distributed around zero in time, indicating absence of bias.
Figure 4.
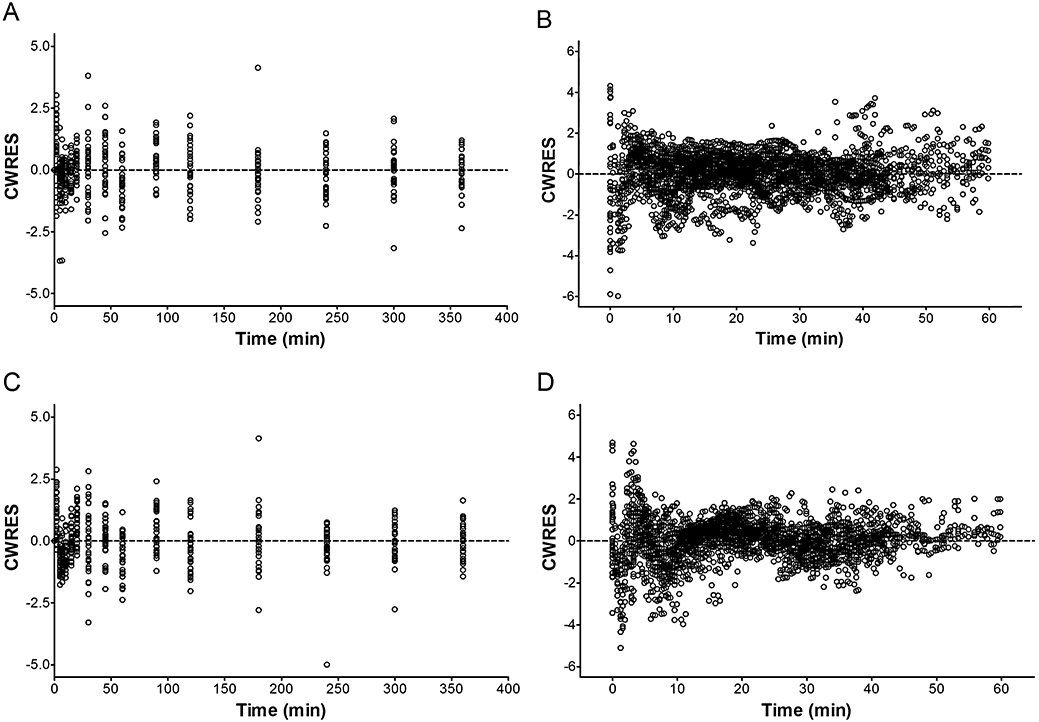
The conditional weighted residuals (CWRES) as a function of time for the final population pharmacokinetic and pharmacodynamic models of microemulsion (A and B) and LCT propofol (C and D). The dashed line is a line of identity. LCT, long-chain triglyceride emulsion.
Population pharmacokinetic and pharmacodynamic parameter estimates and median parameter values (2.5–97.5%) of the nonparametric bootstrap replicates for microemulsion and LCT propofol are summarized in Tables 4 and 5. The predictive checks based on 2000 data sets for pooled dose groups showed that less than 5% of the data of pharmacokinetics (2.44% and 3.56% for microemulsion and LCT propofol respectively) and pharmacodynamics (1.61% and 2.39% for microemulsion and LCT propofol respectively) were distributed outside the 95% prediction intervals. The predictive checks for each dose group are shown in Figures 5 and 6.
Figure 5.
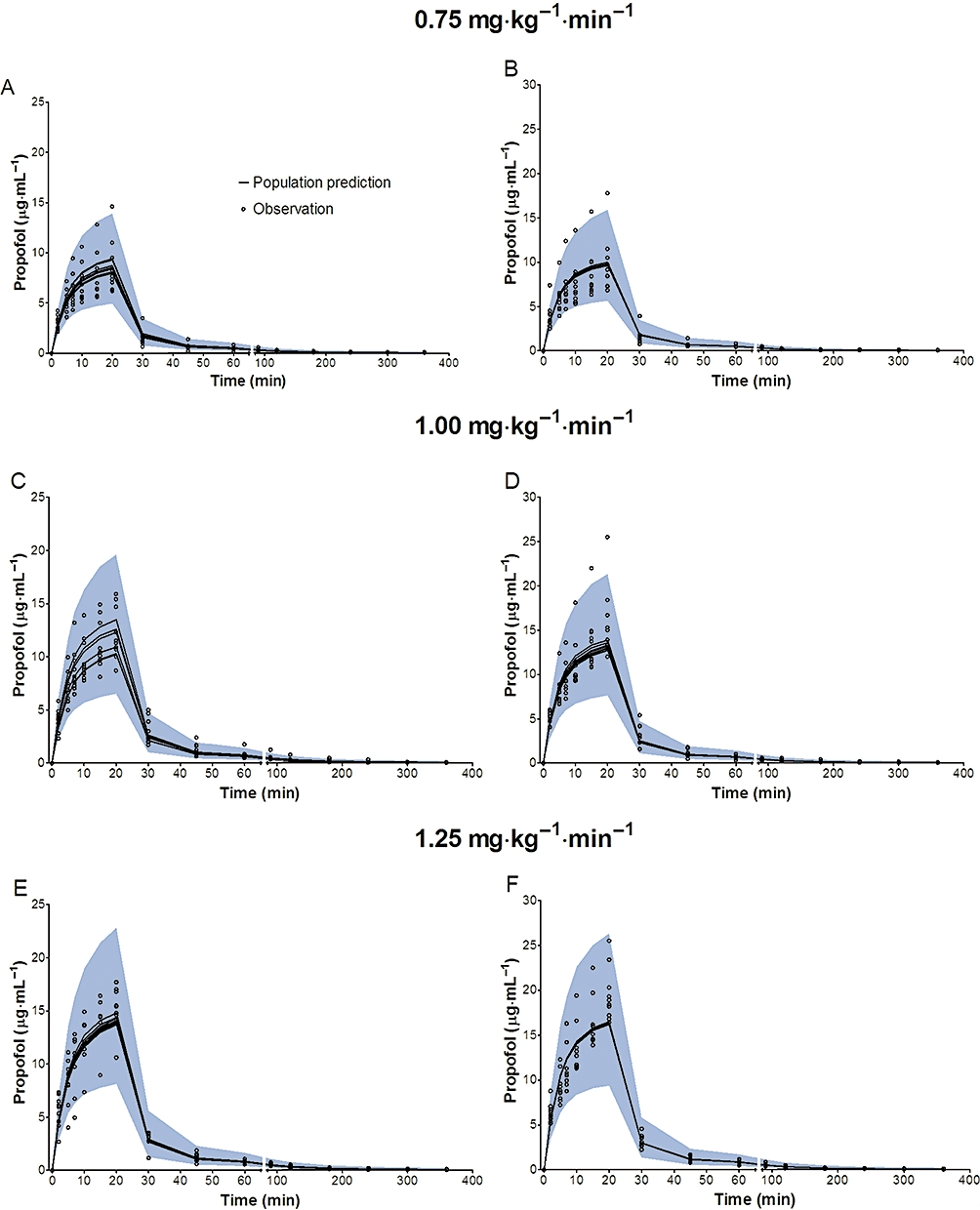
Predictive checks of propofol in plasma based on 2000 datasets at the infusion rate of 0.75 mg·kg−1·min−1, 1.00 mg·kg−1·min−1 and 1.25 mg·kg−1·min−1 in a crossover fashion. Most of the observed values lay within the 95% prediction interval. A small portion of data distributed outside the 95% prediction intervals (A: 2.00%, C: 4.00%, E: 2.67% for microemulsion propofol, and B: 5.33%, D: 2.67%, F: 0.67% for LCT propofol), indicating that the final pharmacokinetic model for both formulations were adequate to describe the time-courses of propofol plasma concentrations. The blue filled area represents the model 95% prediction interval. LCT, long-chain triglyceride emulsion.
Figure 6.
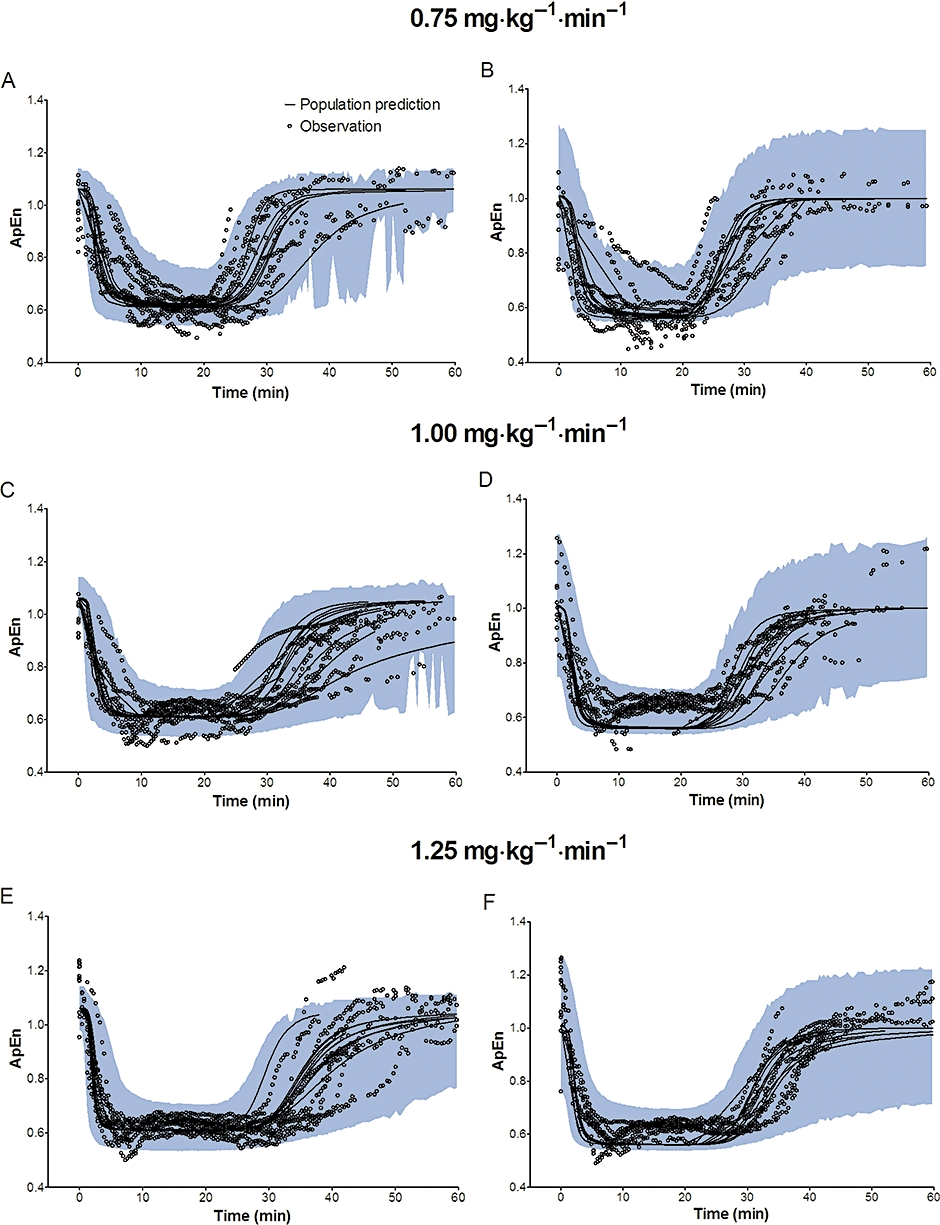
Predictive checks of electroencephalographic approximate entropy (ApEn) based on 2000 datasets at the infusion rate of 0.75 mg·kg−1·min−1, 1.00 mg·kg−1·min−1 and 1.25 mg·kg−1·min−1 in a crossover fashion. Most of the observed values lay within the 95% prediction interval and only a small portion of data distributed outside the 95% prediction intervals (A: 4.97%, C: 5.07%, E: 3.57% for microemulsion propofol, and B: 13.00%, D: 0.86%, F: 2.12% for LCT propofol), indicating that the final pharmacodynamics for both formulations are adequate to describe the time-courses of ApEn. The blue filled area represents the 95% prediction interval from the model. LCT, long-chain triglyceride emulsion.
The 90% CIs for the ratio of arithmetic means of empirical Bayes estimates of pharmacokinetic parameters between microemulsion and LCT propofol are shown in Table 6. A computer simulation of target controlled infusions of microemulsion and LCT propofol is shown in Figure 7.
Table 6.
Comparison of empirical Bayes estimates of pharmacokinetic parameters between microemulsion and long-chain triglyceride emulsion (LCT) propofol
| Parameter | Microemusion propofol | LCT propofol | Ratio*(%) | 90% CI* |
|---|---|---|---|---|
| V1 (L) | 4.49 ± 0.85 | 3.72 ± 0.67 | 120.74 | 112.24–129.23 |
| V2 (L) | 7.19 ± 1.60 | 6.29 ± 2.09 | 114.14 | 101.27–127.01 |
| V3 (L) | 46.10 ± 31.27 | 41.03 ± 17.55 | 112.35 | 85.19–139.50 |
| Vdss (L) | 57.78 ± 30.93 | 51.05 ± 18.50 | 113.18 | 91.24–135.12 |
| Cl (L·min−1) | 0.61 ± 0.10 | 0.54 ± 0.07 | 112.31 | 105.50–119.11 |
| Q2 (L·min−1) | 0.21 ± 0.05 | 0.17 ± 0.06 | 119.66 | 106.16–133.16 |
| Q3 (L·min−1) | 0.14 ± 0.07 | 0.12 ± 0.05 | 124.45 | 100.54–148.36 |
| t1/2α (min) | 3.16 ± 0.40 | 3.05 ± 0.40 | 103.76 | 98.12–109.40 |
| t1/2β (min) | 32.09 ± 4.16 | 32.74 ± 3.29 | 98.00 | 93.84–102.17 |
| t1/2γ (min) | 282.17 ± 102.44 | 314.07 ± 82.21 | 89.84 | 76.92–102.76 |
Based on an analysis of variance with a linear mixed effects model that contained effects for sequence, subject nested within sequence, period and formulation.
Data are expressed as mean ± SD (n= 30, each formulation), which are arithmetic means and SD of empirical Bayes estimates of pharmacokinetic parameters.
CI, confidence interval.
Figure 7.
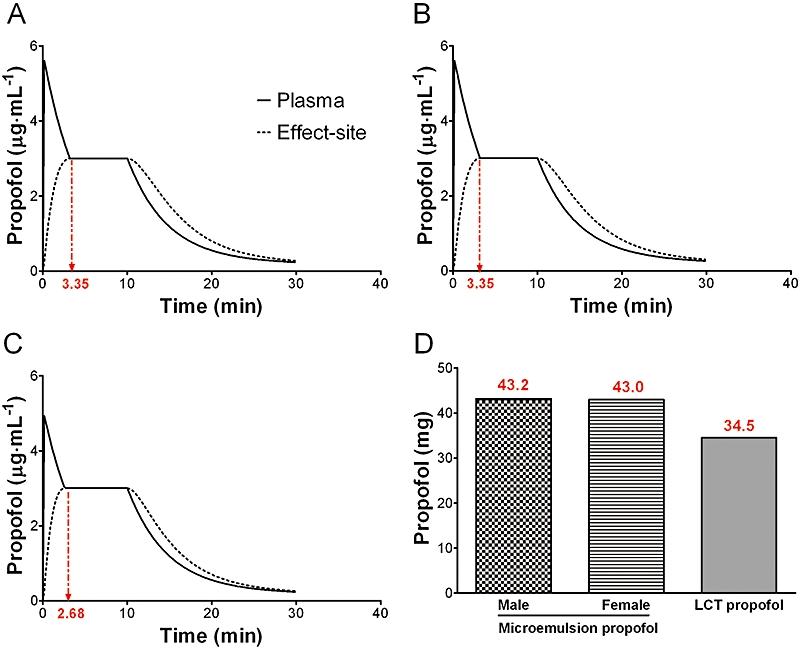
A computer simulation of target controlled infusions of microemulsion and LCT propofol to maintain an effect-site concentration of 3 µg·mL−1 for 10 min in a beagle dog weighing 10 kg. (A) microemulsion propofol, male, (B) microemulsion propofol, female, (C) LCT propofol, (D) total amount of propofol for 10-min period. Dotted red arrows indicate the time when the plasma concentration is equal to the effect-site concentration. LCT, long-chain triglyceride emulsion.
Discussion
The microemulsion formulation of propofol showed incomplete pharmacokinetic bioequivalence to LCT propofol. However, microemulsion propofol was pharmacodynamically bioequivalent to LCT propofol, and showed linear pharmacokinetics and a dose-dependent effect on the ApEn at the applied dose range in beagle dogs.
As hepatic metabolism of propofol is flow limited, the nonlinearity in propofol pharmacokinetics is proposed to be determined by hepatic blood flow and also cardiac output (Lee et al., 2008). Although dose range is an important factor for dose proportionality (Takizawa et al., 2004), hepatic blood flow may have a direct influence on this for drugs such as propofol. In this study, maximal reduction of MAPs from baseline was about 40% in all animals. However, MAP was still maintained within normal range in dogs (Haskins, 1996) and subsequently, hepatic perfusion may not be reduced. In our earlier study, MAP decreased significantly in a dose-dependent manner, which might account for nonlinear pharmacokinetics of microemulsion propofol in rats (Lee et al., 2008). In this study, irrespective of formulations, the differences of MAPs among infusion rates of both propofol formulations were not significant, which may not induce a decrease of hepatic perfusion with an increasing dose. Therefore, microemulsion and LCT propofol might demonstrate linear pharmacokinetics over the dose range, as seen in rats (Lee et al., 2008).
In this study, reformulated microemulsion propofol consistently produced lower plasma concentrations of propofol than that of LCT propofol commencing from 2 min after the start of zero-order infusion to the end of infusion, hence, showing higher V1, V2, V3 and Vdss values than those of LCT propofol. Our previous microemulsion formulation showed a smaller central volume of distribution and less extensive peripheral distribution (smaller V3 and Vdss) than those of LCT propofol. These divergent findings in peripheral distribution of the previous and reformulated microemulsion propofol may be attributed to different polymeric vehicles of propofol. Although pharmacokinetic studies of polyethylene glycol 660 hydroxystearate (Solutol HS 15) and tetrahydrofurfuryl alcohol polyethylene glycol ether (Glycofurol) have not been published, we postulated that the previous microemulsion formulation was less extensively distributed to peripheral tissues, compared with LCT propofol (Kim et al., 2007). On the other hand, PP188 is a highly water-soluble nonionic polymer with preferential distribution to the extracellular fluid and widely distributed throughout the well-perfused organs and tissues in rats and dogs (Grindel et al., 2002b). These phenomena can be seen throughout the duration of infusion (Figure 2) and may account for the incomplete pharmacokinetic bioequivalence (difference in Cmax) between the two formulations as well as the higher Cl, Q2 and Q3 of microemulsion propofol in this study.
The volume of the rapidly equilibrating compartment (V2) of microemulsion propofol was higher than that of LCT propofol, which causes a lower peak effect site concentration of propofol, resulting in slower equilibration between blood and brain as indicated by t1/2ke0 of the microemulsion propofol. For the same reason, higher amounts of microemulsion propofol may be needed to maintain the same plasma or effect-site concentrations of propofol, compared with LCT propofol, as suggested in Figure 6. Morey et al. (2006) reported that significantly greater doses of propofol were required to induce anesthesia with propofol microemulsions, irrespective of surfactant concentration or type, than with propofol macroemulsion.
The pharmacokinetic models of both formulations included body weight as a significant covariate for the volume of central compartment (V1). These may make a target-controlled infusion system in a canine model available, as a weight-dependent model is required for clinical applications (Kim et al., 2007). In particular, sex was another significant covariate for k21 in the pharmacokinetic model of microemulsion propofol, with the typical value of k21 for female being slightly higher than that of male. According to the following equation (5), V2 of a male beagle dog is higher than that of a female beagle dog.
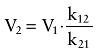 |
(5) |
In dogs, males tend to be physically larger and heavier than females. While fat tissue mass of the males and females was not significantly different, lean tissue mass and bone mineral content was higher in males (Booles et al., 1994). This may explain the higher V2 values in male dogs in this study.
For pharmacodynamic analyses, the effect of isoflurane (0.5%) on the baseline electroencephalographic activity might be not fully excluded. This may be a limitation to this study.
In conclusion, although the pharmacokinetics of microemulsion propofol were not completely bioequivalent to those of LCT propofol, the microemulsion propofol was pharmacodynamically bioequivalent to LCT propofol, in terms of AAC and fractional decrease of ApEn. It also demonstrated dose proportionality and a dose-dependent effect on the ApEn within the dose range applied in this study.
Acknowledgments
This study was supported by grants from the Korea Healthcare Technology R&D Project, Ministry of Health Welfare, Korea (Grant Number: A070001) and from the Industry Trust Research Service between University of Ulsan College of Medicine and Daewon Pharmaceutical Co., Ltd., Seoul, Korea (Grant Number: 2007-0003). We are deeply grateful to Do-Yang Park, A.S. at the Department of Clinical Pharmacology and Therapeutics, Asan Medical Center, University of Ulsan College of Medicine, Seoul, Korea, and Ae-Kyung Hwang, B.S., Hyun-Jeong Park, B.S. and Arum Kim, B.S. in Clinical Research Center of Asan Medical Center, Seoul, Korea for the conduct of the animal experiments and measurements of propofol concentration respectively.
Glossary
Abbreviations:
- ApEn
electroencephalographic approximate entropy
- LCT
long-chain triglyceride emulsion
- MAP
mean arterial pressure
- PP188
purified poloxamer 188
References
- Beal S, Sheiner L. NONMEM User's Guides Part V Introductory Guide. San Francisco, CA: NONMEM Project Group, University of California; 1992. [Google Scholar]
- Beths T, Glen JB, Reid J, Monteiro AM, Nolan AM. Evaluation and optimisation of a target-controlled infusion system for administering propofol to dogs as part of a total intravenous anaesthetic technique during dental surgery. The Veterinary Rec. 2001;148:198–203. doi: 10.1136/vr.148.7.198. [DOI] [PubMed] [Google Scholar]
- Booles D, Poore DW, Legrand-Defretin V, Burger IH. Body composition of male and female Labrador retriever puppies at 20 wk of age. J Nutr. 1994;124:2624S–2625S. doi: 10.1093/jn/124.suppl_12.2624S. [DOI] [PubMed] [Google Scholar]
- Bruhn J, Bouillon TW, Hoeft A, Shafer SL. Artifact robustness, inter- and intraindividual baseline stability, and rational EEG parameter selection. Anesthesiology. 2002;96:54–59. doi: 10.1097/00000542-200201000-00015. [DOI] [PubMed] [Google Scholar]
- Cockshott ID, Douglas EJ, Plummer GF, Simons PJ. The pharmacokinetics of propofol in laboratory animals. Xenobiotica; the fate of foreign compounds in biol systems. 1992;22:369–375. doi: 10.3109/00498259209046648. [DOI] [PubMed] [Google Scholar]
- CTEP. Common Terminology Criteria for Adverse Events (CTCAE) v3.0. Bethesda: Division of Cancer Treatment and Diagnosis (DCTD), National Cancer Institute (NCI), U.S. National Institutes of Health, NIH.
- Devlin JW, Lau AK, Tanios MA. Propofol-associated hypertriglyceridemia and pancreatitis in the intensive care unit: an analysis of frequency and risk factors. Pharmacotherapy. 2005;25:1348–1352. doi: 10.1592/phco.2005.25.10.1348. [DOI] [PubMed] [Google Scholar]
- Dutta S, Ebling WF. Emulsion formulation reduces propofol's dose requirements and enhances safety. Anesthesiology. 1997;87:1394–1405. doi: 10.1097/00000542-199712000-00019. [DOI] [PubMed] [Google Scholar]
- Dutta S, Ebling WF. Formulation-dependent pharmacokinetics and pharmacodynamics of propofol in rats. J Pharm Pharmacol. 1998;50:37–42. doi: 10.1111/j.2042-7158.1998.tb03302.x. [DOI] [PubMed] [Google Scholar]
- EMEA. Guideline on the Investigation of Bioequivalence. London: European Agency for the Evaluation of Medical Products (EMEA); 2008. [Google Scholar]
- FDA. Guidance for Industry: Statistical Approaches to Establishing Bioequivalence. Rockville: US Food and Drug Administration (FDA); 2001. [Google Scholar]
- Franks NP. Molecular targets underlying general anaesthesia. Br J Pharmacol. 2006;147:S72–81. doi: 10.1038/sj.bjp.0706441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grindel JM, Jaworski T, Emanuele RM, Culbreth P. Pharmacokinetics of a novel surface-active agent, purified poloxamer 188, in rat, rabbit, dog and man. Biopharm Drug Dispos. 2002a;23:87–103. doi: 10.1002/bdd.297. [DOI] [PubMed] [Google Scholar]
- Grindel JM, Jaworski T, Piraner O, Emanuele RM, Balasubramanian M. Distribution, metabolism, and excretion of a novel surface-active agent, purified poloxamer 188, in rats, dogs, and humans. J Pharm Sci. 2002b;91:1936–1947. doi: 10.1002/jps.10190. [DOI] [PubMed] [Google Scholar]
- Haskins SC. Monitoring the anesthetized patient. In: Thurmon JC, Tranquilli WJ, Benson GJ, editors. Veterinary Anesthesia. 3rd. Baltimore, MD: Williams & Wilkins; 1996. p. 418. [Google Scholar]
- Hicks CR, Turner VT. Nested and nested-factorial experiments. In: Hicks CR, Turner VT, editors. Fundamental Concepts in the Design of Experiments. 5th. New York: Oxford University Press; 1999. pp. 190–221. [Google Scholar]
- Holford NH, Sheiner LB. Understanding the dose-effect relationship: clinical application of pharmacokinetic-pharmacodynamic models. Clin Pharmacokinet. 1981;6:429–453. doi: 10.2165/00003088-198106060-00002. [DOI] [PubMed] [Google Scholar]
- Hooker AC, Staatz CE, Karlsson MO. Conditional weighted residuals (CWRES): a model diagnostic for the FOCE method. Pharm Res. 2007;24:2187–2197. doi: 10.1007/s11095-007-9361-x. [DOI] [PubMed] [Google Scholar]
- Hummel J, McKendrick S, Brindley C, French R. Exploratory assessment of dose proportionality: review of current approaches and proposal for a practical criterion. Pharm Stat. 2008;8:38–49. doi: 10.1002/pst.326. [DOI] [PubMed] [Google Scholar]
- Jonsson EN, Karlsson MO. Xpose – an S-PLUS based population pharmacokinetic/pharmacodynamic model building aid for NONMEM. Comput Methods Programs Biomed. 1999;58:51–64. doi: 10.1016/s0169-2607(98)00067-4. [DOI] [PubMed] [Google Scholar]
- Kang SH, Poynton MR, Kim KM, Lee H, Kim DH, Lee SH, et al. Population pharmacokinetic and pharmacodynamic models of remifentanil in healthy volunteers using artificial neural network analysis. British J Clin pharmacology. 2007;64:3–13. doi: 10.1111/j.1365-2125.2007.02845.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson MO, Savic RM. Diagnosing model diagnostics. Clin Pharmacol Ther. 2007;82:17–20. doi: 10.1038/sj.clpt.6100241. [DOI] [PubMed] [Google Scholar]
- Kim KM, Choi BM, Park SW, Lee SH, Christensen LV, Zhou J, et al. Pharmacokinetics and pharmacodynamics of propofol microemulsion and lipid emulsion after an intravenous bolus and variable rate infusion. Anesthesiology. 2007;106:924–934. doi: 10.1097/01.anes.0000265151.78943.af. [DOI] [PubMed] [Google Scholar]
- Lee EH, Lee SH, Park DY, Ki KH, Lee EK, Lee DH, et al. Physicochemical properties, pharmacokinetics, and pharmacodynamics of a reformulated microemulsion propofol in rats. Anesthesiology. 2008;109:436–447. doi: 10.1097/ALN.0b013e318182a486. [DOI] [PubMed] [Google Scholar]
- Lindbom L, Pihlgren P, Jonsson EN. PsN-Toolkit – a collection of computer intensive statistical methods for non-linear mixed effect modeling using NONMEM. Comp methods and programs in biomedicine. 2005;79:241–257. doi: 10.1016/j.cmpb.2005.04.005. [DOI] [PubMed] [Google Scholar]
- Minto CF, Schnider TW. Contributions of PK/PD modeling to intravenous anesthesia. Clin Pharmacol Ther. 2008;84:27–38. doi: 10.1038/clpt.2008.100. [DOI] [PubMed] [Google Scholar]
- Morey TE, Modell JH, Shekhawat D, Grand T, Shah DO, Gravenstein N, et al. Preparation and anesthetic properties of propofol microemulsions in rats. Anesthesiology. 2006;104:1184–1190. doi: 10.1097/00000542-200606000-00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noh GJ, Kim KM, Jeong YB, Jeong SW, Yoon HS, Jeong SM, et al. Electroencephalographic approximate entropy changes in healthy volunteers during remifentanil infusion. Anesthesiology. 2006;104:921–932. doi: 10.1097/00000542-200605000-00006. [DOI] [PubMed] [Google Scholar]
- Nolan A, Reid J. Pharmacokinetics of propofol administered by infusion in dogs undergoing surgery. Br J Anaesth. 1993;70:546–551. doi: 10.1093/bja/70.5.546. [DOI] [PubMed] [Google Scholar]
- Park JW, Park ES, Chi SC, Kil HY, Lee KH. The effect of lidocaine on the globule size distribution of propofol emulsions. Anesth Analg. 2003;97:769–771. doi: 10.1213/01.ANE.0000074797.70349.CA. [DOI] [PubMed] [Google Scholar]
- Parke J, Holford NH, Charles BG. A procedure for generating bootstrap samples for the validation of nonlinear mixed-effects population models. Comput Methods Programs Biomed. 1999;59:19–29. doi: 10.1016/s0169-2607(98)00098-4. [DOI] [PubMed] [Google Scholar]
- Pellegrino FC, Sica RE. Canine electroencephalographic recording technique: findings in normal and epileptic dogs. Clin Neurophysiol. 2004;115:477–487. doi: 10.1016/s1388-2457(03)00347-x. [DOI] [PubMed] [Google Scholar]
- Schnider TW, Minto CF, Gambus PL, Andresen C, Goodale DB, Shafer SL, et al. The influence of method of administration and covariates on the pharmacokinetics of propofol in adult volunteers. Anesthesiology. 1998;88:1170–1182. doi: 10.1097/00000542-199805000-00006. [DOI] [PubMed] [Google Scholar]
- Schuttler J, Kloos S, Schwilden H, Stoeckel H. Total intravenous anaesthesia with propofol and alfentanil by computer-assisted infusion. Anaesthesia. 1988;43:2–7. doi: 10.1111/j.1365-2044.1988.tb09059.x. [DOI] [PubMed] [Google Scholar]
- Sheiner LB, Stanski DR, Vozeh S, Miller RD, Ham J. Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharmacol Ther. 1979;25:358–371. doi: 10.1002/cpt1979253358. [DOI] [PubMed] [Google Scholar]
- Takizawa Y, Nishimura H, Morota T, Tomisawa H, Takeda S, Aburada M. Pharmacokinetics of TJ-8117 (Onpi-to), a drug for renal failure (I): Plasma concentration, distribution and excretion of [3H]-(-)epicatechin 3-O-gallate in rats and dogs. Eur J Drug Metab Pharmacokinet. 2004;29:91–101. doi: 10.1007/BF03190582. [DOI] [PubMed] [Google Scholar]
- Yamakage M, Iwasaki S, Satoh J, Namiki A. Changes in concentrations of free propofol by modification of the solution. Anesth Analg. 2005;101:385–388. doi: 10.1213/01.ANE.0000154191.86608.AC. table of contents. [DOI] [PubMed] [Google Scholar]


