Abstract
In ultrasonic targeted imaging, specially designed encapsulated microbubbles are used, which are capable of selectively adhering to the target site in the body. A challenging problem is to distinguish the echoes from such adherent agents from echoes produced by freely circulating agents. In the present paper, an equation of radial oscillation for an encapsulated bubble near a plane rigid wall is derived. The equation is then used to simulate the echo from a layer of contrast agents localized on a wall. The echo spectrum of adherent microbubbles is compared to that of free, randomly distributed microbubbles inside a vessel, in order to examine differences between the acoustic responses of free and adherent agents. It is shown that the fundamental spectral component of adherent bubbles is perceptibly stronger than that of free bubbles. This increase is accounted for by a more coherent summation of echoes from adherent agents and the acoustic interaction between the agents and the wall. For cases tested, the increase of the fundamental component caused by the above two effects is on the order of 8-9 dB. Bubble aggregates, which are observed experimentally to form near a wall due to secondary Bjerknes forces, increase the intensity of the fundamental component only if they are formed by bubbles whose radii are well below the resonant radius. If the formation of aggregates contributes to the growth of the fundamental component, the increase can exceed 17 dB. Statistical analysis for the comparison between adhering and free bubbles, performed over random space bubble distributions, gives p-values much smaller than 0.05.
Keywords: Contrast agent, Targeted imaging, Rigid wall, Acoustic response
1. Introduction
Blood is much less echogenic than tissue. Therefore an ultrasound contrast agent can be introduced in the blood during a medical ultrasonic exam in order to increase the scattering properties of the blood pool [1-4]. Ultrasound contrast agents are micron-sized encapsulated bubbles with a stabilizing shell of albumin, polymer, or lipid. In recent years, targeted ultrasound techniques have progressed with the development of specific contrast agents that are capable of selectively adhering to the desired target site [5-10]. Unlike nontargeted blood pool agents, adherent targeted microbubbles oscillate in the immediate vicinity of, or just attached to, a boundary such as a blood vessel wall [11,12]. Therefore a challenging problem arises as to how to detect the echoes from adherent microbubbles and distinguish them from echoes produced by freely circulating non-adherent agents. Much work has been done on simulating the dynamics of encapsulated microbubbles in an ultrasound field [13-30]. In these studies, however, a contrast microbubble is assumed to be in an infinite medium. The purpose of the present theoretical analysis is to provide a foundation for investigations of the acoustic response from targeted microbubble contrast agents near a boundary. To this end, the equation of radial oscillation for an encapsulated bubble near a plane rigid wall is derived. This equation is then used to simulate the echo from a layer of contrast agent microbubbles localized on a wall. The echo from adherent microbubbles is compared to that from free microbubbles, randomly distributed inside a vessel, in order to reveal differences between the free and adherent cases.
2. Theory
It is well known that theoretically a bubble at a plane rigid wall is a particular case of the two-bubble problem. Therefore we first derive equations of radial motion for two coupled encapsulated bubbles and then apply them to the case of a bubble at a wall.
2.1. Equations of motion for two coupled bubbles
The coupled radial oscillations of two contrast agents were considered previously by Allen et al. [31]. In the present study, we apply a different approach than that of Allen et al., which lets us derive simpler and more suitable equations of motion.
Let us first consider two coupled unencapsulated bubbles. If the translational motion of the bubbles is negligible, their equations of radial motion are given by [32,33]
| (1) |
| (2) |
where Rα is the instantaneous radius of the first bubble, bubble α, Rβ is the instantaneous radius of the second bubble, bubble β, the overdot denotes the time derivative, and ρL is the equilibrium density of the surrounding liquid. The pressure Pα is given by
| (3) |
where P0 is the hydrostatic pressure in the surrounding liquid, σ is the surface tension at the gas-liquid interface, Rα0 is the equilibrium radius of bubble α, γ is the ratio of specific heats of the gas within the bubble, ηL is the shear viscosity of the surrounding liquid, and Pac(t) is the driving acoustic pressure. The term Tα describes the effect of the neighboring bubble, bubble β, on the oscillation of bubble α and is defined by
| (4) |
with d denoting the distance between the centers of the bubbles. Expressions for Pβ and Tβ are obtained from (3) and (4) replacing α with β and vice versa. Equation (4) assumes that d >> R1, R2. It should be noted, however, that, if the translational motion of the bubbles is absent or negligible as with bubbles adherent to a wall, (4) in fact is accurate up to the order (Rα,β/d)3, see [32,33]. Therefore this equation can serve as a plausible estimate up to relatively small separation distances.
Let us now compare (1) and (2) with the equation of radial motion for a single unencapsulated bubble, the Rayleigh-Plesset equation,
| (5) |
The comparison shows that the coupling term Tα can be treated just as a correction to the external acoustic field incident on bubble α. That is, in the case of two interacting bubbles, one can consider that each bubble undergoes the external field which is specified by Pac(t)−ρLTα or Pac(t)−ρLTβ, respectively. All the other terms in the equations for two interacting bubbles are the same as in the Rayleigh-Plesset equation for a single bubble.
Let us now apply this inference to encapsulated bubbles. As an equation for a single encapsulated bubble, which is intended to be generalized to the case of two coupled encapsulated bubbles, we will use the radial equation obtained in [28], which was derived as an improvement to Church’s theory [17]. This equation can be represented as
| (6) |
Here κ = ρL/ρS, c is the speed of sound in the surrounding liquid, and, following Church’s notation, R1 and R2 denote the inner and the outer radii of the bubble shell, respectively. The function H accounts for the acoustic radiation losses of the bubble caused by the compressibility of the surrounding liquid and is defined as [28]
| (7) |
The function G is an analog of the right-hand side of the Rayleigh-Plesset equation for the case of an encapsulated bubble and given by
| (8) |
where Pg0 is the equilibrium gas pressure inside the bubble, R10 and R20 are, respectively, the inner and the outer radii of the bubble shell at rest, and σ1 and σ2 are the surface tension coefficients at the gas-shell and shell-liquid interfaces, respectively. The term S describes the physical properties of the encapsulating shell. Its explicit expression depends on what rheological model is used for the shell, see Section 2.3. Equations (6) - (8) are supplemented with the relationship , which results from the assumption that the shell material is incompressible. The initial conditions for (6) are specified by R1(0) = R10, R2(0) = R20, and .
If the shell thickness RS = R2 − R1 << R1, R2, as is the case with lipid-shelled contrast agents which will be dealt with hereinafter, (6) reduces to an equation of zero-thickness type
| (9) |
where the functions H and G are given by
| (10) |
| (11) |
Comparing (5) and (9), one can see that the only difference between them is the presence of the function H and the shell term S in the right-hand side of (9). As a matter of fact, the function H can be added into (5) as well because it describes acoustic radiation losses of any bubble, no matter whether it is encapsulated or free [34]. It is also clear that the expressions for H and S are independent of whether a neighboring bubble is present or not. These facts mean that (9) can be generalized to the case of two interacting encapsulated bubbles in the same way as (5) to the case of two interacting unencapsulated bubbles, i.e., just replacing Pac(t) with Pac(t)−ρLTα or Pac (t)−ρLTβ for bubbles α and β, respectively. As a result, for two coupled encapsulated bubbles, one obtains
| (12) |
| (13) |
where Tα,β is defined by (4), and Hα,β and Gα,β are given by (10) and (11) in which all the quantities concerning bubbles α and β should be used with the subscripts α and β, respectively.
2.2. A bubble at a wall
As pointed out above, a bubble at a wall is a particular case of the two-bubble problem. Using the method of mirror image, the equation of motion for a bubble at a rigid wall can be obtained from the two-bubble problem, Eqs. (12) and (13), by assuming that the two bubbles are equal, pulsating in phase, and the wall is halfway between them. We will assume below that the real bubble is bubble α and denote its radius by R. As a result, using (12) and (4), the equation of radial motion for an encapsulated bubble at a rigid wall can be written as
| (14) |
where x is the spacing between the center of the bubble and the wall, and H and G are given by (10) and (11).
Summing up the above derivation, (14) allows one to estimate the effect of a boundary on the radial dynamics of an encapsulated bubble. The boundary is treated as a plane rigid wall, the effect of encapsulation is allowed for by the term S in the function G, and the function H takes account of the acoustic radiation losses due to the compressibility of the surrounding liquid. Equation (14) also assumes that the translational motion of the bubble is negligible, the separation distance between the bubble and the wall is large compared to the bubble radius, and the bubble retains the spherical shape at all times.
The above assumptions make it appropriate to consider the applicability of (14) to the purpose of the present study. The first point is the neglect of translational motion in (14). As stated in the Introduction, our purpose is to compare the echo from contrast agent microbubbles at two fixed states: bubbles in free space and bubbles near a wall. Thus the translational motion in itself is beyond our interest in this study. What is more, the pattern of the translational motion in the case under consideration is apparent: A bubble approaches rapidly the wall and then its movement is stopped. Even if the bubble continues to execute insignificant translational motions near the wall, it is evident that their contribution (as a dipole oscillation) to the scattered echo is negligible compared to that of the radial (monopole) motion. This is in fact the prime reason of why the effect of translation can be neglected in (14) when estimating the acoustic response from contrast microbubbles at a wall. The second point is the accuracy of (14) at short distances from the wall. If the translational motion of the bubble is negligible, (14) is accurate up to the order (R/2x)3, see the comments following (4). The next correction to the R/2x term of (14) is of the order (R/2x)4. This correction, as applied to two unencapsulated bubbles, was derived by Harkin et al. [32]. Applying it to a bubble at a wall, one can readily show that the ratio of this fourth-order correction to the R/2x term of (14) is approximately equal to 0.5(R/2x)3. Therefore, even if we set x = 2R0 as we will do in the following for contrast agents near a wall, the correction to the R/2x term of (14) should be in the region of 1 %. The last point is asymmetrical oscillations of microbubbles which are initiated by the neighborhood of the wall. The modeling of this effect is a difficult theoretical problem which is beyond the scope of the present study. It should be noted, however, that even if asymmetrical oscillations occur, the dominant contribution to the scattered pressure field comes from the volume oscillation so that (14) can still be used to obtain a plausible estimate of the scattered echo.
The scattered pressure from a bubble near a wall can be written as
| (15) |
where r1 is the distance from the center of the real bubble and r2 is the distance from the center of the imaginary, mirror bubble. Assuming that the distance between the real bubble and the point of observation is large compared to the spacing between the bubble and the wall, the scattered pressure at the distance r = r1 can be approximately represented as
| (16) |
This equation shows that the scattered pressure is as if we had two identical bubbles pulsating at the same space point. Note, however, that this does not mean that the scattered pressure from a bubble near a wall is twice as large as the scattered pressure from the same bubble in an unbounded medium because the oscillation of the bubble is affected by the wall. Nevertheless (16) shows that the scattered pressure increases as the bubble approaches the wall.
2.3. Shell model
It is easy to show that all existing thin-shelled bubble models boil down to equation (9) with different expressions for the term S in equation (11). In what follows, we will use the shell model proposed by de Jong et al. [16], which can be represented as [29]
| (17) |
where κS is the shell viscosity (in kg/s) and χ is the shell elasticity (in N/m). The expression for Pg0 in this case is given by
| (18) |
Equation (17) is widely used in the literature and shows good agreement with experiments for many cases.
3. Numerical results
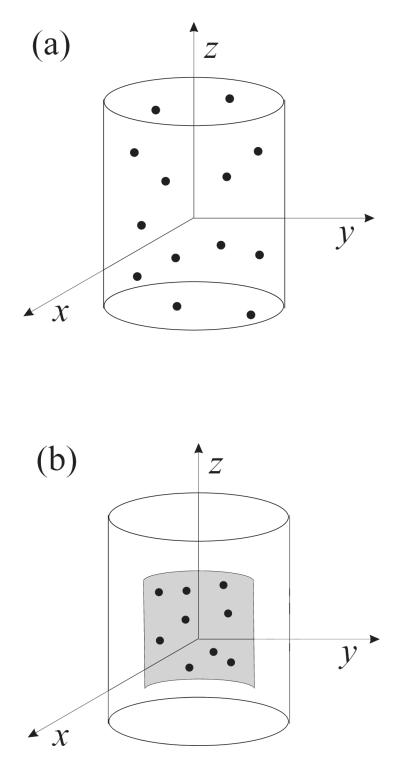
As a guide for the experimental conditions and physical parameters, we have used data from [12,27,29,35]. The values of the physical parameters were the following: P0 =101.3 kPa, ρL =1000 kg/m3, ηL =0.001 Pa s, c =1500 m/s, γ =1.07, and σ = 0.072 N/m. Simulations were carried out to compare the echo from freely circulating contrast agents to that produced by adherent contrast agents. The echo was calculated for a population of 100 microbubbles. Bubbles were assumed to be either randomly distributed inside a vessel (free bubbles) or localized on a vessel wall (adherent bubbles). In the free case, 100 bubbles were assumed to be randomly distributed within a tube with 200 μm in diameter and 400 μm in length, Fig. 1a. In the adherent case, 100 bubbles were assumed to be randomly distributed near the rear part of the tube wall 200 μm in length within a 90-degree angle, Fig. 1b. These parameters correspond to the experimental conditions of [12]. The total echo was calculated at the point lying on the x axis at a distance of 0.01 m from the origin of the coordinates. For each case tested, the calculated echo was averaged by repeating simulations 20 times with randomly varying spatial bubble distributions.
Fig. 1.
Contrast agent microbubbles (a) inside a tube, (b) localized on a tube wall.
The total scattered pressure from the bubble population was evaluated as
| (19) |
where N is the number of bubbles, rn is the position vector of the nth bubble, r is the position vector of the observation point at which the total echo is calculated, and the function Qn(t) is defined by
| (20) |
with Rn(t) denoting the instantaneous radius of the nth bubble. To take into account the finite speed of sound propagation in the liquid, we introduce the time delay τn=∣r − rn∣/c following the approach proposed by Mettin et al. [36]. For bubbles far from the wall, q =1 and Rn(t) for each bubble is calculated from (14) with the dropped last term on the right-hand side. For bubbles near the wall, q = 2 and the nontruncated equation (14) is used.
The experimental observations of Zhao et al. [11,12] show that four obvious features distinguishing the dynamics of adherent and free contrast agents are (i) a more coherent summation of echoes from adherent agents due to their localization on a vessel wall, (ii) acoustic interaction between the wall and adherent agents, (iii) formation of bubble aggregates near the vessel wall, and (iv) asymmetrical oscillations of adherent microbubbles. We examine here the first three differences. The effect of asymmetrical oscillations on the echo is beyond the scope of our study.
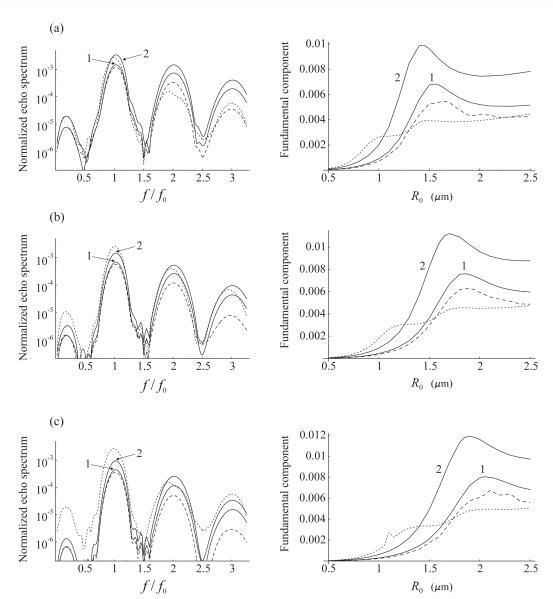
We first assume that the bubble population is monodisperse. The results of the simulations are displayed in Fig. 2. The left column of Fig. 2 shows the Fourier spectrum of the normalized scattered pressure from 100 bubbles with the same radii of 1.1 μm for three different pairs of values for the shell viscosity and elasticity. The right column of Fig. 2 displays the fundamental spectral component as a function of the resting bubble radius under the same conditions as in the corresponding left plot. The normalized scattered pressure is defined as ps/(PaN), where Pa is the amplitude of the driving acoustic pressure. Bubbles are insonified with a 10-cycle Blackman-windowed pulse at the frequency f0=4 MHz and the amplitude Pa = 210 kPa. These acoustic conditions correspond to [12].
Fig. 2.
Fourier spectrum of the scattered pressure from a monodisperse population of 100 bubbles with a radius of 1.1 μm (left column), and the fundamental spectral component as a function of the resting bubble radius under the same conditions as in the corresponding left plot (right column). Bubbles are insonified with a 10-cycle, 4 MHz, 210 kPa Blackman-windowed pulse. The shell parameters are (a) κS=0.5·10−8 kg/s, χ=0.25 N/m; (b) κS=1.0·10−8 kg/s, χ = 0.54 N/m; (c) κS=1.5·10−8 kg/s, χ = 0.8 N/m. The dashed line corresponds to free bubbles. The solid lines correspond to bound bubbles and show the effect of (1) coherent echo summation and (2) coherent echo summation + wall. The dotted line shows the effect of coherent echo summation + wall + bubble aggregates.
The values of the shell viscosity and elasticity were chosen according to estimates available in the literature. Gorce et al. [35] give values of κS=0.72·10−8 kg/s and χ=0.55 N/m. Marmottant et al. [27] obtained values of κS=1.5·10−8 kg/s and χ =1 N/m. Finally, van der Meer et al. [29] report that χ = 0.54 ± 0.10 N/m and the order of magnitude of κS is 10−8 kg/s. These estimates were obtained for two contrast agents. Gorce et al. used SonoVue™ and in the two other papers BR-14 was employed. The experimental observations of Zhao et al. [12] which are referred to here were made for a different contrast agent. Zhao et al. used a home-made contrast agent similar to Definity® [7]. However, all these agents have lipid encapsulation and therefore one can expect that the values of their shell parameters should at least be of the same order of magnitude. This is confirmed by the comparison of the values obtained for SonoVue™ and BR-14. There is one more point to be made. Morgan et al. [21] and van der Meer et al. [29] report that the shell viscosity increases as the resting bubble radius increases. There are also conference reports that the shell elasticity seems to behave similarly [37]. Based on all these facts, three pairs of values for the shell viscosity and elasticity were tested: Fig. 2a κS=0.5·10−8 kg/s, χ = 0.25 N/m; Fig. 2b κS=1.0·10−8 kg/s, χ = 0.54 N/m; Fig. 2c κS=1.5·10−8 kg/s, χ = 0.8 N/m. The order of magnitude of the selected values corresponds to that indicated in the literature, assuming that the shell viscosity and elasticity should increase jointly.
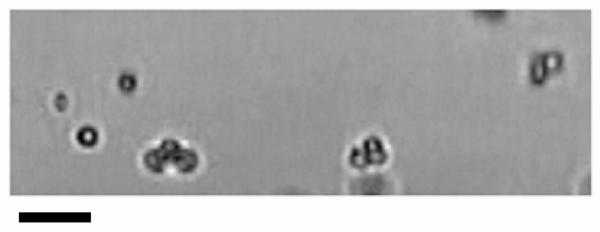
In the left column of Fig. 2, the dashed line shows the spectrum for free bubbles. Curve 1 represents the spectrum for the same bubbles localized near the tube wall as described above. This curve demonstrates the effect of coherent echo summation. Curve 2 is a result of two effects, coherent echo summation and acoustic interaction with the wall, assuming the distance between the bubbles and the wall to be equal to x = 2R0. The dotted curve attempts to evaluate the effect of bubble aggregates. This curve was calculated assuming that, in addition to coherent echo summation and interaction with the wall, some of bound bubbles formed aggregates. An experimental validation of this effect is shown in Fig. 3. This microscopy image illustrates targeted microbubbles bound to the wall of a 200-μm cellulose tube after application of a radiation force pulse of 4 MHz and 50 kPa. Several of the microbubbles have bound to the tube wall as aggregates. The initial microbubble concentration was approximately 4000 microbubbles per microliter. More details of the experiment can be found in [12].
Fig. 3.
Optical observation of the formation of aggregates of targeted bubbles near a tube wall coated with adhesion receptors after an acoustic pulse optimized to produce radiation force. Scale bar represents ~ 10 μm.
Based on the observations made in the course of the experiments reported in [12], it was assumed that amongst 100 bubbles considered, when they approached the wall, 20 remained single while 80 formed twenty 3-bubble and ten 2-bubble aggregates. As currently there is not any more exact theory to describe the interaction between the sound field and a contrast microbubble aggregate, we treated each aggregate as a bubble of larger size, with a volume equal to the total volume of bubbles that formed the aggregate. It is clear that one of the primary factors that define the interaction between the sound field and a bubble aggregate is the resonance frequency of the aggregate. It is also clear that the resonance frequency is dependent on the size of the aggregate. Therefore we believe that though quite rough, our approximation should nevertheless provide qualitative insight into changes that occur in the scattered echo due to the formation of aggregates. The meaning of all the curves in the right column of Fig. 2 is the same as in the left column.
Analysis of Fig. 2 reveals that, for all the values of the shell parameters and the resting bubble radii tested, the coherent echo summation and the acoustic interaction with the wall tend to increase the fundamental spectral component for bound agents compared to free agents. This result is in agreement with the experimental observations of Zhao et al. [12], who suggest that the increase of the fundamental component of adherent agents can be used to distinguish their echo from the echo produced by freely circulating agents. In Fig. 2, the increase of the fundamental component due to the combined effect of coherent echo summation and acoustic interaction with the wall is on the order of 8-9 dB.
The situation with the effect of aggregates is more complicated. The right column of Fig. 2 shows that the presence of aggregates increases the fundamental component only for relatively small bubbles whose radius is well below the resonant radius. This result can readily be explained. For small bubbles, the formation of aggregates improves the resonant matching and therefore the fundamental component increases. For larger bubbles, however, the formation of aggregates makes the resonant matching worse. As a result, the effect of aggregates can even suppress the increase caused by the coherent echo summation and the presence of the wall; cf. the left part of Fig. 2a with those of Figs. 2b and 2c. This means that, especially for bubbles close to resonance, aggregates may be a factor that impedes rather than helps distinguishing adherent and free agents if this discrimination is based on an increase in the fundamental component alone. However, if the formation of aggregates contributes to the growth of the fundamental component, Figs. 2b and 2c show that the increase reaches 13.6 dB and 17.5 dB, respectively.
To estimate the statistical difference between the cases of free and adherent bubbles, the amplitude of the fundamental component for free and adherent agents was calculated over 20 random space bubble distributions for the parameters as in the left column of Fig. 2. For the adherent bubbles, the fundamental amplitude was calculated separately for the cases when the combined effect of the coherent echo summation and the interaction with the wall is taken into account (curve 2), and when all the three effects, including the formation of aggregates (dotted curve), are allowed for. The Student’s t-test was then performed to compare the data sets for the free and adherent bubbles. For all the cases tested, p-values were found to be much smaller than 0.05, which shows that there is really a significant statistical difference between the free and adherent cases.
The case of a polydisperse population has also been tested. The population was assumed to consist of 100 bubbles with a size distribution similar to the commercially available lipid-encapsulated contrast agent Definity®. An experimental measurement of the size distribution of Definity® is shown in Fig. 4. These data were produced by preparing a vial of Definity® according to the manufacture’s recommendation and the size distribution was measured manually using microscopy techniques as described previously [38]. In the simulation, it was assumed that the initial radii of the bubbles take values from 0.25 μm to 3.5 μm with a step of 0.25 μm. As in Fig. 2, the acoustic driving is a 10-cycle, 4 MHz, 210 kPa Blackman-windowed pulse. The shell parameters were set equal to κS=1.0·10−8 kg/s and χ = 0.54 N/m. The Fourier spectrum of the normalized scattered pressure from the polydisperse 100-bubble population is presented in Fig. 5. One can again see that the coherent echo summation and the neighborhood of the wall increase the intensity of the fundamental component. The increase is about 7 dB. Statistical analysis for this case also gives p << 0.05.
Fig. 4.
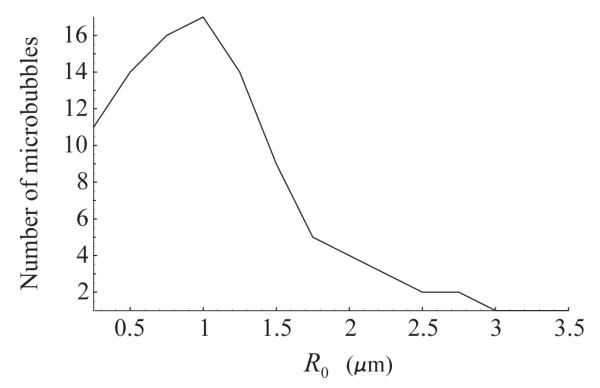
Size distribution of the polydisperse 100-bubble population tested.
Fig. 5.
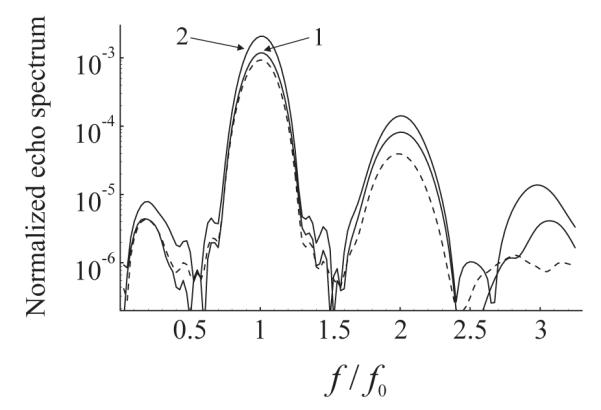
Fourier spectrum of the scattered pressure from a polydisperse 100-bubble population with the size distribution as in Fig. 4 The driving is a 10-cycle, 4 MHz, 210 kPa Blackman-windowed pulse. The shell parameters are κS=1.0·10−8 kg/s and χ = 0.54 N/m. The dashed line shows the spectrum of free bubbles. The solid lines correspond to bound bubbles and show the effect of (1) coherent echo summation and (2) coherent echo summation + wall.
Mention should be made of another difference observed by Zhao et al. [12] in spectral characteristics of free and adherent agents, namely, an increase in the ratio of the fundamental component to harmonics for adherent agents. It may be assumed that this increase is caused by aggregates of microbubbles which form near the tube wall due to secondary radiation forces. Our hypothesis is based on the theoretical results presented in Fig. 6 where the ratio of the fundamental component to the second harmonic is displayed as a function of equilibrium radius for a single encapsulated bubble which is driven under the same acoustic conditions as mentioned above. One can see that for larger bubbles, with radii exceeding approximately 1.2 μm, the fundamental component increases with respect to the second harmonic as the bubble size increases. It is reasonable to assume that the same occurs for aggregates whose resonance frequencies shift away from the driving frequency so that the echo spectrum becomes more linear, with an increasingly stronger fundamental component. Further investigation is required to verify this observation.
Fig. 6.
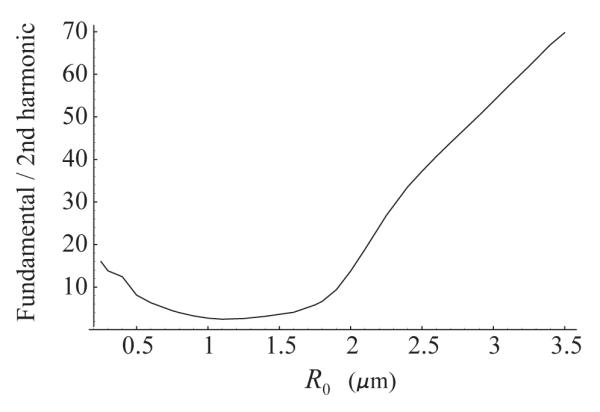
The ratio of the fundamental spectral component to the second harmonic as a function of equilibrium bubble radius. The driving is a 10-cycle, 4 MHz, 210 kPa Blackman-windowed pulse. The shell parameters are κS=1.0·10−8 kg/s and χ = 0.54 N/m.
4. Conclusions
In the present paper, an equation for the radial oscillation of an encapsulated bubble near a plane rigid boundary has been derived. The equation was then used to simulate the acoustic echo from a layer of targeted contrast agent microbubbles localized on a wall. Comparison was made between echo spectra of adherent and freely circulating microbubbles in order to examine differences between the acoustic responses for these two cases. It was shown that the fundamental spectral component of adherent bubbles is perceptibly stronger than that of freely circulating bubbles. This increase is resulted from a more coherent summation of echoes from adherent bubbles and the acoustic interaction between the wall and adherent bubbles. It was also found that bubble aggregates, which are observed experimentally to form near a wall due to secondary Bjerknes forces, increase the intensity of the fundamental component only if they are formed by bubbles whose radii are well below the resonant radius. For larger bubbles, the presence of aggregates can suppress the increase of the fundamental component caused by the coherent echo summation and the presence of the boundary, and thereby impede rather than help distinguishing adherent and free agents. It has been hypothesized that the experimentally observed increase in the ratio of the fundamental component to harmonics for adherent agents is a result of bubble aggregates whose resonance frequencies shift away from the driving frequency so the bubble oscillation becomes more linear.
Acknowledgments
A. A. D. wishes to acknowledge the financial support of the International Science and Technology Center (ISTC) under Contract B-1213. P. A. D. and S. Z. are supported by the NIH Roadmap for Medical Research (Grant R21 EB005325).
Footnotes
PACS: 43.35.Ei; 43.80.Qf; 43.35.Wa; 43.25.Yw
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Becher H, Burns PN. Handbook of Contrast Echocardiography: Left ventricular function and myocardial perfusion. Springer Verlag; New York: 2000. [Google Scholar]
- [2].Goldberg BB, Raichlen JS, Forsberg F, editors. Ultrasound Contrast Agents: Basic Principles and Clinical Applications. Martin Dunitz; London: 2001. [Google Scholar]
- [3].Szabo T. Diagnostic Ultrasound Imaging: Inside Out. Academic; New York: 2004. [Google Scholar]
- [4].Khismatullin DB. Gas microbubbles and their use in medicine. In: Doinikov AA, editor. Bubble and Particle Dynamics in Acoustic Fields: Modern Trends and Applications. Research Signpost; Kerala: 2005. pp. 231–289. [Google Scholar]
- [5].Dayton PA, Ferrara KW. Targeted imaging using ultrasound. J. Magn. Reson. Imaging. 2002;16:362–377. doi: 10.1002/jmri.10173. [DOI] [PubMed] [Google Scholar]
- [6].Bloch SH, Dayton PA, Ferrara KW. Targeted imaging using ultrasound contrast agents: Progress and opportunities for clinical and research applications. IEEE Eng. Med. Biol. Mag. 2004;23:18–29. doi: 10.1109/memb.2004.1360405. [DOI] [PubMed] [Google Scholar]
- [7].Zhao S, Borden MA, Bloch SH, Kruse D, Ferrara KW, Dayton PA. Radiation-force assisted targeting facilitates ultrasonic molecular imaging. Mol. Imaging. 2004;3:135–148. doi: 10.1162/1535350042380317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Rychak JJ, Klibanov AL, Hossack JA. Acoustic radiation force enhances targeted delivery of ultrasound contrast microbubbles: In vitro verification. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005;52:421–433. doi: 10.1109/tuffc.2005.1417264. [DOI] [PubMed] [Google Scholar]
- [9].Christiansen JP, Lindner JR. Molecular and cellular imaging with targeted contrast ultrasound. Proc. IEEE. 2005;93:809–818. [Google Scholar]
- [10].Klibanov AL. Microbubble contrast agents: Targeted ultrasound imaging and ultrasound-assisted drug-delivery applications. Invest. Radiol. 2006;41:354–362. doi: 10.1097/01.rli.0000199292.88189.0f. [DOI] [PubMed] [Google Scholar]
- [11].Zhao S, Ferrara KW, Dayton PA. Asymmetrical oscillation of adherent targeted ultrasound contrast agents. Appl. Phys. Lett. 2005;87:134103. doi: 10.1063/1.2061872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Zhao S, Kruse DE, Ferrara KW, Dayton PA. Acoustic response from adherent targeted contrast agents. J. Acoust. Soc. Am. 2006;120:EL63–EL69. doi: 10.1121/1.2364303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Roy RA, Church CC, Calabrese A. Cavitation produced by short pulses of ultrasound. In: Hamilton MF, Blackstock DA, editors. Frontiers of Nonlinear Acoustics: Proceedings of 12th ISNA; Elsevier, London. 1990. pp. 476–481. [Google Scholar]
- [14].de Jong N, Hoff L, Skotland T, Bom N. Absorption and scatter of encapsulated gas filled microspheres: Theoretical consideration and some measurements. Ultrasonics. 1992;30:95–103. doi: 10.1016/0041-624x(92)90041-j. [DOI] [PubMed] [Google Scholar]
- [15].de Jong N, Hoff L. Ultrasound scattering of Albunex microspheres. Ultrasonics. 1993;31:175–181. doi: 10.1016/0041-624x(93)90004-j. [DOI] [PubMed] [Google Scholar]
- [16].de Jong N, Cornet R, Lancée CT. Higher harmonics of vibrating gas-filled microspheres. Part one: simulations. Ultrasonics. 1994;32:447–453. [Google Scholar]
- [17].Church CC. The effect of an elastic solid surface layer on the radial pulsations of gas bubbles. J. Acoust. Soc. Am. 1995;97:1510–1521. [Google Scholar]
- [18].Ye Z. On sound scattering and attenuation of Albunex bubbles. J. Acoust. Soc. Am. 1996;100:2011–2028. [Google Scholar]
- [19].Frinking PJA, de Jong N. Acoustic modeling of shell-encapsulated gas bubbles. Ultrasound Med. Biol. 1998;24:523–533. doi: 10.1016/s0301-5629(98)00009-x. [DOI] [PubMed] [Google Scholar]
- [20].Hoff L, Sontum PC, Hovem JM. Oscillations of polymeric microbubbles: Effect of the encapsulating shell. J. Acoust. Soc. Am. 2000;107:2272–2280. doi: 10.1121/1.428557. [DOI] [PubMed] [Google Scholar]
- [21].Morgan KE, Allen JS, Dayton PA, Chomas JE, Klibanov AL, Ferrara KW. Experimental and theoretical evaluation of microbubble behavior: Effect of transmitted phase and bubble size. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2000;47:1494–1509. doi: 10.1109/58.883539. [DOI] [PubMed] [Google Scholar]
- [22].Allen JS, May DJ, Ferrara KW. Dynamics of therapeutic ultrasound contrast agents. Ultrasound Med. Biol. 2002;28:805–816. doi: 10.1016/s0301-5629(02)00522-7. [DOI] [PubMed] [Google Scholar]
- [23].Dayton PA, Allen JS, Ferrara KW. The magnitude of radiation force on ultrasound contrast agents. J. Acoust. Soc. Am. 2002;112:2183–2192. doi: 10.1121/1.1509428. [DOI] [PubMed] [Google Scholar]
- [24].Khismatullin DB, Nadim A. Radial oscillations of encapsulated microbubbles in viscoelastic liquids. Phys. Fluids. 2002;14:3534–3557. [Google Scholar]
- [25].Chatterjee D, Sarkar K. A Newtonian rheological model for the interface of microbubble contrast agents. Ultrasound Med. Biol. 2003;29:1749–1757. doi: 10.1016/s0301-5629(03)01051-2. [DOI] [PubMed] [Google Scholar]
- [26].Sarkar K, Shi WT, Chatterjee D, Forsberg F. Characterization of ultrasound contrast microbubbles using in vitro experiments and viscous and viscoelastic interface models for encapsulation. J. Acoust. Soc. Am. 2005;118:539–550. doi: 10.1121/1.1923367. [DOI] [PubMed] [Google Scholar]
- [27].Marmottant P, van der Meer S, Emmer M, Versluis M, de Jong N, Hilgenfeldt S, Lohse D. A model for large amplitude oscillations of coated bubbles accounting for buckling and rupture. J. Acoust. Soc. Am. 2005;118:3499–3505. [Google Scholar]
- [28].Doinikov AA, Dayton PA. Spatio-temporal dynamics of an encapsulated gas bubble in an ultrasound field. J. Acoust. Soc. Am. 2006;120:661–669. doi: 10.1121/1.2215228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].van der Meer SM, Dollet B, Voormolen MM, Chin CT, Bouakaz A, de Jong N, Versluis M, Lohse D. Microbubble spectroscopy of ultrasound contrast agents. J. Acoust. Soc. Am. 2007;121:648–656. doi: 10.1121/1.2390673. [DOI] [PubMed] [Google Scholar]
- [30].Doinikov AA, Dayton PA. Maxwell rheological model for lipid-shelled ultrasound microbubble contrast agents. J. Acoust. Soc. Am. 2007;121:3331–3340. doi: 10.1121/1.2722233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Allen JS, Kruse DE, Dayton PA, Ferrara KW. Effect of coupled oscillations on microbubble behavior. J. Acoust. Soc. Am. 2003;114:1678–1690. doi: 10.1121/1.1600721. [DOI] [PubMed] [Google Scholar]
- [32].Harkin A, Kaper TJ, Nadim A. Coupled pulsation and translation of two gas bubbles in a liquid. J. Fluid Mech. 2001;445:377–411. [Google Scholar]
- [33].Doinikov AA. Translational motion of two interacting bubbles in a strong acoustic field. Phys. Rev. E. 2001;64:026301. doi: 10.1103/PhysRevE.64.026301. [DOI] [PubMed] [Google Scholar]
- [34].Doinikov AA. Equations of coupled radial and translational motions of a bubble in a weakly compressible liquid. Phys. Fluids. 2005;17:128101. [Google Scholar]
- [35].Gorce JM, Arditi M, Schneider M. Influence of bubble size distribution on the echogenicity of ultrasound contrast agents. A study of SonoVue™. Invest. Radiol. 2000;35:661–671. doi: 10.1097/00004424-200011000-00003. [DOI] [PubMed] [Google Scholar]
- [36].Mettin R, Luther S, Kamphausen S, Lauterborn W. Dynamics of delay-coupled spherical bubbles. Proceedings of 15th International Symposium on Nonlinear Acoustics; Goettingen, Germany. 1–4 September 1999; NY: AIP Melville; 2000. pp. 359–362. [Google Scholar]
- [37].Chetty K, Sennoga CA, Hainal JV, Eckersley RJ, Stride E. High speed optical observations and simulation results of lipid based microbubbles at low insonation pressures. Proceedings of the 2006 IEEE International Ultrasonics Symposium; IEEE, Vancouver, Canada. 2006. pp. 1354–1357. [Google Scholar]
- [38].Talu E, Hettiarachchi K, Zhao S, Powell RL, Lee AP, Longo ML, Dayton PA. Tailoring the size distribution of ultrasound contrast agents: possible method for improving sensitivity in molecular imaging. Mol. Imaging. 2007;6:384–392. [PMC free article] [PubMed] [Google Scholar]