An investigation of signal performance enhancements achieved through innovative pixel design across several generations of indirect detection, active matrix, flat-panel arrays

Abstract

Active matrix flat-panel imager (AMFPI) technology is being employed for an increasing variety of imaging applications. An important element in the adoption of this technology has been significant ongoing improvements in optical signal collection achieved through innovations in indirect detection array pixel design. Such improvements have a particularly beneficial effect on performance in applications involving low exposures and∕or high spatial frequencies, where detective quantum efficiency is strongly reduced due to the relatively high level of additive electronic noise compared to signal levels of AMFPI devices. In this article, an examination of various signal properties, as determined through measurements and calculations related to novel array designs, is reported in the context of the evolution of AMFPI pixel design. For these studies, dark, optical, and radiation signal measurements were performed on prototype imagers incorporating a variety of increasingly sophisticated array designs, with pixel pitches ranging from 75 to 127 μm. For each design, detailed measurements of fundamental pixel-level properties conducted under radiographic and fluoroscopic operating conditions are reported and the results are compared. A series of 127 μm pitch arrays employing discrete photodiodes culminated in a novel design providing an optical fill factor of ∼80% (thereby assuring improved x-ray sensitivity), and demonstrating low dark current, very low charge trapping and charge release, and a large range of linear signal response. In two of the designs having 75 and 90 μm pitches, a novel continuous photodiode structure was found to provide fill factors that approach the theoretical maximum of 100%. Both sets of novel designs achieved large fill factors by employing architectures in which some, or all of the photodiode structure was elevated above the plane of the pixel addressing transistor. Generally, enhancement of the fill factor in either discrete or continuous photodiode arrays was observed to result in no degradation in MTF due to charge sharing between pixels. While the continuous designs exhibited relatively high levels of charge trapping and release, as well as shorter ranges of linearity, it is possible that these behaviors can be addressed through further refinements to pixel design. Both the continuous and the most recent discrete photodiode designs accommodate more sophisticated pixel circuitry than is present on conventional AMFPIs – such as a pixel clamp circuit, which is demonstrated to limit signal saturation under conditions corresponding to high exposures. It is anticipated that photodiode structures such as the ones reported in this study will enable the development of even more complex pixel circuitry, such as pixel-level amplifiers, that will lead to further significant improvements in imager performance.

INTRODUCTION

In recent years, an increasing number of medical applications have begun employing flat-panel x-ray imagers based on the principle of a large area active matrix – a concept adapted from active matrix liquid crystal displays (AMLCDs). In an active matrix array, a two-dimensional grid of pixels is addressed by means of thin-film switches, usually based on either hydrogenated amorphous silicon (a-Si:H) or polycrystalline silicon (poly-Si) semiconductor material.

To date, all commercially available active matrix flat-panel imagers (AMFPIs) incorporate a relatively simple design and operating principle:^{1, 2, 3} (i) each pixel has an addressing switch (most commonly a single, a-Si:H thin-film transistor [TFT]) coupled to a pixel storage capacitor; (ii) along a given row of pixels, all the gate contacts of the TFTs are connected to a common gate address line – with one gate line per pixel row; (iii) along a given column of pixels, all the drain contacts of the TFTs are connected to a common data address line – with one data line per pixel column; (iv) an x-ray converter is positioned over the surface of the array so that incident X rays interacting with the converter result in the deposition of signal in the pixel storage capacitors; (v) at the periphery of the array, external gate driver and preamplification circuits are connected to each gate and data line, respectively; (vi) through manipulation of the conductivity of the TFTs via control of the gate line voltages by the drivers, x-ray signal is accumulated in the storage capacitors and then, typically one row at a time, this information is read out via the data lines, subsequently being amplified, multiplexed, and digitized to form an image frame. With this general design and method of operation, AMFPIs may be configured to operate fluoroscopically (i.e., capture, readout, and display of many frames per second) and∕or radiographically (acquisition of a single frame).

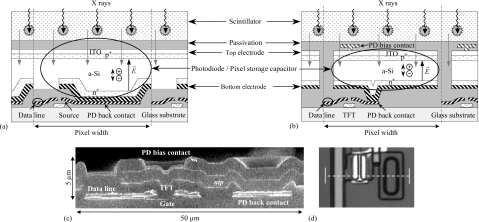
AMFPIs can be divided into two categories based on the form of the x-ray converter: (i) direct detection devices in which the converter consists of a relatively thick layer of photoconductive material (e.g., a-Se);^{2, 3} and (ii) indirect detection devices in which the converter is a scintillator (e.g., CsI:Tl or Gd₂O₂S:Tb) and the pixel storage capacitor takes the form of an a-Si:H photodiode.^{1, 3} In the case of the latter approach, which is the focus of this article, the fraction of the pixel area that is occupied by the photodiode is called the geometric fill factor (FF_geo) while the fraction that is optically sensitive to light from the overlying scintillator is called the optical fill factor (FF_opt). Presently, commercially available indirect detection AMFPIs employ a discrete photodiode, as schematically illustrated in Fig. 1. In such designs, the photodiode competes with the addressing TFT for surface area in the pixel. In addition, a gap must be maintained between the edges of the photodiode and the neighboring address lines and the TFT to minimize parasitic capacitance as well as the chances of unintended contact of pixel structures during fabrication. Furthermore, an overlying metal bias line, which supplies a reverse bias voltage (V_bias) across each photodiode, is commonly positioned over the photodiodes, further reducing FF_opt. (While the bias voltage applied to the top electrode is negative, the symbol V_bias will designate the magnitude of this voltage.) The minimum size of individual features and of the gaps between features are part of the design rules that govern the dimensions of lines, TFTs and photodiodes, and thus FF_opt. Moreover, for a given set of rules, optical fill factor for an array will decrease as the pixel pitch (a_pix) of the design is reduced. Given the types of design rules employed for AMFPIs, the fall-off becomes particularly significant at pitches approaching, and smaller than, 100 μm.

Figure 1.

Schematic drawing of a baseline architecture indirect detection pixel design incorporating a discrete photodiode structure in each pixel. The drawing corresponds to a cross-sectional view, parallel to the direction of the gate address lines, through a part of a pixel containing both the addressing TFT and the photodiode. The locations of the TFT and photodiode are indicated by superimposed ellipses. The direction of the data and photodiode bias lines is orthogonal to the plane of the drawing. Note that the drawing depicts an entire pixel (delimited by a pair of vertical dashed lines and a horizontal, double-headed arrow) as well as portions of adjoining pixels. Finally, note that the drawing is not to scale and that, in particular, the vertical dimensions are significantly exaggerated for reasons of clarity of presentation.

For many medical imaging applications in which AMFPIs are employed, a variety of considerations can combine to make it highly desirable to achieve as high a signal, and thus as large an optical fill factor, as possible. Such considerations include the clinically desired and acceptable exposure level per image frame, the pixel pitch required for the desired spatial resolution, the intrinsic signal and noise properties of the scintillator, and the intrinsic level of nonradiation-related noise (referred to as additive electronic noise, σ_add) from the AMFPI system. Figure 2 shows calculations of detective quantum efficiency, DQE, at zero spatial frequency for hypothetical AMFPI designs, as a function of a_pix, FF_opt, and exposure. The calculations in Fig. 2a are performed for fluoroscopic conditions at exposures (0.1, 1.0, and 3.0 μR per frame) representative of the lower end of the normal fluoroscopic range of 0.1 to 10 μR.^{4, 5} The calculations in Fig. 2b are performed at an average mammographic exposure (10 mR) and at one-tenth of this exposure, corresponding to what might be used for a single exposure in an x-ray tomosynthesis data set.⁶

Figure 2.

Cascaded systems calculations of DQE at zero spatial frequency plotted as a function of pixel pitch using the formalism reported in Ref. 6. Calculations are shown for three values of optical fill factor: 100% (solid lines), 50% (dashed lines), and 25% (dotted lines). (a) Calculations corresponding to an imager with a 600 μm thick CsI:Tl scintillator (75% packing density) operated fluoroscopically at 72 kVp, 20 mm Al filtration, at three values of exposure per frame: 3 μR (black lines), 1 μR (red lines), and 0.1 μR (orange lines). (b) Calculations corresponding to a mammographic imager with a 150 μm thick CsI:Tl scintillator (100% packing density) (Ref. ⁶) operated at 26 kVp, with a Mo∕Mo target∕filter and a 5.0 cm thick BR12 phantom, at two exposures: 10 mR (black lines), and 1 mR (red lines). Finally, the horizontal dot-dashed line corresponds to the theoretical limit on DQE, as defined by the properties of the x-ray converter and the incident x-ray spectrum. Further details relating to assumptions in the calculations appear in the Appendix.

These calculations illustrate a variety of interesting behaviors. Under conditions where the pixel signal is significantly larger than additive noise, the DQE closely approaches the maximum value allowed by the converter (see Refs. ^{5, 6}) – represented by the horizontal dot-dashed line in each figure, which corresponds to the product of the quantum detection efficiency and Swank factor of the CsI:Tl scintillator. In the calculations shown, these conditions are satisfied by a combination of larger pixel pitch, higher exposure, and high optical fill factor. If pitch or exposure decreases, the DQE decreases. (Moreover, the fall-off in DQE is even more pronounced at nonzero spatial frequencies.^{5, 6, 7}) However, for a given pitch, improvements in optical fill factor can substantially improve DQE, with the relative amount of improvement being greater at lower exposures – thus providing strong motivation to maximize FF_opt through improvements in pixel design. In this article, the performance of a variety of indirect detection AMFPI arrays employing progressively more sophisticated pixel designs is reported. These arrays correspond to successive generations of innovative designs developed approximately over a decade. Through a combination of measurements involving optical illumination, x-ray irradiation (employing a scintillator), and in the absence of light or X rays, the properties of the various designs are examined and compared. Finally, an example of a novel pixel circuit design that is facilitated by one of the recent photodiode structures is presented, and the potential for further, significant enhancement of performance through incorporation of increasingly complex pixel circuits is discussed.

METHODS AND MATERIALS

Array designs and electronic acquisition system

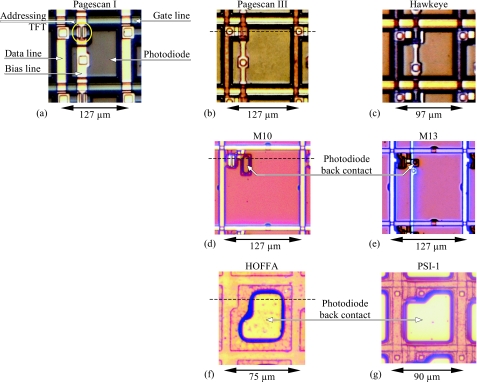
Specifications for the seven indirect detection array designs examined in this study are summarized in Table 1, and photomicrographs of individual pixels for each design are shown in Fig. 3. The designs, developed at the Palo Alto Research Center (PARC) and dpiX, correspond to the use of either a discrete photodiode in each pixel (Pagescan I, Pagescan III, Hawkeye, M10, and M13) or a continuous photodiode (HOFFA and PSI-1). HOFFA and PSI-1 are acronyms for high optical fill factor array and poly-Si imager design number 1, respectively. Compared to Pagescan I [Fig. 3a], which was the first reported large area, high-resolution AMFPI array,⁸ Pagescan III and Hawkeye [Figs. 3b, 3c, respectively] correspond to a later generation employing more aggressive design rules (e.g., narrower address lines and gaps, and smaller addressing TFTs) which facilitated larger optical fill factors.^{9, 10} For these three arrays, the general structure and arrangement of the photodiode in the pixel, which will be referred to as the baseline architecture, is schematically illustrated in Fig. 1. Each photodiode consists of a bottom signal collection electrode, formed from the same metal layer as, and connected to, the source contact of the addressing TFT. This is followed by n-doped, intrinsic, and p-doped a-Si:H layers, patterned so as to be aligned to each other, and referred to as a stacked n-i-p geometry. Finally, there is a top electrode, consisting of a transparent conducting metal (indium tin oxide, ITO), connected to the overlying bias line. The n-i-p stack is in the plane of the addressing TFT and is geometrically configured so as to avoid creating shorts or large parasitic capacitances with other array elements.

Table 1.

Specifications for the five discrete photodiode, and two continuous photodiode array designs examined in this study. The following information is given for each array design: the design name; the type of photodiode structure; the pixel pitch, a_pix; the year of fabrication for the sample array examined; the type of substrate material; the width and length of the pixel addressing TFT (W and L, respectively); the pixel format; the data line capacitance, C_data (determined through measurement or estimation); the data line capacitance per pixel, C_dlpix; the nominal optical fill factor, FF_opt (as determined from pixel design dimensions and expressed in percent, and based on conventions described in the main text); and the geometric fill factor of the photodiode, FF_geo. Note that the substrate material for the first six arrays listed in the table is one of several types of glass (Corning: 7059, 1737F, or 1737G) while the PSI-1 array employs a quartz substrate (Shin-Etsu MicroSi: Viosil-SQ4W525WR). Also note that the pixel design for M10 corresponds to option 2 of Ref. 15, and the design for M13 corresponds to an updated version of option 3 of that reference.

Array	Photodiode type	Pitch,apix (μm)	Year, Ref.	Substrate Type	TFTW×L (μm×μm)	Pixel format (data×gate)	Cdata (pF)	Cdlpix (fF)	Nominal FFopt	FFgeo
Pagescan I	Discrete	127	1994,8	7059	20×11	1536×1920	95	49.5	35%	42.0%
Pagescan III	Discrete	127	1997,9	1737F	15×9	1536×1920	65	33.9	57%	61.0%
Hawkeye	Discrete	97	1998,10	1737F	12×9.5	2048×2048	50	24.4	44%	49.1%
M10	Discrete	127	2003,15	1737 G	15×8	768×768	43	56.0	85%	86.9%
M13	Discrete	127	2004, n∕a	1737 G	15×8	1024×1024	44	42.9	79%	84.3%
HOFFA	Continuous	75	2001,11	7059	15×10	512×512	15	29.3	100%	71.8%
PSI-1	Continuous	90	2003,13	Quartz	10×(5+5)	384×256	2.53	9.9	100%	69.7%

Figure 3.

Photomicrographs of pixels from the various indirect detection array designs evaluated in this article: (a) Pagescan I; (b) Pagescan III; (c) Hawkeye; (d) M10; (e) M13; (f) HOFFA; and (g) PSI-1. In each case, the picture is oriented so that the addressing TFT is located in the upper left-hand corner of the pixel, the gate lines are oriented along the horizontal direction, and the solid, double-headed arrow and accompanying number indicate the pixel pitch. In addition, the locations of the TFT, photodiode, data line, and gate line (which are present for all pixel designs), as well as the bias line (which is present for the discrete pixel designs) are specifically indicated for Pagescan I. The position of the photodiode back contact for M10, M13, HOFFA, and PSI-1 is also indicated. The position of the dashed horizontal line superimposed over (b), (d), and (f) corresponds to the approximate location of the cross-sectional views depicted in Figs. 14b, 4a, respectively.

The HOFFA design [Fig. 3f] uses the continuous n-i-p photodiode structure schematically illustrated in Fig. 4a. HOFFA is an early prototype of this geometry,¹¹ which built upon the experience acquired from the creation of an initial, 64 μm pitch, prototype.¹² A central goal in the design of these arrays was a substantial reduction in the competition between the addressing TFT and the photodiode for area in the pixel, thereby allowing substantial increases in FF_opt. Compared to arrays based on the baseline architecture, both the intrinsic and p-doped a-Si:H layers in HOFFA are extended across the entire array, with no patterning, while the n-doped layer is patterned so as to coincide with the bottom signal collection electrode. Moreover, the bottom electrode occupies a much larger fraction of the pixel area than for the baseline architecture – extending efficient signal collection toward the edges of the pixel. The overall structure is designed to inhibit charge sharing between pixels while increasing FF_opt, ideally, close to 100%, irrespective of pixel pitch. Note that the bottom electrode is a separate metal layer that makes electrical connection to the TFT by virtue of mechanical contact with a metal plane, called the photodiode back contact, formed by an extension of the source contact of the transistor – as illustrated in Fig. 4a. This significantly contributes to nonuniformities in the topology of the continuous photodiode [which are partially illustrated in Fig. 4a] – with the large fraction of photodiode area that is over the photodiode back contact [as is evident in Fig. 3f] at a different height than the fraction occupying the periphery of the pixel. By comparison, the photodiode topology for arrays based on the baseline architecture is highly planar – as portrayed in Fig. 1.

Figure 4.

Illustrations related to the pixel structure of the HOFFA and M10 arrays. (a) Schematic drawing of a pixel design incorporating a continuous photodiode structure, such as that used in HOFFA. The drawing also depicts the photodiode structure for PSI-1, although the details of the addressing TFT for that design differ. (b) Schematic drawing of the M10 pixel design. The drawing also generally applies to the structure for M13, with exceptions noted in the main text. Both drawings follow conventions used in Fig. 1. Also note that nonuniformities in photodiode topology are only partially illustrated. (c) Cross-sectional view, obtained from an SEM photograph, illustrating the structure and topology of a portion of an M10 pixel in the vicinity of the addressing TFT and photodiode back contact. Note that the image is magnified by a factor of ∼2 in the vertical direction, compared to the horizontal direction. Labels superimposed on the image indicate the general position of a variety of design elements, including the region where the source contact of the TFT connects to the back electrode of the photodiode (PD back contact) and the connection between the overlying bias line and the top electrode of the photodiode (PD bias contact). (d) Top microscopic view of a corner of the M10 pixel where the dashed line indicates the position of the cross-sectional image shown in (c). Note that the region illustrated in this image corresponds to the upper left-hand corner of Fig. 3d. The images in (c) and (d) have been adapted from Fig. 3 of Ref. 15.

The pixels for the PSI-1 array [Fig. 3g] employ the same photodiode structure as HOFFA. Although the TFT in PSI-1 uses a poly-Si semiconductor and has a dual gate structure, the pixel circuit is the same as that of the other array designs and, for purposes of this study, the properties of PSI-1 can largely be compared directly to those of the other arrays. Note that the continuous photodiode structure of Fig. 4a allows for the possibility of more complex pixel circuits and PSI-1 was created in connection with other designs incorporating pixel-level amplifiers.^{13, 14}

In the development of the M10 array,¹⁵ in addition to reducing competition between the TFT and the photodiode for area, a goal was to eliminate processing problems that arise in baseline architecture arrays during fabrication of the comparatively thick photodiode next to the addressing TFT – which periodically results in defective pixels. The resulting design for M10, schematically illustrated in Fig. 4b, combines architectural elements of baseline architecture arrays (such as Pagescan I, Pagescan III, and Hawkeye) and the continuous photodiode arrays (i.e., HOFFA and PSI-1). As illustrated in the figure, the M10 pixel employs a discrete photodiode structure consisting of a stacked n-i-p arrangement. In addition, most of the bottom electrode of the photodiode is seen to be positioned above the plane of the addressing TFT, with the source contact of the TFT connected to the bottom electrode by a photodiode back contact that occupies a considerably smaller fraction of the pixel area than for HOFFA or PSI-1 [e.g., compare Figs. 3d, 3f, 3g]. The topology of the photodiode, in the relatively small part of the pixel where it is most nonuniform, is illustrated in the cross-sectional image of an M10 pixel shown in Fig. 4c – corresponding to the pixel region indicated in Fig. 4d. Thus, the goals of the M10 design were pursued by placing a large portion of a discrete photodiode above the plane of the TFT, using narrower lines and gaps, and positioning the bias line over the gate line.

The M13 design [Fig. 3e] builds upon the experience gained from M10. For M13, the bias line was positioned over the photodiode (reducing parasitic capacitance with the gate line and facilitating successful quality control of the arrays), the gap between the bottom signal collection electrode and the data line was slightly increased (reducing data line capacitance), and the area of the photodiode back contact was further significantly reduced (increasing uniformity of the photodiode topology). The first two of these major changes resulted in a slight decrease in FF_opt.

The results reported in this study correspond to data obtained from a single sample array for each design. For the Pagescan III and M13 arrays, the properties of the reported arrays are known, or believed to be representative of other samples of the same design, respectively. The Pagescan I, Hawkeye, M10, HOFFA, and PSI-1 arrays were prototypes made in far more limited numbers, and the properties of the reported samples represented the best behavior among the arrays examined. All arrays were mounted on dedicated printed circuit motherboards, with electrical connections established by means of wirebonding. The electronic acquisition system and the 32-channel preamplifier-multiplexer ASIC used for these measurements have been described previously,^{16, 17} with modifications performed to the acquisition system, as necessary, to facilitate various types of measurements.

Array operational details and experimental conditions

The measurements were performed at a constant room temperature of ∼23 °C, with the acquisition electronics turned on a minimum of 30 min prior to data acquisition to allow the electronics to attain thermal equilibrium with their surroundings. For the six designs incorporating a-Si:H TFTs, measurements were performed for V_bias values ranging from 2 to 6 V, and the gate line voltages were switched between −8 V (V_off-addr) and 10 V (V_on-addr) to render the addressing pixel TFTs nonconducting and conducting, respectively. For the PSI-1 array (with poly-Si TFTs), measurements were performed with V_bias ranging from 1 to 4 V, and V_off-addr and V_on-addr were set to −5 and 15 V, respectively. For each array examined, every gate line was connected to a corresponding gate driver circuit (so that no lines were left floating), and every data line was connected to a corresponding preamplifier channel.

Pixel data were acquired through operation of the arrays both in radiographic and fluoroscopic mode. Each readout of an array resulted in a single “data frame” – referred to as a “dark frame” if the measurement was performed in the absence of light, or as an “image frame” if the sample was exposed to light from an optical source or due to X rays during the frame. Generally, each data frame corresponded to the acquisition of pixel data from the entire array. However, for some measurements, data frames corresponded to readout of consecutive gate lines from only a part of the array – to increase the frame rate by reducing the acquisition time per frame. (Tests performed for each array verified that such partial array readout did not result in leakage of charge from unread, saturated pixels onto the data lines.)

Optical measurements involved the use of a flashing, green LED. The magnitude of the optical signal was controlled by varying the number of LED flashes per image frame, with each flash lasting ∼5 μs. The uniformity of the illumination over the surface of the array, as well as further coarse adjustment of the intensity of the light signal, was controlled through adjustment of the position of the LED above the sample. The x-ray measurements were performed using an x-ray tube (Dunlee, PX1415) operated with a high-frequency generator (Picker, MTX 380), with the source to array distance fixed at 100 cm. The irradiations were performed at 72 kVp, with 20 mm of aluminum filtration added to achieve a half-value layer of ∼7 mm aluminum, corresponding to the standard x-ray spectrum RQA5 in IEC 1267. The exposure at the array surface per x-ray image frame was quantified through measurements with an ion chamber (Keithley, 96035) connected to a dosimeter (Keithley, 35050A). For all x-ray measurements, the same Lanex Regular screen (70 mg∕cm² Gd₂O₂S:Tb, Eastman Kodak) was put into close contact with the surface of the array.

For the various studies described below, the acquisition protocol generally consisted of repeated readout of an array for ∼90 s, to initialize the state of the pixels by minimizing the amount of charge trapped in the a-Si:H of the photodiodes from previous measurements. This was followed by acquisition of a sequence consisting of dark frames, or image frames, or some combination of both.

Techniques for empirical performance evaluations

In order to quantitatively assess and compare the various discrete and continuous photodiode array designs, measurements of a variety of pixel-level signal properties were performed. Each of the properties chosen for examination significantly influences the operation and performance of an AMFPI and is particularly sensitive to the details of a design.³ The measured properties include dark current, the degree of linearity in pixel response, the amount of charge lost to trapping, the amount of trapped charge released per frame, and optical fill factor. In addition, an analysis of those components of pixel-level noise related to array design is presented.

The reported signal results were obtained from measurements that were carried out using methods similar to techniques reported in previous indirect and direct detection array studies.^{18, 19, 20} Pixel dark current, linearity of response, charge trapping, and charge release were all determined as a function of the reverse bias voltage across the photodiode, and the reported results correspond to the average over 10 pixels that exhibited properties and behaviors representative of properly functioning pixels for each array. For the dark current and linearity measurements, the data were further averaged over multiple data frames acquired under identical conditions. (In the case of the sample Pagescan I array examined in this study, measurements of these four properties have previously been reported¹⁹ and are included in Sec. 3 for purposes of comparison.) For each type of measurement and for a given value of V_bias, the methodology is summarized below.

Pixel dark current

In order to determine pixel dark current, dark frames were acquired as a function of frame time, T_frame (the inverse of the frame rate). For each of ∼23 values of T_frame, ranging from ∼0.086 to 30 s (or 100 s in the case of the HOFFA array), approximately 20 data frames were acquired. At a given value of frame time, the slope of a plot of average pixel dark signal, Q_pix-dk, versus T_frame provides a measure of the pixel dark current, I_pix-dk, at that point.¹⁹

Pixel signal response and linearity

In order to examine linearity of pixel response, image frames were acquired as a function of incident light signal provided by a flashing LED, with T_frame fixed at 0.5 s. Data were acquired for ∼25 light levels, chosen so as to provide pixel data ranging from no incident light signal up to saturation of the pixel signal. Data were obtained both in radiographic and fluoroscopic mode, with 8 and 36 image frames acquired per light level, respectively. A linear fit was performed to the data in the first ∼20% of the pixel signal range, and the deviation of the extrapolation of this fit from the measured data provides a measure of the degree of deviation of pixel response from linearity.^{19, 20}

Charge trapping and release

The determination of charge trapping and charge release involved sequences of consecutively acquired data frames, with T_frame fixed at 0.5 s. A given sequence typically comprised of a total of 100 data frames consisting of dark frames, followed by image frames, and ending with further dark frames, with the incident LED light signal kept constant for each image frame of a given sequence. Data were acquired for ∼23 light levels so as to provide results for pixel signal sizes ranging from ∼2% to 99% of saturation. Further details concerning the determination of the amount of trapped and released charge from a given sequence are given in Sec. 3C.

Optical fill factor

For a given array design, the ratio of the area of the exposed surface of the photodiode to the area of the pixel represents the nominal optical fill factor expected for each pixel. While the application of this definition is straightforward for the discrete photodiode designs, the situation is more nuanced for continuous photodiode designs due to the use of unpatterned a-Si:H layers in these structures. For the nominal values of FF_opt for the various array designs, summarized in Table 1, a convention of assigning 100% to the HOFFA and PSI-1 designs was adopted. Given the significant influence that FF_opt can have on the DQE of a system (as illustrated in Fig. 2), it is of interest to examine the degree to which determinations of optical fill factor from measured signal properties are consistent with these nominal FF_opt values.

Two techniques were employed to empirically examine the optical fill factor for each array design. The first technique provided a measure of FF_opt for a given array design relative to one of the other designs. This method is based upon measurement of the pixel signal as a function of exposure, with T_frame fixed at 1.1 s. For a given array, a total of ten fluoroscopic image frames were acquired for each of four exposure rates, resulting in exposures of ∼0.25, 0.52, 0.79, and 1.1 mR per image frame and giving a maximum pixel signal size of less than 3% of saturation. For each exposure, the average pixel signal from ten dark frames, acquired immediately before the image frames, was subtracted from the average pixel signal from the image frames. The slope of a linear fit to a plot of these average pixel signals as a function of exposure provides the x-ray sensitivity, Γ. The value of Γ for a given array, i, is given by

$${\Gamma }_i=q_0{g}_1{g}_2{\mathrm{FF}}_{{\mathrm{opt}}_i}{a}_{{\mathrm{pix}}_i}^2{g}_4,$$ (1)

where q₀ is the number of incident X rays per unit area per unit exposure, g₁ is the x-ray detection efficiency of the scintillator, g₂ is the conversion gain of the scintillator (i.e., the average number of optical photons generated in the scintillator per interacting X ray and escaping the scintillator in the direction of the array), $a_{\mathrm{pix}}^2$ is the pixel area, and g₄ is the coupling efficiency (i.e., the efficiency of penetration of optical photons into the a-Si:H of the photodiode and conversion of those photons into signal that is collected in the pixel capacitance). While the absolute value of FF_opt could, in principle, be determined from Eq. 1, the values for g₂ and g₄ are not known with sufficient precision for the present purposes. However, the ratio of the measured sensitivity of one array to that of another is equal to the ratio of the optical fill factors for those arrays (after accounting for any difference in pixel pitch), given that the other parameters (i.e., g₂ and g₄) are the same for each array. (g₂ is the same since the same screen was used for all sensitivity measurements. In addition, the composition and thickness of the photodiode structures, and of the layers above the photodiodes, are sufficiently similar that it is reasonable to assume that g₄ is the same for all array designs.)

The second technique, which can be used to provide an absolute empirical determination of FF_opt, involves the measurement of the presampled optical modulation transfer function (MTF). MTF is measured both in the gate and data line directions using the angled slit method,²¹ employing a 10 μm wide, 15 mm long slit (National Aperature Inc., Precision Air Slit) illuminated by the flashing LED. Each measured MTF is fit with a function of the form

$$\mathrm{MTF}\left(f\right)=\frac{\mid \sin \left(\pi a_{\mathrm{PD}}f\right)\mid }{\pi a_{\mathrm{PD}}f},$$ (2)

where a_PD is the aperture of the photodiode, which is treated as a fit parameter, and f is spatial frequency. Details of how the fits were performed appear in Sec. 3D. The product of the apertures obtained in the two orthogonal directions, divided by $a_{\mathrm{pix}}^2$, provides a measure of FF_opt, independent of the properties of the x-ray radiation and scintillator. While the first technique for determining FF_opt (involving x-ray sensitivity) uses relatively straightforward measurements of average pixel signal, that method does depend upon a variety of assumptions and only provides values of FF_opt relative to one of the designs. Thus, although the second technique (involving optical MTF determination) requires more elaborate measurement and analysis techniques, it provides absolute values of FF_opt – thereby providing independent, absolute verification of the sensitivity-determined results.

RESULTS

For the measurements of dark current, linearity, charge trapping, and charge release reported below, results for sample arrays of the various designs for several values of V_bias are presented in such a way as to facilitate direct comparisons between the designs. In addition, more extensive detail about the measured properties is presented for M13, the most recent discrete design, and for HOFFA, the continuous photodiode array for which a greater range of data was available.

Pixel dark current

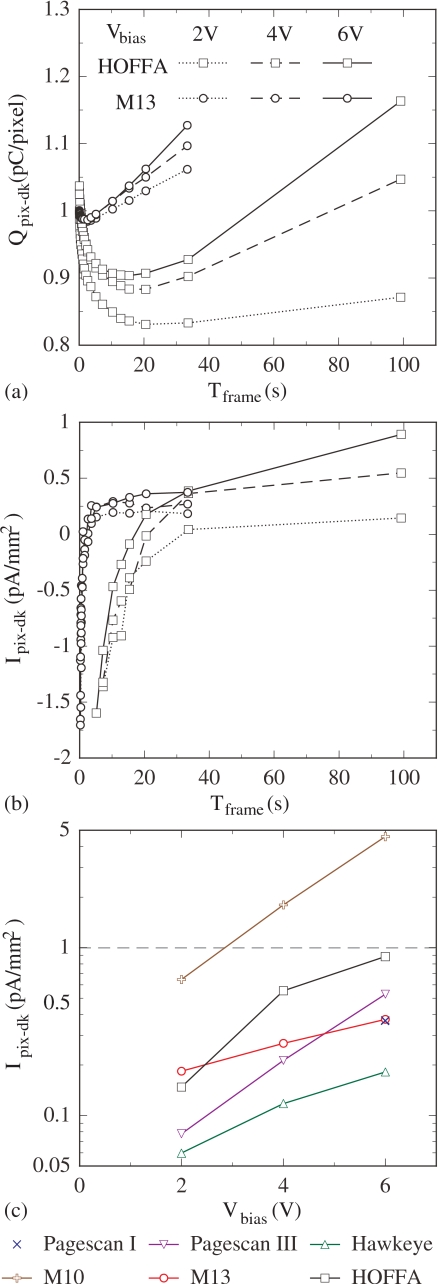
The average pixel dark signal (adjusted by a fixed offset) is plotted as a function of T_frame and V_bias for M13 and HOFFA in Fig. 5a. In the figure, for a given array and V_bias value, Q_pix-dk is observed to undergo an initial decay before slowly increasing. This signal decline is due to a transient current from the TFT originating from the release of trapped charge in the a-Si:H channel of the transistor when the device is switched off.¹⁹ (Such temporal behavior of the dark signal was observed for every array except PSI-1, whose higher mobility poly-Si TFTs exhibit significantly larger leakage current and for which no increase in Q_pix-dk was observed. For that reason, dark current is not reported for PSI-1.) HOFFA exhibits a significantly larger transient signal decline than M13 and the other discrete photodiode arrays. Empirical information obtained from other HOFFA array samples suggests that the larger transient observed from the present HOFFA sample may, at least partially, be the result of a higher density of a-Si:H trapping states in the TFTs of that array. Moreover, the larger transient exhibited by this HOFFA sample, coupled with a relatively modest dark current (see below), results in the dark signal increasing after ∼20 s – much later than the several seconds observed for the discrete arrays in this and previous studies.¹⁹

Figure 5.

Results for pixel dark signal and dark current at V_bias values of 2, 4, and 6 V. (a) Pixel dark signal, Q_pix-dk, plotted as a function of T_frame for the M13 and HOFFA arrays. Note that pixel signal measurements from the arrays do not provide an absolute determination of dark signal due to the contribution of an unknown, constant offset from each preamplifier channel. Thus, to facilitate comparisons between the results of the two arrays, a fixed value has been added to the dark signal data set for each array so as to provide a common starting value (i.e., 1 pC∕pixel at a T_frame of 0.086 s for a V_bias of 2 V). The vertical scale in the plot continues to correctly quantify changes in dark signal as a function of T_frame and V_bias. (b) Pixel dark current, I_pix-dk, derived from the M13 and HOFFA data shown in (a), normalized to the geometric (i.e., full) area of the photodiodes, and plotted as a function of T_frame. (c) Pixel dark current results, determined under conditions where the photodiode contribution dominates, plotted as a function of V_bias for Pagescan III, Hawkeye, M10, M13, and HOFFA. A horizontal dashed line is drawn at a dark current level of 1 pA∕mm² for purposes of comparison. Data from an earlier investigation of the Pagescan I array (Ref. ¹⁹) is also shown in (c) for purposes of comparison, as well as in Figs. 6e, 6f, 8e, 8f. In addition, note that the legend appearing in (a) also applies to (b), and the legend for (c) is shown below that graph. Finally, the lines connecting the data points in the graphs of this figure (as well as in graphs of Figs. 68) are drawn to guide the eye.

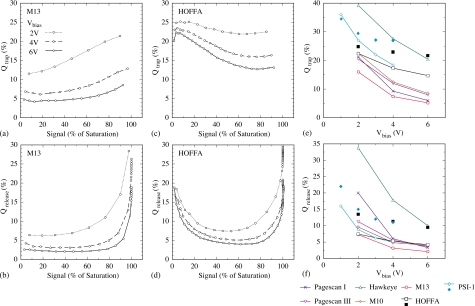
Dark current is plotted as a function of T_frame for M13 and HOFFA in Fig. 5b. These and all reported results for I_pix-dk have been normalized to the full area of the corresponding photodiode (using the geometric fill factors listed in Table 1), to allow direct comparisons between array designs. In the figure, the change in I_pix-dk with T_frame reflects the diminishing contribution of TFT signal transient. At large T_frame, the value of I_pix-dk represents the opposing effects of the photodiode dark current and the TFT leakage current, with the former dominating. In order to minimize the degree to which dark current consumes pixel signal capacity in an AMFPI, an upper limit of ∼1 pA∕mm² is desirable.³ In Fig. 5c, I_pix-dk for each array, determined at large values of T_frame, is plotted as a function of V_bias. As anticipated, the measured dark current is observed to increase with increasing voltage across the photodiode. With the exception of M10 at high V_bias, the magnitude of I_pix-dk remains well below 1 pA∕mm² for all the designs, even at a V_bias of 6 V – indicative of desirable photodiode dark current behavior.

Pixel signal response and linearity

The average pixel signal, Q_pix, is plotted as a function of LED light level and V_bias for M13 and HOFFA in Figs. 6a, 6b, respectively. In each case, data are shown for both radiographic and fluoroscopic mode. For a given array, V_bias, and operational mode, the corresponding pixel response steadily increases with increasing light level, before asymptotically approaching a limit corresponding to the saturation of the pixel at a signal magnitude given by the product of the pixel capacitance, C_PD, and V_bias.¹⁹ In addition, the behavior of the response curves near saturation is consistently different for radiographic mode compared to fluoroscopic mode.

Figure 6.

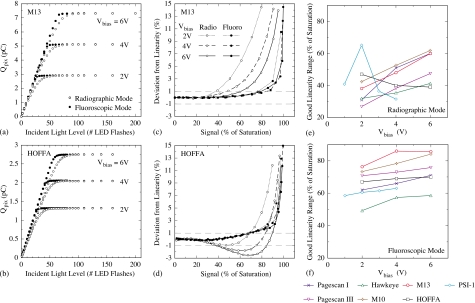
Results for pixel response, as well as deviation from linearity of response, at V_bias values ranging from 1 to 6 V. Pixel signal, Q_pix, is plotted as a function of incident light signal (in units of number of LED flashes) for (a) M13 and (b) HOFFA. In both figures, pixel signal response curves are shown for radiographic and fluoroscopic mode. For each response curve, the contribution of the dark signal has been subtracted. Deviation from linearity is plotted as a function of pixel signal size for (c) M13 and (d) HOFFA, corresponding to an analysis of the response curves in (a) and (b), respectively. The scale of the horizontal axis corresponds to the magnitude of the pixel signal, expressed as a percent of the dark-corrected saturation level – a convention also used in Fig. 8. Note that horizontal dashed lines are drawn at deviation levels of ±1%. The pixel signal size at which the magnitude of the nonlinearity first exceeds 1% is plotted as a function of V_bias for the sample arrays examined in this study for (e) radiographic mode and (f) fluoroscopic mode. Also note that the legends in (a) and (c) also apply to (b) and (d), respectively, and the legend for (e) and (f) is shown below these graphs.

From each set of response data in Figs. 6a, 6b, the degree of deviation of the pixel response from linear behavior, relative to pixel saturation, was determined and the results are plotted as a function of the pixel signal size in Figs. 6c, 6d, respectively. In the case of M13 [Fig. 6c], deviation from linearity systematically becomes larger with increasing pixel signal – slowly at first, then more quickly at higher signal sizes. The range of pixel signal sizes over which deviation from linearity remains small (e.g., less than 1%) increases with increasing V_bias and is also greater for fluoroscopic mode. This pattern is closely followed by all the discrete photodiode sample arrays examined in this study and is also very similar to the linearity behavior observed in earlier studies which included other discrete photodiode array designs.^{19, 22, 23} In particular, the smaller range of good linearity consistently observed in radiographic mode, compared to fluoroscopic mode, is believed to be a consequence of the loss of charge to deep metastable (“trapping”) states in the a-Si:H of the photodiodes.¹⁹ This form of charge trapping becomes more efficient as the electric field across a photodiode decreases²⁴ – which occurs when the pixel storage capacitor is discharged as signal increases, or when V_bias is set lower. In this interpretation, the greater range of good linearity for fluoroscopic mode arises as a result of the fact that fluoroscopic operation brings charge trapping and charge release into approximate equilibrium, whereas, in radiographic mode, signal is lost to trapping, leading to stronger deviation from linearity at lower pixel signal sizes.¹⁹

For HOFFA [Fig. 6d], while its deviation from linearity exhibits the same general pattern as for the discrete arrays, an interesting difference is apparent. In radiographic mode, as the pixel signal response begins to depart from linearity, it first exhibits a small degree of negative deviation, corresponding to superlinear behavior of the pixel response, before reverting to positive deviation, corresponding to the more common sublinear response. This behavior was also observed for PSI-1.

In Figs. 6e, 6f, the signal range over which the pixel response remains highly linear (i.e., up to the point at which deviation first exceeds ±1%) is plotted for the various arrays as a function of V_bias, for radiographic and fluoroscopic mode, respectively. For both modes and at all V_bias values, there is a significant difference in performance between the arrays exhibiting the largest and the smallest ranges of good linearity. The largest ranges are exhibited by discrete designs: up to ∼64% for M10, Pagescan I, and M13 in radiographic mode, and up to 85% for M13 and M10 in fluoroscopic mode. Even the Hawkeye array, which exhibits the smallest values, provides ranges of up to ∼40% and ∼60% for radiographic and fluoroscopic modes, respectively. The two sample arrays with continuous photodiode structures, HOFFA and PSI-1, generally exhibit larger ranges of good linearity than Hawkeye, but lower than the other discrete photodiode arrays. In addition, in fluoroscopic mode, the HOFFA and PSI-1 ranges are only weakly dependent on V_bias. Moreover, in radiographic mode, the HOFFA and PSI-1 ranges generally decrease with increasing V_bias – a consequence of the anomalies in the shape of their corresponding response functions noted above. These interesting behaviors are further discussed in the next section.

Charge trapping and release

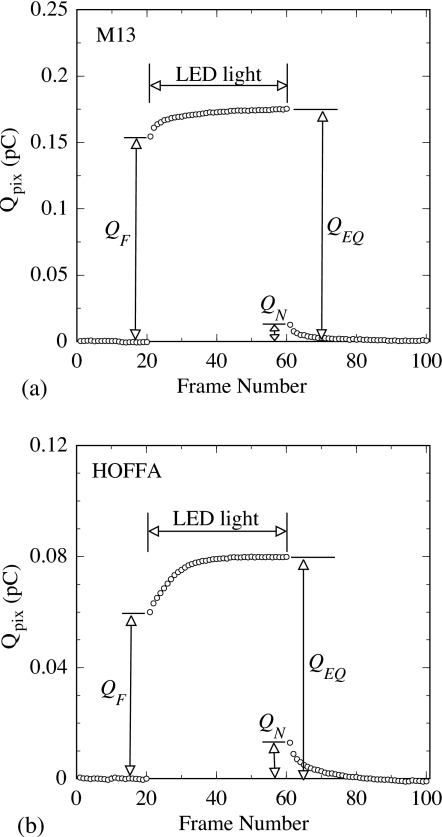
Examples of data frame sequences that were acquired to determine the amount of trapped and released charge are shown in Figs. 7a, 7b for M13 and HOFFA, respectively. For a given sequence, the first few image frames exhibit lower signal sizes due to a loss of charge to trapping, compared to later image frames where the trapping and release of charge come into approximate equilibrium. A measure of the fraction of charge lost to trapping in a radiographic exposure, Q_trap, is given by^{18, 20}

$$Q_{\mathrm{trap}}=(Q_{EQ}-Q_F)∕Q_{EQ},$$ (3)

where Q_EQ is the average pixel signal of the final image frames, #51 to #60, and Q_F is the pixel signal from the first image frame, #21, as illustrated in Fig. 7. In addition, the first few dark frames following the last image frame in the sequence exhibit higher signal sizes than the initial dark frames due to the release of trapped charge. A measure of the relative amount of charge released per frame, Q_release, is given by^{18, 19, 20}

$$Q_{\text{release}}=Q_N∕Q_{EQ},$$ (4)

where Q_N is the pixel signal from the first dark frame (#61) following the last image frame, as illustrated in Fig. 7. Note that Q_release, as defined, is related to the concept of first frame lag that is frequently discussed in the context of fluoroscopic imaging.

Figure 7.

Illustration of pixel data showing charge trapping and charge release. For (a) M13 and (b) HOFFA, pixel signal, Q_pix, is plotted as a function of consecutive frame number for an acquisition sequence consisting of 20 dark frames, followed by 40 image frames (using a flashing LED), and a final 40 dark frames. For the sequences shown, V_bias was set to 2 V and the image frames were acquired at a pixel signal size of ∼6% of saturation. The labels Q_F, Q_N, and Q_EQ are related to pixel signal sizes used in the determination of Q_trap and Q_release, as discussed in the text.

Using the methodology described above, Q_trap and Q_release for the various arrays were determined, and the results appear in Fig. 8. For M13, Q_trap and Q_release are plotted as a function of pixel signal size and V_bias in Figs. 8a, 8b, respectively. The results for Q_trap [Fig. 8a] demonstrate that trapping increases with increasing pixel signal size or decreasing V_bias – consistent with an interpretation of the trapping originating in metastable states in the a-Si:H of the photodiode.¹⁹ Furthermore, the M13 results for Q_release [Fig. 8b] generally exhibit this same pattern of dependence on pixel signal size and V_bias – a result to be expected if the release of charge originates from the same fundamental processes that are responsible for trapping the charge in the first place. Thus, for the discrete photodiode arrays examined in this study, the observed behaviors for linearity, Q_trap and Q_release, are consistent with each other, as well as with the idea of a single, underlying trapping mechanism involving metastable a-Si:H states. The patterns for Q_trap and Q_release, seen for M13, were observed for all the discrete photodiode arrays in the study, and are similar to those observed in an earlier study.¹⁹

Figure 8.

Results for trapped charge, Q_trap, and released charge, Q_release, at V_bias values ranging from 1 to 6 V. Q_trap is plotted as a function of pixel signal size for (a) M13 and (c) HOFFA. Q_release is plotted as a function of signal size for (b) M13 and (d) HOFFA. The amount of (e) trapped charge and (f) released charge at 50% of pixel signal saturation are plotted as a function of V_bias for the arrays examined in this study (open symbols and crosses, with lines). In addition, the amount of trapped and released charge at 10% of saturation is also plotted for HOFFA and PSI-1 (closed symbols). Note that Q_trap results are not shown for signal sizes near saturation, due to limitations in the methodology (Refs. ¹⁸, ¹⁹). Further, note that the legend in (a) also applies to (b), (c), and (d), and the legend for (e) and (f) is shown below these graphs.

For the continuous photodiode array, HOFFA, results for charge trapping and release are plotted as a function of pixel signal size and V_bias in Figs. 8c, 8d, respectively. From these figures, both Q_trap and Q_release are observed to increase when V_bias is set lower – consistent with the behavior of discrete photodiode arrays. However, at low pixel signal sizes (i.e., less than ∼50% of saturation), the amount of trapped and released charge exhibits significant decline from a relatively high level as signal size increases. This differs strongly from the behavior of discrete arrays. Finally, at higher pixel signal sizes (∼80% of saturation), Q_trap and Q_release exhibit varying degrees of increase with increasing signal size. The PSI-1 array generally exhibited the same behavior. Thus, for the continuous photodiode arrays examined in this study, the patterns of behavior for linearity, Q_trap and Q_release, are contrary to a simple model of charge trapping completely dominated by losses to metastable states. The complex behaviors observed for these arrays are not understood, but could be due to an additional, significant charge trapping mechanism associated with the more complicated structure of these continuous photodiodes – for example, in the a-Si:H material in the region between pixels and outside of the footprint of the bottom electrode.

In Figs. 8e, 8f, the amount of trapped and released charge, respectively, is plotted as a function of V_bias for the various arrays. The values reported are at 50% of saturation. In addition, for HOFFA and PSI-1 the values at 10% of saturation are also given, to allow comparison with these anomalously high values at small pixel signal sizes. Generally, the arrays exhibiting the lowest level of charge trapping also demonstrate the lowest level of charge release. Among the discrete photodiode arrays, M13, Pagescan I, Pagescan III, and M10 exhibit the lowest values for Q_trap (less than 10% at 6 V) and Q_release (less than 4% at 6 V) – representing desirable levels of performance.³ In comparison with these discrete array results, HOFFA (which performed slightly better than PSI-1) exhibited higher values for Q_trap (∼15% and 22% at 50% and 10% of saturation, respectively) and for Q_release (∼4% and 10% at 50% and 10% of saturation, respectively). Finally, it is interesting to note that, for a given array and V_bias value, the magnitude of Q_release is always less than that of Q_trap – which is believed to reflect a difference in the time scale required to achieve approximate equilibrium between trapping and release during the image frames, from the time scale for release of the trapped charge in the final dark frames.

Optical fill factor

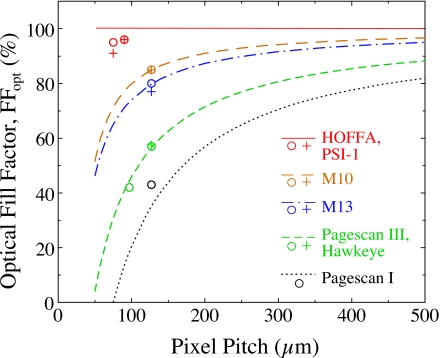
Figure 9 illustrates the results of calculations and measurements of optical fill factor as a function of pixel pitch. Each curve in the figure corresponds to a calculation of the nominal FF_opt to be expected for hypothetical arrays incorporating a common set of design rules and pixel architecture – which, for conciseness, shall be referred to as architectural rules. The architectural rules assumed for a given curve are those employed for a corresponding sample array in this study, where the value predicted by the curve at the pitch of that sample array corresponds to the nominal FF_opt appearing in Table 1. Compared to the predicted fill factors corresponding to the early Pagescan I architectural rules, the various generations of major design changes (exemplified by Pagescan III∕Hawkeye, M10, M13, and HOFFA∕PSI-1) provide significant increases in the nominal values of FF_opt. For the discrete photodiode designs, the indicated improvements are particularly impressive at pitches below ∼100 μm, for example at 50 μm pitch, providing values for FF_opt of ∼46% with M13 rules, compared to ∼4% and 0% for Pagescan III∕Hawkeye rules and Pagescan I rules, respectively. Even at 500 μm pitch, the transition from Pagescan I to M13 rules provides a non-negligible improvement, increasing FF_opt from ∼82% to 95%. In the case of continuous photodiode arrays, such designs offer the possibility of the photodiode sensitive area extending over the entire pixel and, following the convention discussed in Sec. 2C4, the nominal FF_opt for such arrays is depicted as 100%.

Figure 9.

Optical fill factor plotted as a function of pixel pitch for indirect detection AMFPIs incorporating discrete and continuous photodiode structures. The lines correspond to calculations performed for hypothetical array designs, either based on the architectural rules employed to create the discrete photodiode arrays, or on a convention adopted for the continuous photodiode arrays of this study. The symbols correspond to the results of measurements on the various sample arrays. The circle symbols correspond to determinations of fill factor based on x-ray sensitivity measurements, relative to the assumed value of 57% for Pagescan III. The plus symbols correspond to absolute determinations of fill factor for some of the sample arrays based on optical MTF measurements.

The values for optical fill factor determined empirically through x-ray sensitivity measurements, relative to the nominal value of 57% for Pagescan III, are presented in Fig. 9. (Pagescan III was chosen as the basis for comparison since this and very similar designs have been fabricated for many years and the optical fill factor is believed to closely correspond to the nominal value.) For the discrete photodiode arrays, the measured FF_opt results for Hawkeye (42%), M10 (85%), and M13 (80%) are observed to be very close, or equal, to the nominal values predicted by the corresponding architectural rules for those arrays. Interestingly, the measured result for Pagescan I, 43%, is ∼8% higher than the nominal value. Since the arrays are all made with very similar ITO and a-Si:H layers, there is no reason to expect the coupling efficiency, g₄, to differ by this amount and so alternative explanations were considered. The possibility that this relatively large, unexpected, increase in FF_opt could be due to additional x-ray scatter from the greater amount of high atomic number material in the Pagescan I substrate compared to the Pagescan III substrate (the glass types for which are listed in Table 1) was examined, but not supported by Monte Carlo simulations of the interaction of radiation with these substrates involving the EGSnrc and DOSXYZnrc codes.^{25, 26} However, it is suspected that the relatively wide, reflective gate data and bias lines of the Pagescan I design [Fig. 3a] may cause considerable reflection of light between the array and the overlying phosphor screen, not accounted for in g₄, resulting in an enhancement of FF_opt. Finally, the measured FF_opt values for HOFFA (95%) and PSI-1 (96%) are only slightly below the theoretical maximum of 100% – an impressive result given the relatively small pitch of these array designs.

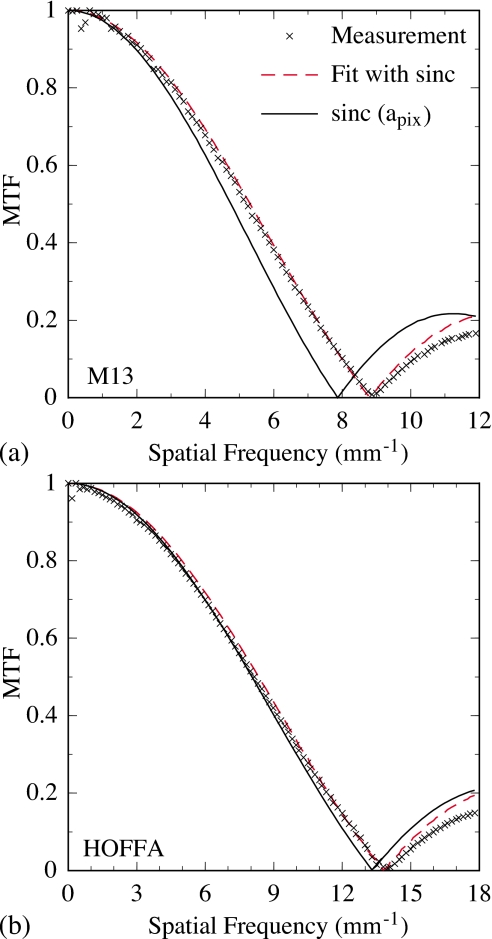
Figures 10a, 10b show presampled MTF results associated with the absolute determination of optical fill factor for M13 and HOFFA, respectively. In each figure, the measured MTF corresponding to the orientation of the slit along the gate line direction is presented, and the dashed line corresponds to a fit to the data using Eq. 2. The fit to these and other array data, carried out manually, was performed so as to closely match the first node (i.e., the first minimum extending to zero) in the data, the spatial frequency of which is set by the effective aperture of the photodiode, a_PD. Data at frequencies beyond the first node were not considered in the fitting. This was due to the fact that small, irregular features in photodiode shape (e.g., created by the intrusion of the bias line and addressing TFT) affect the MTF at higher frequencies, so that a simple sinc function is no longer an accurate model at those frequencies. Finally, the solid line plotted in each figure corresponds to a sinc function calculated with the aperture set to the array pitch, illustrating the MTF that would result if FF_opt were 100%.

Figure 10.

Presampled modulation transfer functions associated with (a) M13 and (b) HOFFA. For each array, measurements of the optical MTF are indicated by the cross symbols, and data are shown up to spatial frequencies slightly beyond the first node. For each set of MTF measurements, the results of a fit of a sinc function to the data are indicated by the dashed lines, as described in the main text. Finally, for each array, a sinc function with an aperture value set to the pixel pitch of the array is plotted as a solid line for purposes of comparison.

As seen in both figures, the shape and magnitude of the fit closely match the MTF data up to the first node. This same pattern and degree of agreement was obtained for the Pagescan III, M10, M13, HOFFA, and PSI-1 arrays for data acquired with the slit oriented in the two orthogonal directions. In Fig. 9, the FF_opt results obtained from the a_PD values determined from these fits for the discrete photodiode arrays Pagescan III (57%), M10 (85%), and M13 (77%) are observed to be close, or equal to the nominal values, as well as to the relative values obtained from sensitivity measurements. (Note that the good agreement of the MTF-determined value of FF_opt for the Pagescan III array with the nominal value for that array, 57%, independently confirms the validity of the assumed value used in the sensitivity-based optical fill factor determinations.) Results for the other two arrays, Pagescan I and Hawkeye, could not be obtained using this method. The wider and more irregular bias lines, and larger TFTs, relative to the pixel size, sufficiently complicate the shape of the exposed regions of their photodiodes that the resulting MTFs exhibit more complex shapes, with no nodes appearing at frequencies that correspond to physically reasonable aperture dimensions. Thus, Eq. 2 was an inappropriate fit model for the data from these arrays, and attempts to use more sophisticated models²⁷ were not successful. For the continuous photodiode arrays, the FF_opt value obtained for PSI-1 (96%) is equal to that obtained from the sensitivity measurement while that obtained for HOFFA (91%) is slightly lower – perhaps reflecting somewhat greater imprecision in the measurement of the MTF for these smaller, 75 μm pitch pixels.

Pixel noise

The additive noise properties of an AMFPI are largely determined by the architectural rules and properties of the array used in the imager.²⁸ It is therefore of interest, in the present context, to investigate the magnitude and relative contribution of several, significant, additive noise components. (Noise on the gate lines, which couples to the data lines at gate line-data line crossovers and which can be significant, is not considered in this analysis as it is highly dependent upon the quality of the gate line voltage supplies as well as on the amount of ambient electromagnetic noise picked up from the environment.) Estimates for pixel shot noise, σ_shot, TFT thermal noise, σ_thermal, and preamplifier noise, σ_preamp, were made based on the architectural rules and properties of the arrays reported in this study.

Shot noise (in electrons) from the pixel dark current, accumulated in the pixel capacitance over a frame time T_frame, is given by

$${\sigma }_{\text{shot}}=\sqrt{I_{\mathrm{pix}\text{-}\mathrm{dk}}{T}_{\text{frame}}∕q},$$ (5)

where q is the charge of an electron (1.602×10⁻¹⁹ C). The resulting calculations of σ_shot corresponding to pixels of the various array designs are given in Table 2. In these calculations, T_frame is assumed to be 1 s, and I_pix-dk values (in units of current per pixel and given in the table) were obtained from Fig. 5c at a V_bias of 6 V.

Table 2.

Estimated values for specific components of pixel noise, corresponding to the architectural rules and properties of the various arrays examined in this paper (column 1). Pixel shot noise at 1 fps, σ_shot (column 5), as determined from Eq. 5 using the measured dark current per pixel at a V_bias of 6 V, I_pix-dk, in column 2. The uncertainty in these shot noise values is approximately ±2.5%, based on an estimated experimental uncertainty of ±5% in the I_pix-dk measurements. Since dark current was not determined for PSI-1, no shot noise value is reported in the table. Thermal noise from the pixel addressing TFT, σ_thermal (column 6), as determined from Eq. 6 using the photodiode capacitance, C_PD, in column 4. C_PD was determined from the thickness of the intrinsic layer of the photodiode (d_PD in column 3), the area of the photodiode (given by the product of the geometric fill factor of the photodiode, FF_geo (Table 1), and the square of the pixel pitch, a_pix (Table 1)), assuming a dielectric constant of 12 for a-Si:H. Preamplifier noise, σ_preamp (column 7) for hypothetical arrays with 30 cm long data lines populated with pixels having the pixel pitch and properties of the arrays listed in column 1, as determined from Eq. 7.

Array	Ipix-dk at 6 V (fA∕pixel)	dPD (μm)	CPD (pC)	σshot (e, rms)	σthermal (e, rms)	σpreamp (e, rms)
Pagescan I	2.50	1.40	0.51	125	404	2040
Pagescan III	5.20	1.50	0.70	180	470	1480
Hawkeye	0.845	1.50	0.33	73	322	1420
M10	64.3	1.50	0.99	634	561	2270
M13	5.08	1.50	0.96	178	553	1800
HOFFA	3.57	1.00	0.43	149	369	2040
PSI-1	n∕a	1.00	0.60	n∕a	436	780

Thermal fluctuations of charge carriers while the channel of the addressing TFT is in its conducting state result in the injection of a random amount of charge into the pixel storage capacitor at the end of pixel readout and initialization (when the transistor is rendered nonconducting). Such fluctuations also cause random variations in charge that are sampled at the end of pixel integration by the preamplifier circuit. The total TFT thermal noise (in electrons) from these two uncorrelated components is given by²⁸

$${\sigma }_{\text{thermal}}=\frac{1}{q}\sqrt{2kT{C}_{\mathrm{PD}}},$$ (6)

where k is the Boltzmann constant (1.38×10⁻²³ m² kg s⁻² K⁻¹), T is temperature (295 K), and C_PD is the photodiode pixel capacitance. Calculations of σ_thermal for the various array designs, and the values of C_PD used in these calculations, are given in Table 2.

In an AMFPI, the signal from each pixel along a data line is typically sampled by a charge-integrating preamplifier whose noise performance is determined by a combination of the preamplifier noise properties and the data line capacitance, C_data. Preamplifier noise (in units of electrons) was estimated using the following expression:

$${\sigma }_{\mathrm{preamp}}=285+15\times C_{\text{data}},$$ (7)

where the values used for the base noise (285 e) and noise slope (15 e∕pF) of the preamplifier correspond to those of a low-noise preamplifier chip specifically designed for AMFPI research.²⁹ In order to provide a basis for comparison of the results, the σ_preamp calculations were performed for hypothetical arrays with 30 cm long data lines, and the results are given in Table 2. For each value of σ_preamp listed in a given row of the table, the number of pixels along the length of the data line was assumed to be given by 30 cm divided by the pitch, a_pix, associated with the corresponding array design for that row. This pixel count, multiplied by the actual data line capacitance per pixel associated with that design, C_dlpix (given in Table 1), provided the value of C_data used in Eq. 7.

For a given array design, the magnitude of the shot noise reported in Table 2 is generally found to be less than 190 e, and is smaller than that of the other two additive noise components. (In the case of M10, while shot noise is larger than TFT thermal noise, due to the large dark current exhibited by this array, it remains relatively small compared to preamplifier noise.) Note that shot noise would decrease at shorter T_frame, corresponding to frame rates above the 1 fps assumed in the calculations. The thermal noise ranges from ∼320 to 560 e across the various designs. With the exception of the calculations corresponding to the PSI-1 array, these thermal noise values are small compared to the estimated preamplifier noise that ranges from 1420 to 2270 e. In the case of PSI-1, the fully self-aligned poly-Si addressing transistor used in the pixel circuit eliminates overlap of the gate and drain contacts that exists in the a-Si:H addressing TFTs in the other array designs. This greatly reduces the data line capacitance per pixel, C_dlpix, as indicated in Table 1, leading to a significant reduction in the estimated preamplifier noise for the hypothetical array to less than 800 e. Note that, compared to the type of a-Si:H TFTs used in the other arrays, fully self-aligned a-Si:H TFT architectures are more complex to implement and not typically manufactured.

Clamp pixel array design

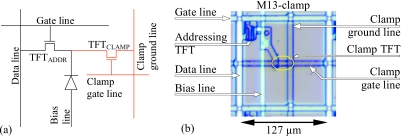
The placement of the discrete photodiode above the plane of the addressing TFT in M10 (illustrated in Fig. 4b) and M13 creates space for the incorporation of other circuit elements in that plane. This new degree of design freedom was explored through development of M13-clamp – an array using the same architectural rules, pixel pitch, addressing transistor, photodiode structure, and pixel format as M13. The pixel circuit of the M13-clamp (which is based on an earlier prototype of the concept)¹⁵ is illustrated in Fig. 11a. Compared to the pixel circuit of a conventional indirect detection AMFPI, the M13-clamp pixel contains a second a-Si:H “clamp” transistor. One contact of this TFT is connected to both the source contact of the addressing TFT as well as to the bottom signal collection electrode of the photodiode. Another contact of the clamp TFT is connected to ground via a dedicated ground line. A negative voltage, V_clamp, is applied to the gate contact of the clamp TFT via a dedicated gate line to control the conductivity of that transistor. A photomicrograph of an M13-clamp pixel appears in Fig. 11b.

Figure 11.

(a) Schematic pixel circuit diagram for the M13-clamp array, with additional circuit elements, indicated in red, beyond those in a conventional indirect detection pixel. The TFT for the clamp circuit has W and L values of 4.5 and 18.5 μm, respectively. (b) Photomicrograph of an M13-clamp pixel, with the same orientation as used in Fig. 3. In the figure, labels are superimposed for the design elements of a conventional AMFPI pixel [as in Fig. 3a], as well as for those circuit elements pertaining to the clamp (clamp TFT, clamp gate line, clamp ground line). The clamp TFT, which is difficult to discern in the photo, is located along the clamp gate line (a portion of which forms the gate contact of this transistor) in the region bounded by the ellipse superimposed on the image.

The purpose and operation of this circuit can be explained as follows. In a conventional AMFPI, as a pixel accumulates signal, the magnitude of the voltage applied across the photodiode decreases, and the magnitude of the voltage across the addressing TFT (initially zero) increases by a corresponding amount. At pixel saturation, the voltage across the photodiode is at or near zero, and no further signal collection can take place. Thus, under conditions where all or part of the array is irradiated to a sufficiently high exposure per image frame, those pixels approaching or reaching saturation will experience considerably greater charge trapping and charge release (as detailed in Sec. 3C). Such conditions, which can occur when fluoroscopic image frames are acquired following a large radiographic exposure, will intensify the effects of image lag and ghosting (also called memory).^{30, 31} In order to limit these effects, the pixel circuit of the M13-clamp is designed to restrict the degree to which the voltage across the photodiode can be decreased. Given the placement of the clamp TFT in the circuit, the increase in voltage that occurs across the addressing TFT during irradiation will also occur across the clamp TFT. If V_clamp is set to a negative value that is smaller in magnitude than V_bias, the clamp TFT will start to exhibit significant leakage before pixel saturation – thus restricting (i.e., clamping) the maximum amount of voltage decrease across the photodiode and limiting undesirable artifacts associated with high levels of charge trapping and release. Note that, for the clamp pixel circuit, the value of V_off-addr supplied to the addressing TFT is typically kept ∼2 V more negative than V_clamp, to guard against an increase in leakage through that transistor at or near the maximum pixel signal level defined by V_clamp. (For a conventional pixel circuit, the magnitude of V_off-addr is typically kept ∼2 V greater than V_bias for the same reason.³)

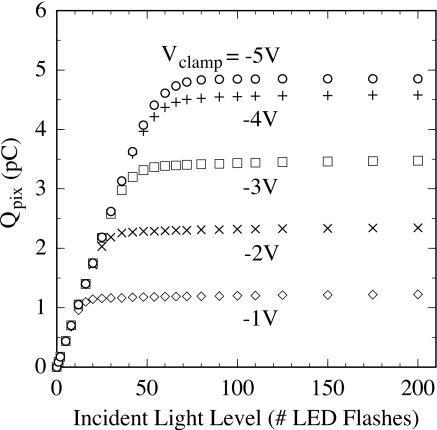
The effect of these circuit modifications is illustrated in Fig. 12. The data shown in the figure were obtained from the significantly better performing sample of two M13-clamp arrays that were examined. This array exhibited pixel properties comparable to those reported in previous sections for M13. In the figure, average pixel response is plotted as a function of LED light level for values of V_clamp ranging from −1 to −5 V, at a V_bias value of 4 V. As long as the magnitude of V_clamp was at least ∼0.5 V greater than V_bias, the M13-clamp pixels were found to exhibit the same behavior as for M13. For example, the fluoroscopic pixel response at a V_clamp value of −5 V (illustrated in the figure) remained unchanged as the magnitude of V_clamp was increased (e.g., to −6, −7, and −8 V, not shown in the figure), and closely corresponds to the fluoroscopic pixel response of an M13 array [see Fig. 6a] operated at the same V_bias, 4 V. However, as the magnitude of V_clamp was reduced (i.e., made less negative than approximately −4.5 V), the maximum signal level of the M13-clamp pixels is observed to decrease by a corresponding amount, as intended and as illustrated in the figure. Thus, by operating the array at a value of V_clamp (e.g., −2 V) smaller in magnitude than V_bias (4 V in this case), the maximum signal capacity of the pixel is limited to a fraction (∼48%) of the normal pixel saturation level – so that the amount of charge trapping and release experienced by the clamp pixel is prevented from reaching the high levels associated with operation much closer to saturation [see Figs. 8a, 8b].

Figure 12.

Measurements of the pixel signal response for the M13-clamp array illustrating the influence of the clamp circuit on pixel behavior. Pixel signal is plotted as a function of incident LED light level (in units of number of flashes) for a V_bias value of 4 V. Results are shown for values of V_clamp set to voltages ranging from −1 to −5 V. The data was acquired in fluoroscopic mode under the same conditions as that reported for the M13 array in Fig. 6a.

DISCUSSION

The evolution in pixel design across the several generations of indirect detection, active matrix flat-panel imaging arrays described in this article has been driven by a variety of motivations. One of the strongest has been the potential for improving DQE performance by increasing optical fill factor, which can be significant under conditions of low exposure and high spatial frequencies. More modest DQE improvements can be achieved by decreasing additive noise through reduction in data line capacitance. Modification of pixel design in pursuit of these objectives, however, is not unconstrained. Issues such as compatibility of potential design changes with the overall fabrication process, yield (i.e., the desire for very low rates of pixel and line defects), and preservation of the ability to inspect and repair arrays at critical points in the circuit impose practical restrictions. The development of these various generations of arrays reflects careful balancing of these considerations.

The Pagescan III and Hawkeye arrays exhibit significantly increased fill factor (57% and 42% at 127 and 97 μm pitch, respectively) relative to what was possible in the earlier generation of designs represented by Pagescan I. This increase was achieved through substantial improvement in the factors governing array design and fabrication (e.g., minimum dimensions, process capability and control) that permitted non-negligible reductions in the size of the addressing transistor, in line widths, and in the gaps between the photodiode and address lines. While further increases in fill factor have been partially assisted by continued reductions in minimum feature size, it was clear that a departure from the baseline architecture (illustrated in Fig. 1) would be necessary to achieve additional, significant improvements in this parameter. The strategy pursued in recent array designs (M10, M13, HOFFA, and PSI-1) involved elevating some or most of the photodiode to a plane positioned completely above that of the addressing TFT – circumventing the zero-sum competition for pixel area between the transistor and the photodiode that is inherent in the baseline architecture.

M10 and M13, which preserve the discrete photodiode structure of the baseline architecture, provide optical fill factors of 85% and ∼79%, respectively. This represents an impressive, absolute increase of 28% and 22%, respectively, over that allowed by the previous-generation Pagescan III array. In addition, the architectural rules associated with M10 and M13 would allow fill factors on the order of 50% at a pitch of 50 μm compared to, at most, a few percent for the architectural rules of earlier generations. Moreover, M13 exhibits excellent properties, with dark current, charge trapping, charge release, and linearity equivalent to that of very high quality, baseline architecture arrays. A key element in the achievement of these favorable properties was establishing a topology for the M13 photodiode as uniform as possible. It is believed that sharp changes in the profile of the top and bottom electrodes create localized distortions in the electric field across the photodiode thickness. This results in large gradients in the field at some points – leading to increased dark current (in regions of high electric field) as well as increased trapping and release (in regions of low electric field). This view is consistent with the significant improvement in properties exhibited by M13 compared to M10, where a decrease in the area of the photodiode back contact in M13 (compared to M10) reduced nonuniformities in the topology of the photodiode.

M13 and M10 further demonstrate an interesting trade-off in two important performance metrics. For M13, a slight increase in the gap between the photodiode and the data line (resulting in an ∼3% reduction in optical fill factor) decreased the data line capacitance per pixel by ∼24%, relative to M10, to a favorably low value of ∼42.9 fF∕pixel. Since the capacitance per pixel directly affects preamplifier noise, and since wider gaps help to reduce line defects as well as facilitate array repair, this is an example of when a small sacrifice in fill factor is quite beneficial.

From the perspective of optical fill factor, the continuous designs are remarkable – providing values only ∼5% below the theoretical maximum of 100%, even at pixel pitches as low as 75 and 90 μm. If fill factor remains relatively independent of pitch, a potential doubling could be achieved at 50 μm compared to that made possible by even the M13 discrete photodiode architectural rules. In our studies, the sample HOFFA and PSI-1 arrays exhibited no indication of degradation in MTF due to charge sharing between pixels. This observation applies to the very low pixel signal sizes (∼5% of pixel saturation) used in those measurements, and is in line with the trend reported in an earlier HOFFA array study in which lateral cross talk between neighboring pixels was found to range from ∼5% at saturation down to values as low as 0.5% (a value approaching the sensitivity of the measurement technique) at 40% of saturation.³²

Although many of the pixel signal properties of the present continuous photodiode arrays are either somewhat poorer (in the case of dark current) or significantly poorer (in the case of charge release, charge trapping, range of linear response) than those of the M13, prospects for significant improvement are good. For example, both HOFFA and PSI-1 have substantial nonuniformity in the topology of their photodiode structure, with this consideration not having been taken into account in their design. Given the apparent effect of topology on performance, it is logical to expect that significant improvements in dark signal, charge trapping, etc. would accrue in continuous photodiode arrays in which uniform topology was maximized. In addition, a reasonable candidate for the origin of the anomalous behavior of charge trapping and release exhibited by HOFFA and PSI-1 at lower pixel signal levels (i.e., initially decreasing with increasing signal size) is the peripheral region of the pixel where the intrinsic layer of the a-Si:H photodiode comes into contact with the oxynitride passivation layer. If unusual trapping effects, or pile-up of charge, is occurring at this boundary, then it may be possible to partially, or completely, eliminate this behavior through some form of surface preparation of the oxynitride, prior to a-Si:H deposition. Alternatively, shaping of the electric field in that region through modification of the nearby bottom electrodes may improve signal performance.

Beyond improvements in DQE performance, and the possibility of indirect detection arrays with pitches approaching 50 μm, the elevation of the photodiode above the plane of the addressing transistor creates the ability to incorporate additional circuit elements into the pixel, with no sacrifice of optical fill factor. The results reported for the M13-clamp array, in which a second transistor was added to the pixel circuit to limit the effects of charge trapping and release, are an early demonstration of the potential benefits to be realized through exploitation of this new degree of design freedom. Further detailed exploration of the behavior of arrays incorporating such pixel clamp circuits, focused on image lag and ghosting, would be interesting and is planned. Similarly, the PSI-1 array is part of a development effort to incorporate an even greater number of additional transistors to create one- and two-stage in-pixel amplifiers that offer potential benefits such as further significant improvement in DQE under some conditions, and even greater restriction on charge trapping and release.^{7, 14, 33, 34} Given the potential benefit of arrays offering such capabilities, further exploration of such possibilities is anticipated.

APPENDIX: ASSUMPTIONS USED IN CASCADED SYSTEMS CALCULATIONS

In the cascaded systems calculations appearing in Fig. 2, the additive noise was assumed to be dominated by the TFT thermal noise of the addressed pixel $\left(\sqrt{2kT{C}_{\mathrm{PD}}}\right)$,²⁸ and by amplifier noise (σ_preamp=285+15×C_data, in units of electrons),²⁹ where C_PD is the capacitance of the photodiode, which is assumed to scale with pitch and optical fill factor, and C_data is the data line capacitance in pF). C_data is assumed to scale with the number of pixels along 30 (24) cm long data lines for the fluoroscopic (mammographic) imager, with a capacitive contribution, C_dlpix, of 42.9 fF∕pixel. In addition, the amount of x-ray attenuation in the detector and the averaged absorbed energy per X ray used in these calculations were obtained from Monte Carlo simulations using the EGS4 code,³⁵ and the light output from the detector per unit radiation, as well as the efficiency for conversion of absorbed x-ray energy to light, was obtained from measurements performed on sample arrays.