Regression Models of Atlas Appearance

Abstract

Models of object appearance based on principal components analysis provide powerful and versatile tools in computer vision and medical image analysis. A major shortcoming is that they rely entirely on the training data to extract principal modes of appearance variation and ignore underlying variables (e.g., subject age, gender). This paper introduces an appearance modeling framework based instead on generalized multi-linear regression. The training of regression appearance models is controlled by independent variables. This makes it straightforward to create model instances for specific values of these variables, which is akin to model interpolation. We demonstrate the new framework by creating an appearance model of the human brain from MR images of 36 subjects. Instances of the model created for different ages are compared with average shape atlases created from age-matched sub-populations. Relative tissue volumes vs. age in models are also compared with tissue volumes vs. subject age in the original images. In both experiments, we found excellent agreement between the regression models and the comparison data. We conclude that regression appearance models are a promising new technique for image analysis, with one potential application being the representation of a continuum of mutually consistent, age-specific atlases of the human brain.

1 Introduction

This paper describes framework for creating models of object appearance. Whereas principal component analysis (PCA) drives the common active shape model (ASM) pioneered by Cootes et al. [1], our framework is instead based on a generalized linear regression model (GLRM). On a high level of abstracting, one can think of the difference between these two approaches as supervised (GLRM) vs. unsupervised (PCA) learning of the model. While regression has been used for non-linear refinement of PCA-based ASMs [2] and for shape regression [3], we believe that this is the first application of regression to generate appearance models.

The immediate benefit of using regression instead of PCA is that it explicitly models the changes of appearance in response to independent variables, such as subject age or sex (see schematic comparison of PCA-based vs. regression shape model in Fig. 1). Such a model is, therefore, able to generate instances linked to specific sets of independent variable values, which we demonstrate herein by creating an appearance regression model of the human brain. Using this model, we are able to generate atlases of the brain for specific ages, sexes, or, in future work, disease conditions.

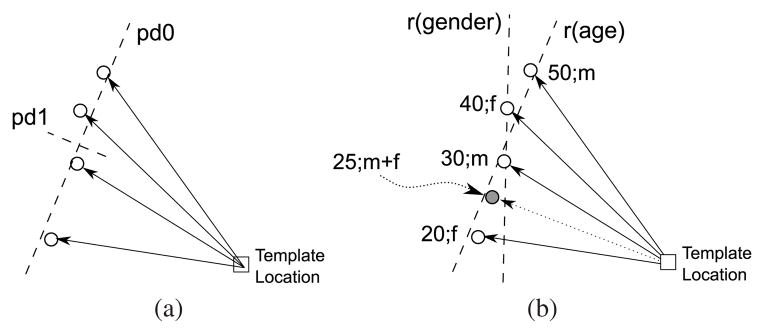
Fig. 1.

Schematic comparison of shape models based on PCA and regression, each using the same mapping of one template point location to four corresponding data point locations. (a) The PCA-based model provides two orthogonal principal directions based entirely on the data point locations. (b) The regression-based model (here, multi-linear model) provides one regression line per independent variable (here, age and sex). The regression lines are not necessarily orthogonal. Unlike the PCA-based model, the regression model can be instantiated for specific independent variable values (here, marked by the solid circle, 25 years of age, half male/half female).

Atlases of human brain anatomy have an important role in studies of brain anatomy and function. They serve as standard reference coordinate systems, to which data from all subjects in typical imaging-based studies are registered for statistical analysis. They can also be used to outline regions of interest, which can then be propagated via registration to images from individual subjects (i.e., atlas-based segmentation [4])

When based on a single individual [5], an atlas represents an anatomy associated with a well-determined set of subject independent variable values (e.g., that person’s age and sex). When an entire group of subjects is used to construct a population atlas [6], on the other hand, then the atlas is representative for an entire range of independent variable values, but it is no longer specific.

For the study of the human brain, the regression-based modeling framework bridges the gap between these two concepts: the atlas regression model covers an entire range of independent variable values, according to the individual images, from which it was created, yet every instance we create from the model corresponds to a specific set of independent variable values. From the same input population we can thus create many different atlases, each specific, but all related to one another by dense mutual coordinate correspondences. Regions of interest outlined on one atlas instance transfer immediately to all other instances from the same model, which enables comparable studies of different subject populations, each of them using a study-appropriate atlas.

The remainder of this paper is organized as follows. Section 2 describes the general mathematical framework behind the regression appearance model. Section 3 describes the application of the regression appearance model to generate atlases from multi-modality MR image data acquired from 36 subjects. Section 4 presents atlases resulting from this population, analyzed in terms of how well they model effects (e.g., age) in the input data. Section 5 discusses of the benefits of regression appearance models and differences between them and PCA-based models.

2 Regression Appearance Model

In this section, we introduce the mathematical framework of the regression appearance model. The purpose of this model is to determine the correspondence between subject independent variables and image appearance based on co-registered images. The principal idea is illustrated by a data flow diagram in Fig. 2. A regression shape model [3] is first constructed from spatial correspondences between the input images via regression over the independent variables associated with them. Correspondences are determined herein via image registrations (see Section 3.3 for details), which relates our model to the statistical deformation model [7], but landmark-based point correspondences are an equally valid input.

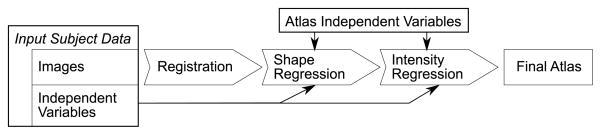
Fig. 2.

Data flow diagram. Coordinate transformations are determined between the input images via image registration. The resulting transformations are then used to create a shape regression model based on the subjects’ independent variable values. The latter are then also used to obtain local regression models of pixel intensities. The combined shape and intensity models are instantiated for selected atlas independent variables to create the final atlas.

When the shape model is instantiated for a particular set of atlas independent variables, all input images can be separately reformatted into the model coordinate space. In this space, we then perform a second regression on the reformatted image intensities at each pixel. The result of instantiating the second regression model is then the final atlas, which combines the two models for shape and intensity appearance.

2.1 Definitions

For k = 1, …, K, let I_k be images from K subjects. For each k, let p⃗_k be a vector of length P, which contains the values of P independent variables for subject k. Numerical independent variables, such as age, are used directly, whereas discrete independent variables, such as sex and diagnosis, are binary dummy-coded as 0 and 1.³

Furthermore, let Ω = {x⃗_n|0 < n ≤ N} be the voxel coordinates of a template grid to which all K images are registered. For each input image I_k, the template space thus relates to the space of I_k via the deformation field U_k = {u⃗_k,n ∈ ℝ³|0 < n ≤ N} such that

$${\overrightarrow{x}}_n\mapsto {\overrightarrow{x}}_n+{\overrightarrow{u}}_{k,n}.$$ (1)

To account for differences in pose, orientation, and scale [7], the pure deformation (excluding affine) component is determined for each pixel n as

$${(d_{k,n}^x,d_{k,n}^y,d_{k,n}^z)}^T={\mathbf{J}}_k^{-1}{\overrightarrow{u}}_{k,n},$$ (2)

where J_k is the Jacobian of the global affine transformation T_k that maps from the template space to the space of image I_k.

2.2 Shape Regression

Shape regression is performed by constructing, via a GLRM [8], a deformation field that maps the original template space into a space corresponding to a given set of subject independent variables. To this end, one needs to solve (via singular value decomposition, see [9], Chapter 15.4) the three regression problems

$${\overrightarrow{b}}_n^x=\mathbf{G}{\overrightarrow{a}}_n^x,{\overrightarrow{b}}_n^y=\mathbf{G}{\overrightarrow{a}}_n^y,\text{and}{\overrightarrow{b}}_n^z=\mathbf{G}{\overrightarrow{a}}_n^z$$ (3)

for ${\overrightarrow{a}}_n^x,{\overrightarrow{y}}_n^z,{\overrightarrow{a}}_n^z$ at each pixel n. Here,

$${\overrightarrow{b}}_n^x={(d_{1,n}^x,\dots ,d_{K,n}^x)}^T,{\overrightarrow{b}}_n^y={(d_{1,n}^y,\dots ,d_{K,n}^y)}^T,\text{and}{\overrightarrow{b}}_n^z={(d_{1,n}^z,\dots ,d_{K,n}^z)}^T$$ (4)

are the observed deformation vector components for the K inputs. The design matrix

$$\mathbf{G}=\left(\begin{array}{cccc}{X}_1({\overrightarrow{p}}_1)& \cdots & X_M({\overrightarrow{p}}_1)& 1\\ ⋮& \ddots & ⋮& ⋮\\ X_1({\overrightarrow{p}}_K)& \cdots & X_M({\overrightarrow{p}}_K)& 1\end{array}\right)$$ (5)

is composed of M functions applied to each of the subject independent variables for k = 1, … K. Later in this paper, we use two particular models: a first-order (linear) and a second-order (quadratic) model. For the linear model, M = P and X_m(p⃗) ≡ p_m. The second-order model contains all functions of the linear model and incorporates as additional functions X all second-order monomials of the elements in p⃗. For example, the first two additional functions could be $X_{P+1}(\overrightarrow{p})\equiv p_1^2$, X_P+2(p⃗) ≡ p₁p₂, and so on. Note that, depending on the application, the model can readily accommodate more complex functions X, such as exponentials and log functions.

After solving the regression problems in Eq. (3), any vector q⃗ ∈ ℝ^P corresponds to a regressed deformation at pixel n defined by the vector-matrix product

$${\overrightarrow{Q}}_{\overrightarrow{q},n}=(X_1(\overrightarrow{q}),\dots ,X_M(\overrightarrow{q}),1)\left({\overrightarrow{a}}_n^{(x)},{\overrightarrow{a}}_n^{(y)},{\overrightarrow{a}}_n^{(z)}\right).$$ (6)

Taken over all n, these deformation vectors define a deformation field, Q_q⃗, that maps coordinates from the original template space to the regression space corresponding to q⃗ via

$${\overrightarrow{x}}_n\mapsto {\overrightarrow{x}}_n+{\overrightarrow{Q}}_{\overrightarrow{q},n}.$$ (7)

In the simplest application of Q_q⃗, its inversion⁴ can be used to reformat the non-regression template into the new coordinate space.

2.3 Intensity Regression

Once the regression-based deformation ${\mathbf{Q}}_{\overrightarrow{\widehat{p}}}$ has been determined for a given independent variable vector q⃗, all K input images can be reformatted directly into the corresponding space by concatenating the numerical inversion of Q_q⃗ with the template-to-subject transformation U_k.

The resulting K reformatted images, now all in the same space with pixel-by-pixel correspondence, can be combined into the final atlas image. Instead of using the usual intensity averaging, however, we use the same regression model already used to construct the regression template coordinate space.

For that, the design matrix, G, is identical to the one used for deformation field regression, b⃗_n contains the intensities of the K corresponding intensities in the reformatted images at pixel n, and the final image intensity is given by scalar multiplication of instantiation variable values q⃗ and fitted parameters a⃗_n.

3 Application to Atlas Generation

3.1 Subjects and Imaging

Images were acquired from 36 subjects, 18 men and 18 women. The average age of the men was 51.3 years (range=20 to 83), that of the women 53.2 years (range=20 to 85). These subjects were subdivided in three distinct age groups: young (25.5±4.3, range = 20 to 33 years), middle-aged (52.4±4.4, range = 46 to 58), and elderly (77.7±4.9, range = 67 to 85 years). Each age group comprised six men and six women. All subjects were right-handed, non-smoking, and healthy, recruited from the local community for ongoing studies in our group.

Four imaging sequences were collected on a 3.0 T GE scanner. For T₁-weighted structural images, acquisition parameters were: 3D axial IR-prep SPoiled Gradient Recalled (SPGR), TR=6.5 ms, TE=1.54 ms, thick=1.25 mm, skip=0, locations=124. For T₂-weighted and proton density-weighted imaging: 2D axial dual-echo fast spin echo (FSE), TR=10,000 ms, TE=14/98 ms, thick=2.5 mm, skip=0, locations=62. Acquisition parameters for diffusion tensor imaging were: 2D echo-planar diffusion-weighted images (DWI), TR=7500 ms, TE=97.6 ms, thick=2.5 mm, skip=0, locations=62, b=0 (5 NEX), plus 15 non-collinear diffusion directions b=860 s/mm² (2 NEX), plus 15 opposite polarity non-collinear diffusion directions b=860 s/mm² (2 NEX) FOV=240 mm, x-dim=96, y-dim=96, reconstructed to 128×128 pixels. For field map computation to spatially unwarp DWI: 2D axial dual-echo gradient echo (GRE), TR=460 ms, TE=3/5 ms, thick=2.5 mm, skip=0, locations=62.

3.2 Image Pre-processing

The SPGR and FSE images were corrected for B₁-induced intensity bias fields by applying a second-order polynomial multiplicative bias field, computed using an in-house implementation of a model-free entropy-minimization algorithm [11]. A brain mask was extracted from the late-echo FSE image using the FSL Brain Extraction Tool, BET [12], which was propagated to the SPGR and early-echo FSE images via co-registration. The skull-stripped SPGR images were then segmented using FAST [13] into probability maps for gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF).

In the DWI, eddy-current distortions were minimized on a slice-by-slice basis by within-slice registration that takes advantage of the symmetry of the opposing polarity acquisition [14]. The individual repeat acquisitions for each diffusion direction were averaged, eliminating the need to account for the cross terms between imaging and diffusion gradients producing 15 images per location for tensor computation. A field map was constructed from the complex difference image between two echoes (3 and 5 ms) of the GRE after unwrapping with FSL’s PRELUDE tool. B₀ inhomogeneity distortion was corrected with FUGUE, the FSL Utility for Geometrically Unwarping EPIs [15]. Tensor fields were then reconstructed, and maps of fractional anisotropy (FA) and mean diffusivity (MD) computed, using Camino [16].

3.3 Groupwise Alignment

The entire intersubject registration procedure is applied to bias-corrected SPGR images. It is described in detail in an earlier paper and is, therefore, only summarized here. An empty template coordinate space, which is defined independently of the N input images, is mapped to each of these images spaces via a coordinate transformation, T_n, for 0 < n ≤ N.

The initial, linear alignments are 9-parameter affine transformations (shift, rotation, anisotropic scale). These were computed using a multi-image generalization of mutual information based on a continuous approximation of joint and marginal image entropies [17]. The nonrigid transformations are represented by free-form deformations based on third-order B-splines [18]. These were computed using a stack entropy image similarity measure [19]. Both registration stages employed a simple but effective multilevel, multi-resolution gradient descent scheme. Both stages also enforced zero sums over all images for each of the transformation parameters, which is a hard constraint based on the regularization term proposed by Studholme & Cardenas [20].

4 Results

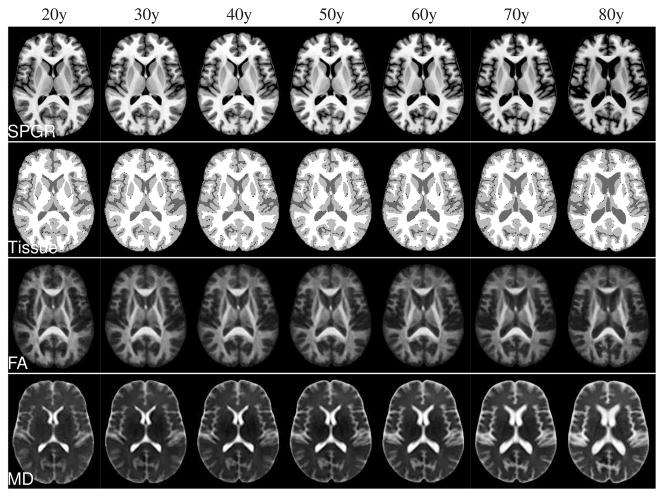
Nonrigid shape (i.e., excluding scale) differences between male and female atlases, while clearly present, were small compared with aging effects (see Fig. 3). All regression atlases shown below are, therefore, mixed-sex atlases with equal male and female contributions. In Fig. 4, representative axial slices are shown from the SPGR, tissue classification, FA, and MD channels of regression atlases created in age increments of 10 years. The regressed tissue classifications were generated by mapping the individual tissue classifications into regressed atlas space, followed by label voting. The typical aging effects (increasing CSF volume, decreasing FA, increasing MD) are readily apparent from these images.

Fig. 3.

Comparison of sex vs. age effects in atlases instantiated from the same 36-subject regression model. Top row: all-male atlases, middle row: male/female mixed-sex atlases, bottom row: all-female atlases. Note that affine differences including scale were eliminated from the model (see text).

Fig. 4.

Discrete instances created from the continuous atlas regression model for ages 20 through 80 years in 10 year increments. Rows from top to bottom: SPGR, maximum-likelihood tissue segmentation, DTI-FA, and DTI-MD.

4.1 First vs. Second Order Models: Comparison with Sub-Population Atlases

One way to assess whether the regression appearance model is effective at modeling the effect of independent variables on brain structure is to compare an atlas generated by the model with one generated from a parameter-matched population of subjects. More precisely, for each of the three 12-subject age groups in our input population, we create a separate brain atlas using the same registration technique outlined in Section 3.3. We then compare the resulting atlas with one generated by the 36-subject regression model for the age defined by the mean age of the 12-subject subgroup.

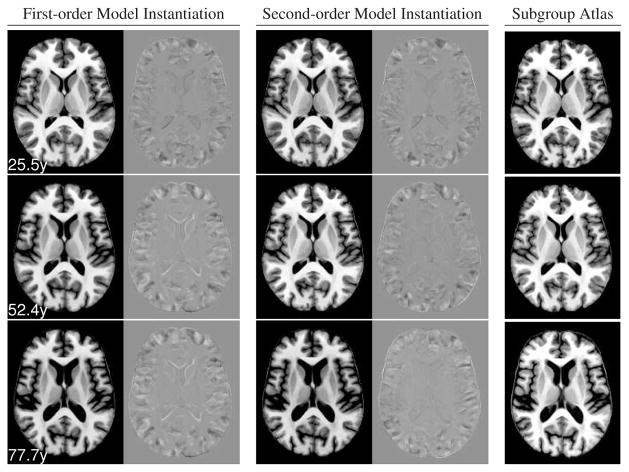
The atlases created by both a first-order and a second-order model are shown with corresponding slices of the respective subgroup atlases in Fig. 5. There are some differences in the cortical folding patterns, which is not surprising given the distinct sets of input individuals. In general, however, and in particular for subcortical structures, all atlases are highly consistent with each other. The second-order model appears to capture the accelerating increase in lateral ventricle volume better than the first-order model, which is particularly evident by comparing difference images between the middle-aged and older atlas images (Fig. 5, second and third row).

Fig. 5.

Comparison of regression atlases instantiated for the mean subject age in each group of the three age groups with atlases computed independently from each group. Top to bottom: young, middle-aged, elderly group. Left column: SPGR for first-order model regression atlas and difference with subgroup atlas. Middle column: SPGR for second-order model regression atlas and difference with subgroup atlas. Right column: subgroup atlas. All difference image are shown using the same gray level scale, centered at zero.

4.2 Age Effects: Regression Atlases vs. Subjects

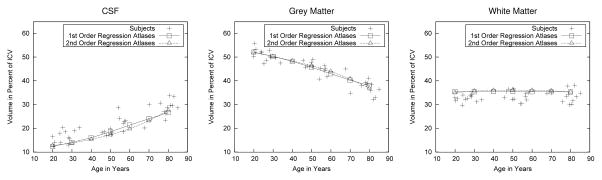
For each subject and for each atlas shown in Fig. 4, we computed the relative volumes of cerebrospinal fluid (CSF), gray matter (GM), and white matter (WM) in percent of intra-cranial volume (ICV). For each of the three “tissue” types, these relative volumes are plotted against age in Fig. 6. There is excellent agreement between the relative volumes in subjects and regression atlases for all three tissue types, albeit with slight overestimation of WM volume and underestimation of CSF volume. Note that the overall effects of increasing CSF volume, decreasing GM volume, but constant WM volume are perfectly consistent with well-established aging effects in the brain [21].

Fig. 6.

Comparison of tissue volume vs. age in subjects and regression atlases. Left to right: CSF, gray matter, white matter. All tissue volumes are relative to the ICV to account for head size differences. Measurements for first-order and second-order regression atlases are connected by line segments. There are no regression lines in these figures, i.e., the lines representing the regression atlases are measurements in their own right and not fits of the subject measurements.

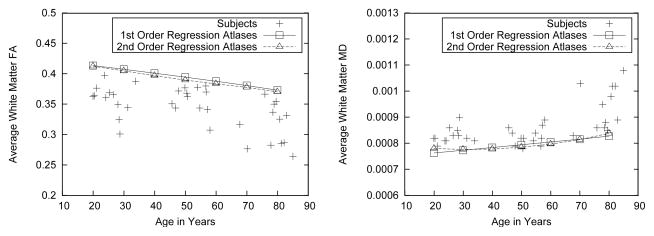
Well-known aging effects of decreasing FA and increasing MD with age are also shown by our subject population and modeled by the regression atlases, as is shown in Fig. 7. We note here that the slope of the age effects is modeled quite accurately, as is (in the second-order regression atlases at least) the well-established increasing speedup of both effects with age.

Fig. 7.

FA and MD vs age effects in regression atlases compared with individual subjects. Left: mean FA, averaged over all pixels classified as white matter in each subject and each atlas. Right: mean MD, averaged over all white matter pixels.

The regression models that we created are consistently over-estimating FA and under-estimating MD compared with the individual input images. We note, however, that simply averaging over all WM pixels is quite crude and ignores effects such as anterior-posterior gradients in aging effects on the brain. More importantly perhaps, the tissue classification in the regression atlases in some sense represents a combination of multiple classifications (one from each input image), which has been shown in other contexts to be more accurate than the individual classifications [22]. Applying more accurate WM maps (i.e., one that includes fewer non-WM pixels) in the regression atlases than in the individual images would certainly explain a bias towards higher FA and lower MD as observed here.

5 Discussion

This paper has described a method for modeling atlas appearance, based on regression rather than PCA. The effectiveness of the framework was demonstrated by applying it to generate models of human brain atlas appearance that depended on subject age and sex. Atlases instantiated from these models showed excellent agreement with three subgroup atlases created from young, middle-aged, and older subjects separately via groupwise registration. The regression atlases also accurately modeled aging effects on tissue volumes and DTI measures observed in the input data, and consistent with the neuroscience literature [21].

It is important to emphasize that the regression model of appearance is not intended, nor able, to replace PCA-based models for every application. Indeed, both methods complement each other: in applications where there are no meaningful independent variables, the PCA-based model is the only one applicable. This is, for example, the case with one standard example of shape models, the training of hand outlines [1]. In cases where controlled independent variables determine the data, however, the regression-based model can make use of this a priori knowledge.

From a theoretical point of view, there are also some relevant differences between the PCA-based and regression-based model: whereas the PCA uses explicit coupling, for example over all pixels in an image or deformation field, via the joint covariance matrix, the regression model uses an implicit coupling via the use of the same regression design matrix at every pixel. The regression model furthermore imposes more intuitive bounds on instantiated values of independent variables, i.e., it is intuitive from the training data, at what point the model instantiation turns from an interpolation into an extrapolation.

As with other regression methods, problems in our framework can arise from correlated independent variables, for example when all diseased subjects are men, and all controls are women. In such cases, the method can be extended to partial least squares regression [23] by first performing PCA on the original independent variables, and then performing regression with respect to the dominant principal components. While this would remedy numerical problems, the model created from such a pathological subject population would suffer from the inability to separate the effects of correlated variables, a problem remedied by study design rather than post-acquisition analysis.

One important application of immediate interest for our work are the popular “optimized VBM” [24] studies, which commonly use study-specific templates for spatial normalization. These templates are generated from the data to be analyzed (or a “normal” subgroup thereof), and thus the results represented within their coordinate systems are not comparable with one another as every study uses its own specific template. Also, quality assurance must be repeated for every study-specific template used. Instead of study-specific templates, our work enables the instantiation of study-appropriate templates from a regression model. All templates instantiated from the same model are guaranteed to be spatially compatible with one another and they have high certainty to be of identical quality.