Improving propensity score weighting using machine learning

Abstract

Machine learning techniques such as classification and regression trees (CART) have been suggested as promising alternatives to logistic regression for the estimation of propensity scores. The authors examined the performance of various CART-based propensity score models using simulated data. Hypothetical studies of varying sample sizes (n=500, 1000, 2000) with a binary exposure, continuous outcome, and ten covariates were simulated under seven scenarios differing by degree of non-linear and non-additive associations between covariates and the exposure. Propensity score weights were estimated using logistic regression (all main effects), CART, pruned CART, and the ensemble methods of bagged CART, random forests, and boosted CART. Performance metrics included covariate balance, standard error, percent absolute bias, and 95% confidence interval coverage. All methods displayed generally acceptable performance under conditions of either non-linearity or non-additivity alone. However, under conditions of both moderate non-additivity and moderate non-linearity, logistic regression had subpar performance, while ensemble methods provided substantially better bias reduction and more consistent 95% CI coverage. The results suggest that ensemble methods, especially boosted CART, may be useful for propensity score weighting.

INTRODUCTION

The propensity score is the probability of receiving a treatment conditional on a set of observed covariates [1]. At each value of the propensity score, the distribution of observed covariates is the same across treatment groups. Thus, by conditioning on the propensity score, one can estimate treatment effects free from confounding due to the covariates that determined the propensity score. Conditioning on the propensity score typically is done by matching on the propensity score, subclassification into strata within which propensity scores are similar, regression adjustment on the propensity score, or weighting by the propensity score [2, 3]. Matching and subclassification approaches rely only on selecting subjects with similar propensity score values, relying less on the precise numerical propensity score values. In contrast, regression adjustment and weighting are especially sensitive to misspecification of the propensity score model due to the incorporation of the actual propensity scores or functions in the outcome model [4–6].

The literature has few guidelines for estimating propensity scores for any of these propensity score techniques. Propensity scores are generally estimated using logistic regression. However, parametric models require assumptions regarding variable selection, the functional form and distributions of variables, and specification of interactions. If any of these assumptions are incorrect, covariate balance may not be achieved by conditioning on the propensity score, which may result in a biased effect estimate [7]. In this paper we examine the use of machine learning methods as one alternative to logistic regression.

Machine learning is a general term for a diverse number of classification and prediction algorithms and has applications ranging from detection of credit card fraud to computerized facial recognition [8, 9]. Contrary to statistical approaches to modeling that assume a data model with parameters estimated from the data, machine learning tries to extract the relationship between an outcome and predictor through a learning algorithm without an a priori data model [10]. The suggestion to use such algorithms for propensity score model construction is not new [2, 11–16]. However, these methods have not been widely applied in the propensity score literature, perhaps because of the “black box” nature of some of the algorithms and difficulty in etiologic interpretations of results [17]. Because decision trees are common in medical research for diagnostic and prognostic purposes [18] and are intuitive to visualize and understand, they are a natural starting point for a discussion of machine learning algorithms.

Decision trees partition a dataset into regions such that within each region, observations are as homogeneous as possible [19]. Decision trees are referred to as classification trees if the predicted outcome is a class or regression trees if the outcome is numerical; we refer to these methods collectively as Classification and Regression Trees (CART). Within each node of the tree, observations will have similar probabilities for class membership. CART has advantageous properties for estimating propensity scores, including the ability to handle categorical, ordinal, continuous, and missing data. It is insensitive to outliers and monotonic transformations of variables. Additionally, interactions and non-linearities are modeled naturally as a result of the splits. However, CART can have difficulty in modeling smooth functions and main effects, and is sensitive to overfitting [20].

Several approaches have been proposed to remedy these limitations. To address overfitting, cost-complexity pruning can be implemented where the number of tree splits is reduced or “pruned” with the idea that a simpler tree will be less sensitive to noise and generalize better to new data [19]. While the single tree implementation of CART and pruned CART can perform poorly as a classifier, the predictive capabilities of a weak classifier can be strengthened when working together with other weak classifiers. Ensemble methods, which are somewhat related to iterative and bootstrap procedures, utilize multiple samplings and passes through data (i.e., multiple trees) to enhance the performance of prediction algorithms and reduce overfitting [8]. Because these methods are complex, we provide only a brief description of ensemble methods with application to CART and provide references for the interested reader. Bootstrap aggregated (bagged) CART involves fitting a CART to a bootstrap sample with replacement and of the original sample size, repeated many times. For each observation, the number of times it is classified into a category by the set of trees is counted, with the final assignment of class membership, or probability thereof, based on an average or majority vote over all the trees [21]. Random forests are similar to bagging but utilize a random subsample of predictors in the construction of each CART [22]. Like bagged CART and random forests, boosted CART goes through multiple iterations of tree fitting on random subsets of the data. However, with each iteration, a new tree gives greater priority to the data points that were incorrectly classified with the previous tree [15, 23].

Because in the real world the true treatment effects within any observational dataset are unknown, simulation-based research is needed to evaluate the performance of machine learning propensity score methods. Using simulated data, Setoguchi et al. compared neural networks, CART, pruned CART, and logistic regression in the context of propensity score matching and found that neural networks produced the least biased estimates in many scenarios [16]. However, they do not consider ensemble methods which perform extremely well in classification and prediction tasks while having desirable statistical properties [8]. Furthermore, it is important to determine whether the performance of machine learning methods in propensity score estimation varies based on how those propensity scores are applied. Finally, Setoguchi et al. do not assess covariate balance. In the present analysis, we evaluate the performance of several decision tree-based algorithms, including ensemble methods, in the context of propensity score weighting.

METHODS

Simulation setup

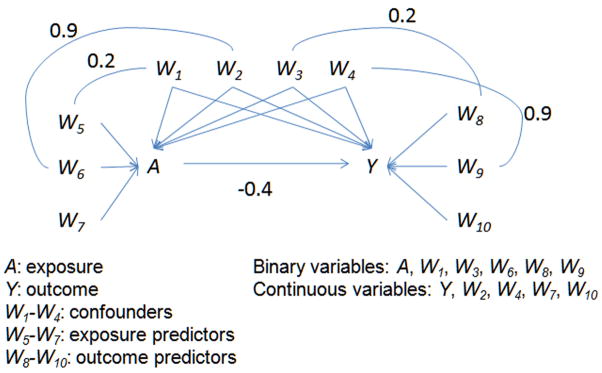
We followed the simulation structure described by Setoguchi and colleagues with slight modifications [16]. For each simulated dataset, ten covariates (four confounders associated with both exposure and outcome, three exposure predictors, and three outcome predictors) W_i were generated as standard normal random variables with zero mean and unit variance. Correlations were induced between several of the variables (Figure 1). The binary exposure A has Pr(A=1|W_i) = 1/(1+exp(−β · f(W_i))). The average exposure probability (in other words, the exposure probability at the average of covariates) was ≈ 0.5 and was modeled from W_i according to the scenarios below, using the formulae provided by Setoguchi et al. The continuous outcome Y was generated from a linear combination of A and W_i such that Y = α_iW_i + γA where the effect of exposure, γ, = −0.4.

Figure 1.

Variable Relationships and Form in Simulation Data Structure

We evaluated the performance of CART-based methods in seven scenarios that differed in degrees of linearity and additivity in the true propensity score model, specified with quadratic terms and interactions. The scenarios were designed such that the true propensity score model had the following properties [16]:

• A: additivity and linearity (main effects only);

• B: mild non-linearity (one quadratic term);

• C: moderate non-linearity (three quadratic terms);

• D: mild non-additivity (three two-way interaction terms);

• E: mild non-additivity and non-linearity (three two-way interaction terms and one quadratic term);

• F: moderate non-additivity (ten two-way interaction terms);

• G: moderate non-additivity and non-linearity (ten two-way interaction terms and three quadratic terms).

To assess the performance of machine learning methods in small, medium, and large-sized datasets, data were simulated for cohort studies of size n=500, n=1000, and n=2000. One thousand datasets of each study size were generated for each of the seven scenarios.

Propensity score estimation methods

We used R version 2.6.1 [24] to estimate propensity scores using the following methods:

• Logistic regression: standard logistic regression with a main effect for each covariate.

• CART: recursive partitioning using the rpart package with default parameters [25].

• Pruned CART: recursive partitioning as described above but with a cost-complexity parameter that controls tree growth. The cost-complexity parameter is automatically chosen to minimize the cross-validated error estimated from a complexity parameter table generated by the plotcp function.

• Bagged CART: bootstrap aggregated CART is implemented using the ipred package [26]. We used 100 bootstrap replicates based on empirical evidence suggesting that with more replicates, misclassification rates improve and test errors are more stable [20].

• Random forests: random forests are implemented using the randomForest package with the default parameters [27].

• Boosted CART: boosted regression trees are implemented using the twang package [28]. We used the parameters recommended by McCaffrey et al., with 20,000 iterations and a shrinkage parameter of 0.0005 [15], with an iteration stopping point that minimizes the mean of the Kolmogorov-Smirnov test statistics.

Estimation of the treatment effect using propensity score weighting

Propensity score weighting is similar to the use of sampling weights in survey data analysis to account for unequal probabilities of inclusion in a study sample. A number of propensity score weighting schemes have been applied in the literature [3, 13, 29, 30]. For example, with inverse probability of treatment weighting, treated persons receive a weight of 1/p_i and untreated persons receive a weight of 1/(1−p_i), where p_i is individual i’s estimated propensity score. In essence, this weights both the treated and untreated groups to look like the combined sample in order to estimate the average treatment effect in the combined sample.

An alternative estimand of interest is the average treatment effect on the treated -- the average treatment effect in a population with a distribution of risk factors similar to that of the treated group. Because this estimand is often of interest in observational studies, we elected to use a weighting scheme with this estimand in mind. We assigned treated persons a weight of 1 while untreated persons are assigned a weight of p_i/(1−p_i) [12, 13, 15, 29]. Thus, persons in the comparison group who are more similar to those in the treatment group are given greater weight and those more dissimilar are downweighted. If the propensity scores are properly estimated, then the weighted covariate distributions between treatment groups should be similar and the average treatment effect can be estimated as the difference of weighted means. Although it is a good idea in practice to perform “doubly robust” linear regression adjustment for covariates after weighting is applied [4, 31], we did not do so in order to better isolate and compare the performance of the various methods with regards to propensity score weighting.

Performance metrics

We evaluated the performance of the various propensity score fitting methods through several measures.

• ASAM: average standardized absolute mean difference, a measure of covariate balance. After weights were applied, the absolute value of the standardized difference of means (standardized by the standard deviation of the particular covariate in the treatment group) between treatment and comparison groups was calculated for each covariate and the average taken across all the covariates. A lower ASAM indicates that the treatment and comparison groups are more similar with respect to the given covariates. We refer to the average value of the 1000 ASAMs in a simulation scenario as the mean ASAM.

• Bias: the percentage difference from the true treatment effect of −0.4. Both absolute bias and bias (either positive or negative) are considered.

• SE: the standard error of the effect estimate. To calculate the standard error of estimates using the weights we used the survey sampling analysis methods implemented by the survey package [32].

• 95% CI coverage: the percentage of the 1000 datasets in which the estimated 95% confidence interval included the true treatment effect.

• Weights: The performance of weighting methods can be adversely affected if weights are extreme, as a result of estimated propensity scores that are close to 0 or to 1. We therefore examined the distribution of weights for the untreated observations.

RESULTS

Simulations of N=1000

Covariate balance

One rule of thumb for assessing the covariate balance between treatment groups is that an absolute standardized difference in means of 0.2 or greater may be of concern [15, 33]. The average covariate balancing performance of logistic regression propensity score models was acceptable, with low mean ASAMs in all scenarios (range: 0.041, 0.094) (Table 1). However, although the mean ASAMs for logistic regression were relatively and absolutely low, if not the lowest, for each scenario, the ASAMs were skewed with a number of high outliers (Figure 2).

Table 1.

Performance Metrics of Propensity Score Estimation Methods in 1000 Simulated Datasets of N=1000.

Metric	Method1	Scenario4
		A	B	C	D	E	F	G
ASAM2	LGR	0.041	0.042	0.058	0.056	0.061	0.068	0.094
	CART	0.159	0.148	0.143	0.171	0.162	0.15	0.143
	PRUNE	0.175	0.164	0.148	0.182	0.173	0.161	0.151
	BAG	0.132	0.127	0.121	0.144	0.141	0.119	0.112
	RFRST	0.08	0.076	0.076	0.089	0.086	0.077	0.075
	BOOST	0.068	0.065	0.067	0.073	0.071	0.065	0.067
Absolute bias	LGR	7.6%	8.3%	13.9%	12.1%	16.0%	16.8%	29.6%
	CART	20.5%	15.2%	18.2%	20.1%	16.9%	22.5%	19.0%
	PRUNE	26.3%	19.5%	19.1%	22.9%	19.1%	23.9%	19.9%
	BAG	12.3%	9.1%	11.0%	11.2%	9.0%	10.2%	9.4%
	RFRST	7.4%	6.2%	8.9%	7.6%	7.3%	7.5%	9.0%
	BOOST	8.1%	6.9%	6.8%	7.0%	6.4%	6.1%	6.2%
Standard error	LGR	0.066	0.066	0.062	0.075	0.076	0.075	0.071
	CART	0.059	0.059	0.068	0.06	0.06	0.061	0.066
	PRUNE	0.057	0.057	0.066	0.059	0.059	0.059	0.065
	BAG	0.055	0.055	0.06	0.056	0.055	0.056	0.058
	RFRST	0.062	0.06	0.064	0.064	0.061	0.063	0.062
	BOOST	0.059	0.058	0.059	0.061	0.059	0.06	0.059
95% CI3 coverage	LGR	97.9%	96.8%	89.7%	88.5%	80.0%	76.0%	32.5%
	CART	63.3%	78.2%	69.5%	63.7%	74.7%	58.3%	67.2%
	PRUNE	49.1%	66.0%	68.0%	56.6%	68.4%	54.9%	65.7%
	BAG	90.9%	96.8%	90.4%	91.8%	95.7%	93.6%	94.7%
	RFRST	98.3%	99.6%	95.3%	98.2%	98.6%	98.4%	95.1%
	BOOST	98.6%	99.8%	99.5%	99.9%	99.9%	100.0%	99.8%

¹LGR – logistic regression, CART – classification and regression tree, PRUNE – pruned CART, BAG – bagged CART, RFRST – random forests, BOOST – boosted CART;

²ASAM – average standardized absolute mean distance;

³CI – confidence interval

⁴A: additivity and linearity; B: mild non-linearity; C: moderate non-linearity; D: mild non-additivity; E: mild non-additivity and non-linearity; F: moderate non-additivity; G: moderate non-additivity and non-linearity.

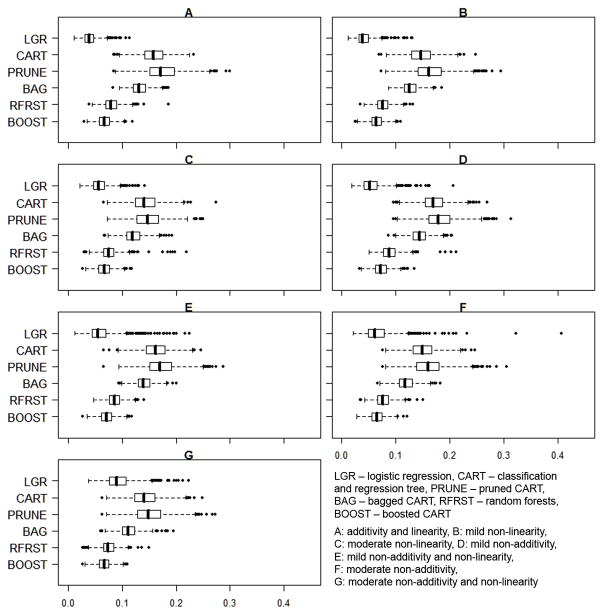
Figure 2.

Distribution of the Average Standardized Absolute Mean Difference by Propensity Score Estimation Method for 1000 Datasets in each of 7 Scenarios (N=1000)

CART and pruned CART propensity score models produced higher mean ASAMs than other methods, with respective ranges of 0.143 to 0.171 and 0.148 to 0.182 across the 7 scenarios. However, CART and pruned CART propensity score models did not provide consistent covariate balance within all datasets, as indicated by the high dispersion of mean ASAMs as well as the large number of high outliers (Figure 2). In contrast, the ensemble methods of bagged CART, random forests, and boosted CARTs produced low mean ASAMs in all scenarios (ranges: bagged CART: 0.112, 0.144; random forests: 0.075, 0.089; boosted CART: 0.065, 0.073) and the ASAMs were much less dispersed than those from the other methods. For example, boosted CART produced no ASAMs > 0.2 in any of the scenarios.

Estimate of effect and standard error

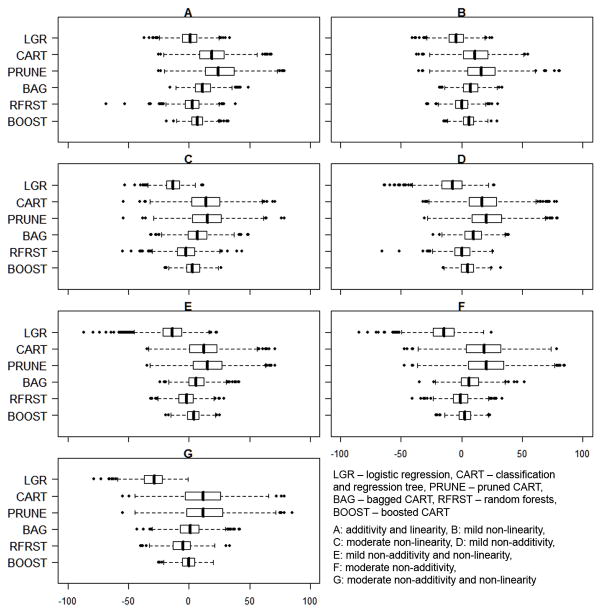
The performance of logistic regression was generally acceptable in the scenario of additivity and linearity (scenario A) with a mean absolute bias of 7.6% and 95% CI coverage of 98.0% (Table 1). However, with increasing non-additivity and non-linearity, logistic regression performed poorly; with moderate non-additivity and nonlinearity (scenario G), logistic regression had a mean absolute bias of 29.6% and 95% CI coverage of 32.5%. Logistic regression propensity score models overestimated the true effect with increasing frequency as non-additivity and non-linearity increased (Figure 3). Both CART and pruned CART had high absolute biases with respective averages of 18.9% and 21.5% across all scenarios as well as low 95% CI coverage (respective averages of 67.8% and 61.2%). In contrast, the ensemble methods displayed low absolute biases as well as high 95% CI coverage. Across all scenarios, bagged CART, random forests, and boosted CART averaged mean absolute biases of 10.3%, 7.7%, and 6.8%, respectively. Boosted CART displayed the best 95% CI coverage with ≥ 98.6% coverage in all scenarios.

Figure 3.

Distribution of the Percent Bias by Propensity Score Estimation Method for 1000 Datasets in each of 7 Scenarios (N=1000)

The superior CI coverage of boosted CART did not come at the expense of relatively large standard errors. The different methods did not yield substantially different SE estimates although logistic regression tended to produce the largest standard errors compared with the other methods (Table 1). For example, logistic regression produced standard errors that ranged on average from 1.06 times (scenario C) to 1.29 times (scenario E) larger than the errors produced by boosted CART, even though both methods had similar performance in terms of coverage rates.

Weights

The average weight did not differ greatly by estimation method (Figure 4). For example, the mean weight assigned to a comparison group observation in Scenario E (mild non-additivity and non-linearity) by method was: logistic regression: 0.90, CART: 0.88, pruned CART: 0.88, bagged CART: 0.67, random forests: 0.92, boosted CART: 0.60. However, in all scenarios, logistic regression and random forests tended to produce a relatively large number of extreme high weights while bagged CART had the fewest number of extreme high weights. For example, in Scenario E, the proportion of comparison group weights greater than ten by method was: logistic regression: 3.5%, CART: 0.9%, pruned CART: 0.7%, bagged CART: 0.0%, random forests: 3.1%, boosted CART 0.7%. This may partially explain the relatively large standard errors produced by the logistic regression approach.

Figure 4.

Distribution of Propensity Score Weights for the Comparison Group for Ten Random Datasets of (N=1000)

Simulations of N=500, N=2000 sample sizes

The comparative results of the differently sized studies did not qualitatively differ from the N=1000 studies (Tables 2 and 3). For all methods, covariate balance increased as the sample size increased. This resulted in less biased effect estimates for all methods. However, because larger sample sizes produced smaller errors and thus attributed greater precision to estimates, the methods that had higher bias (logistic regression, CART, and pruned CART) had notably poor 95% CI coverage in the N=2000 studies: for example, with moderate non-additivity and non-linearity (Scenario G), the 95% CI produced by logistic regression included the true effect size only 2.9% of the time, in contrast with coverage of 99.1% for boosted CART (Table 3).

Table 2.

Performance Metrics of Propensity Score Estimation Methods in 1000 Simulated Datasets of N=500.

Metric	Method1	Scenario4
		A	B	C	D	E	F	G
ASAM2	LGR	0.059	0.057	0.065	0.077	0.078	0.081	0.103
	CART	0.143	0.138	0.152	0.155	0.151	0.142	0.149
	PRUNE	0.179	0.17	0.165	0.184	0.181	0.166	0.165
	BAG	0.129	0.126	0.125	0.143	0.141	0.126	0.121
	RFRST	0.099	0.095	0.093	0.108	0.107	0.101	0.095
	BOOST	0.089	0.085	0.084	0.096	0.094	0.088	0.086
Absolute bias	LGR	11.2%	11.2%	13.8%	15.3%	17.7%	18.1%	30.3%
	CART	19.0%	16.6%	21.8%	19.3%	19.0%	20.1%	21.6%
	PRUNE	27.6%	22.6%	24.5%	24.8%	22.6%	22.9%	23.1%
	BAG	12.6%	10.4%	13.5%	11.6%	10.3%	10.8%	11.4%
	RFRST	10.7%	9.2%	11.4%	10.5%	9.5%	10.5%	11.6%
	BOOST	11.0%	9.6%	9.2%	10.3%	9.3%	9.0%	8.6%
Standard error	LGR	0.094	0.094	0.087	0.105	0.105	0.103	0.102
	CART	0.095	0.096	0.105	0.097	0.098	0.096	0.104
	PRUNE	0.085	0.085	0.097	0.089	0.089	0.088	0.097
	BAG	0.08	0.079	0.085	0.081	0.079	0.081	0.082
	RFRST	0.086	0.083	0.085	0.088	0.084	0.087	0.085
	BOOST	0.084	0.082	0.081	0.086	0.083	0.085	0.083
95% CI3 coverage	LGR	97.0%	97.3%	96.2%	91.1%	87.5%	86.5%	64.3%
	CART	84.5%	88.3%	76.9%	82.4%	84.0%	81.6%	75.7%
	PRUNE	65.3%	75.3%	71.5%	71.2%	75.8%	76.6%	73.8%
	BAG	97.5%	98.2%	95.4%	98.7%	99.1%	99.0%	98.1%
	RFRST	98.5%	99.7%	97.9%	98.5%	98.7%	99.0%	97.0%
	BOOST	99.0%	99.2%	99.5%	99.1%	99.6%	99.9%	99.8%

¹LGR – logistic regression, CART – classification and regression tree, PRUNE – pruned CART, BAG – bagged CART, RFRST – random forests, BOOST – boosted CART;

²ASAM – average standardized absolute mean distance;

³CI – confidence interval

⁴A: additivity and linearity; B: mild non-linearity; C: moderate non-linearity; D: mild non-additivity; E: mild non-additivity and non-linearity; F: moderate non-additivity; G: moderate non-additivity and non-linearity.

Table 3.

Performance Metrics of Propensity Score Estimation Methods in 1000 Simulated Datasets of N=2000.

Metric	Method1	Scenario4
		A	B	C	D	E	F	G
ASAM2	LGR	0.029	0.031	0.052	0.047	0.05	0.057	0.09
	CART	0.177	0.165	0.142	0.186	0.178	0.165	0.153
	PRUNE	0.181	0.171	0.143	0.189	0.182	0.168	0.156
	BAG	0.155	0.146	0.127	0.164	0.158	0.137	0.121
	RFRST	0.062	0.061	0.059	0.068	0.067	0.058	0.057
	BOOST	0.052	0.049	0.054	0.054	0.053	0.048	0.053
Absolute bias	LGR	5.5%	6.8%	13.5%	10.9%	14.7%	16.1%	30.2%
	CART	27.6%	18.8%	16.5%	25.1%	18.9%	32.2%	21.1%
	PRUNE	29.2%	20.9%	16.7%	25.8%	19.9%	32.7%	21.7%
	BAG	19.9%	13.0%	11.3%	16.7%	11.6%	16.3%	9.1%
	RFRST	5.0%	4.5%	7.5%	5.2%	5.2%	5.5%	8.0%
	BOOST	5.6%	4.7%	4.8%	4.7%	4.1%	4.1%	4.7%
Standard error	LGR	0.047	0.047	0.043	0.054	0.053	0.054	0.051
	CART	0.039	0.039	0.045	0.04	0.04	0.041	0.044
	PRUNE	0.039	0.039	0.045	0.04	0.04	0.041	0.044
	BAG	0.038	0.038	0.042	0.038	0.038	0.039	0.04
	RFRST	0.045	0.043	0.048	0.046	0.044	0.046	0.047
	BOOST	0.042	0.041	0.042	0.043	0.042	0.043	0.042
95% CI3 coverage	LGR	98.1%	95.9%	77.6%	78.8%	63.4%	57.6%	2.9%
	CART	18.1%	45.0%	55.6%	27.3%	47.5%	20.4%	41.6%
	PRUNE	15.5%	39.0%	54.4%	26.0%	43.9%	20.0%	40.1%
	BAG	31.6%	69.8%	76.1%	51.9%	78.5%	52.9%	85.8%
	RFRST	99.2%	99.3%	90.8%	98.1%	98.3%	98.2%	89.5%
	BOOST	99.0%	99.9%	99.9%	99.8%	99.9%	99.9%	99.1%

¹LGR – logistic regression, CART – classification and regression tree, PRUNE – pruned CART, BAG – bagged CART, RFRST – random forests, BOOST – boosted CART;

²ASAM – average standardized absolute mean distance;

³CI – confidence interval

⁴A: additivity and linearity; B: mild non-linearity; C: moderate non-linearity; D: mild non-additivity; E: mild non-additivity and non-linearity; F: moderate non-additivity; G: moderate non-additivity and non-linearity.

DISCUSSION

The primary objective of propensity score adjustment is to achieve covariate balance between comparison groups so that valid estimates of the treatment effect can be obtained. Logistic regression propensity score models with only main effect terms generally provided adequate covariate balance. However, the bias reducing capabilities of logistic regression propensity score models substantially degraded when the models did not account for interactions and non-linearities. In contrast, regardless of sample size or the extent of non-additivity or nonlinearity, the ensemble methods of bagged CART, random forests, and boosted CART propensity score models provided excellent performance in terms of covariate balance and effect estimation. The consistently superior performance of boosted CART and random forests leads us to recommend these two machine learning techniques for future consideration in propensity score estimation.

In this study we used only the basic, off-the-shelf versions of each of the methods, since that is likely what most applied researchers would do. It is likely that any method may perform better when implemented by a highly skilled user. For example, logistic regressions with carefully chosen interactions may perform better than the simple main effects-only model used here. Similarly, while random forests sometimes produced large propensity score weights, the estimation algorithm could be calibrated to reduce the likelihood of extreme weights.

In our simulations, the outcome Y is fully determined by the observed covariates W_i and the treatment A, which is not what we normally expect to see in practice but is a common strategy for assessing bias in propensity score settings [34, 35]. However, this fact should have no effect on the performance of the propensity score estimation techniques. To check this supposition we performed a sensitivity analysis on a subset of the data where we added random error to Y such that Y = α_iW_i + γA + ε, ε~N(0,σ). We performed analyses for σ = 0.1 and σ = 0.2, equivalent to 25% and 50%, respectively, of the effect of exposure (γ = −0.4). As expected, this sensitivity analysis showed no changes in the relative performance of the methods considered (results not shown).

Our results suggest that approximately unbiased estimates of the population average treatment effect for the treated can be obtained from machine learning propensity score methods in a variety of scenarios differing by additivity and linearity. These results support the findings presented by Setoguchi et al. in a comparison of logistic regression, neural nets, CART, and pruned CART in propensity score model building [16]. Setoguchi et al. used the propensity score to select matched samples while we use the propensity score to weight the comparison subjects to appear similar to the treated subjects. For both uses of the propensity scores the machine learning methods performed well in a variety of scenarios, indicating the broad applicability of these results. Furthermore, our results indicate that even while machine learning methods are traditionally applied to larger datasets, machine learning methods can also be applied to smaller datasets as well (e.g., N=500).

One interesting observation is that logistic regression often yielded the lowest ASAM but also produced large biases in the estimated treatment effect; conversely, boosted CART often did not have the lowest ASAM but frequently produced better bias reduction. This may have important implications for diagnostic methods to assess propensity score methods: is good covariate balance not enough for ensuring low bias, or is it perhaps that the ASAM is not an adequate measure of balance? For example, in the studies of N=1000, the correlations of ASAM with absolute bias ranged from 0.38 to 0.66 across scenarios. In contrast, the average standardized mean distance calculated using all possible two-way interaction terms (10 choose 2 = 45), not just the covariates themselves, was correlated more strongly with absolute bias in all scenarios, with a range of correlations from 0.56 to 0.72. While further investigation of this issue is needed, these results suggest that covariate balance in interactions may be important to account for in propensity score models and balance checks, particularly when the true outcome models themselves have interaction terms. Although some researchers have recommended checking balance on interactions [36, 37], it is unfortunately rarely done in practice. This may also indicate why logistic regression, with no interaction terms, did not perform well in these simulations.

Boosted CART provided consistently excellent performance in propensity score model building. The efficiency of boosting as a general algorithm to improve estimates is well-known in the machine learning world [20]. What has been less known was whether those benefits would carry over to the world of propensity score estimation and use. As discussed by McCaffrey and colleagues [5, 15], the boosting algorithm we used has a number of features that improves propensity score estimation performance. Boosted CART estimates the propensity score using a piecewise linear combination of multiple CARTs. To reduce prediction error, each successive CART is estimated from a random subsample of the data. In addition, the application of a shrinkage coefficient to downweight each additional CART helps to prevent overfitting. Finally, the use of the piecewise constants has the effect of flattening the estimated propensity scores at the extreme values of the predictors. This minimizes the chance of obtaining predicted probabilities near 0 or 1, thus preventing the high variability in weights that can be problematic for propensity score weighting.

One criticism of machine learning is that the “black box” nature of the algorithms obscures the relationships between predictors and outcome. However, etiologic inference is not a necessary component of propensity score estimation [2]. Therefore, machine learning techniques may be well-suited to the task of creating propensity scores from high-dimensional data where improper parametric specification of relationships may lead to biased estimates. We also note that the available software can offer insight into the relationships among variables. For example, the boosting package twang can analyze the relative contributions of variables to improvements in the model log-likelihood [28] and Elith et al. describe and provide code for visualizing partial dependences and interactions in a boosted regression tree model [23].

In conclusion, our simulation results complement previous work by Setoguchi et al. to show that using machine learning techniques to estimate propensity scores can greatly reduce bias across a range of sample sizes, scenarios, and propensity score application methods. These techniques offer a number of advantages over logistic regression in propensity score estimation and may be implemented using freely available software packages.

Abbreviations

ASAM

average standardized absolute mean distance

CART

classification and regression trees

CI

confidence interval

SE

standard error