Abstract
In quantitative trait locus (QTL) mapping studies, it is mandatory that the available financial resources are spent in such a way that the power for detection of QTL is maximized. The objective of this study was to optimize for three different fixed budgets the power of QTL detection 1 − β* in recombinant inbred line (RIL) populations derived from a nested design by varying (1) the genetic complexity of the trait, (2) the costs for developing, genotyping, and phenotyping RILs, (3) the total number of RILs, and (4) the number of environments and replications per environment used for phenotyping. Our computer simulations were based on empirical data of 653 single nucleotide polymorphism markers of 26 diverse maize inbred lines which were selected on the basis of 100 simple sequence repeat markers out of a worldwide sample of 260 maize inbreds to capture the maximum genetic diversity. For the standard scenario of costs, the optimum number of test environments (E opt) ranged across the examined total budgets from 7 to 19 in the scenarios with 25 QTL. In comparison, the E opt values observed for the scenarios with 50 and 100 QTL were slightly higher. Our finding of differences in 1 − β* estimates between experiments with optimally and sub-optimally allocated resources illustrated the potential to improve the power for QTL detection without increasing the total resources necessary for a QTL mapping experiment. Furthermore, the results of our study indicated that also in studies using the latest genomics tools to dissect quantitative traits, it is required to evaluate the individuals of the mapping population in a high number of environments with a high number of replications per environment.
Introduction
In plant genetics, linkage analysis has been commonly employed to detect quantitative trait loci (QTL). Such approaches have a high power to detect QTL in genome-wide scans (Yu and Buckler 2006). Recently, several attempts have been made for detecting QTL using association mapping methods (e.g., Kraakman et al. 2004; Thornsberry et al. 2001; Vuylsteke et al. 2000) which have the merit of providing a high resolution for QTL detection (Remington et al. 2001). To combine the advantages of both mapping methods, Yu et al. (2008) proposed a nested association mapping (NAM) strategy which uses genome sequence information of recombinant inbred line (RIL) populations derived from several crosses of parental inbreds.
The NAM strategy is based on the idea that the genomes of RILs are mosaics of chromosomal segments of the parental genotypes. Consequently, within chromosomal segments the linkage disequilibrium (LD) information across the parental inbreds is maintained. Thus, if diverse parental inbreds are used, LD decays within the chromosomal segments over a short physical distance (Wilson et al. 2004). Therefore, the QTL mapping strategy using linkage and LD information is expected to have not only a high power to detect QTL in genome-wide approaches but also a high mapping resolution when both linkage and LD information are used.
Exploitation of the advantages of the NAM strategy requires developing, genotyping, and phenotyping of RIL populations from several crosses of diverse parental inbreds. However, this necessitates large financial resources (cf., Yu et al. 2008). Therefore, it is mandatory that the available resources are spent in an optimum way.
Stich et al. (2007) compared RIL populations derived from various mating designs with respect to their power for detecting three-way epistatic interactions in maize. The power 1 − β* is expected to be influenced not only by the mating design from which RIL populations were derived, but also by the number of RILs as well as the heritability on an entry mean basis. To our knowledge, in the context of QTL detection, no study has so far examined the optimum allocation of resources with respect to the number of RILs as well as the number of environments and replications per environment used for phenotypic evaluation.
In the present study, we used computer simulations to optimize for three different fixed budgets the power of QTL detection 1 − β* of RIL populations derived from a nested design by varying (1) the genetic complexity of the trait, (2) the costs for developing, genotyping, and phenotyping RILs, (3) the total number of RILs, and (4) the number of environments and replications per environment used for the phenotypic evaluation of RILs.
Materials and methods
Simulations
Our computer simulations were based on empirical data of 653 single nucleotide polymorphism (SNP) markers of 26 diverse maize inbred lines, namely B73, B97, CML52, CML69, CML103, CML228, CML247, CML277, CML322, CML333, Hp301, IL14H, Ki3, Ki11, Ky21, M37W, M162W, Mo18W, MS71, NC350, NC358, Oh7b, Oh43, P39, Tx303, and Tzi8. These inbreds were selected on the basis of 100 simple sequence repeat markers out of a worldwide sample of 260 maize inbreds to capture the maximum genetic diversity (Liu et al. 2003).
Mating design evaluated
In our simulations, a population of RILs was derived from each of the N C = 25 crosses between B73 and the 25 diverse inbreds, where the total number of RILs was N. This mating design corresponds to that applied in the project “Molecular and Functional Diversity of the Maize Genome” to establish the NAM population (Yu et al. 2008), for which seeds are now available from the Maize Genetics Cooperation Stock Center (E. Buckler, personal communication). The number of RILs per cross N P was calculated as follows: in scenarios with r = N mod N C = 0, N P = N/N C. In contrast, in scenarios with r ≠ 0, we chose for r populations N P = N/N C + 1, whereas for the remaining N C − r populations N P = N/N C.
An interesting property of the above described mating design is that with common-parent-specific (CPS) markers genotyped for the parental inbreds and the RILs, the inheritance of chromosome segments nested within two adjacent CPS markers can be inferred through linkage. Genotyping the founders with additional high-density markers enables the projection of genetic information, capturing LD information, from the parental inbreds to the RILs. This approach is expected to allow high-resolution QTL mapping with a relatively low number of markers in the RILs. However, this strategy is not straightforward to implement for NAM populations, which were derived from other mating designs than the above-described one. Thus, the projection of genetic information based on CPS markers was neglected in our study to facilitate conclusions which are not restricted to the mating design proposed by Yu et al. (2008).
Economic framework and quantitative–genetic parameters
Our simulations assumed a total budget B for (1) developing, (2) genotyping, and (3) phenotyping RILs: B = N(C dev + C geno + ERC fp) + EC env, where R is the number of replications at each of the E environments. C dev, C geno, and C fp are the costs for (1) developing one RIL, (2) genotyping one RIL, and (3) testing one field plot, respectively, and C env are the fixed costs for conducting a field test in one environment. We examined B = 1.25, 2.5, 5 million $. Furthermore, we restricted our simulations to E = 1, 4, 7,…, 19 and R = 1, 2, 3 because higher values are unrealistic in a plant breeding context (cf., Schön et al. 2004). For the standard scenario of costs, we assumed C dev = 30 $, C fp = 15 $, and C env = 25,000 $ (W. Schipprack, personal communication). In view of the fast progress of genotyping and sequencing techniques (Churchill et al. 2004, Shendure et al. 2004), we assumed in our study that all RILs are genotyped with such a high number of markers that each QTL has a marker which is in complete LD with the QTL. We considered it realistic to assume that in the near future, genotyping with such a high number of markers will be available (C geno) for 1,000 $ (Shendure et al. 2004). Eight additional cost scenarios were considered with C dev, C fp, C env being halfed and doubledas well as C geno being quartered and quadrupled (Table 2). Based on the values assumed for E, R, C dev, C geno, C fp, and C env, the total number of RILs N was calculated.
Table 2.
Number of environments (E
opt) and number of replications per environment (R
opt) maximizing the power of QTL detection 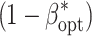 at an experiment-wise error rate of 0.01
at an experiment-wise error rate of 0.01
| Assumptions | Optimum allocation |
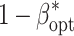 (SE) (SE) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| B | C dev | C geno | C fp | C env | E opt | R opt | N opt | h 2opt | |
| 1.25 | 30 | 1,000 | 15 | 25,000 | 16 | 2 | 563 | 0.941 | 0.992 (0.0014) |
| 15 | 1,000 | 15 | 25,000 | 16 | 2 | 569 | 0.941 | 0.992 (0.0014) | |
| 60 | 1,000 | 15 | 25,000 | 19 | 2 | 457 | 0.950 | 0.992 (0.0014) | |
| 30 | 200 | 15 | 25,000 | 16 | 1 | 1,809 | 0.914 | 0.998 (0.0006) | |
| 30 | 5,000 | 15 | 25,000 | 10 | 3 | 182 | 0.923 | 0.620 (0.0153) | |
| 30 | 1,000 | 7.5 | 25,000 | 19 | 2 | 589 | 0.950 | 0.994 (0.0011) | |
| 30 | 1,000 | 30 | 25,000 | 16 | 2 | 427 | 0.941 | 0.987 (0.0019) | |
| 30 | 1,000 | 15 | 12,500 | 13 | 2 | 766 | 0.929 | 0.993 (0.0012) | |
| 30 | 1,000 | 15 | 50,000 | 10 | 3 | 507 | 0.923 | 0.985 (0.0018) | |
| 2.5 | 30 | 1,000 | 15 | 25,000 | 10 | 2 | 1,692 | 0.909 | 0.998 (0.0007) |
| 15 | 1,000 | 15 | 25,000 | 13 | 2 | 1,548 | 0.929 | 0.998 (0.0007) | |
| 60 | 1,000 | 15 | 25,000 | 10 | 3 | 1,490 | 0.923 | 0.998 (0.0008) | |
| 30 | 200 | 15 | 25,000 | 19 | 2 | 2,531 | 0.950 | 1.000 (0.0003) | |
| 30 | 5,000 | 15 | 25,000 | 19 | 3 | 344 | 0.958 | 0.989 (0.0014) | |
| 30 | 1,000 | 7.5 | 25,000 | 19 | 3 | 1,389 | 0.958 | 0.999 (0.0005) | |
| 30 | 1,000 | 30 | 25,000 | 13 | 2 | 1,202 | 0.929 | 0.996 (0.0008) | |
| 30 | 1,000 | 15 | 12,500 | 13 | 2 | 1,646 | 0.929 | 0.998 (0.0006) | |
| 30 | 1,000 | 15 | 50,000 | 10 | 3 | 1,351 | 0.923 | 0.997 (0.0008) | |
| 5 | 30 | 1,000 | 15 | 25,000 | 10 | 2 | 3,571 | 0.909 | 0.999 (0.0005) |
| 15 | 1,000 | 15 | 25,000 | 7 | 3 | 3,628 | 0.894 | 0.999 (0.0005) | |
| 60 | 1,000 | 15 | 25,000 | 19 | 2 | 2,776 | 0.950 | 0.999 (0.0003) | |
| 30 | 200 | 15 | 25,000 | 10 | 1 | 12,500 | 0.870 | 1.000 (0.0003) | |
| 30 | 5,000 | 15 | 25,000 | 16 | 3 | 800 | 0.950 | 0.997 (0.0008) | |
| 30 | 1,000 | 7.5 | 25,000 | 16 | 2 | 3,622 | 0.941 | 1.000 (0.0002) | |
| 30 | 1,000 | 30 | 25,000 | 10 | 3 | 2,461 | 0.923 | 0.999 (0.0005) | |
| 30 | 1,000 | 15 | 12,500 | 13 | 2 | 3,407 | 0.929 | 1.000 (0.0003) | |
| 30 | 1,000 | 15 | 50,000 | 10 | 3 | 3,041 | 0.923 | 0.999 (0.0005) | |
N opt the optimum number of recombinant inbred lines, h 2opt the optimum heritability on an entry mean basis, B the total budget in million $, C dev, C geno, and C fp the costs for (1) establishing one RIL, (2) genotyping one RIL, and (3) one field plot, respectively, C env the fixed costs for each environment
The number of quantitative trait loci was 50 and the second ratio of variance components (VC2) was used. For a detailed definition of the examined parameters see “Materials and methods”
We assumed the proportions among variance components as σ2g:σ2ge:σ2e = 1:0.5:1 (VC2), where σ2g refers to the genotypic variance, σ2ge to the variance of genotype × environment interactions, and σ2e to the error variance. This ratio was chosen based on the analysis of variance of traits of presumably medium genetic complexity such as grain moisture (Melchinger et al. 1998). However, to cover with our simulations a wide range of quantitative traits, two additional scenarios were considered with interaction and error variance being halved (VC1) and doubled (VC3) in comparison with VC2. Based on E, R, and VC, heritability on an entry mean basis h 2 was calculated as
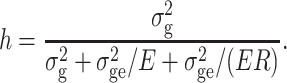 |
Definition of genotypic and phenotypic values
A total of 100 simulation runs was performed for each examined scenario. For each run, three subsets of SNPs (l = 25, 50, 100) were sampled at random without replacement from the linkage map and were defined as QTL. The SNP markers of our study are bi-allelic and, thus, the 25 diverse parental inbreds carry either the same allele as the reference parent B73 or the non-B73 allele. At each QTL, one allele was assigned the genotypic effect zero, whereas the genotypic effect of the other allele was drawn randomly without replacement from the geometric series l(1 − a)[1, a, a 2, a 3,..., a l−1], with a = 0.90 (25 QTL), a = 0.96 (50 QTL), or a = 0.99 (100 QTL) (Lande and Thompson 1990). Because not all of the 25 diverse inbreds have the non-B73 allele, not every QTL segregates in every population. Genotypic values of the inbreds were determined by summing up the effects of the individual alleles.
From the genotypic values of the progenies of each cross, the genotypic variance of RILs within the cross σ2g was calculated. For the progenies of each cross, the phenotypic values of the RILs were generated by adding a realisation from a normally distributed variable 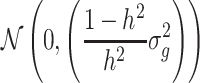 to the genotypic values. The phenotypic values calculated in this way were used for the QTL detection procedure. All simulations were performed with software PLABSOFT (Maurer et al. 2008).
to the genotypic values. The phenotypic values calculated in this way were used for the QTL detection procedure. All simulations were performed with software PLABSOFT (Maurer et al. 2008).
Statistical analyses
The comparison of statistical analyses concerning the power 1 − β* requires an equal experiment-wise error rate α*. To meet this requirement, we applied the following two step procedure for QTL detection. In a first step, stepwise multiple linear regression implemented in PLABQTL (Utz and Melchinger 1996) was used to select a set of cofactors based on the Schwarz Bayesian Criterion (SBC) (Schwarz 1978). We described earlier that we assumed that all RILs are genotyped with such a high number of markers that each QTL has a marker which is in complete LD with the QTL. Therefore, all SNPs, inclusive those treated as QTL, were included in the QTL detection procedures.
In the second step, we calculated a P value for the association of each marker q with the phenotypic value for an F test with a full model against a reduced model:
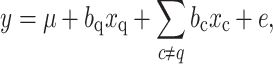 |
where y is the vector of the phenotypic values of all RILs, μ the intercept, b q (b c) the regression coefficient of the qth marker locus (or cth cofactor), x q (x c) an incidence vector of the genotypes of the RILs at the qth marker (cth cofactor), and e the vector of residual errors.
In our study, each combination of B, C
dev, C
geno, C
fp, C
env, l, and VC was designated as scenario. For each combination of E and R within a scenario, the nominal α level was chosen in such a way that the experiment-wise error rate α*, which was determined using the knowledge of where the simulated QTL were, was 0.01. Based on this α level, the power for QTL detection (1 − β*) was calculated as the proportion of QTL correctly identified out of the total number of QTL l, where correctly means that the QTL itself was identified as significant in the final model. Subsequently, we identified for each scenario the number of environments E
opt as well as the number of replicates R
opt for which the maximum power for QTL detection 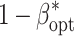 was observed. The optimum heritability h
2opt as well as the optimum number of RILs N
opt arise from E
opt, R
opt, and B.
was observed. The optimum heritability h
2opt as well as the optimum number of RILs N
opt arise from E
opt, R
opt, and B.
Results
The average map distance between the 653 SNP markers was 2.6 cM. The pairwise genetic dissimilarity among the 26 diverse inbreds ranged from 0.58 to 0.75. The average frequency of B73 alleles in the JLAM population was 0.81.
For the standard scenario of costs, E opt ranged across the various examined levels of B and VC from 7 to 19 in the scenarios with l = 25 QTL and R opt varied between two and three (Fig. 1; Table 1). The E opt and R opt values observed for the scenarios with l = 50 and 100 QTL were slightly higher than those observed for the corresponding scenarios with l = 25 QTL. Across the examined levels of l, the increase in the non-genetic variance from VC1 to VC3 resulted in an increase of E opt and R opt. Increasing the budget B from 1.25 to 5 million $ had no influence on E opt and R opt across the examined levels of l and VC.
Fig. 1.
Power to detect quantitative trait loci (QTL) (1 − β*) at an experiment-wise error rate of 0.01 assuming B = 2.5 millon US dollar. The costs for (1) establishing one RIL (C dev), (2) genotyping one RIL (C geno), and (3) testing one field plot (C fp), and the fixed costs for each environment (C env) were 30, 1,000, 15, and 25,000 $, respectively. R is the number of replicates at each of the E environments and VC is the ratio of variance components assumed. For a detailed definition of the examined parameters see “Materials and methods”
Table 1.
Number of environments (E
opt) and number of replications per environment (R
opt) maximizing the power of QTL detection 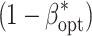 at an experiment-wise error rate of 0.01
at an experiment-wise error rate of 0.01
| Assumptions | Optimum allocation |
 (SE) (SE) |
|||||
|---|---|---|---|---|---|---|---|
| B | l | VC | E opt | R opt | N opt | h 2opt | |
| 1.25 | 25 | 1 | 7 | 3 | 799 | 0.944 | 0.995 (0.0016) |
| 2 | 13 | 3 | 573 | 0.940 | 0.993 (0.0017) | ||
| 3 | 16 | 3 | 486 | 0.906 | 0.982 (0.0026) | ||
| 50 | 1 | 10 | 2 | 752 | 0.952 | 0.996 (0.0009) | |
| 2 | 16 | 2 | 563 | 0.941 | 0.992 (0.0014) | ||
| 3 | 19 | 3 | 411 | 0.919 | 0.970 (0.0026) | ||
| 100 | 1 | 10 | 2 | 752 | 0.952 | 0.996 (0.0006) | |
| 2 | 13 | 3 | 573 | 0.940 | 0.990 (0.0011) | ||
| 3 | 19 | 2 | 484 | 0.905 | 0.938 (0.0035) | ||
| 2.5 | 25 | 1 | 16 | 1 | 1,654 | 0.955 | 0.999 (0.0007) |
| 2 | 16 | 1 | 1,654 | 0.914 | 0.998 (0.0010) | ||
| 3 | 16 | 2 | 1,391 | 0.889 | 0.996 (0.0013) | ||
| 50 | 1 | 10 | 2 | 1,692 | 0.952 | 0.999 (0.0005) | |
| 2 | 10 | 2 | 1,692 | 0.909 | 0.998 (0.0007) | ||
| 3 | 19 | 3 | 1,074 | 0.919 | 0.995 (0.0010) | ||
| 100 | 1 | 7 | 2 | 1,875 | 0.933 | 0.998 (0.0005) | |
| 2 | 16 | 1 | 1,654 | 0.914 | 0.997 (0.0005) | ||
| 3 | 19 | 3 | 1,074 | 0.919 | 0.993 (0.0004) | ||
| 5 | 25 | 1 | 7 | 2 | 3,891 | 0.933 | 1.000 (0.0004) |
| 2 | 16 | 3 | 2,629 | 0.950 | 1.000 (0.0004) | ||
| 3 | 19 | 2 | 2,828 | 0.905 | 0.999 (0.0006) | ||
| 50 | 1 | 7 | 3 | 3,587 | 0.944 | 1.000 (0.0003) | |
| 2 | 10 | 2 | 3,571 | 0.909 | 0.999 (0.0005) | ||
| 3 | 19 | 3 | 2,401 | 0.919 | 0.999 (0.0005) | ||
| 100 | 1 | 10 | 3 | 3,209 | 0.960 | 1.000 (0.0001) | |
| 2 | 10 | 2 | 3,571 | 0.909 | 0.999 (0.0004) | ||
| 3 | 16 | 2 | 3,046 | 0.889 | 0.997 (0.0005) | ||
N opt the optimum number of recombinant inbred lines, h 2opt the optimum heritability on an entry mean basis, B the total budget in million $, l the number of quantitative trait loci, VC the ratio of variance components
The costs for (1) establishing one RIL (C dev), (2) genotyping one RIL (C geno), and (3) testing one field plot (C fp), and the fixed costs for each environment (C env) were 30, 1,000, 15, and 25,000 $, respectively. For a detailed definition of the examined parameters see “Materials and methods”
For the examined levels of B and VC, an increase of l from 25 to 100 reduced 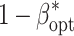 up to 5% of the initial value (Table 1). The increase in the non-genetic variance from VC1 to VC3 decreased
up to 5% of the initial value (Table 1). The increase in the non-genetic variance from VC1 to VC3 decreased 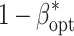 less pronounced than that observed for the increase of l. Increasing the budget B from 1.25 to 5 million $ resulted in an increase of
less pronounced than that observed for the increase of l. Increasing the budget B from 1.25 to 5 million $ resulted in an increase of 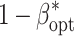 for all examined levels of l.
for all examined levels of l.
For budgets B of 1.25 and 5 million $, the increase of C dev resulted in an increase of E opt (Table 2). The increase of C geno resulted for all examined budgets B in an increase of E opt and/or R opt. For all examined budgets B, the increase of C fp resulted in a decrease of E opt, where the increase of C env resulted in a decrease of E opt and an increase of R opt.
Across all examined levels of B, the increase of C
dev from 15 to 60 $ did not alter 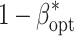 (Table 2). In contrast, a medium decrease of
(Table 2). In contrast, a medium decrease of 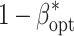 was observed for an increase of C
geno from 200 to 5,000 $, whereas the decreases of
was observed for an increase of C
geno from 200 to 5,000 $, whereas the decreases of 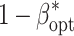 were of small size upon alteration of C
fp and C
env from the low to the high level.
were of small size upon alteration of C
fp and C
env from the low to the high level.
Discussion
Assumptions underlying the simulations
We assumed that all RILs are genotyped with such a high number of markers that each QTL has a marker which is in complete LD with the QTL. Empirical studies based on a NAM population of maize, however,might require a higher number of marker than was used in our study. In this case, it might be necessary to choose a significance threshold that is lower than that of the current study, which in turn reduces 1 − β*. However, this reduction of power estimates is expected to be of similar size for all scenario and, thus, no influence on E opt and R opt is expected.
On the genome-wide level, the most common polymorphisms such as SNPs and insertion/deletions are biallelic (e.g., Cho et al. 1999). Therefore, it is also expected that functional polymorphisms are predominantly biallelic. However, several, tightly linked, biallelic polymorphisms can build up multiple alleles present at QTL (e.g., Harjes et al. 2008). Because such information was not available for the maize inbreds used in our study, we neglected this possibility and assumed the presence of only two alleles at each QTLacross the entire set of maize inbreds. This assumption is expected to increase 1 − β* compared to a scenario with multiple QTL alleles. However, preliminary simulations (data not shown) suggested no or only marginal effects on E opt and R opt.
Power to detect QTL
For scenarios with similar l and h, the power 1 − β* observed in our study was considerably higher than that of Yu et al. (2008). This difference is most likely due to the fact that in our study the phenotypic values were simulated based on population-based heritability estimates. In contrast, in the study of Yu et al. (2008) phenotypic values used for the QTL detection procedure were simulated based on one heritability estimate across all 25 populations. In the latter case, the large difference between the means of the different populations will lead to a low population-based heritability which furthermore reduces 1 − β*. The above-described difference in an assumption leads to the fact that the power estimates of our study and that of Yu et al. (2008) cannot directly be compared although the scenarios seem to be similar with respect to l and h. Furthermore, the different criteria and/or thresholds applied for QTL detection might further contribute to this difference in power estimates.
Mating designs for establishing RIL populations
The results of Stich et al. (2007) revealed considerable differences between RIL populations derived from diallel and different partial diallel designs with respect to the power for detection of three-way epistatic interactions. Due to the high computational burden, however, the simulations of the current study had to be restricted to one mating design. We examined RIL populations derived from a nested design, because this design was used in maize to develop the NAM population (McMullen et al. 2009). Nevertheless, preliminary simulations indicated that the findings of our study are not restricted to RIL populations derived from specific mating designs.
Optimum allocation of resources for NAM
In studies using the latest genomics tools for dissection of quantitative traits, phenotypic information is often generated with low intensity (cf., Aranzana et al. 2005) resulting in low heritabilities on an entry mean basis. However, 1 − β* can be considerably increased by increasing the heritability (cf., Stich et al. 2007). In studies with a fixed budget, however, this implies a reduction in the number of RILs which in turn reduces 1 − β*. Therefore, in studies with a fixed budget, it is an important issue to determine the number of RILs and the corresponding intensity of their phenotypic evaluation for maximizing 1 − β*.
In our simulations, considerable differences were observed between the 1 − β* estimates of experiments with optimally and sub-optimally allocated resources (Fig. 1). This finding is in accordance with results of Knapp and Bridges (1990) who examined based on theoretical considerations the optimum allocation of resources in a linkage mapping context. These results illustrated the potential of improving the QTL detection power without increasing the total resources required for a QTL mapping experiment.
Knapp and Bridges (1990) suggested that in scenarios with residual genetic variance, i.e. not all QTL are detected, 1 − β* is maximized by maximizing the number of genotypes in the segregating population and using one replicate for phenotypic evaluation. This finding, however, is based on the assumption that one replicate is as expensive as one additional genotype. Because this is not true for most experimental situations, we discuss in the following all factors which have the potential to influence the optimum allocation of resources: (1) genetic architecture of the trait, (2) total budget, and (3) costs for establishing, phenotyping, and genotyping RILs.
Genetic architecture of the trait
Our results suggest that in the scenarios with 25 QTL the optimum number of environments E opt as well as the optimum number of replications R opt were slightly lower than those observed for the scenarios with 50 and 100 QTL (Table 1). This finding might be explained by the fact that in the latter scenarios the proportion of the genotypic variance explained by single QTL is considerably lower than in the former scenario. Detecting QTL which explain a low proportion of the genotypic variance, however, requires a higher heritability and consequently more intensive phenotypic evaluation than detecting QTL which explain a high proportion of the genotypic variance.
In addition to the number of QTL l, the genetic architecture of a trait is characterized by the ratio of variance components. Our simulations suggest that across the examined levels of l, E opt and R opt increase with increasing non-genetic variance. This finding might be due to the higher values of E and R, which are required in a scenario with high non-genetic variance in order to obtain a heritability similar to that of a scenario with low non-genetic variance.
In conclusion, our findings suggest that the optimum allocation of resources differs among different traits, which is in accordance with findings of Schön et al. (2004). However, given the high effort to establish NAM populations, the goal is to examine traits of different genetic complexity in the same experiment. Thus, the optimization of the experimental design cannot be performed separately for each trait but must take into account several traits simultaneously.
We detected a high absolute value of the slope of the power curve for values of E < E opt, whereas this value was low for values of E > E opt (Fig. 1). This observation suggested that it is more promising to use a number of environments E which is higher than the optimum than using an E value which is lower than E opt. Furthermore, we observed for traits of low genetic complexity smaller values for E opt and R opt than for traits with high genetic complexity. These findings suggested that it is most promising to optimize the design of NAM populations with respect to the trait with the highest genetic complexity.
Total budget
Our results indicated that in contrast to increasing the genetic complexity of the trait, E opt and/or R opt are hardly affected by changes of the total budget B. This finding might be explained by the fact that even for the low budget B of 1.25 million $ the heritability is not the parameter limiting the power for detection of QTL 1 − β*.
Costs for establishing, genotyping, and phenotyping RILs
Owing to the high computational burden, the influence of altering the costs for establishing, genotyping, and phenotyping RILs was examined only for a trait of medium genetic complexity
The results of our simulations suggested that the increase of C dev resulted in an increase of E opt. Similarly, the increase of C geno resulted for all examined budgets B in an increase of E opt and/or R opt. These observations might be explained by the fact that with the increase of these two costs the price for each RIL increases and, therefore, the phenotyping with a higher intensity becomes advantageous. The opposite explanation is true for the increase of C fp which resulted in a decrease of E opt. The increase of C env which resulted in a decrease of E opt and an increase of R opt might be due to the fact that in this situation the substitution of environments by replications becomes advantageous. Consequently, the results of our simulations suggest that variation of the costs for establishing, genotyping, and phenotyping RILs in a framework, which is realistic in a plant breeding context, has considerable effects on E opt and R opt and, thus, should be considered when planning a QTL mapping experiment.
Comparison with the optimum allocation of resources observed for plant breeding programs
In contrast to the optimum allocation of resources in the context of QTL detection, several studies examined the optimum allocation of resources in plant breeding programs of various crops (e.g., Longin et al. 2006; Tomerius et al. 2008). In such studies, the optimum number of replications R opt was typically one and the optimum number of environments E opt was mostly smaller than 10. The observation that in our study the values for R opt and E opt were substantially higher (Tables 1, 2) might be explained by the fact that for high-resolution QTL mapping, a higher number of marker has to be genotyped. Despite the fact that we assumed genotyping costs C geno which might be realistic in the near future, in our study, between one-third and one-half of the total budget is used for genotyping which in turn makes it advantageous to increase E opt and R opt. This finding indicated that also in studies using the latest genomic tools to dissect quantitative traits, it is required to evaluate the individuals of the mapping population in a high number of environments with a high number of replications per environment.
Conclusions
Our finding of differences in 1 − β* estimates between experiments with optimally and sub-optimally allocated resources illustrated the potential to improve the power for QTL detection without increasing the total resources necessary for a QTL mapping experiment. However, the results of our study suggest that there is no single best allocation for every NAM experiment, but E opt and R opt are strongly influenced by the underlying values of VC, C dev, C geno, C fp, and C env. In contrast, B and l have only marginal effects on the optimum allocation of resources.
Acknowledgments
Funding was provided by the Max Planck Society and the Genome Analysis of the Plant Biological System (GABI) initiative (http://www.gabi.de). We thank Edward S. Buckler for providing the genotypic information of the parental inbreds. Genotyping the parental inbreds used in this study was supported by United States National Science Foundation (DBI-9872631 and DBI-0321467) and United States Department of Agriculture-Agricultural Research Services. The authors appreciate the editorial work of Prof. Dr. B. S. Dhillon whose suggestions considerably improved the style of the manuscript. The authors thank the Plant Computational Biology group of the Max Planck Institute for Plant Breeding Research for use of their computer cluster. The authors thank the associate editor and two anonymous reviewers for their valuable suggestions.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Aranzana MA, Kim S, Zhao K, Bakker E, Horton M, Jacob K, Lister C, Molitor J, Shindo C, Tang C, Toomajia C, Traw B, Zheng H, Bergelson J, Dean C, Marjoram P, Nordborg M. Genome-wide association mapping in Arabidopsis identifies previously known flowering time and pathogen resistance genes. PLoS Genet. 2005;1:e60. doi: 10.1371/journal.pgen.0010060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho RJ, Mindrinos M, Richards DR, Sapolsky RJ, Anderson M, et al. Genome-wide mapping with biallelic markers in Arabidopsis thaliana. Nat Genet. 1999;23:203–207. doi: 10.1038/13833. [DOI] [PubMed] [Google Scholar]
- Churchill GA, Airey DC, Allayee H, Nagel JM, Attie AD, et al. The collaborative cross, a community resource for the genetic analysis of complex traits. Nat Genet. 2004;36:1133–1137. doi: 10.1038/ng1104-1133. [DOI] [PubMed] [Google Scholar]
- Harjes CE, Rocheford TR, Bai L, Brutnell TP, Kandianis CB, et al. Natural Genetic Variation in Lycopene Epsilon Cyclase tapped for maize biofortification. Science. 2008;319:330–333. doi: 10.1126/science.1150255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp SJ, Bridges WC. Using molecular markers to estimate quantitative trait locus parameters: power and genetic variances for unreplicated and replicated progeny. Genetics. 1990;126:769–777. doi: 10.1093/genetics/126.3.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraakman ATW, Niks RE, Van den Berg PMMM, Stam P, Eeuwijk FA. Linkage disequilibrium mapping of yield and yield stability in modern spring barley cultivar. Genetics. 2004;168:435–446. doi: 10.1534/genetics.104.026831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande R, Thompson R. Efficiency of marker-assisted selection in the improvement of quantitative traits. Genetics. 1990;124:743–756. doi: 10.1093/genetics/124.3.743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu K, Goodman M, Muse S, Smith JS, Buckler E, Doebley J. Genetic structure and diversity among maize inbred lines as inferred from DNA microsatellites. Genetics. 2003;165:2117–2128. doi: 10.1093/genetics/165.4.2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longin CFH, Utz HF, Reif JC, Schipprack W, Melchinger AE. Hybrid breeding with doubled haploids: I. One-stage versus two-stage selection for testcross performance. Theor Appl Genet. 2006;112:903–912. doi: 10.1007/s00122-005-0192-z. [DOI] [PubMed] [Google Scholar]
- Maurer HP, Melchinger AE, Frisch M. Population genetical simulation and data analysis with Plabsoft. Euphytica. 2008;161:133–139. doi: 10.1007/s10681-007-9493-4. [DOI] [Google Scholar]
- McMullen MD, Kresovich S, Sanchez Villeda H, Bradbuy P, Li H, Sun Qi, Flint-Garcia S, Thornsberry J, Acharya C, Bottoms C, Brown P, Browne C, Eller M, Guill K, Harjes C, Kroon D, Lepak N, Mitchell SE, Peterson B, Pressoir G, Romero S, Oropeza Rosas M, Solvo S, Yates H, Hanson M, Jones Elizabeth, Smith S, Glaubitz JC, Goodman M, Ware D, Holland JB, Buckler ES. Genetic properties of the maize nested association mapping population. Science. 2009;325:737–740. doi: 10.1126/science.1174320. [DOI] [PubMed] [Google Scholar]
- Melchinger AE, Utz HF, Schön CC. Quantitative trait locus (QTL) mapping using different testers and independent population samples in maize reveals low power of QTL detection and large bias in estimates of QTL effects. Genetics. 1998;149:383–403. doi: 10.1093/genetics/149.1.383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remington DL, Thornsberry JM, Matsuoka Y, Wilson LM, Whitt SR, Doebley J, Kresovich S, Goodman MM, Buckler ES. Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc Natl Acad Sci USA. 2001;98:11479–11484. doi: 10.1073/pnas.201394398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schön CC, Utz HF, Groh S, Truberg B, Openshaw S, Melchinger AE. Quantitative trait locus mapping based on resampling in a vast maize testcross experiment and its relevance to quantitative genetics for complex traits. Genetics. 2004;167:485–498. doi: 10.1534/genetics.167.1.485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. doi: 10.1214/aos/1176344136. [DOI] [Google Scholar]
- Shendure J, Mitra RD, Varma C, Church GM. Advanced sequencing technologies: methods and goals. Nat Rev Genet. 2004;5:335–344. doi: 10.1038/nrg1325. [DOI] [PubMed] [Google Scholar]
- Stich B, Yu J, Melchinger AE, Piepho H-P, Utz HF, Maurer HP, Buckler ES. Power to detect higher-order epistatic interactions in a metabolic pathway using a new mapping strategy. Genetics. 2007;176:563–570. doi: 10.1534/genetics.106.067033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornsberry JM, Goodman MM, Doebley J, Kresovich S, Nielsen D, Buckler ES. Dwarf8 polymorphisms associate with variation in flowering time. Nat Genet. 2001;28:286–289. doi: 10.1038/90135. [DOI] [PubMed] [Google Scholar]
- Tomerius A-M, Miedaner T, Geiger HH. A model calculation approach towards the optimization of a standard scheme of seed-parent line development in hybrid rye breeding. Plant Breed. 2008;127:433–440. doi: 10.1111/j.1439-0523.2008.01493.x. [DOI] [Google Scholar]
- Utz HF, Melchinger AE. PLABQTL: a program for composite interval mapping of QTL. J Quant Trait Loci. 1996;2:1–5. [Google Scholar]
- Vuylsteke M, Kuiper M, Stam P. Chromosomal regions involved in hybrid performance and heterosis: their AFLP®-based identification and practical use in prediction models. Heredity. 2000;85:208–218. doi: 10.1046/j.1365-2540.2000.00747.x. [DOI] [PubMed] [Google Scholar]
- Wilson LM, Whitt SR, Ibáñez AM, Rocheford TR, Goodman MM, Buckler ES. Dissection of maize kernel composition and starch production by candidate gene association. Plant Cell. 2004;16:2719–2733. doi: 10.1105/tpc.104.025700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Buckler E. Genetic association mapping and genome organization of maize. Curr Opin Biotech. 2006;17:155–160. doi: 10.1016/j.copbio.2006.02.003. [DOI] [PubMed] [Google Scholar]
- Yu J, Holland JB, McMullen MD, Buckler ES. Genetic design and statistical power of nested association mapping in maize. Genetics. 2008;178:539–551. doi: 10.1534/genetics.107.074245. [DOI] [PMC free article] [PubMed] [Google Scholar]



