Preparation, characterization, and modeling of α-zirconium phosphonates with ether-functional surfaces

Abstract

Layered α-zirconium(IV) phosphonates were prepared from novel ether-terminal alkyl phosphonic acids, providing nanoplatelets with brush-like polar surfaces. The precursor materials were characterized by NMR, mass spectrometry, and elemental analysis. The derived nanoparticles were examined by XRD, TEM, TGA, and elemental analysis. The experimental compositions were slightly rich in organophosphorus content. In general, the layered materials had good crystallinity, with layer reflections appearing up to (005) and d-spacings consistent with the anticipated α-phase structure. Computer simulations suggest that tailored surface chemistries, including ether functionalities, will offer favorable thermodynamic interactions with polyester polymer matrices.

Introduction

The α-zirconium(IV) phosphonates (ZrP) form a subset of layered hybrid materials¹ that have previously been investigated for applications in catalysis,^2,3 proton conductivity,⁴ and nanocomposites.^5–11 The ZrP core is a versatile substrate for functionalization with a variety of organic substituents. Zirconium itself has useful properties such as high diagnostic X-ray opacity for biomedical applications. However, little advancement has been demonstrated in the specialized engineering of ZrP surfaces for inclusion in structural nanocomposites. Therefore, an approach was developed for producing ZrP nanoplatelets with brush-like functional surfaces having ether terminations, where the ZrP itself was prepared using the hexafluorozirconate-mediated route given by Alberti, et al.⁵ This reaction is known to give the α-phase exclusively.

Nanoplatelet dispersion involves a thermodynamic balance between the self-interaction energy of the layered nanoplatelet system and the guest-host interaction energy of the same material when intercalated or exfoliated by a solvent or polymeric species. In general, favorable enthalpic interactions between the nanoplatelet host and the intercalating guest species are needed to overcome the entropic barrier associated with the confinement of the guest to what is essentially a 2-dimensional surface.^13–17 The net enthalpic interaction among polymer chains and surfaces is most often expressed in terms of the Flory-Huggins parameter, χ, which has a negative value for attractive interactions.

Giannelis et al.⁶ classified the enthalpies of mixing for suface-confined polymers on surfactant-treated nanoplatelets as being either polar or apolar and suggested that apolar interactions are generally repulsive. The polar attractions should be both numerous and large enough in magnitude to overcome the repulsive apolar interactions as well as any entropic barriers due to confinement of the polymer. The changes in free energy density predicted by both mean-field⁷ and self-consistent field^{15, 18, 19} theoretical models, for a given surfactant graft density, suggest that if the polymer-surface interaction is made strongly attractive (χ negative) through polar interactions, then the relatively weak apolar repulsions (χ small, positive) are overcome, and the net free energy becomes increasingly negative as the gallery spacing between the nanoplatelets increases. Thus, polar attractions for a polymer chain confined by two nanoplatelet surfaces are always favorable where intercalation and exfoliation are desired. Furthermore, eliminating undesirable apolar repulsions between the polymer and the surface ligands is a useful tactic for optimizing miscibility in nanocomposite systems.

Among the possible choices of nanoplatelets considered for this study, synthetic α-zirconium phosphonates were selected for their unique applicability to radiopaque biomedical devices. A new method is presented for producing ether-terminal alkyl phosphonic acids with moderate tail lengths. These amphiphiles possess functional dipoles at their terminal ends, providing a potential for favorable polymer interactions, and maintain a central rod-like alkyl segment, which facilitates their ordering into liquid crystalline structures.⁸

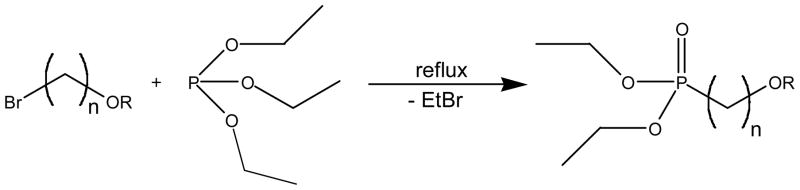
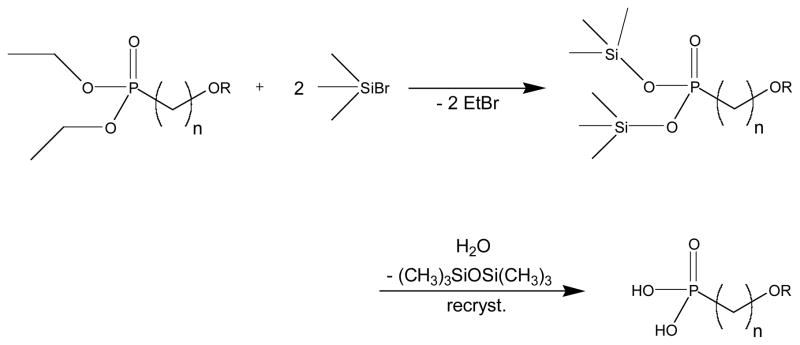
Brominated alkyl chains with ether-functional terminations were prepared for this study by protecting the hydroxy function of the parent alcohols represented in Scheme 1. A similar O-alkylation method was originally described by Diem, et al.⁹ Phosphodiesters were derived using the Michaelis-Arbuzov reaction, shown in Scheme 2. A mild silylation/desilylation route, after McKenna,¹⁰ was preferred for preparing phosphonic acids from the resulting phosphodiesters, as shown in Scheme 3.

Scheme 1.

O-alkylation of brominated primary alcohols (n = 8, 9, 11) by trialkyloxonium tetrafluoroborate salts (R = Me, Et). Suitable acid scavengers include Proton Sponge® or tribenzylamine.

Scheme 2.

General Michaelis-Arbuzov reaction for generating a dialkyl phosphonate.

Scheme 3.

Dealkylation of diethylphosphonate by mild silylation/desilylation reaction after McKenna.¹⁰

Computer simulations were used to predict which of the possible synthetic compounds had the most promising interactivity with host polymer systems for the purpose of preparing nanocomposites. Poojaray and coworkers¹¹ previously solved the structure of zirconium bis-phenyl phosphonate using Reitveld refinement of a synchrotron X-ray powder diffraction pattern. Their crystallographic parameters were adopted for the present study. The equilibrium geometry of the inorganic platelet core, Zr(O₃P)₂, was fixed during the dynamic simulations described below, thereby allowing the interactions among the organic functionalities to be explored independently. The reported equilibrium positions for Zr, P, and O fall within the range of variability reported by Alberti and coworkers,¹² who employed computer-simulated force field adjustments to model structurally related zirconium phosphates.

Experimental

Materials

Octylphosphonic acid (98%, Lancaster), ZrOCl₂·8H₂O (98%, Aldrich), and HF (48% w/w aqueous, Fisher) were purchased and used without further purification. The preparation and characterization of 8-ethoxyoctyl-, 8-methoxyoctyl-, 9-ethoxynonyl-, 9-methoxynonyl-, 11-ethoxyundecyl-, and 11-methoxyundecyl phosphonic acids, according to Schemes 1–3, are detailed in the Supporting Information accompanying this article.

FTIR Spectrophotometry

Attenuated total reflectance (ATR) spectra were acquired with a Nicolet Magna-IR 550 spectrometer (Thermo Scientific Corp., Waltham, MA) equipped with a MIRacle ATR accessory (Pike Technologies, Madison, WI) having a single-reflection diamond-clad ZnSe crystal. The instrument optics were purged with dehydrated air, and the sample was measured in direct reflectance using a screw-driven anvil to force compliance of the sample to the diamond surface. A total of 64 co-added scans were collected for each sample with a resolution of 4 cm⁻¹.

Elemental Analysis

C, H, and O contents for the synthesized phosphonic acids and related ZrP compounds were determined from duplicate analysis by Atlantic Microlab, Inc., Norcross, GA, 30091. P and Zr contents for the ZrP compounds were determined by Galbraith Laboratories, Inc., Knoxville, TN 37950. ZrP samples were dried under vacuum at 100°C prior to testing. Individual values are reported for each sample in the Supporting Information provided with this article.

TGA/DTA

Thermogravimetry was performed using a Q-series SDT-600 DSC/TGA (TA Instruments, New Castle, DE). The samples, weighing ca. 10 mg each, were preconditioned at 100°C under a 100 ml/min flow of dry air. Duplicate burnout experiments were conducted in air with a temperature ramp from 100–1100°C and a ramp rate of 10°C/min. The ash was held at 1100 C for 30 min to ensure complete oxidation.

TEM

Electron micrographs were obtained on a JEOL 1230 (JEOL Ltd., Tokyo, Japan) equipped with a LaB₆ electron gun operated at 80 kV. Images were acquired using a CCD camera system (AMT Corp., Danvers, MA). A catalase crystal standard (Ted Pella, Redding, CA) was imaged to provide an internal reference d-spacing of 8.75 nm. FFT filtering of the images was performed using the open-source ImageJ image analysis package, sponsored by the National Institutes of Health.

Preparation of α-ZrP Nanoplatelets

In a typical reaction, 1.3 g (4 mmol) of ZrOCl₂·8H₂O (98%, Aldrich) was added to 15 mL of deionized water in a 60-ml PTFE digestion vessel (Savillex) equipped with a PTFE condenser. Concentrated aqueous HF was then added such that [F]/[Zr] = 8. After a few minutes, the chosen phosphonic acid, or mixture of phosphonic acids, was added to the previously acidified solution such that [P]/[Zr] = 4. The two-phase reaction mixture was then heated over a 60°C oil bath while stirring with a magnetic stirrer for 1 week in air. The suspension was filtered through a polyethersulfone membrane (0.2 μm pore size), washed with 150 mL of ethanol, and vacuum dried to yield a white, waxy powder (88%, based on ZrOCl₂).

XRD

X-ray diffraction patterns were obtained using a D8 Advance analytical diffractometer (Bruker AXS GmbH, Karlsruhe, Germany) equipped with a Cu-K_α radiation source, a 1.0 mm fixed-divergence slit, a Johansson focusing monochromator, and a standard scintillation detector with a 0.1 mm slit. The source was operated with an acceleration voltage of 36 kV and a filament current of 20 mA. The scan rate was set to 5 s/step with a step size of θ = 0.025°.

Modeling

Computational models were generated with the Cerius^2® software package (version 4.10, rev 05.0120, Accelrys Software, Inc, San Diego, CA). Dynamic simulations were performed on a Silicon Graphics^® Tezro^® workstation (SGI, Sunnyvale, CA) using the Universal 1.02 force field^13–15 and an environmental temperature of 300K.

The zirconium phosphonate moiety was modeled as a single monoclinic unit cell, with a = 9.099Å, b = 5.415 Å, c = 30.235 Å, and β = 101.333°, having the fractional atomic positions provided in Table 1. The c-axis was expanded, and the organic functionalities were inserted subsequent to fixing the positions of Zr, P, and O.

Table 1.

Fractional atomic positions for the zirconium phosphonate moiety based on the lattice parameters given by Poojaray et al.¹¹

	x	y	z
Zr	.25	0.25	0
P	0.438	0.729	.0567
O1	0.565	0.72	.0298
O2	0.338	0.509	.0471
O3	0.347	0.969	.0436

Several models of surface-chain-functionalized nanoplatelets were derived from the same core structure, including phenyl, octyl, 9-ethoxynonyl (EON), and 11-methoxyundecyl (MOUD) surface constituents and their mixtures. Single unit cells were constructed containing a total of eight zirconium atoms and three pairs of symmetric, opposing phosphonates with space group symmetry C2/c. The phenyl ZrP unit cell thus contains three layers wherein the central layer has mirror symmetry with the outer layers through the (010) plane. This central layer was removed from the experimental models, permitting the intralayer gallery size to be varied by adjusting the unit cell size along the c-axis. In order to study layer surfaces with substantial dimensions, the number of unit cells was increased by 6 and 10 in the 〈100〉 and 〈010〉 directions, respectively, to form a new periodic superstructure (nominally 54Å square). This structure was then converted to a single supercell, assigned with P1 symmetry. The supercell’s c parameter was fixed for a given dynamic simulation and adjusted manually between serial simulations. Energy minimizations were performed using the Smart Minimizer tool and the Standard Convergence criterion.

Pair-wise interactions of twin nanoplatelets were compared with and without intercalating polymeric chains. In a typical example, the platelets were first separated far away from one another, with a gallery size in the range of 34–35Å, as measured between the terminal protons extending away from the platelet surfaces. Next, the energy of the expanded platelets was minimized. The pairs were then brought together until a new energy minimum was achieved, giving the total change in free energy due to the net interactions of the surface ligands. After the global energy minimum was obtained, a re-expansion of the basal planes was used to calculate the total enthalpy change without rearrangement of the molecules.

The operation was repeated for each intercalating guest species. As before, a re-expansion of the basal-plane spacing for each energy-minimized system was used to assess the enthalpic energy contribution by not allowing for molecular rearrangements.

Polymers were constructed using the Cerius² homopolymer builder. Oligomeric models included helical isotactic polycaprolactone (PCL, 3000 g/mol, 26 mer units), helical isotactic polyethylene terephthalate (PET, 3000 g/mol, 16 mer units), and random-torsion atactic polymethylmethacrylate (PMMA, 3000 g/mol, 30 mer units). Each oligomer was centered between the nanoplatelet model – surfaces and oriented along the 〈11̂0〉 direction of the supercell.

Results and Discussion

(i) Synthetic Organophosphonates

Phosphodiester intermediates were synthesized at ≥ 94% purity, as characterized by NMR and GC/MS (see Supporting Information). The molecular ions (M-1) were found for all six compounds. The predominant impurity, found mainly in the ethoxy-terminal compounds, was found to be the mono-cleaved phosphonic acid/ester as confirmed by ³¹P NMR (δ 33.2 ppm) and GC/MS (M-28).

Phosphonic acids presented as white, crystalline powders with sharp melting points and 99% or better purity—as confirmed by NMR and CHO analysis (see Supporting Information). Figure 1 presents the ATR absorbance spectra for four of the six ether-terminal phosphonic acids. The methoxy-terminal compounds can be easily distinguished from their ethoxy-terminal counterparts by the shifting of the strong ether-stretching resonance from ca. 940 cm⁻¹ to 1010 cm⁻¹. This is easily explained by the relative bulk of the ethyl group, which shifts the resonance toward higher energy.

Figure 1.

ATR absorbance spectra for the synthetic ether-terminal alkylphosphonic acids showing strong characteristic P-O-H (930 cm⁻¹) and P-C (1090 cm⁻¹) resonances.

(ii) ZrP

The number of ZrP derivatives was limited to preparations from four of the parent compounds (EONPA, MONPA, EOUDPA, and MOUDPA) in addition to octyl-ZrP and octyl/MOUD-ZrP containing 50% (mol/mol) octyl chains. This selection of compounds was informed by the relative cost of development as well as the computational modeling results reported below.

Figure 2 shows ATR spectra for the ether-functional ZrP series. The spectra exhibit a high degree peak refinement due to the crystalline nature of the materials. Note that the same essential resonances are present in all samples, with the dominant peak from the Zr-O-P stretching resonance occurring at 1016 cm⁻¹. Hydroxyl content is not evident for any of the compositions, suggesting well-condensed ZrP structures.

Figure 2.

ATR absorbance spectra for ether-terminal ZrP compounds, as derived from the ZrF₆²⁻ intermediate.

Elemental Analysis

C, H, Zr, and P analyses were used to verify the core composition of the ZrP structures as well as the retention of organophosphorus ligands. The calculated and theoretical empirical formulas are compared in Table 2. The theoretical formulas ignore any variations in stoichiometry at the nanoplatelet edges. Experimental oxygen measurements indicated a false deficiency due to incomplete reduction of the zirconium oxide residue during sample pyrolysis. Therefore, the formula oxygen values were determined by subtraction considering the other four elements present.

Table 2.

Verification of α-phase empirical formula for experimental ZrP compounds.

2(HO)2P(O)R+ZrOCl2 → Zr(O3PR)2+2HCl
R Group	Theoretical α-ZrP Formula	Determined Formula
octyl	C16H34O6P2Zr	C15.6H33.5O5.2P2.1Zr
MON	C20H42O8P2Zr	C22.0H47.1O9.6P2.1Zr
EON	C22H46O8P2Zr	C22.4H47.8O8.2P2.1Zr
MOUD	C24H50O8P2Zr	C25.2H52.9O8.7P2.1Zr
EOUD	C26H54O8P2Zr	C28.7H60.7O9.4P2.1Zr
octyl/MOUD (1:1)	C20H42O7P2Zr	C21.9H46.5O8.3P2.1Zr

The surface-tethered organic chains appear well preserved after the ZrP condensation. All of the materials were slightly enriched in phosphorus as compared to zirconium. Assuming that two dangling phosphonic acid groups exist for each layer of a peripheral unit cell, the average number of dangling bonds for a single layer would be 0.1394 Å⁻¹ based on the lattice parameters a = 9.060 Å and b = 5.297 Å for the crystalline phosphate.¹⁶ For a round disc-shaped layer with a diameter of 80 nm, this would yield 350 dangling bonds for every 4.19×10³ phosphorus atoms. The dangling bonds could, therefore, account for only 0.08% of the total phosphorus. The presence of excess phosphorus, relative to zirconium, therefore suggests that incompletely condensed phosphonic acid groups are trapped within the layer structures of the experimental ZrP.

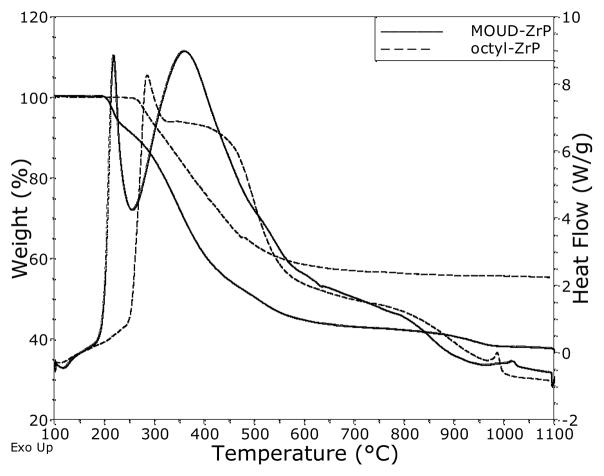
TGA/DTA

Representative TGA/DTA curves are presented in Figure 3. The burnout yields of ZrP₂O₇ are given in Table 3 for comparison with the theoretical values. Samples were preconditioned at 100°C to eliminate contributions from water and other volatile intercalated solvents. The obtained ash was an exact match for ZrP₂O₇ by XRD and showed sharp resonances with no hydroxyl band in the FTIR. As with the elemental analysis above, the theory ignores any deficiency in zirconium at the nanoplatelet edges. In general, the burnout yields match well with the predicted values; however, no correlation can be found between the errors and the relative carbon fractions indicated in Table 2.

Figure 3.

TGA/DTA curves for a) octyl ZrP and b) MOUD-ZrP.

Table 3.

Ceramic yield of ZrP₂O₇ from experimental ZrP compounds based on weight loss in air from 100–1100°C.

Compound	Theoretical Yield (% w/w)	Determined Yield (% w/w)
octyl-ZrP	55.8	55.6
MON-ZrP	47.0	46.4
EON-ZrP	44.8	45.9
MOUD-ZrP	42.8	43.6
EOUD-ZrP	40.9	39.1
octyl/MOUD-ZrP (1:1)	48.4	49.1

Nanoplatelet Structure

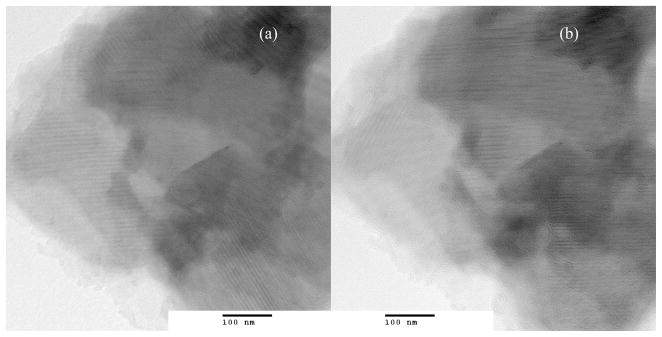
The isolated ZrP compounds remained largely aggregated in dry powder form. In rare instances, an isolated group of platelets could be imaged by TEM, as shown for MOUD-ZrP in Figure 4. The figure shows a stack of layers parallel to the carbon substrate. Different Moire fringes appear depending upon the focus condition. These patterns suggest the interference of two or more ordered arrays scattering multiple electron beams. They confirm that the layers are crystalline in nature; however, the d-spacings of the individual arrays cannot be resolved from these images due to the large number of interacting layers.

Figure 4.

TEM of MOUD-ZrP aggregate showing a) Moire fringes developed by interactions between the electron-dense basal planes and b) rearrangement of the patterns with focus condition due to multilayer interactions.

XRD powder patterns for a series of four ether-terminal alkyl ZrP materials are provided in Figure 5. The primary layer spacings are indicated, as determined from peak positions at their full-width half-maximum (FWHM) values. In general, the intralayer organization is less well defined for the methoxy-terminal compounds than it is either for their ethoxy-terminal counterparts or for zirconium bis-octyl phosphonate. Based on literature values for the monoclinic unit cell dimensions for related phenyl phosphonate compounds,¹¹ the group of peaks in the range of 19–23° 2θ contain the (200) reflection, while those in the 33–35 range contain the (100) and (020) reflections. The peaks present are insufficient to derive an structural solution; however, they are consistent with other structural results for α-ZrP¹¹ as well as the related computer models presented in this paper. The octyl/MOUD-ZrP appears to have the most disorder within the (001) plane structure, as indicated by the single broad peak near 20° 2θ. This disorder is at least partly attributable to the zirconium deficiency noted in the preceding discussion.

Figure 5.

XRD powder patterns for the synthetic ZrP materials with indicated FWHM d-spacings for the (001) reflections.

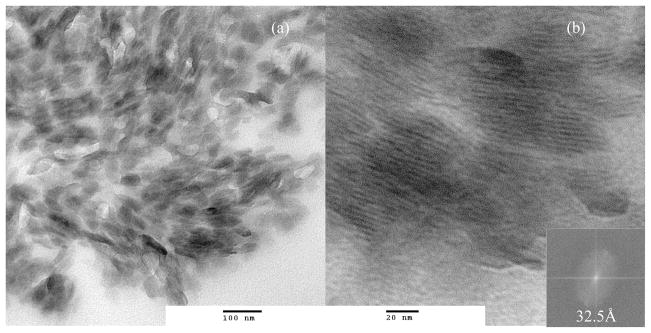
Individual MOUD-ZrP tactoids, of length ca. 60 nm and thickness ca. 30 Å, were imaged within a thermosetting triethyleneglycol dimethacrylate (TEGDMA) matrix, shown in Figure 6. The composite is a simple room-temperature admixture. Image filtering by FFT provided an average interlayer d-spacing of 32.5 Å, which is consistent with the FWHM value from XRD of 32.3 Å. Therefore, the composite does not exhibit intercalation.

Figure 6.

TEM of a) MOUD-ZrP tactoids mechanically dispersed in TEGDMA resin with b) resolved intraplanar d-spacing measured from FFT filter (inset).

The following section discusses the thermodynamic interactions of three different thermoplastic resins with postulated α-ZrP nanoplatelet structures. In order to develop an effective comparison, intercalation of the nanoplatelet galleries by the polymers was assumed. The models do not account for any kinetic barriers to intercalation, and it should not be assumed that such activation energies are small. Nevertheless, it proved instructive to study the thermodynamics of mixing in order to gain insight into the relative stability of the systems in the event that intercalation takes place.

Modeling

In order to examine interactions between α-ZrP and individual polymeric host resins, several nanoplatelet models were developed and compared with the empirical data described above.

The thermodynamic energy minimum for a computational nanoplatelet model is expected to occur at an interlayer spacing equivalent to the (001) d-spacing determined from powder diffraction data for the real material. Typical model spacings are provided in Table 4 and compared with the experimental d-spacings derived from the XRD patterns, shown previously in Figure 5. The agreement between the experimental and calculated spacings is within 2% on average, which is quite good. With one exception, the models retained larger equilibrium spacings than their synthetic counterparts. This could be attributed to the observation made earlier that an excess of phosphorous, related to partially unreacted precursors, appears to be absorbed within the interlayer.

Table 4.

Energy-minimized layer spacings for simulated and real ZrP structures.

Surface phosphonate ligand(s)	Model layer spacing (A)	Experimental (001) X-ray spacing (A)
phenyl	15.4*	15.1†
octyl	24.0	22.8
EON	30.4	29.8
MOUD	32.2	32.3
octyl/MOUD (1:1 interdigitating)	28.9	28.4

^*Three-layer model.

^†Datum from Poojaray et al.¹¹

The equilibrium spacing for the MOUD-ZrP model agrees particularly well with the (001) powder diffraction peak obtained for the synthetic material. Notably, the minimum energy state for that model requires an irreversible rotation of each bond between the third and fourth methylene groups distal to each phosphorus atom. Similar bond rotations proved more easily reversed for the shorter-chain models (e.g. octyl- and EON-ZrP). Re-expansion of the platelet galleries permitted either one surface or the other to lose its compressed conformation in the vicinity of the measured X-ray spacing. The unique compressibility of the MOUD-ZrP model is thus attributable to the stability of a single conformational change.

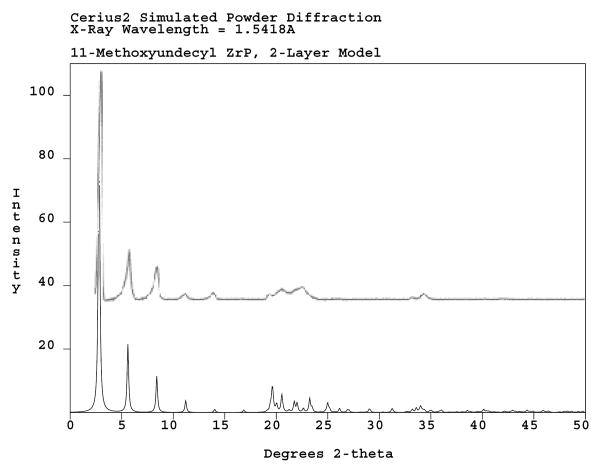
Figure 7 presents a simulated X-ray diffractogram from the MOUD-functional platelet model that shows general similarity with the empirical pattern given in Figure 5. Minor differences in the line intensities occur in the range of 19–23° 2θ.

Figure 7.

Simulated XRD powder pattern for the two-layer MOUD-ZrP model (bottom) with overlaid experimental pattern (see also Figure 5).

For the case of octyl/MOUD-ZrP with a 1:1 ligand ratio, the degree of surface interdigitation could be manipulated by varying the positional substitution of the ligands on the ZrP nanoplatelet core. Given that the model is restricted to having a non-turbostratic relationship^17,18 between the platelet layers, a minor change in symmetry excludes the possibility of interdigitation, as shown in Figure 8. Only the interdigitated model reflects the experimental d-spacing from XRD.

Figure 8.

Interdigitating and porous interfaces between two nanoplatelets presenting mixed octyl/MOUD surfaces in a 1:1 ratio but with reversed substitutional positions among the tail segments.

The mean-field, lattice-based model developed by Vaia and Giannelis⁷ for polymer melt intercalation predicts that the entropy change for small increases in the gallery spacing between nanoplatelets, such as layered silicates, is small. If the platelet surfaces are modified by a tethered surfactant, then an entropic contribution is also derived from the conformational freedom of the surfactant tail segments. As the gallery space increases in volume, the increased conformational freedom afforded to the tail segments increases entropy that offsets the entropy lost to polymer confinement—up to the limit where the gallery spacing permits full extension of the surfactant segments.^6,7 If a solvent is present, then its desorption from the interlayer surfaces also increases entropy.¹⁹ However, a favorable enthalpic interaction between the polymer molecules and the organically modified surfaces is still required for intercalation.⁷

Simulation data in Table 5 show that ether-functional surface terminations increase the enthalpic attraction between nanoplatelets, with the methoxy species showing a stronger effect than the ethoxy. The enthalpic interactions were assessed by increasing the interlayer spacing from the equilibrium position and recalculating the system energy without allowing for conformational changes. Since the total number of states was not varied, the entropic term did not change. After expansion, the total free energy change was determined through re-minimization of the separated platelets with their increased freedom of surface motion. The difference term, shown in the far right column of Table 5, expresses the relative effect of conformational freedom in the models examined. Long-range attractions disappeared completely with expansions of 35 Å or more.

Table 5.

Energy change for gallery expansion in nanoplatelet pairs separated from their minimum-energy positions.

Surface ligand(s)	Energy of Expansion (kcal/mol)
	ΔH (kcal/mol)	ΔG (kcal/mol)	TΔS (kcal/mol)
octyl	1920	721	1199
ethoxynonyl	2450	1913	537
MOUD	3509	1326	2183
octyl/MOUD (1:1 interdigitating)	2937	871	2066

Simulations of polymer intercalation began with PMMA (3000 g/mol). The average interaction potentials with intercalating PMMA are provided in Table 6. The resulting enthalpy changes are highly dependent on the presence of ether dipoles on the nanoplatelet surfaces. Removing the oligomer prior to expansion of the galleries subtracts the oligomer contribution from the total enthalpic interaction of the intercalated system. In all cases, the platelet contribution is small compared to that of the guest.

Table 6.

Energy changes for ZrP systems after gallery expansion, expressed with and without intercalating PMMA.

Surface ligand(s)	Energy of Expansion (kcal/mol)
	ΔHintercalate	ΔGintercalate	ΔHplatelet
octyl	518	200	19
MOUD	1107	654	443
octyl/MOUD (1:1 interdigitating)	854	875	241

Overall, the greatest free energy change was observed for the octyl/MOUD-ZrP system with an interdigitating surface arrangement. Therefore, additional intercalating candidates were evaluated with that model, as depicted in Figure 9. Energy changes are reported in Table 8 for a reduction in basal-plane spacing of 25 Å, giving a nominal gallery opening of 12 Å. The equilibrium basal-plane spacings for each intercalated system fell within 0.2 Å of each other.

Figure 9.

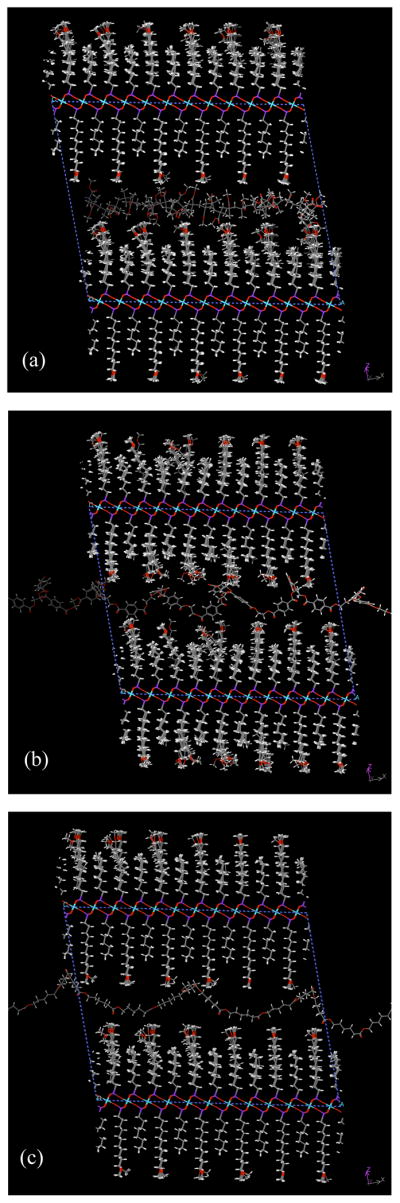
Perspective of intercalated 3000g/mol oligomeric species: a) PMMA b) PET, and c) PCL as viewed down the b axis of the supercell.

PMMA provided the smallest reduction in free energy among the three oligomers despite having a greater enthalpic attraction. It is notable that the dipole density for the three oligomeric species differs considerably, in the order of PMMA > PET > PCL. The energetic contribution of the densely arranged carboxylic ester side chains in PMMA was expected to be significant, with many of side chains extending into the interstitial spaces of the mixed-surface model. In practice, the potential benefit appears to be outweighed by the platelet surface’s ability to accommodate the more rigid helical chains. This result is highly encouraging for the development of composites with crystallizable polyester components.

Balasz and coworkers ²⁰ determined that nanoplatelet surfaces bearing longer surfactant segments provided a deeper free energy minimum than shorter segments with χ ≤ 0. This finding is in basic agreement with the results of Vaia and Giannelis⁷ and demonstrates that the entropic increase due to increasing conformational freedom in the tethered surfactant segments can balance favorably against the entropic penalty of polymer confinement. Such a context is helpful in understanding why the nanoplatelet models are accommodating to relatively rigid oligomer segments. Although the surface structure of uniform alkyl ZrP is highly paraffinic, the improvement in chain mobility within a mixed nanoplatelet surface, such as octyl/MOUD-ZrP, substantially alters in the entropic profile of the system.

Conclusions

Layered α-zirconium(IV) phosphonate nanoplatelets were successfully prepared by the conventional ion exchange between novel ether-terminal alkylphosphonic acids and a ZrF₆²⁻ intermediate. The materials exhibited regular interlayer d-spacings and varying degrees of intralayer order attributed to phosphorus defects. The ether-functional materials are anticipated to be useful for the preparation of polyester-matrix nanocomposites due to the high density of dipoles within the organophilic nanoplatelet surface.

Computer modeling was employed to compare the relative thermodynamic interactions between postulated ZrP nanoplatelets and oligomeric polymer chains. The simulation results suggest a nanoplatelet architecture for reducing the free energy associated with polymer intercalation. Dipole/dipole interactions, based on ether functionality, are useful for increasing enthalpic attractions between nanoplatelets and intercalating polymers. Mixtures of surface chains, especially long surface chains, increase a nanoplatelet’s ability to accommodate intercalating polymers through self-disorder and by providing greater access to dipole sites. Simultaneously, mixed surfaces inhibit nanoplatelet aggregation by reducing the enthalpy of self attraction.

Synthetic octyl/MOUD-ZrP is promising for further study in nanocomposite systems, including those with crystallizable polymer matrices.

Table 7.

Differential energy values for the interdigitating octyl/MOUD-functional nanoplatelet pair undergoing contraction of the gallery containing a individual oligomer (3000 g/mol) species.

Oligomer Species
PMMA		PCL		PET
ΔG (kcal/mol)	ΔH (kcal/mol)	ΔG (kcal/mol)	ΔH (kcal/mol)	ΔG (kcal/mol)	ΔH (kcal/mol)
−875	−853	−941	−381	−979	−770