Fast Implementations of Reconstruction-Based Scatter Compensation in Fully 3D SPECT Image Reconstruction

Abstract

Accurate scatter compensation in SPECT can be performed by modeling the scatter response function during the reconstruction process. This method is called reconstruction-based scatter compensation (RBSC). It has been shown that RBSC has a number of advantages over other methods of compensating for scatter, but using RBSC for fully 3D compensation has resulted in prohibitively long reconstruction times. In this work we propose two new methods that can be used in conjunction with existing methods to achieve marked reductions in RBSC reconstruction times. The first method, Coarse-Grid Scatter Modeling, significantly accelerates the scatter model by exploiting the fact that scatter is dominated by low frequency information. The second method, Intermittent RBSC, further accelerates the reconstruction process by limiting the number of iterations during which scatter is modeled. The fast implementations were evaluated using a Monte Carlo simulated experiment of the 3D MCAT phantom with Tc-99m tracer, and also using experimentally acquired data with Tl-201 tracer. Results indicated that these fast methods can reconstruct, with fully 3D compensation, images very similar to those obtained using conventional RBSC methods, and in reconstruction times that are an order of magnitude shorter. Using these methods, fully 3D iterative reconstruction with RBSC can be performed well within the realm of clinically realistic times (under 10 minutes for 64 × 64 × 24 image reconstruction).

I. Introduction

Accurate 3D reconstruction in SPECT requires compensation for the effects of attenuation, detector response and scatter. While accurate and efficient methods of compensating for the first two of these effects exist, compensating for the effects of scatter is more difficult. A promising approach to scatter compensation, reconstruction-based scatter compensation (RBSC), involves modeling the scatter response function (SRF) in the projector (and backprojector) of an iterative reconstruction algorithm (Frey and Tsui, 1993; Frey et al., 1993; Beekman et al., 1993; Beekman et al., 1996; Floyd et al., 1985; Welch et al., 1995). In effect, scatter compensation is achieved by mapping scattered photons back to their point of origin. Iterative RBSC has been found to result in images with both less bias and reduced variance as compared to subtraction-based scatter compensation methods (Frey et al., 1992). The major shortcoming of RBSC is that scatter models tend to be very computationally intensive. In addition, iterative recovery of image features is slowed when scatter is modeled (hence, more iterations are required). These two effects result in greatly increased reconstruction times, even in the 2D case. When inter-slice scatter is modeled and fully 3D reconstructions are performed, the reconstruction times can become prohibitive.

There are a number of approaches that may help reduce the reconstruction time when performing RBSC. Perhaps the most obvious approach is to use fast scatter models. Substantial research has been performed in this area (Beekman et al., 1996; Hutton et al., 1996; Frey and Tsui, 1996; Welch et al., 1995), but only limited success has been achieved. Another approach is to change the way in which RBSC is implemented. For example, there has been much recent interest in using an unmatched projector / backprojector pair with RBSC; i.e., to model the SRF in the projector but not the backprojector (Kamphuis et al., 1996; Zeng et al., 1997; Welch and Gullberg, 1997). The use of accelerated iterative algorithms (Hudson and Larkin, 1994; Lalush and Tsui, 1996; Byrne, 1996) also falls along these lines. Finally, a third approach would be to limit the size of the reconstruction problem. For example, Frey and Tsui (1997) demonstrated that 3D reconstructions can be limited to including only slices within 3–5 cm of the organ or interest.

We present here two new methods that fall along the lines of the first two approaches listed above, and then incorporate all of these approaches into a single scheme for fast 3D iterative reconstruction with RBSC. The first of the new methods is called Coarse-Grid Scatter Modeling (CGSM), and makes use of the fact that the scatter component of SPECT projection data tends to be dominated by low frequency information. Using CGSM can lead to an order of magnitude reduction in processor time required to model the SRF in the projector or backprojector of an iterative algorithm. The second new method is called Intermittent RBSC. It is based upon the observation that, during iterative reconstruction, scatter effects in the image estimate are reduced in a small number of iterations, whereas resolution loss due to detector response blurring takes many iterations to recover. The Intermittent RBSC method exploits this observation by limiting the number of iterations in which the SRF is modeled. The name arises because scatter-modeling is performed intermittently during the iterative reconstruction process. It should be noted that a method similar to Intermittent RBSC was developed independently by Hutton and Lau (1997).

In this paper we first describe and present some verification of the CGSM and Intermittent RBSC methods. We then incorporate these methods into fast 3D iterative reconstruction schemes that use the Ordered-Subsets Expectation-Maximization (OSEM) algorithm (Hudson and Larkin, 1994) and the Effective Source Scatter Estimation (ESSE) model (Frey and Tsui, 1996). The performance of the fast reconstruction schemes were evaluated and compared to the conventional implementation of Full RBSC in which the 3D SRF is modeled (without using the coarse-grid approach) in both the projector and backprojector for every iteration. Also included is a comparison to the method of Forward RBSC, which uses an unmatched projector/backprojector pair where the 3D SRF is modeled in the forward projector only. This evaluation was carried out using (1) a Monte Carlo simulated phantom experiment with Tc-99m tracer and (2) experimentally acquired data using an anthropomorphic torso phantom and Tl-201 tracer. The processor times required to reconstruct with each of the methods are given and compared. Finally, conclusions are drawn as to the effectiveness of the proposed methods and to the utility of using RBSC in the clinic.

II. Methods

The CGSM and Intermittent RBSC methods will be described in the context of OSEM reconstructions. We first present several definitions here for clarity. The scatter component of the projection data is defined to be the component of the projection data that is due to photons that have scattered (via Compton scatter or coherent scatter) at least once in the patient prior to being detected. The phrase scatter estimate refers to an estimate of the scatter component. It may be estimated either by modeling the SRF and projecting the current image estimate (a process which we call projecting the scatter estimate), or by other means (for example, by acquiring and scaling data acquired in additional energy windows). The reconstructed image estimate is represented using cubic voxels, and projection data are represented using square pixels.

A. Coarse-Grid Scatter Modeling

The distribution of scattered photons in SPECT has been studied extensively (Floyd et al., 1984; Frey and Tsui, 1991), and it is well known that the SRF contains a small peaked component surrounded by long, substantial tails. In terms of the frequency response, the scatter component of SPECT projection data tends to be dominated by low frequency information, though there is some higher frequency information present. The CGSM method takes advantage of this by performing the bulk of the calculations required to project (and backproject) the scatter estimate using a larger voxel size than is used to represent the image estimate. The use of larger voxels greatly reduces the size of the image matrix, leading to a corresponding decrease in the number of computations required to project the scatter estimate.

The basic idea behind CGSM is to collapse the 3D image matrix by a factor of n in each direction, project the scatter estimate using this larger voxel size, then expand and interpolate the projected scatter component back to the normal pixel size. However, due to the presence of the peaked component in the SRF and high frequency structures in the image, simple collapsing and projecting leads to some inaccuracies in the scatter estimate. The coarse-grid approach can be incorporated into the scatter model, as described below, to minimize the inaccuracies resulting from the use of a larger voxel size. Such incorporation works well with the ESSE scatter model (Frey and Tsui, 1996), and while it may be possible to incorporate CGSM into other available scatter models, we have not attempted to do so.

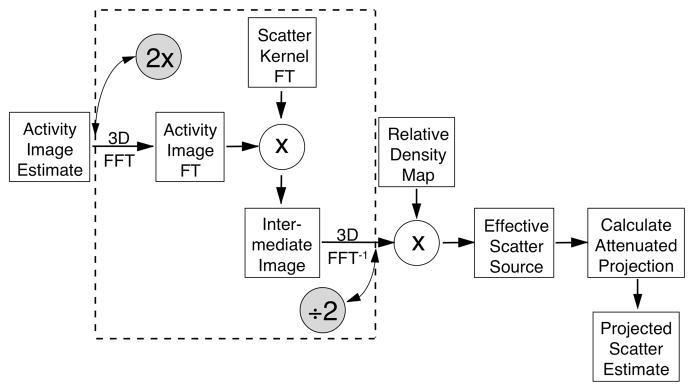
Figure 1 summarizes the major steps required to project an image estimate using the ESSE scatter model. The ESSE model differs from other scatter models in that it does not explicitly calculate a projection space SRF for each voxel in the image. Rather, the ESSE model works by calculating an “effective scatter source” that is dependent upon the current image estimate, the attenuation map, the projection angle, and the ESSE scatter kernel. The simple attenuated projection of the effective scatter source provides the projected scatter component. The spatial variance and object-dependence of the scatter response is accounted for in part during the calculation of the effective source, and also in part by the attenuated projection operation. If the effective scatter source is added to the current image estimate, then a single attenuated projection can be performed, resulting in the primary+scatter projection data. While the processor time required to compute an attenuated projection is quite modest, the time required to compute the effective scatter source is substantial.

Figure 1.

Diagram indicating the basic steps of the ESSE scatter model. The model inputs the activity image estimate, the relative density map and the ESSE scatter kernel, and outputs the projected scatter estimate. When Coarse-Grid Scatter Modeling is incorporated into the ESSE model, the operations within the dashed-line box are performed using a larger voxel size than the other operations. The shaded circles indicate where the coarse-grid collapse and expansions are performed.

Computation of the effective scatter source can be broken into two parts: (1) convolution of the current image estimate with the ESSE scatter kernels (this is actually done for several terms of a Taylor series expansion, as described by Frey and Tsui, 1996), and (2) weighting by the relative density map to account for some of the effects of nonuniform attenuation (this step accounts for much of the object-dependence of scatter). Step (1) involves the convolution of large 3D images and dominates the computational effort required by the ESSE model. It is here that we have incorporated coarse-grid scatter modeling. The convolution of step (1) is performed by computing the Fourier transforms of the kernel and image and multiplying them in the frequency domain. The Fourier transforms are computationally intensive, especially for large 3D images. Using Fast Fourier Transform (FFT) techniques, collapsing the images by a factor of n leads to a speedup of approximately n³log₂(n³) in the FFTs. We therefore collapse the image and kernel by a factor of n prior to performing the convolution, and then expand with interpolation by a factor of n after the convolution. This shown graphically in Figure 1. Note that only the convolution step is affected by the use of a larger voxel size. The density weighting and projection steps are performed with the regular voxel size, which avoids many of the inaccuracies that would be introduced if all steps were performed using the larger voxel size.

Using the ESSE model, another step can be taken to minimize the inaccuracies that may result from using CGSM. The ESSE scatter kernel is described fully in (Frey and Tsui, 1996), and generally consists of a very sharp peak surrounded by a mass of low frequency data. The peak is limited in extent to only a pixel or two, and it accounts for very small angle and coherent scattering events that occur near to the source of primary photon emission. For scatter kernels that have such a peak (which is generally present in photopeak energy windows), the kernel can be decomposed into two parts: a part representing the peak (which is very nearly a delta-function), and the remainder (which is predominantly low-frequency). The convolution (step (1) above) is likewise broken into two parts: the peak portion of the kernel is treated as a delta-function for the convolution, and the low frequency portion of the kernel is convolved using the coarse-grid technique described above. This approach yields nearly the same speedup factor as when the kernel is not broken into parts, but the high frequency information in the kernel is retained with more accuracy.

B. Intermittent RBSC

The second method we are introducing, Intermittent RBSC, is based upon the observation that the projected scatter estimate converges in relatively few iterations. In this context, “converge” means to approach the final value obtained after many OSEM iterations. To demonstrate this property, we have reconstructed Monte Carlo simulated data of the 3D MCAT phantom (Terry et al., 1990; Tsui et al., 1994) and studied the scatter estimates as projected at each iteration. The SIMIND (Ljungberg and Strand, 1989) Monte Carlo program was used, and the various parameters of the simulation are described in Table I. The reconstruction was performed using the OSEM algorithm with 4 angles per subset, a 64³ image matrix, and Full RBSC. The OSEM subsets were chosen to maximize the angular distance between successive subsets; i.e., the first subset included angle indices (1,17,33,49), the second included indices (9,25,41,57), the third (2,18,34,50), and so on.

Table I.

Parameters describing the Monte Carlo simulated phantom experiment.

– 140.5 keV Te-99m emissions – 643 image matrix with 0.625 cm pixels – LEGP parallel hole collimator – Energy resolution 10% FWHM at 140 keV – 20% wide energy window centered on 140 keV – 64 × 64 projection matrix with 0.625 cm bins – 64 projection views evenly spaced over a 180° are from 45° LPO to 45° RAO – Simulated 3D effects of non-uniform attenuation, depth-dependent detector response, and scatter – Followed up to 10 orders of scatter, both coherent and incoherent – Simulated 11 × 109 photon histories to obtain data with low simulation noise – Scaled data and simulated Poisson noise for a scan that acquired ~200,000 counts in a typical cardiac slice

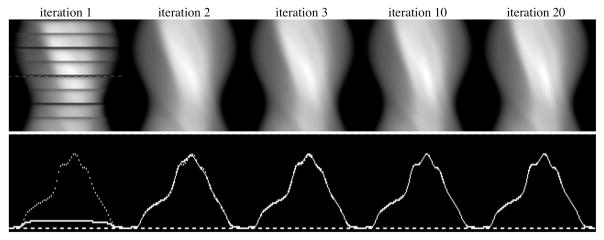
The images shown in Figure 2 are sinograms of the projected scatter estimates for a single slice as projected during the OSEM reconstruction. The sinograms are shown as projected during iterations 1, 2, 3, 10 and 20. One obvious feature that needs explanation is the presence of dark bands on the sinogram projected during the first OSEM iteration. The reconstruction was performed using a uniform initial estimate, the height of which was set to the mean of the projection data. Due to attenuation effects, this initial estimate had voxel values that were quantitatively much lower than in the converged reconstructed image, hence the projected scatter estimates for the early OSEM subsets were grossly underestimated (as compared to the “converged” scatter estimate projected at iteration 20). This gross quantitative inaccuracy was corrected by the first few subsets of the OSEM reconstruction, and therefore the projected scatter estimates for the first few subsets appear as dark bands on the sinograms of Figure 2.

Figure 2.

Scatter estimate sinograms (top row) and profiles across the angle indicated (bottom row) as projected during OSEM iterations 1, 2, 3, 10 and 20. The profiles for each iteration were drawn with a solid line, and the profile for the “converged” scatter estimate at iteration 20 was overdrawn on each using a dotted line. The images demonstrate the rapid convergence of the scatter estimate with iteration. The dark bands appearing on the sinogram for iteration 1 are explained in the text.

It is easily seen from the images and profiles of Figure 2 that the projected scatter estimates were nearly fully converged after only 2 or 3 iterations of OSEM. As additional proof of this, we have calculated the normalized mean square error (NMSE) between the projected scatter estimates at each of these iterations (using all 64 slices) and the scatter component of the Monte Carlo simulated projection data. The NMSEs were found to be 0.1753, 0.0250, 0.0247, 0.0246 and 0.0246 for iterations 1, 2, 3, 10 and 20 respectively. Again, the NMSE results indicate that the projected scatter estimates were nearly fully converged after only 2 or 3 OSEM iterations. The idea behind the Intermittent RBSC method is to exploit this behavior by only projecting the scatter estimate during iterations in which it is likely to change, and to hold the scatter estimate constant for the remaining iterations.

We describe here the details of the Intermittent RBSC method in the context of the OSEM algorithm, but the key points are applicable to other iterative reconstruction algorithms as well. The OSEM algorithm can be written as:

$${\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{new}}={\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{old}}\frac{1}{{\displaystyle \sum _{k\in S_n}}{\mathbf{F}}_{ki}}\sum _{l\in S_n}\frac{{\mathbf{F}}_{li}{\stackrel{\sim }{\mathbf{p}}}_l}{{\displaystyle \sum _{m=1}^N}{\mathbf{F}}_{lm}{\stackrel{\sim }{\mathbf{x}}}_m^{\mathit{old}}}$$ (1)

where

x̃ = the reconstructed image estimate vector,

N = the dimension of the vector x̃,

p̃ = the measured projection data vector

F = the projection matrix (the relevant imaging equation is Fx = p).

The symbol S_n represents the set of projection data points for the current subset, and the superscripts old and new on x̃ are used to indicate the previous and current (updated) image estimates, respectively.

Throughout this paper we have modeled non-uniform attenuation and the distance-dependent collimator-detector response in all projection and backprojection matrices. In the conventional implementation of RBSC, the SRF is modeled in both the projection and backprojection matrices, and these matrices are equal. We call this case Full RBSC. The superscripts a, d and s will be used to denote modeling of attenuation, 3D collimator-detector response and 3D scatter, respectively. The OSEM algorithm for Full RBSC is given in eq. 2:

$${\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{new}}={\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{old}}\frac{1}{{\displaystyle \sum _{k\in S_n}}{\mathbf{F}}_{ki}^{(\mathit{ads})}}\sum _{l\in S_n}\frac{{\mathbf{F}}_{li}^{(\mathit{ads})}{\stackrel{\sim }{\mathbf{p}}}_l}{{\displaystyle \sum _{m=1}^N}{\mathbf{F}}_{lm}^{(\mathit{ads})}{\stackrel{\sim }{\mathbf{x}}}_m^{\mathit{old}}}.$$ (2)

It has also been suggested that RBSC can be implemented by modeling the SRF in the projection matrix only, and not in the backprojection matrix. This is referred to as using an unmatched projector/backprojector pair, and we call this case Forward RBSC. The OSEM algorithm for Forward RBSC is given in eq. 3:

$${\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{new}}={\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{old}}\frac{1}{{\displaystyle \sum _{k\in S_n}}{\mathbf{F}}_{ki}^{(ad)}}\sum _{l\in S_n}\frac{{\mathbf{F}}_{li}^{(ad)}{\stackrel{\sim }{\mathbf{p}}}_l}{{\displaystyle \sum _{m=1}^N}{\mathbf{F}}_{lm}^{(\mathit{ads})}{\stackrel{\sim }{\mathbf{x}}}_m^{\mathit{old}}}.$$ (3)

An equivalent formulation of Forward RBSC can be written if the projection step is separated into two parts— projection of the primary (unscattered) component, and projection of the scattered component:

$${\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{new}}={\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{old}}\frac{1}{{\displaystyle \sum _{k\in S_n}}{\mathbf{F}}_{ki}^{(ad)}}\sum _{l\in S_n}\frac{{\mathbf{F}}_{li}^{(ad)}{\stackrel{\sim }{\mathbf{p}}}_l}{{\displaystyle \sum _{m=1}^N}{\mathbf{F}}_{lm}^{(ad)}{\stackrel{\sim }{\mathbf{x}}}_m^{\mathit{old}}+{\displaystyle \sum _{m=1}^N}{\mathbf{F}}_{lm}^{(s)}{\stackrel{\sim }{\mathbf{x}}}_m^{\mathit{old}}}.$$ (4)

This form of Forward RBSC is very similar to the case in which an a priori scatter estimate is used to perform scatter correction (Lange and Carson, 1984; Bowsher et al., 1996):

$${\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{new}}={\stackrel{\sim }{\mathbf{x}}}_i^{\mathit{old}}\frac{1}{{\displaystyle \sum _{k\in S_n}}{\mathbf{F}}_{ki}^{(ad)}}\sum _{l\in S_n}\frac{{\mathbf{F}}_{li}^{(ad)}{\stackrel{\sim }{\mathbf{p}}}_l}{{\displaystyle \sum _{m=1}^N}{\mathbf{F}}_{lm}^{(ad)}{\stackrel{\sim }{\mathbf{x}}}_m^{\mathit{old}}+{\stackrel{\sim }{\mathbf{s}}}_l}.$$ (5)

where s̃ represents the a priori scatter estimate. The only difference between eqs. 4 and 5 is that the scatter estimate s̃ in eq. 5 is determined a priori, whereas the scatter estimate in eq. 4 is projected from the current image estimate at each iteration.

The Intermittent RBSC method is a hybrid of eqs. 4 and 5, where the scatter estimate is recalculated by projecting the current image estimate during some iterations (i.e. using eq. 4), but is held constant for the other iterations (i.e. using eq. 5). The advantage is that the scatter estimate is only projected during the iterations in which it is likely to change (e.g., the first two or three OSEM iterations). For the remaining iterations the scatter estimate is held constant, and the algorithm runs as fast as when using eq. 5 alone.

C. Fast Reconstruction Scheme

The CGSM and Intermittent RBSC methods have been incorporated into fast 3D reconstruction schemes that takes advantage of each of the methods. These schemes will be compared to the more standard implementations of Full RBSC and Forward RBSC, as well as to the case in which no scatter compensation is performed. All of the cases studied used the OSEM algorithm with four angles per subset and a rotation-based projector/backprojector pair (Zeng et al., 1991; Frey et al., 1993). The effects of nonuniform attenuation and the 3D depth-dependent detector response were modeled in both the projector and backprojector in all cases. The methods differed only in the ways in which scatter was modeled and at which iterations this modeling occurred. The methods are named and summarized in Table II. In addition to what has already been discussed, Table II includes a pair of methods with the label ‘Full/Intermittent RBSC’. These methods differed from Intermittent RBSC in that the SRF was modeled in backprojector as well as the projector for iterations 1 and 2. Again, scatter was modeled in neither the projector nor the backprojector for the other iterations.

Table II.

Names and descriptions of the implementations of RBSC studied.

Name	CGSM collapse factor	SRF modeled in projector at iterations:	SRF modeled in backprojector at iterations:
No Scatter Compensation	n/a	n/a	n/a
Full RBSC	n/a	all	all
Forward RBSC	n/a	all	none
Forward RBSC, 2x	2	all	none
Intermittent RBSC	n/a	1,2	none
Intermittent RBSC, 2x	2	1,2	none
Full/Intermittent RBSC	n/a	1,2	1,2
Full/Intermittent RBSC, 2x	2	1,2	1,2

III. Results

A. CGSM Evaluation

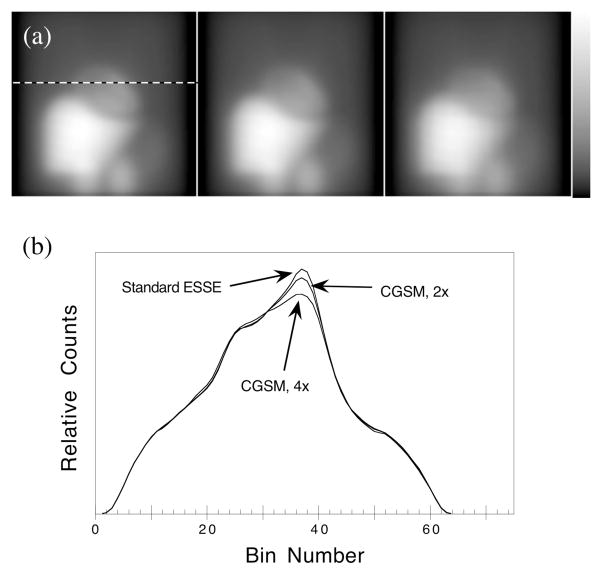
The accuracy of the CGSM method was evaluated by projecting images of the 3D MCAT phantom and comparing the CGSM projected scatter estimates to those projected with the standard ESSE model. The projected scatter estimates for a single view are shown in Figure 3. The images show qualitatively that the scatter estimates for the standard ESSE model and the CGSM, 2× (‘2×’ indicating a collapse factor of 2 was used) method were very similar, but the CGSM, 4× method resulted in some loss of definition and structure. The profiles of Figure 3 demonstrate that, with a collapse factor of 2, the CGSM method slightly underestimated the height of the peak in the scatter estimate, and this effect was more pronounced when using a collapse factor of 4. This reduced peak height was expected when using coarse-grid techniques, and its effect upon the reconstructed image will be discussed in the next section.

Figure 3.

Projected scatter estimates for a single view of the MCAT phantom (a) and horizontal profiles(b). The scatter estimates were projected using the standard ESSE scatter model (left), and using CGSM with collapse factors of 2 (center) and 4 (right). The profiles were drawn at the position indicated by the dashed line.

To further demonstrate the accuracy of the CGSM method, we have calculated the normalized mean-square error (NMSE) of the projected scatter estimates with respect to the Monte Carlo simulated data (Table I). The NMSE for the standard ESSE model was 0.0101, and the NMSE for the CGSM methods were 0.0103 and 0.0136 for collapse factors of 2 and 4, respectively. These data indicate that the accuracy of the ESSE scatter model was not substantially degraded by using the CGSM, 2× technique.

The time savings for the CGSM method was also studied. Projecting the scatter estimate for a 64 × 64 × 24 image using the standard ESSE model took 415 processor seconds on a Sun Ultra 2200 (200 MHz clock speed). The time was reduced to 45 s. and 37 s. with the CGSM collapse factors of 2 and 4, respectively. The reason that a collapse factor of 4 did not lead to a more significant reduction in processor time is that, when using CGSM with a collapse factor of 2 or greater, the calculation was no longer dominated by the FFTs. Thus only modest reductions in processor times were obtained when using larger collapse factors for problems of this size. For images represented with smaller voxels and larger matrix dimensions, using a collapse factor of 4 may prove to be useful. These results show that the CGSM, 2× method projected scatter estimates nearly as accurately as the standard ESSE model, but with approximately a 9-fold reduction in processor time.

B. 3D MCAT Phantom Experiment

1. Noise-free reconstructions

Each of the methods of Table II were used to reconstruct the simulated projection data (Table I) of the 3D MCAT phantom. Sample transaxial slices reconstructed from the essentially noise-free simulated data are shown in Figure 4. Due to differences in the rates of iterative convergence, the Full RBSC images are shown at 8 iterations; the Full/Intermittent RBSC, 2× image is shown at 7 iterations; and all other images are shown at 6 iterations. These numbers of iterations were chosen to give similar image quality from subjective evaluation. The images of Figure 4 have some interesting properties. The image reconstructed without scatter compensation had a general overestimation of counts and loss of contrast due to the presence of scatter, and these effects were much reduced for each of the scatter-compensated images. All of the scatter compensated images were both qualitatively and quantitatively very similar in the region near the heart. However, there were some small differences in the background between the forward RBSC images and the Full RBSC images. For example, the lungs were best defined in the Full RBSC case, and they were somewhat better defined for the Full/Intermittent RBSC, 2× image than for the other methods. This result indicates that there may be some minor loss of image quality when scatter modeling is not included in the backprojector. However, we stress that the images in the region of the heart were very similar for all the scatter compensated cases.

Figure 4.

Sample transaxial slices of the noise-free reconstructions for the simulated MCAT phantom experiment. Top row, left to right: No Scatter Compensation (6 iterations); Full RBSC (8 it.); Full RBSC, 2× (8 it.); Full/Intermittent RBSC, 2× (7 it.). Bottom row, left to right: Forward RBSC (6 it.); Forward RBSC, 2× (6 it.); Intermittent RBSC (6 it.); Intermittent RBSC, 2× (6 it.).

The noise-free images were further analyzed by calculating the left ventricle myocardium-to-chamber contrast (LV Contrast). The LV Contrast was calculated by drawing regions-of-interest (ROIs) over the myocardium (MY) and chamber (CH) for each slice that contained the heart, averaging the counts in each ROI, and then computing:

$$\mathbf{LV}\mathbf{contrast}=\frac{\mathbf{MY}-\mathbf{CH}}{\mathbf{MY}+\mathbf{CH}}.$$ (6)

It should be noted that the LV Contrast computed in this way is closely related to the average spatial resolution over the myocardium—images with better spatial resolution will better localize the counts in the myocardium, leading to a higher LV Contrast.

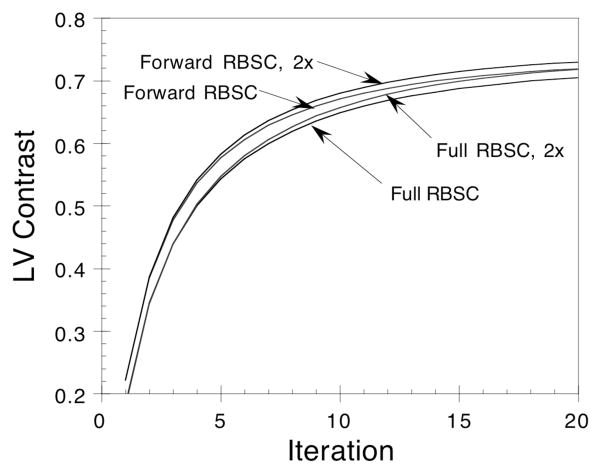
The LV Contrast is plotted versus iteration in Figure 5 for the cases of Full RBSC and Forward RBSC both with and without CGSM. The figure shows that contrast is recovered more quickly with iteration for the Forward RBSC methods than for the Full RBSC methods. This effect has been seen previously when using an unmatched projector/backprojector pair, and this is why the Full RBSC images were shown after more iterations in Figure 4. The CGSM method resulted in a slight over-estimation of LV Contrast as compared to the results when the standard ESSE model was used. This is easily explained by the loss of high frequency information in the scatter estimate when using CGSM (recall Figure 3)—the projected scatter component is slightly underestimated in the region of the myocardium, resulting in a slight over-estimation of the activity in the myocardium in the reconstructed image. The result is a small, artificial increase in LV Contrast when using the CGSM methods. The effect of this behavior on lesion detection has not been studied.

Figure 5.

Plot of LV Contrast versus iteration for Full RBSC and Forward RBSC with and without CGSM (indicated by ‘2x’). A coarse-grid collapse factor of 2 was used for the CGSM methods. The CGSM methods result in slightly overestimated LV Contrast as compared to the standard methods.

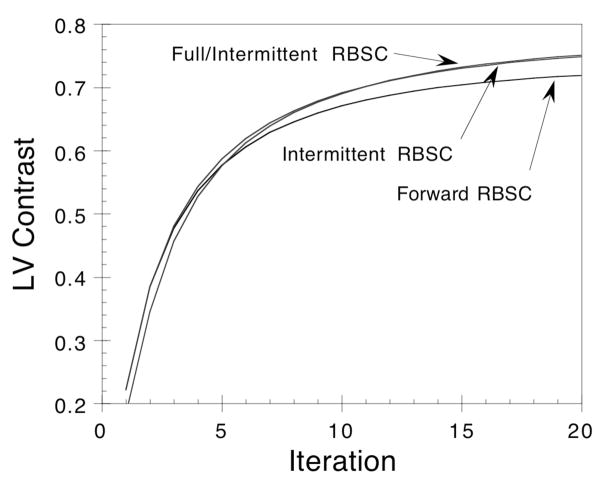
The LV Contrasts for Intermittent RBSC, Full/Intermittent RBSC and Forward RBSC are plotted versus iteration in Figure 6. The curves for Intermittent RBSC and Full/Intermittent RBSC were nearly identical, and these methods resulted in somewhat higher LV Contrast than did Forward RBSC. The results were found to be nearly identical when CGSM was used with the Intermittent RBSC methods, hence these cases are not shown. The increase in LV Contrast for the Intermittent RBSC methods is due, at least in part, to two effects. First, since the scatter estimate is held constant after the first two iterations, the Intermittent RBSC methods may have faster rates of iterative convergence than Forward RBSC. Second, the Intermittent RBSC scatter estimates, while nearly converged, were not fully converged. At later iterations, the Intermittent RBSC scatter estimates had less high frequency structure than did the scatter estimates for Forward RBSC. The result was artificially increased LV Contrast for the Intermittent RBSC methods (for the same reason as described for the CGSM method earlier).

Figure 6.

Plot of LV Contrast versus iteration comparing Intermittent RBSC methods to Forward RBSC. The Full/Intermittent RBSC and Intermittent RBSC curves are nearly identical.

2. Noise Analysis

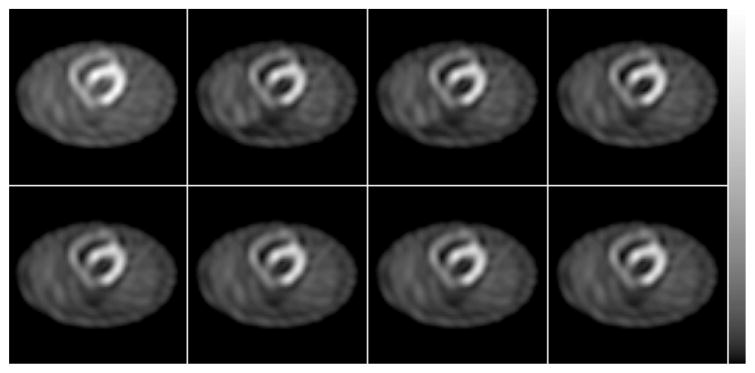
It is very important when performing scatter compensation to consider the effects that the compensation will have upon reconstructed image noise. The reconstructed image noise levels were studied for each of the methods by reconstructing 100 independent noise realizations and computing reconstructed variance images. In order to reduce the computational effort required by this series of reconstructions, only a single 2D slice was reconstructed for each method and noise realization. However, we modified the simulation so that the 3D contribution of scatter was included and accurately modeled in the slice. Sample reconstructed transaxial slices of the noisy reconstructions are shown in Figure 7, where the images have been smoothed with a Butterworth filter of order 5 and cut-off 0.25/cm. Some differences in the noise intensity and texture can be seen in these images, but again the scatter compensated images are all very similar in the region of the heart.

Figure 7.

Reconstructions of noisy projection data for the simulated MCAT phantom experiment. Top row, left to right: No Scatter Compensation (6 iterations); Full RBSC (8 it.); Full RBSC, 2x (8 it.); Full/Intermittent RBSC, 2x (7 it.). Bottom row, left to right: Forward RBSC (6 it.); Forward RBSC, 2x (6 it.); Intermittent RBSC (6 it.); Intermittent RBSC, 2x (6 it.).

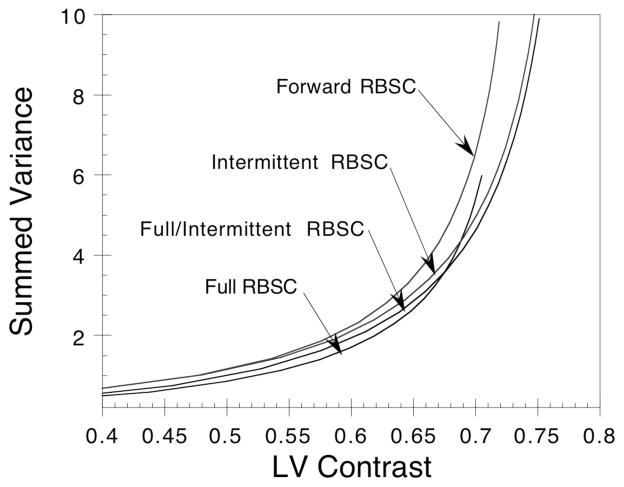
The reconstructed variance images for Full RBSC (8 iterations), Forward RBSC (6 it.), Intermittent RBSC (6 it.) and Full/Intermittent RBSC (7 it.) are shown in Figure 8. Since the CGSM method had very little effect upon the reconstructed image noise, separate variance images for the cases which used CGSM are not shown here. The profiles of Figure 8 show that the Full RBSC method resulted in a somewhat lower variance image than did the other methods. Since this difference could be due to differences in iterative convergence at these iterations, we have summed the voxels of each variance image and plotted the result as a function of LV Contrast in Figure 9. Plotting variance versus LV Contrast instead of versus iteration helps ensure that the noise levels are being compared at iterations that result in similar noise-free image quality. The figure demonstrates that each of the methods behaves similarly, with Full RBSC resulting in the lowest variance and Forward RBSC resulting in the highest variance at similar LV Contrast. The fast methods (Intermittent RBSC and Full/Intermittent RBSC) fell in between the standard methods, except at the later iterations where the fast methods had artificially increased LV Contrast. The differences in variance were also accompanied by substantial differences in noise texture—the cases that modeled scatter in the backprojector led to more correlated noise than the cases not modeling scatter in the backprojector. Such differences in noise texture may greatly affect the performance of the images for tasks such as lesion detection, and further studies such as an observer study with ROC analysis would be required before conclusions regarding lesion detection could be drawn. As such, we drawn no conclusions regarding the noise properties of the proposed methods other than to say that they resulted in variance levels falling in between those for Full RBSC and Forward RBSC.

Figure 8.

Reconstructed variance images over 100 noise realizations (top row) and horizontal profiles across each (bottom row) for the cases of (from left to right): Full RBSC (8 iterations), Forward RBSC (6 it.), Intermittent RBSC (6 it.) and Full/Intermittent RBSC (7 it.). The profiles were drawn at the position indicated by the dashed lines, and all profiles were displayed using the same vertical scale.

Figure 9.

Sum of the voxels in the reconstructed variance images plotted as a function of LV Contrast for each of the methods shown in Figure 8.

C. Anthropomorphic Phantom Experiment

The fast implementations of RBSC were also tested by reconstructing experimentally acquired data of a plastic and water anthropomorphic phantom with cardiac insert (Data Spectrum Corp., Hillsborough, NC). The phantom was filled with a water and Tl-201 solution with relative activity ratios of 20:10:1 in the heart:liver(bowel):body. Two cold lesions were placed in the myocardial wall: one in the basal portion of the septal wall, and another in the inferior mid-ventricular wall close to the liver. The experiment was performed on a GE Optima dual-head SPECT system equipped with a Gd-153 scanning line source for transmission measurements. A LEGP parallel hole collimator was used, and 128 evenly spaced views were acquired over a 360° arc. About 1.15 × 10⁵ counts per cardiac slice were acquired using a 32% wide energy window centered on 76 keV. The images were reconstructed using OSEM with 4 angles per subset, and a post-reconstruction Butterworth filter was applied with order 5 and cut-off 0.25/cm.

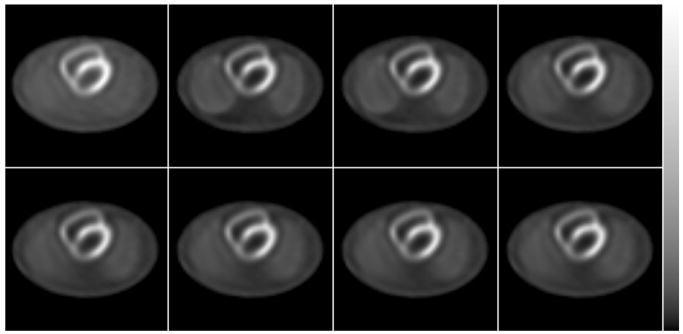
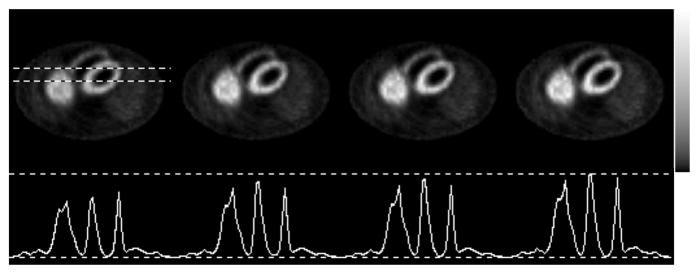
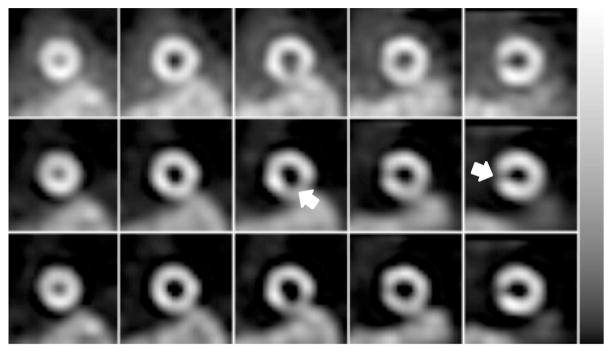
The experimental data was reconstructed using three methods: (i) No Scatter Compensation (6 iterations), which demonstrates the effects of scatter; (ii) Full RBSC (8 it.), which demonstrates the improvement in image quality obtained using the standard implementation of RBSC; and (iii) Full/Intermittent RBSC, 2× (7 it.), which is the fast implementation of RBSC that resulted in the best tradeoff between bias, noise and reconstruction time. The reconstructed images were oriented into short-axis slices and are shown in Figure 10. The scatter compensated images had much better contrast than the uncompensated images, and the lesions were better defined for the scatter compensated images. The fast Full/Intermittent RBSC, 2× method reconstructed images that were quite similar to those for the standard Full RBSC case, though there were some minor differences. The images for the fast method had slightly better contrast, but these images had somewhat larger noise effects in the region of the liver/bowels.

Figure 10.

Every other short-axis slice reconstructed for the Tl-201 phantom experiment using No Scatter Compensation (top row); Full RBSC (middle row); and Full/Intermittent RBSC, 2× (bottom row). The images of each row have been displayed using the grayscale shown at the right. The phantom had two cold lesions (arrows) in the myocardium—one in the basal septal wall, and another in the inferior mid-ventricular wall.

D. Reconstruction Times

All of the reconstructions presented in this paper used a C program with user-specified reconstruction options. In all cases a rotation-based projector-backprojector pair was used, and the reconstructions were performed on one CPU of a Sun Ultra 2200. With this setup, reconstruction of a 64 × 64 image with 24 slices required about 13 processor seconds per iteration when modeling non-uniform attenuation in the projector and backprojector. Modeling the 3D depth-dependent detector response required an additional 18 s. per iteration, and performing Full RBSC with the standard implementation of the 3D ESSE model (without CGSM) required an additional 830 s. per iteration.

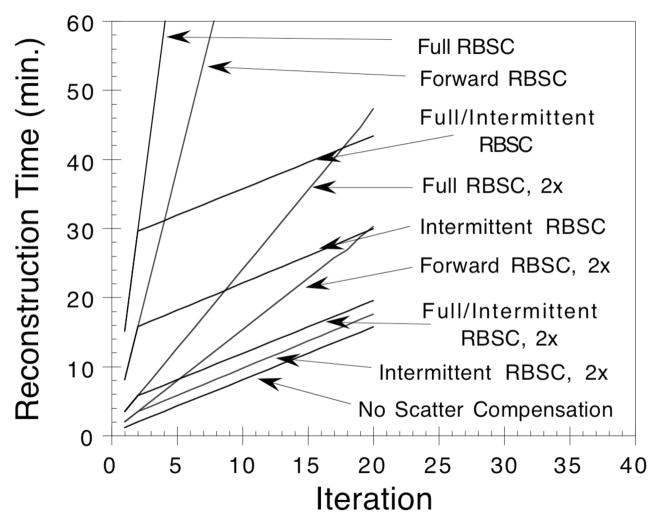
The fast RBSC implementations proposed use two approaches to reduce the reconstruction time. The CGSM method changes the way in which the scatter model is calculated, leading to approximately a 9-fold reduction in processor time (415 s. down to 45 s.) required to project (or backproject) the scatter estimate when a collapse factor of 2 is used. The Intermittent RBSC method limits the number of iterations in which scatter needs to be modeled, resulting in a significant reduction in processor time required for the other iterations. The methods can also be used in conjunction to achieve further reductions in reconstruction times. In Figure 11 we plot reconstruction times versus iteration for the methods studied; the times required to reconstruct 6–8 iterations (depending on the method) are summarized in Table III. The data clearly demonstrate the substantial reductions in reconstruction times that were achieved using the fast implementations of RBSC proposed in this paper.

Figure 11.

Reconstruction times plotted as a function of iterations for each of the methods studied.

Table III.

Total processor times required to reconstruct a 64 × 64 × 24 image for each implementation of RBSC studied.

Method	# Iterations	Reconstruction time (c.p.u. min.)
No Scatter Compensation	6	5.9
Full RBSC	8	131.8
Full RBSC, 2x	8	21.7
Forward RBSC	6	53.8
Forward RBSC, 2x	6	10.9
Intermittent RBSC	6	19.7
Intermittent RBSC, 2x	6	7.4
Full/Intermittent RBSC	7	34.2
Full/Intermittent RBSC, 2x	7	10.4

IV. Discussion

We have shown that fast implementations of RBSC can reconstruct images that are very similar to those reconstructed using standard RBSC methods, and that these reconstructions can be performed in greatly reduced processor times. The proposed methods have some flexibility in how they are implemented, and the methods can be optimized for different imaging situations. For example, we found that a CGSM collapse factor of 2 resulted in a marked speedup with little loss of accuracy in the scatter model, but using a larger collapse factor provided little additional benefit. This result may differ when using a larger image matrix with smaller voxels—in that case, a larger CGSM collapse factor could likely be used (at least during the early iterations) to gain a greater speedup without a corresponding loss of accuracy. However, the peak in the scatter kernel may need to be handled differently when using CGSM with small voxel sizes.

The Intermittent RBSC method can be implemented in a number of different ways, and the best implementation will depend upon a number of factors. The Intermittent RBSC method is based upon the observation that the projected scatter estimates converge in relatively few iterations. In our case, we found that the projected scatter estimate was nearly fully converged after only two OSEM iterations. However, this result may change for different imaging situations, and some study will be required before implementing Intermittent RBSC with different reconstruction algorithms, different image matrix sizes, and so on. In some cases, it may be necessary to consider implementations in which the scatter estimate is projected during the first two iterations, held constant for a few iterations, then projected one more time for a final update. The reconstruction time required to use Intermittent RBSC is dependent upon the number of iterations for which the scatter estimate is projected (updated), so different speedup factors may result from different implementations.

V. Summary and Conclusions

In summary, we have proposed and evaluated two methods of accelerating reconstruction times when using iterative reconstruction-based scatter compensation. The first method, Coarse-Grid Scatter Modeling (CGSM), is based upon the observation that the scattered component of SPECT projection data is dominated by low frequency information. When incorporated into a scatter model such as ESSE, CGSM can lead to an order of magnitude reduction in processor times required for scatter modeling. The second method is called Intermittent RBSC, and reduces reconstruction times by limiting the number of iterations during which scatter is modeled in the projector (and/or backprojector). Our results indicated that scatter may only need to be modeled during the first two iterations, leading to a substantial reduction in reconstruction times.

The proposed methods were evaluated using both Monte Carlo simulations and a real phantom experiment. The fast implementations of RBSC reconstructed images very similar to those reconstructed using standard implementations, and these reconstructions could be performed in clinically acceptable reconstruction times. Fully 3D reconstruction of a 64 × 64 × 24 image required about 10 minutes (one processor, Sun Ultra 2200) using the fast implementations of RBSC, which is a marked improvement as compared to the 1–2 hours required to reconstruct with conventional RBSC methods. Since RBSC has been shown previously to have a number of advantages over other scatter compensation methods, these fast implementations of RBSC may be an excellent choice for clinical use.