THE ROLE OF THE RIGHT AND LEFT PARIETAL LOBES IN THE CONCEPTUAL PROCESSING OF NUMBERS

Abstract

Neuropsychological and functional imaging studies have associated the conceptual processing of numbers with bilateral parietal regions (including the intraparietal sulcus, IPS). However, the processes driving these effects remain unclear because both left and right posterior parietal regions are activated by many other conceptual, perceptual, attention and response-selection processes. To dissociate parietal activation that is number-selective from parietal activation related to other stimulus or response-selection processes, we used fMRI to compare numbers and object names during exactly the same conceptual and perceptual tasks while factoring out activations correlating with response times. We found that right parietal activation was higher for conceptual decisions on numbers relative to the same tasks on object names, even when response time effects were fully factored out. In contrast, left parietal activation for numbers was equally involved in conceptual processing of object names. We suggest that left parietal activation for numbers reflects a range of processes, including the retrieval of learnt facts that are also involved in conceptual decisions on object names. In contrast, number-selectivity in the right parietal cortex reflects processes that are more involved in conceptual decisions on numbers than object names. Our results generate a new set of hypotheses that have implications for the design of future behavioral and functional imaging studies of patients with left and right parietal damage.

INTRODUCTION

The parietal regions, especially the intraparietal sulcus (IPS) have been shown to be a major site of activation in neuroimaging studies of numerical processing (e.g. Dehaene et al., 2003; Nieder, 2005). For instance, comparing or estimating symbolic and non-symbolic magnitudes, and performing arithmetical operations all activate parietal cortex (e.g. Dehaene et al., 2003). Whether the left and right parietal lobes are similarly involved in number processing is currently a matter of debate. The essential involvement of the left parietal areas for number processing comes from studies investigating how number tasks are affected by permanent neurological damage in patients or temporary disruption following transcranial magnetic stimulation, TMS. For instance, left parietal damage has been observed in patients who are impaired at processing numerical quantities (i.e. quantities expressed by numbers) but able to process continuous quantities, such as the physical size of objects (e.g. Cipolotti et al., 1991; Dehaene & Cohen, 1991; Lemer et al., 2003; Polk et al., 2003). Moreover, TMS studies have reported impaired performance in terms of increased response times in number comparison when the left IPS regions are stimulated (e.g. Andres et al., 2005; Cappelletti et al., 2007).

On the other hand, the right parietal lobe has been shown to be equally (e.g. Ansari et al., 2006; Castelli et al., 2006; Thioux et al., 2005) or even more strongly activated than the left in several imaging studies (e.g. Cohen Kadosh et al., 2008a; Le Clec’H et al., 2000; Naccache & Dehaene, 2001). Further evidence of the involvement of the right parietal areas comes from TMS studies (e.g. Cappelletti et al., 2007; under review) and from investigations on developmental dyscalculia showing that this is associated with right parietal dysfunctions (Molko et al., 2003; Price et al., 2008; Rotzer et al., 2008).

Numerical and non-numerical processing in the left and right parietal lobes

There are several reasons for the inconsistencies of previous results in terms of the involvement of the left and right parietal areas. In the case of neuroimaging studies, one reason may be that stimuli or tasks with different cognitive demands were used, for instance comparing numbers or physical sizes relative to reading numbers or letters, therefore leading to different patterns of activation (e.g. Chochon et al., 1999; Dehaene et al., 1999; Simon et al., 2002). A second reason may be that the left and right parietal areas play different roles in numerical processing, with the left parietal cortex more engaged in exact, language-dependent number processing, and the right parietal cortex more involved in approximate number processing (e.g. Dehaene et al., 1999). Although this distinction explains the performance of some neuropsychological patients (e.g. Dehaene & Cohen, 1991; Lemer et al., 2003; Polk et al., 2001), some cases of developmental dyscalculia (e.g. Kucian et al., 2006), and some TMS results (Cappelletti et al., 2007), it still does not account for discrepant results in imaging studies that were not based on the exact vs approximate dichotomy.

A third reason why the involvement of the left and right parietal lobe in numerical processing is unclear at least in neuroimaging studies may be because other conceptual, perceptual and response-selection processes have been shown to recruit parietal regions similar to those involved in number processing (e.g. Bunge et al., 2002; Corbetta & Shulman, 2002; Culham & Kanwisher, 2001; Ritcher et al., 2000; Wojciulik & Kanwisher, 1999). That is, extracting and comparing learnt information from stimuli or selecting a response such as a left or right key press might engage the same parietal areas irrespective of the cognitive task performed. It is therefore unclear to what extent parietal activations during numerical tasks are specific to numerical processing or merely a reflection of other non-numerical processes including response selection.

Three approaches have recently been used to dissociate number processing from other processes that correlated with reaction times (RTs). The optimum approach is to equate RTs across different tasks, i.e. equate task difficulty across tasks in order to achieve similar RTs (e.g. Pinel et al., 2006; Thioux et al., 2005). In this context, differences between stimuli can not be attributed to differences in RTs. However, it is not always possible to satisfactorily equate response times and in these circumstances, the second approach attempts to correct for response time differences by using regression analysis to factor out the effect of response times from number processing (Göbel et al., 2004). Using this approach, Göbel et al. (2004) found that the main effect of response times over three different tasks (number comparison, vertical line judgment on numbers and vertical line judgment on non-numbers) activated the same left IPS areas as the main effect of number comparison relative to either of the other two tasks. No number selective activations in the right parietal lobe were reported. On this basis the authors argued that number selectivity was indistinguishable from processes associated with RT changes in the IPS. We note, however, that the RT effects reported by Göbel et al. (2004) were in the left IPS, therefore they do not explain the right IPS activation previously associated with number processing.

The third approach avoids confounds associated with these RT-correlated processes by using a fMRI adaptation (fMRIA) paradigm, which avoids participants having to make a response. This technique is based on the observation that the BOLD signal is reduced when the same stimulus is presented repeatedly in a passive viewing, suggesting that a neuronal population is sensitive to a particular feature of the stimuli (e.g. Grill-Spector et al., 2006). This paradigm has recently become popular in numerical cognition research although has yielded inconsistent results. For instance, reports that quantity processing activate the parietal lobe bilaterally (e.g. Ansari et al., 2006; Cantlon et al., 2006; Piazza et al., 2004) contrast with those reporting left-lateralized parietal activations (e.g. Cohen-Kadosh et al., 2007 for abstract quantity processing) or even no number-selective activations (e.g. Shuman & Kanwisher, 2004). However, number-selectivity was beyond the scope of most of these studies as no comparison of numerical and non-numerical quantity processing was carried out. Moreover, although these fMRIA paradigms are simple and elegant, they were designed to look at passive number processing rather than the cognitive processes involved in more complex numerical tasks. Therefore, they do not allow more specific hypotheses on the role of the parietal regions in number processing to be tested.

One of these hypotheses is whether the parietal lobes are engaged in processing numerical meanings not requiring magnitude manipulation, for instance hours (e.g. 7.15 a.m.), dates (e.g. 2006) and mathematical constants (e.g. 3.14). Evidence suggesting that quantity and non-quantity number meanings may be distinct comes from lesion studies (e.g. Cappelletti et al., 2008; Dehaene & Cohen, 1991), although no investigations have so far tested quantity and non-quantity number meanings with the same stimuli and task demands. Another hypothesis is that the parietal lobes respond to numbers irrespective of the task performed on them, i.e. irrespective of whether the task requires conceptual manipulation or not (e.g. Eger et al., 2003).

We therefore aimed to: 1) test whether there is any parietal region whose activation is higher for numbers in one condition relative to another, i.e. number selectivity; 2) dissociate numerical processes from processes associated with RTs in the parietal lobe; 3) investigate whether the parietal regions involved in quantity processing with numbers are also engaged in other conceptual operations that do not involve quantity manipulation; and 4) contrast the involvement of the parietal lobes in these conceptual operations with numbers (both quantity and non-quantity) with perceptual operations with the same numerical stimuli.

The present study

The present investigation of the conceptual processing of numbers included three novel experimental features. First, to dissociate parietal activation that was number-selective from activation that might be driven by response time effects, our statistical analyses factored out response times within and across conditions and subjects. Second, we tested numerical (e.g. ‘23.07’) and non-numerical stimuli (i.e. object names, e.g. ‘desk’) on identical conceptual and perceptual tasks in order to compare both stimuli under the same task demands and to identify parietal activation that was number-selective, i.e. higher for numbers than object names. Third our non-quantity conceptual tasks with numbers required the extraction of learnt information but could not be based on a quantity strategy. We reasoned that if any parietal activation is driven by quantity processing then this should be higher for the quantity than non-quantity tasks for numbers, object names or both. Moreover, if parietal activation is higher for numbers than object names, then it is number selective. In contrast, if any parietal activation is common to quantity and non-quantity conceptual tasks on both numbers and object names then this could be related to other processes including the extraction and comparison of learnt information.

METHODS

Participants

Participants were 22 right-handed volunteers comprising 10 males and 12 females with a mean age of 54.6 (range 23-62). All participants were neurologically normal native English speakers who gave informed consent and were screened prior to testing to ensure they were scanner compatible with normal or corrected to normal vision. The study was approved by the National Hospital and Institute of Neurology’s joint ethics committee.

Experimental design

The experimental design independently manipulated stimulus type (numerals, e.g. ‘23.07’ or object names, e.g. ‘desk’) and task. In all conditions, participants were simultaneously presented with two stimuli (either numbers or written object names). One stimulus was presented above a central fixation point and the other stimulus was presented below fixation. Above both stimuli was a two-word question. One word referred to the type of information that needed to be attended to (see below) and the other word indicated the type of stimulus (number or object).

The tasks were categorized on 2 levels (see Figure 1A and 1B). The first level distinguished between (i) conceptual tasks that necessitate access to the abstract meaning associated with a number/object name, from (ii) a perceptual task that involved a decision on the color of the physical stimulus (rather than its meaning). The second level distinguished between conceptual tasks that involved the extraction of either (i) quantity or (ii) non-quantity information.

Figure 1. Experimental design.

The same experimental tasks were used with pairs of (A) Arabic numbers and (B) object names, and can be distinguished at 2 levels: 1. conceptual vs perceptual tasks; 2.within conceptual tasks, quantity vs non-quantity tasks. For each task, one of two possible questions was presented in different blocks in counterbalanced order (i.e. larger/smaller, more/less, summer/winter, working/sleeping). In each trial (C), participants viewed pairs of stimuli presented one above the other with a fixation cross in the middle of the computer screen. Both Arabic numbers and object names were each presented in one of four possible colors (red, yellow, blue, green). Subjects were instructed to indicate with a button press which of the two stimuli was the correct response to a question consisting of two keywords presented above the upper stimulus before and during the stimulus display. The 6 different conditions (3 tasks × 2 stimuli) were blocked (6 trials per block) and fully counterbalanced between and within subjects. In each task, the first block consisted of 6 trials with numerical stimuli (or object names), followed by another 6-trial block of the same task with object names (or numerical stimuli) in a counterbalanced order. Presentation of blocks of the same task with both stimuli was followed by about 16-second rest period where subjects were asked to maintain fixation on a cross in the middle of the computer screen. Trials where the correct answer was the upper or the lower stimulus were presented in equal proportion. Timing parameters refer to paradigm 2.

The quantity tasks required decisions about relative size or numerosity (i.e. how many items?). The non-quantity tasks also required the extraction of learnt information but could not be based on a quantity strategy. This was possible by using non-quantity questions that focused on times and dates, both of which are on a circular rather than linear dimension. Thus to identify a sleeping time, a simple quantity strategy (i.e. bigger number=later time=sleeping time) may not work as the target number could be either smaller (e.g. ‘2.40’ vs ’11.05’) or bigger in magnitude (e.g. ‘9.22’ vs ’23.29’) than the other number in the pair. Likewise, in the case of dates the first month (January) is closer in time to the twelfth (December) than the third (March). Times were represented as two numbers referring to the hour followed by two numbers referring to the minute (e.g. 13.07 = seven minutes past one). Likewise, dates were represented as two numbers referring to the day followed by two numbers referring to the month (e.g. 13.07 = 13^th July). For objects, we distinguished between items that were used at night for sleeping (e.g. “bed”) versus items that were used during office hours for working (e.g. “desk”). With respect to seasons, we distinguished between summer objects (e.g. “sunglasses”) versus winter objects (e.g. “gloves”). We then selected questions that could be used for both the number stimuli and object name stimuli, see Figure 1A and 1B for examples. Specifically, there were a total of 4 different quantity questions for numbers: (i) larger number? (ii) smaller number? (iii) more numbers? (vi) less numbers?; with the same 4 questions for object names: (i) larger object? (ii) smaller object? (iii) more objects? (vi) less objects? Likewise, we also included 4 different non-quantity questions for numbers: (i) summer month? (ii) winter month? (iii) working time? (vi) sleeping time? The same 4 non-quantity questions were also used for object names: i.e. (i) summer object? (ii) winter object? (iii) working object? (vi) sleeping object?

Our range of tasks/questions allowed us to minimize differences in the type of information that was extracted from numbers and object names but there were also some subtle differences. For example, for numbers the questions “more vs less?” and “larger vs smaller?” are equivalent but for object names, “more?” questions referred to the number of items (i.e. a numerosity judgments) whereas “larger?” questions referred to the size of the object. We therefore investigated whether the type of question (e.g. numerosity versus size) influenced our effects of interest, i.e. the effects of [conceptual versus perceptual] and [quantity versus non-quantity]. As our behavioral and imaging results did not reveal any significant effects of question type on our effects of interest, our final analyses (see below) summed over question type within the quantity and non-quantity conditions.

Stimuli

A total of 144 Arabic numbers and 144 object names were generated (see Appendix 1). Arabic numbers were presented as pairs of 1 or 2 digits, each separated by a dot, e.g. 23.07. They referred to a linear dimension of quantity, to dates (e.g. 23^rd July) or to times (e.g. seven minutes past eleven at night). Numbers indicating quantites ranged from 1 to 31 for the first half of the numerical expression and from 01 to 59 for the second part (i.e. from 1.01 to 23.59). Numbers indicating dates were chosen to represent either summer or winter days in the Northern hemisphere; therefore summer dates included the months of June, July, and August, winter dates included the months of December, January and February. Dates were expressed in terms of day and month separated by a dot (e.g. 23.07). Numerals referring to a date ranged from 01 to 31 for the first half of each numerical expression and from 01 to 12 for the second part (i.e. from 01.01 to 31.12). Numbers indicating times were chosen to refer to either a sleeping or a working time approximately in terms of a 8am to 6pm job. Therefore, working times were chosen between 8am and 6pm, and sleeping times between 10pm and 7am. Times were expressed in terms of 24-hour clock with the first pair of digits referring to the hour and the other two digits, separated by a dot, referring to the minutes past the hour (e.g. 16.30 is half past four in the afternoon). Numbers referring to a time ranged from 00 to 23 for the first half of each numerical expression and from 01 to 59 for the second part (i.e. from 00.01 to 23.59). Our numerical stimuli differed from those used in previous studies as we employed non-integer numbers. This decision was motivated by the nature of our non-quantity categorical tasks where non-integer numbers allow us to represent dates and times. To keep the stimuli constant across task, we also used the same non-integer numbers in the quantity task. Therefore we were not able to compare integer and non-integer numbers but this was not the aim of the current experiment.

APPENDIX 1. Experimental stimuli used.

‘Ant’	Flies’	‘Radiator’
‘Armchair’	‘Folder’	‘Reindeer’
‘Barbeque’	‘Fork’	‘Sailing boat’
‘Bath’	‘Gloves’	‘Scarf’
‘Bed’	‘Hammer’	‘Screwdriver’
‘Bedroom’	‘Heater’	‘Seal’
‘Bed-sit’	‘Holly berries’	‘Shawl’
‘Bedspread’	‘Hostel’	‘Sheets’
‘Bee’	‘Hotel’	‘Shelter’
‘Bikini’	‘Husky’	‘Shelves’
‘Bird Nest’	‘Ice lolly’	‘Shoes’
‘Biscuits’	‘Ice skates’	‘Shorts’
‘Blanket’	‘Igloo’	‘Skipole’
‘Blinds’	‘Jacket’	‘Sledge’
‘Boots’	‘Jumper’	‘Slippers’
‘Briefcase’	‘Ladybird’	‘Snowboard’
‘Bunk bed’	‘Lampshade’	‘Snowflake’
‘Butterfly’	‘Lawn-mower’	‘Snowman’
‘Cactus’	‘Lizard’	‘Socks’
‘Calculator’	‘Mango’	‘Sofa’
‘Candle’	‘Mattress’	‘Spade’
‘Car’	‘Melon’	‘Spoon’
‘Chalet’	‘Mince pies’	‘Stamps’
‘Cheque’	‘Mittens’	‘Stapler’
‘Cherries’	‘Moon’	‘Stars’
‘Chestnuts’	‘Mouse pad’	‘Stool’
‘Clogs’	‘Mug’	‘Strawberry’
‘Coat’	‘Newspaper’	‘Suit’
‘Coconut’	‘Nightdress’	‘Sunflowers’
‘Coffee maker’	‘Notepad’	‘Sunglasses’
‘Computer’	‘Office’	‘Sweater’
‘Cot’	‘Paint-brush’	‘Swim cap’
‘Couch’	‘Papaya’	‘Swimming pool’
‘Cricket bat’	‘Paperclips’	‘Swimsuit’
‘Cricketball’	‘Parasol’	‘Teabags’
‘Curtains’	‘Peach’	‘Teddy’
‘Cushion’	‘Pen’	‘Telephone’
‘Deck chair’	‘Penguin’	‘Tent’
‘Desk’	‘Picnic basket’	‘Thermos’
‘Diary’	‘Pillow’	‘Tinsel’
‘Dormitory’	‘Pine tree’	‘Toothbrush’
‘Drill’	‘Pineapple’	‘Toothpaste’
‘Duvet’	‘Pliers’	‘Towels’
‘Earplugs’	‘Printer’	‘Umbrella’
‘Envelope’	‘Pumpkin’	‘Uniform’
‘Fax’	‘Purse’	‘Wallet’
‘Fireplace’	‘Pyjamas’	‘Watermelon’
‘Flip-flops’	‘Quilt’	‘Woolly hat’
‘00.01’	‘2.11’	‘30.11’
‘00.16’	‘2.12’	‘31.01’
‘00.25’	‘2.40’	‘31.07’
‘01.01’	‘2.47’	‘31.08’
‘1.03’	‘2.49’	‘31.10’
‘1.06’	‘21.01’	‘4.08’
‘1.07’	‘21.05’	‘4.25’
‘1.09’	‘21.06’	‘4.52’
‘1.11’	‘21.58’	‘5.02’
‘1.32’	‘22.02’	‘5.06’
‘1.36’	‘22.10’	‘5.08’
‘10.01’	‘22.30’	‘5.09’
‘10.15’	‘23.11’	‘5.10’
‘10.41’	‘23.29’	‘5.30’
‘11.05’	‘23.30’	‘5.55’
‘11.07’	‘23.45’	‘6.03’
‘11.08’	‘23.48’	‘6.04’
‘11.45’	‘24.01’	‘6.50’
‘12.02’	‘24.03’	‘6.54’
‘12.07’	‘25.02’	‘6.56’
‘12.11’	‘25.03’	‘7.00’
‘12.51’	‘26.01’	‘7.05’
‘13.02’	‘26.06’	‘7.08’
‘13.07’	‘26.07’	‘7.10’
‘13.12’	‘27.01’	‘7.12’
‘13.24’	‘27.06’	‘7.28’
‘13.51’	‘27.08’	‘7.38’
‘14.07’	‘28.02’	‘7.43’
‘14.10’	‘28.08’	‘7.44’
‘14.43’	‘28.09’	‘7.50’
‘14.57’	‘28.11’	‘7.58’
‘15.09’	‘29.03’	‘8.01’
‘15.19’	‘29.06’	‘8.05’
‘16.02’	‘29.07’	‘8.10’
‘16.06’	‘29.08’	‘8.11’
‘16.30’	‘29.08’	‘8.12’
‘17.00’	‘29.11’	‘8.15’
‘17.02’	‘3.02’	‘8.25’
‘17.03’	‘3.03’	‘8.32’
‘17.07’	‘3.08’	‘8.45’
‘17.55’	‘3.10’	‘8.47’
‘18.03’	‘3.17’	‘8.52’
‘18.08’	‘3.20’	‘8.56’
‘18.20’	‘30.03’	‘9.08’
‘18.55’	‘30.05’	9.11’
‘2.02’	‘30.06’	‘9.11’
‘2.06’	‘30.09’	‘9.22’
‘2.08’	‘30.10’	‘9.56’

Object name stimuli referred to concrete, countable objects whose size could be unambiguously identified and that could be used in both the quantity (e.g. larger object: ‘sailing boat’ or ‘desk’?) and non-quantity tasks (e.g. working object: ‘sailing boat’ or ‘desk’?).

Irrespective of stimulus (numbers versus words) or task (quantity, non-quantity or perceptual), the two stimuli were presented in two different colors. Possible colors were red, yellow, blue, and green. Subjects needed to attend to the color in the perceptual task to make the color decision response but they were instructed to ignore the color in the quantity and non-quantity conceptual tasks.

Task instructions

Participants were told that they would see pairs of numbers or object names and that above the stimuli, a two-word question would be presented before a during a block of 6 trials, see Figure 1C. On every trial, participants were instructed to make a key press response to indicate which stimulus was the answer to the question. They were asked to press the upper key of a two-button keypad to select the upper stimulus and the lower key to select the lower stimulus. Trials where the correct answer was the upper or the lower stimulus were presented in equal proportion.

Participants were also told that the number stimuli could indicate either: i) quantities, ii) dates, or iii) times. The instructions for the number stimuli were as follows: For the larger/smaller and more/less questions, participants were told that numbers referred to an amount and that they should choose the larger (or smaller) number in each pair irrespective of the wording of the question (i.e “larger” or “more”). In this context, they were encouraged not to process the numbers according to any specific contextual meaning, for instance ‘money’. In contrast, for summer/winter questions, participants were told that each number indicated either a summer or a winter month in the Northern hemisphere (all participants were British and raised in the UK). They were told that summer months were ‘June’, ‘July’, and ‘August’ and winter moths were ‘December’, ‘January’ and ‘February’ and that these months followed a day (1-31) separated with a dot (13.07) rather than the more familiar slash (13/07). They were instructed to select either the summer or the winter month in each pair of stimuli depending on the question. For the working/sleeping questions, participants were told that working or sleeping times were in terms of a 24-hour clock; and that working times were between 8am and 6pm, and sleeping times were between 10pm and 7am. Participants were discouraged from considering jobs that include night shifts. Finally, in the perceptual (color-decision) task, participants were asked to choose the stimulus whose color corresponded to the color indicated by the question above the stimuli. Subjects were instructed to select the stimulus according to the color of the ink and not according to the color of the object (e.g. they should not select red just because the object name was strawberries or tomatoes etc).

For object names, the instructions were the same as those for the numbers except that the processing required for “more/less” questions was not the same as that required for “larger/smaller” questions. Instead, during the more/less questions participants were instructed to select the stimulus that was more (or less) numerous than the other, for example ‘socks versus thermos’, ‘stars vs moon’, ‘bed vs blanket’, ‘deck chair vs swimming pool’, ‘snowflakes vs snowman’ or ‘cherries vs melon’. Prior to the fMRI experiment, participants underwent a practice session in order to familiarize themselves with the task procedure.

Presentation parameters

The 6 different conditions (quantity, non-quantity and perceptual-decision tasks x 2 stimuli) were blocked (6 stimuli per block) and fully counterbalanced between and within subjects. We used a blocked rather than an event related design to minimize the cognitive cost of switching from one task to another and to maximize efficiency (Friston et al., 1999). Although it may be possible that blocking stimuli introduces strategic differences in the way the stimuli are processed, these strategic effects can be dissociated from stimulus effects because the same stimuli were used in all three tasks, thus allowing us to distinguish between task dependent effects and task independent stimulus effects.

Six pairs of stimuli with a fixation between them were presented in each block. Each block began with a question that appeared before the first trial and remained on the screen for the duration of the block. A fixation was then presented between blocks (see Figure 1C). We used two versions of the same experiments (paradigm 1, P1 and paradigm 2, P2). These paradigms differed in terms of number of subjects studied, the hand they used to respond, and timing parameters (see Table 1). The advantage of including two different sets of parameters is that we can conclude that any effects that are consistent for both paradigms can not be attributed to hand of response, stimulus duration or participants’ age.

Table 1. Experimental tasks.

Details of paradigm 1 (P1) and paradigm 2 (P2) in terms of participants and timing parameters.

	Paradigm 1	Paradigm 2
Participants
Number	14	8
Age	Average= 58.7 range 22-74	Average= 50.4 range 22-69
Gender	Males 7, females 7	Males 3, females 5
Handiness	Right	Right
Hand of response	Right	Left
Timing parameters
Duration of each stimulus pair	2.65s	4s
Fixation between stimulus pairs	500ms	1s
Total time to respond	3.15s	5s
Total time for each block	18.9s (6 pairs × 3.15s)	30s (6 pairs × 5s)
Question before beginning of each block	3.78s	2.7s
Fixation between blocks	11.34s	16.2s
Number of scans per run	216	260
Number of runs	3	4
Total scanning time	40.8 minutes	46.8 minutes

Data acquisition

MR images were acquired using a 1.5T Siemens Sonata MRI scanner (Siemens Medical, Erlangen, Germany). All three tasks (quantity, non-quantity, perceptual-decision) for each stimulus (numbers and object names) were presented within a run of 216 (P1) or 260 scans (P2) with each subject participating in three (P1) or four (P2) runs. Participants’ eyes were monitored using a compatible eye tracker device to ensure that they kept awake during the scanning sessions. A gradient echo planar image sequence was used to acquire functional images (repetition time (TR) 3780 ms (P1), 2700 ms (P2); echo time (TE) 50 ms; field of view 192×192 mm; 64×64 matrix). Forty two (P1) and thirty (P2) oblique axial slices of 2 mm thick (1 mm gap), tilted approximately 20 degrees were acquired. Our final resolution was therefore 3×3×3mm voxels. High resolution anatomical reference image was acquired using a T1 weighted 3D Modified Driven Equilibrium Fourier Transform (MDEFT) sequence (repetition time (TR) 12.24 ms; echo time (TE) 3.56 ms; field of view 256×256 mm; voxel size 1×1×1 mm).

Data analysis

For both P1 and P2, functional image analysis was performed using Statistical Parametric Mapping software (SPM5 software, Wellcome Trust Centre for Neuroimaging, London; http//www.fil.ion.ucl.ac.uk/spm).

The first four (P1) and six (P2) volumes of each fMRI session were discarded and the remaining 212 (P1) and 254 (P2) volumes were used for the analysis. Scans were realigned, unwarped and spatially normalized (Friston et al., 1995) to the Montreal Neurological Institute (MNI) standard space. Functional images were then smoothed in the spatial domain with a Gaussian kernel of 6 mm FWHM to improve the signal to noise ratio. A high pass filter was used with a cutoff period of 128 s.

The aim of our analysis was to examine whether: (1) there were number-selective activations, i.e. activations specific for [numbers>object names] for conceptual and/or perceptual decision tasks; (2) these activations were distinct from effects driven by RT correlated processes. As we established that there was no difference between the subtasks used (see Methods section), we conducted 2 first level analyses. In one analysis, response times were modeled as a covariate for each condition. In the other analysis response times were modeled over numbers and object names for (a) the conceptual task and (b) the perceptual task separately. In each first level analysis, each event related stick function was convolved with a canonical hemodynamic response function and activation for each condition was compared to fixation according to the general linear model (Friston et al., 1995). For each of the two first level analyses we conducted two second level Analysis of Variance (ANOVA) to identify effects at the group level. To control for any correlation between conditions, a correction was made for non-sphericity using standard SPM5 procedures. Moreover, in each ANOVA contrasts from P1 were modeled separately from P2 so that we could test for any interaction with the paradigm.

Analysis SET 1: RTs modeled separately for each condition

At the first level the functional data were modeled in an event related fashion with 12 regressors corresponding to the correct responses to each of the 12 condition types (3 tasks: 2 conceptual and 1 perceptual x 2 stimuli x P1 and P2) and a thirteenth regressor modeling all incorrect responses. In addition, for each subject, response times for each trial were entered as a covariate (parametric modulation) that interacted with condition. This allows us to compare the effect of RTs in different conditions. First level contrasts were then entered into two second level ANOVAs to identify four different effects at the group level.

ANOVA 1 modeled the main effects of conditions and interactions with 12 different conditions (6 per experimental paradigm). In addition, age and mean response times per subject for each condition were entered as 2 continuous covariates (i.e. across conditions). From this analysis, we identified effects that were:

(A) Common to numbers and object names by identifying the main effect of conceptual tasks (over quantity and non-quantity numbers and object names) relative to fixation. To ensure that these effects were not driven by one condition only, we used the inclusive masking option in SPM to identify the main effect of conceptual tasks relative to fixation in areas that were activated by both (i) conceptual tasks on numbers and (ii) conceptual tasks on object names at p<0.01.

(B) Number selective (i.e. more activated by numbers than object names) over task and for each task separately (i.e. conceptual and perceptual).

ANOVA 2: modeled the effect of RT correlated processes. The design matrix was almost identical to ANOVA 1, except that (i) the contrast images corresponded to the effect of RTs for each condition, rather than the effect of condition relative to fixation and (ii) we did not include the covariate that modeled the mean RT correlated processes for each subject. From this analysis we identified effects of RTs that were

(C) Common to all conceptual tasks

(D) Number selective (i.e. more activated by numbers than object names) over task and for each task separately.

Analysis SET 2: RTs modeled over conditions

Analysis set 1 (described above) allowed us to look at how the effect of RT correlated processes differed for different conditions. However, if these effects varied across condition (task or stimulus), then differences between conditions are confounded by RT differences. For example, if conceptual decisions on numbers take longer than conceptual decisions on object names, then increased activation for numbers might be a consequence of more difficult response selection or other RT related processes. Although our behavioral data did not indicate longer RTs for numbers than object names, we further ensured that our number selective areas were not confounded with RT related effects by conducting a second set of analyses that modeled these effects across numbers and object names. In this context, number selective areas were identified after the main effect of RTs has been factored out.

In order to do this, we used a different design matrix at the first level. This modelled the functional data in an event related fashion with 5 regressors corresponding to (1) the correct responses to the semantic and (2) perceptual conditions across stimulus type, (3) numbers versus object names, (4) quantity versus non-quantity tasks and (5) all incorrect responses. Response times were entered as covariates on the first and second regressors thereby modeling RT related effects over numbers and object names but separately for semantic and perceptual trials.

These first level contrasts were then entered into two second level ANOVAs to identify effects at the group level.

ANOVA 3: Number selectivity when the main effect of RT related processes was removed

This involved a t-test on the contrast images for [numbers > object names on the conceptual tasks], i.e. one contrast for each participant. From this analysis we extracted the effect sizes for number > object names for each subject in the left and right parietal regions (sphere 8mm radius) centered on the peak co-ordinates for number selectivity. A t-test comparing the left versus right hemisphere effects allowed us to report the interaction of number selectivity with hemisphere.

ANOVA 4: RT related effects over conditions

We examined the effect of RT related processes for each task (i.e. semantic and perceptual) over numbers and object names.

Statistical threshold

For the main effect of task and number selectivity, regions were identified using a statistical threshold of p<0.05 corrected for multiple comparisons across the entire brain using family-wise error correction. We also lowered the threshold to p<0.001 uncorrected in the parietal lobes to fully characterize our effects. However, we only draw conclusions from effects that survived a corrected level of significance.

RESULTS

Behavioral data

An analysis of variance (Anova) on the mean accuracy, with stimulus type and task type as within-subject variables and experimental paradigm as between-subject variable, revealed a main effect of task (F(2,40) = 41.54; p<0.001), no effect of stimulus type (p>0.1), but a significant interaction between task and stimuli (F(2,20) = 33.26; p<0.05). Pair wise comparisons demonstrated a significantly higher accuracy for the perceptual decision relative to conceptual task for both numbers (t(21) = 9.17, p<0.001) and object names (t(21) = 8.25, p<0.001), for quantity relative to non-quantity for numbers (t(21) = 2.07, p<0.05) and for non-quantity relative to quantity for object names (t(21) = 2.00, p<0.05). P1 and P2 did not differ (F(1,20) = 0.98; p=0.98).

The identical analysis on mean response latencies identified significant main effects of task (F(2,40) = 467.19; p< 0.001), stimulus type (F(1,20) = 10.64; p<0.005), and a task-by-stimulus interaction (F(2, 40) = 160.38; p< 0.001). P1 and P2 did not differ (F(1,20) = 3.45; p=0.08). Pairwise comparisons of RTs demonstrated significantly faster RTs for perceptual decision relative to both conceptual tasks on numbers (t(21) = 15.82, p<0.001) and object names (t(21) = 12.15, p<0.001), for quantity relative to non-quantity conceptual tasks for numbers (t(21) = 6.26, p<0.001) and for non-quantity relative to quantity for object names (t(21) = 13.04, p<0.001). Slower RTs for numbers than object names were therefore only observed on the non-quantity conceptual task. On the quantity task, RTs were longer for object names than numbers. Therefore, any effect of number selectivity that is task independent cannot be explained by RTs.

In sum, perceptual judgments with numbers and object names resulted in the fastest and most accurate performance. More errors and slower RTs emerged when participants performed non-quantity judgments with numbers (e.g. summer month: ‘23.07’ or ‘10.02’?) and quantity judgments with object names (e.g. larger object: ‘sailing boat’ or ‘desk’?).

Functional imaging results

ANALYSIS SET 1: When RTs were modeled for each condition separately

A) Main effect of conceptual task

Both conceptual tasks (quantity and non-quantity) on both types of stimuli (numbers and object names) increased activation in bilateral posterior IPS. In addition, these tasks activated bilateral occipital, right frontal and cerebellar regions (Table 2; Figure 2, yellow areas).

Table 2. Main effect of task.

Activations common to all conceptual tasks relative to fixation, specific for quantity and non-quantity judgments, and for numbers and object names.

		Coordinates			Common Conceptual	Quantity only	Non-quantity only	Numbers only	Object names only
Area	Hem	x	y	z	Z scores
Occipital	R	24	−104	2	6.5	5.7	6.2	5.7	6.2
	R	28	−92	−4	5.7	4.8	5.6	5.5	5.0
	R	14	−106	6	5.7	5.4	5.3	5.0	5.5
		14	−106	16	5.5	5.7	4.5	4.0	6.0
	L	−18	−102	0	7.5	6.8	7.0	5.6	6.8
	L	−32	−96	−2	5.7	5.1	5.4	4.8	5.7
	L	−24	−88	−10	5.8	5.0	5.8	4.7	5.9
Posterior IPS	R	30	−58	56	6.6	5.0	4.9	3.8	3.5
	L	−26	−64	54	5.3	5.1	4.9	5.3	4.1
Inferior frontal	R	46	26	22	5.0	3.7	5.4	5.4	3.7
Cerebellum	R	38	−76	−20	5.3	5.0	4.9	4.7	5.0
		22	−78	−20	4.8	4.1	4.7	3.5	5.2

Legend: In bold significant at p<0.05 corrected for multiple comparisons. H = Hemisphere, L = Left; R = Right

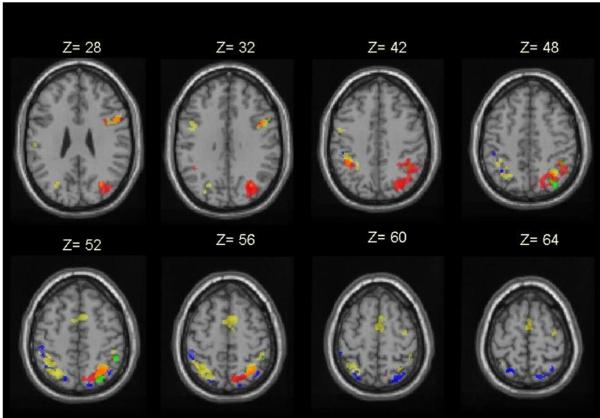
Figure 2. Main effect of conceptual task, number selectivity and RT effects (analysis 1).

Activations rendered onto a template of axial sections (from z=28 to z=64) showing activations for conceptual decisions common to numbers and object names (yellow), numbers > object names (i.e. number selectivity, red), RT effects for all conceptual decisions for numbers and object names (blue) and RT effects for numbers > object names (green) averaged for paradigm 1 and 2 (p<0.001). Left is left.

B) Number selectivity

There was no main effect of numbers more than object names across conceptual and perceptual tasks but there was an interaction between stimulus (numbers > object names) and task (conceptual > perceptual). This is because number selectivity was significant for conceptual decision (but not perceptual decisions) in the right posterior IPS extending into the right angular gyrus, right superior parietal and right supramarginal gyri. There was also a significant number selective activation in the left supramarginal gyrus and the right inferior frontal cortex (Table 3, analysis 1). These effects were observed for both quantity and non-quantity number processing consistent with the absence of an interaction between [number > object names] and [quantity >. non-quantity tasks].

Table 3. Number selectivity.

Activations for numbers > object names (number selectivity) for conceptual tasks only, conceptual > perceptual judgments, quantity and non-quantity judgments only in Analysis 1 (RTs modeled separately for numbers and object names) and for conceptual tasks only in Analysis 2 (RTs modeled over number & object names).

					Analysis 1				Analysis 2
	Coordinates				Conceptual only	Conceptual> perceptual	Quantity only	Non-quantity only	Conceptual only	No. of voxels^
Area	H	x	y	z	z-scores
Posterior IPS	R	28	−70	32	6.0	4.9	6.1	4.8	4.7	340
		32	−66	32	4.2	3.8	4.0	3.2	4.3
		32	−80	34	4.6	4.4	3.4	3.2	4.4
Angular gyrus	R	42	−78	34	3.4*	n.s.	3.8*	3.1*	3.7
		38	−78	30	4.6	4.0	4.5	3.5	3.9
		32	−76	42	5.2	4.4	4.0	4.6	n.s.	433
		30	−62	46	3.9	3.0	2.8	3.2	4.2
		32	−56	42	n.s.	n.s.	n.s.	n.s.	4.5
Superior parietal	R	22	−68	56	5.5	4.9	4.9	4.1	4.3
		18	−70	56	5.4	4.7	4.2	3.3	3.4
		32	−64	54	5.1	4.1	5.1	5.0	3.2
Supramarginal gyrus	R	48	−48	40	3.8	3.4	3.7	2.1	3.4
		44	−44	48	4.0	2.8	2.6	2.8	3.3
	L	−40	−44	40	5.4	4.8	4.5	4.8	n.s.
		−52	−4	46	3.2	1.7	1.8	1.7	n.s.

Legend: In bold significant at p<0.05 corrected for multiple comparisons, H = Hemisphere, L = Left; R = Right

^{^}p<0.001

^*Within 4mm

The anatomical location of the number selective effects is illustrated in red in Figure 2. Relative to the main effect of conceptual decisions for both numbers and object names, number selectivity was right lateralized and extended more inferiorly in the parietal lobes.

C) The main effect of RT related processes (over numbers and object names)

Nothing reached significance at p<0.05 corrected for multiple comparisons across the whole brain. At a more lenient statistical threshold in the parietal lobes (p<0.001), a main effect of RTs (over numbers and object names) was observed in bilateral superior parietal cortex and very dorsal parts of the angular and supramarginal gyri. The more dorsal locations of RT effects relative to number selective effects (reported in B above) are illustrated in blue in Figure 2.

D) Number selective RT effects

At an uncorrected threshold only (p<0.001), there were only two areas in the right dorsal angular gyrus and the right dorsal supramarginal gyrus where activation correlated with number RTs more than object name RTs (Table 4, analysis 1, and green areas in Figure 2).

Table 4. Reaction-time effects.

Activations for response time related effects for conceptual judgments for number and object names together and numbers > object names in Analysis 1 (RTs modeled separately for numbers and object names) and for conceptual judgments for number and object names together in Analysis 2 (RTs modeled over number & object names).

						Analysis 1			Analysis 2
	Coordinates					Numbers & object names	Numbers > words		Numbers & object names
Area	H	x	y	z	BA	z-scores		No. of voxels^	z-scores	No. of voxels^
Superior parietal	R	26	−70	60	7	3.9	n.s.	65	3.4	494
		28	−72	50		2.8	n.s.		4.0
		34	−62	60		3.7	n.s.		4.0
		16	−80	54		4.1	n.s.	16	2.6
Dorsal angular gyrus		34	−70	50		n.s.	3.9	43	4.5
		40	−64	52		3.4	n.s.		4.5
		36	−62	52		3.2	3.1		4.5
		40	−56	54		3.1	n.s.		4.5
Dorsal supramarginal		50	−44	54	40	n.s.	3.7	22	3.9
Posterior IPS	R	30	−70	32		ns	ns		3.9
Superior parietal	L	−24	−60	64	7	4.1	n.s.	41	2.5	71
Dorsal angular gyrus		−34	−56	50		4.3	n.s.	30	3.5
		−30	−52	46		2.8	n.s.		4.0
		−0	−52	56		3.5	n.s.		3.8
		−34	−60	46		3.0	n.s.		3.5
Dorsal supramarginal		−48	−36	56	40	3.8	n.s.	56	3.3
Frontal	R	44	8	28		2.5	n.s.		5.7	137
	L	−48	28	20		2.5	n.s.		4.0	60

Legend: H = Hemisphere, L = Left; R = Right

^{^}p<0.001

^*Within 4mm

Critically, the effects of condition (analysis A and B) and RTs (analysis C and D) never overlap, even when the threshold is lowered to p<0.05 uncorrected. This is because the first level analyses modeled the effect of RTs as co-variates on the main effect of conditions, therefore condition effects are those after RTs are factored out. Conversely, RT related effects are those after condition effects are modeled out.

ANALYSIS SET 2: When RTs were modeled over numbers and object names

Number-selectivity

After the main effect of RT related processes (over numbers and object names) was factored out, right parietal activation for numbers relative to object names remained significant after correction for multiple comparisons across the whole brain in extent (Table 3, Analysis 2; and red areas in Figure 3). However, consistent with the findings of Göbel et al. (2004), number selectivity was no longer significant in the left parietal cortex, the highest peak being at (−30, −76, 28, Z-score = 2.8 (7 voxels on the left at p<0.01 versus 2988 voxels on the right at p<0.01). The greater effect of number selectivity in the right compared to the left hemisphere was shown in a significant hemisphere by numerosity interaction (t(20) = −2.592, p< 0.02, see Methods for details).

Figure 3. Number selectivity and RT effects (analysis 2).

Activations rendered onto a template of axial sections (from z=28 to z=64) showing number selectivity (red) once RT-related effects have been factored out, and RT effects summed over numbers and object names (blue) averaged for paradigm 1 and 2 (p<0.001). Left is left.

Response time related effects (over numbers and object names)

Longer RTs increased activation in bilateral frontal and dorsal parietal areas (Table 3, analysis 2; and blue areas in Figure 3). These effects were significant after correction for multiple comparisons in either height or extent.

In sum, our results have dissociated number-selective right-parietal activation from other stimulus-independent task effects and RT related effects. These effects were consistent across paradigm 1 and 2. In other words, we can also exclude explanations in terms of hand of response, stimulus duration and participants’ age.

DISCUSSION

In this study, we aimed to dissociate parietal activation that was number-selective from parietal activation driven by other conceptual and response-related processes and to compare these results in the left and right hemispheres. Number-selective activation was identified by comparing numbers to object names during the same conceptual and perceptual tasks. Activation related to increasing RTs was identified by correlating RTs over numbers and object names separately (stimulus-independent effects) or for each stimulus separately (stimulus-dependent effects). Below, we discuss three novel findings from this study which can be summarized as follow.

First, in several right parietal regions, activation was selective for conceptual decisions on numbers even when RT-related processes were fully factored out. Second, the right parietal number-selective effects were task-dependent because they were observed during quantity and non-quantity conceptual tasks but not during a low level color decision task. Third, we demonstrate a different pattern of effects in the left and the right parietal cortex which has implications for the functional role of the left and right hemispheres and for the design of future patient and functional neuro-imaging studies.

Throughout the discussion, we describe the anatomical locations of the different effects in terms of their relative position to one another. This is because the functional dissociation that we have observed does not fit neatly with anatomical labels or boundaries. For example, different regions of the angular gyri expressed either number selectivity, response time related effects or stimulus-independent task effects. Likewise, different parts of the intraparietal sulcus and supramarginal gyri showed either number selective or stimulus independent effects.

Number-selectivity in the parietal lobes

Number selective effects were observed during conceptual tasks in the right posterior intraparietal sulcus extending into the right angular and supramarginal gyri. These effects dissociated from other activations in more dorsal right parietal regions, and throughout the left intraparietal sulcus.

Our finding of number-selective activations was in the context of several novel features of our experimental design and analysis. The experimental design carefully matched the numerical and non-numerical conditions by using identical tasks with numbers and object names (with the exception of ‘more/larger number’ vs ‘more/larger object’). These tasks included quantity judgments, perceptual judgments and a novel non-quantity conceptual task that required the extraction of learnt information (e.g. Does ‘10.07’ indicate a summer month? Does ‘10.07’ indicate a working time?) but was unlikely to be based on a quantity strategy. Our rationale for including this non-quantity task was as follows: If parietal activation was driven by quantity processing then it should be higher for the quantity than non-quantity tasks for numbers, object names or both. Our results did not identify any areas that met these criteria. In contrast, our results showed that in many left parietal and dorsal right parietal regions activations were common to quantity and non-quantity conceptual tasks on both numbers and object names, suggesting that this could be related to other processes including the extraction of learnt information.

Another novel aspect of our approach is that our statistical analysis factored out any activation that correlated with response times within and across conditions and subjects, even though the overall mean response times for numbers and object names were not significantly different. The only other study that used a similar approach (Göbel et al., 2004) claimed that number selectivity in the left parietal lobe could not be distinguished from response time effects. We replicate the pattern of effects observed by Göbel et al. (2004) in the left hemisphere, i.e. left parietal activation is not number selective when response times are factored out. However, our final conclusion contrasts with that of Göbel et al. (2004) because we observed number-selectivity in the right parietal lobe that was not reported by Göbel et al. This key difference in our results is likely to be due to differences between our tasks and theirs. Specifically, we used the same conceptual tasks on both numbers and object names whereas Göbel et al. contrasted number comparison with two low-level perceptual tasks, i.e. vertical orientation judgment on numbers and non-numbers.

Task-dependent number selectivity in the right parietal lobe

Our observation that number selectivity in the right parietal lobe emerged only during the conceptual but not the perceptual tasks is consistent with the theoretical proposals that the parietal areas are engaged in the conceptual representation of numbers (Dehaene, 1998; Dehaene & Cohen, 1995). However, it differs from studies that observed similar parietal activations for numbers during conceptual and perceptual tasks (e.g. Göbel et al., 2004; Eger et al., 2003; Shuman & Kanwisher, 2004; Tang et al., 2006; Thioux et al., 2005). One possible explanation for this discrepancy is that previous tasks considered to be non-conceptual (such as ‘stimulus detection’, i.e. distinguishing number stimuli from another types of stimuli, Eger et al., 2003), activated the parietal lobes because they actually required conceptual processing in the form of identity recognition. Moreover, other non-conceptual tasks involved visual search processes (e.g. Göbel et al., 2004; Tang et al., 2006; Thioux et al., 2005) that previous studies have shown to activate the superior parietal lobes (e.g. Coull et al., 2003; Pollman et al., 2003).

Our key result was that number-selective right parietal activation was still observed during both the quantity and non-quantity conceptual tasks involving numbers, after controlling for task and response time effects. This suggests that right parietal activation might reflect conceptual processing that is involved in numbers more than object names. Recently, Ischebeck et al. (2008) provided evidence for the role of intraparietal areas in processing the ordinal aspect of numbers by demonstrating greater intraparietal activation during the generation of the names of the months, which requires an ordered sequence, compared to the generation of non-ordered names of animals. Critically, they found no significant difference between ordered generation of months and numbers. Likewise, Gevers et al (2003) provided similar evidence based on chronometric techniques. Our study involved processing of ordered sequences, although not in terms of generating ordered information, and this processing may occur automatically in the presence of numbers but not in the presence of object names. In addition, our study suggests that number selective conceptual processing is more related to the right than left parietal lobes.

Number processing in the left parietal lobe

Conceptual decisions on numbers and object names resulted in equal activation of the left angular and supramarginal gyri as well as bilateral dorsal areas in the intraparietal sulcus, where activation correlated with response times irrespective of the stimulus. Therefore this suggests that the left parietal lobe is involved in numerical processing although not exclusively. By showing left and right parietal activations, our results draw together previous observations of number selectivity in the right parietal lobe (e.g. Chochon et al., 1999; Dehaene et al., 1996; Fias et al., 2003; Le Clec’H et al., 1999; Nacchache & Dehaene, 2001; Pinel et al., 2001; Thioux et al., 2005) with other types of processing in the left parietal lobe (Göbel et al., 2004). However, our results may appear to conflict with functional imaging studies that have reported left parietal number-selective effects (e.g. Ansari et al., 2006; Cantlon et al., 2006; Cohen Kadosh et al., 2007; Piazza et al., 2004, 2007) and neuropsychological studies suggesting numerical impairments following left but not right parietal lesions (e.g. Cipolotti et al., 1991; Dehaene & Cohen, 1991; Lemer et al., 2003; Polk et al., 2003).

There are many possible reasons for the inconsistencies between studies. Number-selective effects can be driven by many different processes and they therefore depend on the nature of both the task and the stimuli. For example, in some of the studies reporting number activations in the left parietal lobe the direct comparison between numerical and non-numerical stimuli was beyond the scope of the study, therefore it was unclear to what extent the effects were selective for numbers (Ansari et al. 2006; Chochon et al., 1999; Cohen Kadosh et al., 2007; Piazza et al., 2004, 2007; Simon et al., 2002). In other studies, numerical and non-numerical stimuli have been directly compared but in conditions differing in task demands (e.g. Chochon et al., 1999; Le Clec’H et al., 2000; Pesenti et al., 2000; Thioux et al., 2005). For instance, number quantity processing (e.g. which is larger: 3 or 4?) was compared to non-quantity tasks such as number reading or addition (e.g. Chochon et al., 1999; Dehaene et al., 1999; Simon et al., 2002), or to decisions on continuous, non-countable features (e.g. luminance or physical size, Cohen Kadosh et al., 2008a; Fias et al., 2003; Pinel et al., 2004). The increased left parietal activation for number comparison reported by these studies might have reflected a more general process of the extraction and comparison of learnt information (consistent with the present findings for left parietal). Such general processes may have been more involved in number comparisons in these past studies because reading and addition can be based on rote verbal memory, while luminance and physical size judgments can be based on comparison of analogue magnitudes that do not need to be extracted from symbolic stimuli. Our suggestion is therefore that left parietal activation during conceptual tasks reflects the extraction and comparison of learnt information irrespective of stimulus-type. As demonstrated by our results, left parietal activation does not depend on whether information is extracted and compared from numbers or object names, when response times are controlled. We also note that our left parietal activations are very similar to the brain networks previously described for either number comparison or distance effects (e.g., Pesenti, et al., 2000; Pinel et al., 1999), consistent with the idea that these left-lateralized activations reflect the extraction and the comparison of numerical information.

Our results have provided new evidence that these processes are not specific for numerical stimuli, but they occur irrespectively of the stimulus used. Moreover, our results are in keeping with the proposal that the left parietal lobe is more engaged in exact processing symbolic, language-based numerical information, as opposed to the right parietal lobe being more involved in approximate, pre-verbal numerical representations (Chochon et al., 1999; Cohen Kadosh et al., 2007; Izard et al., 2008; Stanescu-Cosson et al., 2000). Exact representation of symbolic numbers requires extraction of information from the numerical symbols before processing and we suggest that the left parietal regions may be the locus where this occurs, although not just for numerical stimuli (see also Cohen Kadosh et al., 2008b for a similar proposal).

How do these conclusions fit with the neuropsychological literature that has reported number-selective deficits following left parietal damage? Is it the case that left parietal damage impairs the extraction and comparison of learnt information whereas right parietal damage impairs the processing of number semantics? At present the answer is unclear because patients with difficulties processing numbers have not been tested on conceptual tasks such as those used in our fMRI experiment. It is therefore possible that left parietal lesions impair performance on such conceptual tasks involving object names (as well as numbers). However, it is also possible that left parietal lesions could impair performance on numbers more than object names even when the same tasks are used. This could arise if, after brain damage, a novel strategy was learnt that was more effective when the task was performed on object names than numbers. Along the same lines, the left and right parietal lobes may recover in different ways after brain damage such that, for instance, following right parietal lesions the undamaged left parietal areas may still be able to extract and compare symbolic numbers thereby masking the loss of number processing in the right hemisphere. Likewise, left parietal regions may not be able to fully compensate the role of the right parietal regions as shown by cases of developmental dyscalculia which present with right parietal dysfunction (e.g. Molko et al., 2003; Price et al., 2008; Rotzer et al., 2008).

Another reason why numerical impairments are more often associated with left rather than right parietal lesions may be due to the fact that left-lesioned patients are routinely tested with symbolic number tasks rather than approximate non-symbolic number tasks (e.g. Cipolotti et al., 1991; Delazer & Benke, 1997). Nevertheless, when the latter tasks have been used, selectively spared ability to approximate non-symbolic numbers has been reported in patients with left parietal lesions (e.g. Dehaene & Cohen, 1991; Lemer et al., 2003; Polk et al., 2001). Similarly, the scarcity of neuropsychological patients with right parietal lesions and numerical impairments may be partly due to the fact that these patients are routinely tested with exact, symbolic number tasks, such as number comparison and arithmetical operations, which are usually preserved as they may be performed by intact left parietal regions (e.g. Priftis, et al., 2006; Vuilleumier et al., 2004; Zorzi et al., 2002, 2006). The results of our study have therefore generated a new set of hypotheses that need to be investigated with future behavioral and functional imaging studies with patients.

Summary and Conclusions

In summary, both left and the right parietal regions are activated during conceptual decisions on numbers. On the basis of our own analyses and previous functional imaging data, we propose that the left parietal number activation reflects a range of processes correlating with RTs, including the extraction and comparison of learnt information. On the other hand, the right parietal number activation is more involved in conceptual processing of numbers than object names. These findings motivate the investigation of new hypotheses to be tested in patients with left and right parietal damage. They also highlight the importance of controlling for task and response time effects when searching for number selective effects.