A Metabolite-Sensitive, Thermodynamically Constrained Model of Cardiac Cross-Bridge Cycling: Implications for Force Development during Ischemia

Abstract

We present a metabolically regulated model of cardiac active force generation with which we investigate the effects of ischemia on maximum force production. Our model, based on a model of cross-bridge kinetics that was developed by others, reproduces many of the observed effects of MgATP, MgADP, Pi, and H⁺ on force development while retaining the force/length/Ca²⁺ properties of the original model. We introduce three new parameters to account for the competitive binding of H⁺ to the Ca²⁺ binding site on troponin C and the binding of MgADP within the cross-bridge cycle. These parameters, along with the Pi and H⁺ regulatory steps within the cross-bridge cycle, were constrained using data from the literature and validated using a range of metabolic and sinusoidal length perturbation protocols. The placement of the MgADP binding step between two strongly-bound and force-generating states leads to the emergence of an unexpected effect on the force-MgADP curve, where the trend of the relationship (positive or negative) depends on the concentrations of the other metabolites and [H⁺]. The model is used to investigate the sensitivity of maximum force production to changes in metabolite concentrations during the development of ischemia.

Introduction

For the heart to fulfill its function as a pump, its musculature must cyclically develop force, shorten, and relax. This cycle is achieved by the expenditure of metabolic energy via pathways, the end-products of which are inhibitory to the cycle. Such inhibition becomes particularly crucial during periods of hypoxia or ischemia when the reduction in supply of adenosine triphosphate (ATP) from mitochondrial oxidative phosphorylation, and the attendant accumulation of inorganic phosphate (Pi), adenosine diphosphate (ADP), and protons may interfere with the cyclic interactions between actin monomers and myosin heads protruding from the thick filaments (1).

Our aim is to develop a thermodynamically consistent and metabolite-sensitive model of cardiac cross-bridge cycling to explore the influence of these metabolites on force production under physiological and ischemic conditions. There are a number of criteria that such a model must meet. The cycling action of cross-bridges is driven by the free energy released from the hydrolysis of ATP into ADP and Pi (i.e., free energy transduction). Firstly, therefore, the model must incorporate a free energy-transducing thermodynamic cycle, with pathways that allow it to be driven in both forward and backward directions (2). This excludes fading-memory models that do not explicitly represent the cross-bridge cycle (3,4). Secondly, the model must be thermodynamically consistent as defined by Hill (5), where a constraint is introduced to relate the rate constants of the model to the free energy of ATP hydrolysis. Thirdly, the model must explicitly incorporate the regulatory effects of MgATP and its hydrolysis products, MgADP, Pi, and H⁺. Sliding-filament models, derived from the seminal work of Huxley (6), are based on strain-dependent distributions of cross-bridge populations, and have been extended to include metabolite interactions (7). However, the explicit representation of a spatial dimension (cross-bridge strain) requires the solution of partial differential equations (PDEs), which renders them computationally expensive and not ideal for integrating into cell or tissue models. More recently, mean-field models have been proposed that ignore the microscopic details of cross-bridge population distributions and, instead, ascribe the behavior of the entire cross-bridge population to an average cross-bridge cycle, removing the need for PDEs.

In this study, we extend the recent mean-field model by Rice et al. (8) such that it conforms to the criteria listed above. The Rice et al. (8) model describes Ca²⁺ activation and cross-bridge cycling kinetics and can reproduce a range of myofilament behavior including length- and temperature-dependent effects. This model provides a foundation onto which a biochemical scheme of ATP hydrolysis is integrated to develop a thermodynamically consistent and metabolite-sensitive model of cross-bridge cycling kinetics (which we denote as the Extended Model). The Extended Model introduces three new parameters that are fitted using cardiac data from the literature and validated against a range of metabolic and sinusoidal length change protocols. The model is then used to investigate the effects of changing metabolite concentrations, observed after the onset of ischemia, on the development of active force.

Methods

A schematic of the four-state model by Rice et al. (8) is shown in Fig. 1 A. Rice et al. parameterized their model for rat cardiac tissue, and include a parameter xbmod_species (which multiplies all rate constants) to adjust to different species. Consistent with our previous studies (9–11), we develop a model parameterized for guinea pig myocardium, setting xbmod_species = 0.2, effectively slowing the kinetics by fivefold from rat, following the findings of Palmer and Kentish (12). We parameterize and validate against guinea pig data where possible.

Figure 1.

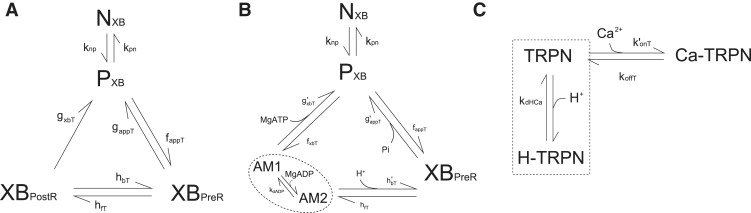
(A) Original model from Rice et al. (8). (B) The original model is modified to include metabolite dependence (i.e., Extended Model). AM1 and AM2 are two strongly-bound rapid-equilibrium states (dotted ellipse). The rate constants g′_appT, g′_xbT, and h′_bT are true first-order rate constants that are independent of metabolite concentrations whereas g_appT, g_xbT, and h_bT from the original model are pseudo-first-order rate constants that are assumed to be implicit functions of MgATP, MgADP, Pi, and H⁺ (see text for details.) (C) Schematic of the competitive binding of H⁺ to the Ca²⁺ binding site on troponin C. TRPN and H-TRPN are assumed to be in rapid-equilibrium (dotted rectangle). The on-rate for Ca²⁺ binding, k′_onT, is modified to include the H⁺ regulation.

The original model implicitly assumes that cross-bridge cycling is irreversible by omitting a reverse step between states P_XB and XBpostR. To account for the full (reversible) thermodynamic cycle we add a reverse transition step, f_xbT (Fig. 1 B), to allow transitions from state P back to state XBpostR, representing the release of MgATP as the myosin-head transitions from a weakly attached state back to a strongly attached state. The value of f_xbT is determined by the thermodynamic constraint that links the rate constants in the cycle to the hydrolysis of MgATP (5),

$$\frac{{\prod {\alpha }_{\text{i}}}^{+}}{{\prod {\alpha }_{\text{i}}}^{-}}=e^{\frac{-\Delta G_{\text{ATP}}}{RT}},$$ (1)

where α_i⁺ and α_i⁻ are the pseudo first-order forward and backward rate constants for state i and

$$\Delta G_{\text{ATP}}=\Delta G_{\text{ATP}}^{\text{0}}+RT\ln \frac{\left[\text{MgADP}\right]\left[\text{Pi}\right]\left[{\text{H}}^{+}\right]}{\left[\text{MgATP}\right]},$$ (2)

where ΔG⁰_ATP is the standard free energy of MgATP hydrolysis and H⁺ is the proton released during ATP hydrolysis, which we label the metabolic proton. (The equation for f_xbT is given in the Appendix.)

Metabolite dependencies are incorporated into the transition rates between steps of the cycle using mass-action kinetics. We will assume that normal physiological metabolic conditions are given by MgATP = 5 mM, MgADP = 36 μM, Pi = 2 mM, and pH = 7.15, and that the parameters and outputs from Rice et al. (8) correspond to these conditions.

MgATP

The binding of MgATP in striated muscle detaches the cross-bridge from the strongly-bound state after execution of the power stroke (13–16). Measurements of isometric force have shown a descending trend with increasing concentrations of MgATP, consistent with the dissociation of strongly-bound cross-bridges (17,18). In the Extended Model (Fig. 1 B), the MgATP binding step is therefore placed in the transition from state XB_PostR to state P_XB (g_xbT), during which the strongly-bound cross-bridge becomes detached. It is also assumed that hydrolysis of ATP occurs at this step. The Rice et al. (8) parameter for the transition, g_xbT, is adjusted to account for physiological MgATP concentrations using the formulation

$${g^{\prime }}_{\text{xbT}}=\frac{g_{\text{xbT}}}{{\text{MgATP}}^{\prime }},$$ (3)

where g′_xbT represents the true first-order rate constant, MgATP′ is the physiological MgATP concentration, and g_xbT is the pseudo-first order rate constant from the Rice et al. (8) model. Following mass-action kinetics, the MgATP-dependent transition rate from state XB_PostR to state P_XB is therefore given by

$${g^{\prime }}_{\text{xbT}}\times \left[\text{MgATP}\right]\text{.}$$ (4)

Under normal metabolic conditions, when [MgATP] = MgATP′, this gives g′_xbT = g_xbT. This formulation is applied to the other metabolite dependencies described below. The equation for this transition rate is not yet complete as g′_xbT is also modified by MgADP (see below).

Inorganic phosphate

Biochemical and mechanical experiments in both skeletal (17,18) and cardiac muscle (19,20) have demonstrated that increasing [Pi] leads to a decrease in isometric force. Under isometric conditions, the sole force-producing state in the model in the literature (21,22) is XB_PostR, whereas XB_preR remains as a strongly-bound state that can contribute to cross-bridge stiffness. The binding of Pi can therefore be placed at either h_bT or g_appT, because either will drive the cross-bridge cycle away from XB_PostR and decrease isometric force with increasing [Pi]. We find that placing the Pi-binding step at g_appT produces a better quantitative fit to the data (see below). The adjustment of the original rate constant to account for [Pi] is given by

$${g^{\prime }}_{\text{appT}}=\frac{g_{\text{appT}}}{P{i}^{\prime }},$$ (5)

where the parameters are defined equivalently to those in Eq. 3.

pH

Changes in pH have been shown to affect the force-Ca curve in two distinct ways: A decrease of pH leads to a decrease in the Ca²⁺ sensitivity as well as a decrease in the maximum force generated at saturating levels of Ca²⁺ (23,24). To incorporate these effects, we include two distinct mechanisms of sensitivity to pH. We assume that the decrease in Ca²⁺ sensitivity with decreasing pH is due to the competitive binding of H⁺ to the single Ca²⁺ binding site on troponin C (Fig. 1 C) (25,26), modeled as a rapid equilibrium reaction identically for both populations of troponin with dissociation constant k_dHCa and cooperativity m. This modifies the rate constant for the binding of Ca²⁺ to troponin C,

$${k^{\prime }}_{\text{onT}}=\frac{k_{\text{dHCa}}^{\text{m}}+H^{\prime \text{m}}}{k_{\text{dHCa}}^{\text{m}}+{\left[{\text{H}}^{+}\right]}^{\text{m}}}\times k_{\text{onT}},$$ (6)

where k′_onT is the new apparent rate constant for Ca²⁺ binding, k_onT is the original Ca²⁺ binding rate constant, and H′ is the reference proton concentration. The apparent rate constant for Ca²⁺ binding affects the transition rates responsible for activation of the cross-bridge cycle (k_pnT and k_npT). The two parameters that govern the mechanism of competitive H⁺ binding, k_dHCa and m, are determined using data from the literature (see below).

The inclusion of competitive H⁺ binding can account for the shift in Ca²⁺ sensitivity but cannot reproduce the change in maximum tension at saturating Ca²⁺ concentration. This effect can be incorporated by assigning one of the (reverse) rate constants in the cross-bridge cycle (Fig. 1 A) to be associated with the release of the metabolic H⁺ (a by-product of the ATP hydrolysis reaction; see Eq. 2). The two positions at which this reaction could occur are h_bT and g_appT, as both can lead to a decrease in force with an increase in H⁺ concentration. We locate H⁺ release at the reverse isomerization step, h_bT, because this produces a drop in force of a magnitude that is in better agreement with the data (see below). The adjustment of the rate constant to account for the physiological H⁺ concentration is given by

$${h^{\prime }}_{\text{bT}}=\frac{h_{\text{bT}}}{H^{\prime }},$$ (7)

where the parameters are defined equivalently to those in Eq. 3. The H⁺-dependent transition from XB_PostR to XB_PreR is therefore given by

$${h^{\prime }}_{\text{bT}}\times \left[{\text{H}}^{+}\right]\text{.}$$ (8)

Note that the equation for this transition rate is not yet complete, as h′_bT is also modified by MgADP (see below).

MgADP

Mechanical measurements have shown that MgADP binds to attached cross-bridges (27–30) that remain attached after the binding event (31). Increasing MgADP concentrations also leads to an increase in steady-state isometric force development in both skeletal (17,32) and cardiac (21,33) muscle preparations. The only transition between strongly-bound states in the four-state Rice et al. (8) model where the MgADP binding event could be placed is from XBpostR to XBpreR. This, however, leads to a decrease in isometric force development because XBpreR is a lower-force state than XBpostR. The four-state model therefore contains an insufficient number of states to represent the binding of MgADP. Hence, we expand state XBPostR into two force-producing substates, AM1 and AM2, to create a five-state model (Fig. 1 B), where we assume that the two substates contribute equally to total force and sum to produce the same force as state XBpostR, and MgADP is assumed to bind to state AM1. This five-state construction is equivalent to the four-state model when binding and unbinding of MgADP is rapid (states AM1 and AM2 are in rapid equilibrium). We model the MgADP binding step with a single parameter representing the MgADP dissociation constant, k_dADP. This modifies the rates of transitions leaving state XB_PostR, i.e., g′_xbT and h′_bT, by

$$\frac{k_{\text{dADP}}+MgAD{P}^{\prime }}{k_{\text{dADP}}+\left[\text{MgADP}\right]}$$

and

$$\left(\frac{k_{\text{dADP}}+MgAD{P}^{\prime }}{MgAD{P}^{\prime }}\right)\times \left(\frac{\left[\text{MgADP}\right]}{k_{\text{dADP}}+\left[\text{MgADP}\right]}\right),$$

respectively, where MgADP′ is the normal physiological MgADP concentration and the dissociation constant k_dADP is constrained by fitting the model to isometric force data (see below). Incorporating Eq. 4, the complete MgATP and MgADP-dependent transition from XB_PostR to P_XB is given by

$$\left[\text{MgATP}\right]\times {g^{\prime }}_{\text{xbT}}\times \left(\frac{k_{\text{dADP}}+MgAD{P}^{\prime }}{k_{\text{dADP}}+\left[\text{MgADP}\right]}\right)\text{.}$$ (9)

By incorporating Eq. 8, the complete H⁺ and MgADP-dependent transition from XB_PostR to XB_PreR is determined as

$$\left[{\text{H}}^{+}\right]\times {h^{\prime }}_{\text{bT}}\times \left(\frac{k_{\text{dADP}}+MgAD{P}^{\prime }}{MgAD{P}^{\prime }}\times \frac{\left[\text{MgADP}\right]}{k_{\text{dADP}}+\left[\text{MgADP}\right]}\right)\text{.}$$ (10)

A full description of the model formulation and equations that have been modified from Rice et al. (8) is given in the Appendix and the Supporting Material, and a detailed description of all model parameters is given in the Supporting Material.

Parameter estimation and model selection

Previous studies have suggested that placement of the Pi-binding step at either g_appT or h_bT provides plausible explanations for the isometric force-Pi data (19,20,34). We found that the Extended Model best fits the data when the Pi binding step is placed at g_appT (Fig. 2 A). There is also evidence demonstrating a decrease in stiffness with increased [Pi], which is consistent with the binding of Pi causing the dissociation of cross-bridge attachment (3,35). This leaves the binding location of the metabolic H⁺ along with the three new parameters, k_dADP, k_dHCa, and m, to be determined.

Figure 2.

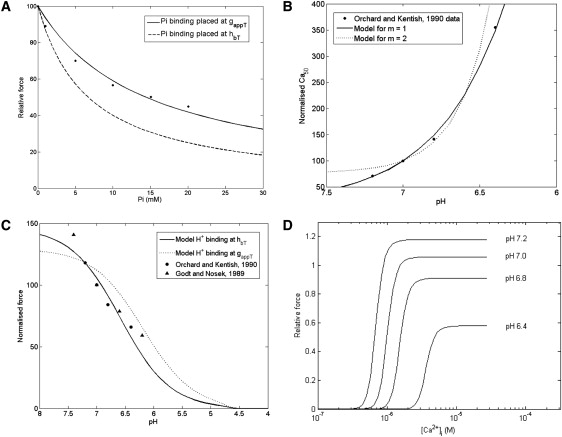
(A) Comparing the effect of modeling the Pi binding step at either g_appT or h_bT on the force-Pi curve. The data points are from rabbit papillary muscle (21). Other conditions in the simulations: [MgATP] = 5 mM, [MgADP] = 36.3 μM, pH = 7.15, [Ca²⁺]_i = 200 μM (maximum activation), SL = 2.2 μM, and T = 22°C. (B) Best fit of the relative Ca²⁺ sensitivities (Ca₅₀) of the Extended Model to data from Orchard and Kentish (24), at m = 1 (k_dHCa = 2 × 10⁻⁵ mM) and at m = 2 (k_dHCa = 1.8 × 10⁻⁴ mM²). The Ca₅₀ values on the y axis are normalized to the Ca₅₀ at pH = 7. (C) Model simulation of maximum steady-state force (under saturated Ca²⁺ conditions) as a function of pH. The model simulations correspond to the placement of the metabolic H⁺ release step at either g_appT or h_bT in the cross-bridge cycle. The simulations are normalized to force at pH 7.2 (see Fig. S1 in Supporting Material for original data). (D) Model simulation of steady-state force-Ca curves as a function of pH. Other conditions in the simulations of panels B–D: SL = 2.1 μM; T = 30°C. Note that metabolite concentrations are set to their reference values.

Experiments in cardiac muscle preparations have measured an increase in isometric force of ∼10–15% when [MgADP] is increased from zero to saturating concentrations in the millimolar range (21). We constrain the MgADP dissociation constant, k_dADP, to give a 13% increase in isometric force when [MgADP] is increased from 0 to 3 mM (21). This produces a k_dADP value of 4 μM, which compares well with those measured by Johnson and Adams (36) (14 μm at 23°C and 5 μm at 15°C) and with Kardami et al. (37) (8 μm at 5°C) (which were obtained from bovine cardiac preparations using independent assaying methodologies).

To determine the parameters governing the competitive binding of H⁺ to the Ca²⁺ binding sites on troponin C, we use the guinea pig force-Ca data of Orchard and Kentish (24). For reasons considered in the Discussion, the slopes of the force-Ca data are relatively flat (n = 2) when compared to the curves produced by the Rice et al. (8) model (n = 7). Therefore, we fit the relative change in Ca²⁺ sensitivity (Ca₅₀) brought about by changes in H⁺ concentration. Fig. 2 B shows the result of fitting the Extended Model to the normalized data from Orchard and Kentish (24). The Ca₅₀ values for the data set have been normalized to the Ca₅₀ at pH = 7. The best fit to the data is obtained at m = 1 and k_dHCa = 2 × 10⁻⁵ mM. For increasing values of m, the curve becomes more concave and does not fit the data as well. The value of 1 for the cooperativity constant, m, can be interpreted as the binding of a single H⁺ to the Ca²⁺ binding site and, in this model, is favored over the binding of two or more H⁺.

Fig. 2 C shows model simulations when the metabolic H⁺ is released at either g_appT or h_bT (Fig. 1 B). Both simulations are qualitatively consistent with the data inasmuch as a decrease of pH leads to a decrease in maximum steady-state force. However, quantitatively, the placement of the H⁺ release step at h_bT produces better agreement with the data from Orchard and Kentish (24) (guinea pig trabeculae) and Godt and Nosek (21) (rabbit papillary). Fig. 2 D shows the overall effect of pH on the force-Ca curve, giving the expected decrease in Ca²⁺ sensitivity and maximum force with decreasing pH, comparable to experimental data from Orchard and Kentish (24) (shown in the Supporting Material—but exhibiting a much steeper slope, because the experimental data of Orchard and Kentish (24) are from skinned preparations).

Results

Force redevelopment and MgATP

The Extended Model was used to predict the effect of varying MgATP concentration on the isometric force response and the rate of tension redevelopment after a sudden length change (Fig. 3 A). An increase in MgATP concentration leads to a decrease in the normalized force, because this favors the detachment of strongly-bound cross-bridges (g′_xbT) and thereby reduces the proportion of cross-bridges in the strongly-bound state. The model simulations show that the force-MgATP curve is sensitive to low levels of MgADP concentration, because decrease of MgADP represents a reduction in the competition for the strongly-bound state AM1 that results in a large drop in force with increasing MgATP. The data-set from Ebus et al. (18) lies within the family of curves simulated by the model at low to physiological MgADP concentrations. Fig. 3, B and C, shows the force redevelopment after the imposition of a sudden length change, which is assumed to detach almost all the strongly-bound cross bridges thus reducing the developed force to zero, at three different MgATP concentrations. Rapid detachment of cross-bridges is simulated (at time t = 300 ms) by decreasing 1000-fold the forward transition rates, f_appT and h_fT, and increasing 1000-fold the backward rate constants, g′_appT and h′_bT, for a period of 5 ms. Fig. 3 B shows that the steady-state force increases with decreasing MgATP concentration, consistent with Fig. 3 A, whereas Fig. 3 C shows that the rate of tension redevelopment decreases with decreasing MgATP concentration. These predictions are consistent with the results of Ebus et al. (18) (Fig. 3 D), who also demonstrated a decrease in rate of tension redevelopment with decreasing MgATP concentrations.

Figure 3.

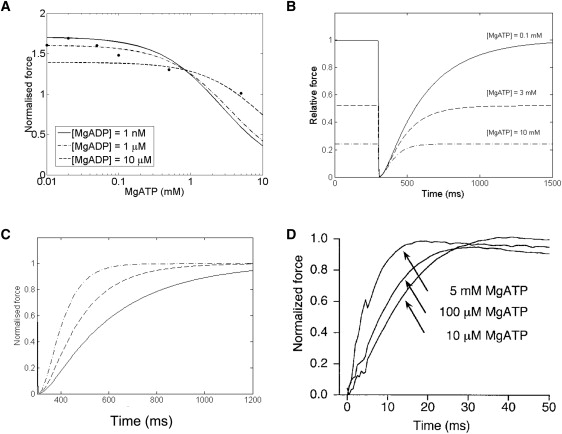
(A) Model simulations of isometric force as a function of MgATP concentration at different MgADP concentrations. The data points are from rat ventricular tissue (18) for which MgADP concentration is not specified and therefore assumed to be low/zero. The simulated curves are normalized to the maximum force from the data. Other conditions in the simulation: [Pi] = 0 mM, pH = 7, [Ca²⁺] = 200 μM, SL = 2.1 μM, and T = 20°C. (B) Model simulations of the time course of isometric force recovery after a sudden length change as a function of MgATP concentration. The change in length is applied at 300 ms (see text for details). The curves are normalized to the maximum force at [MgATP] = 0.1 mM. Other conditions are: [MgADP] = 1 μM, [Pi] = 2 mM, pH = 7, [Ca²⁺] = 200 μM, SL = 2.1 μM, and T = 20°C. (C) Same simulation as panel B, except that each curve has been normalized to its own maximum force so that the rate of force redevelopment at different MgATP concentrations can be compared to data shown in panel D. (D) Experimental data reproduced with permission from Fig. 5A of Ebus et al. (18).

Sinusoidal length perturbations

Kawai et al. (3) used sinusoidal length perturbation over a range of frequencies to determine the complex stiffness of cardiac muscle at different MgATP and Pi concentrations (in ferret myocardium). We imposed a sinusoidal length change with an amplitude of 0.25% of L₀, the imposed sarcomere length (2.28 μm) in the Extended Model, including both passive and active components of tension. Fig. 4 shows the two components of complex stiffness, dynamic modulus (Fig. 4 A) and phase shift (Fig. 4 B), as a function of perturbation frequency at different Pi concentrations, compared with the experimental data from Kawai et al. (3). (Similar plots showing the comparison between model and data for dynamic modulus and phase shift at different MgATP concentrations can be found in the accompanying Supporting Material, and provide further validation of the dependence of cross-bridge cycling on MgATP.)

Figure 4.

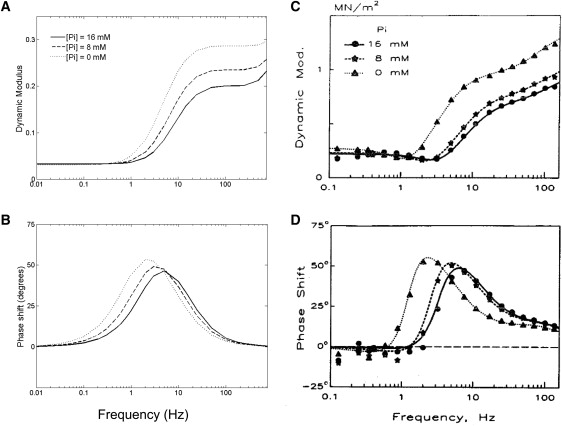
Two measures of complex stiffness: dynamic modulus (A) and phase shift (B), calculated for the model as a function of perturbation frequency and [Pi]. (C and D) Experimental data from ferret cardiac muscle (reproduced with permission from Wolters Kluwer Health, from Kawai et al. (3)). Dynamic modulus is calculated as the amplitude of the normalized force oscillation in response to a sinusoidal length change protocol with an amplitude of 0.25% L₀ (where L₀ is set at 2.28 μm). Other conditions in the simulations: [MgATP] = 5 mM, pH = 7.15, [Ca²⁺] = 200 μM, and T = 20°C. We also assume [MgADP] = 0, as there was no mention of its presence in the experimental protocol described by Kawai et al. (3).

Our simulations reproduce, qualitatively and semiquantitatively, features observed in the experimental data. Both demonstrate that with increasing frequency the dynamic modulus increases, whereas the phase shift increases toward a peak before decreasing. Dynamic modulus is a measure of muscle stiffness, which is directly proportional to force and is therefore a function of the fraction of cross-bridges in the strongly-bound state and their mean distortions. In the model, stiffness increases with frequency because the average distortion of the strongly-bound cross-bridges increases before they can detach.

The response to a change in [Pi] (and in [MgATP]; see Supporting Material) is very similar to the experimental observations. Stiffness decreases with increasing [Pi] (Fig. 4 A), whereas the peaks of the phase shifts move to a lower frequency. Increasing [Pi] (or [MgATP]) leads to a decrease in stiffness at a given stimulation frequency because it favors detachment of cross-bridges (reducing the proportion in the strongly-bound state, and hence, stiffness). An increase in [Pi] favors detachment of cross-bridges (from XB_PreR) in the anti-clockwise direction, whereas an increase in [MgATP] favors detachment (from XB_PostR) in the clockwise direction.

Force development during ischemia: sensitivity analysis

A key motivation for our study was to investigate the effects of changing metabolite concentrations during ischemia on the development of active force. Befroy et al. (38) measured [PCr], [ATP], and pH, and developed pressure, during 20 min of zero-flow global ischemia in perfused guinea pig hearts. These data were used by Terkildsen et al. (10) to calculate the time courses for [ADP] (using the creatine kinase equilibrium constant) and [Pi] (assuming conservation of the total phosphate pool). These time courses are shown in the first column of Fig. 5 (rows A–D), with the corresponding isometric force at maximum Ca²⁺ activation ([Ca²⁺] = 200 μM; row E) calculated from the model. The simulation shows force decreasing rapidly to ∼10% of its preischemic value after ∼10 min, consistent with the pressure measurements from Befroy et al. (38) and Allen and Orchard (1).

Figure 5.

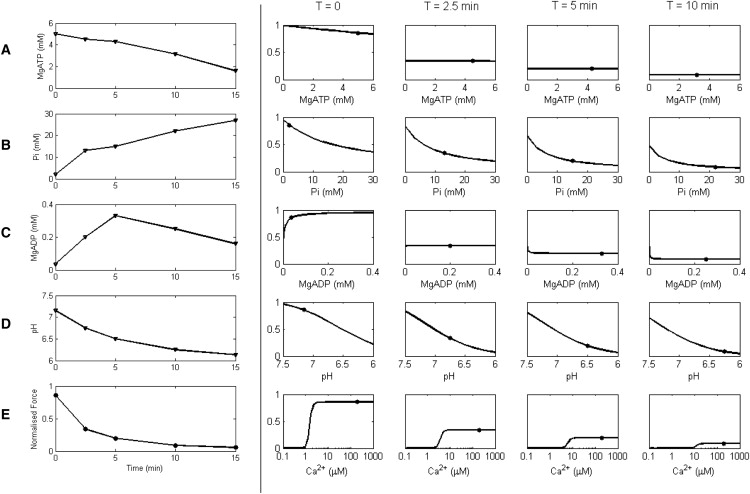
Production of force during ischemia. Imposed ischemic time courses for metabolites, pH, and simulated force are shown in the first column. The time courses for the change in (A) [MgATP], (B) [Pi], (C) [MgADP], and (D) pH are redrawn at five distinct time points (T = 0, 2.5, 5, 10, and 15 min) from Befroy et al. (38) and Terkildsen et al. (10). These time courses are then used to simulate the isometric force response (row E). The other four columns show the sensitivity of maximal force to [MgATP], [Pi], [MgADP], pH, and [Ca²⁺] at four different time points during ischemia. The y axis of each plot shows normalized force. Each column illustrates a particular time point after the onset of ischemia. (Solid circles) Force and respective metabolite, pH, or Ca²⁺ level at that time point. (Curves) Effect on force (sensitivity) of changing values of [MgATP], [Pi], [MgADP], pH, or [Ca²⁺] (rows A–E), while keeping the others constant. For plots A–D, [Ca²⁺] is held at 200 μM to achieve maximum force. Other conditions in the simulations: SL = 2.2 μM and T = 25°C.

To investigate the relative effects of the metabolites and pH on the maximum force during ischemia, we performed a sensitivity analysis at times T = 0 (normoxic conditions), and T = 2.5, 5, and 10 min after the onset of ischemia. Each curve shows the change in maximum force (y axis) as one metabolite is varied (x axis), whereas the others are held at their respective values for that time point (shown as solid circles on the sensitivity curves). For example, row B shows the negative inotropic effect of increasing [Pi] on force when [MgATP], [Pi], and pH are kept constant, whereas row C shows an initially positive effect of [MgADP] on force, with a small but negative effect on force after a few minutes of ischemia. Row E shows the effect of calcium on force at each time point post-onset of ischemia, showing that the calcium level required to achieve the diminishing maximal force also increases during the progression of ischemia.

These results indicate that the maximum force is most sensitive to changes in [Pi] and pH (the curves for [Pi] and pH have steepest gradient over the physiological range). The initial rapid decrease in maximum force after the onset of ischemia is primarily caused by increasing [Pi] and decreasing pH. We note, however, that these effects are not additive due to the nonlinear dependencies among variables in the model. Force is not strongly sensitive to MgATP or MgADP. At T = 0, increasing [MgATP] leads to a decrease in force, whereas after T = 2.5 min, force becomes insensitive to [MgATP]. For [MgADP], at T = 0 force increases with increasing [MgADP], becoming almost insensitive at T = 2.5 min, and starts to decrease after T = 5 min. These changes in the sensitivity to [MgATP] and [MgADP] over the time course of ischemia are due to the changing [Pi] and pH levels. The switch from increasing to decreasing sensitivity to [MgADP] is a consequence of the MgADP-binding step occurring between two strongly-bound states. The shift to the right (higher Ca) in the force-Ca curve (Row E) demonstrates the reduction of sensitivity to Ca²⁺ during ischemia. This is brought about primarily by the increased inhibition of Ca²⁺ binding to troponin C, due to falling pH (Fig. 2 D).

Discussion

The position of the MgATP and MgADP binding steps within the cross-bridge cycle are well constrained by data from the literature. MgATP was assumed to bind at g_xbT because this transition detaches a strongly-bound cross-bridge, consistent with experimental observations (7,18). Experimental observations have also shown that the cross-bridge head remains strongly attached after the MgADP binding event, and that increasing [MgADP] leads to an increase in isometric force (21,31,33), which leads us to introduce a new state into the original cross-bridge scheme from Rice et al. (8). The binding positions for Pi and the metabolic H⁺ in the cross-bridge cycle are not as well characterized in the literature. Data indicate that an increase in the concentrations of either Pi or H⁺ will lead to a decrease in isometric force (21–24). This qualitative behavior can be satisfied by placing either of these binding events at g_appT or h_bT (Fig. 1), and we have determined a scheme that gives the best fit to experimental data (Fig. 2, A and C). Pi binding at g_appt is further supported by the sinusoidal length perturbation simulations in Fig. 4 that reproduce the qualitative, and many of the quantitative, aspects of the experimental data. (MgATP binding is also further supported by these simulations—see Supporting Material.) These simulations demonstrate the recruitment and distortional stiffnesses identified by Campbell et al. (39), who analytically derived the frequency response of the Razumova et al. (40) model—a precursor to the Rice et al. (8) model. The distortional stiffness rises with increasing frequency because the cross-bridges are stretched further before they can detach, whereas the recruitment stiffness is a function of the fractional occupancies of the strongly-bound cross-bridge states (XB_PreR and XB_PostR). Increasing either [MgATP] or [Pi] leads to a decrease in the fractional occupancy of these strongly-bound states, resulting in a decrease in stiffness, as is observed in the experimental data of Kawai et al. (3).

Decreasing pH, as occurs during ischemia, has been shown to affect the force-Ca curves in two distinct ways, shifting the force-Ca curve to the right (reducing Ca²⁺ sensitivity) (23–26,41), and decreasing the maximum force at saturating Ca²⁺ (23,24). We have shown that competitive binding of H⁺ for the Ca²⁺-binding site on troponin C can account for the pH-dependent shift in Ca₅₀ and that the release of the ATP hydrolysis-derived proton directly affects kinetics of the cross-bridge cycle, leading to a decrease in maximum force with decreasing pH. Together, these mechanisms can reproduce the experimentally observed steady-state pH-dependent force-Ca curves (Fig. 2 D). This is consistent with the study by Crampin and Smith (9), who also used two distinct mechanisms to capture the pH-dependent force-Ca data, but did so by using a phenomenological model for force generation. Our model also suggests that only one H⁺ binds to the Ca²⁺ binding site and that the release of the metabolic H⁺ occurs during the power-stroke and after the release of Pi.

Model limitations

This model of Ca²⁺ activation and cross-bridge kinetics is a mean-field representation of cooperative spatial interactions between regulatory proteins and cross-bridge action. Rather than explicitly describing these spatial interactions, which would require computationally intensive PDEs, the model achieves this by using a mean value to represent the population as a whole and, in doing so, can be described using a set of ordinary differential equations. The gains, in terms of computational efficiency, of this approach are offset by the limitations imposed on modeling the feedback behavior. Rice et al. (42) have shown that mean-field models generate hysteresis artifacts not seen in real muscle when global feedback on Ca²⁺-binding affinity is incorporated, i.e., allowing strongly-bound cross-bridges to influence explicitly the affinity of Ca²⁺ binding. Nevertheless, feedback mechanisms onto the Ca²⁺ affinity for troponin C are necessary for simulating observed phenomena such as ADP-contraction (33,43,44) and spontaneous oscillatory contractions (45,46). These phenomena have been successfully simulated using models with different feedback mechanisms, although it must be pointed out that these models are designed to study these specific phenomena only and cannot simulate other behavior such as force-Ca relations (33,46).

Inversion of the force-MgADP relationship

One of the unexpected outcomes from this modeling study is the dependence of the force-MgADP relationship on the other metabolites: MgATP, Pi, and H⁺. Fig. 3 A shows a reversal point at [MgATP] = 0.9 mM where the MgADP-dependent curves intersect. At this point, isometric force is insensitive to the MgADP concentration. For [MgATP] < 0.9 mM, an increase in MgADP concentration leads to a decrease in force, whereas for [MgATP] > 0.9 mM, increasing MgADP increases force. Varying [MgADP] and [Pi] will shift the position of this reversal point. This effect is not limited to MgATP, because the trend of the force-MgADP curve also depends on [H⁺] and all the other parameters in the cross-bridge cycle. This reversal behavior is unique to the MgADP binding step, as the sensitivity of force to [MgATP], [Pi], and [H⁺] will exhibit only a unidirectional response. This emergent feature of the model appears consistent with data showing a biphasic force-MgADP curve that initially increases with increasing MgADP before inverting and decreasing as MgADP is further increased (Fig. 5 from Shimizu et al. (43)). Our model is able to reproduce this biphasic behavior qualitatively if we assume that [Pi] is increasing commensurate with [MgADP] (see Fig. S2 in Supporting Material). The increasing [Pi] tilts the balance of XB_PostR toward AM2 such that further increases in [MgADP] will increase the fraction of cross-bridges in state XB_PreR (which is a non-force-generating state under isometric conditions). The mechanism underlying this behavior is centered around the placement of the MgADP binding step between the two strongly-bound substates that make up XB_PostR (AM1 and AM2). The direction of the force-MgADP relationship depends on the balance between the competition for these two states. An analysis of this reversal point and the conditions under which it occurs is provided in the Supporting Material.

Reversibility

In our model of the cross-bridge cycle, the value of f_xbT is calculated to be minute. The small magnitude of this reverse rate constant restricts the cross-bridge from cycling backward to any appreciable extent. Despite this, it is obligatory to include f_xbT to ensure that the cycle is thermodynamically consistent. Simulation of muscle stretch under conditions where the free energy was artificially set to be positive produced a very small reversal flux. This is consistent with many studies in the literature that have attempted, but failed, to generate ATP through the application of external work (47–50). Our model shows that the cross-bridge cycle can reverse, albeit at a very low rate, and this is primarily due to the kinetics of the cross-bridge cycle.

Implications for ischemia

Our simulation of ischemia shows an exponential-like decrease in force that falls to ∼10% after 10 min of ischemia (Fig. 5). These results are consistent with the experimental data of Befroy et al. (38) from perfused guinea pig hearts. We have isolated the effects of the metabolic changes on the cross-bridge cycle from effects of changing Ca²⁺ levels by setting a high [Ca²⁺]. By considering each of the metabolite time courses separately, the sensitivity analysis suggests that [Pi] and pH are the primary contributors to the rapid fall in maximum tension during ischemia (Fig. 5). However, the metabolic changes that occur during ischemia also have direct effects on SERCA and the Na-pump, whereas falling pH directly inhibits the ryanodine receptors and indirectly leads to a rise in intracellular [Na⁺] (see (9) and references therein). Inhibition of SERCA and elevation of intracellular [Na⁺] will contribute to a rise in the diastolic Ca²⁺ concentration and the amplitude of the Ca²⁺ transient although the force production decreases. Row E of Fig. 5 shows that an increase in [Ca²⁺] cannot restore the loss of contractile strength brought about by the rise in [Pi] and fall in pH. Furthermore, the fall in pH greatly reduces the sensitivity of the force-Ca response, pushing the Ca₅₀ past 10 μM after 10 min of ischemia.

The model developed here incorporates metabolite dependence into a model of cooperative activation and cross-bridge kinetics, which can reproduce a range of important metabolite/force/length/Ca²⁺ characteristics. The model is constructed using ordinary differential equations, making it ideal for integrating into whole-cell models of excitation-contraction. The simulations of ischemia in this study were carried out by imposing the time course of metabolic changes onto our model. The next step is to integrate this cross-bridge model into a cellular framework and to couple it to a model of mitochondrial oxidative phosphorylation, such that the metabolic time courses are driven by the mitochondria which, in turn, drive the cross-bridge model. Along with published models of the cardiac Na-pump (2,10) and SERCA (11), this metabolite-sensitive model of the cross-bridge cycle provides a platform on which to develop a whole-cell model of cardiac electrophysiology and Ca²⁺ dynamics that is capable of simulating the effects of compromised energetics during ischemia.

The model is available in the CellML repository at http://models.cellml.org/workspace/tran_2009. A MATLAB (The MathWorks, Natick, MA) version of the code is also available from the authors. Full details and further analysis of the model are available in the Supporting Material.

Appendix

All parameters in the Extended Model are as given in Rice et al. (8), except xbmod_species = 0.2, as described above. Three new parameters are introduced: k_dHCa = 2 × 10⁻⁵ mM, m = 1, and k_dADP = 4 μM.

The following ordinary differential equations describing the cross-bridge kinetics are modified from Eqs. 14–17 from Rice et al. (8):

$$\begin{array}{c}\frac{d}{dt}{P}_{\text{XB}}=k_{\text{npT}}\times N_{\text{XB}}+{\alpha }_3^{+}\times X{B}_{PostR}+{\alpha }_1^{-}\times X{B}_{\text{PreR}}-\left(k_{\text{pnT}}+{\alpha }_1^{+}+{\alpha }_3^{-}\right)\times P_{\text{XB}}\\ \frac{d}{dt}X{B}_{\text{PreR}}={\alpha }_1^{+}\times P_{\text{XB}}+{\alpha }_2^{-}\times X{B}_{\text{PostR}}-\left({\alpha }_1^{-}+{\alpha }_2^{+}\right)\times X{B}_{\text{PreR}}\\ \frac{d}{dt}X{B}_{\text{PostR}}={\alpha }_3^{-}\times P_{\text{XB}}+{\alpha }_2^{+}\times X{B}_{\text{PreR}}-\left({\alpha }_2^{-}+{\alpha }_3^{+}\right)\times X{B}_{\text{PostR}}{N}_{\text{XB}}=1-\left(P_{\text{XB}}+X{B}_{\text{PreR}}+X{B}_{\text{PostR}}\right)\text{.}\end{array}$$

where the values α₁⁺ = f_appT, α₂⁺ = h_fT, α₁⁻ = [Pi] × g′_appT, α₃⁻ = f_xbT, and α₂⁻, α₃⁺ are defined by Eqs. 9 and 10, respectively. The values f_appT and h_fT, are rate constants from Rice et al. (8) and g′_xbT, g′_appT, and h′_bT are defined in Eqs. 3, 5, and 7, respectively. The f_xbT is calculated using the constraint from Eq. 1,

$$f_{\text{xbT}}=\frac{k_{\text{dADP}}\times f_{\text{appT}}\times h_{\text{fT}}\times {g^{\prime }}_{\text{xbT}}}{{g^{\prime }}_{\text{appT}}\times {h^{\prime }}_{\text{bT}}\times k_{\text{MgATP}}},$$ (11)

where k_MgATP = 15,400 mM² is the equilibrium constant for the ATP hydrolysis reaction and is defined as

$$k_{\text{MgATP}}=e^{-\Delta G^0/RT}\text{.}$$

ΔG⁰ = 10.3 KJ mol⁻¹ is the standard free energy change, taking into account [H⁺] in the hydrolysis reaction (Eq. 2), R is the universal gas constant, and T = 298 K.

The differential equations governing the rate of change of the mean distortions, Eqs. 29 and 30 of Rice et al. (8), are also modified:

$$\begin{array}{c}\frac{d}{dt}xX{B}_{\text{PreR}}=\frac{1}{2}\frac{dSL}{dt}+\frac{\mathit{\varphi }}{X{B}_{\text{PreR}}^{\text{DutyFract}}}\left[-\left({\alpha }_1^{+}\times xX{B}_{\text{PreR}}\right)+{\alpha }_2^{-}\times \left(xX{B}_{\text{PostR}}-x_0-xX{B}_{\text{PreR}}\right)\right]\\ \frac{d}{dt}xX{B}_{\text{PostR}}=\frac{1}{2}\frac{dSL}{dt}+\frac{\mathit{\varphi }}{X{B}_{\text{PostR}}^{\text{DutyFract}}}\left[{\alpha }_2^{+}\times \left(xX{B}_{\text{PreR}}+x_0-xX{B}_{\text{PostR}}\right)\right]\text{.}\end{array}$$

Addition of f_xbT modifies Eqs. 31 and 32 of Rice et al. (8), used to calculate the steady-state occupancies of XB_PreR and XB_PostR:

$$\begin{array}{c}X{B}_{\text{PreR}}^{\text{DutyFract}}=\frac{{\mathit{\alpha }}_3^{-}{\mathit{\alpha }}_2^{-}+{\mathit{\alpha }}_3^{+}{\mathit{\alpha }}_1^{+}+{\mathit{\alpha }}_2^{-}{\mathit{\alpha }}_1^{+}}{{\Sigma }_{\text{XB}}^{\text{DutyFract}}}\\ X{B}_{\text{PostR}}^{\text{DutyFract}}=\frac{{\mathit{\alpha }}_1^{+}{\mathit{\alpha }}_2^{+}+{\mathit{\alpha }}_3^{-}{\mathit{\alpha }}_1^{-}+{\mathit{\alpha }}_3^{-}{\mathit{\alpha }}_2^{+}}{{\Sigma }_{\text{XB}}^{\text{DutyFract}}}\\ {\Sigma }_{\text{XB}}^{\text{DutyFract}}={\mathit{\alpha }}_1^{+}{\mathit{\alpha }}_2^{+}+{\mathit{\alpha }}_3^{-}{\mathit{\alpha }}_1^{-}+{\mathit{\alpha }}_3^{-}{\mathit{\alpha }}_2^{+}+{\mathit{\alpha }}_3^{-}{\mathit{\alpha }}_2^{-}+{\mathit{\alpha }}_3^{+}{\mathit{\alpha }}_1^{+}+{\mathit{\alpha }}_2^{-}{\mathit{\alpha }}_1^{+}+{\mathit{\alpha }}_2^{+}{\mathit{\alpha }}_3^{+}+{\mathit{\alpha }}_3^{-}{\mathit{\alpha }}_1^{-}+{\mathit{\alpha }}_3^{+}{\mathit{\alpha }}_1^{-}\text{.}\end{array}$$

Equations 33 and 34 in Rice et al. (8), used to normalize the force output, become

$$\begin{array}{c}X{B}_{\text{PreR}}^{\text{Max}}=\frac{f_{\text{xb}}{h}_{\text{b}}+g_{\text{xb}}{f}_{\text{app}}+h_{\text{bT}}{f}_{\text{app}}}{{\Sigma }_{\text{XB}}^{\text{Max}}}\\ X{B}_{\text{PostR}}^{\text{Max}}=\frac{f_{\text{app}}{h}_{\text{f}}+f_{\text{xb}}{g}_{\text{app}}+f_{\text{xb}}{h}_{\text{b}}}{{\Sigma }_{\text{XB}}^{\text{Max}}}\\ {\Sigma }_{\text{XB}}^{\text{Max}}=h_{\text{f}}{g}_{\text{xb}}+h_{\text{b}}{g}_{\text{app}}+g_{\text{xb}}{g}_{\text{app}}+f_{\text{xb}}{h}_b+g_{\text{xb}}{f}_{\text{app}}+h_{\text{b}}{f}_{\text{app}}+f_{\text{xb}}{g}_{\text{app}}+f_{\text{app}}{h}_{\text{f}}+f_{\text{xb}}{h}_{\text{b}}\text{.}\end{array}$$

In the Extended Model, the normalizing force is therefore determined by the force at the reference physiological metabolite levels under optimal conditions (see (8) for details). The value f_xb is defined similarly to Eq.11, except that the base value of the rate constant is used, i.e., f_app instead of f_appT.