Sodium Perchlorate Effects on the Helical Stability of a Mainly Alanine Peptide

Abstract

Sodium perchlorate salt (NaClO₄) is commonly used as an internal intensity standard in ultraviolet resonance Raman (UVRR) spectroscopy experiments. It is well known that NaClO₄ can have profound effects on peptide stability. The impact of NaClO₄ on protein stability in UVRR experiments has not yet been fully investigated. It is well known from experiment that protein stability is strongly affected by the solution composition (water, salts, osmolytes, etc.). Therefore, it is of the utmost importance to understand the physical basis on which the presence of salts and osmolytes in the solution impact protein structure and stability. The aim of this study is to investigate the effects of NaClO₄, on the helical stability of an alanine peptide in water. Based upon replica-exchange molecular dynamics data, it was found that NaClO₄ solution strongly stabilizes the helical state and that the number of pure helical conformations found at room temperature is greater than in pure water. A thorough investigation of the anion effects on the first and second solvation shells of the peptide, along with the Kirkwood-Buff theory for solutions, allows us to explain the physical mechanisms involved in the observed specific ion effects. A direct mechanism was found in which ClO₄⁻ ions are strongly attracted to the folded backbone.

Introduction

The presence of ions in water impacts the conformation and activity of proteins, but the physical mechanisms involved in such effects are not yet completely understood. Hribar-Lee et al. recently provided an explanation of the effects of simple ions on protein solubility (1), but the effects of more complex ions, containing both charged and hydrophobic groups, is still unknown.

It has been well accepted for more than a century that ions have the ability to change the structure of water. The arrangement of water molecules around a protein is determined by hydrogen bonding, which is altered by the presence of ions. According to the traditional picture, water molecules solvate cations by orienting their oxygen atoms toward the ion, whereas they solvate anions by adopting the opposite configuration. Such reorientations perturb the hydrogen-bonded network. These observations started with Franz Hofmeister in 1888, who noted that some salts tend to precipitate eggwhite proteins from solution (salting out), whereas others enhance eggwhite protein solubility (salting in) (2). Hofmeister also found that ions varied in their ability to unfold proteins and to affect surface tension. The Hofmeister series ranks ions according to their “salting-out” tendency for proteins. For anions, the ranking is

$${\mathrm{H}}_2{\text{PO}}_4^{-}>{\text{SO}}_4^{2-}>{\mathrm{F}}^{-}>{\text{Cl}}^{-}>{\text{Br}}^{-}>{\text{NO}}_3^{-}>{\mathrm{I}}^{-}>{\text{ClO}}_4^{-}>{\text{SCN}}^{-}$$

and for cations

$${\text{Mg}}^{2+}>{\text{Li}}^{+}>{\text{Na}}^{+}\sim {\mathrm{K}}_{+}>{\text{NH}}_4^{+}$$

The traditional explanation for the Hofmeister series introduced the now-questioned concepts of “structure-making” and “structure-breaking” ions (3,4).

The basic idea is that large, low-charge-density ions, such as I⁻ and NH₄⁺ (called chaotropes or structure breakers), disrupt “water structure” whereas small or high-charge-density ions, such as F⁻ and Mg²⁺ (called kosmotropes or structure makers), impose order on the hydrogen-bonded network. Salting out and salting in of proteins is explained on the basis of entropic changes induced in their hydration shells by the addition of ions or by a reduction in the strength of hydrogen bonding of water molecules caused by the dissolved ions. Salting out is a result of competition for solvation between the salt and the protein, where an ion's ability to confiscate waters of solvation is related to its effect on the water structure.

However, this concept of ions changing the water structure has recently been questioned. For example, a recent x-ray absorption spectroscopy study of cation hydration demonstrates that ions significantly perturb the electronic structure of adjacent water molecules, but that there appears to be no significant distortion of the water hydrogen-bond network beyond the first solvation shell (5). This local view of the effects of ions on water structure is supported by a first-principles simulation (6), as well as by a femtosecond-pump-probe spectroscopic study showing that ions do not influence the rotational dynamics of water molecules outside the first solvation shell (7), and that the presence of ions does not lead to an enhancement or a breakdown of the hydrogen-bonded network in liquid water.

Thus, instead of trying to understand the Hofmeister series on the basis of “global” changes in solvent structure induced by ionic solutes, it seems far more logical to consider the effects that these ions have on the local hydration of protein residues. Recent work shows that the Hofmeister effect must be understood in terms of specific interactions between ions and proteins. Pinna et al. (8) studied the effect of adding sodium salts of various anions to buffer solutions of lipase. They showed that the enzymatic activity is altered as a result of specific anion interactions with the enzyme surface.

Harano and Kinoshita indicated that excluded-volume effects can play a significant role in protein stability by compensating the entropic cost of protein compaction (9,10). The idea is that large particles (proteins) and small particles (water molecules and/or ions) tend to phase separate to minimize the volume of space that is inaccessible to the small particles surrounding each of the large particles. This exclusion results in a reduction of translational entropy of the small particles.

Rösgen et al. (11) stated that water is not the only denaturing agent in aqueous solutions. The authors contend that along with the expected change in protein hydration that occurs upon denaturation, in the presence of ions there occurs a competition between the ions and protein for water hydration. The protein hydration change going from folded (F) to unfolded (U) can be represented as ${\Delta }_{\mathrm{F}}^{\mathrm{U}}\left(G_{\text{PW}}\right)$, and the protein-ion solvation change can be determined as ${\Delta }_{\mathrm{F}}^{\mathrm{U}}\left(G_{\text{PS}}\right)$. Here (G_PX) represents the Kirkwood-Buff integral for the protein in water (X = W) or for the protein in a salt solution (X = S). Moreover, the competition between protein hydration and protein solvation is what determines whether a compound stabilizes or destabilizes proteins. The change of solvation preference of the protein upon unfolding ${\Delta }_{\mathrm{F}}^{\mathrm{U}}\left(G_{\text{PW}}-G_{\text{PS}}\right)$ is the key factor in describing protein stability.

Alanine peptides form highly stable helices in aqueous solutions and the behavior of ions solvating alanine-based peptides has been specifically investigated in the past. Yu et al. studied the impact of sodium and chloride ions on a 13-residue alanine peptide (12). They observed that polyalanine has differential binding affinity to different types of ions. This preferential binding is dependent upon the conformation of the polypeptide and the ion concentration.

Using circular dichroism, Maison et al. reported a notable helix stabilization caused by chaotropic anions in alanine peptides with no charged groups (13). Furthermore, they showed that ClO₄⁻ ion induces a strong helix-stabilizing effect. They attributed this effect to the anion binding to the N-terminal cap of the peptide.

Ma et al. (14) studied the conformational changes that NaClO₄ induces in poly-L-lysine. They found that increasing the NaClO₄ concentration shifts the melting temperature (T_m) of the unfolding transition to higher values, indicating an increased stability of the helical conformations at higher NaClO₄ concentration. They suggested that the neutralization of the lysine NH₃⁺ groups by efficient ion pairing with ClO₄⁻ is what impacts the energy landscape, changing the relative order between equilibrium peptide conformations.

In summary, the features cited in attempting to explain the Hofmeister effect are structure-making/breaking effects, excluded-volume effects, protein-solvation changes upon unfolding, and ion-binding effects. It is still not clear, from the studies just described, which is the fundamental mechanism of salt stabilization/destabilization. To provide insight into this issue, we report our results on the peptide AP, which is a 21-residue alanine-arginine peptide. AP was chosen because it has been extensively studied both experimentally and computationally (15–22). Mikhonin et al. used UVRR spectroscopy to study the amide vibrations during α-helix melting. Using the dependence of the amide III₃ frequencies with the Ψ Ramachandran angle, they determined the helix population for different temperatures (23). In their initial experiments, AP was immersed in a 0.2M NaClO₄ solution. The reason to include NaClO₄ is that in the Raman technique, Raman excitation profiles are measured relative to an internal frequency standard. ClO₄⁻ has been shown to be a good preresonance enhancement and it is used to determine absolute Raman excitation profiles and absolute Raman cross sections in the visible through UV spectral region down to 220 nm.

We examine here the effects of NaClO₄ on AP helical stability, what kind of conformations AP adopts in the presence of this salt, and the physical stabilization mechanisms. We performed replica-exchange molecular dynamics (REMD) simulations of AP starting in its folded α-helix conformation for a total of 480 ns, sampling the folded and extended states in NaClO₄ solution and in TIP3P explicit water for comparison purposes.

Methods

The system studied is the alanine peptide AP: AAAAA(AAARA)₃A, where A represents alanine and R arginine. The simulations were performed using the AMBER 10 package (24) with a modified version of the AMBER-99 force field, ffSB99 (25). This force field has improved Φ/Ψ dihedral parameters, which have been shown to represent more accurately peptides such as glycine and alanine (25). The force field parameters given by Baaden et al. (26) have been used to describe ClO₄⁻ anions, with the atomic charges fitted to electrostatic potentials calculated at the Hartree-Fock level using a 6-31G^∗ basis set.

The peptide was simulated in two solutions: an explicit water molecule solution and a 0.2 M NaClO₄solution. For both solutions, the initial state was the α-helical state.

The simulations in explicit water were constructed immersing the peptide in a cubic box containing 2317 TIP3P water molecules. The TIP3P representation was chosen because the force field used was optimized with TIP3P water molecules. Previous studies sampled folded and unfolded states of AP using boxes with similar dimensions. Three Cl⁻ atoms were added to counterbalance the peptide charge.

The 0.2M NaClO₄ solution was prepared by adding the NaClO₄ ion coordinates to the peptide coordinates, then adding three Cl⁻ atoms to counterbalance the charge, and finally adding the water molecules in the cubic box. The resulting ClO₄⁻ ion/peptide ratio is 9.

The energy of both systems was minimized for a total of 16,000 steps. After the minimization, a 50-ps NVT equilibration was run at 300 K with the peptide fixed, to equilibrate the solutions. Next, the total volume and density were adjusted with another 50-ps NPT run with the total pressure set to 1 atm. The concentration of salt after the NPT simulation was calculated at 0.2 M. Production runs for both systems were carried out under NVT conditions.

We used a time step of 2 fs, and trajectory data was saved every 1 ps. The simulated systems were canonical ensembles at 300 K, and periodic boundary conditions were used. All bonds involving hydrogen atoms were constrained using SHAKE, with a tolerance of 0.0005 Å. REMD simulations were performed using 48 replicas at constant volume covering a range of temperatures from 270 K to 505 K. The intervals between replicas were adjusted to have a uniform acceptance ratio >20%. Exchanges were attempted every 100 integration steps. Following the procedure of García and Sanbonmatsu (20), each replica was run for 10 ns, with a total sampling time of 480 ns, and data collection for both cases began after 3 ns of MD simulation to eliminate initial biasing. The trajectories were divided into five blocks in which all the measured quantities were averaged and a standard deviation was assigned to each calculated quantity.

For the ion distribution analysis, trajectories were generated using the amber utility ptraj, centering the peptide to the origin of the box, and then imaging the whole system (placing atoms outside the periodic box back in the box).

Results

Testing the force fields

AP

As mentioned in the Methods section, the peptide was described using the ffSB99 amber force field (25), optimized for alanine peptides. To test how this force field describes the unfolding of AP in pure water, we calculate in this section the Lifson-Roig (LR) parameters (27) for the simulation of AP in TIP3P water and compare them with parameters calculated in previous works (28,29).

Using the standard Zimm-Bragg model, the partition function can be written as

$$q_n=\sum _{k=1}^{n-2\min \left(k,n-k-1\right)}\sum _{j=1}{\Omega }_{j,k}{\sigma }^j{s}^k,$$

where Ω_j,k counts the number of ways to put k helical hydrogen bonds into j segments, σ is the helix nucleation parameter, and s is the helix propagation parameter. The fractional helicity, θ, can be expressed in terms of the partition function as

$$\theta =\left(\frac{\delta q_n}{\delta s}\right)\left(\frac{s}{q_n}\right)\frac{1}{n-2},$$

where n indicates the number of residues. The average number of helical segments in terms of q_n is

$$j=\left(\frac{\partial q_n}{\partial \sigma }\right)\left(\frac{\sigma }{q_n}\right)\text{.}$$

With these two quantities (θ and j), calculated from the REMD simulations, we computed σ and s. Using our calculated Zimm-Bragg parameters σ and s, we determined the LR parameters v and w (30) using the relationships

$$s=\frac{w}{1+v},\sigma =\frac{v^2}{{\left(1+v\right)}^4}\text{.}$$

Fig. 1 shows our calculated LR parameters as a function of temperature.

Figure 1.

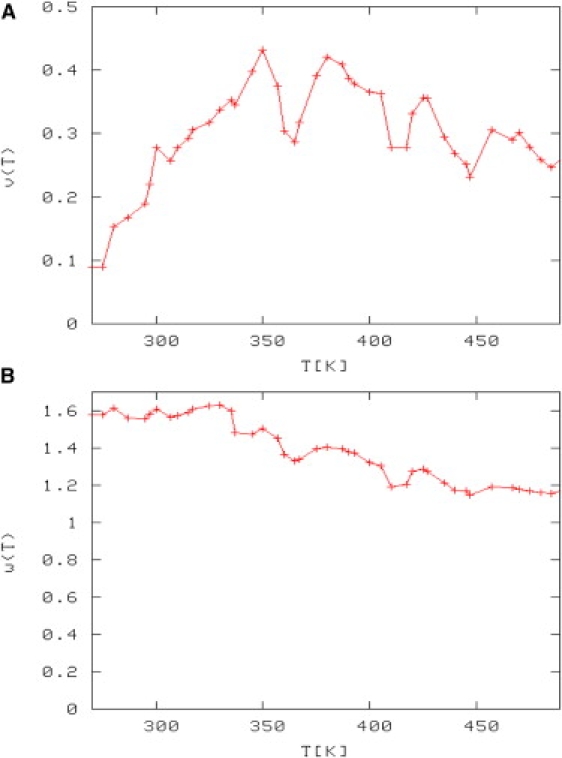
(A) LR nucleation parameter (v). (B) LR helix propagation (w) as a function of temperature.

At T = 300 K, the calculated LR parameter values are w (helix propagation) = 1.61 and v (helix nucleation) = 0.28. Nymeyer and Garcia (28) obtained w = 2.12 and v = 0.27 using the PARM 94 force field. Using a modified PARM 94 force field, the values reported were w = 1.67 and v = 0.13. A more recent calculation of these parameters was reported by Sorin et al. (29), who obtained w = 1.26 and v = 0.26 at T = 305 K, and our values at that temperature are w = 1.56 and v = 0.26. Our calculated parameters are in good agreement with previous calculations (28,29).

ClO₄⁻

The force-field parameters have been tested by our group previously (31) through a study of the behavior of NaClO₄ in aqueous solution at various concentrations ranging from 0.08 to 1.60 mol/L. The structure of the aqueous sodium perchlorate solution at different concentrations was well characterized in terms of its radial distribution functions (RDFs), its hydrogen-bond network, and its activity.

AP angular distributions

In this section, we compare the number of helical states found in a canonical ensemble at room temperature in the two different solutions studied, explicit water and NaClO₄ solution. It was shown in a previous work (19) that the number of helical states for AP can be correctly characterized computationally, as well as experimentally, by Ψ, defined as the set of dihedral angles ψ_j at each peptide residue. For example, a pure α-helical state has a Ψ = {−42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°, −42°}. It was shown that Ψ accurately distinguishes the folded and unfolded state in AP. The folded states were defined as α-helix like states with Ψ < 0°, whereas the unfolded states are polyproline II (PPII) configurations with Ψ ∼ 150°. We have shown in previous articles that AP immersed in a TIP3P water molecule box unfolds from the α-helix state, characterized by Ψ < 0°, enters into a transition region described by 0° ≤ Ψ ≤ 50°, and finally reaches the unfolded region of PPII states characterized by Ψ ∼ 150° (19,23).

The angular distributions from the REMD simulations for the peptide in explicit TIP3P water and in NaClO₄ solution were analyzed in this work constructing the (Φ,Ψ) normalized distributions shown in Fig. 2.

Figure 2.

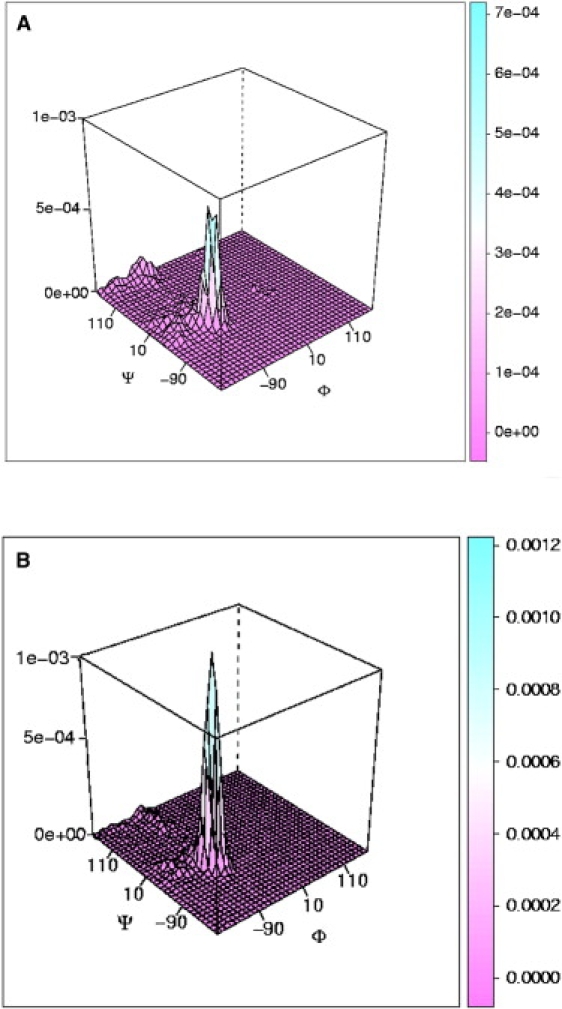
Normalized probability of the dihedral angle (Φ,Ψ) values sampled during the simulations at 300 K for (A) AP in TIP3P water and (B) AP in NaClO₄ solution.

During the unfolding of AP, two states are mainly populated in TIP3P water and the NaClO₄ solution. The highest peak in Fig. 2, A and B, represents the folded state, with the ψ-angle in the α-helical region, whereas the smaller peak is associated with the unfolded state. The unfolded state is a PPII conformation, in which Φ and Ψ values associated with PPII are the most populated states. The peak associated with folded states is centered at Ψ = −37° ± 1° for AP in TIP3P and Ψ = −41° ± 1° for AP in NaClO₄ solution. The latter value is usually associated with pure α-helices. The implication is that helical AP in NaClO₄ solution is more stable and that the helical states populated are mainly pure helices, whereas in TIP3P water a mix of folded states (pure α-helices, 3₁₀, and turns) are populated. This result is consistent with recent UVRR experiments in which the most prominent difference between pure water and NaClO₄ spectra occurs for the AmIII₃ band at ∼1200 cm⁻¹, a band associated with turns, which is present in pure water but absent in NaClO₄ (32).

It is important to mention also that UVRR distributions (23) report more PPII than helical states at 300 K. It is very likely that one cause of this difference between our calculations and the experiments is due to an overstabilization of the helical states by the force field used in the dynamics. Best et al. (33) investigated the differences in short alanine peptide conformational preferences obtained from 12 currently used molecular dynamics force fields and NMR experiments. They found that most current force fields do overpopulate the α-helical region. Specifically, for the force field used in this work (ffSB99), the α-helical content in Ala₅ dropped from 15.7% to 7% after reweighting to match experiments. On the other hand, they also reported that within the 12 force fields studied, ffSB99 is in the group with lower χ² values, which means that the deviation from experiment is comparable to the error derived from the corrections. The TIP3P water model used in this work might be another cause of difference in helical content between experiment and computation. As an example of the influence of the water model on the description of protein secondary structures, we mention that in a study of the Trp-cage protein using the TIP3P water model, a loop-type configuration at the C-terminus of the protein was reported (34), whereas in a different study of the same protein using a TIP4P-Ew water model, the loop-type configuration was not observed (35).

Average helical contents

Based on the calculated (Φ, Ψ) distributions, we define a state as helical if Ψ < 0 and nonhelical otherwise.

Using this definition, we calculated the fractional helical content per snapshot averaged over the entire trajectory. The helical content values for each studied temperature for AP in water and for AP in NaClO₄ solution are shown in Fig. 3, A and B, respectively. For the lowest temperature studied, 270 K, we found 75% of helical content for AP in TIP3P and 91% for AP in NaClO₄, that is, 20% more helical content than in pure water. This result is consistent with UVRR experiments, where the non-PPII fraction (α-helix, 3₁₀, and π states) measured for AP in NaClO₄ was 30% greater than that in deionized water (Fig. 3 C). This difference was related to the absence of a band associated with turn structures at ∼1200 cm⁻¹ in NaClO₄ solution. The conclusion from the experiment is supported by our analysis, in which no turn states are found in the NaClO₄ simulation.

Figure 3.

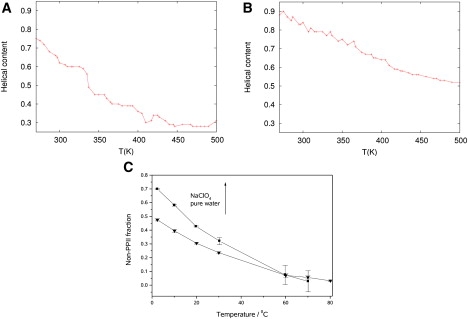
(A and B) Helical content per snapshot averaged over the entire trajectory versus temperature for (A) AP in TIP3P water and (B) AP in NaClO₄ solution. (C) Non-PPII states of AP in 0.2 M NaClO₄ compared with non-PPII states in pure water. The temperature-dependent basis spectra of the PPII-like conformations were calculated using the method of Lednev et al. (56). We then digitally smoothed and subtracted the appropriate amount of the PPII-like conformation basis spectra from the measured and smoothed UVRR of AP.

Circular dichroism spectra

We calculated the peptide circular dichroism (CD) spectra as another way to compare qualitatively the folding of AP in both TIP3P and NaClO₄ solution. The CD spectra were calculated according to the procedure of Woody and Sreerama (36). Briefly, a matrix method (37) was used in which the rotational strengths are calculated using a transition parameter set derived from a combination of experimental and theoretical parameters. The experimental data were used to describe the two amide ππ^∗ transitions, and parameters derived from intermediate neglect of the differential overlap model parameterized for spectroscopy (INDO/S) wave functions were used for the nπ^∗ transitions. The bandwidths used were 10.5 nm for the nπ^∗ transitions, 11.3 nm for the π₀π^∗ transitions, and 7.2 nm for the π₊π^∗ transitions (38). These transition parameters were used in calculating oligonucleotide CD spectra, reproducing most of the features of A-, B-, and Z-conformation CD, with particularly good agreement between theory and experiment for B and Z conformations.

The CD spectrum for each temperature studied was calculated at every snapshot and an average was taken over the whole trajectory. The average spectra versus temperature for both TIP3P and NaClO₄ solutions are shown in Fig. 4. In both solutions, the spectra are characterized by two negative bands at 204 nm and 222 nm and a positive band at 190 nm. The 222 nm band becomes less negative as the temperature increases, indicating helix melting. The spectrum in TIP3P agrees reasonably well with the experiments (Fig. 4 C), with the 204 nm and 222 nm bands and the temperature dependence quite well reproduced. The spectra associated with the peptide in NaClO₄ solution (Fig. 4 B) shows deeper bands at 204 nm and, in addition, melting behavior is observed at higher temperatures compared to AP in TIP3P (Fig. 4 B), providing further evidence of helical stabilization.

Figure 4.

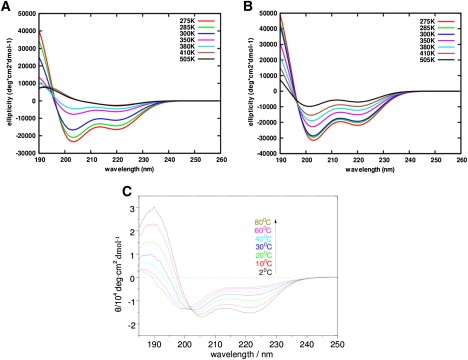
(A and B) Averaged CD spectra for AP in TIP3P explicit water (A) and in NaClO₄ solution (B), shown only at selected temperatures 275 K, 285 K, 300 K, 350 K, 380 K, 410 K, and 505 K, for better clarity. (C) CD spectra for AP in pure water from CD experiments.

Fig. 5 shows the average value of θ₂₂₂ as a function of temperature for AP in TIP3P water and in NaClO₄ solution. It is observed that the α-helical content increases by at least 25% when the peptide is immersed in a NaClO₄ solution. CD experiments show an α-helical content increase between 10% and 25%, depending on the NaClO₄ concentration (32).

Figure 5.

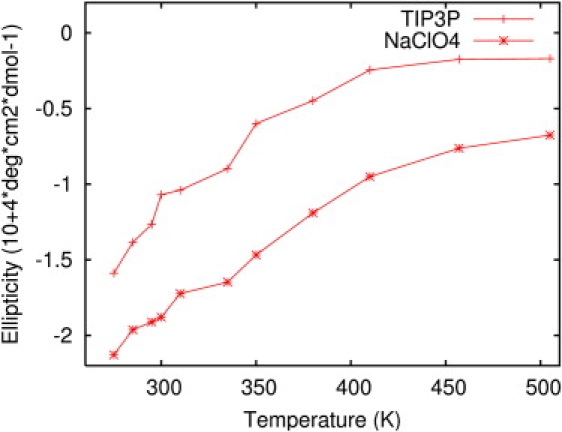
Averaged ellipticity, θ₂₂₂, for AP in TIP3P water and in NaClO₄ solution.

Physical mechanisms involved in the helical stabilization effects

Water structure

The traditional picture of ions modifying the conformational preferences of peptides involves changes in the water structure. We found that the global structure of water is not modified by the presence of perchlorate ions in the solution, as shown in Fig. 6. The O-O and O-H radial distributions show that the water structure changed insignificantly for AP in the NaClO₄ solution.

Figure 6.

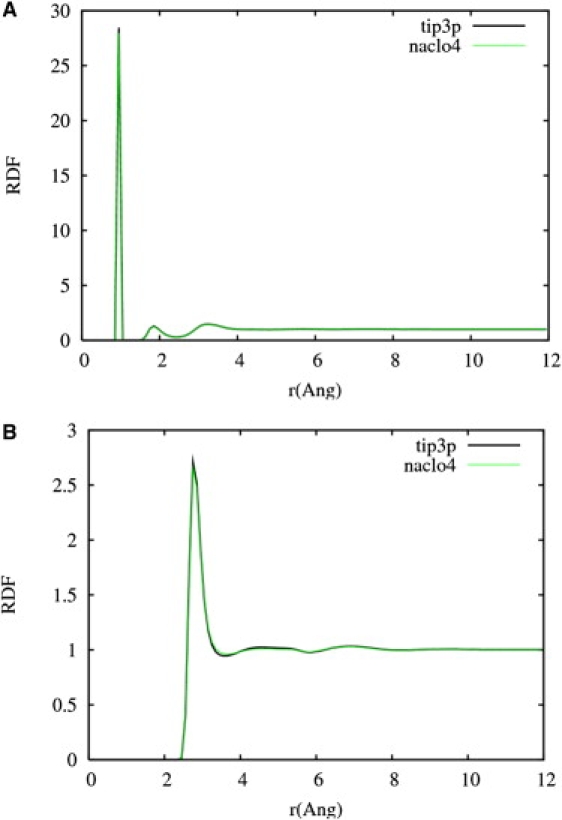
RDFs for O-H (A) and O-O (B) in TIP3P solution (black line) and NaClO₄ solution (green line). No significant global changes in the water structure are observed.

Ion distributions around AP

One of the first molecular dynamics simulations that explicitly included salts (39) showed an accumulation of chloride ions around the N-terminus of a zwitterionic bis(penicillamine) derivative, DPDPE. Also, several chlorides were found to be associated with multiple amide hydrogen atoms, and the chloride-chloride contacts were stabilized by the presence of bridging water molecules between them. These structures had been reported already in studies focused on ion pairing (40,41). To investigate possible ion associations with the peptide, we computed the average closest distances between the anions (ClO₄⁻) and each C_β at alanine and NH₂ at arginine over the 300 K trajectory. With these distances, a histogram was computed for each residue. The 21 histograms are shown in Fig. 7. ClO₄⁻ ions distribute on average around the backbone (between 3 Å and 8 Å apart), and the distribution with higher probability is observed around the terminal NH₃⁺ (residues 1–3). As Fig. 7 B shows, there is some ion association with the Arg⁹, less with Arg¹⁴, and none with Arg¹⁹ (indicated by the random distributions of ions around the side chains). This result can be rationalized by considering the partial charges assigned to the terminal NH₃⁺ and to the side-chain atoms. The partial charge assigned to the terminal NH₃⁺ is +0.74, whereas the Arg NH₂ charge is +0.03. This charge assignment represents the difference between the positive localized charge at the terminal and the more delocalized positive charge at the side chains.

Figure 7.

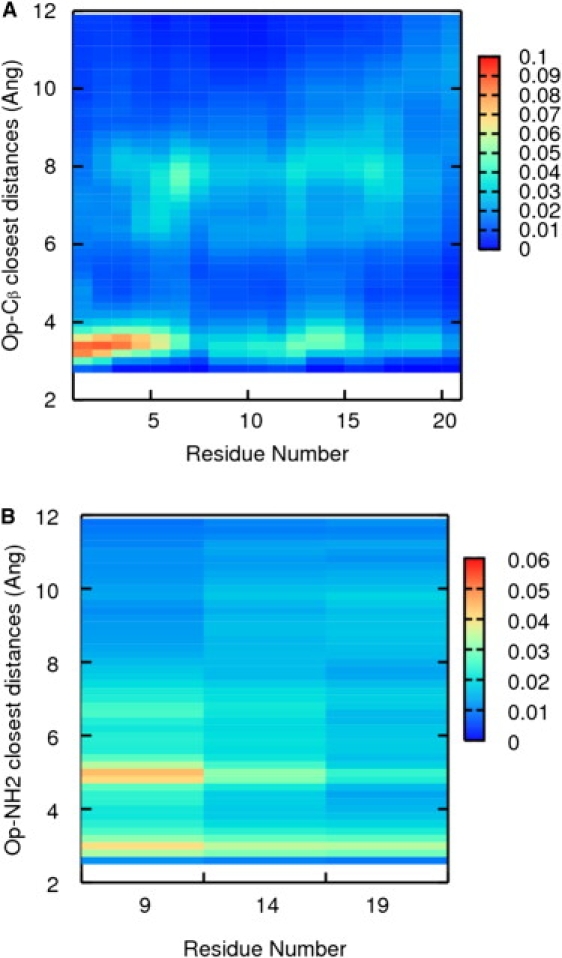
Color maps representing the average closest distances between (A) the O atoms at ClO₄⁻ and each backbone C_β and (B) the O atoms at ClO₄⁻ and each NH₂ at each arginine during the simulation at 300 K. The color represents the probability range, from least probable (blue) to most probable (red).

The anion distribution around the peptide was also computed by calculating the spatial occupancy maps for the anions during the 300 K simulation using Chimera. For this calculation, all the frames in the trajectory at 300 K were computed. The regions of space that are highly populated by the anions relative to the peptide in the ensemble are represented as a three-dimensional grid of values, or volume data, and the resulting map is called an “occupancy map”. This map reproduces the finding that the region with highest occupancy is around the N-terminal -NH₃⁺. The map also shows that the regions around the C-terminal-COO^- and the Arg¹⁹ are the ones with the least probability of becoming populated by the anions. See Fig. S1 in the Supporting Material.

Local peptide hydration

The ion/water ratio in the simulation box is 0.004, but we observed that this density is not homogeneous in the simulation. Three regions can be easily identified by a trajectory inspection where the ions distribute differently. Based on these observations, we defined three different volumes inside the simulation box. Volumes I and II contain the peptide and solvent molecules at distances of <5 Å and <10 Å, respectively, from the peptide backbone, and volume III contains the whole box. The ion/water ratio is higher in volume I: 0.01 compared to 0.004 in volumes II and III. The change in the ion/water ratio inside the simulation box is evidence of a preferential hydration mechanism. It can be assumed that the ions are competing with the water molecules to solvate the peptide. A similar result was observed by Hua et al. for an aqueous urea solution (42), where an increased osmolyte/water ratio in the region near lysozyme was observed. The authors attribute the accumulation of urea in the proximity of lysozyme to a more favorable van der Waals interaction energy between urea and lysozyme, and they state that that interaction is the dominant interaction that drives urea molecules to the protein surface.

Kirkwood-Buff analysis

An alternative approach to investigate the mechanisms of salt effects on protein stability is the Kirkwood-Buff (KB) theory (43). KB theory has been recently applied to investigate protein solvation properties in liquid mixtures (11,44–50). Using structural properties of the solution, such as the pair correlation function between particles, KB theory can be used to calculate the thermodynamical properties of the system. The structural parameters, G_PW, in this theory are called the “KB integrals”, obtained in this case by integrating the deviation of protein-water distribution (g_PW(r)) from bulk density over the total solution volume (Eq. 1):

$$G_{\mathrm{PW}}=4\pi {\int }_0^{\infty }\left(g_{\mathrm{PW}}^{\mu VT}\left(r\right)-1\right)r^{2}dr\approx 4\pi {\int }_0^{R_c}\left(g_{\mathrm{PW}}^{\mathrm{NPT}}\left(r\right)-1\right)r^{2}dr,$$ (1)

where P refers to the peptide and W to water. R_c defines a cutoff where the local cosolvent and solvent density around the peptide differs from the bulk density. Beyond R_c, g_PW(r) ≈ 1.

Positive G_PW indicates an excess of water around the peptide, whereas negative G_PW indicates a depletion of water around the peptide. The change in peptide hydration upon unfolding, ${\Delta }_{\mathrm{F}}^{\mathrm{U}}{G}_{\text{PW}}=G_{\text{PW}}^{\mathrm{U}}-G_{\text{PW}}^{\mathrm{F}}$, can be used to determine the more hydrated state and the change in hydrated molar volumes. However, water is not the only factor that induces unfolding. There is another contribution of opposite sign, the change in preferential solvation of the peptide by the ions, ${\Delta }_{\mathrm{F}}^{\mathrm{U}}{G}_{\text{PS}}$ (45). In this model, it is the competition between protein hydration (${\Delta }_{\mathrm{F}}^{\mathrm{U}}{G}_{\text{PW}}$) and ion solvation (${\Delta }_{\mathrm{F}}^{\mathrm{U}}{G}_{\text{PS}}$) that determines whether a salt stabilizes or destabilizes the peptide. In summary, the change in solvation preference of the peptide upon unfolding, ${\Delta }_{\mathrm{F}}^{\mathrm{U}}\left(G_{\text{PW}}-G_{\text{PS}}\right)$, is the crucial factor to be considered when monitoring the unfolding (51,52).

The distribution of salt molecules around the peptide can also be tracked by replacing W with S in Eq. 1. When the peptide hydration and solvation change upon unfolding are known, the change in the peptide excess chemical potential with respect to a change in the salt concentration can be calculated (46):

$$\frac{1}{RT}\left(\frac{\partial {\mu }^{ex}}{\partial c_{\mathrm{S}}}\right)=\frac{G_{\mathrm{PW}}-G_{\mathrm{PS}}}{1-c_{\mathrm{S}}\left(G_{\mathrm{WS}}-G_{\mathrm{SS}}\right)}\text{.}$$ (2)

The numerator on the righthand side of Eq. 2 times the salt concentration is called the preferential interaction parameter: Γ = −c_S(G_PW − G_PS), where Γ indicates the peptide state's preference for positive correlations with either water or salt, indicating, as explained previously, whether the salt will stabilize or destabilize a specific conformation.

The preferential interaction parameter can also be related to the free energy of unfolding.

The change in peptide hydration upon unfolding was determined by looking at the RDFs between the backbone C_α and the water molecules in both solutions. An RDF was constructed for each simulated temperature. For this analysis, it is useful to note that low-temperature simulations sample mainly folded states, whereas high-temperature simulations sample unfolded states, making possible a relation between high temperatures and unfolded states and low temperatures and folded states. Fig. 8 A shows the degree of AP hydration in pure water. We note that there is no significant change in the first and second peaks as the temperature increases, implying that the peptide hydration is not changing significantly upon unfolding in pure water. In Fig. 8 B, it can be observed, through the higher probabilities in the first and second peaks, that the peptide is getting more hydrated as the temperature increases, demonstrating that the peptide is significantly more hydrated when unfolded in NaClO₄ solution. The change in peptide hydration is more pronounced in NaClO₄ solution (a 20% increase in the probability is observed for the peptide in NaClO₄, whereas a 2% increase is observed for the peptide in TIP3P water). By comparing Fig. 8, A and B, it can also be seen that at low temperatures, the peptide is more hydrated in TIP3P water than in NaClO₄ solution.

Figure 8.

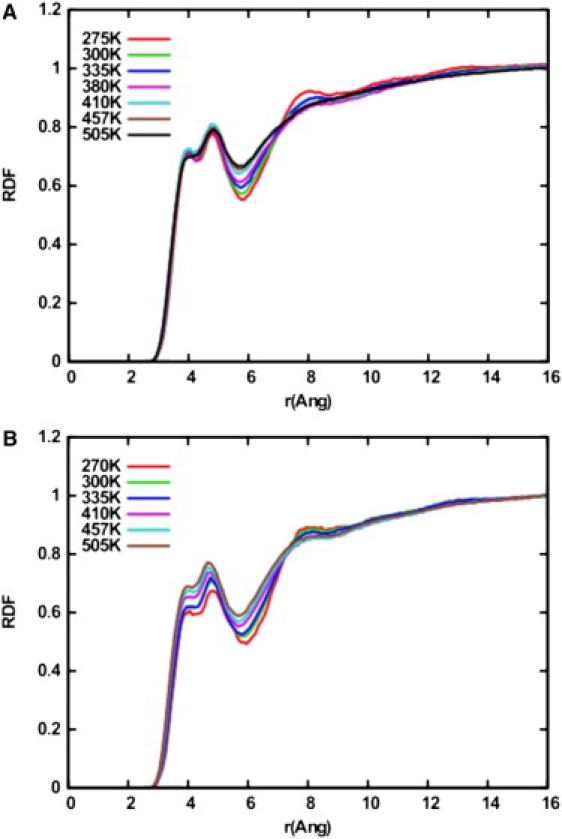
RDFs between the backbone Cα and water molecules for (A) AP in TIP3P and (B) AP in NaClO₄ solution.

The change in peptide hydration as the temperature increases can also be calculated with the KB integral. Using Eq. 1, the change in AP hydration between 270 K and 505 K for volumes I and II is positive and is four times greater in NaClO₄ solution than in TIP3P water.

The ClO₄⁻ anions show a behavior opposite that of water molecules. As the temperature increases, the distributions in the first and second region decrease, showing that more ions solvate the first and second shells of AP when it is folded (Fig. 9). The change in the peptide's ion solvation calculated by the KB integral is negative and significantly greater in volume II than in volume I.

Figure 9.

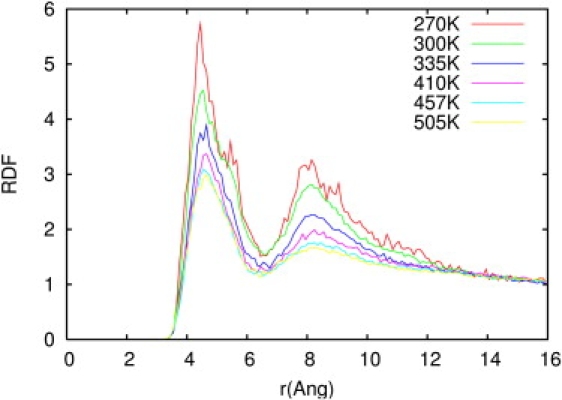
RDFs between the backbone Cα and the center of mass of the ClO₄⁻ ions for selected temperatures from 270 K to 505 K.

The anion-peptide RDF displayed in Fig. 9 still shows structure up to distances of 14 Å. This structure is amplified in the KB integrals, resulting in considerable error in the calculated integrals. The calculation of high-precision KB integrals demands long simulation time and large simulation boxes due to the difficulty in reaching convergence (53). To support the qualitative analysis presented above, we performed a 100 ns simulation of AP in a new, bigger box with dimensions 93 × 82 × 81 ų, which contained 99 ions and 16,744 water molecules. The concentration was maintained at 0.2 M, equal to that in the smaller box. With this new system, the calculated KB integrals and Г converged at a distance of 18 Å (Fig. S2, A and B). Г is negative at distances <3.5 Å (peptide-anion distance) due to the excluded-volume effect, then increases sharply and becomes positive, indicating a greater number of anions than water molecules around the first solvation shells of the peptide, until it reaches a plateau.

The preferential interaction parameter Γ is positive for both regions, which means that $G_{\text{PW}}^{{\text{NaClO}}_4}<G_{\text{PS}}^{{\text{NaClO}}_4}$, indicating a significant affinity of ClO₄⁻ ions for AP. The change in the interaction parameter is evidence of differences in the peptide solvation preferences upon unfolding. The helical states are preferentially solvated by the anions, whereas the unfolded states are more hydrated.

According to Ben-Naim (54), the excess (or deficit) number of molecules i around a central molecule j is directly proportional to G_ij:

$$\Delta n_{ij}=c_i{G}_{ij},$$

where c_i is the bulk molar concentration of component i. $G_{\text{PS}}^{{\text{NaClO}}_4}$ > 0 for all of the temperatures studied, and its value decreases as the temperature increases, indicating an excess of ClO₄⁻ ions around the peptide surface for low temperatures (where AP is folded), which decreases as the peptide unfolds.

Discussion

Our results reveal that a competition exists between ions and water molecules to solvate the peptide AP. For AP in NaClO₄, we observe that the solvation preference of the peptide changes significantly upon unfolding.

The behavior of the ions at the peptide/water interface changes as the temperature increases. For temperatures below the melting temperature, ClO₄⁻ ions are able to penetrate the peptide's first solvation shell (volume I), excluding the water from the peptide surface. And although the first Arg (Arg⁹) shows some ion association, the backbone and the positive N-terminus are the regions that significantly attract the ions.

In view of these results, we believe that the α-helix stabilization observed in AP when immersed in NaClO₄ solution is a local and direct effect that can be studied by the behavior of the ions near the peptide/water interface.

Jungwirth et al. reported similar effects studying the behavior of ions near a water/air interface (55). They showed that the behavior of ions near a water/air interface follows an inverse Hofmeister series and can be explained by means of surface tensions and surface potentials. Specifically, they studied the variations of the surface tension of aqueous solutions of amphiphilic organic substances with concentration. They found that inorganic salts increase the surface tension of the solution/air interface; ions are repelled, leaving an ion-free region at the interface. They also found that although this change in surface tension is not very sensitive to the identity of the monovalent cation, it is anion-specific. The number of ions in the interfacial region decreases in the order

$${\text{\#ClO}}_4^{-}<{\text{\#I}}^{-}<{\text{\#Br}}^{-}<{\text{\#Cl}}^{-}\text{.}$$

Based on our results and the observations of Jungwirth, we would predict that helix stability is greatest in the presence of perchlorate and least stabilized in the presence of sulfate.

Summary

We have studied the effects of NaClO₄ on the helical stability of the 21-residue alanine-based peptide AP and compared the results with those for the peptide in pure water. In particular, we examined the stability of the folded and unfolded states in this solution. A strong helical stabilization effect was found for AP in NaClO₄. In view of these results, its use when measuring protein conformations has to be carefully considered.

Finally, a KB analysis was performed, and preferential interaction parameters were calculated for folded and unfolded states. The preferential interaction parameters indicate that the unfolded state (PPII) is more hydrated than the folded state. AP's backbone has a strong ion solvation preference in NaClO₄ solution.

The strong stabilization found for NaClO₄ can be explained as follows: ClO₄⁻ ions compete with water molecules to solvate the peptide. The ion solvation effect is stronger than that of hydration, and the peptide surface “loses” water, or gets dry. A less hydrated peptide promotes more intrapeptide hydrogen bonding, which leads to greater helical stability.