A Modeling Study of T-Type Ca²⁺ Channel Gating and Modulation by L-Cysteine in Rat Nociceptors

Abstract

L-cysteine (L-cys) increases the amplitude of T-type Ca²⁺ currents in rat T-rich nociceptor-like dorsal root ganglia neurons. The modulation of T-type Ca²⁺ channel gating by L-cys was studied by fitting Markov state models to whole-cell currents recorded from T-rich neurons. The best fitting model tested included three resting states and inactivation from the second resting state and the open state. Inactivation and the final opening step were voltage-independent, whereas transitions between the resting states and deactivation were voltage-dependent. The transition rates between the first two resting states were an order of magnitude faster than those between the second and third resting states, and the voltage-dependency of forward transitions through resting states was two to three times greater than for analogous backward transitions. Analysis with the best fitting model suggested that L-cys increases current amplitude mainly by increasing the transition rate from resting to open and decreasing the transition rate from open to inactivated. An additional model was developed that could account for the bi-exponential time course of recovery from inactivation of the currents and the high frequency of blank sweeps in single channel recordings. This model detected basically the same effects of L-cys on channel gating as the best fitting model.

Introduction

T-type Ca²⁺ channels (T-channels) expressed in nociceptors are an important factor in the transmission of pain information. Various agents that decrease or increase T-channel activity in peripheral tissues also decrease or increase, respectively, thermal pain threshold (1). L-cysteine (L-cys), an endogenous thiol-containing amino acid, produces a large increase in the amplitude of T-type Ca²⁺ currents (T-currents) evoked from nociceptor-like dorsal root ganglion (DRG) cells (2). In vivo, L-cys in the blood plasma may come into contact with peripheral nociceptor terminals via plasma extravasation after trauma, burns, or inflammation (3). There is evidence that L-cys acts on T-channels via chelation of Zn²⁺ bound to a critical metal-binding histidine residue (H191) on the external side of domain I of the channel protein (4). Only the Ca_V3.2 T-channel isoform is modulated by Zn²⁺ binding, and thus susceptible to upregulation via Zn²⁺ chelation by L-cys (4,5).

The L-cys-induced changes in T-channel gating that result in up-regulation of T-currents are poorly understood. L-cys is reported to cause a large increase in peak T-channel mediated conductance and shift the V_1/2 of activation by ∼−5 mV. However, steady-state inactivation, deactivation, and recovery from inactivation are not significantly affected by L-cys (2). By itself, the shift in V_1/2 of activation does not explain the large increase in peak conductance.

In this study, the effects of L-cys on T-channel gating were investigated by fitting whole-cell T-currents with Markov state models. This strategy was used in the hope that it could detect L-cys-induced changes in T-channel gating that were undetected by the electrophysiological protocols used previously. T-currents used for model fitting were acquired from a subpopulation of small diameter rat DRG cells, previously named T-rich DRG cells (2). Studies on Ca_V3.2 mouse knockouts and T-channel blockade by Ni²⁺ suggest that T-currents in T-rich DRG cells (and most other small diameter DRG cells) are mediated nearly exclusively by the Ca_V3.2 isoform (2,4,6,7).

To fit Markov state models to T-currents, we used a method developed recently for model-based fitting of macroscopic (whole-cell) currents (8). This method provides reliable estimates for transition rates, as do other similar methods (9,10). However, the method used here is fast, allowing the simultaneous fitting of whole-cell current records evoked by different voltage protocols that target different transition rates. Also, the method is freely available online, allowing for easy replication and extension of our work by others.

In this study, the information extracted from a battery of whole-cell T-channel recordings allowed the ranking of different Markov state models based on goodness of fit, and direct estimation of transition rates before and after channel modulation by L-cys. What we believe is a new model was developed that could account for the activation, deactivation, and inactivation from resting and open states of Ca_V3.2 type T-channels. Results with this model regarding the effects of L-cys on Ca_V3.2 channel gating were compared to those generated by fitting of a previously developed, more complex model (11). The previous model was tuned to fit our data and also to account for the bi-phasic time course of Ca_V3.2 channel recovery from inactivation, or the large number of blank sweeps typically observed in single T-channel recordings.

Materials and Methods

The T-current records, used for fitting with models and for comparison with model-based simulations in this study, were acquired from T-rich DRG cells as part of a previous study by Nelson et al. (2). The preparation of rat DRG cells, identification of T-rich cells, and the solutions and equipment used in data acquisition are described in that study (2).

Description of current records used

T-currents used for direct iterative fitting by Markov state models were evoked by protocols for voltage-dependency of current activation and deactivation, before and after treatment with L-cys. The T-currents were carried by 10 mM Ba²⁺. The original data files representing voltage-dependency of activation (activation records) contained currents evoked by voltage commands (VCs) to −80 mV through +50 mV, from a holding potential (HP) of −90 mV. The HP of −90 mV removed almost all inactivation (2). The original data files representing the voltage-dependency of deactivation (deactivation records) contained tail currents elicited by VCs to −50 mV through −160 mV, after 15 ms VCs to −35 mV from HP −90 mV to fully activate the current (2). Data on steady-state inactivation and the time course of recovery from inactivation were also taken from the previous study (2) for comparison to model-based simulations. In the original protocol for steady-state inactivation, DRG cells were held at −90 mV and given 3.5 sec conditioning potentials (CPs) to −95 mV through −50 mV, followed by VCs to −30 mV to assess inactivation (2). In the original protocol for the time course of recovery from inactivation, DRG cells were held at −90 mV and given 300 ms CPs to −0 mV to inactivate the current. After a variable recovery period at −90 mV, ranging from 2–10,000 ms, DRG cells were given VCs to −30 mV to assess recovery (2).

Models tested

Various Markov state models were tested for their goodness of fit to control T-current records to examine the plausibility of various published hypotheses regarding T-channel inactivation. Model A (Fig. 1 A), which allows for inactivation from the open state only, was compared to Models B–E (Fig. 1, B–E), which allow for inactivation from both open and resting states (12). Model B was compared to Models C–E, to examine whether resting states and the open state undergo transitions to the same or to different resting states (12). Models C, D, and E were compared to each other to examine the possibility that some resting states have a higher probability than others of undergoing transition to inactivated states (11).

Figure 1.

Different Markov state models fitted to T-type Ca²⁺ channel currents. The letters C, O, and I represent resting, open, and inactivated states, respectively. The arrows represent kinetic rate constants. The rate constants held voltage-dependent are designated by α (kC1C2 and kC2C3), β (kC3C2 and kC2C1), and δ (kOC3). The number of free parameters in Models A–F, is 10, 13, 11, 13, 13, and 10, respectively. The normalized sums of squares averaged 2962 ± 473, 1686 ± 209, 1881 ± 278, 1173 ± 122, and 1249 ± 149, for Models A–E, respectively.

Model F (Fig. 1 F) was adapted from a previous model developed by Burgess et al. (11), based on whole-cell currents and gating currents mediated by Ca_V3.2 T-channels. Model F was tuned to fit our data and to also account for the bi-phasic time course of recovery from inactivation of Ca_V3.2 channels (13). Then Model F was fitted to control and L-cys records for comparison to the best fitting model from the above A–E series, regarding detected L-cys-induced changes in T-channel gating. A variant of Model F (Model Fa) was tuned to account for the large number of blank sweeps typically observed in single T-channel recordings, and then also used for comparison regarding detected L-cys induced changes in T-channel gating (11,13,14).

Several constraints were placed on Models A–F. The final opening step kC3O, and transitions between open/resting states and inactivated states (kCI and kIC) were constrained as voltage-independent, to reflect the saturation of the time to peak current and macroscopic inactivation rate at positive VCs observed in this study (Fig. S1, B and C, in the Supporting Material), and previous studies (15). kOC3 was set as voltage-dependent to reflect the lack of saturation of tail-current decay rate at negative voltages observed in the data used in this study (Fig. S1 D), and in previous studies (15). To reduce the number of free parameters, the voltage-dependence of kOC3 was fixed at −0.015 mV⁻¹, reflecting the estimates obtained when Model D (Fig. 1 D) was fitted to control (−0.014 ± 0.001 mV⁻¹) and L-cys records (−0.015 ± 0.001 mV⁻¹) with kOC3 as a free parameter. Also to reduce free parameters, the transitions among the three resting states (C1, C2, and C3) were constrained to have the same voltage-dependency in the forward direction, and the same voltage dependency in the backward direction. Microscopic reversibility was enforced in each model that incorporated a loop, i.e., the product of the rate constants in the forward direction equaled that in the backward direction. Enforcement of microscopic reversibility over a range of voltages required scaling of voltage-dependence terms within loops, so that the sum of the terms in the forward direction equaled the sum of the terms in the backward direction (Fig. 1, B–F). These constraints were automatically handled by the fitting software. In all models except Model Fa (see below), all channels were assumed to reside in C1 before the onset of the initial VC.

Several additional constraints were placed on Model F, both to reduce the number of free parameters and to conform the model—in some respects—to the model developed by Burgess et al. (11). kOC3 was scaled equal to kI4I3 (see Fig. 5 A), reflecting the report that the off-gating current had a similar time constant of relaxation as the whole-cell tail current (11). Also, kC2I2 was scaled as 50% of kC3I3, and kI2C2 was scaled at 25 times of kI3C3 (see Fig. 5 A). Although qualitatively similar to the Burgess model, the above scalings between resting and inactivated states were arrived at through trial and error, to make Model F fit our data reasonably well (see Fig. 5 B). In contrast to the Burgess model, kC1I1 and kI1C1were fixed at 0.0008^sec−1 and 0.02^sec−1, respectively (Fig. 5 A). Finally, to reduce the number of free parameters, the following transition rates were scaled as equal; kC1C2 = kI1I2, kC2C3 = kI2I3, and kC3O = kI3I4. Regarding Model Fa, kC1I1 and kI1C1 were scaled as equal, and the initial channel distribution was set to 50% in C1 and 50% in I1, and the channel number was doubled to compensate for reduced channel availability.

Figure 5.

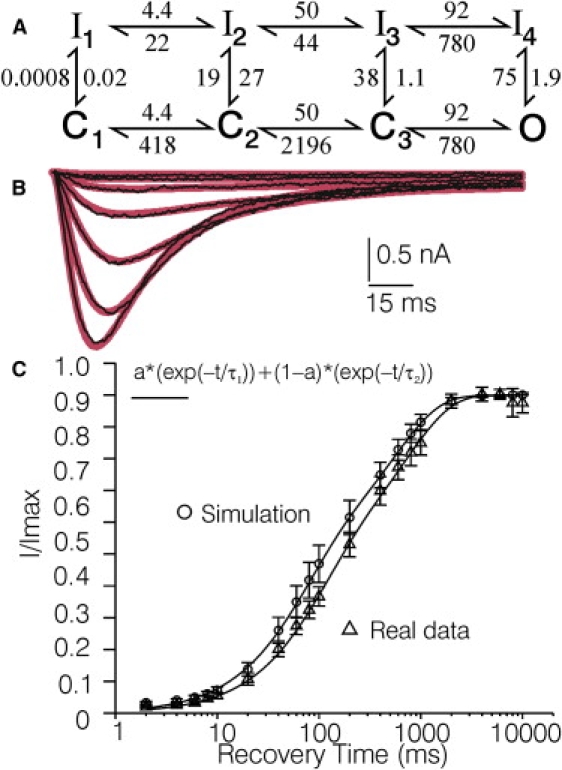
Simulations with Model F of recovery from inactivation. (A) Model F, with the averaged optimized rate constants corresponding to a voltage of −90 mV, obtained by fitting Model F to the six control records. (B) Same control current records as shown in Fig. 4 (thin black lines and corresponding simulation (thick lines) based on fitting Model F to the same records). (C) Recovery data simulated with Model F, superimposed on real recovery data acquired from five different T-rich DRG cells (2). Fitting the simulated data with a double exponential function indicated that 47 ± 8% of the current recovered with fast time constant (66 ± 4 ms), and 53 ± 8% recovered with a slower time constant (580 ± 112 ms). The same procedure applied to the real data indicated that 51 ± 8% of the T-current recovered with a fast time constant (105 ± 18 ms), whereas 49 ± 8% recovered with a slower time constant (981 ± 173 ms). The error bars represent the SE.

Model fitting

Models were represented mathematically and fitted to the current records using the MAC algorithm in the QuB software suite (13), which can be downloaded freely from www.qub.buffalo.edu. Six sets of activation records, each acquired from a different DRG cell before and after L-cys treatment in the study by Nelson et al. (2), were used for fitting. The activation records were restricted to those evoked by VCs to −70 mV through −35 mV, to limit the number of data points fitted. Also, the upper limit of −35 mV was chosen to avoid contamination of the T-currents with high-threshold Ca²⁺ currents (see Discussion). Each control and L-cys activation record was paired with the same control or L-cys deactivation record, respectively, which was an average of data acquired from seven different DRG cells in the study by Nelson et al. (2). The currents included in deactivation records were restricted to those evoked by VCs to −140 mV through −80 mV, to limit the number of data points fitted. The pairing of the activation and deactivation records is described in detail in the Fig. 3 legend. The paired records will be referred to as “control records” and “L-cys records.” To speed fitting, the records (originally acquired at 10 kHz) were down-sampled to 2 kHz. The shortest delay between VC onset and the occurrence of evoked net inward current (observed at −35 mV) averaged 1.08 ± 0.04 ms for controls, and 0.95 ± 0.022 ms after L-cys treatment. These delays were represented by two data points (1 ms) set to zero current. Longer delays associated with less depolarized VCs were also represented by setting the corresponding data points to zero current.

Figure 3.

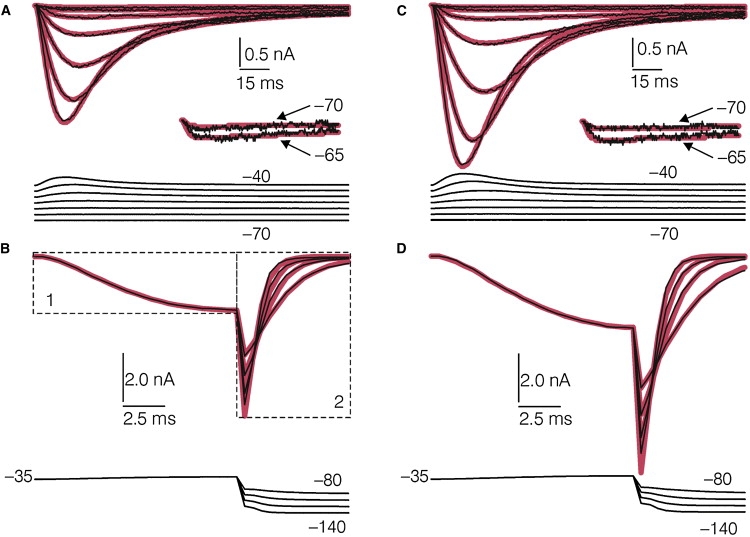
Fit of Model D to control and L-cys records, (thin black lines, real data; thick lines, model predictions). (A) Control activation records corresponding to VCs to −70 mV through −40 mV. The inset shows scaled up currents corresponding to −70 mV and −65 mV. (B) Box 1, first 15 ms of a control activation record corresponding to a VC to −35 mV taken from the same data file as the records shown in A; box 2, control deactivation records corresponding to VCs to −140 to −80 mV (average of data acquired from seven DRG cells). The deactivation records were scaled so that their amplitudes were the same, relative to the amplitude of the activation current shown in box 1 at 15 ms, as the relative corresponding amplitudes of the activation and deactivation records in the original averaged file. For fitting, the scaled deactivation records corresponding to the different VCs (box 2) were individually spliced to the ends of five repeats of the activation record (box 1) to form a continuous file. This file was then spliced to the end of the file containing the activation records shown in A, and the entire resulting continuous file was fitted simultaneously. (C and D) Same as A and B except after L-cys treatment. The insets below each set of current records in A–D represent the voltage records corrected for 3.5 MΩ R_S.

For each data point in a given current record, the fitting algorithm was provided with the value of the command voltage, corrected for series resistance (R_S). Because the actual R_S was unknown, an estimate for each control record was obtained by fitting Model D (Fig. 1 D) to each record after the corresponding voltage record was adjusted to reflect R_S increasing from 0 MΩ to 5 MΩ in 500 μΩ increments. The best fits were obtained when assuming uncompensated R_S averaging 3.5 MΩ (range = 2.5–4 MΩ). The individual R_S values corresponding to best fit for each record were used for subsequent comparisons of goodness of fit of different models and analyses of the effects of L-cys on T-channel gating.

To calculate whole cell current amplitude at different voltages, the MAC algorithm requires input regarding unitary conductance, reversal potential, and the number of available channels. T-channel unitary conductance (g) was estimated using averaged tail currents from the study by Nelson et al. (2) corresponding to VCs to −90 mV through −50 mV. Assuming 3.5 MΩ R_S, the corrected voltage range was ≈−76 mV through −41 mV (Fig. S1 A), which overlapped with that of the activation records used for fitting. The number of open channels corresponding to tail current amplitude at −40 mV was estimated by dividing this amplitude (extrapolated from a graph of tail current amplitude versus corrected voltage) by −0.35, which is the unitary T-channel current amplitude (i) determined in a single channel study by Balke et al. (16) with 10 mM extracellular Ca²⁺. Then i, corresponding to the other corrected voltages, was calculated by dividing the respective tail current amplitudes by the channel number. The resulting relationship of i versus voltage was relatively linear (Fig. S1 A), and corresponded to g of 5.95 pS and a reversal potential (V_r) of −19 mV. Thus an ohmic model (i = g ^∗(V − V_r), where V = corrected membrane voltage) was used in MAC to calculate i at different voltages.

The above assumptions regarding I and V_r are somewhat greater and smaller, respectively, than the values of 4.7 pS and +35 mV observed in the study by Balke et al. (16). However, in that study, T-channels were activated with VCs ranging from −40 mV to −10 mV, which is more positive than the range of voltages used here. The discrepancies could be explained if there was some rectification in the g/V relationship over the voltage range from −75 mV to −10 mV (Fig. S1 A), as has been observed in previous studies of T-channel-mediated tail current amplitude (15).

The number of available T-channels in a given DRG cell was estimated with the formula: $N=I_{\max }/i\times P_{o,\max }\times \left(g/g_{\max }\right)$, where I_max = peak current amplitude evoked by a VC to −40 mV, P_o,max = peak open probability = 0.15 (14,15,17), and g/g_max = fraction of maximal whole-cell T-channel conductance observed at VC −40. I_max and g/g_max corresponding to VC −40 mV were extrapolated for each data set from I/V and g/V plots. The assumptions regarding the number of available channels for the six sets of activation records averaged 59,601 ± 6528 (SE).

Rate constants (k) were calculated in MAC based on the voltage record that accompanied each current, using the equation: k = k₀ × exp(k₁ × V), where k is the rate constant [s⁻¹] at a given voltage V, and k₀ [s⁻¹] is the rate constant at zero potential. For convenience, the voltage was expressed in mV. The exponential factor k₁ [mV⁻¹] is equal to zδe/k_BT, where z = the valence of the gating charge moved over a fraction δ of the electric field, e = the charge of an electron, k_B is Boltzmann constant, and T is the absolute temperature. When reporting the degree of voltage-dependence in the results, the values of k₁ are written as shown in MAC (i.e., 0.01, 0.06). Larger absolute values correspond to a greater degree of voltage-dependence (8).

Goodness of fit of a given model to a current record was assessed via a direct comparison of the current amplitude versus time predicted by the model (given a set of parameters) to the real current amplitude versus time. Discrepancies between the real and predicted currents were quantified as the unweighted sum of squares according to the formula: sum of squares = Σ(I_t − μ_t)², where I_t = real current amplitude at a given time point, and μ_t = the isochronal predicted current amplitude. The optimizer used in MAC used the sum of squares as criterion to search for optimum values for the free parameters (8). The best fit was defined as the set of parameters last estimated before successive iterations failed to further minimize the sum of squares. Strategies used to avoid local minima and detect multiple solutions included starting fits with different seed values, and restarting fits after perturbation of selected optimized values. Regarding the parameter values reported, no alternate solutions were empirically detected where the sum of squares was minimized to a similar degree. There was a strong positive correlation between the sum of squares terms associated with the best fits of the various models to the six sets of records and the corresponding amplitudes of currents evoked with a VC to −40 mV (for control data, Model D, r = 0.834, p = 0.042, Bartlett χ² statistic). Therefore, to reduce variation within groups, the sum of squares terms were normalized by dividing the sum of squares for each data set by the current amplitude corresponding to VC −40 mV for that data set.

Results

In a fitting session with a given model, the real current records and various assumptions (voltage records corrected for putative series resistance, number of available channels, unitary conductance, reversal potential, initial channel distribution, model topology, scalings, fixed parameters, and seed values for free parameters) were fed into MAC. Subsequently, MAC returned optimized values for the free parameters, a set of predicted current traces superimposed on the real data, and the sum of squares describing goodness of fit.

Initial observations regarding model optimization

There are several important details regarding patterns of rate constant amplitude, voltage-dependency, and series resistance that visibly improved the fit of each respective model (shown in Fig. 1, A–F) to the current records. Models with three resting states, versus two or four, best explained the initial delay and rapid phase of current activation. In addition, best fits to the initial delay and rapid phase of current activation resulted when there was a relatively slow transition from C1 to C2, a relatively fast transition from C2 to C3, followed by a relatively slow final opening step (Table 1). This pattern emerged when kC1C2, kC2C3, kC2C1, and kC3C2 were unconstrained, free parameters. Applying an equality constraint to the forward rates connecting the three resting states resulted in visibly poor fits to the initial rapid increase in current amplitude. Interestingly, the pattern of slow, fast, slow transitions regarding the channel activation sequence is the same as proposed in the Burgess model (see Table 1 for a comparison). Furthermore, visibly better fits resulted when the voltage-dependency of the forward transitions among the resting states was greater than that of the corresponding backward transitions. This pattern also emerged when fitting models to the current records with the voltage-dependency of the forward transitions independent from that of the backward transitions. Finally, adjusting the voltage values for the error caused by the putative uncompensated R_S resulted in visibly better fits with Model D.

Table 1.

Values for kinetic rate constants and voltage-dependencies derived from fitting different models to T-type Ca²⁺ channel currents

Parameter	Model Dcontrol	Model DL-cys	Model Fcontrol	Model Facontrol	Burgess model
NC	56,901	56,901	56,901	113,802	87,000
kC1C2	168 ± 30	152 ± 23	207 ± 30	216 ± 30	203
kC2C1	112 ± 19	90 ± 30	103 ± 17	103 ± 16	71
kC2C3	2095 ± 167	2191 ± 246	2353 ± 264	2236 ± 334	4557
kC3C2	396 ± 22∗	292 ± 27	559 ± 62	537 ± 63∗	3588
kC3O	128 ± 6∗	229 ± 41	92 ± 9∗	86 ± 9∗	420
kOC3	333 ± 12	350 ± 13	368 ± 13	370 ± 13	45
kOI	263 ± 6∗	178 ± 16	75 ± 28∗	64 ± 28∗	58
kIO	2.8 ± 0.6∗	1.3 ± 0.2	1.9 ± 0.7∗	0.8 ± 0.3∗	0.08
kC1I1			0.0008	0.02	0.6
kI1C1			0.02	0.02	0.2
kC2I2	46 ± 11∗	88 ± 19	19 ± 3∗	20 ± 3∗	3.4
kI2C2	0.6 ± 0.2∗	2.5 ± 0.9	27 ± 5	14 ± 3	0.7
kC3I3			38 ± 7∗	41 ± 7∗	58
kI3C3			1.1 ± 0.2	0.4 ± 0.1	0.08
kI2I4	14 ± 8	5 ± 1	—	—	—
kI4I2	3 ± 1∗	0.6 ± 0.3	—	—	—
kI1I2			207 ± 30	216 ± 30	4
kI2I1			5.7 ± 1∗	69 ± 8	0.9
kI2I3			2353 ± 264	2236 ± 334	28
kI3I2			11± 1	11 ± 1	0.15
kI3I4			92 ± 9	86 ± 9	420
kI4I3			368 ± 13	370 ± 13	45
Vd fwd	0.073 ± 0.001∗	0.077 ± 0.001	0.078 ± 0.001	0.077 ± 0.001	0.052, 0.055
Vd bkwd	−0.031 ± 0.002∗	−0.045 ± 0.005	−0.028 ± 0.003∗	−0.029 ± 0.003∗	−0.02, −0.122
Vd kOC3	−0.015	−0.015	−0.015	−0.015	−0.028

Rate constants are expressed as transitions^sec−1. For voltage-dependent transitions, rate constants correspond to −40 mV.

^∗ Control value significantly changed by L-cys, in the same direction as shown for Model D, Wilcoxon test. p < 0.05, n = 6. For Models D, F, and Fa, Vd fwd and Vd bkwd refer to the voltage-dependence of forward and backward transitions through the resting states, respectively. For the Burgess model, the two numbers corresponding to each Vd fwd and Vd bkwd represent different values for transitions between C1 and C2 versus C2 and C3. The voltage dependence terms shown for the Burgess model were calculated using data provided in Burgess et al. (11), and are analogous to the voltage-dependence terms used in MAC. The N_C parameter represents the average number of available channels calculated for the six DRG cells (see Materials and Methods), except for the Burgess model, where the value shown represents the number of channels resulting in a peak current equal to the average peak current observed for the six DRG cells (−1730 pA), in response to a VC to −35 mV, given the optimized parameters in the Burgess model. For Models D, F, and Fa, the data are expressed as the mean ± SE. Values for the Burgess model are reported in Burgess et al. (11).

Comparison of goodness of fit across different models

With the above initial optimizations in force, Models A–E, were compared regarding their goodness of fit to the control records. After a final series of optimization sessions, statistical analysis of the normalized sum of squares indicated that Model D fit the control records better than Models A–C, but not better than Model E (paired t-test with Bonferroni correction, p < 0.05). Fits with Models A–C exhibited marked underestimations of the peaks and macroscopic inactivation rates of currents evoked by VCs to −70 mV, through −60 mV. On the other hand, both Models D and E fit the currents evoked by all VCs very closely (see Fig. 3). However, Model D fit the L-cys records significantly better than Model E (paired t-test, p < 0.05), and thus was considered the best fitting model overall. The kinetic rate constants and their voltage-dependencies for fits of Model D to the control records are shown in Table 1. For comparison, Table 1 also contains analogous values from the Burgess model (11), which incorporated data on Ca_V3.2 whole-cell currents and gating currents.

Effects of L-cys treatment on T-current shape

L-cys treatment greatly increased the amplitude of the T-currents, increased the macroscopic current inactivation rate, and decreased the current amplitude at the end of the records relative to peak current (Fig. 2). The putative peak voltages reached during analogous VCs were not exactly the same between control and L-cys records, due to greater corrections of the L-cys voltage traces for R_S. However, the L-cys-induced changes in macroscopic current inactivation could not be explained solely by differences in peak voltage. The differences in macroscopic current inactivation between control and L-cys records were greatest for the smallest VCs, where there was little difference regarding the corrected peak voltage (Fig. 2, D–F).

Figure 2.

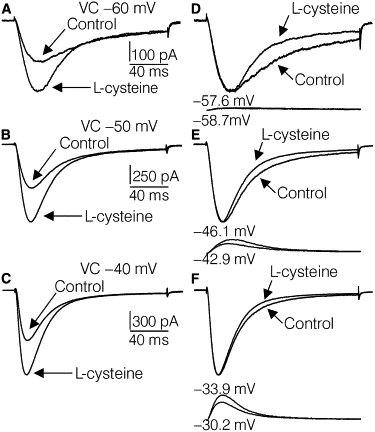
L-cys-induced shape changes in T-currents. (A–C) Effects of L-cys treatment on T-currents evoked by VCs to −60 mV, −50 mV, and −40 mV. The current records shown are averages from the six sets of current records used for model fitting. (D–F) Same currents as shown in A–C except the control currents have been scaled at their peaks to match the corresponding L-cys treatment currents. In D–F, the traces below the currents show the VCs after correction for 3.5 MΩ of R_S. The numbers above and below the traces represent the peak membrane voltage for L-cys and control conditions, respectively.

Effects of L-cys treatment on T-channel gating

Changes in currents induced by L-cys were analyzed in terms of channel gating by fitting Model D to the control and L-cys records. An example of the close fit of Model D to control and L-cys records is shown in Fig. 3. The other five data sets were also fitted closely by Model D. The results (Table 1) suggest that L-cys treatment induced a significant increase in the rate of the final opening step (kC3O), and significant decreases in the rate of inactivation from the open state (kOI4), and in the rate of the backward transition from C3 to C2 (kC3C2). L-cys treatment also significantly increased the transition rates between C2 and I2 (both kC2I2 and kI2C2), increased the voltage-dependency of transitions between the resting states (both forward and backward), and decreased the transition rates from I4 back to the open state (kI4O) and from I4 to I2 (kI4I2).

Simulations of individual L-cys-induced changes on current shape

The consequences regarding current shape of changes in individual parameters by L-cys treatment was analyzed with simulations where the transition rates were changed one at a time. According to these simulations, peak current amplitude would be increased by an increase in kC3O, or by a decrease in kOI4 or kC3C2 (Fig. 4, A–C). Conversely, peak current would be decreased by an increase in inactivation from the resting state (kC2I2), or by an increase in the voltage-dependency of forward or backward transitions through the resting states (Fig. 4, D–F). Because all VCs were to negative voltages, increases in voltage-dependency actually decrease forward rates and increase backward rates.

Figure 4.

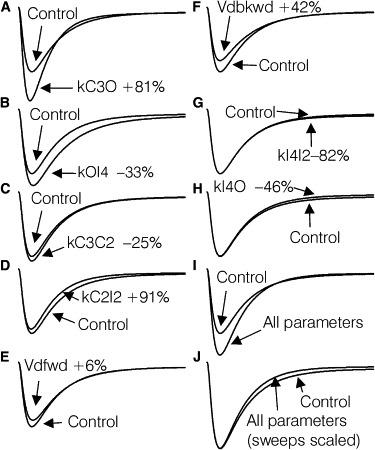
Effects of changing parameters in Model D on simulated current shape. (A–H) Each panel contains a simulated control current corresponding to a VC of −40 mV, and an analogous simulated current reflecting a change in one parameter. The parameters indicated were changed individually according to the average change induced by L-cys treatment in Model D when fitted to the six sets of control and L-cys records. (I) Effect of simultaneously making all the changes depicted in A–H. (J) Same simulations shown in I except the control simulation has been scaled at the peak to match the L-cys simulation.

According to the simulations, L-cys induced changes in several parameters that would be expected to target aspects of current shape in addition to amplitude. An increase in kC3O would increase both the rate of rise and inactivation of the macroscopic current, and thus decrease time to peak current (Fig. 4 A). An increase in kC2I2 would also increase the inactivation rate and decrease time to peak current (Fig. 4 D). Conversely, a decrease in kOI4 would decrease the inactivation rate, thus increasing time to peak current (Fig. 4 B). Finally, a decrease in kI4O would decrease the current amplitude during the last ≈2/3 of the record, whereas a decrease in kI4I2 would have the opposite effect over the last ≈1/3 of the record (Fig. 4, G and H).

When those parameters significantly altered by L-cys were simultaneously changed to their corresponding L-cys treatment values, the net simulated effect was a large increase in peak current amplitude (Fig. 4 I), an increase in the macroscopic inactivation rate, and a decrease in current amplitude toward the end of the record, relative to the peak current (Fig. 4 J). Overall, the simulations suggest that the primary cause of the increase in peak current amplitude is the increase in kC3O, whereas the reductions in kOI4 and kC3C2 made smaller contributions.

Analysis of L-cys induced gating changes with Model F

Model F (Figs. 1 F and 5 A) was developed to see what putative L-cys induced changes in T-channel gating would result from fitting a model that incorporated a putative mechanism accounting for the bi-phasic time course of recovery. After setting the constraints outlined in the Materials and Methods, Model F was fitted to the control and L-cys records (Fig. 5 B). Recovery data were simulated using the six sets of optimized control parameters obtained and the same protocol used to generate recovery data in the real experiments (see Materials and Methods). The sum of the fractions of channels residing in the resting states after each recovery period (as calculated with MAC), divided by the same fraction after 10 s of recovery, was assumed to reflect the fraction of recovery. Fits of a double exponential function to the simulated recovery data resulted in similar time constants and corresponding magnitudes as fits of a double exponential function to the real data (Fig. 5 C). Similar to the real data (2), the simulated time course of recovery was not affected significantly by fitting Model F to control versus L-cys records. After optimization, Model F also accurately simulated steady-state inactivation observed for T-channels before and after L-cys treatment in the study by Nelson et al. (2).

The optimized control values obtained for kC1C2, kC2C1, kC2C3, kC3C2, and kC3O and kOC3 with Model F, closely resemble those obtained with Model D (Table 1). Also, the voltage-dependence of the control transitions between the resting states was very similar between Model D and Model F. Finally, fits with Model F exhibited a pattern of L-cys-induced changes in the transition rates similar to that yielded by Model D (Table 1). The only discrepancy between the two models (with respect to common parameters) was that kC3C2 and the voltage-dependency of forward transitions through the resting states were not significantly changed in fits with Model F.

Analysis of L-cys-induced gating changes with Model Fa

Model Fa was developed to see what putative L-cys-induced changes in T-channel gating would result from fitting a model that could account for the large number of blank sweeps typically observed in single T-channel recordings. With kC1I1 set equal to kI1C1, 50% of the channels initially in I1 and 50% in C1, and channel number doubled, Model Fa was fitted to the control records. Single channel activity during 160 ms VCs to −35 mV, simulated using the six sets of optimized control parameters obtained, indicated that blank sweeps would be observed with a probability of 0.55 ± 0.04. Simulations with Model F under the same conditions indicated that blank sweeps would be observed with a lower probability of 0.29 ± 0.04. Model Fa yielded a similar pattern of control parameters and L-cys induced changes in parameters, as did Models F and D (Table 1).

Discussion

The main thrust of this study was to examine possible gating mechanisms by which L-cys treatment increases T-current amplitude in T-rich DRG cells. To this end, Markov state models were fitted to whole-cell T-current records acquired in a previous study (2). A new model was developed (Model D) that is fairly simple, yet can account closely for the change over time of Ca_V3.2-mediated T-currents elicited by protocols that emphasize channel activation and deactivation over a fairly wide range of voltages. In several respects, the rate constants and voltage-dependencies obtained by fitting Model D to T-current records are similar to those reported for a more complex model (Burgess model), that was based on Ca_V3.2 mediated whole-cell currents and gating currents (11). The results of analyses with Model D suggest what we believe is a new idea—L-cys treatment increases T-current amplitude primarily by increasing the rate of channel transitions toward the open state, and to a lesser degree by decreasing the rate of channel transitions away from the open state. These results were not dependent on the exact configuration of Model D. Significant L-cys-induced changes in the same parameters were also detected with Models F and Fa, which were endowed with more complex topologies than Model D to provide putative explanations for additional T-channel behaviors.

The modeling results suggest that a neuromodulator can alter current amplitude and time course by affecting channel behaviors that occur predominately during stimulus-induced transitions through different states. Such mechanisms can be difficult to detect using typical electrophysiological protocols. The only effect of L-cys treatment on T-channels detected by a battery of electrophysiological studies was a ≈−5 mV shift in V_1/2 for activation (2), and even this may be an overestimation because VCs were not corrected for R_S. In any case, a negative shift in V_1/2 would not explain the large L-cys induced increase (≈ 60%) in peak conductance, observed at voltages that produce maximal channel activation (Fig. S2 A). An alternate possibility is that L-cys induced an increase in unitary conductance. However, when expressed as percent increase over control levels, T-channel-mediated whole-cell conductance increased proportionally to VC amplitude, reaching a plateau around −60 mV (Fig. S2 B). In contrast, an increase in unitary conductance would be expected to result in a relatively constant percent increase in conductance versus voltage. Finally, L-cys treatment changes current shape, which is not expected if the underlying mechanism were limited to an increase in channel availability or unitary conductance. Thus, the available data are consistent with what we believe is a novel idea that the gating mechanisms underlying L-cys-induced increase in T-current amplitude are in force only when channels are undergoing transitions through the activation-inactivation sequence.

The validity of the optimized parameters depends on the fitted records representing the behavior of a single class of ion channel. Several previous observations suggest this is predominantly the case regarding the T-current records in this study. As mentioned in the Introduction, several previous studies suggest that T-currents in T-rich DRG cells and other small diameter rat DRG cells are nearly exclusively mediated by the Ca_V3.2 T-channel isoform (2,4,6,7). In addition, there should be little contamination by high-threshold Ca²⁺ currents in T-rich DRG cells, where peak high-threshold Ca²⁺ current amplitude is on average only ≈8% of the peak T-current amplitude (2). Also, these small high-threshold Ca²⁺ currents would only be partially activated by the strongest VCs used in acquisition of the current records fitted. Assuming an average R_S of 3.5 MΩ, membrane voltages would have reached an average of ≈−25 mV at the peaks of L-cys records corresponding to VCs of −35 mV. VCs to −25 mV would be expected to evoke high-threshold Ca²⁺ currents in rat DRG cells with amplitudes averaging ∼20% of their peak amplitude observed at 0 mV (18). Thus, we estimate that on average maximal contamination by high-threshold Ca²⁺ current of the current records used for fitting was <2%.

Several observations suggest that Model D was not overparameterized. Removal of any given state from the model markedly decreased goodness of fit. Also, no alternate solutions with equal goodness of fit were detected by starting fits with different sets of seed values for the free parameters, or perturbing optimized parameters and refitting. Although Model D contains 13 free parameters, additional simulations to those shown in Fig. 4 demonstrated that each differed, (in most cases markedly, in some cases subtly), regarding the regions and aspects of the predicted current encoded. It seems likely that these differences were amplified across the different voltages used, although this was not addressed with simulations. Thus, it seems that fitting Model D to the current records was considerably more comprehensive in detecting changes in current shape and converting this information into a meaningful form, versus exponential fits and current amplitude measurements. At most, ∼5 or 6 parameters could be assessed by these latter methods, and interpretation of such data in terms of channel gating would be difficult.

The goodness of fit studies involving Models A–E provide some insight regarding T-channel inactivation. Models A and B (with optimized parameters) could not closely simulate the T-current records used for fitting, especially those corresponding to small amplitude VCs. The results with Model A suggest that inactivation from the resting state is an important determinant regarding current amplitude versus time versus voltage as previously suggested (12,15). Results with Model B shed doubt on the idea (12) that resting states and the open state undergo transition to the same inactivated state. The comparisons of Models C, D, and E suggest that inactivation from the resting state is poorly represented by configurations where the resting state closest to the open state preferentially undergoes inactivation. This result is inconsistent with the Burgess model (and Model F), where the resting states progressively closer to the open state exhibit progressively higher probabilities of undergoing inactivation. It seems that the overall strategy used (models + current records) does not differentiate well between inactivation from C3 and inactivation from the open state. In Model F (and Model C), the increase in kC3I3, relative to that in Model D, is compensated for by a large decrease in kOI4, relative to that in Model D (Table 1). In any case, the ability of Models D and E to closely simulate the current records is consistent with idea that inactivation of T-channels resembles an “inactivation particle” scenario (11). According to this scenario, transition to inactivated states from resting and open states involves an interaction of some part of the channel with the channel pore. Thus, the various inactivation states are identical to their corresponding resting and open states, except for the conformational change that blocks Ca²⁺ flux. However, the various inactivation states are different from each other, in that inactivation occurs at different stages of activation (11).

Model D could not account for the bi-phasic time course of recovery from inactivation of Ca_V3.2 channels (13) because it contains only one pathway for recovery. Model F was able to roughly simulate recovery from inactivation data acquired in real experiments (Fig. 5). However, the fast and slow time constants obtained by fitting a double exponential to the simulated data were significantly faster than the corresponding time constants obtained from real recovery data. This discrepancy may have arisen from the fact that the records fitted with Model F were acquired from different T-rich DRG cells than the real recovery data, and also that the records used for fitting contained little information about recovery from inactivation.

However, this study supports the idea that multiple recovery pathways can account for two very different time courses of recovery. The distribution of channels within Model F, after the various simulated recovery times, suggests a scenario where ∼50% of the channels become “trapped” in I1 after ∼100 ms of recovery. Due to the fixing of kI1C1 at a low level in Model F, the fastest route for channels in I1 to undergo recovery to C1 is via I2 and C2. This alternate path generates the slow time constant for recovery. Other scenarios could be that the channels trapped in I1 undergo transition directly to C1 according to the slow time constant, or that channels accumulate in and are released slowly from some other inactivation state. For the channels to recover with two markedly different time courses, they must somehow become separated into different pools that release them at different rates.

A prominent aspect of the Burgess model is that the ratio of kC1I1 to kI1C1 is such that at hyperpolarizing membrane potentials (−120 mV) a given channel will reside in I1 ∼75% of the time and in C1 ∼25% of the time. This configuration provides an explanation for the large fraction of null sweeps observed in single channel recordings (4,11). Reports of null sweep frequency in response to strong VCs range from 75% to 40% in patches containing or corrected for 1 T-channel (13,14,16,17,19). As illustrated in Table 1, configuring Model F so that 50% of the channels resided in I1 and 50% in C1 at hyperpolarized membrane potentials (Model Fa) had little effect on the rate constants overall, or on the effects of L-cys on the rate constants. Furthermore, simulations of single channel activity with Model Fa suggest that over 50% of the sweeps would be blank. However, ∼30% blank sweeps were observed given the same simulation with Model F, suggesting that there are other factors that result in blank sweeps. These may include channels bypassing the open state due to inactivation from the resting state, or simply not reaching the open state due to large energy barriers along the activation pathway.

Changes in the transitions leading to and/or away from the open state may be a common mechanism by which neuromodulators up- and downregulate ion channel activity. In this study, the idea that L-cys increases T-current amplitude by increasing the rate of the final opening step and reducing the rate of inactivation from the open state was supported by analysis with three significantly different models. In addition, a previous modeling study suggested that serotonin increases TTX-resistant Na⁺ currents in rat nociceptors by the same mechanism (20). Conversely, another modeling study accounted for a reduction in TTX-sensitive Na⁺ currents in rat striatal neurons via cAMP-dependent phosphorylation as an increase in the rate of transition from the open state to the inactivated state (21). These types of changes in channel gating could increase or decrease current amplitude in the absence of changes in the voltage-dependency of channel activation or steady-state inactivation, as measured using standard electrophysiological protocols.