Bicarbonate and ammonia changes in brain during spreading depression

Abstract

An alkaline, followed by an acid-going transient, characterizes acid–base changes in the interstitial space during spreading depression in a variety of brain structures. In rat, such changes are associated with a significant rise in brain lactate content. How brain proton buffers behave during spreading depression is unknown. Techniques to significantly improve the response time of gas permeable membrane semnimicroelectrodes for carbon dioxide and ammonia are reported. Measurements with such electrodes, when coupled to measurements of hydrogen ion concentration (from microelectrodes), permit rapid changes to be determined in bicarbonate concentration or ammonia and ammonium ion concentration, respectively. Bicarbonate concentration fell from 30 ± 1 (n = 16) to 14 ± 1 mM (n = 16) during spreading depression. On the other hand, ammonia concentration rose from 2.3 ± 0.1 to 4.4 ± 0.3 μM (n = 17) while ammonium ion concentration rose from 116 ± 11 (n = 17) to 382 ± 30 μM (n = 17) during spreading depression. Bicarbonate changes probably reflect titration of brain bicarbonate stores by accumulated lactic acid. Similar physicochemical changes do not explain the rise in ammonia and ammonium ion concentrations. Instead, elevation of the latter can only result from an increase in ammonia content of the interstitial space.

Introduction

Acid–base homeostasis is an essential requirement of living systems. To survive, cells must continuously adjust their hydrogen ion concentration within a narrow physiologic range. Such regulation is accomplished by a combination of metabolic activities, physicochemical H⁺ buffering, and plasma membrane exchange transport (antiport) of H⁺-related (Stewart 1981) ionic species (Siesjö and Messeter 1971). Based on indirect measurements, failure of such antiport during ischemia was recently proposed as a necessary step toward excessive accumulation of acid in glia with subsequent lethal injury to affected brain (Kraig et al. 1986). Direct measurements of rat brain cell [H⁺] (Kraig and Nicholson 1987) now lend support to this hypothesis; levels of acid that occur in ischemic brain cells are sufficient to induce necrosis when injected directly into normal brain (Kraig et al. 1987). Thus extreme acidosis is likely to be a necessary concomitant of brain infarction from ischemia. It follows that by understanding how such extreme levels of [H⁺] are achieved one may begin to recognize the molecular mechanisms by which brain necrosis from ischemia occurs. More generally, a knowledge of how cells fail to adjust their [H⁺] (or that of their microenvironment) during various disease states may also reveal important clues as to the pathogenesis of these same maladies. The last assumption stems from the fact that H⁺ homeostasis is a crucial activity of viable cells and tissues. For these reasons we continue to study the disruption of brain acid–base homeostasis created by spreading depression.

Spreading depression is associated with an alkaline, then acid-going shift in interstitial [H⁺], [H⁺]_o (Kraig et al. 1983; Mutch and Hansen 1984; Kraig et al. 1985a). In rat neocortex, lactate accumulates to 7 mmol/kg (Mutch and Hansen 1984) and associated hydrolysis of high-energy phosphate stores (Alberti and Cuthbert 1982) probably accounts for the increased proton production of brain undergoing spreading depression. However, how the brain makes use of volatile H⁺ buffers, i.e., bicarbonate (HCO₃⁻) and ammonia (NH₃), in response to this acid load is unknown. This lack of knowledge is partly due to technical difficulties associated with measuring NH₃ or HCO₃⁻. In theory, NH₃ may be measured directly with a gas permeable membrane electrode. On the other hand, HCO₃⁻ cannot as yet be measured directly. (We discovered that the HCO3⁻ exchanger sold by World Precision Instruments (IE-310) actually predominantly sensed carbonate ions over bicarbonate. This ion exchanger is presumably that originally described by Khuri et al. (1974). When IE-310 was incorporated into double-barrelled ion-selective microelectrodes it did result in a millivolt output from the ion barrel that was proportional to the logarithm of either the [HCO₃⁻] or carbonate concentrations of test solutions. To differentiate which of these two ionic species the exchanger was indeed responding to, we performed the following experiment. A standard glass pH electrode (Thomas 4094-L15) and an ion-selective microelectrode made with IE-310 were placed in a solution of 26 mM sodium bicarbonate. Next, CO₂ was bubbled through the solution. As noted by Stewart (1981), increasing the CO₂ tension of a sodium bicarbonate solution will result in only an infinitesimal rise in [HCO₃⁻] (at biological concentrations). However, the rise in CO₂ tension will also cause an order of magnitude drop in the carbonate concentration. We observed that the IE-310 measures predominantly carbonate and not HCO₃⁻. However, the IE-310 exchanger performs poorly even as a carbonate sensor. Estimates of the selectivity of IE-310 for carbonate over other anions typically present in the brain indicate that the exchanger is not capable of making accurate measurements of carbonate concentrations in vivo because of significant ionic interferences.)

Methods

Electrode characteristics

The CO₂ electrode used in experiments reported here (MI-720; Microelectrodes, Inc., Londonderry, NH) has been described in detail (Kraig et al. 1986). To accurately record potentially rapid brain tissue CO₂ tension (Pt_CO2) changes during spreading depression, the response time (t₉₅) of the CO₂ electrode had to be decreased from the 30–40 s previously reported (Kraig et al. 1986). Such a reduction was accomplished by adding carbonic anhydrase (10 mg/mL, EC 4.2.1.1.; Sigma Chemical Co., St. Louis, MO) to the backfill solution of 5 mM sodium bicarbonate and 20 mM sodium chloride. Carbonic anhydrase reduced the t₉₅ of the CO₂ electrode to approximately 5 s (Fig. 1).

Fig. 1.

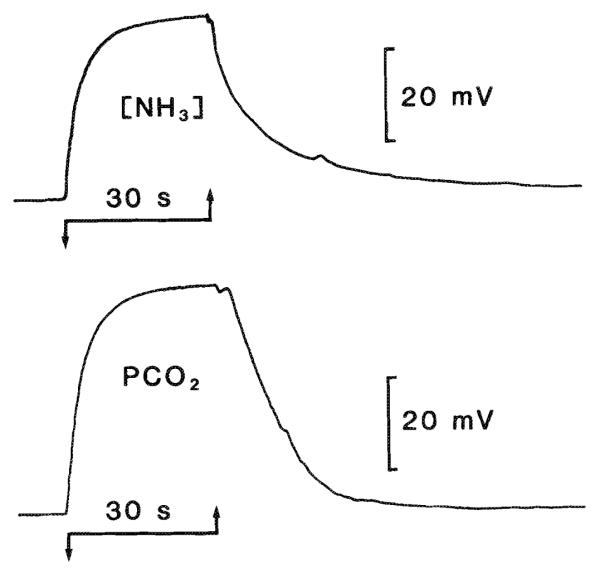
Response time of NH₃ and CO₂ semimicroelectrodes. Electrodes were placed in a loose fitting plastic tube (5 cm long and 0.4 cm internal diameter) connected to one port of a three-way stopcock. The other two ports received humidified gas at different concentrations. In this way, gas streams that passed the active surface of the electrode could be rapidly switched from one concentration to another. For example, the top trace shows the response of an NH₃-sensitive electrode to changes in [NH₃] created by bubbling nitrogen gas through 10 mM ammonium chloride (downgoing arrow) or 1 M ammonium chloride (upgoing arrow).t₉₅ (the time for the electrode to reach 95% of its final value after a step change in concentration of the measured species) was approximately 10 s. The CO₂ electrode t₉₅ (lower trace) was improved from the 30–40 s previously reported (Kraig et al. 1986) to about 5 s by adding 10 mg/mL of carbonic anhydrase (EC 4.2.1.1.; Sigma) to the backfill solution. 5% CO₂ – 95% oxygen initially flowed past the CO₂ electrode (downgoing arrow) followed by 101% CO₂ (upgoing arrow).

[HCO₃⁻] was derived from simultaneous measurements of [H⁺]_o and Pt_CO2 according to the Hendersen equation (Kraig et al. 1986):

$${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}=\frac{S^{\prime }{K_1}^{\prime }P{\mathrm{t}}_{{\mathrm{co}}_2}}{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{o}}}$$ [1]

where S’, the solubility constant for CO₂ (mM/mmHg), when corrected for temperature and molality, can be approximated by

$$S^{\prime }=0.4650t^{-0.7426}$$ [2]

K₁’ is the first ionization equilibrium constant for carbonic acid, which when corrected for [H⁺] can be approximated by

$${K_1}^{\prime }=\left(\ln \right[{\mathrm{H}}^{+}]∕16.0381)∕(-2.6481\times {10}^7)$$ [3]

We are unaware of previous reports that describe the use of an NH₃-selective electrode for (i) in vivo measurements of brain [NH₃] or (ii) simultaneous use of such an electrode with [H⁺] measurements to allow calculations of brain ammonium ion concentration ($\left[{\mathrm{NH}}_4^{+}\right]$). Therefore, we will describe the theory behind an NH₃-selective microelectrode in more detail here. An MI-740 semimicroelectrode (Microelectrodes, Inc., Londonderry, NH) was used to make NH₃ measurements. To improve the t₉₅ of this electrode, we replaced the polypropylene membrane supplied with the electrode with one made from a new form of Teflon (Chemfluor Lab Tape; ChemPlast, Inc., Wayne, NJ). This change in membrane decreased the t₉₅ from approximately 50 to 10 s (Fig. 1). The backfill solution was 5 mM ammonium hydroxide and 20 mM sodium chloride. Electrodes were connected to unity gain, high-performance buffer amplifiers whose outputs were filtered by 10 Hz active (Burr Brown) filters (Kraig et al. 1983). NH₃ electrodes were calibrated in a place remote from the animal and in situ by passing Ringer solutions with varying amounts of ammonium chloride (Fig. 2) over the active surface of the NH₃ electrode while simultaneously measuring solution [H⁺]. Normal Ringer solutions (Kraig et al. 1983) to which 100 or 300 μM of ammonium chloride was added were used to calibrate NH₃ electrodes in situ.

Fig. 2.

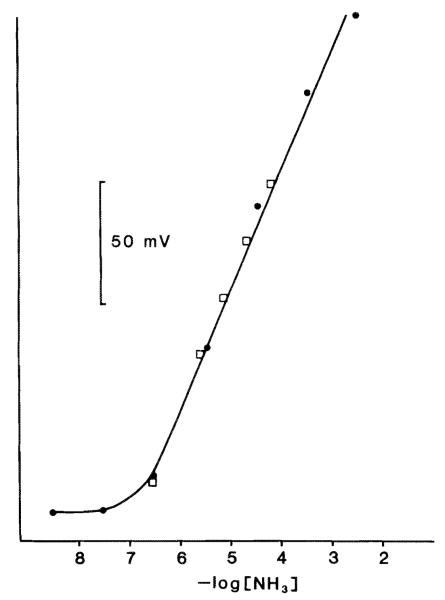
Response of an NH₃-sensitive electrode to changes in [NH₃]. ●, serial dilutions of ammonium chloride solutions; □, normal Ringer solutions with varying amounts of added ammonium chloride. The graph shows the linearity (r = 0.998) and sensitivity (57 mV/decade change in [NH₃]) down to approximately 0.5 μM [NH₃].

Determination of [NH₃] and calculation of $\left[{\mathrm{NH}}_4^{+}\right]$ were carried out as follows, Total NH₃, (NH₃)_t, of calibrating solutions was specified by adding a known amount of ammonium chloride to a known volume of Riniger solution so that

$${\left({\mathrm{NH}}_3\right)}_t=\left[{\mathrm{NH}}_3\right]+\left[{\mathrm{NH}}_4^{+}\right]$$ [4]

$$\left[{\mathrm{NH}}_3\right]={\left({\mathrm{NH}}_3\right)}_t{K}^{\prime }∕\left[{\mathrm{H}}^{+}\right]$$ [5]

$$\left[{\mathrm{NH}}_4^{+}\right]=\left[{\mathrm{NH}}_3\right]\left[{\mathrm{H}}^{+}\right]∕K^{\prime }$$ [6]

K¹’ the ionization equilibrium constant, in low ionic strength media when corrected for temperature (Sillén 1964) can be predicted by an Arrhenius plot that is described by the following equation:

$$K^{\prime }={10}^{\left(\right(-2.7257\times {10}^3∕T)-(9.8207\times {10}^{-2}\left)\right)}$$ [7]

where T is in degrees Kelvin. The NH₃ electrode response was linear (r = 0.998) and sensitive (57 mV/decade changes in [NH₃]) down to approximately 0.5 μM (Fig. 2). NH₃ electrode responses showed no interference to changes in CO₂ tension up to 100% CO₂. Similarly, CO₂ electrode responses showed no interference when exposed to 1 M ammonium hydroxide.

Animal preparation and recording

Male Wistar rats were prepared as previously decribed (Kraig et al. 1986) with the following modifications. A twisted wire, surface bipolar (platinum–iridium) stimulating electrode was placed greater than 1 mm away from the recording electrodes and near the lambdoid suture. After calibration of the H⁺-selective microelectrode (Kraig et. al. 1983; Kraig et al. 1985b) and the CO₂ semimicroelectrode (Kraig et al. 1986), the electrode array was advanced so that the CO₂ electrode’s active surface gently touched the pial surface. The H⁺-selective microelectrode was angled by about 20° from vertical and positioned so that it recorded from adjacent interstitial space 300 μm below the pial surface and immediately beneath the surface of the CO₂ electrode. Next, Ringer superfusion was stopped and the superfusion cup drained of Ringer and refilled with light mineral oil. The latter retarded egress of CO₂ from the brain surface (R. P. Kraig, unpublished observations; Matschinsky et al. 1968). NH₃ electrodes were poisoned by mineral oil (i.e., mineral oil seeped into the active surface to prevent NH₃ from penetrating the Chemfluor membrane and reaching the backfill solution). Thus, to measure [NH₃], after calibration and placement of NH₃ electrodes on the pial surface normal Ringer superfusion was continued. It is possible that [NH₃] measured with the electrode yielded artificially low brain values. However, NH₃ diffuses very slowly from solutions at biological pH levels of 7.4 or lower, so we consider the loss of NH₃ from the surface of the brain to be minor. Arterial pH, oxygen tension (Pa_o2), and carbon dioxide tension (Pa_CO2) were stabilized and measured with a Corning 158 blood gas analyzer. Blood glucose was measured with a Glucometer. Spreading depression was evoked by a 100 Hz bipolar surface stimulation for less than 5 s.

Results and discussion

Animals were moderately hypercapnic and mildly hypotensive (systolic blood pressure) (Table 1) as a result of halothane anesthesia and continued spontaneous ventilation. General anesthesia raises Pa_CO2 because of a depression in central nervous system ventilatory drive stimuli (Smith 1971). Similarly, anesthetic levels of halothane induce arterial hypotension (Deutsch 1971). We confirmed these effects in our experiments by noting that animals did not withdraw to pin prick of a hindlimb when Pa_CO2 was approximately 60 Torr (1 Torr = 133.32 Pa) and arterial blood pressure was approximately 100 mmHg. In addition, animals were normoxic, normoglycemic, and had normal hematocrits and body temperatures. Brain physiologic variables (Table 2) of [H⁺]_o (reported as interstitial pH, pH_o, Pt_CO2, and [HCO₃⁻]_o were similar to those previously reported (Kraig et al. 1983, 1985a, 1985b, 1986). [NH₃]_o, and ${\left[{\mathrm{NH}}_4^{+}\right]}_{\mathrm{o}}$ have not been previously reported. Values for [NH₃]_o and ${\left[{\mathrm{NH}}_4^{+}\right]}_{\mathrm{o}}$, when taken together, represent (NH₃]_t, which was 118 μM (Table 2) under normal conditions. This value represents (NH₃)_t of a single brain compartment, the interstitial space. Similar (NH₃)_t values for whole brain (i.e., 188 μM; Benjamin 1982) are somewhat higher than that for interstitial space reported here. Such a higher value for whole brain (NH₃)_t probably results from the more acid environment (i.e., higher cellular $\left[{\mathrm{NH}}_4^{+}\right]$) of brain cells. Nonetheless, such close agreement between two widely differing methods to determine (NH₃)_t supports our contention that simultaneous measurements of [NH₃] and [H⁺] provide an accurate and rapid technique for measurement of [NH₃] and estimate of $\left[{\mathrm{NH}}_4^{+}\right]$ and (NH₃)_t in real time. Furthermore, the ease and reproducibility of such measurements, though not generally recognized (Siesjö 1985), should encourage others to apply similar measurements to areas of interest. Perhaps the most important aspect of the present combined electrode experiments is the speed in which changes in carbonic acid buffer species and ammonia buffer species can be measured.

Table 1.

Blood physiologic variables

Variable	Mean ± SE
n	8
pH	7.35±0.02
PaCO2 (Torr)	60±2
PaO2 (Torr)	112±5
Glucose (mM)	7.1±0.6
Hematocrit (%)	43±0.4
Systolic blood pressure (mmHg)	106±2
Rectal temperature (°C)	37±0.5

Note: Pa_CO2, arterial PCO₂; Pa_O2, arterial PO₂; n, number of animals.

Table 2.

Brain physiologic variables

Variable	Mean ± SE	Time to peak	Time to resolve (min)
Before spreading depression
pHo	7.30±0.01 (n = 33)
PtCO2, (Torr)	64±2 (n = 16)
${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ (mM)	30±/ (n = 16)
[NH3]o (μM)	2.3±0.1 (n = 17)
$\left[{\mathrm{NH}}_4^{+}\right]$o (μM)	116±11 (n = 17)
Peak during spreading depression
pHo
Alkaline	7.49±0.01 (n = 33)	—	—
Acid	6.93±0.02 (n = 33)	9±0.5 s	11.9±0.8
PtCO2 (Torr)	79±2 (n = 16)	37±2 s	6.6±1.3
${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ (mM)	14±1 (n = 16)	—	—
[NH3]o (μM)	4.4±0.3 (n = 17)	1.8±0.1 min	20.8±2.1
$\left[{\mathrm{NH}}_4^{+}\right]$o (μM)	382±30 (n = 17)	—	—

Note: Pt_CO2, brain tissue PCO₂; n number of spreading depressions.

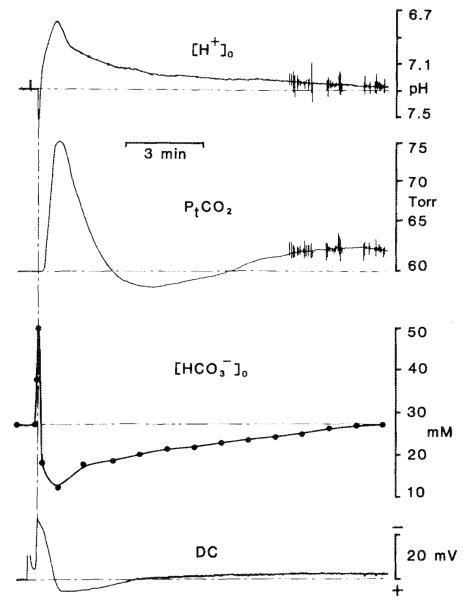
Changes in carbonic acid buffer species of [H⁺]_o, Pt_CO2, and calculated [HCO₃⁻]_o during spreading depression are shown in Fig. 3. Base-line Pt_CO2 values were not as high compared with blood (Tables 1 and 2) as previously reported (Kraig et al. 1986). This discrepancy may have resulted because more care was taken here to only gently apply the CO₂ electrode to the pial surface. In so doing a small interface of cerebral spinal fluid may have been present between the brain and the active surface of the electrode that could reduce Pt_CO2 measurements. Alternatively, the Pt_CO2 values previously reported (Kraig et al. 1986) may have been artificially elevated because of mild ischemia from compression created by the electrode surface (as originally suggested by Pontén and Siesjö 1966). Nonetheless, Pt_CO2 values reported here and those reported previously (Kraig et al. 1986) show an incremental increase above Pa_CO2 that is similar to values recently reported by Smith et al. (1986). Notice that the alkaline shift is not associated with any change in Pt_CO2. This result provides further support for the suggestion that blood flow fluctuations are unlikely to cause any influence in [H⁺]_o measurements (Kraig et al. 1983; Nicholson et al. 1985). ${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ rose to approximately 52 mM during the alkaline shift and fell to 14 mM during the acid shift. If ${\mathrm{HCO}}_3^{-}$ remains as the sole H⁺ buffer of the interstitial space during spreading depression, then ${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ changes closely approximate SID changes. SID is defined as the sum of strong (i.e., fully ionized) cations minus the sum of strong anions. (Understanding of the physicochemical acid–base behavior of biological solutions is often difficult because of complex interactions of numerous acids and bases. Stewart (1981) presented a conceptual framework that employs the formalisms of solution chemistry to clearly define dependent and independent variables in biological acid–base systems. Such categorization clearly defines those variables affected by and those variables that effect acid–base status in living cells and tissue. Dependent variables are internal to a system and are defined by equations relevant to the system as well as by externally imposed independent variables. Dependent variables include H⁺, hydroxyl ions, carbonate ions, ${\mathrm{HCO}}_3^{-}$, anions of weak acids, and undissociated weak acids. Stewart goes on to define independent variables as quantities whose values are imposed on a system from the outside. Independent variables do not affect one another but determine the values of dependent variables. Independent variables include Pt_CO2, the total weak acid concentration, and SID. Eight equations are necessary to fully define acid–base in a biological solution (Stewart 1981; also see Kraig et al. 1983, 1985a). In the interstitial space, where ${\mathrm{HCO}}_3^{-}$ is the principal H⁺ buffer species, SID is closely approximated by ${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$.) Furthermore, such SID changes would represent the independent variable responsible for [H⁺]_o changes (since Pt_CO2, the other independent variable, did not change). Thus, the alkaline shift of spreading depression could be accounted for by a large shift in ${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ (Kraig et. al. 1983). On the other hand, if partially ionized substances (weak acids or bases) also buffer the interstitial space during spreading depression, the ${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ changes alone would account for [H⁺]_o changes. Briefly stated, [H⁺]_o under these latter conditions would also depend on any changes in weak acids or bases (as the third independent variable).

Fig. 3.

Changes in carbonic acid buffer species during spreading depression. The uppermost trace shows [H⁺]_o changes after spreading depression elicited by 100 Hz bipolar surface stimulation for 5 s on the parietal cortex. The [H⁺]_o recording was made 300 μm beneath the parietal–pial surface. In this example, [H⁺]_o reached a peak acid level of pH 6.79 before returning to base line. The DC signal (lowermost trace) was recorded from the reference barrel of the H⁺-selective double-barrelled microelectrode. The negative DC shift was used as a time mark to gauge the time to [H⁺]_o, Pt_CO2, or [NH₃] peak changes and their resolution. Pt_CO2 (second trace from the top) was recorded from the adjacent parietal surface. Here Pt_CO2 rose to 79 Torr before returning to base line in a damped oscillatory fashion. ${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ changes (second trace from the bottom) were calculated according to Eq. 4. Solid dots represent specific calculated points. In this example ${\left[{\mathrm{HCO}}_3^{-}\right]}_{\mathrm{o}}$ rose to approximately 52 mM during the alkaline transient () and fell to a low of 13 mM before returning to base line.

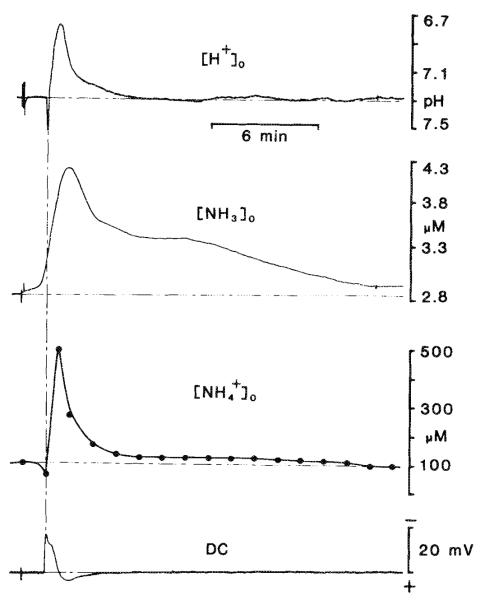
[NH₃]_o and ${\left[{\mathrm{NH}}_4^{+}\right]}_{\mathrm{o}}$ changes during spreading depression have not been reported previously. This lack, in part, probably stems from the inability of standard enzymatic techniques used to measure (NH₃)_t (Benjamin 1982) to resolve the spatial and temporal changes seen during spreading depression (Fig. 4). The micromolar range rise in (NH₃)_t during spreading depression adds little to the H⁺ buffer capacity of brain compared with the millimolar quantities of ${\mathrm{HCO}}_3^{-}$ present. More importantly, [NH₃]_o rose during spreading depression. Physicochemical buffering of the rise in [H⁺]_o would cause a fall in [NH₃]_o during spreading depression and an associated rise in ${\left[{\mathrm{NH}}_4^{+}\right]}_{\mathrm{o}}$. Instead, the elevation of [NH₃]_o during spreading depression can only result from an increase in (NH₃)_t of the interstitial space. The source of the rise in [NH₃]_o is unknown. However, of the at least 15 enzymatic reactions in mammalian brain that can generate NH₃, three are the most important (Cooper and Plum 1987): (i) purine nucleotide cycle; (ii) glutaminase reaction; (iii) glutamate dehydrogenase reaction. Fumarate and α-ketoglutarate generated in reactions i and iii, respectively, are further metabolized through the tricarboxylic acid cycle. Thus, increased ammonia content of the interstitial space seen during spreading depression may result from alternative fuel consumption by brain (Tilden 1983).

Fig. 4.

Simultaneous [H⁺]_o and [NH₃]_o changes during spreading depression. NH₃ and ${\mathrm{NH}}_4^{+}$ changes in brain measured in real time have not been previously reported because the enzyme-based or chemical techniques typically used only measure whole brain ammonia content (i.e., NH₃ plus ${\mathrm{NH}}_4^{+}$). These techniques for total ammonia require that brain samples be frozen rapidly in liquid nitrogen. The difficulties inherent in such procedures can be overcome if [H⁺] and [NH₃] are measured simultaneously in living tissue. The uppermost trace shows spreading depression elicited by 100 Hz bipolar surface stimulation for 5 s. Here [H⁺]_o reached a peak of pH 6.73 before returning to base line. A concomitant DC signal is shown in the lowermost trace. [NH₃]_o changes were recorded from a surface electrode placed adjacent to the H⁺-selective microelectrode. Initially [NH₃]_o (second record from the top) was approximately 2.8 μM before spreading depression and reached a peak value of approximately 4.2 μM before returninig to base line several minutes later. Notice that the time scale here is smaller than that of Fig. 3. ${\left[{\mathrm{NH}}_4^{+}\right]}_{\mathrm{o}}$ changes were calculated accordinig to Eqs. 1-3 and show that ${\left[{\mathrm{NH}}_4^{+}\right]}_{\mathrm{o}}$ (second trace from the bottomn) began at approximately 100 μM and reached a peak value of greater than 500 μM in this example before returning to base line.