Abstract
Context:
Because anterior cruciate ligament (ACL) injuries can occur during deceleration maneuvers, biomechanics research has been focused on the lower extremity kinetic chain. Trunk mass and changes in trunk position affect lower extremity joint torques and work during gait and landing, but how the trunk affects knee joint and muscle forces is not well understood.
Objective:
To evaluate the effects of added trunk load and adaptations to trunk position on knee anterior shear and knee muscle forces in landing.
Design:
Crossover study.
Setting:
Controlled laboratory environment.
Patients or Other Participants:
Twenty-one participants (10 men: age = 20.3 ± 1.15 years, height = 1.82 ± 0.04 m, mass = 78.2 ± 7.3 kg; 11 women: age = 20.0 ± 1.10 years, height = 1.72 ± 0.06 m, mass = 62.3 ± 6.4 kg).
Intervention(s):
Participants performed 2 sets of 8 double-leg landings under 2 conditions: no load and trunk load (10% body mass). Participants were categorized into one of 2 groups based on the kinematic trunk adaptation to the load: trunk flexor or trunk extensor.
Main Outcome Measure(s):
We estimated peak and average knee anterior shear, quadriceps, hamstrings, and gastrocnemius forces with a biomechanical model.
Results:
We found condition-by-group interactions showing that adding a trunk load increased peak (17%) and average (35%) knee anterior shear forces in the trunk-extensor group but did not increase them in the trunk-flexor group (peak: F1,19 = 10.56, P = .004; average: F1,19 = 9.56, P = .006). We also found a main effect for condition for quadriceps and gastrocnemius forces. When trunk load was added, peak (6%; F1,19 = 5.52, P = .030) and average (8%; F1,19 = 8.83, P = .008) quadriceps forces increased and average (4%; F1,19 = 4.94, P = .039) gastrocnemius forces increased, regardless of group. We found a condition-by-group interaction for peak (F1,19 = 5.16, P = .035) and average (F1,19 = 12.35, P = .002) hamstrings forces. When trunk load was added, average hamstrings forces decreased by 16% in the trunk-extensor group but increased by 13% in the trunk-flexor group.
Conclusions:
Added trunk loads increased knee anterior shear and knee muscle forces, depending on trunk adaptation strategy. The trunk-extensor adaptation to the load resulted in a quadriceps-dominant strategy that increased knee anterior shear forces. Trunk-flexor adaptations may serve as a protective strategy against the added load. These findings should be interpreted with caution, as only the face validity of the biomechanical model was assessed.
Keywords: lower extremities, anterior cruciate ligament injuries
Key Points.
The biarticular hamstrings muscles provided the mechanistic link for how trunk position modulates knee anterior shear forces.
Hamstrings muscle forces and knee anterior shear forces were modulated by an interaction between trunk load and the kinematic trunk adaptation to the load.
Added trunk loads increased the demands on quadriceps and gastrocnemius muscle forces regardless of trunk-adaptation strategy.
Future researchers need to investigate how trunk position, independent of trunk load, affects knee joint and muscle forces in landing.
Anterior cruciate ligament (ACL) injuries commonly occur during high-impact jumping and landing activities and carry an estimated annual cost of $1 billion.1,2 Because of the high economic cost and the devastating nature of the injury, researchers are working to identify biomechanical factors that lead to abnormally high knee joint loads, so they can apply these findings to clinical practice and try to minimize the incidence of ACL injuries. Anterior shear forces in the knee cause the tibia to translate anteriorly relative to the femur and to load the ACL.3,4 The quadriceps muscles load the ACL, with the greatest loads occurring during the last 30° of terminal knee extension, and the anterior shear force that this muscle produces via the patellar tendon can rupture an intact ACL.5 Conversely, the hamstrings muscles apply a posterior force to the proximal tibia and, therefore, can reduce knee anterior shear force and ACL strain.3,4,6,7 Because evidence has shown that the lower extremity muscles biomechanically affect ACL loading, researchers8–12 have mainly focused on the effects of these muscles on knee joint forces during abrupt deceleration tasks, such as vertical landing and stop jumping. However, because the kinetic chain is a complex, multisegmented system involving the trunk, pelvis, and lower extremity,13 anterior shear forces in the knee may be affected by other biomechanical sources in the kinetic chain and ultimately may contribute to ACL injuries.14 Specifically, trunk biomechanics may influence knee joint and muscle forces during tasks known to cause ACL injury, such as landing.
Zazulak et al15 prospectively studied the link between trunk biomechanics and knee injury. They found that poor trunk control predicted knee ligament injury (injury to any knee ligament) and ACL injury. In response to a sudden force release from the trunk in an upright, semi-sitting position, trunk displacement was greater in participants sustaining ACL injuries than in participants without ACL injuries. In addition, a regression analysis15 incorporating multiple trunk biomechanical measures (ie, displacements in sagittal and frontal planes) and a history of low back pain predicted knee ligament injury with 91% specificity and 68% sensitivity. Because trunk control was assessed under artificial conditions in which pelvic and lower extremity segments were restricted, a mechanistic understanding of how trunk biomechanics relate to knee joint biomechanics in a dynamic environment was limited. Other researchers have shown that both trunk position16,17 and trunk mass18 affect lower extremity biomechanical demands, which raises the question of which biomechanical component of the trunk predominantly affects the lower extremity kinetic chain.
To assess how trunk biomechanics relate to lower extremity biomechanics during landing, Kulas et al19 recently compared the effects of flexed and extended trunk adaptations with the effects of an added trunk load (10% body mass) on lower extremity joint kinematics, moments, and powers. Although the added trunk load increased knee extensor moments (18%) and work (14%) during drop landings, regardless of whether participants adapted to the load by increasing or decreasing their trunk-flexion angles, the magnitude of the increases in knee extensor moments and work were 2 to 3 times greater in participants who landed with a more-extended trunk (24%–28%) than in participants who adapted to the load by flexing their trunks more (4%–9%). This evidence indicated that trunk-control strategies affect knee joint forces through alterations in muscle forces, specifically the biarticular hamstrings. However, clinical interpretations of ACL injury potential were speculative, considering that knee joint and muscle forces were not reported.
We wanted to explore the clinical implications of this previous work19 and formulated an overall hypothesis that added trunk loads and trunk-position adaptations to the added trunk load affect knee joint and muscle forces in landing. Therefore, the purpose of our study was to assess the effects of an added trunk load and of kinematic trunk adaptations on anterior shear forces in the knee and on quadriceps, hamstrings, and gastrocnemius muscle forces during landing. The added trunk load served as a controlled experimental manipulation to further challenge segmental trunk control, allowing us to explore how trunk mass, trunk-position adaptations to the added mass, or a combination of both (mass-by-position interaction) affect knee joint and muscle forces. Inverse-dynamics–based methods of calculating knee anterior shear forces include joint reactions but do not include the shear forces produced by muscles that cross the knee and, thus, they probably underestimate the true shear forces; therefore, we used a biomechanical knee model that estimated anterior shear forces by including both shear forces produced by muscles and joint reaction forces.20 We hypothesized that as individuals adapted to the added trunk load by landing with less trunk flexion, they would produce less hamstrings force, resulting in greater knee anterior shear force. Conversely, we hypothesized that individuals who adapted to the added trunk load by landing with greater trunk flexion would produce greater hamstrings forces, resulting in less knee anterior shear force. Alternatively, we hypothesized that if trunk-position adaptations to the added load did not affect knee joint and muscle forces, similar effects of the added load would be observed in both kinematic trunk-adaptation groups.
METHODS
Participants
Ten men (age = 20.3 ± 1.15 years, height = 1.82 ± 0.04 m, mass = 78.2 ± 7.3 kg) and 11 women (age = 20.0 ± 1.10 years, height = 1.72 ± 0.06 m, mass = 62.3 ± 6.4 kg) who were recreationally active people participated in our study. We defined recreationally active as participating in jumping and landing activities at least 3 times per week for 30 minutes each time. All participants self-reported that they were healthy and had no history of lower extremity or low back injuries. All participants provided written informed consent, and the study was approved by the University and Medical Center Institutional Review Board.
Protocol
Participants were instructed to wear black spandex shorts, T-shirts, and their own athletic shoes. We measured their heights and masses. Using a PALM skeletal alignment and leg-length discrepancy instrument (Palpation Meter; Performance Attainment Associates, Lindstrom, MN), we measured pelvic depth and trunk depth, because these values were necessary to construct the biomechanical model. After we collected all anthropometric measurements, participants were familiarized with the drop-landing task. They balanced on the right foot on top of a 45-cm box with their toes in line with the front edge. Participants were instructed to roll forward until they felt themselves start to freefall and to land with the right foot on and left foot off of the force plate. We also instructed them to land in a natural, smooth, coordinated manner. Participants practiced the landings until they were comfortable with the task. For biomechanical analysis, reflective markers were placed bilaterally on the greater trochanters, iliac crests, anterior-superior iliac spines, and acromion processes. We also placed 1 marker on each of the following areas: first and fifth metatarsal heads, medial and lateral malleoli, knee joint line, and sacrum. Clusters of markers mounted onto rigid plates were also affixed to the foot, shank, and thigh (Figure 1).21 A fitted weight vest with 4 markers on its posterior aspect was placed firmly over the trunk. Next, a static calibration trial, with the participant standing in anatomic neutral and with arms crossing the chest, was collected. The markers on the medial and lateral metatarsal heads, malleoli, knee joint lines, bilateral greater trochanters, iliac crests, and acromion processes were removed. All remaining markers were used to track the foot, shank, thigh, pelvic, and trunk segments during the landing task.
Figure 1.
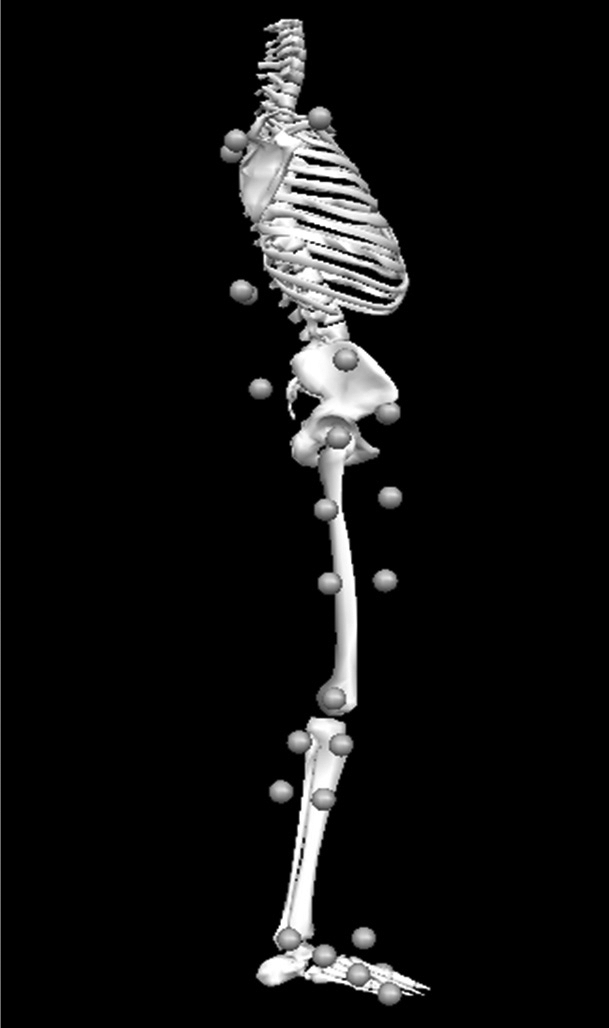
Lateral view of marker set. Medial markers on the right leg and left sides of the trunk and pelvis are not shown. The clusters of markers on the foot (3), lower leg (4), and femur (4) were used to track motion of the lower extremity during dynamic landing trials. Markers on the right and left anterior-superior iliac spines and sacrum were used to track the motion of the pelvis. A group of 4 markers on the posterior trunk tracked motion of the trunk segment.
Participants performed 8 double-leg landings under 2 conditions: no load and trunk load. The no-load condition was performed with no mass added to the trunk vest, whereas the trunk-load condition was performed with 10% body mass added symmetrically (anteriorly and posteriorly) to the trunk vest. The 2 conditions were counterbalanced across participants to control for potential effects (ie, learning or fatigue) associated with the order of the conditions. All kinematic data were acquired at 240 Hz using a 6-camera motion analysis system (model MCU240 ProReflex motion capture cameras and Qualisys Track Manager [QTM] software; Qualisys AB, Gothenburg, Sweden), whereas ground reaction forces were sampled at 960 Hz (model LG6-4-2000; Advanced Medical Technology Inc, Watertown, MA).
Data Reduction
All kinematic and analog data were exported from the QTM software and imported into Visual3D 3-dimensional biomechanical modeling and calculation software program (version 3.19; C-Motion Inc, Rockville, MD). We constructed a 5-segment biomechanical model in which we modeled the foot, shank, and thigh as frusta of right cones and modeled the pelvis and trunk as cylinders. Segment inertial properties and anthropometrics were based on the models of Hanavan22 and Dempster,23 respectively. All raw kinematic (marker position) and analog (ground reaction force) data were low-pass filtered using a second-order, bidirectional Butterworth filter at 6 Hz and 50 Hz, respectively.19 Lower-end cutoff frequencies (ie, 6 Hz) may result in oversmoothing (attenuation of the true signal) and may affect first-order and second-order calculations necessary for inverse-dynamics analysis. However, raw kinematic data collected during running, cutting, and landing applications traditionally have been low-pass filtered at 5 Hz to 18 Hz.12,24–27 Although it is not uncommon to filter the analog data for landing applications,19,27 we chose 50 Hz19 as a low-pass cutoff frequency because we identified higher-frequency noise in our force plate data. Magnitude and temporal comparisons between original and filtered analog data showed that signal attenuation due to the filtering was minimal.
Cardan angles for the hip, knee, and ankle were calculated in an x (flexion-extension), y (adduction-abduction), z (internal-external rotation) sequence. Trunk-flexion angle was calculated as the angle between the trunk segment and a vertical line in the laboratory coordinate system. Joint moments at the hip, knee, and ankle were calculated using standard inverse-dynamics procedures.20 Time of initial contact was denoted as 10 N of vertical ground reaction force determined during postprocessing. The end of the deceleration phase of landing was determined kinematically when the pelvic segment reached its lowest vertical position. All dependent-variable calculations occurred during this period. Means of the first 5 acceptable trials for each condition were used for analyses. Trials that showed obvious marker tracking errors were considered unacceptable.
Knee Muscle and Joint Force Estimations
We used a biomechanical knee model to estimate knee muscle and knee anterior shear forces.28–30 This moment-driven knee model, which was first used and fully explained by DeVita and Hortobágyi,28 has 2 main components. First, muscle forces are estimated from joint moments and pertinent physiologic data reported from the literature. The physiologic data include muscle moment arms according to joint position, muscle physiologic cross-sectional areas, and direction of muscle forces according to segment positions. Second, the estimated muscle (hamstrings, quadriceps, and gastrocnemius) forces and joint reaction forces are applied to the tibia. The knee anterior shear forces (acting parallel to the surface of the tibia) are calculated from the combined shear forces produced from muscle and joint reaction forces20 and represent the resultant anterior-posterior draw force acting on the proximal tibia.31 The Appendix provides a full description of the model.
This model has several limitations. First, the model does not take into account muscle activation and contraction dynamics when estimating muscle forces. Second, although the model does take into account muscle cocontraction from agonist and antagonist muscles crossing the knee, muscle cocontraction is not included when estimating hamstrings and gastrocnemius muscle forces from the hip and ankle joint moments, respectively. Third, the knee biomechanical model does not incorporate the ACL itself and its orientation relative to the tibia. Because of the limitations of this biomechanical knee model (and of all biomechanical models reported in the literature), the validity of its muscle and joint-force estimates is uncertain. The criterion standard for validating any biomechanical model is to compare estimates with in vivo forces; however, this is rarely feasible. Therefore, we determined the level of face validity of our model estimates by comparing the knee joint and muscle forces estimated for our study, the study in which this model was originally introduced,28 and those of other studies in which different techniques were used (Table 1).
Table 1.
Peak Knee Anterior Shear and Leg Muscle Forcesa
The biomechanical knee model was initially developed to estimate knee muscle and joint forces in individuals who had ACL reconstruction and were walking with or without a functional knee brace and in healthy control participants.28 The knee model produced muscle and joint forces comparable with forces reported by others; therefore, the face validity was considered reasonable.28 However, related reports10–12,32,33 of anterior shear forces in the knee during high-impact activities have varied widely from 0.24 to 9.37 body weights. These large discrepancies can be partially explained by differences in the knee shear force calculations and inherent task differences. Several investigators10,11,45 ultimately have derived the anterior shear forces from the resultant joint reaction forces. However, joint forces result from the combined effects of the joint reaction forces and muscle forces.20 Therefore, anterior shear forces in these data10,11,45 may be considered underestimates, as the additional shear forces induced by muscle contractions were not included.20 This is the primary reason we elected to estimate anterior shear forces using our biomechanical knee model, which takes into account the shear forces due both to the joint reactions and to the muscles crossing the knee. Cowling and Steele44 estimated the anterior shear forces through the combined effects of the patellar tendon force and joint reaction forces but did not account for antagonist muscle forces provided by the hamstrings muscles. More complex musculoskeletal models4,12,42,43 that account for muscle, ground reaction, and tibiofemoral contact forces acting on the tibia to produce anterior shear forces have been used in countermovement jumping, walking, squat-to-stand, and landing activities to estimate muscle and joint forces.
Although more complex, these musculoskeletal models also have different sets of limitations, which include using an inextensible patellar tendon,46 and the knee has been represented as a hinge joint with 1 degree of freedom.42 Because the biomechanical knee model that we used produced estimates that were at or within the wide variability of published data, we believe that our estimates of knee joint and muscle forces are reasonable. However, as with all biomechanical models, reasonable estimates do not ensure a valid model (validated to in vivo data), so the reader should be aware of how the model was validated and of the model's limitations and assumptions.
Average knee anterior shear forces were calculated as the anterior shear impulse divided by the landing impulse time. Peak and average anterior shear forces were normalized to body weights. The rationale for calculating and reporting both peak and average forces was that although peak forces occurring early during landing are presumed to be the primary cause of ACL injury, the exact magnitude or time that causes injury is unclear. However, the average force calculated across the entire deceleration period of landing (approximately 150–250 milliseconds) represents an overall estimation of the total stress on the knee joint and knee musculature. Therefore, both peak and average measurements more fully characterize the extent to which the trunk relates to knee joint and muscle forces during landing.
Participants were categorized into either the trunk-flexor or trunk-extensor group based on their responses to the trunk-load condition relative to the no-load condition. We used a Δ score, calculated as the difference between mean peak trunk-flexion positions in the trunk-load and no-load conditions, to classify each participant. Participants landing with more or less trunk flexion in the trunk-load condition than in the no-load condition were assigned to the trunk-flexor (n = 11) group or the trunk-extensor (n = 10) group, respectively. A 2-tailed, independent-samples t test showed group differences in peak trunk flexion angle Δ scores (trunk-extensor group = 5.56° ± 3.93°, trunk-flexor group = −3.65° ± 2.16°; P < .001). These results confirmed the presence of 2 different kinematic trunk-flexion–adaptation groups.
Data Analyses
We calculated 2 × 2 analyses of variance (ANOVAs) with repeated measures on condition (no load, trunk load) and between-groups comparisons (trunk flexor, trunk extensor) for peak and average quadriceps, hamstrings, gastrocnemius, and knee anterior shear forces. Tukey honestly significant different post hoc tests were calculated when interactions were found. We used SPSS (version 13.0; SPSS Inc, Chicago, IL) for data analysis. The α level was set a priori at .05.
RESULTS
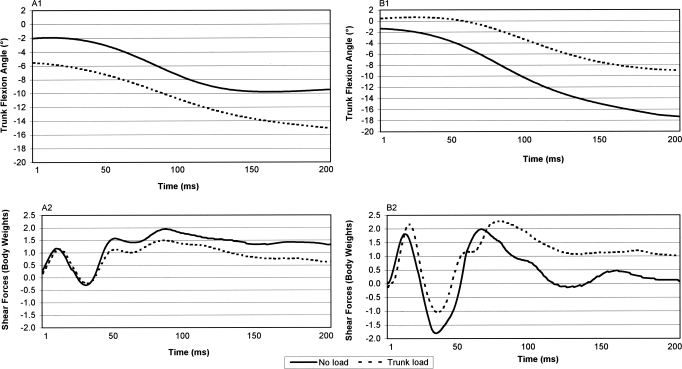
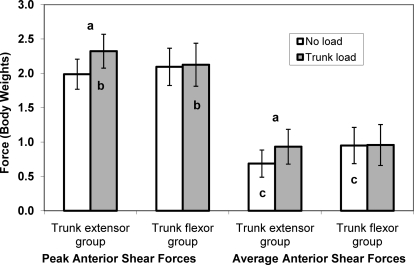
Figure 2 displays representative data for 1 participant in each of the trunk-adaptation groups. We found condition-by-group interactions showing that adding a trunk load increased peak and average knee anterior shear forces in the trunk-extensor group but not in the trunk-flexor group (peak: F1,19 = 10.56, P = .004; average: F1,19 = 9.56, P = .006; Figure 3). Compared with the trunk-flexor group, the extensor group had higher peak knee anterior shear forces in the trunk-load condition, but we found no group differences in the no-load condition. Additionally, compared with the trunk-flexor group, the trunk-extensor group had lower average knee anterior shear forces in the no-load condition, but we found no group differences in the trunk-load condition.
Figure 2.
Representative trunk flexion and shear forces in each trunk adaptation group. Data are presented for A, 1 individual in the trunk flexor adaptation group and B, 1 individual in the trunk extensor group. Positive values represent trunk extension and anterior shear forces. Negative values represent trunk flexion and posterior shear forces. Knee shear forces are normalized to body weight.
Figure 3.
Peak and average anterior shear forces across conditions and between groups. Vertical bars represent 95% confidence intervals. a Indicates increase across no-load to trunk-load conditions. b Indicates group differences in the trunk-load condition. c Indicates group differences in the no-load condition. a–c Collectively used to explain the condition-by-group interactions for both peak and average variables (both P < .01).
We found main effects for peak (F1,19 = 5.52, P = .030) and average (F1,19 = 8.83, P = .008) quadriceps forces, demonstrating that the added trunk load increased quadriceps muscle force regardless of group (Table 2). Peak quadriceps force increased from 7.83 ± 1.45 body weights in the no-load condition to 8.31 ± 1.91 body weights in the trunk-load condition. Similarly, average quadriceps force increased from 4.90 ± 1.07 body weights in the no-load condition to 5.27 ± 1.25 body weights in the trunk-load condition.
Table 2.
Main Effects for Quadriceps and Gastrocnemius Muscle Forces Across Conditionsa
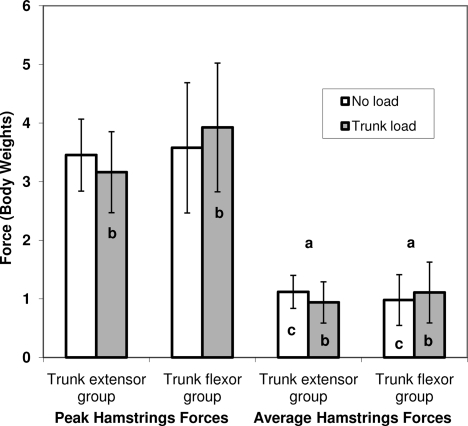
We found condition-by-group interactions for peak (F1,19 = 5.16, P = .035) and average (F1,19 = 12.35, P = .002) hamstrings muscle forces (Figure 4). Tukey post hoc testing showed that the peak hamstrings forces were greater in the trunk-flexor group than in the trunk-extensor group during the trunk-load condition, but the groups were not different in the no-load condition. Peak hamstrings force did not change within either group across conditions. Average hamstrings muscle forces increased in the trunk-flexor group but decreased in the trunk-extensor group across no-load and trunk-load conditions. In addition, compared with the trunk-flexor group, the trunk-extensor group had higher average hamstrings forces in the no-load condition and lower average hamstrings forces in the trunk-load condition.
Figure 4.
Peak and average hamstrings forces across conditions and between groups. Vertical bars represent 95% confidence intervals. a Indicates increase across no-load to trunk-load conditions. b Indicates group differences in the trunk-load condition. c Indicates group differences in the no-load condition. a–c Collectively used to explain the condition-by-group interactions for both peak (P < .05) and average variables (P < .01).
We found a main effect for condition for average gastrocnemius muscle forces. Added trunk load increased average (F1,19 = 4.94, P = .039) but not peak (F1,19 = 2.08, P = .165) gastrocnemius muscle forces regardless of trunk-adaptation group (Table 2). Average gastrocnemius forces increased from 0.79 ± 0.21 body weights to 0.83 ± 0.24 body weights across the no-load and trunk-load conditions.
DISCUSSION
Our overall hypothesis was that added trunk loads and trunk-position adaptations to the load affect knee joint and muscle forces in landing. We assessed the effects of an added trunk load and kinematic trunk adaptations on anterior shear forces in the knee and on quadriceps, hamstrings, and gastrocnemius muscle forces during landing. Our main finding was that added trunk loads selectively increased knee anterior shear forces depending on trunk-adaptation strategy. After 10% body mass was added to a trunk vest, peak and average knee anterior shear forces increased by 17% and 35%, respectively, in the trunk-extensor group, but peak (2%) and average (1%) knee anterior shear forces did not increase in the trunk-flexor group. Although quadriceps and gastrocnemius forces increased regardless of group (ie, main effect for added load), condition-by-group interactions on hamstrings forces showed that average hamstrings forces decreased by 16% across conditions in the trunk-extensor group and increased by 13% in the trunk-flexor group. Because we found main effects (trunk-load condition) and condition-by-group interactions (trunk-load condition and both trunk position adaptations) of the trunk on knee joint and knee muscle forces, we accept our overall hypothesis.
Trunk-Load Accommodation Strategies and Knee Injury Potential
The trunk extensor group increased peak and average knee anterior shear forces by 17% and 35%, respectively. These increases indicated that the trunk-extensor group used an accommodation strategy that might increase ACL injury potential. Conversely, the trunk-flexor group exhibited an accommodation strategy that minimized the increases in knee anterior shear forces (peak = 2%, average = 1%). Therefore, the trunk-flexor accommodation seemed to be a safe strategy to minimize additional forces on the knee. To clarify the biomechanical consequences of these 2 different kinematic trunk adaptations to the added external trunk load, we will explain the muscular adaptations leading to the resultant knee anterior shear forces.
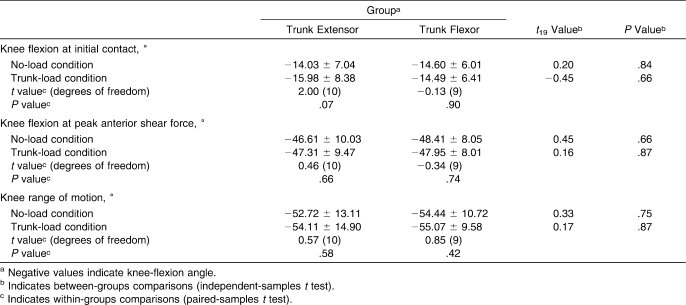
The added trunk load increased peak (6%) and average (8%) quadriceps muscle forces and average (4%) gastrocnemius muscle forces regardless of kinematic trunk-adaptation group. Because the knee extensor and ankle plantar-flexor muscles are the primary muscles that eccentrically contract to reduce the mechanical energy during vertical landing tasks,28,47,48 increased trunk mass concomitantly increases the energetic demands of these extensor muscles during landing.19 However, in vivo evidence has shown3,49,50 that the quadriceps and gastrocnemius muscles are antagonists to the ACL when knee-flexion angles are small (approximately 0°–45°). In addition, DeMorat et al5 showed that aggressive quadriceps loading in cadavers can rupture the ACL when the knee angle is at 20° of flexion. Therefore, our quadriceps muscle force results may be attributed to changes in knee-flexion angle across conditions and between groups but may not be attributed to the added trunk mass. Supplemental 2-tailed t tests on knee-flexion angle at initial contact, the time of peak anterior shear force, and total knee joint motion revealed no differences across conditions or between groups (all P > .05; Table 3). These results showed that quadriceps demands were increased by the additional trunk mass and were not a function of changes in knee-flexion angle. In addition, the different knee anterior shear force responses between groups cannot be explained by quadriceps forces or differences in knee kinematics alone.
Table 3.
Knee Kinematics (Mean ± SD)
The differential muscle response between groups was that hamstrings force production was increased in the trunk-flexor group but decreased in the trunk-extensor group. Figure 5 shows the differential hamstrings response to the added trunk load compared with similar group responses of the quadriceps and gastrocnemius to the added trunk load by illustrating the percent change across loading conditions and between groups. The protective effect of the hamstrings on knee anterior shear forces and ACL strain in vivo has been documented.3,4 Although the ability of the hamstrings to protect the ACL depends on knee-flexion position, Beynnon et al3 showed that when quadriceps activation is coupled with hamstrings activation, the strain on the ACL can be reduced by 36% at 15° and by 85% at 30° of knee flexion. Because our data showed that both groups had similar knee kinematics at peak knee anterior shear forces, we assumed that trunk load and trunk position did not influence hamstrings muscle moment arms at the knee and were not different between groups. Therefore, the increases and decreases in hamstrings force production observed in the trunk-flexor and trunk-extensor groups, respectively, can be explained by the changes in trunk-flexion angle. Our suggestion corresponds with the findings of Oddsson and Thorstensson.51 They showed that during fast, voluntary trunk-flexion movements performed from standing, hamstrings muscle activation is augmented. To better understand the link between trunk-flexion position and hamstrings force production in our study, we performed a supplementary correlation analysis between peak trunk-flexion position and hamstrings force impulse during the no-load condition only (ie, independent of trunk load). The correlation between peak trunk-flexion angle and hamstrings impulse was 0.80 (R2 = 0.64, P < .001), meaning that as trunk-flexion angle increased, hamstrings force also increased. Although defining the relationships between trunk-flexion angle and hamstrings force production was not our specific intention, this relationship nevertheless helps to clarify the mechanism by which increases in trunk flexion can ultimately affect knee anterior shear forces in landing. It is also important to note that our definition of trunk motion did not include the hip and was considered pure segmental motion of the trunk. Therefore, the influence of trunk flexion on hamstrings muscle function was made possible because pure segmental trunk flexion was correlated with hip-flexion and hip-extension moments,19 which affect hamstrings muscle moment arms and force production.
Figure 5.
Knee muscle force responses across conditions and between groups. Arrows indicate increases or decreases based on the results of the 2 × 2 analyses of variance for average muscle-force–dependent variables.
When considering the combined effects of the hamstrings and quadriceps forces on the knee joint within each group, the trunk-extensor group exhibited an adaptation to the trunk load that can be characterized as a quadriceps-dominant strategy that might ultimately increase ACL injury risk. Within this trunk-adaptation strategy, the increases in concomitant quadriceps forces (due to additional trunk mass) and decreases in hamstrings forces (due to trunk position adaptation) indicated that the muscular responses combined to increase the knee anterior shear forces during landing. Conversely, the trunk-flexor group increased both quadriceps and hamstrings muscle forces and, therefore, exhibited no increases in knee anterior shear forces. These results demonstrated that the trunk-flexor group adapted to the added load through augmentation of hamstrings force production, thereby offsetting the increases in quadriceps forces and ultimately resulting in no increases in knee anterior shear forces. In contrast, the trunk-extensor group exhibited a quadriceps-dominant strategy explained by both increased quadriceps forces and decreased hamstrings forces, culminating in the observed 17% to 35% increases in knee anterior shear forces.
Clinical Relevance
The clinical relevance of this study is 2-fold. First, from an injury mechanism perspective, the results showed that despite the presence of additional trunk mass, trunk position played a more integral role than trunk mass alone in determining knee anterior shear forces. This is helpful for the clinician, because trunk position is more readily modifiable and, therefore, trainable in an environment of injury prevention or rehabilitation. Second, from a rehabilitation and injury prevention perspective, weight vests are commonly used and marketed for lower extremity strength training. Our results indicated that using moderate levels of added mass (10% body mass) may have long-term benefits for strengthening the quadriceps and gastrocnemius muscles. Therefore, future studies on the use of trunk vests for lower extremity strengthening are warranted. However, because the effects of a weighted trunk vest on knee joint forces depend on how an individual positions the trunk, proper supervision from a certified athletic trainer is warranted.
Limitations
Our biomechanical model had several limitations. First, our model estimated muscle and anterior shear forces, and only the face validity of the model was addressed (Table 1). However, face validity alone does not ensure a valid model, because it cannot be assumed that model estimates from the literature are valid. Other investigators52–54 have validated their models by comparing the models' musculoskeletal simulation outputs (temporal and magnitude comparisons) with experimental data, such as joint moments, kinematics, and muscle-activation patterns. Because our model did not produce simulated kinematic, kinetic, and muscle-activation variables, we could not use these validation techniques. Simulation models can produce similar experimental kinematics and kinetics, which indirectly indicate muscle-force validity, but the validity of the exact magnitude of the simulated individual muscle forces is difficult to interpret because no standard for validating muscle-force estimations exists.55
Second, our model estimated muscle forces from hip, knee, and ankle joint moments and from physiologic data reported in the literature; hence, it did not take into account muscle activation and the length-tension and force-velocity properties.56 Thus, the model could have inaccurately estimated knee muscle and joint (anterior shear) forces. In pilot work conducted in our laboratory, we compared muscle forces computed with our moment-driven method and muscle forces computed using traditional Hill-type muscle-modeling techniques, which incorporate kinematics, muscle activations, and muscle length-tension and force-velocity properties. Although the moment-driven model consistently overestimated quadriceps and hamstrings muscle forces compared with the Hill-type model, the net effects of the estimated muscle forces (ie, quadriceps to hamstrings force ratios) were similar (1.53 versus 1.48). The mean difference in anterior shear force estimates were within 0.17 body weights (range, 13.7–19.4 body weights). These absolute differences correspond with a difference of 12.7% (range, 11.7%–13.7%).
Third, the biomechanical model did not directly calculate forces on the ACL; rather, the model estimated anterior shear forces acting perpendicular to the tibia based on predicted muscle forces and joint reactions. The ACL is the primary restraint against anterior tibial translation due to anteriorly directed shear forces,57 and anteriorly directed knee forces increase strain on the ACL.3 Although the exact magnitude of ACL force is unknown, the use of knee anterior shear forces to indirectly estimate ACL loads seems justified. Given the limitations of the biomechanical knee model, our results should be interpreted as estimates. Future work is needed to more strongly validate this model and may include (1) using the muscle forces generated from our model to drive forward-dynamics–based simulations of landing and to compare model outputs (kinematics, kinetics) with experimental data and (2) comparing the temporal relationship between simulated muscle forces and that of experimental muscle activations to ensure reasonable on-off characteristics. In addition, face validity could also be improved as new in vivo data become available.
We did not manipulate trunk-flexion position directly, so our results cannot be attributed to trunk position alone. Rather, our findings for knee anterior shear forces and hamstrings muscle forces are explained by the interactions between trunk load and trunk-adaptation strategy. Therefore, future studies are warranted to examine the effects of trunk position on knee anterior shear and knee muscle forces independent of trunk load.
CONCLUSIONS
Adding a trunk load of 10% body mass increased quadriceps and gastrocnemius muscle demands, regardless of kinematic trunk adaptation group. However, the effects of the trunk load on hamstrings muscle forces and knee anterior shear forces were dependent on trunk adaptation strategy. These results supported the role of trunk position as an important factor modulating hamstrings forces and, thus, knee anterior shear forces. Hence, the trunk-flexor strategy may be viewed as a protective strategy for minimizing ACL injury risk. Conversely, because knee anterior shear forces increase strain on the ACL, the trunk-extensor adaptation may be viewed as a strategy that increases ACL injury risk. Because both trunk load and kinematic trunk-adaptation strategies affected knee joint and knee muscle forces, we accept our hypothesis that added trunk loads and trunk-position adaptations to the load affect knee joint and muscle forces in landing. These data provide evidence for the concept that changes in the alignment of proximal body segments during landing affect lower extremity joint mechanics and injury potential. Therefore, in future studies aimed at understanding biomechanical factors leading to high knee joint loads, researchers should consider the role of the trunk as it relates to knee injury risk.
Acknowledgments
We thank Paul Zalewski for his valuable contributions toward participant recruitment, data collection, and data reduction for this project.
Appendix. Biomechanical Knee Model
The biomechanical knee model, originally developed by DeVita and Hortobágyi,28 is a moment-driven model because it uses the joint moments from the inverse dynamic analysis to determine the muscle forces. The 2 primary steps of the model require that researchers (1) determine the forces in the gastrocnemius, hamstrings, and quadriceps muscles and (2) apply these forces along with the joint reaction forces to the tibia to determine the knee joint forces. The gastrocnemius forces are determined from the plantar-flexor moment at the ankle joint, and it is assumed that this moment is produced by the triceps surae (gastrocnemius and soleus muscles). Muscle moment arm values for each ankle joint angle are derived from the literature32,33 according to ankle joint position. Next, gastrocnemius forces are calculated based on their proportion to the total physiologic cross-sectional area (PCA) of the triceps surae.34 The direction of the gastrocnemius forces is determined from the line of the tibia and the knee position and is expressed as the angle (α) between the gastrocnemius forces and the tibia. The proximal end of the gastrocnemius is attached 0.020 m superior and 0.023 m posterior to the knee joint on the femur.35 The resultant direction of the gastrocnemius forces on average is about α = 3° from parallel with the tibia.
Hamstrings forces are calculated from the hip extensor moment during the landing movement. The hip extensor moment is assumed to be produced by the hamstrings and gluteus maximus muscles, and it is also assumed that the hip flexors do not cocontract when a hip extensor moment is present. The estimated hamstrings forces account for (1) the hamstrings PCA relative to the total PCA (hamstrings + gluteus maximus) and (2) the hamstrings moment arm at the hip relative to the gluteus maximus moment arm. The total hamstrings proportion to the hip extensor moment is calculated as
where Hp is the proportion of the hip extensor moment generated by the hamstrings; Ham PCA and GM PCA are the hamstrings and gluteus maximus PCAs, respectively; and Hd and GMd are the hamstrings and gluteus maximus moment arms, respectively. Values for muscle PCAs34 and the hamstrings and gluteus maximus moment arms according to hip joint angle36,37 are attained from the literature. The average proportion of the hip extensor moment generated by the hamstrings is 0.63 using Equation 1.
The hamstrings forces are then calculated as
where Hp is the proportion of the hip extensor moment generated by the hamstrings, Het is the hip extensor moment, and Hd is the hamstrings moment arm. The direction of the hamstrings forces is a line parallel to the femur and at angle β to the tibia.
The quadriceps forces via the patellar tendon are calculated from the observed net knee joint moment, the hamstrings and gastrocnemius forces, and moment arms relative to the knee of the hamstrings, gastrocnemius, and quadriceps tendon:
where Kt is the net knee moment from inverse dynamics; Q, H, and G are the quadriceps tendon, hamstrings, and gastrocnemius muscle forces, respectively; and Qd, Hd, and Gd are the respective moment arms for the quadriceps tendon, hamstrings, and gastrocnemius as they cross the knee.
The forces in the quadriceps via the quadriceps tendon are calculated as
where Q, H, and G are the quadriceps tendon, hamstrings, and gastrocnemius muscle forces, respectively; Kt is the net knee moment from inverse dynamics; and Hd, Gd, and Qd are the respective moment arms for the hamstrings, gastrocnemius, and quadriceps tendon as they cross the knee.
Moment arms at the knee are obtained from the literature38–41 by averaging the values from several studies and for each knee joint angle. The direction of the patellar tendon forces (φ) is determined from the literature41 and is also a function of knee angle.
After the muscle forces are estimated, all muscle forces and the joint reaction forces (estimated through inverse dynamics) are partitioned into the anterior-posterior shear (perpendicular to the tibia in the sagittal plane) components and summed:
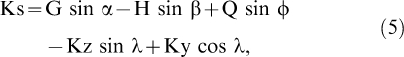 |
where Ks are the shear forces at the knee; G, H, Q are the gastrocnemius, hamstrings, and quadriceps tendon muscle forces, respectively; and Kz and Ky are the vertical and horizontal knee joint reaction forces, respectively. The Ks are positive when the shear force applies an anterior load to the tibia (ie, anterior shear force).
REFERENCES
- 1.Krosshaug T., Nakamae A., Boden B. P., et al. Mechanisms of anterior cruciate ligament injury in basketball: video analysis of 39 cases. Am J Sports Med. 2007;35(3):359–367. doi: 10.1177/0363546506293899. [DOI] [PubMed] [Google Scholar]
- 2.US Department of Health and Human Services, Centers for Disease Control and Prevention, National Center for Injury Prevention and Control. CDC Injury Research Agenda. http://www.cdc.gov/ncipc/pub-res/research_agenda/01_foreword.htm. Published June 2002. Accessed June 16, 2009.
- 3.Beynnon B. D., Fleming B. C., Johnson R. J., Nichols C. E., Renström P. A., Pope M. H. Anterior cruciate ligament strain behavior during rehabilitation exercises in vivo. Am J Sports Med. 1995;23(1):24–34. doi: 10.1177/036354659502300105. [DOI] [PubMed] [Google Scholar]
- 4.Shelburne K. B., Torry M. R., Pandy M. G. Muscle, ligament, and joint-contact forces at the knee during walking. Med Sci Sports Exerc. 2005;37(11):1948–1956. doi: 10.1249/01.mss.0000180404.86078.ff. [DOI] [PubMed] [Google Scholar]
- 5.DeMorat G., Weinhold P., Blackburn T., Chudik S., Garrett W. Aggressive quadriceps loading can induce noncontact anterior cruciate ligament injury. Am J Sports Med. 2004;32(2):477–483. doi: 10.1177/0363546503258928. [DOI] [PubMed] [Google Scholar]
- 6.Pandy M. G., Shelburne K. B. Dependence of cruciate-ligament loading on muscle forces and external load. J Biomech. 1997;30(10):1015–1024. doi: 10.1016/s0021-9290(97)00070-5. [DOI] [PubMed] [Google Scholar]
- 7.MacWilliams B. A., Wilson D. R., DesJardins J. D., Romero J., Chao E. Y. Hamstrings cocontraction reduces internal rotation, anterior translation, and anterior cruciate ligament load in weight-bearing flexion. J Orthop Res. 1999;17(6):817–822. doi: 10.1002/jor.1100170605. [DOI] [PubMed] [Google Scholar]
- 8.Cowling E. J., Steele J. R., McNair P. J. Effect of verbal instructions on muscle activity and risk of injury to the anterior cruciate ligament during landing. Br J Sports Med. 2003;37(2):126–130. doi: 10.1136/bjsm.37.2.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chappell J. D., Yu B., Kirkendall D. T., Garrett W. E. A comparison of knee kinetics between male and female recreational athletes in stop-jump tasks. Am J Sports Med. 2002;30(2):261–267. doi: 10.1177/03635465020300021901. [DOI] [PubMed] [Google Scholar]
- 10.Yu B., Lin C. F., Garrett W. E. Lower extremity biomechanics during the landing of a stop-jump task. Clin Biomech (Bristol, Avon) 2006;21(3):297–305. doi: 10.1016/j.clinbiomech.2005.11.003. [DOI] [PubMed] [Google Scholar]
- 11.Sell T. C., Ferris C. M., Abt J. P., et al. The effect of direction and reaction on the neuromuscular and biomechanical characteristics of the knee during tasks that simulate the noncontact anterior cruciate ligament injury mechanism. Am J Sports Med. 2006;34(1):43–54. doi: 10.1177/0363546505278696. [DOI] [PubMed] [Google Scholar]
- 12.Pflum M. A., Shelburne K. B., Torry M. R., Decker M. J., Pandy M. G. Model prediction of anterior cruciate ligament force during drop-landings. Med Sci Sports Exerc. 2004;36(11):1949–1958. doi: 10.1249/01.mss.0000145467.79916.46. [DOI] [PubMed] [Google Scholar]
- 13.Zatsiorsky V. M. Kinetics of Human Motion. Champaign, IL: Human Kinetics; 2002. [Google Scholar]
- 14.Griffin L. Y., Albohm M. J., Arendt E. A., et al. Understanding and preventing noncontact anterior cruciate ligament injuries: a review of the Hunt Valley II meeting, January 2005. Am J Sports Med. 2006;34(9):1512–1532. doi: 10.1177/0363546506286866. [DOI] [PubMed] [Google Scholar]
- 15.Zazulak B. T., Hewett T. E., Reeves N. P., Goldberg B., Cholewicki J. Deficits in neuromuscular control of the trunk predict knee injury risk: a prospective biomechanical-epidemiologic study. Am J Sports Med. 2007;35(7):1123–1130. doi: 10.1177/0363546507301585. [DOI] [PubMed] [Google Scholar]
- 16.Grasso R., Zago M., Lacquaniti F. Interactions between posture and locomotion: motor patterns in humans walking with bent posture versus erect posture. J Neurophysiol. 2000;83(1):288–300. doi: 10.1152/jn.2000.83.1.288. [DOI] [PubMed] [Google Scholar]
- 17.Lieberman D. E., Raichlen D. A., Pontzer H., Bramble D. M., Cutright-Smith E. The human gluteus maximus and its role in running. J Exp Biol. 2006;209(pt 11):2143–2155. doi: 10.1242/jeb.02255. [DOI] [PubMed] [Google Scholar]
- 18.Lees A. Methods of impact absorption when landing from a jump. Eng Med. 1981;10(4):207–211. [Google Scholar]
- 19.Kulas A., Zalewski P., Hortobágyi T., DeVita P. Effects of added trunk load and corresponding trunk position adaptations on lower extremity biomechanics during drop-landings. J Biomech. 2008;41(1):180–185. doi: 10.1016/j.jbiomech.2007.06.027. [DOI] [PubMed] [Google Scholar]
- 20.Winter D. A. Biomechanics and Motor Control of Human Movement. New York, NY: Wiley-Interscience; 1990. pp. 89–90. 2nd ed. [Google Scholar]
- 21.Cappozzo A., Cappello A., Della Croce U., Pensalfini F. Surface-marker cluster design for 3-D bone movement reconstruction. IEEE Trans Biomed Eng. 1997;44(12):1165–1174. doi: 10.1109/10.649988. [DOI] [PubMed] [Google Scholar]
- 23.Dempster W. T. Space Requirements of the Seated Operator: Geometrical, Kinematic, and Mechanical Aspects of the Body With Special Reference to the Limbs. Wright-Patterson Air Force Base, OH: Wright Air Development Center Technical Report 55–159; 1955. [Google Scholar]
- 24.James C. R., Bates B. T., Dufek J. S. Classification and comparison of biomechanical response strategies for accommodating landing impact. J Appl Biomech. 2003;19(2):106–118. doi: 10.1123/jab.19.2.106. [DOI] [PubMed] [Google Scholar]
- 25.Ferber R., Davis I. M., Williams D. S., III Gender differences in lower extremity mechanics during running. Clin Biomech (Bristol, Avon) 2003;18(4):350–357. doi: 10.1016/s0268-0033(03)00025-1. [DOI] [PubMed] [Google Scholar]
- 26.Decker M. J., Torry M. R., Wyland D. J., Sterett W. I., Steadman J. R. Gender differences in lower extremity kinematics, kinetics and energy absorption during landing. Clin Biomech (Bristol, Avon) 2003;18(7):662–669. doi: 10.1016/s0268-0033(03)00090-1. [DOI] [PubMed] [Google Scholar]
- 27.Hewett T. E., Myer G. D., Ford K. R., et al. Biomechanical measures of neuromuscular control and valgus loading of the knee predict anterior cruciate ligament injury risk in female athletes: a prospective study. Am J Sports Med. 2005;33(4):492–501. doi: 10.1177/0363546504269591. [DOI] [PubMed] [Google Scholar]
- 28.DeVita P., Hortobágyi T. Functional knee brace alters predicted knee muscle and joint forces in people with ACL reconstruction during walking. J Appl Biomech. 2001;17(4):297–311. [Google Scholar]
- 29.Messier S., DeVita P., Cowan R. E., Seay J., Young H. C., Marsh A. P. Do older adults with knee osteoarthritis place greater loads on the knee during gait? A preliminary study. Arch Phys Med Rehabil. 2005;86(4):703–709. doi: 10.1016/j.apmr.2004.05.015. [DOI] [PubMed] [Google Scholar]
- 30.Messier S. P., Gutekunst D. J., Davis C., DeVita P. Weight loss reduces knee-joint loads in overweight and obese older adults with knee osteoarthritis. Arthritis Rheum. 2005;52(7):2026–2032. doi: 10.1002/art.21139. [DOI] [PubMed] [Google Scholar]
- 31.McLean S. G., Huang X., Su A., van den Bogert A. J. Sagittal plane biomechanics cannot injure the ACL during sidestep cutting. Clin Biomech (Bristol, Avon) 2004;19(8):828–838. doi: 10.1016/j.clinbiomech.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 32.Rugg S. G., Gregor R. J., Mandelbaum B. R., Chiu L. In vivo moment arm calculations at the ankle using magnetic resonance imaging (MRI) J Biomech. 1990;23(5):495–501. doi: 10.1016/0021-9290(90)90305-m. [DOI] [PubMed] [Google Scholar]
- 33.Spoor C. W., van Leeuwen J. L., Meskers C. G., Titulaer A. F., Huson A. Estimation of instantaneous moment arms of lower-leg muscles. J Biomech. 1990;23(12):1247–1259. doi: 10.1016/0021-9290(90)90382-d. [DOI] [PubMed] [Google Scholar]
- 34.Yamaguchi G. T., Sawa G. U., Moran D. W., Fessler M. J., Winters J. M. A survey of human musculotendon actuator parameters. In: Winters J. M., Woo S. L. Y., editors. Multiple Muscle Systems: Biomechanics and Movement Organization. New York, NY: Springer-Verlag; 1990. pp. 717–778. [Google Scholar]
- 35.Seireg A., Arvikar R. J. A mathematical model for evaluation of forces in lower extremities of the musculo-skeletal system. J Biomech. 1973;6(3):313–326. doi: 10.1016/0021-9290(73)90053-5. [DOI] [PubMed] [Google Scholar]
- 36.Duda G. N., Brand D., Freitag S., Lierse W., Schneider E. Variability of femoral muscle attachments. J Biomech. 1996;29(9):1185–1190. doi: 10.1016/0021-9290(96)00025-5. [DOI] [PubMed] [Google Scholar]
- 37.Németh G., Ohlsén H. In vivo moment arm lengths for hip extensor muscles at different angles of hip flexion. J Biomech. 1985;18(2):129–140. doi: 10.1016/0021-9290(85)90005-3. [DOI] [PubMed] [Google Scholar]
- 38.Herzog W., Read L. J. Lines of action and moment arms of the major force-carrying structures crossing the human knee joint. J Anat. 1993;182(pt 2):213–230. [PMC free article] [PubMed] [Google Scholar]
- 39.Nissell R. Mechanics of the knee: a study of joint and muscle load with clinical applications. Acta Orthop Scand Suppl. 1985;216:1–42. [PubMed] [Google Scholar]
- 40.Spoor C. W., van Leeuwen J. L. Knee muscle moment arms from MRI and from tendon travel. J Biomech. 1992;25(2):201–206. doi: 10.1016/0021-9290(92)90276-7. [DOI] [PubMed] [Google Scholar]
- 41.Yamaguchi G. T., Zajac F. E. A planar model of the knee joint to characterize the knee extensor mechanism. J Biomech. 1989;22(1):1–10. doi: 10.1016/0021-9290(89)90179-6. [DOI] [PubMed] [Google Scholar]
- 42.Shelburne K. B., Pandy M. G. Determinants of cruciate-ligament loading during rehabilitation exercise. Clin Biomech (Bristol, Avon) 1998;13(6):403–413. doi: 10.1016/s0268-0033(98)00094-1. [DOI] [PubMed] [Google Scholar]
- 43.Anderson F. C., Pandy M. G. Storage and utilization of elastic strain energy during jumping. J Biomech. 1993;26(12):1413–1427. doi: 10.1016/0021-9290(93)90092-s. [DOI] [PubMed] [Google Scholar]
- 44.Cowling E. J., Steele J. R. The effect of upper-limb motion on lower-limb muscle synchrony: implications for anterior cruciate ligament injury. J Bone Joint Surg Am. 2001;83(1):35–41. doi: 10.2106/00004623-200101000-00005. [DOI] [PubMed] [Google Scholar]
- 45.Chappell J. D., Herman D. C., Knight B. S., Kirkendall D. T., Garrett W. E., Yu B. Effect of fatigue on knee kinetics and kinematics in stop-jump tasks. Am J Sports Med. 2005;33(7):1022–1029. doi: 10.1177/0363546504273047. [DOI] [PubMed] [Google Scholar]
- 46.Shelburne K. B., Pandy M. G. A musculoskeletal model of the knee for evaluating ligament forces during isometric contractions. J Biomech. 1997;30(2):163–176. doi: 10.1016/s0021-9290(96)00119-4. [DOI] [PubMed] [Google Scholar]
- 47.Zhang S. N., Bates B. T., Dufek J. S. Contributions of lower extremity joints to energy dissipation during landings. Med Sci Sports Exerc. 2000;32(4):812–819. doi: 10.1097/00005768-200004000-00014. [DOI] [PubMed] [Google Scholar]
- 48.Minetti A. E., Ardigò L. P., Susta D., Cotelli F. Using leg muscles as shock absorbers: theoretical predictions and experimental results of drop landing performance. Ergonomics. 1998;41(12):1771–1791. doi: 10.1080/001401398185965. [DOI] [PubMed] [Google Scholar]
- 49.Fleming B. C., Renstrom P. A., Beynnon B. D., et al. The effect of weightbearing and external loading on anterior cruciate ligament strain. J Biomech. 2001;34(2):163–170. doi: 10.1016/s0021-9290(00)00154-8. [DOI] [PubMed] [Google Scholar]
- 50.Fleming B. C., Renstrom P. A., Ohlen G., et al. The gastrocnemius muscle is an antagonist of the anterior cruciate ligament. J Orthop Res. 2001;19(6):1178–1184. doi: 10.1016/S0736-0266(01)00057-2. [DOI] [PubMed] [Google Scholar]
- 51.Oddsson L., Thorstensson A. Fast voluntary trunk flexion movements in standing: primary movements and associated postural adjustments. Acta Physiol Scand. 1986;128(3):341–349. doi: 10.1111/j.1748-1716.1986.tb07987.x. [DOI] [PubMed] [Google Scholar]
- 52.Lloyd D. G., Besier T. F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J Biomech. 2003;36(6):765–776. doi: 10.1016/s0021-9290(03)00010-1. [DOI] [PubMed] [Google Scholar]
- 53.McLean S. G., Su A., van den Bogert A. J. Development and validation of a 3-D model to predict knee joint loading during dynamic movement. J Biomech Eng. 2003;125(6):864–874. doi: 10.1115/1.1634282. [DOI] [PubMed] [Google Scholar]
- 54.Chumanov E. S., Heiderscheit B. C., Thelen D. G. The effect of speed and influence of individual muscles on hamstring mechanics during the swing phase of sprinting. J Biomech. 2007;40(16):3555–3562. doi: 10.1016/j.jbiomech.2007.05.026. [DOI] [PubMed] [Google Scholar]
- 55.Xiao M., Higginson J. S. Muscle function may depend on model selection in forward simulation of normal walking. J Biomech. 2008;41(15):3236–3242. doi: 10.1016/j.jbiomech.2008.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zajac F. E. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng. 1989;17(4):359–411. [PubMed] [Google Scholar]
- 57.Butler D. L., Kay M. D., Stouffer D. C. Comparison of material properties in fascicle-bone units from human patellar tendon and knee ligaments. J Biomech. 1986;19(6):425–432. doi: 10.1016/0021-9290(86)90019-9. [DOI] [PubMed] [Google Scholar]