Two perspectives on the twist of DNA

Abstract

Because of the double-helical structure of DNA, in which two strands of complementary nucleotides intertwine around each other, a covalently closed DNA molecule with no interruptions in either strand can be viewed as two interlocked single-stranded rings. Two closed space curves have long been known by mathematicians to exhibit a property called the linking number, a topologically invariant integer, expressible as the sum of two other quantities, the twist of one of the curves about the other, and the writhing number, or writhe, a measure of the chiral distortion from planarity of one of the two closed curves. We here derive expressions for the twist of supercoiled DNA and the writhe of a closed molecule consistent with the modern view of DNA as a sequence of base-pair steps. Structural biologists commonly characterize the spatial disposition of each step in terms of six rigid-body parameters, one of which, coincidentally, is also called the twist. Of interest is the difference in the mathematical properties between this step-parameter twist and the twist of supercoiling associated with a given base-pair step. For example, it turns out that the latter twist, unlike the former, is sensitive to certain translational shearing distortions of the molecule that are chiral in nature. Thus, by comparing the values for the two twists for each step of a high-resolution structure of a protein-DNA complex, we may be able to determine how the binding of various proteins contributes to chiral structural changes of the DNA.

INTRODUCTION

The structure of a DNA molecule is often described as a succession of base pairs, each represented as a rectangular plane.¹ A knowledge of the relative locations of origins positioned within these planes and the relative orientations of the short and long axes of the rectangles allow one to determine for each pair of adjacent base pairs in the molecule—a so-called base-pair step—the numerical values of six rigid-body parameters, three translational: shift, slide, and rise and three angular: tilt, roll, and twist.^{2, 3, 4, 5, 6, 7}

Some 40 years ago mathematicians defined a “twist” which, shortly after its introduction, was applied to DNA and used, like the step-parameter twist mentioned above, to characterize the secondary structure of the molecule.^{8, 9, 10} This twist was defined as the value of a certain integral involving two continuous space curves. In the application to DNA, the structure of which at that time was often depicted in terms of space curves.¹¹ One of the curves was taken to be the axis of the double helix, and the other curve was one of the strands winding about this axis. Using this framework, one then went on to compute the twist of the DNA, a unitless scalar representing the number of times the strand wound about the helical axis.

Here we are concerned with differences in the properties of these two twists, the step-parameter twist and the twist of the preceding paragraph, which, because of its connection with the global shape of the helical axis of a closed DNA molecule, a plasmid, for example, we shall refer to as the twist of supercoiling. In the next section we begin by reviewing the definition of the twist of supercoiling, and its well-known connection with the writhing number and the linking number.^{12, 13} Then, after characterizing two space curves consistent with today’s picture of DNA as a succession of discrete rectangular planes, we go on to describe a method for the computation of the twist of supercoiling for a single base-pair step. We also point out how easy it is to compute the writhe for the case of a closed molecule with an axial curve envisioned as a succession of line segments connecting the origins of the base pairs.

Of particular interest is the difference in properties between the step-parameter twist and the twist of supercoiling. We note that in a relaxed, undeformed configuration of a DNA molecule, the two twists are expected to be close in value for all base-pair steps. However, we find that although translations of the base pairs leave the step-parameter twist unchanged, that is not generally the case for the twist of supercoiling. It, instead, is sensitive to translational distortions that are chiral in nature. To illustrate the point, we compare the values of the two types of twist for base-pair steps in a model DNA structure having both a bend and a shear. We find in this case a base-pair step for which the value of the step-parameter twist and the twist of supercoiling are significantly different.

THE TWIST OF SUPERCOILING

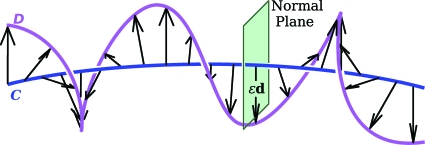
As we pointed out above, in much of the early theoretical work describing the equilibrium configurations of DNA, the atomistic details of the molecule were ignored, and instead, the structure of the molecule was, in fact, described in terms of two space curves. The tertiary structure of the molecule was represented, as shown in Fig. 1, by the shape of a smooth space curve C mirroring the shape of the axis of the double helix.

Figure 1.

Schematic representation of DNA. The double-helical axis is given by curve C and one of the helical strands by curve D. For the purpose of calculation of the twist of D about C, D is to be thought of as being traced out by the head of a vector εd(s_C) everywhere normal to the tangent vector t_C(s_C).

A second curve D, identified with one of the helical strands, was that traced out by the head of a vector εd(s_C), where ε is a constant, and d(s_C) is a unit vector normal to the tangent t_C(s_C) to C at a position having an arc length s_C along C.

The t_C(s_C), d(s_C) pairs associated with two nearby points along C having arc lengths s_C and s_C+ds_C are, in general, somewhat rotated with respect to each other. The relative rotational orientation of the two pairs before and after a small change in arc length ds_C is such that there exists a single rotation of the initial pair (at s_C) by a small angle about some axis that leads to t_C(s_C+ds_C) and d(s_C+ds_C). The vector dΩ, the differential of the Darboux vector Ω, points in the direction of this axis of rotation and has a magnitude equal to the small angle of rotation. The change dt_C(s_C) and dd(s_C) that the vectors t_C(s_C) and d(s_C) undergo during this change in arc length ds_C is simply the cross product of dΩ with the vector itself. That is, if v_C(s_C) stands for either t_C(s_C) or for d(s_C),

$$d{\mathbf{v}}_C\left(s_C\right)=d\mathbf{\Omega }\times {\mathbf{v}}_C\left(s_C\right).$$ (1)

For the case of the tangent, Eq. 1 leads to the equation

$$d\mathbf{\Omega }={\mathbf{t}}_C\left(s_C\right)\times d{\mathbf{t}}_C\left(s_C\right)+\left(d\mathbf{\Omega }\cdot {\mathbf{t}}_C\left(s_C\right)\right){\mathbf{t}}_C\left(s_C\right).$$ (2)

One of the Frenet–Serret equations, the three equations relating the tangent to the principal normal n_C(s_C) and the binormal b_C(s_C) (=t_C(s_C)×n_C(s_C)), allows us to write dt_C(s_C)=n_C(s_C)κ_C(s_C)ds_C where κ_C(s_C) is the curvature of C. The first term on the right-hand side of Eq. 2 then becomes

$${\mathbf{t}}_C\left(s_C\right)\times d{\mathbf{t}}_C\left(s_C\right)={\mathbf{b}}_C\left(s_C\right)\kappa \left(s_C\right)d{s}_C.$$ (3)

The second term in that equation, the one containing the component of dΩ along t_C(s_C), is proportional to the twist density. Replacing t_C(s_C) by d(s_C) in Eq. 2 and then taking the projection of the resulting expression for dΩ along the tangent shows that

$$d\mathbf{\Omega }\cdot {\mathbf{t}}_C\left(s_C\right)=\left(\mathbf{d}\left(s_C\right)\times d\mathbf{d}\left(s_C\right)\right)\cdot {\mathbf{t}}_C\left(s_C\right).$$ (4)

The twist T(D,C), in units of number of turns, of D about a length l of C is

$$T\left(D,C\right)=\left(\frac{1}{2\pi }\right){\int }_{s_{C_1}}^{s_{C_2}}d\mathbf{\Omega }\cdot {\mathbf{t}}_C\left(s_C\right),$$ (5)

where s_C2−s_C1=l.

If the curves C, given by r_C(s_C), and D, given by r_D(s_D), are closed, the conventional twist is simply related to two other integrals,^{12, 13} so-called Gauss integrals, the linking number L(D,C),

$$L\left(D,C\right)=\left(\frac{1}{4\pi }\right)∯\frac{{\mathbf{t}}_D\left(s_D\right)\times {\mathbf{t}}_C\left(s_C\right)\cdot \left({\mathbf{r}}_D\left(s_D\right)-{\mathbf{r}}_C\left(s_C\right)\right)}{{\mid {\mathbf{r}}_D\left(s_D\right)-{\mathbf{r}}_C\left(s_C\right)\mid }^3}d{s}_{D}d{s}_C,$$ (6)

and the writhing number W(C), or writhe for short,

$$W\left(C\right)=\left(\frac{1}{4\pi }\right)∯\frac{{\mathbf{t}}_C\left(s_C\right)\times {\mathbf{t}}_C\left(s_C^{\prime }\right)\cdot \left({\mathbf{r}}_C\left(s_C\right)-{\mathbf{r}}_C\left(s_C^{\prime }\right)\right)}{{\mid \left({\mathbf{r}}_C\left(s_C\right)-{\mathbf{r}}_C\left(s_C^{\prime }\right)\right)\mid }^3}d{s}_{C}d{s}_C^{\prime }.$$ (7)

The linking number is an integer, a topological invariant, equal to the number of times that the curve D passes through a surface bounded by C.¹⁴ (In computing this sum each pass-through is assigned a value of either +1 or −1 according to a convention consistent with the form of the Gauss integral.) This integer remains unchanged for all distortions in shape of the curves C and D as long as the curves do not intersect each other during the distortions. The writhe, a property of closed curve C alone, is a measure of the chiral distortion of the curve from planarity. Fuller pointed out that its value is also what one would get by averaging, over all orientations of a plane P, the sum of the signed self-crossings occurring in the planar curves resulting from the perpendicular projection of C on P.¹⁰

The connection between the twist, the writhe, and the linking number mentioned above is given by the well-known equation⁹ (For another derivation, see Appendix A.),

$$L\left(D,C\right)=W\left(C\right)+T\left(D,C\right).$$ (8)

Some additional mathematical properties of the twist, writhe, and linking number integrals are discussed in a more recent paper.¹⁵

THE TWIST OF SUPERCOILING FOR THE MULTISTEP DNA MOLECULE

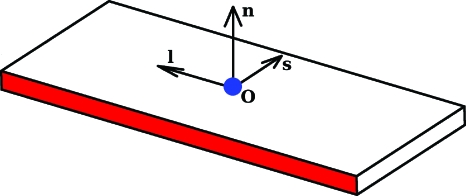
As we have mentioned, details of the structure of DNA are now more realistically represented, not in terms of smooth space curves, but as a sequence of base pairs. Two adjacent base pairs enclose a base-pair step. Various mathematical procedures have been formulated for going from the atomic coordinates (determined from high-resolution structural measurements and simulations) of two associated bases to a base-pair plane such as that shown in Fig. 2. Each plane contains an origin o from which a triad of mutually orthogonal unit vectors emanate, a short axis s, a long axis l, and a normal n(=s×l). The method employed here for determining the position and orientation of these planes is the one agreed upon by DNA structural and computational biologists in 1999 at the Tsukuba Workshop on Nucleic Acid Structure and Interactions and subsequently reviewed and approved by the International Union of Biochemistry and Molecular Biology Commission on Biochemical Nomenclature.¹⁶

Figure 2.

The vectors associated with a base-pair plane: an origin o and a mutually orthogonal triad of unit vectors, the short axis s, the long axis l, and the normal n.

We begin the application of the concept of the twist of supercoiling, described above, to a succession of base-pair planes by imagining that there are simply line segments connecting the origins of adjacent base pairs. How then can a smooth curve C be chosen that gives such a picture of the DNA, a picture that seems to show a curve with a discontinuous change in its tangent at each base pair? That is, for each base pair, the i^th for example, the incoming line segment has a unit tangent we call t_(i−1). The tangent of the outgoing segment is t_(i). Both of these vectors are defined in terms of the origins o_i−1, o_i, and o_i+1 of the i^th base pair and the two base pairs adjoining it,

$${\mathbf{t}}_{\left(i-1\right)}=\frac{{\mathbf{o}}_i-{\mathbf{o}}_{i-1}}{\mid {\mathbf{o}}_i-{\mathbf{o}}_{i-1}\mid },$$ (9)

$${\mathbf{t}}_{\left(i\right)}=\frac{{\mathbf{o}}_{i+1}-{\mathbf{o}}_i}{\mid {\mathbf{o}}_{i+1}-{\mathbf{o}}_i\mid }.$$

(Note: Subscripts enclosed in parentheses label base-pair steps and those not enclosed in parentheses label individual base pairs.)

We can envision a limiting process, shown in Fig. 3, in which we start with a curve along which the tangent changes smoothly from t_(i−1) to t_(i) in the vicinity of base pair i as one moves along a circular arc lying in a plane spanned by these two vectors, i.e., lying in the plane having as its normal b_i given by

$${\mathbf{b}}_i=\frac{{\mathbf{t}}_{\left(i-1\right)}\times {\mathbf{t}}_{\left(i\right)}}{\mid {\mathbf{t}}_{\left(i-1\right)}\times {\mathbf{t}}_{\left(i\right)}\mid }.$$ (10)

Then the arc of the circle is allowed to decrease to zero as its curvature increases to infinity, with the tangent vectors t_(i−1) and t_(i) remaining unchanged. This process is repeated at each base pair. Thus, base pair i+1 has an incoming tangent t_(i) and an outgoing tangent t_(i+1) determined as in Eq. 9 from the origins of base pairs i+1 and i+2. When the tangent becomes t_(i) the curve abruptly becomes a line segment of length ∣o_i+1−o_i∣ directed along t_(i). At base pair i+1 the curvature abruptly becomes infinitely large again but with the tangent still changing smoothly from t_(i) to t_(i+1), along a circular arc lying in a plane with

$${\mathbf{b}}_{i+1}=\frac{{\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(i+1\right)}}{\mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(i+1\right)}\mid }$$ (11)

as its normal.

Figure 3.

The passage from a smooth curve with circular segments of curvature κ to the entirely linear segments that connect the origins of the base-pair planes consistent with a high-resolution structure of DNA.

We now can define in greater detail the nature of a single step, the i^th. At base pair i curve C for the step begins at that point in the circular arc where the tangent, call it ${\tilde{\mathbf{t}}}_i$, is midway between t_(i−1) and t_(i), i.e.,

$${\tilde{\mathbf{t}}}_i=\frac{{\mathbf{t}}_{\left(i-1\right)}+{\mathbf{t}}_{\left(i\right)}}{\mid {\mathbf{t}}_{\left(i-1\right)}+{\mathbf{t}}_{\left(i\right)}\mid },$$ (12)

and ends at the corresponding point at base pair i+1, i.e., where the tangent is

$${\tilde{\mathbf{t}}}_{i+1}=\frac{{\mathbf{t}}_{\left(i\right)}+{\mathbf{t}}_{\left(i+1\right)}}{\mid {\mathbf{t}}_{\left(i\right)}+{\mathbf{t}}_{\left(i+1\right)}\mid }.$$ (13)

The unit vector ${\mathbf{d}}_i^{\mathbf{l}}$ at the beginning of the step we first take to be in the direction of the projection of the long axis l_i on the plane containing o_i perpendicular to ${\tilde{\mathbf{t}}}_i$. The unit vector ${\mathbf{d}}_{i+1}^{\mathbf{l}}$ at the end of the step points along the projection of l_i+1 on the plane containing o_i+1 perpendicular to ${\tilde{\mathbf{t}}}_{i+1}$,

$${\mathbf{d}}_i^{\mathbf{l}}=\frac{\left({\mathbf{l}}_i\cdot {\mathbf{b}}_i\right){\mathbf{b}}_i+\left({\mathbf{l}}_i\cdot {\tilde{\mathbf{t}}}_i\times {\mathbf{b}}_i\right)\left({\tilde{\mathbf{t}}}_i\times {\mathbf{b}}_i\right)}{\mid \left({\mathbf{l}}_i\cdot {\mathbf{b}}_i\right){\mathbf{b}}_i+\left({\mathbf{l}}_i\cdot {\tilde{\mathbf{t}}}_i\times {\mathbf{b}}_i\right)\left({\tilde{\mathbf{t}}}_i\times {\mathbf{b}}_i\right)\mid }$$ (14)

and

$${\mathbf{d}}_{i+1}^{\mathbf{l}}=\frac{\left({\mathbf{l}}_{i+1}\cdot {\mathbf{b}}_{i+1}\right){\mathbf{b}}_{i+1}+\left({\mathbf{l}}_{i+1}\cdot {\tilde{\mathbf{t}}}_{i+1}\times {\mathbf{b}}_{i+1}\right)\left({\tilde{\mathbf{t}}}_{i+1}\times {\mathbf{b}}_{i+1}\right)}{\mid \left({\mathbf{l}}_{i+1}\cdot {\mathbf{b}}_{i+1}\right){\mathbf{b}}_{i+1}+\left({\mathbf{l}}_{i+1}\cdot {\tilde{\mathbf{t}}}_{i+1}\times {\mathbf{b}}_{i+1}\right)\left({\tilde{\mathbf{t}}}_{i+1}\times {\mathbf{b}}_{i+1}\right)\mid }.$$

Let us call ${\alpha }_i^{\mathbf{l}}$ the angle (in radians) that ${\mathbf{d}}_i^{\mathbf{l}}$ makes with b_i, and ${\alpha }_{i+1}^{\mathbf{l}}$ the angle that ${\mathbf{d}}_{i+1}^{\mathbf{l}}$ makes with b_i+1, or, more precisely,

$$\text{cos}{\alpha }_i^{\mathbf{l}}={\mathbf{b}}_i\cdot {\mathbf{d}}_i^{\mathbf{l}},\text{sin}{\alpha }_i^{\mathbf{l}}={\tilde{\mathbf{t}}}_i\cdot {\mathbf{b}}_i\times {\mathbf{d}}_i^{\mathbf{l}}$$ (15)

and

$$\text{cos}{\alpha }_{i+1}^{\mathbf{l}}={\mathbf{b}}_{i+1}\cdot {\mathbf{d}}_{i+1}^{\mathbf{l}},\text{sin}{\alpha }_{i+1}^{\mathbf{l}}={\tilde{\mathbf{t}}}_{i+1}\cdot {\mathbf{b}}_{i+1}\times {\mathbf{d}}_{i+1}^{\mathbf{l}}.$$

These vectors and angles are pictured in Fig. 4.

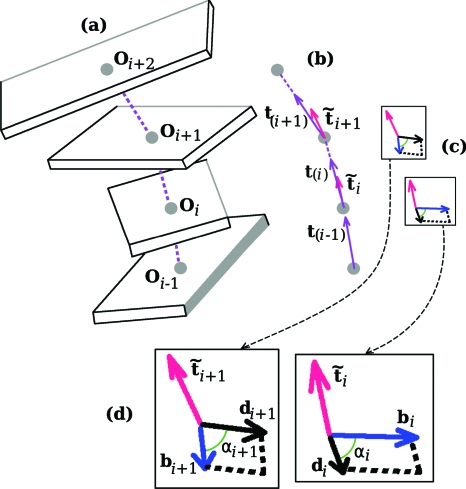
Figure 4.

The vectors involved in the calculation of the twist of supercoiling of the DNA base-pair step bounded by the i^th and the (i+1)^st planes. Shown in (a), the four base-pair plane origins needed for the determination of the three vectors depicted in (b), t_(i−1),t_(i), and t_(i+1), which, in turn, are needed for specifying ${\tilde{\mathbf{t}}}_i$ and ${\tilde{\mathbf{t}}}_{i+1}$. These last two are normal to the two planes seen in (c). Each of these planes contains a d vector and a b vector. Two of the angles needed for the twist calculation as given by Eq. 16 are denoted in (d), an enlargement of (c).

To determine the twist of supercoiling of the i^th base-pair step we carry out five rotations during which ${\mathbf{d}}_i^{\mathbf{l}}$ is converted to ${\mathbf{d}}_{i+1}^{\mathbf{l}}$. All of the vectors involved during this process can be thought of as emanating from a single point. For each of the rotations of the d¹ vector, the rotational axis, dΩ, also passing through this point, will either (a) lie along a tangent which is not changing its direction, or (b) the axis will coincide with one of the two constant b vectors. For a-type rotations, according to Eq. 5, the twist of supercoiling is simply the angle of rotation while for b-type rotations with the axis perpendicular to the tangent, the twist is zero. We start with the plane containing ${\mathbf{d}}_i^{\mathbf{l}}$ and b_i. The normal to this plane is ${\tilde{\mathbf{t}}}_i$. The sequence of five rotations is as follows: (i) rotation of ${\mathbf{d}}_i^{\mathbf{l}}$ about ${\tilde{\mathbf{t}}}_i$ until the angle between d¹ and b_i changes from ${\alpha }_i^{\mathbf{l}}$ to ${\overline{\alpha }}_{\left(i\right)}^{\mathbf{l}}$ where ${\overline{\alpha }}_{\left(i\right)}^{\mathbf{l}}=\left({\alpha }_i^{\mathbf{l}}+{\alpha }_{i+1}^{\mathbf{l}}\right)∕2$; (ii) rotation of d¹ about b_i until the normal to the plane containing these vectors changes from ${\tilde{\mathbf{t}}}_i$ to t_(i). At this point the plane contains b_i+1 as well as b_i; (iii) rotation of d¹ about t_(i) until d¹ makes an angle of ${\overline{\alpha }}_{\left(i\right)}^{\mathbf{l}}$ with b_i+1; (iv) rotation of d¹ about b_i+1 until the normal changes from t_(i) to ${\tilde{\mathbf{t}}}_{i+1}$; and (v) rotation of d¹ about ${\tilde{\mathbf{t}}}_{i+1}$ until the angle between d¹ and b_i+1 changes from ${\overline{\alpha }}_{\left(i\right)}^{\mathbf{l}}$ to ${\alpha }_{i+1}^{\mathbf{l}}$. The d¹ vector has now become ${\mathbf{d}}_{i+1}^{\mathbf{l}}$. There is a nonzero twist associated with the a-type rotations (i), (iii), and (v), since, for each of these steps, the vector dΩ is directed along the tangent. Rotations (ii) and (iv), on the other hand, since the axis of rotation is perpendicular to the tangent, are b-type rotations with zero twist. In the case of rotation (i) and (v) the twist angle is $\Delta {\alpha }_{\left(i\right)}^{\mathbf{l}}∕2$ where $\Delta {\alpha }_{\left(i\right)}^{\mathbf{l}}={\alpha }_{i+1}^{\mathbf{l}}-{\alpha }_i^{\mathbf{l}}$. For rotation (iii) the angle of rotation, which we call β_(i), has as its cosine and sine: cos β_(i)=b_i⋅b_i+1 and sin β_(i)=t_(i)⋅b_i×b_i+1. The twist of supercoiling of the base-pair step associated with these rotations $T_{\left(i\right)}^{\mathbf{l}}$ (in units of number of turns) is, thus,

$$T_{\left(i\right)}^{\mathbf{l}}=\frac{\Delta {\alpha }_{\left(i\right)}^{\mathbf{l}}+{\beta }_{\left(i\right)}}{2\pi }.$$ (16)

The beginning and ending d vectors in the rotations leading to the twist given by Eq. 16 are those defined in Eqs. 14, 15, the unit vectors in the direction of the projections of the long axes l_i and l_i+1 onto the planes perpendicular to ${\tilde{\mathbf{t}}}_i$ and ${\tilde{\mathbf{t}}}_{i+1}$, respectively.

For an unnicked closed DNA molecule with n_B base pairs, Eq. 8 tells us that

$$\sum _{i=1}^{n_B}{T}_{\left(i\right)}^{\mathbf{l}}=L\left(D,C\right)-W\left(C\right).$$ (17)

If one now were to calculate the T_(i)’s for the same five rotations but using as the d-vectors those derived from the short axes s_i and s_i+1, we would find that for a single step the two twists, call them $T_{\left(i\right)}^{\mathbf{l}}$ and $T_{\left(i\right)}^{\mathbf{s}}$, would be somewhat different. The sum ${\sum }_{i=1}{T}_{\left(i\right)}^{\mathbf{s}}$, however, would have exactly the same value as that obtained before, that given by the right-hand side of Eq. 17. We define the twist of supercoiling of the step, T_(i), as the average of $T_{\left(i\right)}^{\mathbf{l}}$ and $T_{\left(i\right)}^{\mathbf{s}}$. Clearly, Eq. 17 is also satisfied for T_(i)’s so defined. The average of ${\alpha }_i^{\mathbf{l}}$ and ${\alpha }_i^{\mathbf{s}}$ will be denoted as α_i.

In the calculation of the twist of supercoiling for the case of a DNA molecule with an open helical axis, for the initial step we take ${\tilde{\mathbf{t}}}_1$ to be in the direction of t₍₁₎, and for the final step we take ${\tilde{\mathbf{t}}}_{n_B}$ in the direction of t_(nB−1). The step-parameter twist of the base pair step can be derived in a similar way. In this case the d vectors are the long and short axes themselves. Carrying out the rotations starting with l_i and ending with l_i+1 gives the same value for the twist as starting with s_i and ending with s_i+1. There is thus no need to do the averaging indicated in the definition of the twist of supercoiling. Figure 5 shows the vectors and angles that play a role in the determination of the step-parameter twist.

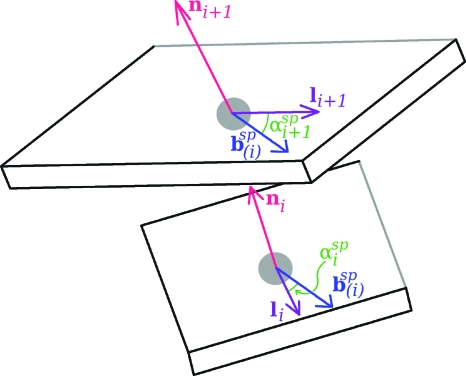
Figure 5.

The vectors needed for the calculation of the step-parameter twist of the same step shown in the previous figure. Here knowledge of the direction of the two normals allows the determination of the single vector ${\mathbf{b}}_{\left(i\right)}^{sp}$, which lies in each of the two base-pair planes. Also indicated are the two angles needed for the use of Eq. 18 for the twist calculation.

The analog of ${\tilde{\mathbf{t}}}_i$ and ${\tilde{\mathbf{t}}}_{i+1}$ are the normals n_i and n_i+1, and b_i and b_i+1 become the single vector, ${\mathbf{b}}_{\left(i\right)}^{sp}={\mathbf{n}}_i\times {\mathbf{n}}_{i+1}∕\mid {\mathbf{n}}_i\times {\mathbf{n}}_{i+1}\mid$. The step-parameter twist $T_{\left(i\right)}^{sp}$ of the step (in units of number of turns) thus, is, simply,

$$T_{\left(i\right)}^{sp}=\frac{\Delta {\alpha }_{\left(i\right)}^{sp}}{2\pi },$$ (18)

where $\Delta {\alpha }_{\left(i\right)}^{sp}$ is the difference between the angle ${\alpha }_{i+1}^{sp}$ that l_i+1 (or s_i+1) makes with ${\mathbf{b}}_{\left(i\right)}^{sp}$ and the angle ${\alpha }_i^{sp}$ that l_i (or s_i) makes with ${\mathbf{b}}_{\left(i\right)}^{sp}$.

THE WRITHE OF THE CLOSED MULTISTEP DNA MOLECULE

The shape of the closed axial curve of the DNA molecules we are dealing with, consistent with the smooth space curves we have described, is a succession of line segments connecting the origins of the base pairs. A method for computing the writhe of such a segmented closed curve was elegantly put forth many years ago by Levitt.¹⁷ Here we get an equivalent result using a different approach. We first note that for this type of curve, the Gauss integral [Eq. 7] for the writhe for a molecule with n_B base pairs, and therefore, n_B base pair steps, takes the form of a sum of contributions w_(i)(j) of all pairs of base-pair steps,

$$W\left(C\right)=\sum _{i,j}{w}_{\left(i,j\right)}$$ (19)

with

$$w_{\left(i,j\right)}=\left(\frac{1}{2\pi }\right)\int \int \frac{{\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\cdot {\mathbf{r}}_{\left(i,j\right)}\left(s_{\left(i\right)},s_{\left(j\right)}\right)}{{\mid {\mathbf{r}}_{\left(i.j\right)}\left(s_{\left(i\right)},s_{\left(j\right)}\right)\mid }^3}d{s}_{\left(i\right)}d{s}_{\left(j\right)},$$ (20)

where

$${\mathbf{r}}_{\left(i,j\right)}\left(s_{\left(i\right)},s_{\left(j\right)}\right)={\mathbf{r}}_{\left(i\right)}\left(s_{\left(i\right)}\right)-{\mathbf{r}}_{\left(j\right)}\left(s_{\left(j\right)}\right)={\mathbf{X}}_{\left(i,j\right)}+{\mathbf{t}}_{\left(i\right)}{s}_{\left(i\right)}-{\mathbf{t}}_{\left(j\right)}{s}_{\left(j\right)}$$ (21)

is a vector which points from a point on the j^th line segment to a point on the i^th. The constant vector X_(i,j) is perpendicular to each of the tangents. Its magnitude is thus the distance of closest approach of the segments. Terms involving a base-pair step with itself, and terms involving pairs of adjacent steps are zero.

Given Eq. 21, Eq. 20 can be cast into the form

$$w_{\left(i,j\right)}=\left(\frac{1}{2\pi }\right){\int }_{s_{\left(i\right)}\left(1\right)}^{s_{\left(i\right)}\left(2\right)}{\int }_{s_{\left(j\right)}\left(1\right)}^{s_{\left(j\right)}\left(2\right)}\frac{{\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\cdot {\mathbf{X}}_{\left(i,j\right)}}{{\mid {\mathbf{X}}_{\left(i,j\right)}+{\mathbf{t}}_{\left(i\right)}{s}_{\left(i\right)}-{\mathbf{t}}_{\left(j\right)}{s}_{\left(j\right)}\mid }^3}d{s}_{\left(i\right)}d{s}_{\left(j\right)},$$ (22)

where s_(i)(1), s_(i)(2), s_(j)(1) and s_(j)(2) denote the arc lengths of the endpoints of the segments.

The three vectors t_(i), t_(j), and r_(i.j)(s_(i),s_(j)) determine a dihedral angle μ_(i.j)(s_(i),s_(j)) we define as follows in terms of its sine and cosine,

$$\text{sin}{\mu }_{\left(i,j\right)}=-\frac{{\mathbf{r}}_{\left(i,j\right)}\cdot \left({\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\right)\times \left({\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\right)}{\mid {\mathbf{r}}_{\left(i,j\right)}\mid \mid {\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\mid \mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\mid }=-\frac{\mid {\mathbf{r}}_{\left(i,j\right)}\mid \left({\mathbf{r}}_{\left(i,j\right)}\cdot {\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\right)}{\mid {\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\mid \mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\mid },$$ (23)

$$\text{cos}{\mu }_{\left(i,j\right)}=\frac{\left({\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\right)\cdot \left({\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\right)}{\mid {\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\mid \mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\mid }.$$

It follows from its definition that μ_(i.j)(s_(i),s_(j)) is the angle between the vectors normal to two planes, the one spanned by r_(i.j)(s_(i),s_(j)) and t_(i) and the one spanned byr_(i.j)(s_(i),s_(j)) and t_(j).

In Appendix B, it is shown that the integrand in the integral appearing in Eq. 22 is equal to −∂²μ_(i,j)∕∂s_(i)∂s_(j) so that the contribution to the writhe of base-pair step i and base-pair step j, w_(i,j), is simply related to the four dihedral angles associated with the endpoints of the steps, i.e.,

$$w_{\left(i,j\right)}=\left(\frac{1}{2\pi }\right)\left(-{\mu }_{\left(i,j\right)}\left(s_{\left(i\right)}\left(2\right),s_{\left(j\right)}\left(2\right)\right)+{\mu }_{\left(i,j\right)}\left(s_{\left(i\right)}\left(2\right),s_{\left(j\right)}\left(1\right)\right)-{\mu }_{\left(i,j\right)}\left(s_{\left(i\right)}\left(1\right),s_{\left(j\right)}\left(1\right)\right)+{\mu }_{\left(i,j\right)}\left(s_{\left(i\right)}\left(1\right),s_{\left(j\right)}\left(2\right)\right)\right).$$ (24)

We note that w_(i,j) has the same sign as t_(i)×t_(j)⋅X_(i,j).

COMPARISON OF THE TWIST OF SUPERCOILING AND THE STEP-PARAMETER TWIST

Like $T_{\left(i\right)}^{sp}$ of Eq. 18, the twist of supercoiling of a step in the form as expressed in Eq. 16 is independent of the direction of propagation along the DNA molecule. However, whereas $T_{\left(i\right)}^{sp}$ does not depend at all on the properties of the two steps adjacent to the i^th base-pair steps, T_(i) depends on the previous step (i−1), and on the following step (i+1). In particular, ${\tilde{\mathbf{t}}}_i$ depends on the origin o_i−1 and ${\tilde{\mathbf{t}}}_{i+1}$ depends on o_i+2. For Eq. 17 to be satisfied for unnicked closed DNA molecules, the twist of supercoiling must depend on the way the tangent vectors are changing. In the case of the step-parameter twist, on the other hand, the sum ${\sum }_{i=1}{T}_{\left(i\right)}^{sp}$ has no particular significance.

Because in relaxed DNA, the normals of the base pairs and the associated $\tilde{\mathbf{t}}$ vectors are approximately collinear, for each step we expect the two twists to be close in value. When the base pairs are forced to undergo translations of a chiral nature, however, unlike the step-parameter twist, which is unaffected by pure translations, we expect the twist of supercoiling to change.

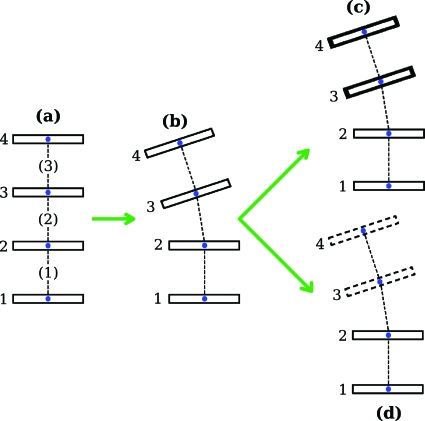
To demonstrate how differences in values of the step-parameter twist and the twist of supercoiling can arise we consider the simple model depicted in Fig. 6. We start with a DNA molecule with four base pairs having origins that are equally spaced and collinear, Fig. 6a. In addition, the base-pair planes are oriented so that their normals coincide with the t-vectors. Here, for each of the three steps, the twist of supercoiling equals the step-parameter twist. To change the structure to that labeled (b), base pairs 3 and 4 are first rotated as a unit by 9° about an axis lying in base pair 2 and passing through the origin of that base pair, and then rotated as a unit by 9° about an axis parallel to the first axis but lying in base pair 3 and passing through the origin of that base pair. After this total bend of 18° is introduced, the origins of the base pairs are no longer collinear, but they remain coplanar. (In the figure the common plane of the origins is taken to be the plane of the page.) A calculation shows that for the new structure neither the step-parameter twist nor the twist of supercoiling for each of the three steps has changed in value so that the equality seen in (a) of the two types of twist for each step carries over to (b). Finally, base pairs 3 and 4 are translated in a direction perpendicular to the plane on which they had been lying in (b) either up to give (c), or by the same amount down to give (d). This shearing motion has no effect on the step-parameter twists, but the connection between the twist of supercoiling and the writhing number in closed molecules given by Eq. 17 demands that the chirality that now characterizes the positions of the origins in the structures (c) and (d) leads to a change in the value of the twist of supercoiling. We find that if the size of the translational shear is taken to be half as large as the spacing between the base pairs in (a), that the twist of supercoiling of the middle step, (2), of the structure with the right-handed jog, (c), is 4.3° greater in value than the step-parameter twist for that step, and 4.3° lower in value for the middle step of the structure with the left-handed jog, (d). Shearing of this magnitude is typical of values seen in high resolution structures. For the two steps, (1) and (3), adjacent to the middle step in both (c) and (d), the two types of twist are now very close in value but not exactly equal.

Figure 6.

Construction of a model DNA structure characterized by a chiral deformation. Image labeled (a) shows four equally spaced and parallel base-pair planes having their origins lying on a line. The sequence of base-pair planes in (b) depicts the structure after the bend described in the text is introduced. The four origins are still coplanar, and the viewing direction is chosen to be normal to this plane. A translation of base pairs 3 and 4 as a single unit along the viewing direction, depending on the direction of the motion, results either in (c), a structure with a right-handed jog, or (d), one with a left-handed jog.

We have pointed out that there is not one, but various procedures that have been proposed for going from the measured atomic coordinates of two associated bases to the ideal base-pair plane containing an origin o and the vectors s and l. The approach employed here is the one agreed upon by the international structural and computational biology community.¹⁶ The question arises—how might the results reported here change had we used a different method. For one thing, the values of the step-parameter twists would not have changed by any significant amount. These twists are defined in terms of the vectors s, l, and n only, and it turns out that s, l, and n are little dependent on which method is chosen.⁶ The twists of supercoiling, however, also depend on the position of the origins. In the absence of distortions such as buckling, which change the angle between the normals of the bases when viewed in projection along a plane perpendicular to the short, pseudodyad axis of the base pair, the various methods used to describe the spatial arrangements of DNA bases and base pairs introduce a coordinate frame with an origin located in the midst of the hydrogen-bonding of the base pairs. In this case, the values of the twist of supercoiling, like those of the step-parameter twist, would be method independent.

The origins introduced in three analysis schemes—NUPARM (a Nucleid Acid Parameter Determination Program) from Bansal and associates,^{18, 19} CEHS (the Cambridge University Engineering Department Helix Computation Scheme) from El Hassan and Calladine,⁴ and FREEHELIX (a computation of base-steps parameters “totally independent of any choice of helix axis”) from the Dickerson laboratory⁵—lie midway between the positions of two carbon atoms, one on each base (C6 on pyrimidine and C8 on purine) near the DNA backbone. For these three methods, buckling has the effect of moving the origin outside of the hydrogen-bonded region of the base pair. By contrast, the origins defined here would remain near the center of the purine-pyrimidine complex.

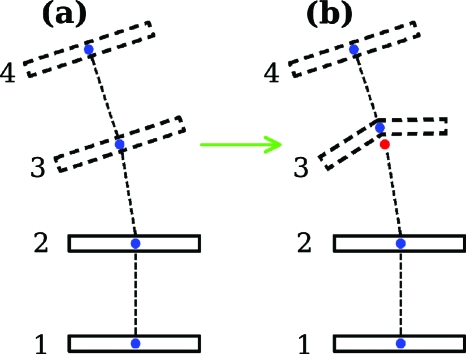
In Fig. 7 an example is given of a protein-induced structural distortion that would not have changed the twist of supercoiling for a DNA step had the NUPARM, CEHS, or FREEHELIX schemes been employed (origin shown as a red dot), but do produce such a change with the method we use here (origin shown as a blue dot). The structure labeled (a) in Fig. 7 is identical to structure (d) in Fig. 6, the one with the left-handed jog. During the passage to Fig. 7b, base-pair 3 is subjected to a buckling-type distortion. Before the distortion the two origins are superimposed, but after the distortion, they are separated. For the placement of the two origins shown, we find that our method gives a twist of supercoiling for the middle step in the buckled structure Fig. 7b greater than what it was in structure Fig. 7a. For the other method, the twist of supercoiling is insensitive to this particular structural change, one commonly found when a protein inserts an amino acid side group between two base pairs.²⁰

Figure 7.

Structural deformation of DNA leading to a twist of supercoiling change dependent on the method used to determine the position of the origin, the method used here, or that in which the origin lies on a line connecting two carbon atoms on the bases. In structure (a), the same as structure (d) in Fig. 6, both methods lead to an origin for all four base pairs located in the same position. However when base pair 3 is buckled as shown to form structure (b), the origin determined by our method (blue dot) moves, but that of the other method (red dot) does not. One then observes a method-dependent twist of supercoiling for the middle step.

SUMMARY

We have defined a twist of supercoiling consistent with the high-resolution atomic structure of DNA starting from the original definition of the twist of one smooth space curve about another. The twist of supercoiling is to be distinguished from one of six step parameters, also called the twist, now in common usage to describe DNA structure. The twist of supercoiling, unlike the step-parameter twist, is connected to the topological invariant, the linking number, and the writhing number of closed DNA molecules. Given this association, the twist of supercoiling, as we show, must be sensitive to chiral structural distortions. We give an example of a chiral distortion that has no effect on the step-parameter twist. In fact, in future work, we plan to compare the values of these two twists for DNA steps in a selection of protein-DNA complexes to gain insight into details of the distortion that the proteins may be inducing.

APPENDIX A: A DERIVATION OF EQUATION 8, THE FUNDAMENTAL EXPRESSION OF DNA TOPOLOGY

We begin the derivation of Eq. 8 by expressing the connection between curve D and curve C, by writing for r_D,

$${\mathbf{r}}_D\left(s_D\right)={\mathbf{r}}_C\left(s_C^{\prime }\right)+\epsilon \mathbf{d}\left(s_C^{\prime }\right),$$ (A1)

where ε is a constant and $\mathbf{d}\left(s_C^{\prime }\right)$ is a unit vector perpendicular to the tangent ${\mathbf{t}}_C\left(s_C^{\prime }\right)$ to curve C, i.e., $\mathbf{d}\left(s_C^{\prime }\right)\cdot {\mathbf{t}}_C\left(s_C^{\prime }\right)=0$. Equation A1 implies that the unit tangent t_D(s_D) to curve D is of the form

$${\mathbf{t}}_D\left(s_D\right)=k\left({\mathbf{t}}_C\left(s_C^{\prime }\right)+\epsilon \frac{d\mathbf{d}\left(s_C^{\prime }\right)}{d{s}_C^{\prime }}\right),$$ (A2)

where k is the reciprocal of the magnitude of the vector contained in the parentheses. These two expressions are substituted into the integrand appearing in the Gauss integral form for the linking number, Eq. 6. We then allow ε to approach zero. Beyond a certain point in this limiting process curve C and curve D no longer can intersect each other, and thereafter the linking number remains unchanged.¹⁰ The factor k approaches one as ε approaches zero. We also find that, in this limit, the terms in the integrand that are linear in ε are zero. Thus one can write for the linking number

$$L\left(D,C\right)=W\left(C\right)+\underset{\epsilon \to 0}{\text{lim}}\left(\frac{{\epsilon }^2}{4\pi }\right)∯\frac{\mathbf{d}\left(s_C\right)\times \frac{d\mathbf{d}\left(s_C\right)}{d{s}_C}\cdot {\mathbf{t}}_C\left({s^{\prime }}_C\right)}{{\left({\mid {\mathbf{r}}_C\left(s_C\right)-{\mathbf{r}}_C\left(s_C^{\prime }\right)\mid }^2+{\epsilon }^2\right)}^{3∕2}}d{s}_C^{\prime }d{s}_C,$$ (A3)

where W(C) is the writhing number as given in Eq. 7. Furthermore, because

$$\underset{\epsilon \to 0}{\text{lim}}\frac{{\epsilon }^2}{{\left({\mid {\mathbf{r}}_C\left(s_C\right)-{\mathbf{r}}_C\left(s_C^{\prime }\right)\mid }^2+{\epsilon }^2\right)}^{3∕2}}=\underset{\epsilon \to 0}{\text{lim}}\frac{{\epsilon }^2}{{\left({\left(s_C-s\right)}^2+{\epsilon }^2\right)}^{3∕2}}=2\delta \left(s_C-s_C^{\prime }\right),$$ (A4)

where $\delta \left(s_C-s_C^{\prime }\right)$ is a Dirac delta function, the integration over $s_C^{\prime }$ in the second term of Eq. A3 can be readily carried out:

$$\underset{\epsilon \to 0}{\text{lim}}\left(\frac{{\epsilon }^2}{4\pi }\right)∯\frac{\mathbf{d}\left(s_C\right)\times \frac{d\mathbf{d}\left(s_C\right)}{d{s}_C}\cdot {\mathbf{t}}_C\left(s_C^{\prime }\right)}{{\left({\mid {\mathbf{r}}_C\left(s_C\right)-{\mathbf{r}}_C\left(s_C^{\prime }\right)\mid }^2+{\epsilon }^2\right)}^{3∕2}}d{s}_C^{\prime }d{s}_C=\left(\frac{1}{2\pi }\right)∯\delta \left(s_C-s_C^{\prime }\right)\mathbf{d}\left(s_C\right)\times \frac{d\mathbf{d}\left(s_C\right)}{d{s}_C}\cdot {\mathbf{t}}_C\left(s_C^{\prime }\right)d{s}_C^{\prime }d{s}_C=\left(\frac{1}{2\pi }\right)\oint \mathbf{d}\left(s_C\right)\times \frac{d\mathbf{d}\left(s_C\right)}{d{s}_C}\cdot {\mathbf{t}}_C\left(s_C\right)d{s}_C.$$ (A5)

This completes the proof of Eq. 8.

APPENDIX B: DERIVATION OF THE EXPRESSION THAT FACILITATES THE PASSAGE FROM EQUATION 22 TO EQUATION 24, THE CONTRIBUTION TO THE WRITHE IN TERMS OF DIHEDRAL ANGLES

We begin by deriving an expression for −∂μ_(i,j)∕∂s_(j). Since, for example,

$$\frac{\partial \text{\hspace{0.17em}cot}\mu }{\partial s_{\left(j\right)}}=\frac{d\text{\hspace{0.17em}cot}\mu }{d\mu }\frac{\partial \mu }{\partial s_{\left(j\right)}},$$ (B1)

we see that

$$-\frac{\partial \mu }{\partial s_{\left(j\right)}}={\text{sin}}^2\mu \frac{\partial \text{\hspace{0.17em}cot}\mu }{\partial s_{\left(j\right)}}.$$ (B2)

Given the definition of the dihedral angle [Eq. 23], and the fact that t_(i)×t_(j)⋅r_(i,j) is independent of s_(i) and s_(j), this last equation can be rewritten as

$$-\frac{\partial \mu }{\partial s_{\left(j\right)}}=-\frac{{\mid {\mathbf{r}}_{\left(i,j\right)}\mid }^2\left({\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\cdot {\mathbf{r}}_{\left(i,j\right)}\right)}{{\mid {\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\mid }^2{\mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\mid }^2}\times \frac{\partial }{\partial s_{\left(j\right)}}\left(\frac{\left({\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\right)\cdot \left({\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\right)}{\mid {\mathbf{r}}_{\left(i,j\right)}\mid }\right).$$ (B3)

After noting that the explicit dependence of r_(i,j) on s_(i) and s_(j) as given in Eq. 21 leads to the fact that

$${\mid {\mathbf{r}}_{\left(i,j\right)}\mid }^2={\mid {\mathbf{X}}_{\left(i,j\right)}\mid }^{\mathbf{2}}+s_{\left(i\right)}^2+s_{\left(j\right)}^2-2\left({\mathbf{t}}_{\left(i\right)}\cdot {\mathbf{t}}_{\left(j\right)}\right)s_{\left(i\right)}{s}_{\left(j\right)},$$ (B4)

$${\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\cdot {\mathbf{r}}_{\left(i,j\right)}={\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\cdot {\mathbf{X}}_{\left(i,j\right)},$$

$${\mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\mid }^2={\mid {\mathbf{X}}_{\left(i,j\right)}\mid }^{\mathbf{2}}+{\mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\mid }^2{s}_{\left(j\right)}^2,$$

$${\mid {\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\mid }^2={\mid {\mathbf{X}}_{\left(i,j\right)}\mid }^{\mathbf{2}}+{\mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\mid }^2{s}_{\left(i\right)}^2,$$

$$\left({\mathbf{r}}_{\left(i,j\right)}\times {\mathbf{t}}_{\left(j\right)}\right)\cdot \left({\mathbf{t}}_{\left(i\right)}\times {\mathbf{r}}_{\left(i,j\right)}\right)=-\left(\left({\mathbf{t}}_{\left(i\right)}\cdot {\mathbf{t}}_{\left(j\right)}\right){\mid {\mathbf{X}}_{\left(i,j\right)}\mid }^{\mathbf{2}}+{\mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\mid }^2{s}_{\left(i\right)}{s}_{\left(j\right)}\right).$$

We find, after performing the indicated differentiation with respect to s_(j) in Eq. B3 and simplifying the resulting expression, that

$$-\frac{\partial \mu }{\partial s_{\left(j\right)}}=\frac{\left({\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\cdot {\mathbf{X}}_{\left(i,j\right)}\right)\left(s_{\left(i\right)}-\left({\mathbf{t}}_{\left(i\right)}\cdot {\mathbf{t}}_{\left(j\right)}\right)s_{\left(j\right)}\right)}{\left({\mid {\mathbf{X}}_{\left(i,j\right)}\mid }^{\mathbf{2}}+{\mid {\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\mid }^2{s}_{\left(j\right)}^2\right)\mid {\mathbf{r}}_{\left(i,j\right)}\mid }.$$ (B5)

Differentiating Eq. B5 again, this time with respect to s_(i), yields

$$-\frac{{\partial }^2{\mu }_{\left(i,j\right)}}{\partial s_{\left(i\right)}\partial s_{\left(j\right)}}=\frac{{\mathbf{t}}_{\left(i\right)}\times {\mathbf{t}}_{\left(j\right)}\cdot {\mathbf{X}}_{\left(i,j\right)}}{{\mid {\mathbf{r}}_{\left(i.j\right)}\mid }^3}.$$ (B6)