Optical Determination of Anisotropic Material Properties of Bovine Articular Cartilage in Compression

Abstract

The precise nature of the material symmetry of articular cartilage in compression remains to be elucidated. The primary objective of this study was to determine the equilibrium compressive Young’s moduli and Poisson’s ratios of bovine cartilage along multiple directions (parallel and perpendicular to the split line direction, and normal to the articular surface) by loading small cubic specimens (0.9×0.9×0.8 mm, n=15) in unconfined compression, with the expectation that the material symmetry of cartilage could be determined more accurately with the help of a more complete set of material properties. The second objective was to investigate how the tension-compression nonlinearity of cartilage might alter the interpretation of material symmetry. Optimized digital image correlation was used to accurately determine the resultant strain fields within the specimens under loading. Experimental results demonstrated that neither the Young’s moduli nor the Poisson’s ratios exhibit the same values when measured along the three loading directions. The main findings of this study are that the framework of linear orthotropic elasticity (as well as higher symmetries of linear elasticity) is not suitable to describe the equilibrium response of articular cartilage nor characterize its material symmetry; a framework which accounts for the distinctly different responses of cartilage in tension and compression is more suitable for describing the equilibrium response of cartilage; within this framework, cartilage exhibits no lower than orthotropic symmetry.

INTRODUCTION

As the load-bearing material of diarthrodial joints, articular cartilage helps to absorb mechanical shocks and distribute high joint loads more evenly across the underlying bony structures, while maintaining minimal friction and wear (Mankin et al., 1994; Mow and Ateshian, 1997; Ateshian et al., 1998). Articular cartilage is a structurally and compositionally complex material. Most of the biochemical constituents of articular cartilage (e.g., glycosaminoglycans, collagen and water) are inhomogeneously distributed, giving the tissue a layered character (Weiss et al., 1968; Redler and Zimny, 1970; Bullough and Jagannath, 1983; Maroudas et al., 1969; Venn, 1977; Muir, 1980; Buckwalter et al., 1985; Hardingham and Fosang, 1992). These variations in the structure and composition of cartilage are closely related to the inhomogeneous and anisotropic mechanical and electrochemical properties of the tissue.

Despite the intensive study of articular cartilage in the field of biomechanics, the exact nature of cartilage as a material remains to be elucidated. There are still no established answers to some of the most basic questions such as the nature of the material’s symmetry that are commonly asked for a classical material. As greater efforts have been placed on the study of tissue anisotropy in tension, it has been shown that the equilibrium tensile modulus of articular cartilage is significantly greater for specimens harvested parallel to the split-line directions than for those perpendicular to the split lines (Kempson et al., 1968, 1973; Woo et al., 1976, 1979; Roth and Mow, 1980; Huang et al., 1999); the tensile modulus has also been investigated along the depth-direction (Basser et al., 1998; Narmoneva et al., 1999), but has not yet been related to the other two directions. Nevertheless, since the tensile properties of cartilage have been found to differ along two of these three mutually perpendicular directions (Huang et al., 1999; Narmoneva et al., 1999; Korhonen et al., 2001), it is likely that the highest symmetry of cartilage is at best orthotropic, with its three planes of symmetry defined in situ by the split-line direction in a plane tangent to the surface (1-direction), the direction perpendicular to the split-line direction in the same tangent plane (2-direction), and the direction normal to this plane (3-direction), i.e. the “radial” (or depth) direction of the cartilage layer (Soltz and Ateshian, 2000). In further support of cartilage anisotropy in tension, several studies (Woo et al., 1979; Chang et al., 1999; Elliott et al., 1999; Huang et al., 1999) have demonstrated that Poisson’s ratio for cartilage in uniaxial tension exceeds 0.5, which is permissible only for anisotropic materials (e.g., Lai et al., 1993). For human humeral head cartilage, Huang et al. (1999) reported an average Poisson’s ratio value of ν₊₁₂ = 1.3 for uniaxial tension along the 1-direction and measurement of the contraction along the 2-direction, and a similar average of ν₊₂₁ = 1.3 for the converse configuration, in the superficial zone of cartilage; in the middle zone, these values reduced to ν₊₁₂ = 1.2 and ν₊₂₁ = 1.0. For human patellar cartilage, Chang et al. (1999) reported average values of ν₊₁₂ = 0.9 and ν₊₁₃ = 1.8 in the surface-to-middle zone, and ν₊₁₂ = 0.5 and ν₊₁₃ = 0.7 in the deep zone, whereas Elliot et al. (1999) reported ν₊₁₂ = 2.2 in the superficial zone and ν₊₁₂ = 0.6 in the middle zone.

In contrast to tensile measurements, there are only a few preliminary studies that have investigated the anisotropy of cartilage in compression. Jurvelin et al. (1996) have reported measurements of the compressive modulus of cartilage in unconfined compression, on cylindrical specimens whose axis was oriented either along the radial 3-direction (which is the most commonly tested direction in compression studies) or along a direction parallel to the cartilage surface (though no relation to the split-line direction was reported). They found the compressive modulus of human knee cartilage in the 3-direction to be smaller (0.58MPa versus 0.85MPa), suggesting that cartilage is also anisotropic in compression. However, in a study by Soltz et al. (1999) where immature bovine carpometacarpal joint cartilage cubes were tested in unconfined compression along the 1-, 2-, and 3-directions, no significant differences were found in the compressive moduli among the three direction (with mean values ranging from 0.41MPa along the 1-direction to 0.47MPa in the 3-direction). From compression experiments, Poisson’s ratio at equilibrium has been found to be small in human and bovine articular cartilage (Jurvelin et al., 1997; Wang et al., 2000b; Wong et al., 1998; Wong, 1999). Optical measurements from unconfined compression have yielded an average equilibrium Poisson’s ratio of 0.18 in bovine humeral head cartilage (Jurvelin et al., 1997) and 0.06 in bovine carpometacarpal joint cartilage (Wang et al., 2000b).

While these results suggest that cartilage does not exhibit the same anisotropy in compression as it does in tension, the nature of the anisotropy of cartilage in compression remains undetermined. The primary objective of this study, therefore, is to determine the equilibrium compressive Young’s moduli and Poisson’s ratios of bovine cartilage along multiple directions (1-, 2- and 3-directions) by loading cubic specimens in unconfined compression, with the expectation that the material symmetry of cartilage can be determined more accurately with the help of a more complete set of material properties. Optimized digital image correlation (DIC) is adopted to accurately determine the resultant strain fields within the specimens under loading. It is noted that the studies reported above on the tensile and compressive properties of articular cartilage confirm that the cartilage moduli and Poisson ratios can be very different in tension and compression. Thus, the second objective of this study is to investigate how the tension-compression nonlinearity of cartilage might alter the interpretation of material symmetry (Curnier et al., 1995; Soltz and Ateshian, 2000). Based on previous findings in the literature as reviewed above, it is hypothesized in the current study that the material symmetry of cartilage is no lower than orthotropic.

MATERIALS AND METHODS

Specimen Preparation

Healthy shoulder joints from 2- to 3-month-old calves were obtained from a local slaughterhouse 4–8 hours post-mortem. A steel trephine with a 4-mm diameter core was used to harvest cartilage-bone plugs with the core axis perpendicular to the articular surface. The plugs were then rinsed with phosphate buffered saline (PBS) and protease inhibitors (PI) and frozen at −80 °C for storage until the day of use. On the day of testing, plugs were thawed to room temperature by immersion in freshly prepared PBS + PI solution. Using a freezing stage (Hacker Instruments, Fairfield, NJ, USA) mounted on a sledge microtome (Model 1400; Leitz, Rockleigh, NJ, USA), a full-thickness plug was microtomed to remove residual subchondral bone and vascularized deep zone only, leaving the articular surface intact. Optical measurement of the thickness (h₀) of the plug after microtoming showed a range of 0.6 to 1.2 mm. The plug was allowed to equilibrate in PBS + PI for up to 30 minutes.

Prior to testing, the split-line direction (1-direction) was determined using a needle, and marked with a cut parallel to the split lines in the 2-plane (the plane perpendicular to the 2-direction, Figure 1a). A cubic specimen was sharply excised relative to the split-line direction using a custom cutting device with razor blades in a cruciform configuration (Figure 1c,d). One of the two cube faces in the 2-plane was marked using Trypan Blue dye (0.4% in PBS). During all subsequent testing, specimen orientation was determined using this marked face and the easily discernible articular surface (3-plane). The dimensions of each specimen were measured optically using a calibrated 4x microscope objective with a resolution of 1.66 μm/pixel. Totally, 15 cubic specimens from eight different animals were used in this study. The average dimensions of these specimens are 0.91 ± 0.05 mm along 1-direction, 0.89 ± 0.03 mm along 2-direction and 0.82 ± 0.15 mm along the radial 3-direction.

Figure 1.

(a) Specimen preparation; (b) unconfined compression loading device; (c) custom cutting device for preparation of cubic specimen (d); and (e) a cubic specimen surface imaged between two glass platens. Note that the texture as seen in (e) was used in the optimized DIC to determine the deformation field of the specimen within the imaging plane.

Mechanical Testing

Cubic specimens were sandwiched between the two glass platens of a custom unconfined compression microscopy device (Wang et al., in press), and bathed in PBS+PI contained in an immersion chamber with glass window at bottom (Figure 1b,e). The microscopy device was fixed to a motorized stage (ProScan H128 Series; Prior Scientific, Rockland, MA, USA) of an inverted microscope (Olympus IX70; Olympus America, Melville, NY, USA) equipped with a DeltaRam high speed monochrometer, a DAPI filter cube, and a Uplan 4x objective (Olympus America, Melville, NY, USA). The device was aligned so that the platens were perpendicular to one of the moving axes (e.g., x-axis) of the motorized stage. The optical path of the microscope was adjusted through the immersion chamber and the face of the cubic specimen between the platens was focused and visualized.

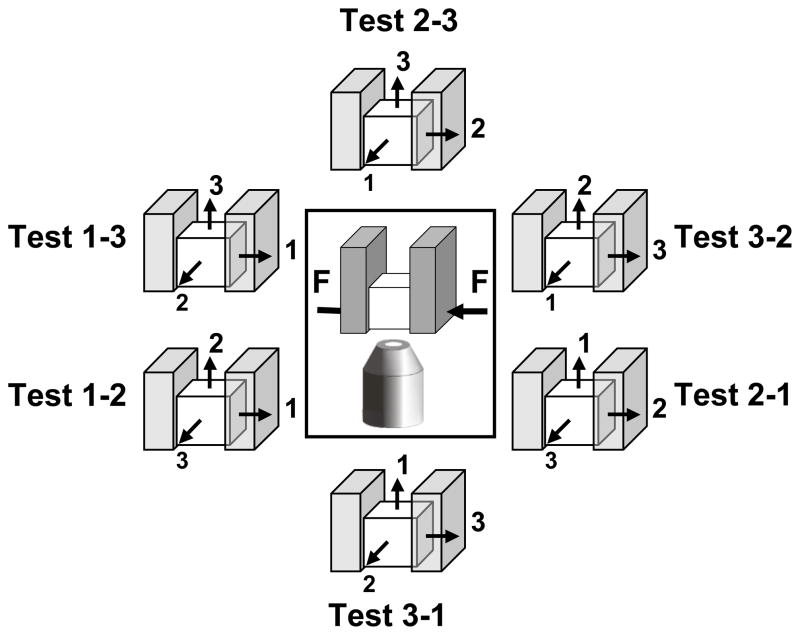
Six tests were performed on each specimen in random order, each test requiring re-positioning of the sample (Figure 2). Each test was denoted by two indices, where the first index indicates the loading direction and the second index denotes the specimen face that was observed. At the beginning of each test, a compression of ~5% of the initial specimen thickness (h₀) was applied as tare load and the image of the face of interest was acquired for the specimen in its equilibrium state. The displacements required to achieve specimen compression of 10 and 15% of h₀ were then applied successively by advancing the loading platen at approximately 1 μm/sec. Following each increment in compression, the specimen was allowed to equilibrate for 20 minutes before being imaged, see Figure 3.

Figure 2.

The six tests performed on a typical cubic specimen, each requiring re-positioning of the cubic specimen. The schematic drawing within the frame indicates the loading and observation directions; and the drawings surrounding the frame illustrate the orientations of the cubic specimen in the six tests.

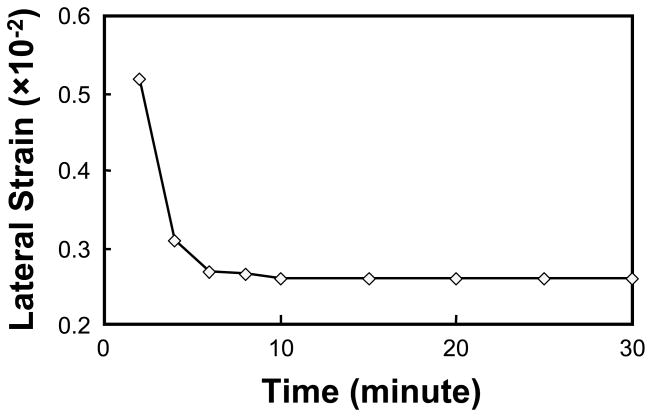
Figure 3.

Lateral strain history of a typical cubic specimen when compressed 5% along the 1-direction. It is noted that the specimen reaches equilibrium within 20 minutes after the load application.

Data Analysis

An optimized digital image correlation technique was applied to the images to generate the displacement data (Chu et al., 1985; Wang et al., in press). A thin-plate spline smoothing algorithm with generalized cross-validation (Craven and Wahba, 1979; Wahba, 1986; Bates et al., 1987) was applied to the displacement data to provide continuous and differentiable displacement fields (U(x,y) and V(x,y)) for performing strain analyses. The axial normal strain (E_xx, along the loading direction), the lateral normal strain (E_yy, perpendicular to the loading direction) and the shear strain (E_xy) were determined from U(x,y) and V(x,y) using the standard expressions for infinitesimal strain,

$$E_{xx}=\frac{\partial U}{\partial x},E_{yy}=\frac{\partial V}{\partial y},E_{xy}=\frac{1}{2}\left(\frac{\partial U}{\partial y}+\frac{\partial V}{\partial x}\right).$$ (1)

For each test (x-y; x,y = 1,2,3), an apparent Poisson’s ratio (ν_{− xy}) and an apparent Young’s modulus (E_−Yx) were obtained using

$${\nu }_{-xy}=-\frac{E_{yy}}{E_{xx}}\text{and}{E}_{-Yx}=\frac{{\sigma }_{xx}}{E_{xx}}$$ (2)

where σ_xx is the normal stress measured on the face perpendicular to the loading x-direction. The Young’s moduli (for compressive increments of 5–10% and 10–15%) obtained from test x-y (x,y = 1,2 or 3) and test x-z (x,z = 1,2 or 3) were averaged to yield a final Young’s modulus E_−Yx for the specimen along the x-direction (no significant difference was found in E_−Yx from both measurements). Along the depth direction (3-direction) it was observed that the axial normal strain (E_xx) was not uniform due to the inhomogeneity of the tissue (Guilak et al., 1995; Schinagl et al., 1996, 1997). For this direction, an average normal strain was evaluated from the superficial one third of the sample thickness and from the remaining two thirds to yield two distinct strain measures, subsequently used to calculate the apparent properties of the tissue in these two distinct zones. Statistical analyses were performed in this study using two-way ANOVA for the effects of loading direction and applied compressive strain, using repeated measures and a significance level of α=0.05, followed by Tukey HSD Post Hoc tests.

Constitutive Model

To investigate the anisotropy of articular cartilage in compression, a sufficiently general material symmetry is first hypothesized which subsumes all higher symmetries. The experimental measurements are then employed to determine whether the fundamental relations of each material symmetry are satisfied or violated. Due to the tension-compression nonlinearity of articular cartilage, a more general framework than linear elasticity is required to investigate the material symmetry. The octantwise orthotropic conewise linear elastic (CLE) model was developed by Curnier et al. (1995) to describe “bimodular” materials which exhibit tension-compression nonlinearity, with linear but distinct responses in tension and compression. It was combined with the biphasic theory of Mow et al. (1980) in our recent study (Soltz and Ateshian, 2000) to successfully predict the transient response of articular cartilage in unconfined compression under a simplified cubic symmetry assumption. In the current study, only the equilibrium response of cartilage is investigated to determine whether it can be described within the general framework of the octantwise orthotropic CLE theory. The constitutive stress-strain relation for such a material is given by

$${\mathbf{\sigma }}^e(\mathbf{E})={\lambda }_{aa}[{\mathbf{A}}_a:\mathbf{E}]tr({\mathbf{A}}_a\mathbf{E}){\mathbf{A}}_a+{\lambda }_{ab}tr({\mathbf{A}}_a\mathbf{E}){\mathbf{A}}_b+{\mu }_a({\mathbf{A}}_a\mathbf{E}+\mathbf{E}{\mathbf{A}}_a),$$ (3)

with summations implicit over a and b (a,b=1,2,3; b ≠ a), and λ_ab =λ_ba; σ^e is the Cauchy stress tensor, E is the infinitesimal strain tensor, tr(.) is the trace operator which yields the first invariant of its tensorial argument, and ${\mathbf{A}}_a:\mathbf{E}=tr({\mathbf{A}}_a^T\mathbf{E})$. A_a is a texture tensor corresponding to each of the three preferred material directions defined by the unit vector a_a (a_a · a_a = δ_ab, Kronecker delta, no sum over a, · denoting the dot product of vectors), with A_a = a_a ⊗ a_a (⊗ denoting the dyadic product of vectors). The three preferred directions are taken to be as in the above experimental protocol: a₁ parallel to the split line direction, a₂ perpendicular to the split line direction, and a₃ normal to the articular cartilage surface. The term A_a:E represents the component of normal strain along the direction a_a. Tension-compression nonlinearity is embodied in the functional dependence of λ_aa on A_a:E,

$${\lambda }_{aa}[{\mathbf{A}}_a:\mathbf{E}]=\{\begin{array}{ll}{\lambda }_{-aa},\hfill & {\mathbf{A}}_a:\mathbf{E}<0\hfill \\ {\lambda }_{+aa},\hfill & {\mathbf{A}}_a:\mathbf{E}>0\hfill \end{array}$$ (4)

This signifies that the material properties λ_aa differ whether the normal strain component along the direction a_a is compressive or tensile. The material properties of this model are the twelve constants λ₋₁₁,λ₊₁₁,λ₋₂₂,λ₊₂₂,λ₋₃₃,λ₊₃₃,λ₂₃,λ₁₃,λ₁₂,μ₁,μ₂,μ₃ (three more than orthotropic linear elasticity). There are eight fourth-order elasticity tensors for this orthotropic octantwise linear elasticity model, since A_a:E could be either negative or positive along any of the three possible directions, a=1, 2 or 3. The convexity of the energy potential is ensured by the positive definiteness of each of these eight elasticity tensors.

To derive the Young’s moduli and Poisson’s ratios from these relations, a rectangular prismatic beam can be considered with its edges aligned along the preferred directions of material symmetry. For example, when applying uniaxial compression along the 1-direction with frictionless loading platens, and with traction free lateral surfaces (unconfined compression), and recognizing that the strain fields for this simple configuration are homogeneous, the following set of equations can be posed:

$$\begin{array}{ll}{\sigma }_{11}^e=H_{-A1}{E}_{11}+{\lambda }_{12}{E}_{22}+{\lambda }_{13}{E}_{33}\hfill & {\sigma }_{23}^e=({\mu }_2+{\mu }_3)E_{23}=0\hfill \\ {\sigma }_{22}^e={\lambda }_{12}{E}_{11}+H_{+A2}{E}_{22}+{\lambda }_{23}{E}_{33}=0\hfill & {\sigma }_{13}^e=({\mu }_1+{\mu }_3)E_{13}=0\hfill \\ {\sigma }_{33}^e={\lambda }_{13}{E}_{11}+{\lambda }_{23}{E}_{22}+H_{+A3}{E}_{33}=0\hfill & {\sigma }_{12}^e=({\mu }_1+{\mu }_2)E_{12}=0\hfill \end{array},$$ (5)

where H_±Aa = λ_±aa + 2μ_a (a= 1,2,3; no sum) are the aggregate moduli in tension and compression. These equations derive from Eqs.(3)–(4) above and from the boundary conditions. Note that in unconfined compression along the 1-direction, it is expected that E₁₁ < 0, E₂₂ ≥ 0, and E₃₃ ≥ 0; consequently, λ₁₁ [E₁₁] = λ₋₁₁, λ₂₂ [E₂₂] = λ₊₂₂ and λ₃₃ [E₃₃] = λ₊₃₃ as reflected in the aggregate moduli in Eq.(5) above. The only non-zero traction component for this configuration is ${\sigma }_{11}^e$; these expressions can be solved for the unknown strain components, from which the Young’s moduli and Poisson’s ratios along the 1-direction can be obtained, $E_{-Y1}={\sigma }_{11}^e/E_{11}$, ν₋₁₂ =−E₂₂/E₁₁, and ν₋₁₃ =−E₃₃/E₁₁. From a similar analysis for unconfined compression loading along the 2- and 3-directions, all the properties can be obtained as summarized below.

$$\begin{array}{l}{E}_{-Y1}=-\frac{H_{+A3}{\lambda }_{12}^2+H_{+A2}(-H_{-A1}{H}_{+A3}+{\lambda }_{13}^2)+{\lambda }_{23}(-2{\lambda }_{12}{\lambda }_{13}+H_{-A1}{\lambda }_{23})}{H_{+A2}{H}_{+A3}-{\lambda }_{23}^2},\\ E_{-Y2}=-\frac{H_{+A1}{\lambda }_{23}^2+H_{+A3}(-H_{-A2}{H}_{+A1}+{\lambda }_{12}^2)+{\lambda }_{13}(-2{\lambda }_{23}{\lambda }_{12}+H_{-A2}{\lambda }_{13})}{H_{+A3}{H}_{+A1}-{\lambda }_{13}^2},\\ E_{-Y3}=-\frac{H_{+A3}{\lambda }_{13}^2+H_{+A1}(-H_{-A3}{H}_{+A2}+{\lambda }_{23}^2)+{\lambda }_{12}(-2{\lambda }_{13}{\lambda }_{23}+H_{-A3}{\lambda }_{12})}{H_{+A1}{H}_{+A2}-{\lambda }_{12}^2}.\end{array}$$ (6)

$$\begin{array}{l}{\nu }_{-12}=\frac{H_{+A3}{\lambda }_{12}-{\lambda }_{13}{\lambda }_{23}}{H_{+A2}{H}_{+A3}-{\lambda }_{23}^2},{\nu }_{-13}=\frac{H_{+A2}{\lambda }_{13}-{\lambda }_{12}{\lambda }_{23}}{H_{+A2}{H}_{+A3}-{\lambda }_{23}^2},\\ {\nu }_{-21}=\frac{H_{+A3}{\lambda }_{12}-{\lambda }_{13}{\lambda }_{23}}{H_{+A1}{H}_{+A3}-{\lambda }_{13}^2},{\nu }_{-23}=\frac{H_{+A1}{\lambda }_{23}-{\lambda }_{12}{\lambda }_{13}}{H_{+A1}{H}_{+A3}-{\lambda }_{13}^2},\\ {\nu }_{-31}=\frac{H_{+A2}{\lambda }_{13}-{\lambda }_{12}{\lambda }_{23}}{H_{+A1}{H}_{+A2}-{\lambda }_{12}^2},{\nu }_{-32}=\frac{H_{+A1}{\lambda }_{23}-{\lambda }_{12}{\lambda }_{13}}{H_{+A1}{H}_{+A2}-{\lambda }_{12}^2}.\end{array}$$ (7)

The following should be noted: (a) Unlike the case of linear orthotropic elastic materials, ν_−ab/E_−Ya ≠ ν_−ba/E_−Yb in general for a bimodular material. However, it can be verified from Eq.(7) that ν₋₁₂ν₋₂₃ν₋₃₁ = ν₋₁₃ν₋₃₂ν₋₂₁ must always hold. (b) Poisson’s ratios in compression are independent of the compressive aggregate moduli. (c) The expressions in Eqs.(6)–(7), derived from uniaxial compression, are insufficient to solve for the shear moduli μ_a (a=1,2,3) (shear tests would be appropriate to achieve such measurements). (d) The equivalent expressions for the Young’s moduli and Poisson’s ratio in tension can be trivially obtained by substituting the subscripted ‘−’ signs with ‘+’ signs, and vice versa, in the above expressions. (e) When H_+A1 = H_−A1, H_+A2 = H_−A2, and H_+A3 = H_−A3, the classical expressions for a linear orthotropic elastic material are recovered and in that case ν_ab/E_Ya = ν_ba/E_Yb is satisfied (no distinction being made between tension and compression in linear elasticity).

Because of the relation ν₋₁₂ν₋₂₃ν₋₃₁ = ν₋₁₃ν₋₃₂ν₋₂₁, the six expressions in Eq.(7) are not independent from each other, thus knowledge of the six Poisson’s ratios cannot be used to yield unique solutions for the six moduli which appear in those expressions, H_+A1,H_{+ A2},H_{+ A3},λ₂₃,λ₁₃,λ₁₂. It follows therefore that experimental determination of the three Young’s moduli and six Poisson’s ratios in compression is not sufficient to yield unique solutions for the six aggregate moduli (H_±Aa,a=1,2,3) and three ‘off-diagonal’ moduli (λ₂₃,λ₁₃,λ₁₂). Unlike a linearly elastic material which has the same properties in tension and compression, a bimodular CLE material requires additional tests to fully characterize the aggregate and off-diagonal moduli.

To determine the material symmetry of articular cartilage in this study, it will first be verified whether ν₋₁₂ν₋₂₃ν₋₃₁ = ν₋₁₃ν₋₃₂ν₋₂₁ is statistically satisfied by the experimental data. If that is found to be the case, the general framework of octantwise orthotropic CLE theory may be found appropriate for this tissue. Next, it will be verified whether ν_−ab/E_−Ya = ν_−ba/E_−Yb is statistically satisfied, and if so, it may be concluded that the framework of orthotropic linear elasticity is sufficient to explain the experimental findings. If further simplifications are observed from the experimental data, it may then be determined whether the material satisfies higher symmetry (e.g., transverse isotropy or isotropy). Conversely, if none of the above relations are satisfied, it would be concluded that cartilage has a material symmetry lower than orthotropy; or alternatively, that neither the framework of linear elasticity nor that of octantwise orthotropic CLE theory is suitable for the equilibrium response of articular cartilage. The measurements of Poisson’s ratios and Young’s moduli in compression are reported in the Results section below, while the nature of the material symmetry of cartilage is presented in the Discussion that follows.

RESULTS

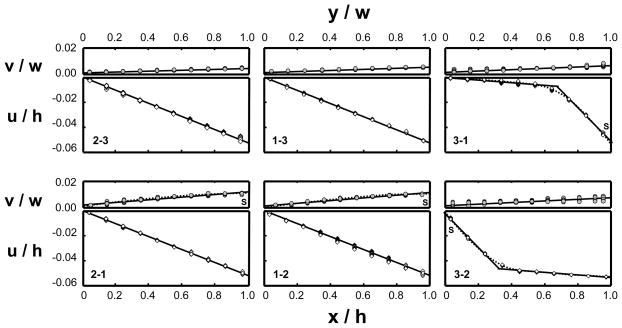
Prior to each of the six tests performed on the cubic specimens, specimen dimensions were re-measured. No permanent deformation was observed and the specimens were found to recover fully to their original dimensions after load removal from previous loading. The determination of material properties relies on the description of the deformation inside a tissue specimen under loading. The displacement distributions resulting from the six tests on a typical cubic sample are plotted in Figure 4 as a function of normalized coordinates. Consistently for all specimens, compression tests along the 1- and 2-directions (1-2, 2-1, 1-3, and 2-3) produced linear displacement distributions in the axial compression (denoted by u in the figure, irrespective of the specific loading direction), indicating homogeneous strain fields, and thus homogeneous moduli along those directions. In contrast, in compression tests along the 3-direction (3-1 and 3-2) the axial displacement was highly nonlinear, with the axial strain highest at the articular surface and decreasing toward the deep zone. This inhomogeneity of cartilage in compression along its depth direction is consistent with observations in several other studies (Guilak et al., 1995; Schinagl et al., 1996, 1997; Wang et al., 2000a, 2001c). Compared to the other tests, the lateral expansion (denoted by v) in the 3-1 and 3-2 tests varied significantly through the depth (3-direction), as can be more clearly observed from Figure 5(a, b).

Figure 4.

The displacement distributions determined for a typical specimen from the six tests. The top plot of each figure is the lateral expansion normalized by the width of the specimen along the lateral direction (v/w) and plotted versus the normalized position along the lateral direction (y/w); the bottom plot of each figure is the axial displacement normalized by the height of the specimen along the axial direction (u/h) and plotted versus the normalized position along the axial direction (x/h). The slope of each solid line represents the average strain. The dotted lines indicate inhomogeneous displacement distributions. The S’s in the figures indicate the articular surface of the specimen when observed.

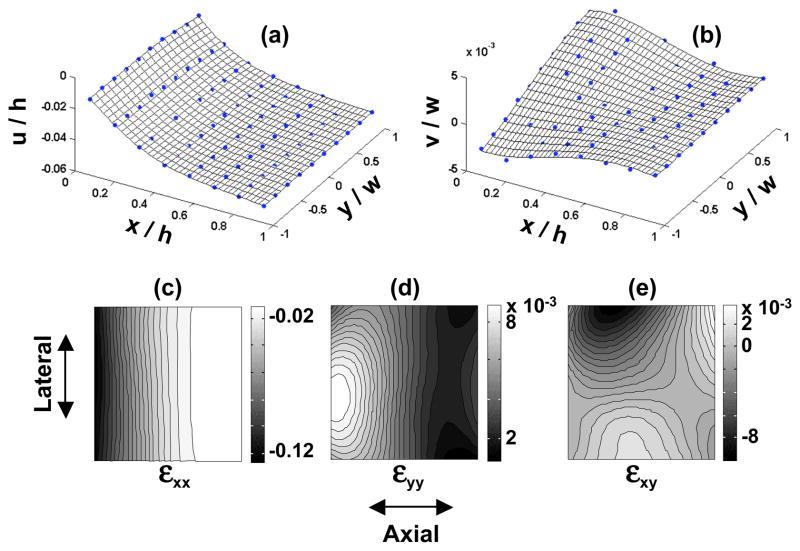
Figure 5.

The displacement fields (a, b) determined from the test where the 3-direction of a typical specimen was compressed; and the resultant strain fields within the imaging plane (c, d, e). The meshes in (a) and (b) are the thin-plate smoothing spline fit of the displacement data.

For the purpose of evaluating the compressive moduli along each direction, the axial strain along the 1- or 2-direction was determined from the slope of the nearly linear displacement distribution using linear regression analysis; for the 3-direction, the nonlinear depth-dependent displacement was amenable to subdivision into two zones (top one-third and bottom two-thirds of the tissue thickness), within each of which a linear regression could produce a representative measure of the slope (Table 1). All lateral strains were determined from linear regression of the measured displacement distributions along the lateral direction. Table 2 summarizes the measurements of all the strains for the six tests performed on each of the 15 cubic specimens. The measured lateral strains were all positive and always smaller in magnitude than the axial compressive strains.

Table 1.

Summary of the R² values from the linear regressions of the displacement data for strain determination, from the six tests on all 15 cubic specimens.

Test		2-3	1-3	3-1		2-1	1-2	3-2
				Top	Bottom			Top	Bottom
Axial Compression	R2	0.987	0.992	0.960	0.942	0.985	0.989	0.966	0.944
	STD	0.011	0.005	0.021	0.036	0.014	0.008	0.032	0.037
Lateral Expansion	R2	0.647	0.669	0.813	0.716	0.840	0.796	0.823	0.763
	STD	0.157	0.198	0.175	0.236	0.132	0.153	0.172	0.159

STD = standard deviation; Top = the top one-third of the tissue thickness; Bottom = the bottom two-third of the tissue.

Table 2.

Measured average strains (± standard deviation) from the six tests performed on 15 cubic specimens. The strains were determined from two compression levels: 5–10% compression and 10–15% compression. The applied strains listed in the table were calculated as: ε_app = 0.05 h₀/(1 − α)h₀, where h₀ is the tissue thickness in the absence of load; α is the compression level of the reference state (α=0.05 for 5–10% compression; α=0.1 for 10–15% compression).

Test	Measured Strains
	5 – 10% Compression		10 – 15% Compression
	Axial (%)	Lateral (%)	Axial (%)	Lateral (%)
2-3	−5.11 ± 0.26	0.22 ± 0.09	−5.40 ± 0.21	0.15 ± 0.06
1-3	−5.18 ± 0.23	0.27 ± 0.08	−5.26 ± 0.27	0.19 ± 0.09
3-1 (Top)	−8.96 ± 1.58	0.51 ± 0.20	−9.89 ± 1.75	0.38 ± 0.14
3-1 (Bottom)	−1.53 ± 0.65	0.45 ± 0.18	−1.89 ± 0.76	0.31 ± 0.11
2-1	−5.02 ± 0.33	1.49 ± 0.31	−5.17 ± 0.47	1.34 ± 0.28
1-2	−5.12 ± 0.35	1.46 ± 0.33	−5.13 ± 0.26	1.21 ± 0.30
3-2 (Top)	−9.87 ± 1.11	0.54 ± 0.19	−11.13 ± 2.25	0.43 ± 0.11
3-2 (Bottom)	−1.59 ± 0.76	0.48 ± 0.17	−1.89 ± 0.65	0.37 ± 0.08
Applied	~5.26		~5.56

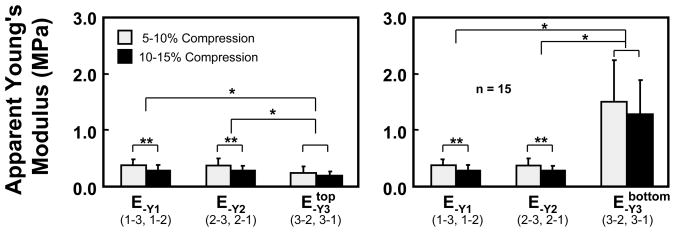
The measured axial strains and the recorded applied stresses were used to determine the average apparent Young’s moduli for the cubic specimens along each direction as per Eq.(2). These results are summarized in Figure 6 and Table 3, where those moduli are reported at two compression levels (i.e., when measured incrementally from 5–10% compression and 10–15% compression) for all 15 specimens; along the 3-direction, two distinct values are reported, corresponding to the average modulus of the top one-third and bottom two-thirds of the sample. At both compression levels, no significant difference was found between E_−Y1 and E_−Y2, but these moduli were significantly greater than E_−Y3 in the top layer of the sample, and significantly smaller than E_−Y3 in the bottom layer. Furthermore, it was observed that the moduli determined at the higher compression level were statistically smaller than those at the lower compression level along the 1- and 2-directions (p < 0.001).

Figure 6.

The apparent Young’s moduli determined for the three directions at two compression levels along with results of statistical comparisons (* p<0.01; ** p< 0.001).

Table 3.

Summary of measured properties in unconfined compression for all 15 specimens, including means and standard deviations (STD) at two levels of compression (5–10% and 10–15%). A two-layer model is used in the depth direction of the articular layer (3-direction) to account for the strong inhomogeneity observed along that direction.

Parameter	5–10% Compression		10–15% Compression
	Mean	STD	Mean	STD
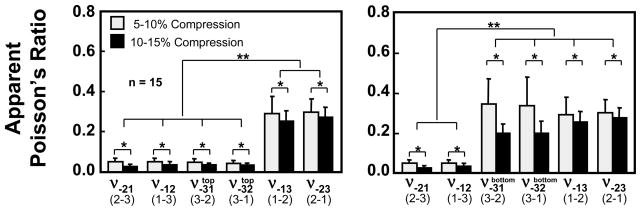
ν−21	0.045	0.018	0.028	0.011
ν−12	0.053	0.016	0.035	0.016
ν−13	0.293	0.095	0.237	0.060
ν−23	0.307	0.060	0.261	0.056
ν−31 (top)	0.048	0.017	0.036	0.006
ν−31 (Bottom)	0.361	0.132	0.212	0.050
ν−32 (top)	0.043	0.015	0.033	0.009
ν−32 (Bottom)	0.363	0.148	0.223	0.058
E−Y1	0.385 MPa	0.103 MPa	0.291 MPa	0.101 MPa
E−Y2	0.377 MPa	0.127 MPa	0.286 MPa	0.083 MPa
E−Y3 (top)	0.229 MPa	0.102 MPa	0.194 MPa	0.049 MPa
E−Y3 (bottom)	1.509 MPa	0.725 MPa	1.272 MPa	0.605 MPa

The equilibrium apparent Poisson’s ratios measured at the two compression levels from the six uniaxial compression tests are shown in Figure 7 and Table 3, with significant differences observed as indicated; as for the modulus along the 3-direction, two distinct values are provided for each of ν₋₃₁ and ν₋₃₂ corresponding to the top one-third and bottom two-thirds of the layer. In the top one-third, for both compression levels, it was observed that ν₋₂₁ ≈ ν₋₁₂ ≈ ν₋₃₁ ≈ ν₋₃₂ < ν₋₁₃ ≈ ν₋₂₃, where ≈ denotes that there was no statistical difference observed in the corresponding means, whereas < denotes a statistically significant effect; conversely, in the bottom two-third, it was found that ν₋₂₁ ≈ ν₋₁₂ < ν₋₃₁ ≈ ν₋₃₂ ≈ ν₋₁₃ ≈ ν₋₂₃. The increase in compression caused a significant decrease in all the apparent Poisson’s ratios (p < 0.01), indicating a nonlinear behavior of the tissue at equilibrium.

Figure 7.

The apparent Poisson’s ratios determined from compressions along the three directions at two compression levels along with results of statistical comparisons (* p<0.01; ** p<0.001).

One-way ANOVA demonstrated no significant difference between the products ν₋₁₂ν₋₂₃ν₋₃₁ and ν₋₁₃ν₋₃₂ν₋₂₁ (in the top one-third, p = 0.27 for Poisson’s ratios measured from 5–10% compression and p = 0.40 for those measured from 10–15% compression; in the bottom two-third, p = 0.23 and 0.37, respectively). The ratios ν_−ab/E_−Ya and ν_−ba/E_−Yb are presented in Table 4, in the top and bottom layers, at both compression levels, along with the corresponding p-values for the statistical test of hypothesis ν_−ab/E_−Ya ≠ ν_−ba/E_−Yb (paired two-tailed Student’s t-test with α = 0.05), demonstrating that this equality does not hold in general.

Table 4.

Summary of the ratios ν_−ab/E_−Ya for all 15 specimens, and p-values for statistical tests of the hypothesis ν_−ab/E_−Ya ≠ ν_−ba/E_−Yb.

For 5–10% compression:
ν−ab/E−Ya	Mean (×10−7)	STD (×10−7)	p-value
ν−12/E−Y1	1.31	0.44	0.73
ν−21/E−Y2	1.43	0.10
ν−31/E−Y3 (Top)	2.19	0.59	0.00016
ν−13/E−Y1	7.38	2.21		0.00016
ν−31/E−Y3 (Bottom)	2.11	0.44
ν−32/E−Y3 (Top)	2.02	0.70	0.0016
ν−23/E−Y2	8.14	3.80		0.0023
ν−32/E−Y3 (Bottom)	2.08	0.74

For 10–15% compression:
ν−ab/E−Ya	Mean (×10−7)	STD (×10−7)	p-value
ν−12/E−Y1	1.26	0.63	0.096
ν−21/E−Y2	0.85	0.45
ν−31/E−Y3 (Top)	1.97	0.68	0.0015
ν−13/E−Y1	8.93	4.98		0.00055
ν−31/E−Y3 (Bottom)	2.25	1.56
ν−32/E−Y3 (Top)	1.79	0.88	5.9×10−5
ν−23/E−Y2	9.99	3.93		1.6×10−5
ν−32/E−Y3 (Bottom)	2.35	1.97

DISCUSSION

The testing configuration employed in this study allowed the characterization of three Young’s moduli and six Poisson’s ratio on the same specimen, using an optical technique and digital image correlation analysis to measure the tissue strains. The inhomogeneity of articular cartilage through its depth (the 3-direction) increases the complexity of characterizing its intrinsic material properties. Among all six tests performed on the cubic specimens, compression along the 3-direction produced the most inhomogeneous deformations within the imaging plane (Figure 5, c, d, e). The axial strain changed primarily along the depth direction. The greatest compressive axial strain, which always happened near the surface, could be an order of magnitude higher than the axial strain in the deep layer. In contrast, the lateral strains were always positive and much smaller (at least an order) in magnitude. It was found, for the purpose of this study, that the axial strain field along the 3-direction could be reasonably analyzed using a two-layer model, with different properties assumed for the top 1/3 and the bottom 2/3 layers. Strictly, the material properties reported in this study represent apparent properties because inhomogeneous specimens were analyzed using formulas derived under the assumption of homogeneity, albeit using a two-layer model.

The compressive Young’s moduli reported in Figure 6 are in the typical range of compressive properties for bovine articular cartilage, demonstrating that the infrequently measured E_−Y1 and E_−Y2 are on the same order of magnitude as the more commonly measured E_−Y3, particularly in the top layer. The depth-dependent inhomogeneity of E_−Y3 is consistent with the study of Guilak et al. (1995) and our own recent results (Wang et al., 2000a, 2000b, 2001c), and it parallels that observed for H_−A3 by Schinagl et al. (1996, 1997), who also found that the compressive modulus in the superficial zone is smaller than that in the deep zone. Only a few recent studies have reported direct measurements of Poisson’s ratios and those have typically been obtained from compressive tests along the 3-direction (Jurvelin et al., 1997; Wong et al., 1998; Wong, 1999); nevertheless, just as for the case of E_−Y3, Poisson’s ratios ν₋₃₁ and ν₋₃₂ (Figure 7) measured in the top layer (ν₋₃₁ ≈ ν₋₃₂ ≈ 0.04) and bottom layer (ν₋₃₁ ≈ ν₋₃₂ ≈ 0.28) bracket the values reported previously from homogeneous analyses in the literature (e.g., 0.18 in the study of Jurvelin et al., 1997). In contrast, to our knowledge the present results of ν₋₂₁ ≈ ν₋₁₂ ≈ 0.04 and ν₋₁₃ ≈ ν₋₂₃ ≈ 0.28 represent new findings in the literature.

With regard to the characterization of material symmetry, the results of Table 4, showing that ν_−ab/E_−Ya ≠ ν_−ba/E_−Yb, clearly indicate that the framework of linear orthotropic elasticity is generally unsuitable for describing the equilibrium elastic response of articular cartilage. This result should not come as a surprise in light of the more recent realization that the disparity in the tensile and compressive moduli of articular cartilage has a major influence on its mechanical response to loading, whether in unconfined compression (Soulhat et al., 1999; Soltz and Ateshian, 2000), or other loading configurations (Ateshian and Soltz, 1999; Huang et al., 2001). The octantwise orthotropic CLE theory of Curnier et al. (1995), whose salient equations are summarized above, provides one possible framework for describing this kind of material, while still helping characterize its material symmetry. In this context, the finding from this study that ν₋₁₂ ν₋₂₃ ν₋₃₁ ≈ ν₋₁₃ ν₋₃₂ ν₋₂₁ means that the framework of the octantwise orthotropic CLE theory is not violated and may indeed serve as a proper model for describing the equilibrium response of articular cartilage. However, satisfying this equality is a necessary but not sufficient condition to demonstrate that this framework is suitable for cartilage. As alluded to in the methods section, a more rigorous test would entail the additional experimental characterization of the tensile moduli of cartilage along the three assumed directions of material symmetry which, together with the compressive moduli and Poisson’s ratios reported here, would allow a validation of the expressions in Eqs.(6)–(7) together with a verification of the positive definiteness of each of the eight possible elasticity tensors that can result from the permutation of λ_−aa and λ_+aa (a=1,3).

Nevertheless, even in the absence of direct measurements of the tensile moduli, there are several observations of the experimental data that permit a rather elaborate analysis that can provide supporting evidence in favor of this framework. Since the experimental responses differed in the top and bottom layers, the ensuing analysis needs to similarly discriminate between the two layers.

Top Layer

In the top layer, the following relations were found to be satisfied statistically by the experimental data:

$$E_{-Y1}\approx E_{-Y2},{\nu }_{-21}\approx {\nu }_{-12}\approx {\nu }_{-31}\approx {\nu }_{-32},{\nu }_{-13}\approx {\nu }_{-23}.$$ (8)

These expressions are purely a result of experimental observation and do not represent a fundamental theoretical requirement. However, they can be used to establish phenomenological relations between the set of experimentally determined {E_−Ya,ν_−ab} and the material constants {H_±Aa,λ_ab} (a,b=1,3, a≠b). Substituting the expressions of Eqs.(6)–(7) into these identities, and further assuming for simplicity that

$$H_{-A2}\approx H_{-A1},{\lambda }_{23}\approx {\lambda }_{13},$$ (9)

results in the following relations between {E_−Ya,ν_−ab} and {H_±Aa,λ_ab},

$$\begin{array}{l}{E}_{-Y1}\approx E_{-Y2}\approx H_{-A1}-{\lambda }_{12}+\frac{{\lambda }_{13}(H_{+A1}-{\lambda }_{12})}{H_{+A1}+{\lambda }_{12}},E_{-Y3}\approx H_{-A3}-\frac{2{\lambda }_{13}^2}{H_{+A1}+{\lambda }_{12}},\\ {\nu }_{-21}\approx {\nu }_{-12}\approx {\nu }_{-31}\approx {\nu }_{-32}\approx \frac{{\lambda }_{12}}{H_{+A1}+{\lambda }_{12}},{\nu }_{-13}\approx {\nu }_{-23}\approx \frac{{\lambda }_{12}}{{\lambda }_{13}}-\frac{H_{+A1}}{H_{+A1}+{\lambda }_{12}},\end{array}$$ (10)

along with the restriction that

$$H_{+A2}\approx H_{+A1}\text{and}{H}_{+A3}\approx \frac{(H_{+A1}+{\lambda }_{12}-{\lambda }_{13}){\lambda }_{13}^2}{H_{+A1}({\lambda }_{12}-{\lambda }_{13})+{\lambda }_{12}^2}.$$ (11)

Note that the expressions of Eq.(10) represent four equations in the five unknowns H_+A1,H_{− A1},H_−A3,λ₁₂,λ₁₃; thus, even with the knowledge of the complete set of material properties {E_−Ya,ν_−ab}, the complete set {H_±Aa,λ_ab} remains indeterminate as mentioned earlier. But the simplification achieved here allows a straightforward parametric analysis whereby, e.g., H_+A1 is parameterized to calculate the complete set of material constants {H_±Aa,λ_ab} given the experimental set {E_−Ya,ν_−ab}, by solving the nonlinear set of equations in Eq.(10) for each given H_+A1. Then the positive definiteness of each of the eight possible elasticity tensors can be verified by checking that the eigenvalues of the eight matrices

$$\left[\begin{array}{ccc}{H}_{\pm A1}& {\lambda }_{12}& {\lambda }_{13}\\ {\lambda }_{12}& H_{\pm A2}& {\lambda }_{23}\\ {\lambda }_{13}& {\lambda }_{23}& H_{\pm A3}\end{array}\right]$$ (12)

are all positive. One such parametric analysis is presented in Table 5, using representative values of {E_−Ya,ν_−ab} from the experimental data set. It can be noted from the results in this table that positive definiteness of the elasticity tensors can be achieved for 0< H_{+ A1} < 7.4 MPa, which is entirely plausible in light of other findings in the literature which show that the tensile modulus in the 1-direction is on this order of magnitude in the range of small strains. The values of the remaining estimated parameters are also reasonable, with the upper bound on the “off-diagonal moduli” (λ₁₂,λ₂₃,λ₁₃) on the order of 0.3 MPa, which agrees with the direct measurements of λ₂₃,λ₁₃ as reported by Khalsa and Eisenberg (1997). Interestingly, the predicted value of H_+A3 in the top layer is consistently smaller than H_+A1, which remains to be verified from future experiments. This indicates that the tissue exhibits significantly lower tensile stiffness along the 3-direction than along the other two directions; the functional implication of this finding remains to be explored, but the fact that the 3-direction of cartilage experiences primarily compressive loading seems to be consistent with this result. Conversely, given the complete set {H_±Aa,λ_ab} generated from this parametric analysis, it is also possible to predict the response of the tissue to tensile loading to yield the data set {E_+Ya,ν_+ab}, as presented in Table 5 as well. The most salient results of this analysis are that the tensile Poisson’s ratios ν₊₁₂ ≈ ν₊₂₁ increase to a peak value of ~0.31 at H_+A1 ~5 MPa, but turn negative at H_+A1≥7.0 MPa; experimental values of these Poisson’s ratios have been found to be positive and typically higher than the values in this table, as reviewed in the Introduction. The range of ν₊₁₃ ≈ ν₊₂₃ is found to be much greater however, encompassing that described in recent experimental studies, and spanning beyond the value of 0.5 which is an upper bound on Poisson’s ratio only for isotropic or cubic symmetry. The finding that E_+Y1 ≈ E_+Y2 in Table 5 is also inconsistent with the well known experimental finding that the tensile modulus along the split line direction is typically greater than perpendicular to the split line direction (Kempson et al., 1968, 1973; Woo et al., 1976, 1979; Roth and Mow, 1980; Huang et al., 1999), but this limitation along with that for the range of ν₊₁₂ ≈ ν₊₂₁ stem from the simplifying assumptions of Eq.(9) and should not be construed to reflect a fundamental limitation of the theoretical framework. Without these simplifications the parametric analysis would necessarily involve more than one parameter, which would limit its clarity and usefulness.

Table 5.

Estimates of the material constants {H_±Aa,λ_ab} and {E_+Ya,ν_+ab} in the top one-third layer of the articular cartilage, from an analysis where H_+A1 is varied parametrically over its valid range, given that E_−Y1 ≈ E_−Y2 ≈ 0.335 MPa, E_−Y3 ≈ 0.211 MPa, ν₋₂₁ ≈ ν₋₁₂ ≈ ν₋₃₁ ≈ ν ₋₃₂ ≈ 0.04, and ν₋₁₃ ≈ ν₋₂₃ ≈ 0.28 based on the experimental data. All moduli are given in MPa.

H+A1, H+A2	H+A3	H−A1, H−A2	H−A3	λ12	λ13, λ23	E+Y1, E+Y2	E+Y3	ν+12, ν+21	ν+23, ν+13	ν+31, ν+32
0.50	0.07	0.34	0.21	0.03	0.02	0.50	0.07	0.07	0.09	0.06
1.00	0.14	0.35	0.21	0.05	0.04	0.99	0.14	0.13	0.17	0.11
1.50	0.22	0.36	0.22	0.08	0.06	1.47	0.20	0.18	0.24	0.15
2.00	0.29	0.36	0.22	0.10	0.08	1.95	0.26	0.22	0.30	0.18
2.50	0.36	0.37	0.22	0.13	0.11	2.43	0.32	0.25	0.36	0.21
3.00	0.43	0.38	0.22	0.16	0.13	2.91	0.37	0.27	0.41	0.24
3.50	0.50	0.38	0.22	0.18	0.15	3.38	0.43	0.29	0.47	0.26
4.00	0.58	0.39	0.22	0.21	0.17	3.85	0.48	0.31	0.52	0.28
4.50	0.65	0.40	0.23	0.23	0.19	4.32	0.54	0.31	0.58	0.30
5.00	0.72	0.40	0.23	0.26	0.21	4.79	0.59	0.31	0.64	0.32
5.50	0.79	0.41	0.23	0.28	0.23	5.25	0.64	0.29	0.72	0.33
6.00	0.87	0.42	0.23	0.31	0.25	5.72	0.69	0.25	0.82	0.35
6.50	0.94	0.43	0.23	0.34	0.27	6.18	0.74	0.15	1.00	0.36
7.00	1.01	0.43	0.23	0.36	0.29	6.63	0.79	−0.12	1.40	0.37
7.30	1.05	0.44	0.24	0.38	0.31	6.89	0.82	−0.63	2.12	0.38

Bottom Layer

In the bottom layer, the following relations were found to be satisfied by the experimental data:

$$E_{-Y1}\approx E_{-Y2},{\nu }_{-21}\approx {\nu }_{-12},{\nu }_{-31}\approx {\nu }_{-32}\approx {\nu }_{-13}\approx {\nu }_{-23}.$$ (13)

Using the same approach as for the top layer, and making the same additional simplifying assumptions of Eq.(9), the following relations are found between {E_−Ya,ν_−ab} and {H_±Aa,λ_ab}:

$$\begin{array}{l}{E}_{-Y1}\approx E_{-Y2}\approx H_{-A1}-\frac{{\lambda }_{12}^2}{H_{+A1}}-\frac{{\lambda }_{13}^2(H_{+A1}-{\lambda }_{12})}{H_{+A1}(H_{+A1}+{\lambda }_{12})},E_{-Y3}\approx H_{-A3}-\frac{2{\lambda }_{13}^2}{H_{+A1}+{\lambda }_{12}},\\ {\nu }_{-12}\approx {\nu }_{-21}\approx \frac{{\lambda }_{12}}{H_{+A1}}-\frac{{\lambda }_{13}^2}{H_{+A1}(H_{+A1}+{\lambda }_{12})},{\nu }_{-31}\approx {\nu }_{-32}\approx {\nu }_{-13}\approx {\nu }_{-23}\approx \frac{{\lambda }_{13}}{H_{+A1}+{\lambda }_{12}}.\end{array}$$ (14)

with the additional constraints of

$$H_{+A2}\approx H_{+A1}\text{and}{H}_{+A3}\approx H_{+A1}+\frac{{\lambda }_{13}^2-{\lambda }_{12}^2}{H_{+A1}}.$$ (15)

A parametric analysis whereby the set {H_±Aa,λ_ab} is estimated from typical experimental data for {E_−Ya,ν_−ab} as H_+A1 is varied, and the corresponding estimates of {E_+Ya,ν_+ab}, are presented in Table 6. As for the top layer, an acceptable range for H_+A1, which preserves the positive definiteness of all eight elasticity tensors, is found to lie within the bounds 0 < H_+A1 < 3.25 MPa; however, for positive values of all the tensile Poisson’s ratios, the upper bound on H_+A1 is 2.3 MPa. Once again, this result is consistent with literature findings that the tensile modulus of cartilage along the 1-direction decreases with depth from the articular surface (Akizuki et al., 1986), thus it seems quite plausible to have the upper bound on H_+A1 decrease accordingly. A close examination of the results of Table 6 leads to similar conclusions as for the top layer, namely that the results are compatible with literature findings, with some agreements stronger than others, though none presenting any fundamental contradiction between theory and experiments.

Table 6.

Estimates of the material constants {H_±Aa,λ_ab} and {E_+Ya,ν_+ab} in the bottom two-third layer of the articular cartilage, from an analysis where H_+A1 is varied parametrically over its valid range, given that E_−Y1 ≈ E_−Y2 ≈ 0.335 MPa, E_−Y3 ≈ 1.39 MPa, ν₋₂₁ ≈ ν₋₁₂ ≈ 0.04, and ν₋₃₁ ≈ ν₋₃₂ ≈ ν₋₁₃ ≈ ν₋₂₃ ≈ 0.28 based on the experimental data. All moduli are given in MPa.

H+A1, H+A2	H+A3	H−A1, H−A2	H−A3	λ12	λ13, λ23	E+Y1, E+Y2	E+Y3	ν+12, ν+21	ν+23, ν+13	ν+31, ν+32
0.50	0.54	0.38	1.48	0.06	0.16	0.48	0.43	0.13	0.09	0.35
0.75	0.81	0.41	1.52	0.10	0.24	0.70	0.59	0.16	0.13	0.47
1.00	1.08	0.43	1.57	0.13	0.32	0.92	0.72	0.18	0.17	0.57
1.25	1.35	0.45	1.61	0.16	0.39	1.14	0.84	0.18	0.20	0.64
1.50	1.63	0.48	1.66	0.19	0.47	1.35	0.95	0.17	0.24	0.71
1.75	1.90	0.50	1.70	0.22	0.55	1.56	1.05	0.14	0.28	0.76
2.00	2.17	0.52	1.74	0.26	0.63	1.77	1.14	0.10	0.33	0.81
2.25	2.44	0.55	1.79	0.29	0.71	1.97	1.23	0.02	0.39	0.85
2.50	2.71	0.57	1.83	0.32	0.79	2.16	1.31	−0.08	0.47	0.89
2.75	2.98	0.59	1.88	0.35	0.87	2.34	1.38	−0.26	0.58	0.92
3.00	3.25	0.62	1.92	0.39	0.95	2.49	1.46	−0.56	0.77	0.95
3.20	3.47	0.63	1.96	0.41	1.01	2.57	1.51	−1.00	1.03	0.97

Taking together that ν₋₁₂ ν₋₂₃ ν₋₃₁ ≈ ν₋₁₃ ν₋₃₂ ν₋₂₁ and that the experimental results on {E_−Ya,ν_−ab} produce self-consistent estimates of {H_±Aa,λ_ab} from the parametric analyses of Tables 5–6, it appears reasonable to conclude that the experimental findings of this study can be properly interpreted in the framework of the octantwise orthotropic CLE theory. Thus, despite the experimental observation that ν_−ab/E_−Ya ≠ ν_−ba/E_−Yb, it is still possible to conclude that articular cartilage exhibits no lower symmetry than orthotropy, when using a constitutive model which recognizes the tissue’s tension-compression nonlinearity response. The experimental finding that some of the material constants exhibit the approximate identities summarized in Eqs.(8) and (13), for the top and bottom layers respectively, suggests that further refinements in the characterization of material symmetry may be achieved in the future, if tensile moduli are measured along with the compressive properties reported here.

It is not intended that the specific constitutive model employed in this study be considered the most ideally suited for describing cartilage, in view of the fact that this model assumes strain-independent moduli and Poisson’s ratios in tension as well as in compression, whereas experimental findings from this and other studies suggest otherwise. Similarly, the parametric results listed in Tables 5–6 offer encouraging support for this general framework but do not exhibit sufficient flexibility to describe the wider range of cartilage material responses observed at higher tensile strains. However, as commonly done in the study of materials, the modeling assumption of a linear (but distinct) response in tension and compression can represent the first foray into more elaborate future modeling assumptions.

A useful advantage of the application of optimized digital image correlation in this study is the increased accuracy of strain measurements. Unlike the surface-to-surface measurement adopted in other optical measurements, this technique does not require any thresholding and edge detection on the recorded images. With respect to the experimental protocol, it was found that the axial compressive strains measured from digital image correlation were close to but typically smaller than the nominal compressive strains applied via the loading platens; this suggests incomplete mating of the loading platen with the specimen surface as well as potential errors from initial thickness measurements. All material properties were determined from the true strain measurements derived from digital image correlation, to eliminate any potential errors from these sources.

This study also demonstrated that the compressive Young’s moduli decreased with increasing applied strain; this apparent strain-softening of the tissue was statistically significant along the 1- and 2-directions and also notable along the 3-direction, when the compression increased from 5–10% to 10–15% of the initial thickness. Such strain-softening of cartilage has been observed in other studies (Schinagl et al., 1997; Bursac et al., 1999) and has been explained as the transition from tension to compression by overcoming the pre-stretched state resulting from the osmotic pressure; we address this phenomenon in much greater detail in a forthcoming study (Wang et al., 2001b).

In conclusion, the main findings of this study are that (a) with the proper methodology, it is possible to measure the unconfined compression Young’s moduli and Poisson’s ratio of articular cartilage along three mutually perpendicular directions, as performed on bovine samples in the current study, to gain greater insight into the material symmetry of cartilage; (b) the framework of linear orthotropic elasticity (as well as higher symmetries of linear elasticity) is not suitable to describe the equilibrium response of articular cartilage nor characterize its material symmetry; (c) a framework which accounts for the distinctly different responses of cartilage in tension and compression, such as the octantwise orthotropic conewise linear elasticity theory of Curnier et al. (1995), may be more suitable for describing the equilibrium response of cartilage; within this framework, cartilage exhibits no lower than orthotropic symmetry.