Skip to main content
PMC home page
The Journal of Chemical Physics logoLink to The Journal of Chemical Physics
. 2008 Jun 27;128(24):244112. doi: 10.1063/1.2940738

Hartree–Fock orbitals significantly improve the reaction barrier heights predicted by semilocal density functionals

Benjamin G Janesko 1,a), Gustavo E Scuseria 1
PMCID: PMC2809668  PMID: 18601322

Abstract

Semilocal density functional theory predictions for the barrier heights of representative hydrogen transfer, heavy-atom transfer, and nucleophilic substitution reactions are significantly improved in non-self-consistent calculations using Hartree–Fock orbitals. Orbitals from hybrid calculations yield related improvements. These results provide insight into compensating for one-electron self-interaction error in semilocal density functional theory.

INTRODUCTION

Kohn–Sham density functional theory (DFT) using semilocal exchange-correlation (XC) functionals is an indispensable tool for computational chemistry and solid state physics.1 Semilocal XC functionals include the local spin-density approximation (LSDA) constructed from the electron density, generalized gradient approximations (GGAs) constructed from the density and density gradient, and meta-GGAs incorporating the kinetic energy density and∕or density Laplacian.2 DFT has been extensively applied to predicting reaction energies and reaction barrier heights.3, 4, 5 An early investigation6 of the F+H2→HF+H hydrogen transfer found that non-self-consistent calculations using Hartree–Fock (HF) orbitals and the BLYP (Refs. 7, 8) GGA predicted an accurate reaction energy and a slightly overestimated barrier height. However, subsequent investigations indicated that self-consistent calculations with semilocal XC functionals significantly underestimate the barriers of reactions such as hydrogen transfers, heavy-atom transfers, and nucleophilic substitutions.4, 5, 9

This reaction barrier underestimation is connected to the one-electron self-interaction error (1e-SIE) intrinsic to semilocal density functionals. 1e-SIE is defined as an erroneous nonzero electron-electron interaction energy in one-electron systems due to incomplete cancellation between the Coulomb and XC interactions of an electron with itself.10 Semilocal DFT reaction barriers can be significantly improved by explicit Perdew–Zunger self-interaction correction9, 10, 11, 12 (PZ-SIC) or by admixture of a large fraction (∼50%) of 1e-SIE-free HF exchange.13, 14, 15, 16 Because 1e-SIE mimics nondynamical electron correlation in covalent bonds,17, 18, 19 molecular thermochemistry tends to be optimized by a scaled down PZ-SIC (Ref. 12) or a smaller fraction (∼10%–25%) of HF exchange.20, 21, 22 Functionals incorporating 100% long-range HF exchange23, 24 or a fraction of middle-range HF exchange25 appear to balance the desirable versus undesirable effects of 1e-SIE, providing accurate treatments of both molecular thermochemistry and reaction barrier heights.26 The role of many-electron self-interaction error in such systems has recently been highlighted.27, 28, 29

Unfortunately, both PZ-SIC and admixture of HF exchange have a significant computational cost relative to semilocal DFT, especially in solids.30 This has led to extensive research on semilocal functionals that incorporate the desirable nondynamical correlation effects of 1e-SIE while avoiding its undesirable effects on reaction barriers. However, the most accurate extant GGA (Refs. 31, 32, 33, 34) and meta-GGA (Refs. 35, 36, 37) functionals are highly parameterized and sometimes fail to reproduce exact conditions.2 Further investigation of how 1e-SIE affects reaction barriers may provide insight into developing more accurate and less empirical semilocal XC functionals.

This article represents one such investigation. We show that non-self-consistent calculations combining semilocal XC functionals with 1e-SIE-free HF orbitals significantly improve many reaction barriers. Orbitals from hybrid functionals incorporating a fraction of HF exchange yield similar improvements. The improvements appear to result from cancellation between the 1e-SIE of transition states versus reactants, arising from the relatively localized transition state electronic structures obtained from HF calculations.

COMPUTATIONAL DETAILS

We investigate forward and reverse reaction barrier heights from the HTBH38∕04 set of 19 hydrogen transfer reactions and the NHTBH38∕04 set of 6 heavy-atom transfer reactions, 8 nucleophilic substitution reactions, and 5 unimolecular and association reactions.38, 39 Geometries and experimental values for these sets are taken from Ref. 39. We also test the small, representative AE6 set of atomization energies and BH6 set of hydrogen transfer reaction barrier heights.40 Geometries and experimental values for these data sets are taken from Refs. 40, 41.

We present results for the following density functionals: LSDA [Vosko–Wilk–Nusair correlation functional V (Ref. 42)], the nonempirical Perdew–Burke–Ernzerhof43 (PBE) and RPBE (Ref. 44) GGAs, the PBEh (Refs. 45, 46) and PBE half-and-half (“HandH”) global hybrids, and the accurate one-parameter long-range-corrected hybrid LC-ωPBE.26 “PBE-75” denotes a PBE global hybrid with 75% HF exchange. RPBE, PBEh, PBE-HandH, PBE-75, and LC-ωPBE use the PBE correlation functional. We also present results from the HCTH407 GGA,33 which is taken as representative of the latest empirical GGAs. Calculations use a development version of the GAUSSIAN electronic structure program47 and (unless noted otherwise) the 6-311++G(3df,3pd) basis set. Open-shell systems are treated spin unrestricted. Errors are calculated as theory-experiment.

RESULTS

Table 1 compares self-consistent and post-HF errors in reaction barrier heights. The table shows mean and mean absolute errors in forward and reverse barrier heights of the HTBH38∕04 and NHTBH38∕04 test sets. Post-HF calculations dramatically improve LSDA and the nonempirical PBE and RPBE GGAs. The largest improvements occur for hydrogen transfer, nucleophilic substitution, and heavy-atom transfer reaction barriers. To our knowledge, this effect has never been systematically reported or investigated. Hydrogen transfer and nucleophilic substitution barriers were previously shown to be improved by explicit PZ-SIC.9

Table 1.

Mean and mean absolute errors in self-consistent (SCF) and post-HF 6-311++G(3df,3pd) reaction barrier heights of the HTBH38∕04 and NHTBH38∕04 test sets.

Functional HTBH38 hydrogen transfer Non-hydrogen-transfer reactions of the NHTBH38 set
Nucleophilic substitution (16) Heavy-atom transfer (12) Unimolecular and association (10) Full NHTBH38
SCF Post-HF SCF Post-HF SCF Post-HF SCF Post-HF SCF Post-HF
Mean absolute errors (kcal∕mol)
LSDA 17.9 10.2 8.4 1.3 23.8 12.9 6.1 3.5 12.7 5.5
PBE 9.7 3.5 6.8 1.6 15.3 8.6 3.5 2.5 8.6 4.0
RPBE 6.8 2.0 5.5 2.6 12.5 7.6 2.8 2.7 7.0 4.2
HCTH407 5.8 1.9 2.5 5.0 9.3 7.4 2.3 4.3 4.6 5.6
PBEh 4.6 1.7 1.9 3.1 7.0 5.6 2.3 2.5 3.6 3.7
PBE-HandH 1.5 2.0 2.4 4.5 2.2 5.4 2.7 2.9 2.4 4.4
LC-ωPBE 1.3 2.6 2.8 5.8 1.9 7.2 2.3 3.3 2.4 5.6
Mean errors (kcal∕mol)
PBE −9.7 −3.1 −6.8 1.6 −15.3 −0.7 −3.1 1.8 −8.5 0.9
HCTH407 −5.8 0.6 −2.5 5.0 −9.3 6.1 −0.9 4.3 −4.2 5.2
LC-ωPBE −0.5 2.4 2.8 5.8 −0.6 7.2 1.4 3.3 1.4 5.6
Open in a new tab

Table 2 demonstrates that post-HF and self-consistent semilocal DFT calculations yield similar results for thermochemistry and reaction energies. The table presents post-HF and self-consistent errors in HTBH38∕04 and NHTBH38∕04 reaction energies and AE6 atomization energies. These properties are largely orbital independent, with LSDA and PBE somewhat improved post-HF. This is consistent with Refs. 9, 11, which show that 1e-SIE has a minimal effect on reaction energies. Post-HF calculations tend to overcorrect atomization energies of the RPBE and HCTH407 GGAs.

Table 2.

Errors in HTBH38∕04 and NHTBH38∕04 reaction energies and AE6 atomization energies; details as in Table 1.

Functional HTBH38 NHTBH38 AE6
SCF Post-HF SCF Post-HF SCF Post-HF
Mean absolute error (kcal∕mol)
LSDA 6.7 6.4 6.7 4.6 77.0 68.5
PBE 3.2 3.0 3.7 2.0 15.1 10.2
RPBE 1.8 1.7 2.8 1.6 9.7 14.6
HCTH407 1.8 1.8 2.6 1.6 5.6 9.7
PBEh 1.6 1.5 2.2 1.7 6.1 5.3
PBE-HandH 1.5 1.5 3.2 3.2 10.7 12.6
LC-ωPBE 1.8 1.8 2.0 1.6 4.9 6.5
Mean error (kcal∕mol)
PBE 0.1 0.1 1.6 1.1 11.9 4.4
HCTH407 −0.5 −0.5 0.9 0.3 −2.6 −9.7
LC-ωPBE 0.1 0.2 −1.0 −1.3 −2.2 −6.5
Open in a new tab

The results in Table 2 are unsurprising at first glance. Semilocal DFT energies of covalently bound molecules are known to be rather insensitive to orbital choice.1 However, the point is of central importance. Post-HF calculations with semilocal DFT functionals appear to reduce the undesirable effects of 1e-SIE on reaction barriers while largely maintaining its desirable simulation of the nondynamical correlation effects essential to thermochemistry.

The effects in Table 1 are not restricted to post-HF calculations but occur to some extent for hybrid DFT orbitals and densities. Table 3 presents mean absolute errors in the small, representative BH6 set of hydrogen transfer reaction barrier heights.40 For each method X=PBE, PBE-HandH, LC-ωPBE, PBE-75, and HF; the table presents results of self-consistent calculations and of non-self-consistent “post-X” PBE using orbitals and densities from method X. All of the functionals yield orbitals and densities that improve PBE hydrogen transfer barriers. This is a notable contrast to the self-consistent calculations, where removing too much 1e-SIE (and its associated simulation of nondynamical correlation17, 18, 19) degrades the results.

Table 3.

BH6 hydrogen transfer reaction barrier height mean absolute errors (kcal∕mol). “SCF” denotes self-consistent calculations. “Post-X PBE” denotes non-self-consistent PBE calculations using orbitals from a self-consistent calculation with method X.

  SCF Post-X PBE
PBE 9.6 9.6
PBEh 4.9 9.2
LC-ωPBE 1.5 8.7
PBE-HandH 1.3 8.2
PBE-75a 2.7 6.7
HF 12.1 3.4
Open in a new tab
a

PBE global hybrid, 75% HF exchange.

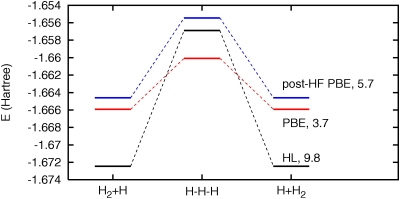
The accurate post-HF reaction barriers appear to result from an improved cancellation of 1e-SIE between reactants and transition states. To illustrate, Fig. 1 presents an energy level diagram of the H2+H→H+H2 reaction. The figure compares self-consistent and post-HF PBE to high-levelab initio calculations.48 For self-consistent PBE (red), the reactant energies are significantly above the high-level results (black), while the transition state energy is below the high-level result and far too low relative to the reactants. This error is due in part to the spurious Coulomb self-repulsion present in PBE, a repulsion that is smaller in the relatively delocalized transition state. Non-self-consistent PBE calculations with HF orbitals (blue) apparently have a more localized transition state with significantly increased Coulomb self-repulsion.49 This extra self-repulsion improves the cancellation of 1e-SIE between transition state and reactants. The resulting post-HF reaction barrier is significantly closer to the high-level calculation, even though the post-HF total energies are still rather inaccurate.

Figure 1.

Figure 1

Open in a new tab

Energy level diagram for the H2+H→H+H2 reaction. PBE (red), post-HF PBE, and high-level (HL) ab initio calculations. Classical reaction barriers (kcal∕mol) are given in the labels; other details are in the text.

An important caveat to these results is that HF electronic structures tend to be too localized, yielding overestimated reaction barrier heights.4, 5 The accurate post-HF results shown here thus enjoy a degree of error compensation. This may explain the relatively poor post-HF barriers obtained for PBE-HandH and LC-ωPBE, which already include substantial HF exchange. It may also explain the overcorrected HCTH407 reaction barriers. HCTH407 is parametrized to a data set including accurate 1e-SIE-free XC potentials of atoms and small molecules and thus presumably incorporates some sort of effective 1e-SIC.32, 33 In this context, we note that Baerends and co-workers found that semilocal DFT calculations using accurate ab initio electronic structures significantly underestimate hydrogen transfer50 and nucleophilic substitution51 reaction barriers, with results comparable to self-consistent semilocal DFT. Despite this, the post-X results of Table 3 indicate that a more general principle is at work.

The results in Table 1 should provide a caution to the common practice of benchmarking density functionals using non-self-consistent calculations. Reaction barrier heights can apparently be strongly orbital dependent, such that non-self-consistent calculations may give an incorrect picture of a functional’s performance.

DISCUSSION

In this work, we suggest that localizing semilocal DFT electronic structures can compensate for some undesirable effects of self-interaction error. We show that non-self-consistent semilocal DFT calculations using HF orbitals dramatically improve many reaction barriers without degrading thermochemistry. These improvements are in many respects a consequence of error compensation. Semilocal DFT calculations of reaction barrier heights always rely on a cancellation between the 1e-SIE of reactants versus transition states. HF orbitals and densities appear to increase the self-Coulomb repulsion in semilocal DFT transition states, improving this cancellation of 1e-SIE. (It is interesting to note in this context that the exact energy can in principle be obtained directly from the HF density matrix.52)

Of course, we do not advocate post-HF methods for production calculations. Rather, we suggest that these results provide insight into “working around” the 1e-SIE intrinsic to semilocal density functionals. Explicit constraints counteracting self-Coulomb-induced delocalization may provide improved 1e-SIE cancellation without the need to evaluate HF exchange. While such error compensations must be treated with care, they are essential in applications where high-level, 1e-SIE-free methods are computationally intractable.

ACKNOWLEDGMENTS

The authors thank Jochen Heyd for useful discussions. This work was supported by a training fellowship from the National Library of Medicine to the Keck Center for Interdisciplinary Bioscience Training of the Gulf Coast Consortium (NLM Grant No. 5T15LM07093), NSF CHE-0457030, and the Welch Foundation (C-0036).

References

  1. Scuseria G. E. and Staroverov V. N., in Theory and Applications of Computational Chemistry: The First 40 Years, edited by Dykstra C. E., Frenking G., Kim K. S., and Scuseria G. E. (Elsevier, Amsterdam, 2005). [Google Scholar]
  2. Perdew J. P. and Schmidt K., in Density Functional Theory and its Application to Materials, edited by Van Doren V., Van Alsenoy C., and Geerlings P. (American Institute of Physics, New York, 2001). [Google Scholar]
  3. Ziegler T., Chem. Rev. 10.1021/cr00005a001 91, 651 (1991). [DOI] [Google Scholar]
  4. Andersson S. and Grüning M., J. Phys. Chem. A 10.1021/jp040448c 108, 7621 (2004). [DOI] [Google Scholar]
  5. Grüning M., Gritsenko O. V., and Baerends E. J., J. Phys. Chem. A 10.1021/jp031227u 108, 4459 (2004). [DOI] [Google Scholar]
  6. Scuseria G. E., J. Chem. Phys. 10.1063/1.463977 97, 7528 (1992). [DOI] [Google Scholar]
  7. Becke A. D., Phys. Rev. A 10.1103/PhysRevA.38.3098 38, 3098 (1988). [DOI] [PubMed] [Google Scholar]
  8. Lee C., Yang W., and Parr R. G., Phys. Rev. B 10.1103/PhysRevB.37.785 37, 785 (1988). [DOI] [PubMed] [Google Scholar]
  9. Patchkovskii S. and Ziegler T., J. Chem. Phys. 10.1063/1.1468640 116, 7806 (2002). [DOI] [Google Scholar]
  10. Perdew J. P. and Zunger A., Phys. Rev. B 10.1103/PhysRevB.23.5048 23, 5048 (1981). [DOI] [Google Scholar]
  11. Johnson B. G., Gonzales C. A., Gill P. M. W., and Pople J. A., Chem. Phys. Lett. 10.1016/0009-2614(94)87024-1 221, 100 (1994). [DOI] [Google Scholar]
  12. Vydrov O. A., Scuseria G. E., Perdew J. P., Ruzsinszky A., and Csonka G. I., J. Chem. Phys. 10.1063/1.2176608 124, 094108 (2006). [DOI] [PubMed] [Google Scholar]
  13. Truong T. N. and Duncan W., J. Chem. Phys. 10.1063/1.468299 101, 7408 (1994). [DOI] [Google Scholar]
  14. Bell R. L. and Truong T. N., J. Chem. Phys. 10.1063/1.467862 101, 10442 (1994). [DOI] [Google Scholar]
  15. Lynch B. J., Fast P. L., Harris M., and Truhlar D. G., J. Phys. Chem. A 10.1021/jp000497z 104, 4811 (2000). [DOI] [Google Scholar]
  16. Kang J. K. and Musgrave C. M., J. Chem. Phys. 10.1063/1.1415079 115, 11040 (2001). [DOI] [Google Scholar]
  17. Becke A. D., J. Chem. Phys. 10.1063/1.464304 98, 1372 (1993). [DOI] [Google Scholar]
  18. Gritsenko O. V., Schipper P. R. T., and Baerends E. J., J. Chem. Phys. 10.1063/1.474864 107, 5007 (1997). [DOI] [Google Scholar]
  19. Cremer D., Mol. Phys. 10.1080/00268970110083564 99, 1899 (2001). [DOI] [Google Scholar]
  20. Becke A. D., J. Chem. Phys. 10.1063/1.464913 98, 5648 (1993). [DOI] [Google Scholar]
  21. Stephens P. J., Devlin F. J., Chabalowski C. F., and Frisch M. J., J. Phys. Chem. 10.1021/j100096a001 98, 11623 (1994). [DOI] [Google Scholar]
  22. Perdew J. P., Ernzerhof M., and Burke K., J. Chem. Phys. 10.1063/1.472933 105, 9982 (1996). [DOI] [Google Scholar]
  23. Savin A., in Recent Developments and Applications of Modern Density Functional Theory, edited by Seminario J. M. (Elsevier, Amsterdam, 1996), pp. 327–357. [Google Scholar]
  24. Iikura H., Tsuneda T., Yanai T., and Hirao K., J. Chem. Phys. 10.1063/1.1383587 115, 3540 (2001). [DOI] [Google Scholar]
  25. Henderson T. M., Izmaylov A. F., Scuseria G. E., and Savin A., J. Chem. Phys. 10.1063/1.2822021 127, 221103 (2007). [DOI] [PubMed] [Google Scholar]
  26. Vydrov O. A. and Scuseria G. E., J. Chem. Phys. 10.1063/1.2409292 125, 234109 (2006). [DOI] [PubMed] [Google Scholar]
  27. Ruzsinszky A., Perdew J. P., Csonka G. I., Vydrov O. A., and Scuseria G. E., J. Chem. Phys. 10.1063/1.2387954 125, 194112 (2006). [DOI] [PubMed] [Google Scholar]
  28. Mori-Sánchez P., Cohen A. J., and Yang W., J. Chem. Phys. 10.1063/1.2403848 125, 201102 (2006). [DOI] [PubMed] [Google Scholar]
  29. Vydrov O. A., Scuseria G. E., and Perdew J. P., J. Chem. Phys. 10.1063/1.2723119 126, 154109 (2007). [DOI] [PubMed] [Google Scholar]
  30. Heyd J. and Scuseria G. E., J. Chem. Phys. 10.1063/1.1760074 121, 1187 (2004). [DOI] [PubMed] [Google Scholar]
  31. Becke A. D., J. Chem. Phys. 10.1063/1.475007 107, 8554 (1997). [DOI] [Google Scholar]
  32. Hamprecht F. A., Cohen A. J., Tozer D. J., and Handy N. C., J. Chem. Phys. 10.1063/1.477267 109, 6264 (1998). [DOI] [Google Scholar]
  33. Boese A. D. and Handy N. C., J. Chem. Phys. 10.1063/1.1347371 114, 5497 (2001). [DOI] [Google Scholar]
  34. Handy N. C. and Cohen A. J., Mol. Phys. 10.1080/00268970010018431 99, 403 (2001). [DOI] [Google Scholar]
  35. Van Voorhis T. and Scuseria G. E., J. Chem. Phys. 10.1063/1.476577 109, 400 (1998). [DOI] [Google Scholar]
  36. Proynov E., Chermette H., and Salahub D. R., J. Chem. Phys. 10.1063/1.1321309 113, 10013 (2000). [DOI] [Google Scholar]
  37. Zhao Y. and Truhlar D. G., J. Chem. Phys. 10.1063/1.2370993 125, 194101 (2006). [DOI] [PubMed] [Google Scholar]
  38. Zhao Y., Lynch B. J., and Truhlar D. G., J. Phys. Chem. A 10.1021/jp049908s 108, 2715 (2004). [DOI] [Google Scholar]
  39. Zhao Y., Gónzales-García N., and Truhlar D. G., J. Phys. Chem. A 10.1021/jp045141s 109, 2012 (2005). [DOI] [PubMed] [Google Scholar]
  40. Lynch B. J. and Truhlar D. G., J. Phys. Chem. A 10.1021/jp035287b 107, 8996 (2003); [DOI] [Google Scholar]; Lynch B. J. and Truhlar D. G., J. Phys. Chem. A 10.1021/jp0379190108, 1460 (2004). [DOI] [Google Scholar]
  41. Lynch B. J., Zhao Y., and Truhlar D. G., J. Phys. Chem. A 109, 1643 (2005). [DOI] [PubMed] [Google Scholar]
  42. Vosko S. H., Wilk L., and Nusair M., Can. J. Phys. 58, 1200 (1980). [Google Scholar]
  43. Perdew J. P., Burke K., and Ernzerhof M., Phys. Rev. Lett. 10.1103/PhysRevLett.77.3865 77, 3865 (1996); [DOI] [PubMed] [Google Scholar]; Perdew J. P., Burke K., and Ernzerhof M., Phys. Rev. Lett. 10.1103/PhysRevLett.78.139678, 1396 (1997). [DOI] [PubMed] [Google Scholar]
  44. Hammer B., Hansen L. B., and Nørskov J. K., Phys. Rev. B 10.1103/PhysRevB.59.7413 59, 7413 (1999). [DOI] [Google Scholar]
  45. Ernzerhof M. and Scuseria G. E., J. Chem. Phys. 10.1063/1.478401 110, 5029 (1999). [DOI] [Google Scholar]
  46. Adamo C. and Barone V., J. Chem. Phys. 10.1063/1.478522 110, 6158 (1999). [DOI] [Google Scholar]
  47. Frisch M. J., Trucks G. W., Schlegel H. B.et al. , Gaussian Development Version, Revision F.02, Gaussian, Inc., Wallingford, CT, 2006.
  48. Figure 1 energies are obtained with the aug-cc-pVTZ basis and geometries from Ref. 38. High-level calculations are CCSD(T), which were found in Ref. 11 to give a transition state energy within microhartree of full CI.
  49. As expected, the post-HF PBE total energies in Fig. 1 are always above self-consistent PBE.
  50. Schipper P. R. T., Gritsenko O. V., and Baerends E. J., J. Chem. Phys. 10.1063/1.479707 111, 4056 (1999). [DOI] [Google Scholar]
  51. Gritsenko O. V., Ensing B., Schipper P. R. T., and Baerends E. J., J. Phys. Chem. A 10.1021/jp001061m 104, 8558 (2000). [DOI] [Google Scholar]
  52. Levy M., in Density Matrices and Density Functionals, edited by Erdahl R. and V. H.Smith, Jr. (D. Reidel Publishing Co., Dordecht, Holland, 1987), pp. 479–498. [Google Scholar]

Articles from The Journal of Chemical Physics are provided here courtesy of American Institute of Physics

RESOURCES