The effects of molecular diffusion in ultrafast two-dimensional nuclear magnetic resonance

Abstract

The so-called “ultrafast” nuclear magnetic resonance (NMR) methods enable the collection of multidimensional spectra within a single scan. These experiments operate by replacing traditional t₁ time increments, with a series of combined radiofrequency-irradiation∕magnetic-field-gradient manipulations that spatially encode the effects of the indirect-domain spin interactions. Barring the presence of sizable displacements, the spatial patterns thus imparted can be read out following a mixing period with the aid of oscillating acquisition gradients, leading to a train of t₂-modulated echoes carrying in their positions and phases the indirect- and the direct-domain spin interactions. Both the initial spatial encoding as well as the subsequent spatial decoding procedures underlying ultrafast NMR were designed under the assumption that spins remain static within the sample during their execution. Most often this is not the case, and motion-related effects can be expected to affect the outcome of these experiments. The present paper focuses on analyzing the effects of diffusion in ultrafast two-dimensional (2D) NMR. Toward this end both analytical and numerical formalisms are derived, capable of dealing with the nonuniform spin manipulations, macroscopic sample sizes, and microscopic displacements involved in this kind of sequences. After experimentally validating the correctness of these formalisms these were used to analyze the effects of diffusion for a variety of cases, including ultrafast experiments on both rapidly and slowly diffusing molecules. A series of prototypical schemes were considered including discrete and continuous encoding modes, constant- and real-time manipulations, homo- and heteronuclear acquisitions, and single versus multiple quantum modalities. The effects of molecular diffusion were also compared against typical relaxation-driven losses as they happen in these various prototypical situations; from all these situations, general guidelines for choosing the optimal ultrafast 2D NMR scheme for a particular sample and condition could be deduced.

INTRODUCTION

Two-dimensional nuclear magnetic resonance (2D NMR) plays an essential role in contemporary elucidations of molecular structure and dynamics.^{1, 2} 2D NMR is based on the classic Jeener–Ernst scheme,^{2, 3, 4}

$$\text{preparation}-\text{evolution}\left(t_1\right)-\text{mixing}-\text{acquisition}\left(t_2\right),$$

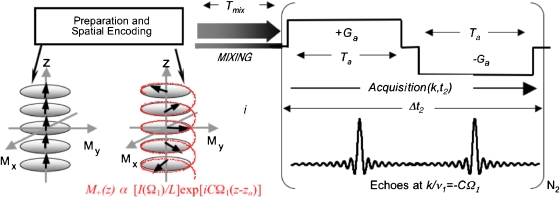
affording a 2D time-domain signal S(t₁,t₂) by incrementation of an indirect-domain evolution parameter followed by digitization as a function of a direct-domain acquisition time. Built into this NMR scheme is a need for collecting multiple t₁-incremented scans, regardless of sensitivity considerations. To alleviate this constraint a number of proposals have been made during the years, geared at reducing the number of acquisitions required to complete a 2D NMR experiment.^{5, 6} Included among these proposals is an “ultrafast” alternative, capable of completing multidimensional NMR acquisitions within a single transient.^{7, 8} Lying at the core of these experiments is a departure from traditional time-domain indirect-domain encoding schemes and their replacement by a spatial encoding and subsequent decoding of the indirect-domain interactions. A generic solution-state ultrafast 2D NMR implementation is illustrated in Fig. 1; spins are allowed here to impart their indirect-domain evolution effects along a particular sample direction (e.g., the z axis), originating site-specific patterns of spin magnetization of the form

$$M_{+}\left(z\right)\propto [I\left({\Omega }_1\right)∕L]\exp \left[iC{\Omega }_1(z-z_0)\right].$$ (1)

Ω₁ is here the frequency whose I(Ω₁) spectrum one is attempting to measure, and $C\propto t_1^{\max }∕L$ is a controllable parameter depending on the overall indirect-domain encoding time $t_1^{\max }$ and the sample length L. Following a conventional mixing period T_mix that preserves this spatial pattern, the indirect-domain frequencies that acted on each site can be revealed by subjecting spins to an additional acquisition gradient G_a. Defining an acquisition wavenumber $k={\gamma }_a{\int }_0^t{G}_a\left(t^{\prime }\right)d{t}^{\prime }$ and assuming that G_a acts along the same direction as used to impart the Ω₁-driven winding of the spin coherences, results in a signal

$$S\left(k\right)\approx [I\left({\Omega }_1\right)∕L]{\int }_L\exp \left[iC{\Omega }_1(z-z_0)\right]\exp \left[ikz\right]dz\approx I\left({\Omega }_1\right)\exp [-iC{\Omega }_1{z}_0]\delta [C{\Omega }_1+k],$$ (2)

which reflects, via a series of echoes positioned atk=−CΩ₁, the I(Ω₁) spectrum that is being sought. Having translated in such manner the indirect-domain encoding process into a gradient-driven readout opens in turn the opportunity to extract full 2D NMR spectra within a single scan. Indeed the time T_a over which the G_a readout gradient needs to be applied in order to provide the indirect-domain information is fairly short; k_max=γ_aG_aT_a needs to equate the maximum spectral window _SW1to be explored scaled by the C coefficient, leading to typical times $T_a\approx t_1^{\max }{\mathrm{SW}}_1∕{\gamma }_a{G}_{a}L$ on the order of 10²–10³ μs. The indirect-domain readout can therefore be done and undone numerous times over the course of the data acquisition by oscillating G_a, leading to a mixed frequency∕time-domain S(k∕ν₁,t₂) interferogram. From here, the full I(Ω₁,Ω₂) 2D NMR spectrum being sought can be retrieved by one-dimensional (1D) Fourier analysis versus t₂.

Figure 1.

Schematic description of ultrafast 2D NMR experiments. Field gradients are used to create windings of magnetizations based on the indirect-domain evolution frequencies (left); these are preserved as either phase or amplitude modulations during the mixing process (center), and finally read out by a train of oscillating acquisition gradients creating site-specific Ω₁-dependent echoes modulated as a function of t₂ (right). All these spatially dependent patterns and manipulations are susceptible to influence by motions, particularly by the unavoidable effects of the random molecular diffusion considered in this study.

It follows from this summary that a key component in the implementation of single-scan 2D NMR spectroscopy lies in assuming that the z position of every spin has stayed constant throughout the course of the full experiment: From the beginning of the encoding, through the mixing process, and until concluding the acquisition. Otherwise, should this stop being the case, constructive interference processes like the one embodied by Eq. 2 will fail to materialize and signal losses or other forms of peak distortions would follow. So far all the pulse sequence derivations and all the different proposals that have been made for carrying out ultrafast NMR’s spatial encoding and its subsequent decoding,^{9, 10, 11, 12, 13, 14, 15} were put forward under the assumption that the spins’ positions did indeed remain fixed throughout the various manipulations. This proved a reliable approximation, yet ignoring the effects that motions could have—and, in particular, the Brownian molecular diffusion that is ubiquitous in liquids—prevents one from making a full description of these experiments. Therefore, unless molecular diffusion is fully accounted for and compared vis-à-vis other potential sources of signal losses such as T₂ transverse relaxation, the unambiguous prediction of which gradient-based strategy is best suited to carry out a particular kind of single-scan 2D NMR acquisition, may not be possible. Accordingly, this paper seeks to provide a quantitative analysis of the effects brought about by random diffusion on ultrafast 2D NMR. To do so, and given the numerous different schemes that have been proposed for carrying out ultrafast 2D NMR and the complex, spatially dependent spin magnetization patterns that the combined radiofrequency (rf), gradient, and chemical shift effects impose through the course of these schemes, we decided to begin by modifying the usual diffusion-based NMR analysis so as to fit into it the peculiar nature of these kinds of experiments. The following paragraph presents a summary of this derivation, which results in an analytical framework capable of examining the impact of diffusion on arbitrary ultrafast 2D NMR sequences. With this theory at hand we then chose to highlight the effects of diffusion for three different, prototypical ultrafast 2D NMR schemes: A discrete approach relying on multiple gradient oscillations during the encoding and decoding processes,⁹ a continuous real-time scheme imparting an amplitude modulation of the spin coherences via a bipolar ±G_e gradient oscillation,¹¹ and a constant-time phase-modulated scheme employing a pair of adiabatic π sweeps in conjunction with a ±G_e oscillation.¹⁰ These analytical predictions are validated with both experiments and numerical simulations in Sec. 3; Sec. 4 further exploits these analytical derivations with a comprehensive evaluation of diffusion-induced effects on a variety of scenarios, including small- and macromolecular 2D experiments as well as homo- and heteronuclear 2D correlations. Finally, given what we believe is its novel ability to compute microscopic diffusion effects over macroscopically heterogeneous samples and length scales, an Appendix is also devoted to describing a new numerical algorithm derived for simulating diffusion in these kinds of experiments.

ANALYTICAL DESCRIPTION OF DIFFUSION EFFECTS IN SINGLE-SCAN 2D NMR

Overall theoretical framework

This treatment will focus on spins undergoing random molecular diffusion, while subject to the effects of time-, space-, and frequency-dependent manipulations. To maintain the problem within an analytical setting while giving it sufficient generality to treat all these variables, we chose to present it while relying on the Bloch equations; extensions to more complex situations involving multispin coherences or multiple-axis gradients can be made in a relatively straightforward manner. The differential rotating-frame equations arising within this semiclassical framework are well known;^{16, 17, 18} for a site’s transverse magnetization these are

$$\frac{\partial }{\partial t}{M}_{+}(t,z)=-i[{\Omega }_1+\gamma G\left(t\right)z]M_{+}(t,z)-\frac{M_{+}(t,z)}{T_2}+D\frac{{\partial }^2}{\partial z^2}{M}_{+}(t,z).$$ (3)

This expression includes the various definitions introduced in the preceding section, as well as Torrey’s diffusion term governed by the D coefficient. In the absence ofthis term the fate of a magnetization is simplyM₊(t,z)=M₀ exp[−iϕ(t,z)]exp[−t∕T₂], with the dynamic evolution phase given by the integral over the acting frequencies,

$$\varphi (t,z)={\int }_0^t[{\Omega }_1+\gamma G\left(t^{\prime }\right)z]d{t}^{\prime }.$$ (4)

In the presence of diffusion within a time-dependent linear field gradient γG(t)z, Karlicek and Lowe showed that this solution needs to be modified into¹⁹

$$M_{+}(t,z)=M_0\exp [-i\varphi (t,z)]\exp (-\frac{t}{T_2})A\left(t\right),$$ (5)

with

$$A\left(t\right)=\exp [-D{\int }_0^t{K}^2\left(t^{\prime }\right)d{t}^{\prime }]$$ (6)

an attenuating function given by a wavenumber $K\left(t^{\prime }\right)={\int }_0^{t^{\prime }}\gamma G\left(t^{″}\right)d{t}^{″}$.

The actual derivation of this wavenumber follows from having to track the changes arising in the resonance frequencies of the spins, as they undergo random diffusion. The treatment put forward by Karlicek and Lowe called for taking a first spatial derivative of the frequency Ω₁+γG(t)z that left solely γG(t); hence the simple form taken by K(t). In the more generic scenario of a uniform sample being subject to a nonlinear, time-dependent field B(t,z), Loening et al. derived an extended form for the attenuation function that is similar to Eq. 6 but with the wavenumber now given by $K(t^{\prime },z)=\gamma {\int }_0^{t^{\prime }}[\partial B(t^{″},z)∕\partial z]d{t}^{″}$.²⁰ For the case of ultrafast experiments like the ones to be considered here, one has to account for an even more general scenario whereby, unlike in hitherto proposed diffusion experiments, spins are no longer treated in a homogeneous fashion. Instead spins now become a subject to time- and frequency- (i.e., space-) dependent manipulations, which make the effects of diffusion heterogeneous throughout the sample. To handle this extra complexity we notice that the K wavenumbers in the above-mentioned treatments were meant to reflect time integrals of the decay brought about by local spatial variations in the spins’ frequencies; equivalently, such effects could be described by the spatial derivatives ∂ϕ(t,z)∕∂z of dynamic evolution phases like the one introduced in Eq. 4. Consequently, and considering the proven convenience of describing the ultrafast experiments based on the phase variations experienced by spins in proximity to arbitrary positions z₀,⁸ we approach the diffusion problem by introducing an effective K_local wavenumber describing the local phase variability experienced by spins under these manipulations as

$$\varphi (t,z_0+\delta z)=\varphi (t,z_0)+\frac{d\varphi (t,z_0)}{dz}\delta z+O\left(\delta z^2\right)\approx \varphi (t,z_0)+K_{\text{local}}(t,z_0)\delta z.$$ (7)

The ensuing diffusion-induced decay will then, up to first order, be independent of the uniform local phase and be solely given by K_local. With this modification a full derivation based on the arguments that lead to Eq. 6 results in a new attenuating function,

$$A(t,z)=\exp [-D{\int }_0^t{K}_{\text{local}}^2(t^{\prime },z)d{t}^{\prime }]=\exp [-D{\int }_0^t{\left(\frac{d\varphi (t^{\prime },z)}{dz}\right)}^{2}d{t}^{\prime }].$$ (8)

We find this generic expression useful, as it enables one to analyze the diffusion effects expected for arbitrary ultrafast 2D schemes by a simple operation on the corresponding ϕ(t,z) evolution phase functions. The following paragraphs exploit this to derive the diffusion attenuation thus expected from three prototypical encoding schemes: A discrete real-time approach using multiple fast gradient oscillations over the t₁ period, a continuous real-time (amplitude-modulated) approach based on the application of two identical π∕2 chirped pulses, and a constant-time (phase-modulated) experiment involving a hard excitation followed by two identical π-swept pulses. The effects expected from diffusion upon applying a ±G_a oscillating gradient waveform over the course of the t₂ acquisition are also presented.

Rapid oscillating gradients: Diffusion effects in the discrete real-time encoding and square-wave decoding processes

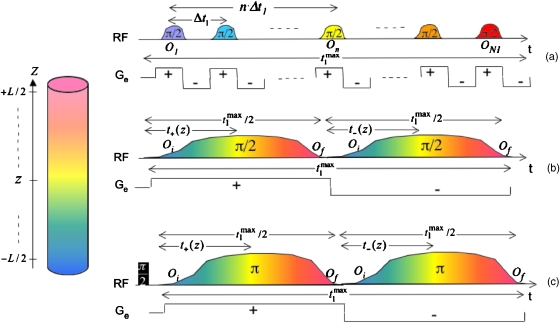
We begin by considering the effects of diffusion on two ultrafast-related processes that employ trains of rapidly oscillating gradients, and which arise within two complementary frameworks. One of these involves imparting an Ω₁-derived spatial encoding of the shift interactions by a train of soft rf pulses applied in conjunction with a synchronous oscillating gradient waveform;⁹ the other involves a periodic decoding of the indirect-domain spectrum as a function of t₂ by means of an oscillating square-wave gradient, corresponding to the G_a-related portion of Fig. 1. The encoding process relies on applying a ±G_e square-wave gradient waveform of period Δt₁, together with a frequency-shifted rf pulse train triggering the indirect-domain time evolution of N₁ independent slices throughout the initial portion of each oscillation [Fig. 2a]. Assuming for simplicity a magnetization model based on the linear approximation^{2, 18} and an instantaneous excitation of each voxel at the instant of the corresponding rf pulse’s action, leads to time- and space-dependent phase functions

$$\varphi (t,z=z_0+n\Delta z+\delta z)=\{\begin{array}{l}0,0⩽t⩽n\Delta t_1\\ {\int }_{n\Delta t_1}^t[{\Omega }_1+{\gamma }_e{G}_e\left(t^{\prime }\right)z]d{t}^{\prime },& n\Delta t_1⩽t⩽N_1\Delta t_1.\end{array}\phantom{\}}$$ (9)

Here n, Δz, and δz are each slice’s index, spacing, and local coordinates, respectively, z₀ is the position of the first slice to be excited, and all positions are dictated by the gradient G_e and offset values {O_i}_1⩽i⩽N1 used to impart the excitation. Substituting this phase expression into Eq. 8 yields the amplitude attenuation affecting each slice at the conclusion of the spatial encoding due to the effects of diffusion,

$$A(t=N_1\Delta t_1,z_n)=\exp [-{\gamma }_e^{2}D{\int }_{n\Delta t_1}^{N_1\Delta t_1}{\left({\int }_{n\Delta t_1}^{t^{\prime }}{G}_e\left(t^{″}\right)d{t}^{″}\right)}^{2}d{t}^{\prime }].$$ (10)

This expression can be further simplified thanks to the gradients’ bipolar rectangular waveform. The diffusion-related contribution experienced during each oscillation cycle Δt₁ by every spin packet that has gone through an excitation will therefore be constant, and equal to

$$\alpha =\exp \{-D{\int }_0^{\Delta t_1}{[k_0+{\gamma }_e{G}_e{t}^{\prime }U(\frac{\Delta t_1}{2}-t)+{\gamma }_e{G}_e(\Delta t_1-t)U(t-\frac{\Delta t_1}{2})]}^{2}d{t}^{\prime }\}=\exp \{-2D[\frac{\Delta t_1}{2}{k}_0^2+{\gamma }_e{G}_e\frac{\Delta t_1^2}{4}{k}_0+\frac{{\gamma }_e^2{G}_e^2\Delta t_1^3}{24}]\}.$$ (11)

Here U is a step function that accounts for the sign reversal undergone by G_e a time Δt₁∕2 within the bipolar cycle, and k₀ is the spin-packet’s wavenumber at the beginning of the cycle. This wavenumber will be different from zero owing to the incomplete dephasing∕rephasing process that each slice experiences during its first excitation cycle. According to the linear approximation k₀’s value will be −γ_eG_eΔt₁∕4, leading to $\alpha =\exp \{-{\gamma }_e^{2}D(G_e^2\Delta t_1{}^3∕48)\}$. With this attenuation factor at hand, one can derive the full attenuation experienced by spins in the z_n slice at the conclusion of the indirect evolution time $t_1^{\max }=N_1\Delta t_1$ as

$$A(t=t_1^{\max },z_n)=\exp [-{\gamma }_e^{2}D\frac{G_e^2\Delta t_1^3}{96}]{\alpha }^{N_1-n}.$$ (12)

Figure 2.

Description of the combined gradient∕rf manipulations underlying the indirect-domain spatial encoding strategies considered in this work. (a) Discrete real-time scheme involving a train of π∕2 pulses applied in synchrony with an oscillating ±G_e waveform. (b) Continuous real-time scheme whereby chirped excitation and storage π∕2 pulses are applied in the presence of a single bipolar ±G_e oscillation. (c) Idem but based on a phase-modulated, constant-time spin evolution imparted by a pair of chirped π pulses. Spatiotemporal encoding efficiencies for the different sequences are C=N₁Δt₁∕L, $t_1^{\max }∕L$, and $2t_1^{\max }∕L$, respectively; the timings n Δt₁, t₊(z), and t₋(z) refer to the fate of the lightest (yellow) z coordinate.

Following this initial encoding event, additional windings may be imposed on the spins as a result of either chemical shift evolution effects—which are not, however, significant within each of the excited discrete elements because of the uniformity of these voxels’ excitation—and∕or due to the actions of a purging gradient. These effects are usually related to a shifting of the indirect-domain spectrum and∕or to coherence pathway selection processes, and therefore the spacing of their winding is on the order of ${\mathrm{SW}}_1{t}_1^{\max }∕L$; i.e., small vis-à-vis γ_eG_eΔt₁. Still they add up to an additional wavenumber k₁, which could be associated with significant diffusion-driven losses when considered over relatively long mixing periods T_mix. We therefore follow Eq. 6 and add them in this treatment as an additional, spatially homogeneous diffusion-related attenuation term exp[−Dk₁²T_mix]. Finally, during the acquisition period, an additional diffusion-related contribution may arise due to the presence of the oscillatory readout gradient G_a acting throughout t₂. Arguments analogous to the ones just used to derive Eq. 11 can be employed to derive the gradient-induced decay brought about by this second acquisition oscillation. Relying on the notation used in Fig. 1 and assuming that this time the acquisition commences with a k₀=0, this t₂-related attenuation factor becomes

$$\beta =\exp \{-2D\frac{{\gamma }_1^2{G}_a^2{T}_a^3}{3}\}.$$ (13)

With this expression at hand, one can then describe the overall effects incurred by diffusion on a particular slice z_n at the center of the mth bipolar acquisition gradient echo as

$$A(t=t_1^{\max }+T_{\text{mix}}+m\Delta t_2,z_n)=\exp [-D(\frac{{\gamma }_e^2{G}_e^2\Delta t_1^3}{96}+k_1^2{T}_{\text{mix}})]{\alpha }^{N_1-n}{\beta }^m.$$ (14)

Notice that this function should be further weighted by the appropriate relaxation-driven losses and then integrated over the full sample length L, in order to give the ensemble description of the overall signal attenuation. The former procedure involves additional multiplication by simple factors such as [exp(−Δt₁∕T_2,e)]^N₁−n+1, exp(−T_mix∕T_relax), or[exp(−Δt₂∕T_2,a)]^m, while the latter involves a simple summation. All of these factors are further dealt with below within the framework of a comprehensive comparison among the different ultrafast encoding schemes.

Diffusion in continuous, real-time amplitude-modulated encoding sequences

A continuous, real-time spatial encoding with amplitude modulation of the t₁ evolution can also be carried out by sweeping an identical pair of frequency-chirped π∕2 pulses, acting within the positive and negative lobes of a ±G_e bipolar gradient waveform.¹¹ The first of these pulses will progressively excite magnetizations as a function of their z position, while the second pulse does a “first in–last out” storage of the evolved coherences. Overall this leads, by the time when the mixing period begins, to a shift-induced but gradient-free winding of amplitude-modulated magnetizations [Fig. 2b]. The mechanism of action of these swept-rf∕bipolar gradient combinations has been discussed elsewhere in detail,^{8, 11} and hence, we only focus here on diffusion-specific considerations of their effects. The evolution imparted by the first linearly swept π∕2 pulse on the spins can be expressed by the time- and space-dependent excitation phase,

$${\varphi }_{\mathrm{exc}}(t,z)=\{\begin{array}{l}0,0⩽t⩽t_{+}\left(z\right)\\ {\phi }_{\mathrm{rf}}\left[t_{+}\left(z\right)\right]+({\Omega }_1+{\gamma }_e{G}_{e}z)[t-t_{+}\left(z\right)],& t_{+}\left(z\right)⩽t⩽t_1^{\max }∕2.& \end{array}\phantom{\}}$$ (15)

This expression follows from the assumption that an instantaneous spin excitation happens at a time t₊(z), corresponding to the moment when the rf offset O(t) matches the spins’ resonance frequency Ω₁+γ_eG_ez (see Refs. ^{21, 22} for further details). In addition to an explicit z-dependence, ϕ_exc also depends on the φ_rf(t) phase accumulated by the transmitter up to this time, which acts as reference for the excitation, and on the overall time $t_1^{\max }∕2$ taken by the sweep to excite the full sample length L. With these last two parameters given ϕ_exc(t,z) can be deduced at arbitrary times; assuming, for instance, a sweep rate R extending over a symmetric range O_i=−γ_eG_eL∕2→O_f=+γ_eG_eL∕2 and lasting a time $t_1^{\max }∕2$, it follows that

$$t_{+}\left(z\right)=\frac{{\Omega }_1+{\gamma }_e{G}_{e}z-O_i}{R},$$ (16)

the accumulated transmitter phase is then

$${\phi }_{\mathrm{rf}}\left(t\right)={\int }_0^{t}O\left(t^{\prime }\right)d{t}^{\prime }=O_{i}t+\frac{1}{2}R{t}^2,$$ (17)

and the local K wavenumber during the course of the excitation becomes

$$K_{\text{local}}(t,z)=\frac{d{\varphi }_{\mathrm{exc}}(t,z)}{dz}=\{\begin{array}{l}0,0⩽t⩽t_{+}\left(z\right)\\ {\gamma }_e{G}_e[t-t_{+}\left(z\right)],& t_{+}\left(z\right)⩽t⩽t_1^{\max }∕2.\end{array}\phantom{\}}$$ (18)

Following this first excitation pulse, diffusion will also act during the second storage period of the encoding. The rf sweep here involved is identical to that of the first chirp, except for the fact that it is applied under the presence of a −G_e gradient. It will therefore act on the spins at a z-dependent instant

$$t_{-}\left(z\right)=\frac{{\Omega }_1-{\gamma }_e{G}_{e}z-O_i}{R}$$ (19)

after its initiation, and the overall phase accumulated over its course will be

$${\varphi }_{\text{store}}(\frac{t_1^{\max }}{2}+t,z)=\{\begin{array}{l}{\varphi }_{\mathrm{exc}}(\frac{t_1^{\max }}{2},z)+({\Omega }_1-{\gamma }_e{G}_{e}z)t,0⩽t⩽t_{-}\left(z\right)\\ {\phi }_{\mathrm{rf}}\left[t_{-}\left(z\right)\right]-({\Omega }_1-{\gamma }_e{G}_{e}z)[t-t_{-}\left(z\right)]-{\varphi }_{\mathrm{exc}}(\frac{t_1^{\max }}{2},z),& t_{-}\left(z\right)<t⩽t_1^{\max }∕2.\end{array}\phantom{\}}$$ (20)

Notice that since this pulse involves a storage process it yields, at $t=t_1^{\max }∕2$, a magnetization pattern that is amplitude modulated along the z-axis of the Bloch sphere according to the cosine of ${\varphi }_{\text{store}}(t_1^{\max },z)$. Differentiating Eq. 20 with respect to z and using the various definitions given above yields the local wavenumber affecting spins during the course of the storage process,

$$K_{\text{local}}(\frac{t_1^{\max }}{2}+t,z)=\frac{d{\varphi }_{\text{store}}(\frac{t_1^{\max }}{2}+t,z)}{dz}=\{\begin{array}{ll}-{\gamma }_e{G}_e[t-\frac{t_1^{\max }}{4}+\frac{{\gamma }_e{G}_{e}z+{\Omega }_1}{R}],& 0⩽t⩽t_{-}\left(z\right)\\ \frac{2{\gamma }_e{G}_e{\Omega }_1}{R},t_{-}\left(z\right)⩽t⩽t_1^{\max }∕2.\end{array}\phantom{\}}$$ (21)

Substituting Eqs. 18, 21 into Eq. 8 provides the full argument of the exponential attenuation for these kind of experiments,

$$D{\int }_0^{t_1^{\max }}{K}_{\text{local}}^2\left(t^{\prime }\right)d{t}^{\prime }=\frac{D{\gamma }_e^2{G}_e^2}{3}\{{(\frac{t_1^{\max }}{4}-\frac{{\gamma }_e{G}_{e}z+{\Omega }_1}{R})}^3+{(\frac{2{\Omega }_1}{R}-\frac{t_1^{\max }}{4})}^3+{(\frac{t_1^{\max }}{4}-\frac{{\gamma }_e{G}_{e}z+{\Omega }_1}{R})}^3+3{\left(\frac{2{\Omega }_1}{R}\right)}^2(\frac{t_1^{\max }}{2}+\frac{{\gamma }_e{G}_{e}z-{\Omega }_1}{R})\}.$$ (22)

Recalling in turn that $R=2{\gamma }_e{G}_{e}L∕t_1^{\max }$ and that in typical ultrafast experiments the indirect-domain spectral range of Ω₁’s is small compared to the chirp’s spectral width γ_eG_eL allows one to further simplify this expression into

$$D{\int }_0^{t_1^{\max }}{K}_{\text{local}}^2\left(t^{\prime }\right)d{t}^{\prime }\approx \frac{D{\gamma }_e^2{G}_e^2{\left(t_1^{\max }\right)}^3}{12}{(\frac{1}{2}-\frac{z}{L})}^3.$$ (23)

This expression still does not account for the potential contribution of purge gradients that may have been imparted during the indirect-domain evolution, or for the winding effects of the chemical shift Ω₁. As already noted for the discrete encoding case these effects may not be significant from a diffusional standpoint vis-à-vis G_e-derived losses during the course of t₁, but they may certainly affect intensities following a long mixing period $T_{\text{mix}}⪢t_1^{\max }$. Describing all purge gradient windings by a common wavenumber k₁ yields the full spatially dependent degradation of the magnetization incurred by diffusion effects up to the acquisition stage,

$$A\left(z\right)=\exp \{-D[\frac{{\gamma }_e^2{G}_e^2{\left(t_1^{\max }\right)}^3}{12}{(\frac{1}{2}-\frac{z}{L})}^3+{(k_1+\frac{2{\gamma }_e{G}_e{\Omega }_1}{R})}^2{T}_{\text{mix}}]\}.$$ (24)

During the course of the acquisition, the presence of a ±G_a oscillating gradient train will lead to additional losses; one can use arguments analogous to those employed in the discrete scheme to derive the decays felt by spins at position z upon executing the mth signal acquisition cycle as

$$A(t=t_1^{\max }+T_{\text{mix}}+m\Delta t_2,z)=\exp \{-D[\frac{{\gamma }_e^2{G}_e^2{\left(t_1^{\max }\right)}^3}{12}{(\frac{1}{2}-\frac{z}{L})}^3+{(k_1+\frac{2{\gamma }_e{G}_e{\Omega }_1}{R})}^2{T}_{\text{mix}}]\}{\beta }^m,$$ (25)

where once again $\beta =\exp \{-2D(\gamma _a{}^2{G}_a^2{T}_a^3∕3)\}$. Notice that just as its discrete analog Eq. 14, this expression still does not include the potential signal losses arising from T₁ and T₂ relaxation during the periods of longitudinal storage or transverse evolution. For the mixing and acquisition periods these will be as in the discrete case; for the indirect domain we remark for completion that since the time spent by the spins in the transverse plane will be given by the spatially dependent function

$$t_{\text{evolution}}\left(z\right)=\frac{t_1^{\max }}{2}-t_{+}\left(z\right)+t_{-}\left(z\right)=\frac{t_1^{\max }}{2}-2\frac{{\gamma }_e{G}_{e}z}{R},$$ (26)

an additional z-dependent attenuation factor of the form $\exp [-(t_1^{\max }∕T_{2,e})(z∕L-1∕2)]$ will be incurred.

Diffusion effects under a continuous, constant-time phase-modulated encoding

Another class of continuous spatial encoding scheme whose diffusion effects deserve addressing concerns the use of constant-time sequences. In parallel to the continuous real-time scheme just described this method also imparts its spatial encoding by employing two identical chirped pulses acting in unison with a bipolar gradient.¹⁰ The amplitudes of these pulses, however, are now tuned so as to invert rather than excite∕store the transverse spin packets, which will have to be created at the beginning of the experiment by a hard π∕2 rotation. Using the definitions in Fig. 2c and analogous conventions as in Eqs. 15, 20, one can express the phase accumulated by the spins during the first gradient period as⁸

$${\varphi }_{\mathrm{enc}}^{+}(t,z)=\{\begin{array}{l}({\Omega }_1+{\gamma }_e{G}_{e}z)t,0⩽t⩽t_{+}\left(z\right)\\ {\phi }_{\mathrm{rf}}\left[t_{+}\left(z\right)\right]+[{\phi }_{\mathrm{rf}}\left[t_{+}\left(z\right)\right]-{\varphi }_{\mathrm{enc}}^{+}(t_{+}\left(z\right),z)]+({\Omega }_1+{\gamma }_e{G}_{e}z)(t-t_{+}\left(z\right)),& t_{+}\left(z\right)⩽t⩽t_1^{\max }∕2,\end{array}\phantom{\}}$$ (27)

while following the second negative gradient, the accumulated phase becomes

$${\varphi }_{\mathrm{enc}}^{-}(t,z)=\{\begin{array}{l}{\varphi }_{\mathrm{enc}}^{+}(t^{\left(\pi \right)},z)+({\Omega }_1-{\gamma }_e{G}_{e}z)t,0⩽t⩽t_{-}\left(z\right)\\ {\phi }_{\mathrm{rf}}\left[t_{-}\left(z\right)\right]+[{\phi }_{\mathrm{rf}}\left[t_{-}\left(z\right)\right]-{\varphi }_{\mathrm{enc}}^{-}(t_{-}\left(z\right),z)]+({\Omega }_1-{\gamma }_e{G}_{e}z)(t-t_{-}\left(z\right)),& t_{-}\left(z\right)⩽t⩽t_1^{\max }∕2.\end{array}\phantom{\}}$$ (28)

The various definitions appearing in these expressions, including the times t₊(z) and t₋(z) when the first and second rf sweeps reach the resonance frequency of spin packets at a particular z coordinate (assuming each of these sweeps begins at its own time zero), as well as the transmitter phases φ_rf taken by the B₁ field at the time of these π-flips, are similar to those given in Eqs. 16, 17, 19. Taking then the spatial derivatives of these phases yields the relevant K wavenumbers,

$$K_{\text{local}}(t,z)=\{\begin{array}{l}\gamma G_{e}t,0⩽t⩽t_{+}\left(z\right)\\ \gamma G_e[t-2t_{+}\left(z\right)],& t_{+}\left(z\right)⩽t⩽t_1^{\max }∕2\end{array}\phantom{\}}$$ (29)

and

$$K_{\text{local}}(\frac{t_1^{\max }}{2}+t,z)=\{\begin{array}{l}-\gamma G_e[t+2t_{+}\left(z\right)-\frac{t_1^{\max }}{2}],0⩽t⩽t_{-}\left(z\right)\\ -\gamma G_e[t-2(t_{+}\left(z\right)+t_{-}\left(z\right))+\frac{t_1^{\max }}{2}],& t_{-}\left(z\right)⩽t⩽t_1^{\max }∕2.\end{array}\phantom{\}}$$ (30)

As before, substituting Eqs. 29, 30 into Eq. 8 provides the full argument of the exponential attenuation function,

$$D{\int }_0^{t_1^{\max }}{K}_{\text{local}}^2\left(t^{\prime }\right)d{t}^{\prime }=\frac{D{\gamma }_e^2{G_e}^2{\left(t_1^{\max }\right)}^3}{2}\{{(-\frac{z}{L})}^3+(\frac{1}{2}-\frac{2{\Omega }_1}{{\gamma }_e{G}_{e}L}){\left(\frac{z}{L}\right)}^2+[\frac{1}{4}+\frac{2{\Omega }_1}{{\gamma }_e{G}_{e}L}+{\left(\frac{{\Omega }_1}{{\gamma }_e{G}_{e}L}\right)}^2]\left(\frac{z}{L}\right)+\frac{{\Omega }_1}{2{\gamma }_e{G}_{e}L}+\frac{5}{2}{\left(\frac{{\Omega }_1}{{\gamma }_e{G}_{e}L}\right)}^2-2{\left(\frac{{\Omega }_1}{{\gamma }_e{G}_{e}L}\right)}^3+\frac{1}{24}\}.$$ (31)

Assuming once again that γ_eG_eL⪢Ω₁, this expression yields a simplified form

$$D{\int }_0^{t_1^{\max }}{K}_{\text{local}}^2\left(t^{\prime }\right)d{t}^{\prime }=\frac{D{\gamma }_e^2{G_e}^2{\left(t_1^{\max }\right)}^3}{2}[{(-\frac{z}{L})}^3+\frac{1}{2}{\left(\frac{z}{L}\right)}^2+\frac{1}{4}\left(\frac{z}{L}\right)+\frac{1}{24}].$$ (32)

When considering as above that potential purging-gradient∕shift effects may be active during a relatively long T_mix mixing period, and when factoring in the losses that will be incurred by the presence of the ±G_a oscillating acquisition gradient train, one obtains the analog of Eq. 25 but for this constant-time scheme:

$$A(t=t_1^{\max }+T_{\text{mix}}+m\Delta t_2,z)=\exp \{-D[\frac{{\gamma }_e^2{G}_e^2{\left(t_1^{\max }\right)}^3}{2}[{(-\frac{z}{L})}^3+\frac{1}{2}{\left(\frac{z}{L}\right)}^2+\frac{1}{4}\left(\frac{z}{L}\right)+\frac{1}{24}]+{(k_1+\frac{4{\gamma }_e{G}_e{\Omega }_1}{R})}^2{T}_{\text{mix}}]\}{\beta }^m,$$ (33)

with $\beta =\exp \{-2D(\gamma _a{}^2{G}_a^2{T}_a^3∕3)\}$. This expression accounts for the larger spatiotemporal C efficiency active in this case, but still ignores potential losses arising from T₁ and T₂ relaxations. For the mixing and direct acquisition domains these will be as before; for the indirect domain and unlike what was seen in the previous cases these will now be z-independent, owing to the fact that all spin packets spend the entire $t_1^{\max }$ encoding period precessing in the transverse plane. Therefore, an additional spatially independent attenuation factor $\exp (-t_1^{\max }∕T_{2,e})$ needs to be considered, at the time of computing the overall signal intensity losses.

EXPERIMENTAL AND NUMERICAL VERIFICATIONS

Prior to exploiting the theoretical models just derived to judge diffusion penalties under various prototypical ultrafast 2D NMR conditions, these derivations were subject to a number of verifications and tests. These in turn involved two complementary routes: An experimental one where confidence was sought based on a (necessarily limited) series of comparisons, and a numerical one which—like the analytical expressions above—has the flexibility to accommodate a large number of different situations as well as arbitrary diffusion and spin-relaxation parameters.

To validate experimentally the theoretically derived attenuation profiles, multiple measurements were conducted on a solution of 0.01% H₂O∕D₂O using a Varian iNova^® 500 MHz NMR spectrometer. These measurements were carried out at room temperature using a conventional 5 mm gradient-equipped probe possessing a sample length L≈1.80 cm, conditions for which a literature-derived D=1.9×10⁻⁹ m²∕s self-diffusion coefficient could be assumed in the data analysis.²³ In order to quantitatively evaluate the models’ correctness, and keeping in mind the equal G_a-derived effects that all sequences predict for the signals, experimental data were analyzed by focusing on the results afforded by the first m=1 echo of an ultrafast 2D acquisition. Given the different z-dependencies predicted by Eqs. 14, 25, 33 for the diffusion effects—as well as relaxation losses that as mentioned are also distinctive for different encoding schemes—data were analyzed by subjecting the signals to a Fourier analysis that provided the spatial distribution of their decays. The local attenuations displayed by the resulting 1D profiles were further normalized by referencing them versus 1D images acquired on simple pulsed gradient-echo sequences, devoid from spatial encoding manipulations.

As a complement to these experimental verifications, further backup for the analytical derivations was sought in numerical simulations of full ultrafast experiments that simultaneously consider the effects of coherent manipulations, of diffusion, and of relaxation. Several methods have been proposed for calculating diffusion effects in NMR,^{24, 25, 26} including a convolution algorithm which we adopted as basis for the calculations. An attractive starting point of such algorithm is its reliance on a discretization of both the space and time domains, a feature already built-in in previous ultrafast simulations,^{9, 21, 22} whereby spin packets placed at a series of equispaced z positions throughout the sample were propagated under the effects of piecewise constant Bloch equations with varying rf- and gradient-related coefficients. A problem, however, arises upon introducing random Brownian motions into such algorithms: Given the minute distances $\delta z\approx \sqrt{2D\Delta t}$ over which typical diffusion coefficients will displace spins during the relatively short propagation times Δt that are dictated by rf and gradient manipulations, an extremely large number of microscopic elements spread over the full sample range L becomes necessary for reproducing the macroscopic spin signal. The calculation of arbitrary pulse sequences with diverse spatial and temporal features therefore becomes a highly demanding computational task, ill suited to use as a tool for systematic tests and verifications. In order to deal with this feature—which is absent in conventional calculations owing to the spatial uniformity with which the rf and gradients in standard diffusion measurements treat the spins throughout the sample’s volume—a novel algorithm was developed based on phase-continuity requirements and on the reliance on an analytical diffusion kernel for describing the effects of motion at a microscopic level. Further details on this algorithm, which allowed us to carry out calculations using spatial increments Δz exceeding by orders of magnitude the diffusion-dictated δz distances and whose operation was extensively tested before employment on these ultrafast 2D evaluations, are presented in the Appendix.

Figure 3a compares the behavior observed from a typical set of real-time modulation experiments carried out using continuous spatial encoding pulses of different durations against predictions arising from both the analytical and numerical models. For simplicity these experiments involved a very short, mixing-less storage period, and hence they are mainly meant to describe the diffusion and relaxation losses over the t₁ encoding. As expected the amplitude-modulated nature of the encoding yields maximal values of 1∕2 for the normalized profiles; also expected is the asymmetric nature of the attenuation, as both diffusion and T₂ relaxation bias the losses at one end of the sample (in this case the z>0 edge that was first excited) over the other. Relevant to our discussion is the fact that the analytical predictions follow very closely the experimental observations; this in spite of containing no adjustable parameters once the experimentally dictated gradient strengths, timings, known diffusion coefficient, and an a priori measured T₂^*=0.37 s value, are all given. Also following very closely the experimental profiles are the numerical simulations, calculated using the same predefined parameters. In fact, the sole significant deviation between the numerical∕theoretical profiles and the experimental diffusion-weighted images arises at the edges of the sample and reflects the fact that neither simulations nor derivations considered the smoothed-out profiles used as envelops of the experimental chirped rf sweeps. Complementing these amplitude-modulated tests, Fig. 3b shows a second set of experiments, this one obtained with the constant-time, phase-modulated pulse sequence approach. Once again the experimental and numerical results in this set show quantitatively similar profiles to the theoretical function derived in Sec. 2D; notice that these profiles are different in both amplitude and shape from the counterparts arising in the real-time ultrafast experiments, lacking the latter’s differential T₂z-weighting and reaching a maximum at |z|≈L∕6 rather than at one of the sample’s edges. Notice as well that by contrast to the real-time case, Fig. 3b reveals a minor systematic deviation between the analytical model and experimental results for the shorter-$t_1^{\max }$ experiment. We ascribe this to the fact that the chirped rf sweeps in these experiments are characterized by larger adiabaticity parameters,¹⁰ for which the “instantaneous” spatial and temporal locality assumptions underlying Sec. 2 are less justified. Numerical simulations on the other hand make no assumptions regarding the pulses’ localized nature, and therefore are less constrained in reproducing the experimental results.

Figure 3.

Experimental and numerical verifications of the theoretical models derived in Eqs. 25, 33 utilizing (a) a real-time and (b) a constant-time spatial encoding sequence. These experiments are extensions of the basic schemes illustrated in Figs. 2b, 2c, incorporating a number of extra purging gradients to ensure cleaner single-scan profiles. Rather than obtaining a full 2D interferogram, a single echo (i.e., the first t₂ point) was collected and Fourier analyzed to obtain the spatial profiles illustrated under each sequence. The experiments employed rf pulses sweeping from O_i=+50 toO_f=−50 kHz programmed on the basis of the Shinnar–LeRoux algorithm (Ref. ²⁷) with a finite envelop whose smoothing was not accounted for in the theoretical analyses (hence the departures of the experimental data at the sample’s edges). Further details on the numerical simulation procedure used to carry these comparisons are given in the Appendix.

COMPARING DIFFUSION AND RELAXATION LOSSES AMONG ULTRAFAST 2D SCHEMES

Having validated the theoretical derivations of Sec. 2, these were employed for evaluating the diffusion and relaxation losses expected for the typical parameters involved in 2D ultrafast experiments. The present section discusses the main features observed during such survey paying specific attention to (i) the magnitude of the diffusion-related losses, (ii) their relative effects vis-à-vis competing relaxation losses, and (iii) the optimized pulse sequence approach to be used in different instances to maximize sensitivity. While not exhaustive of all sequences or cases of relevance, we focus here on, certain representative instances including 2D homo- and heteronuclear NMR experiments, as well as experiments on both small (e.g., organic) molecules and on proteins∕biopolymers.

A common feature of the various schemes treated in Sec. 2 is their reliance on the use of an oscillatory gradient during the course of the acquisition. An idea of the impact that diffusion will have upon using this gradient waveform can be gathered from evaluating first the sensitivity losses associated with the discrete excitation scheme, which also employs oscillating gradients during the course of both its indirect- and direct-domain evolution periods. An attractive feature of beginning such comparison with this scheme stems from the fact that, given the sequence’s discreteness, it can lead to analytical expressions for both the overall diffusion- and for the relaxation-related losses. Indeed the total echo signal S observed in these cases for the mth acquisition cycle will be given by a summation of Eq. 14 over all the 1⩽n⩽N₁ excited slices,

$$S(t=t_1^{\max }+T_{\text{mix}}+m\Delta t_2)=\sum _{n=1}^{N_1}\exp [-D(\frac{{\gamma }_e^2{G}_e^2\Delta {t_1}^3}{96}+k_1^2{T}_{\text{mix}})]{\alpha }^{N_1-n}{\beta }^m=\exp [-D(\frac{{\gamma }_e^2{G}_e^2\Delta {t_1}^3}{96}+k_1^2{T}_{\text{mix}})]\frac{1-{\alpha }^{N_1}}{1-\alpha }f{\beta }^m,$$ (34)

where f is a fixed number representing the fraction of spins that has been excited within each slice Δz, as dictated by the shape chosen for doing the selective pulse excitation. We recall that β here represents the losses associated with one Δt₂=2T_a acquisition decoding cycle [Eq. 13]; the decoding acquisition conditions that define β are in turn a function of the desired 2D spectral parameters, and for the discrete excitation case they must fulfill γ_aG_aT_a=Δt₁(N₁∕L)SW₁.⁹ Taking this as well as the potential acquisition T_2,a relaxation effects into account leads to

$$\beta =\exp \{-2D\frac{{{\gamma }_a}^2{G}_a^2{T}_a^3}{3}\}\exp \{-\frac{2T_a}{T_{2,a}}\}=\exp \{-[D\frac{\mathrm{S}{\mathrm{W}}_1^2\Delta t_1^2}{3}{\left(\frac{N_1}{L}\right)}^2+\frac{1}{T_{2,a}}]\Delta t_2\}.$$ (35)

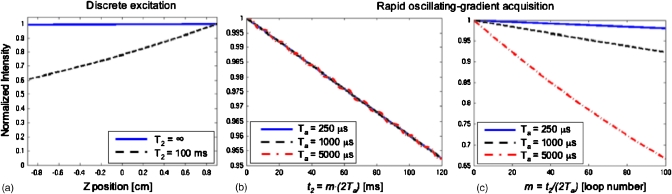
With these equations at hand we proceed to consider the most unfavorable of all diffusion-derived scenarios, involving a ¹H homonuclear experiment on a small molecule possessing a waterlike diffusion coefficient of 10⁻⁹ m²∕s. Given this low molecular weight assumption we also considered relatively long T₂’s and desired spectral width and resolutions of 2000 and 20 Hz, respectively, for each of the domains. For the discrete excitation case one also needs to recall that spectral widths and resolutions dictate the gradient amplitude and number N₁ of pulses that will be needed throughout the encoding, according to γ_eG_eL∕N₁=ΔO≈2∕Δt₁.²⁸ This leads to a relatively high gradient G_e≈52 G∕cm and a total duration $t_1^{\max }\approx 50\mathrm{ms}$, for the realization of such discrete encoding conditions. Even under such relatively demanding high-gradient, long-encoding, fast-diffusion conditions, Fig. 4a illustrates the spatial profiles that can be expected in the absence and presence of T_2,e relaxation; as adumbrated⁹ these diffusion losses remain negligible throughout the encoding period. Also worth exploring are the β-driven diffusion losses expected to arise in such cases during the acquisition period; Figs. 4b, 4c illustrate these for a relaxation-free scenario as a function of different T_a=Δt₂∕2 periods, assuming that the SW₁ spectral window (i.e., the G_aT_a product) is kept constant throughout these changes. Figure 4b demonstrates that (i) diffusion-related losses will also in this case be very small and (ii) that even if one was to choose differing T_a values, diffusion losses will remain constant when viewed as a function of the overall acquisition time t₂=mΔt₂. This follows again from Eqs. 34, 35, which predict that only when viewed as a function of the index m will modest diffusion losses show up in the long-T_a limit [Fig. 4c]. Of more significance and still covered by Eq. 14 (even if not contemplated in this particular set of calculations) may end up being in these discrete cases k₁-derived losses associated with diffusion over relatively long T_mix mixing periods.

Figure 4.

(a) Attenuation profiles predicted by Eq. 12 for the discrete encoding experiment executed on a small molecule, in the presence and absence of T₂ relaxation effects. Calculation parameters were as described in the text: SW₁=2 kHz, Δt₁=0.5 ms, N₁=100, L=18 mm, G_e=52 G∕cm, D=10⁻⁹ m²∕s. [(b) and (c)] Different renderings of the diffusion-related losses expected during the course of the acquisition, for different values of T_a=Δt₂∕2. In all cases the parameters of panel (a) were assumed; i.e., the γ_aG_aT_a product was kept constant at 55.5 cm⁻¹. Notice the very minor and identical decay arising for different T_a’s under such conditions (center); only for long T_a’s and many ±G_a gradient repetitions m do these losses become notable (right).

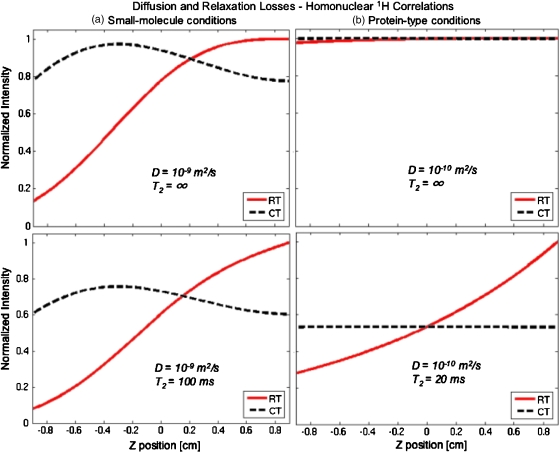
It follows that diffusion’s main influence will arise when gradients remain constant over relatively long periods of time, as happens to be the case for the continuous encoding schemes treated above. To evaluate the sensitivity of such experiments to diffusion, we focus first on small molecules and consider a mixingless homonuclear ¹H correlation experiment where D=10⁻⁹ m²∕s, T_2,e=0.1 s, and spectral width∕resolution requirements are 2000∕20 Hz, respectively. Giving the differing spatiotemporal C ratios of the real- and the constant-time encoding schemes,^{10, 11} fulfilling such resolution requirements implies that the $t_1^{\max }$ encoding durations need to be set at 25 and 12.5 ms, respectively. Unlike in the discrete encoding scheme, however, where also the G_e’s amplitudes were uniquely set by these spectroscopic requirements, both continuous encoding schemes have the freedom to set encoding gradient at more or less arbitrary amplitudes over the duration of their rf sweeps. The only constraints that we find necessary for carrying then out a proper exploitation of the full sample length and achieving a good rf pulse performance is setting the rf sweep widths used for spatial encoding large relative to the spectral spread of the shifts to be encoded; i.e., γ_eG_eL⪢SW₁. For the calculations the rf sweeps were thus given realistic bandwidths of 40 kHz, corresponding to the application of G_e=±5.2 G∕cm gradients over a 1.8 cm sample length. The profiles of the diffusion-related losses arising under such small molecule conditions in the presence and absence of T₂ relaxation effects are shown in Fig. 5a for the real- and the constant-time encoding sequences. As can be appreciated the real-time scheme shows higher diffusion-related losses vis-à-vis its constant-time counterpart, reflecting the longer $t_1^{\max }$ duration demanded by the former to achieve the same spectral resolution as the latter. Nevertheless it is also clear that under these conditions the diffusion losses are in all cases tolerable and not much larger than those arising from T₂ relaxation.

Figure 5.

Comparison between the predictions made by the real-time (RT) and the constant-time (CT) analytical models described in the text for diffusion losses, upon executing homonuclear single-scan 2D correlation on (a) small molecule (left-hand panels) and (b) macromolecular (right-hand panel) spin systems. To put these diffusion effects in perspective, relaxation-free and realistic T₂-derived effects are also compared in corresponding top and bottom panels. The real-time plots assumed the sequence in Fig. 2b with G_e=5.2 G∕cm, $t_1^{\max }=25$ and 50 ms for the large and small molecule experiments, respectively, O_i=−O_f=−20 kHz (notice the sign reversal vis-à-vis in the experiments in Fig. 3) and L=1.80 cm. The constant-time plots used the sequence in Fig. 2c with the same values except for $t_1^{\max }=12.5$ and 25 ms for the large and small molecules, experiments.

In addition to these cases the analytical formalism was used to explore biomolecular scenarios such as those expected when dealing with proteins, where diffusion can be expected to be slower, relaxation times shorter, and spectral resolution demands less stringent than in low molecular weight experiments. A representative homonuclear ¹H test might then involve D≈10⁻¹⁰ m²∕s,²⁹T₂≈20 ms, and spectral width and resolution requirements of 2000 and 40 Hz, respectively. Ultrafast-derived profiles calculated using these spectral and diffusion parameters in the presence and absence of transverse relaxation are displayed in Fig. 5b. Notice that the slower diffusive motion experienced now by the spins coupled to the shorter $t_1^{\max }$ durations required by this kind of experiments due to their limited resolution needs, results in minor diffusion-related losses–approximately 1% of the integrated signal intensity even for the more lossy real-time encoding scheme. By contrast, and owing to the shorter T₂ values, the constant-time scheme becomes more susceptible to relaxation-derived losses than its real-time encoding counterpart in spite of its more efficient spatial C-encoding value.

In addition to homonuclear protocols, ultrafast sequences have been applied within the context of heteronuclear 2D correlations involving indirect- and direct-domain evolutions of nuclei with differing Larmor frequencies. Most often sensitivity considerations suggest keeping ¹H as nucleus of observation, leaving the lower-γ species as targets for the spatial encoding. Taking, for example, a 2D ¹⁵N–¹H heteronuclear single-quantum correlation³⁰ (HSQC) as a test case, the fact that γ_e (i.e., γ_N) will be smaller by approximately an order of magnitude compared with that of γ_a (γ_H) makes a strong reduction on the effect of the diffusion-related encoding losses. Indeed typical HSQC spectroscopy conditions for an indirect-domain characterization would then involve SW₁≈1000 Hz (≈20 ppm on a 11.7 T magnet) and a resolution of ≈20 Hz. This in turn calls for sweeping the chirped rf pulses over ≈20 kHz ranges for either 25 or 50 ms $t_1^{\max }$; when translated in terms of ¹⁵N encoding this corresponds to a gradient amplitude G_e≈26 G∕cm. The diffusion losses that under the influence of such parameters can be expected for the z profiles in the presence and absence of T₂ relaxation are illustrated in Fig. 6 for both small- and macro-molecules. Qualitatively speaking these graphs are all similar to those arising in homonuclear cases, albeit less affected by diffusion losses.

Figure 6.

Idem as in Fig. 5 but for heteronuclear HSQC correlations involving a spatial encoding of the ¹⁵N with G_e=26.1 G∕cm, $t_1^{\max }=50$ and 25 ms for the real- and constant-time experiments, and O_i=−O_f=−10 kHz.

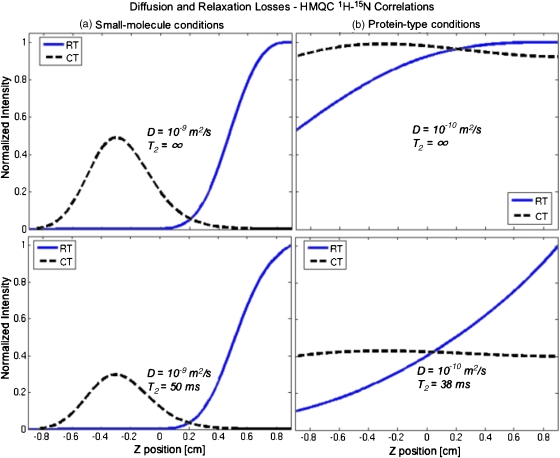
The immunity of these experiments against diffusion stems from the small gyromagnetic ratio involved in γ_e. Certain widespread heteronuclear 2D experiments such as the multiple-quantum correlation (HMQC) sequence,³⁰ however, involve the simultaneous evolution of two nuclei with different magnetic moments (e.g., ¹⁵N and ¹H)—even if only one of these becomes encoded in the indirect domain. In parallel to the HSQC protocol, excitation gradients in this HMQC case will have to be set relatively strong in order to impart the desired spatial encoding on the low-γ ¹⁵N nuclei. And although the diffusion-driven gradient losses arising directly from the nitrogen may still remain relatively small, the proton portion of the t₁ spin coherence may significantly magnify the diffusion effects. In order to evaluate such phenomena spectral parameters identical to those assumed for the HSQC experiments were taken and used to simulate ultrafast HMQC acquisitions where both the diffusion- and the relaxation-driven decays of the ¹⁵N and ¹H components making up the MQ coherence were assumed independent of each other. Spatial profiles thus calculated for small- and for protein-sized molecules are shown in Fig. 7. Most evident from these calculations is the fact that in the case of small molecules, the relatively long encoding durations needed to achieve proper spectral resolution couple to the large diffusivities and strong gradients that are required, to yield substantial diffusion-driven losses that make both continuous versions of the ultrafast HMQC scheme impractical. For more slowly diffusing proteins on the other hand, the shorter durations demanded from $t_1^{\max }$ as well as the smaller diffusion coefficients, make the decays tolerable and comparable to the losses arising from T₂ transverse relaxation.

Figure 7.

Idem as in Fig. 6 but for heteronuclear HMQC correlations; the effective MQ T₂ values indicated reflect hypothetical values dictated by the sum of ¹H₊ and ¹⁵N₊ transverse relaxation rates assumed in Figs. 56.

All the plots given so far were presented as relative signal losses imparted a function of the spins’ positions throughout the sample. This representation highlights the spatially dependent nature of ultrafast NMR and gives a fair idea of the ensuing attenuation. In practical experiments, however, sensitivity will effectively be reflected by the strength of the G_a-driven echoes following their t₂ Fourier transform. As shown in Eq. 2 these signals represent an integration over the full sample; Table 1 presents this alternative way of comparing the various schemes heretofore treated by providing the integrated attenuations that will characterize different ultrafast acquisitions as a result of diffusion-related losses.

Table 1.

Integrated diffusion-induced losses for various ultrafast 2D acquisition protocols, neglecting T₂ decay and under spectral conditions akin to those described in Sec. 4.

Target	Encoding strategy	Homonuclear correlation	HSQCa correlation	HMQCa correlation
Small Moleculeb	Real timec	0.687	0.889	0.242
Small Moleculeb	Constant timed	0.883	0.969	0.144
Proteine	Real timec	0.993	0.987	0.865
Proteine	Constant timed	0.998	0.997	0.961

^aAssuming ¹⁵N–¹H correlations.

^bD=10⁻⁹ m²∕s.

^cWith $t_1^{\max }=50\mathrm{ms}$.

^dWith $t_1^{\max }=25\mathrm{ms}$.

^eD=10⁻¹⁰ m²∕s.

CONCLUSIONS

Spatially selective pulses applied in the presence of oscillating gradients lie at the heart of liquid-phase single-scan 2D NMR experiments. The assumption of static spins proves valuable in the conceptual and developmental aspects of this methodology, yet the fact that this is solely an approximation should not be ignored. Molecules will inevitably change their positions throughout the course of the spatial encoding and decoding processes and, while certain systematic motions such as flow and∕or convection can be minimized, random diffusive motions cannot and will therefore influence the outcome of any ultrafast experiment. The present work addressed these phenomena in a systematic way by providing a general analytical and numerical basis capable of evaluating diffusion effects for arbitrary spatially selective pulse sequences, and then using these to evaluate the effects of translational motions for three prototypical pulse schemes often employed in ultrafast 2D NMR acquisitions. For these cases it was shown that the losses incurred by diffusion affect mainly the indirect domains of the continuous spatial encoding schemes as well as mixing-related processes, while remaining negligible during the direct domain as long as one employs fast acquisition gradient oscillations. Even for the continuous encoding sequences, diffusion-related losses remained comparable or smaller that those arising from natural T₂ relaxation. A main exception to this behavior arose upon considering the execution of HMQC-type sequences on small molecules, where the demands for relatively strong G_e gradients couple with the diffusion losses associated with ¹H coherences to severely reduce the fraction of spins in the sample that can actually contribute to the echo formation during the course of the acquisition period. Naturally, thesame approach employed here to analyze these three prototypical approaches could also be employed to examine diffusion and∕or convection effects in the remaining 2D single-scan sequences hitherto proposed, on new pulsed approaches to ultrafast 2D NMR, or on higher-dimensional versions of these single-scan experiments.

While the drastic attenuations that diffusion brings to the HMQC-derived spatial profiles may bear a poor prognosis for constant-gradient ultrafast experiments of this kind, they also suggest that a new tool may be here found for the computation of diffusion coefficients—operating, like its 2D counterparts, within a single scan. Indeed if sequences can be devised where spatial profiles of the kind illustrated in Figs. 567 strongly depend on the diffusion coefficients, a new window of opportunity would open up in the single-scan characterization of molecular Brownian motions at a site-resolved level. In particular, it turns out that the non-monotonic, T₂-independent profiles afforded by constant-time experiments illustrated in Figs. 67, provide a practical starting point for the site-specific single-scan quantification of diffusion coefficients. And the analytical derivations presented in this work serve as proper starting points to perform their quantitative evaluation. Further extensions of these concepts and demonstrations of their practical use will be described in an upcoming study.

APPENDIX: AN EFFICIENT APPROACH TO THE NUMERICAL PROPAGATION OF HETEROGENEOUS DIFFUSION EFFECTS

As hinted to in Sec. 3, computing numerically the time and space dependencies that arise in ultrafast 2D NMR acquisitions is a considerable challenge if one wishes to include the effects of molecular diffusion. Consider as an example the evaluation of the spins’ behavior upon applying a frequency-chirped pulse lasting 50 ms and sweeping a 40 kHz bandwidth while in the presence of a field gradient. Nyquist-type criteria would suggest solving Bloch’s equations by taking ≈25 μs Δt time increments and propagating the combined rf∕gradient∕shift effects over ≈2000 time steps. A typical ultrafast 2D NMR simulation would then mimic the signal arising from a macroscopic sample by coadding these time responses for a few 100's of z elements, equally spaced over a typical L≈2 cm sample length. On the other hand incorporating the effects of diffusion onto these calculations would require following over the full macroscopic sample volume, the fate of spin packets at a spacingthat is now dictated by diffusion lengths $\delta z\approx \sqrt{2D\Delta t}\approx {10}^{-5}\mathrm{cm}$—leading to a need to consider 10 000's of different z elements and to an orders-of-magnitude increase in the time needed for the computation. In order to deal with such complications we decided to modify an existing convolution algorithm,²⁶ so as to enable its use even while retaining a $\Delta z⪢\sqrt{2D\Delta t}$ spatial resolution.

Convolution algorithms cope with NMR diffusion effects by calculating magnetization components for each element z₀ at a time t+Δt, based on a coherent propagation of the z₀ magnetization over an interval Δt and on an additional convolution of the resulting vector by contributions that may have diffused from neighboring spatial elements. In other words these methods still need to discretize both space and time and solve diffusion-free Bloch equations, but will then account for diffusion effects by convolving at each time increment the resulting spatial pattern with a normalized kernel K(δz,Δt), reflecting a weighted migration among neighboring positions according to

$$S(z_0,t+\Delta t)=\int d{z}^{\prime }S(z^{\prime },t)K(z_0-z^{\prime },\Delta t).$$ (A1)

Here S(z,t) represents the spatial distribution of either the transverse or longitudinal magnetization at a time t, and K is the diffusion-correcting kernel possessing a spatial span on the order of $\sqrt{2D\Delta t}$. For instance, a kernel derived by Gudbjartsson and Patz using conditional random walk assumptions²⁶ and adopted for the present study reads

$$K(\delta z,\Delta t)=\frac{1}{\sqrt{4\pi D\Delta t}}\exp [-\frac{{\left(\delta z\right)}^2}{4D\Delta t}-{\gamma }^2{G}^2\frac{\Delta t^3}{12}+i\gamma G\delta z\Delta t],$$ (A2)

with D the diffusion coefficient and G the active gradient’s amplitude. Taking into consideration that the integral in Eq. A1 needs to be calculated using discrete elements, it follows that accurate results will only be obtained if one carries out its Riemann integration by employing a high δz resolution dictated by D and Δt. To avoid such a taxing demand we decided to modify these calculations—retaining still the kernel formalism but now switching to spatial incrementations $\Delta z⪢\sqrt{2D\Delta t}$—by exploiting the very local nature of the diffusion effect over the considered Δt time scales. To compute diffusion effects at the very short δz distances demanded by Eq. A2, a Taylor expansion of S around z₀ was then used, whereby longitudinal or transverse magnetizations at these diffusion-relevant length scales were interpolated as

$$S(z=z_0+\delta z)=A\left(z\right)e^{i\Phi \left(z\right)}\cong [A\left(z_0\right)+A^{\prime }\left(z_0\right)\delta z+\frac{A^{″}\left(z_0\right)}{2}\delta z^2]e^{i[\Phi \left(z_0\right)+{\Phi }^{\prime }\left(z_0\right)\delta z+{\Phi }^{″}\left(z_0\right)∕2\delta z^2]}.$$ (A3)

The relevant derivatives could then be evaluated on the basis of values computed for the nearest neighbors at larger Δz incrementations, defined by requirements based on the continuity of the amplitude and phase of the spin’s magnetization rather than by diffusion considerations. Amplitudes, for instance, were assumed

$$A^{\prime }\left(z_0\right)=\frac{A(z_0+\Delta z)-A(z_0-\Delta z)}{2\Delta z},$$ (A4)

$$A^{″}\left(z_0\right)=\frac{A(z_0+\Delta z)-2A\left(z_0\right)+A(z_0-\Delta z)}{\Delta z^2},$$

and similarly for the phase coefficient derivatives. With these first- and second-order derivatives at hand, Eq. A2 could be analytically evaluated to quantify the effects of diffusion from neighboring elements. It predicts that diffusion-related changes in the longitudinal magnetization will be given by

$$M_z(z_0,t+\Delta t)=M_z(z_0,t)+M_z^{″}(z_0,t)D\Delta t,$$ (A5)

while analogous effects on the transverse magnetization will be

$$M_{+}(z_0,t+\Delta t)=I(z_0,t)e^{i\Phi (z_0,t)}[A(z_0,t)+i{A}^{\prime }(z_0,t)\frac{D\Delta t(\gamma G\Delta t+{\Phi }^{\prime }(z_0,t))}{1-2i{\Phi }^{″}(z_0,t)D\Delta t}+A^{″}(z_0,t)\frac{D\Delta t(1-2iD\Delta t{\Phi }^{″}(z_0,t)-2D\Delta t{(\gamma G\Delta t+{\Phi }^{\prime }(z_0,t))}^2)}{{(1-2i{\Phi }^{″}(z_0,t)D\Delta t)}^2}],$$ (A6)

where

$$I(z_0,t)=\frac{1}{\sqrt{1-2i{\Phi }^{″}(z_0,t)D\Delta t}}\exp [-\frac{D\Delta t{(\gamma G\Delta t+{\Phi }^{\prime }(z_0,t))}^2}{1-2i{\Phi }^{″}(z_0,t)D\Delta t}-\frac{{\gamma }^2{G}^{2}D\Delta t^3}{12}].$$ (A7)

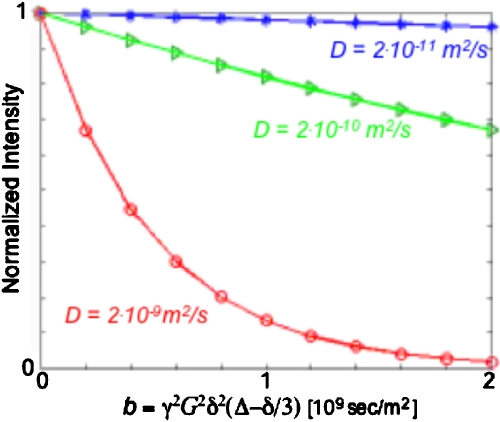
With these expressions accounting for the effects of diffusion over a time increment Δt, the reminder of the calculation on the fate of transverse or longitudinal magnetizations could be evaluated using classical diffusion-free propagation routines. Figure 8 illustrates the good reproduction that such numerical model, used throughout the simulations that accompanied this work, yields for the very well characterized case of a classical pulsed-gradient spin-echo experiment¹⁸ assuming different diffusion coefficients.

Figure 8.

Comparison between the classical exp[−bD] predictions expected from a pulsed-gradient spin-echo experiment for a variety of D diffusion coefficients (solid lines) and numerical predictions arising for the corresponding cases from the model introduced in the Appendix (points). Calculation parameters assumed δ=5 ms, Δ=30 ms, γ=4.257 kHz∕G, and a maximum gradient |G|=20 G∕cm.