Density-fragment interaction approach for quantum-mechanical∕molecular-mechanical calculations with application to the excited states of a Mg²⁺-sensitive dye

Abstract

A density-fragment interaction (DFI) approach for large-scale calculations is proposed. The DFI scheme describes electron density interaction between many quantum-mechanical (QM) fragments, which overcomes errors in electrostatic interactions with the fixed point-charge description in the conventional quantum-mechanical∕molecular-mechanical (QM∕MM) method. A self-consistent method, which is a mean-field treatment of the QM fragment interactions, was adopted to include equally the electron density interactions between the QM fragments. As a result, this method enables the evaluation of the polarization effects of the solvent and the protein surroundings. This method was combined with not only density functional theory (DFT) but also time-dependent DFT. In order to evaluate the solvent polarization effects in the DFI-QM∕MM method, we have applied it to the excited states of the magnesium-sensitive dye, KMG-20. The DFI-QM∕MM method succeeds in including solvent polarization effects and predicting accurately the spectral shift caused by Mg²⁺ binding.

INTRODUCTION

The accurate description of the electronic structure of large molecules is an important topic in the field of quantum chemistry, and is required for the accurate understanding of chemical phenomena. In this subject, many methods have been proposed so far.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18} The most well-known and commonly used approach is the quantum-mechanical∕molecular-mechanical (QM∕MM) method.^{19, 20, 21, 22} In this method, the electronically important part is described by quantum mechanics (QM), while the rest of the system is described by molecular mechanics (MM). The QM∕MM method has been applied to many large systems such as proteins and solvent, and has had great success in providing understanding of the mechanisms of numerous chemical and biological systems.

However, the interactions included in the total QM∕MM Fock^{23, 24} or Kohn–Sham²⁵ (KS) matrix $F_{\mu \nu }^{\mathrm{QM}∕\mathrm{MM}}$ are the electrostatic (ES) interactions between the electrons in the QM region and the fixed partial charges on the MM atoms $V_{\mu \nu }^{{\mathrm{ES}}_{\mathrm{QM}∕\mathrm{MM}}}$,

$$F_{\mu \nu }^{\text{QM}∕\text{MM}}=F_{\mu \nu }^{\text{QM}}+V_{\mu \nu }^{{\text{ES}}_{\text{QM}∕\text{MM}}},$$ (1)

$$V_{\mu \nu }^{{\text{ES}}_{\text{QM}∕\text{MM}}}=\int d{r}_1{\varphi }_{\mu }^{*}\left(1\right)\left[\sum _{A∊\text{MM}}^{N_{\text{atom}}}\frac{-Q_A}{\mid r_1-R_A\mid }\right]{\varphi }_{\nu }\left(1\right).$$ (2)

Therefore, this approximation $V_{\mu \nu }^{{\mathrm{ES}}_{\mathrm{QM}∕\mathrm{MM}}}$ is limited because the polarization effects on the MM atoms cannot be included, which may result in inaccurate structures, analyses, and predictions. (The van der Waals interactions are not included in the total QM∕MM Fock or KS matrix, but into the total energy.)

On the other hand, we have also seen significant development based on a fully QM description for large-scale calculations.^{6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18} One of the authors (W.Y.) has developed the linear-scaling treatment, the divide-and-conquer (DC) method.^{26, 27, 28} In this method, the entire system is first divided into several subsystems and their electron densities are calculated separately. Then the total electronic structure is reconstructed by considering the interactions between the electron densities of the individual subsystems. The DC method is thus a linear scaling approach based on molecular fragments. It is a rigorous approach because its accuracy can be systematically controlled by increasing the buffer size for each fragment and hence decreasing the error in fragment truncation. The DC method has been used for many chemical applications by the Yang laboratory^{29, 30, 31, 32, 33} and elsewhere.^{34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45} There are also several approximate fragment approaches.^{6, 8, 12, 46, 47, 48, 49, 50, 51, 52, 53}

In this paper, we propose a density-fragment interaction (DFI) approach for large-scale calculations based on a mean-field treatment of the electronic interaction between the fragments. In addition, the DFI scheme is combined with the QM∕MM method, which we call the DFI-QM∕MM method. Like the DC method, the DFI approach is based on the interaction of electron densities, which overcomes the inadequacies associated with the fixed point-charge treatment in the conventional QM∕MM method. Hence, a self-consistent method is adopted to equally include the electron density interactions between the individual QM fragments. As a result, the polarization effects of not only the active site but also the surrounding environment including the solvent and protein can be described. Also, the DFI approach can be easily used to perform excited state calculations because the number of electrons and the orbital picture are maintained.

In order to compare the DFI-QM∕MM method with the conventional QM∕MM method, we have applied each approach to the magnesium-sensitive dye, KMG-20.⁵⁴ KMG-20 is known to have a unique optical property such that the absorption wavelength is redshifted with a corresponding increase in intensity upon binding with Mg²⁺. This behavior is used as a magnesium probe in the living cell. Thus, we have focused on the excited states of KMG-20 and have carried out the calculations using time-dependent density functional theory⁵⁵ (TD-DFT) with the B3LYP (Ref. ⁵⁶) functional. As a result, the DFI-QM∕MM method yielded more reasonable spectra than those predicted by the conventional QM∕MM method. Based on these results, we investigated the solvent polarization effect on the excitation energy and the oscillator strength. In addition, we also analyzed the mechanism of spectral tuning in KMG-20 by Mg²⁺ binding. In this paper, we also discuss the differences between the present method and the DC method.

THEORY

The DFI-QM∕MM method and the total Hamiltonian

We begin by explaining the concept of the DFI-QM∕MM method. Figures 1a, 1b provide simple representations of the conventional QM∕MM and DFI methods, respectively. In the conventional method, the total system is divided into a QM subsystem and a MM subsystem. On the other hand, the DFI method has many QM subsystems, and the rest of the system is described by MM. In this paper, these QM regions are called fragments, and they are abbreviated as F_a(a=1,2, …,N_frag). As shown in Fig. 1b, the basic idea of the present method is “many” QM∕MM treatment that each fragment interacts to the other fragments and the MM subsystem. This is the most important point, compared with the conventional QM∕MM method.

Figure 1.

Cartoon representations of (a) QM∕MM, (b) DFI-QM∕MM, and (c) self-consistent method between fragments.

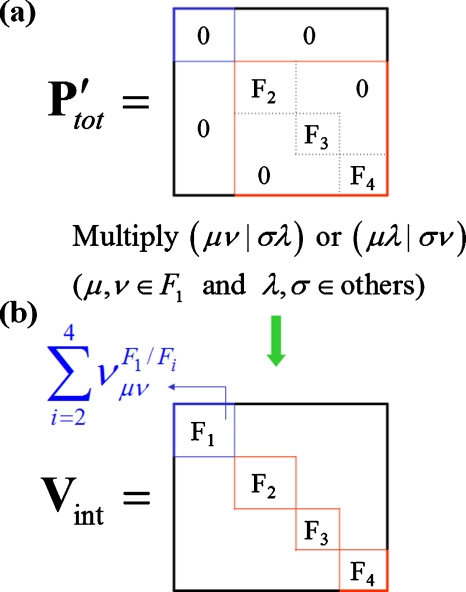
The block diagonal forms of the total one-electron density and Hamiltonian matrixes (Fig. 2) reflect, of course, the mean-field approximation for the interactions between fragments.

Figure 2.

Schematic illustrations of (a) the total density matrix and (b) the interaction matrix. Four fragments are assumed in this figure.

The total Hamiltonian of the DFI-QM∕MM method, ${\widehat{H}}_{\mathrm{tot}}^{\mathrm{DFI}\text{‐}\mathrm{QM}∕\mathrm{MM}}$, is given as follows:

$${\widehat{H}}_{\text{tot}}^{\text{DFI}-\text{QM∕MM}}=\sum _a^{N_{\text{frag}}}{\widehat{H}}_{F_a}+\sum _{a>b}^{N_{\text{frag}}}{\widehat{H}}_{F_a∕F_b}+\sum _a^{N_{\text{frag}}}{\widehat{H}}_{F_a∕\text{MM}}+{\widehat{H}}_{\text{MM}},$$ (3)

where ${\widehat{H}}_{F_a}$, ${\widehat{H}}_{F_a∕F_b}$, ${\widehat{H}}_{F_a∕\mathrm{MM}}$, and ${\widehat{H}}_{\mathrm{MM}}$ denote the Hamiltonian for the fragment a, the interaction Hamiltonian between fragments a and b, the interaction between fragment a and the MM subsystem, and the MM Hamiltonian, respectively. Each term in Eq. 3 is expressed as follows:

$${\widehat{H}}_{F_a}=-\frac{1}{2}\sum _{i∊F_a}^{N_{\text{elec}}}{\nabla }_i^2-\sum _{i∊F_a}^{N_{\text{elec}}}\sum _{A∊F_a}^{N_{\text{nucl}}}\frac{Z_A}{r_{iA}}+\sum _{i>j∊F_a}^{N_{\text{elec}}}\frac{1}{r_{ij}}+\sum _{A>B∊F_a}^{N_{\text{nucl}}}\frac{Z_A{Z}_B}{r_{AB}},$$ (4)

$${\widehat{H}}_{F_a∕F_b}=\sum _{i∊F_a}^{N_{\text{elec}}}\sum _{j∊F_b}^{N_{\text{elec}}}\frac{1}{r_{ij}}-\sum _{i∊F_a}^{N_{\text{elec}}}\sum _{A∊F_b}^{N_{\text{nucl}}}\frac{Z_A}{r_{iA}}-\sum _{A∊F_a}^{N_{\text{nucl}}}\sum _{i∊F_b}^{N_{\text{elec}}}\frac{Z_A}{r_{Ai}}+\sum _{A∊F_a}^{N_{\text{nucl}}}\sum _{B∊F_b}^{N_{\text{nucl}}}\frac{Z_A{Z}_B}{r_{AB}},$$ (5)

$${\widehat{H}}_{F_a∕\text{MM}}=-\sum _{i∊F_a}^{N_{\text{elec}}}\sum _{A∊\text{MM}}^{N_{\text{atom}}}\frac{Q_A}{r_{iA}}+\sum _{A∊F_a}^{N_{\text{nucl}}}\sum _{B∊\text{MM}}^{N_{\text{atom}}}\frac{Z_A{Q}_B}{r_{AB}}+\sum _{A∊F_a}^{N_{\text{atom}}}\sum _{B∊\text{MM}}^{N_{\text{atom}}}{V}_{AB}^{\text{vdW}}+\sum _{A,B,C∊F_a,\text{MM}}{V}_{\text{ABC}}^{\text{angle}}+\sum _{A,B,C,D∊F_a,\text{MM}}{V}_{ABCD}^{\text{torsion}},$$ (6)

$${\widehat{H}}_{\text{MM}}=\sum _{A>B∊\text{MM}}^{N_{\text{atom}}}\left[V_{AB}^{\text{ES}}+V_{AB}^{\text{vdW}}\right]+\sum _{A,B∊\text{MM}}{V}_{AB}^{\text{bond}}+\sum _{A,B,C∊\text{MM}}{V}_{\text{ABC}}^{\text{angle}}+\sum _{A,B,C,D∊\text{MM}}{V}_{ABCD}^{\text{torsion}}.$$ (7)

Here, we can clearly see the difference between DFI-QM∕MM and QM∕MM. Since the QM∕MM total Hamiltonian ${\widehat{H}}_{\mathrm{tot}}^{\mathrm{QM}∕\mathrm{MM}}$ is expressed as follows,l

$${\widehat{H}}_{\text{tot}}^{\text{QM}∕\text{MM}}={\widehat{H}}_{\text{QM}}+{\widehat{H}}_{\text{QM}∕\text{MM}}+{\widehat{H}}_{\text{MM}}={\widehat{H}}_{F_a}+{\widehat{H}}_{F_a∕\text{MM}}+{\widehat{H}}_{\text{MM}},$$ (8)

the difference between Eqs. 3, 8 is in the second term of Eq. 3, ${\widehat{H}}_{F_a∕F_b}$. Therefore, we must develop an approach to describe this newly added interaction, ${\widehat{H}}_{F_a∕F_b}$. Note that in writing the fragment Hamiltonians in Eqs. 4, 5, 6, we have assumed that a fixed number of electrons are assigned to each fragment.

Treatment of the interaction matrix

In quantum chemistry, the Hartree–Fock–Roothaan^{23, 24} method is often used at the first step for obtaining the electronic structure and various properties. Similarly, we first present the Fock matrix of the DFI-QM∕MM method, $F_{\mu \nu }^{F_a,\mathrm{DFI}\text{‐}\mathrm{QM}∕\mathrm{MM}}$, to consider the treatment of the interactions mentioned above,

$$F_{\mu \nu }^{F_a,\text{DFI}-\text{QM}∕\text{MM}}=F_{\mu \nu }^{F_a}+\sum _{b\ne a}^{N_{\text{frag}}}{V}_{\mu \nu }^{F_a∕F_b}+V_{\mu \nu }^{{\text{ES}}_{F_a∕\text{MM}}}=\left[H_{\mu \nu }^{F_a,\text{core}}+G_{\mu \nu }^{F_a}\right]+\sum _{b\ne a}^{N_{\text{frag}}}{V}_{\mu \nu }^{F_a∕F_b}+V_{\mu \nu }^{{\text{ES}}_{F_a∕\text{MM}}}=H_{\mu \nu }^{\prime \text{core}}+G_{\mu \nu }^{F_a}.$$ (9)

Here, $F_{\mu \nu }^{F_a}$, $V_{\mu \nu }^{F_a∕F_b}$, and $V_{\mu \nu }^{{\mathrm{ES}}_{F_a∕\mathrm{MM}}}$ denote the gas-phase Fock matrix for fragment a, the interaction matrix between fragments a and b, and the interaction matrix between fragment a and the MM subsystem, respectively. Each term is expressed as follows:

$$F_{\mu \nu }^{F_a}=H_{\mu \nu }^{F_a,\text{core}}+G_{\mu \nu }^{F_a},$$ (10)

$$H_{\mu \nu }^{F_a,\text{core}}=\int d{r}_1{\varphi }_{\mu }^{F_a^{\ast }}\left(1\right)\left[-\frac{1}{2}{\nabla }_1^2\right]{\varphi }_{\nu }^{F_a}\left(1\right)+\int d{r}_1{\varphi }_{\mu }^{F_a^{*}}\left(1\right)\left[\sum _{A∊F_a}^{N_{\text{nucl}}}\frac{-Z_A}{\mid r_1-R_A\mid }\right]{\varphi }_{\nu }^{F_a}\left(1\right)=T_{\mu \nu }^{F_a}+V_{\mu \nu }^{F_a,\text{nucl}},$$ (11)

$$G_{\mu \nu }^{F_a}=\sum _{\lambda ,\sigma ∊F_a}{P}_{\lambda \sigma }^{F_a}\left(\mu \nu \mid \sigma \lambda \right)-\frac{1}{2}\sum _{\lambda ,\sigma ∊F_a}{P}_{\lambda \sigma }^{F_a}\left(\mu \lambda \mid \sigma \nu \right),$$ (12)

$$V_{\mu \nu }^{F_a∕F_b}={\mu }_{\mu \nu }^{F_a∕F_b}+{\nu }_{\mu \nu }^{F_a∕F_b},$$ (13)

$${\mu }_{\mu \nu }^{F_a∕F_b}=\int d{r}_1{\varphi }_{\mu }^{F_a^{*}}\left(1\right)\left[\sum _{A∊F_b}^{N_{\text{nucl}}}\frac{-Z_A}{\mid r_1-R_A\mid }\right]{\varphi }_{\nu }^{F_a}\left(1\right),$$ (14)

$${\nu }_{\mu \nu }^{F_a∕F_b}=\sum _{\lambda ,\sigma ∊F_b}{P}_{\lambda \sigma }^{F_b}\left(\mu \nu \mid \sigma \lambda \right)-\frac{1}{2}\sum _{\lambda ,\sigma ∊F_b}{P}_{\lambda \sigma }^{F_b}\left(\mu \lambda \mid \sigma \nu \right),$$ (15)

$$V_{\mu \nu }^{{\text{ES}}_{F_a∕\text{MM}}}=\int d{r}_1{\varphi }_{\mu }^{F_a^{*}}\left(1\right)\left[\sum _{A∊\text{MM}}^{N_{\text{atom}}}\frac{-Q_A}{\mid r_1-R_A\mid }\right]{\varphi }_{\nu }^{F_a}\left(1\right),$$ (16)

$$H_{\mu \nu }^{\prime \text{core}}=H_{\mu \nu }^{F_a,\text{core}}+\sum _{b\ne a}^{N_{\text{frag}}}{V}_{\mu \nu }^{F_a∕F_b}+V_{\mu \nu }^{{\text{ES}}_{F_a∕\text{MM}}}.$$ (17)

In Eqs. 12, 15, the two-electron integrals based on the atomic orbitals (AOs) ϕ_i(i=μ,ν,λ,σ) are defined as follows,

$$\left(\mu \nu \mid \lambda \sigma \right)\equiv \int d{r}_{1}d{r}_2{\varphi }_{\mu }^{*}\left(1\right){\varphi }_{\nu }\left(1\right)r_{12}^{-1}{\varphi }_{\lambda }^{*}\left(2\right){\varphi }_{\sigma }\left(2\right),$$ (18)

and the density matrix of fragment a, $P_{\lambda \sigma }^{F_a}$, is expressed by the AO coefficients $C_{\lambda i}^{F_a}\left(i=1,2,\dots N_{\mathrm{AO}}^{F_a}\right)$ included in the ith molecular orbital (MO) ${\phi }_i^{F_a}$ as

$$P_{\lambda \sigma }^{F_a}=2\sum _{i∊F_a}^{N_{\text{elec}}∕2}{C}_{\lambda i}^{F_a}{C}_{\sigma i}^{F_a^{*}},$$ (19)

$${\phi }_i^{F_a}=\sum _{\lambda =1}^{N_{\text{AO}}}{C}_{\lambda i}^{F_a}{\varphi }_{\lambda }^{F_a}.$$ (20)

In the DFI-QM∕MM method, we note three important points. First, ${\mu }_{\mu \nu }^{F_a∕F_b}$ and ${\nu }_{\mu \nu }^{F_a∕F_b}$ in Eq. 13 are different from the second term $V_{\mu \nu }^{F_a,\mathrm{nuc}}$ in Eq. 11 and $G_{\mu \nu }^{F_a}$ expressed by Eq. 12, respectively. $V_{\mu \nu }^{F_a,\mathrm{nuc}}$ and $G_{\mu \nu }^{F_a}$ are the internal contributions from the nuclei and electrons in fragment a to the electrons in fragment a, respectively, whereas ${\mu }_{\mu \nu }^{F_a∕F_b}$ and ${\nu }_{\mu \nu }^{F_a∕F_b}$ are the external interactions from the nuclei and electrons in fragment b to the electrons in fragment a, respectively. In other words, ${\mu }_{\mu \nu }^{F_a∕F_b}$ and ${\nu }_{\mu \nu }^{F_a∕F_b}$ are the interaction matrices between two fragments, which correspond to the second and the first terms of ${\widehat{H}}_{F_a∕F_b}$ in Eq. 5, respectively. Second, the expression for ${\nu }_{\mu \nu }^{F_a∕F_b}$ is based on the HF method. The first and second terms in Eq. 15 correspond to the Coulomb and exchange interactions, respectively. If we employ the HF method for the fragments, this expression is not problematic. However, if DFT is employed, the exchange terms must be removed from ${\nu }_{\mu \nu }^{F_a∕F_b}$ as follows:

$${\nu }_{\mu \nu }^{F_a∕F_b}=\sum _{\lambda ,\sigma ∊F_b}{P}_{\lambda \sigma }^{F_b}\left(\mu \nu \mid \sigma \lambda \right).$$ (21)

This is because the exchange interactions in DFT are described in other ways such as in the Becke’s⁵⁷ 1988 exchange functional. Even if a hybrid method such as the B3LYP (Ref. ⁵⁶) functional is used, the contributions from exchange are eliminated from the fragment-fragment interactions because the balance between the HF and DFT exchange contributions is broken due to the lack of the fragment-fragment interactions in the DFT exchange contributions. If the expression in Eq. 15 is adopted, we need to include the fragment-fragment DFT exchange-correlation term. In this study, only the Coulomb interactions are included in the two-electron contributions in DFT calculations. Third, it should be noted that the sizes of the MM subsystems that contribute to the ES interactions are different from the conventional QM∕MM and DFI-QM∕MM methods, as shown in Eqs. 2, 16, respectively. The ES contributions included in Eq. 16 are formed by the electrons in fragment a and the MM atoms, which do not belong to any of the fragments. Therefore, the ES effects from the MM atoms that correspond to the other fragments are removed from Eq. 2 to avoid double counting. As a result, we find that the modified one-electron contributions, $H_{\mu \nu }^{\prime \mathrm{core}}$, given by Eq. 17 plays the most significant role in the DFI-QM∕MM method, and that the two-electron integral contributions in $G_{\mu \nu }^{F_a}$ do not require modification.

In order to clarify our description of the DFI-QM∕MM method, an example (N_frag=4) is illustrated in Fig. 2. Here, we consider only ${\nu }_{\mu \nu }^{F_a∕F_i}\left(i=b,c,\dots ,N_{\mathrm{frag}}\right)$ since it is the most difficult part of $H_{\mu \nu }^{\prime \mathrm{core}}$ to describe due to the two-electron contributions (e.g., one electron in fragment a and the other in fragment b). As shown in Fig. 2a, the individual fragment density matrices $P_{\lambda \sigma }^{F_i}$, which have a dimension$N_{\mathrm{AO}}^{F_i}\times N_{\mathrm{AO}}^{F_i}\left(i=a,b,c,\dots ,N_{\mathrm{frag}}\right)$, are calculated separately and are set diagonally. The N_AO×N_AO total density matrix abbreviated as ${\mathbf{P}}_{\mathrm{tot}}^{\prime }$ is then constructed. Here, it is noted that the density matrix of fragment a is set as the zero matrix (i.e., $P_{\lambda \sigma }^{F_a}=0$) to prevent $G_{\mu \nu }^{F_a}$ shown in Eq. 12 from being counted twice. In other words, if $P_{\lambda \sigma }^{F_a}$ is not set to zero, we do not have to calculate $G_{\mu \nu }^{F_a}$ in Eq. 9. The present algorithm uses the zero matrix scheme, as shown in Fig. 2, in order to satisfy the expression in Eq. 10. Next, the N_AO×N_AO total interaction matrix, which is abbreviated as V_int, is constructed by the product of ${\mathbf{P}}_{\mathrm{tot}}^{\prime }$ and the two-electron integrals, as shown in Eq. 15 and Fig. 2b. Finally, the $N_{\mathrm{AO}}^{F_a}\times N_{\mathrm{AO}}^{F_a}$ portion is extracted from V_int and then becomes the $\sum {\nu }_{\mu \nu }^{F_a∕F_i}\left(i=b,c,d,\dots .,N_{\mathrm{frag}}\right)$ to be included in $H_{\mu \nu }^{\prime \mathrm{core}}$.

Self-consistent method of the fragment interactions

As mentioned above, the contribution from fragment b (or c,d, …, etc.) to fragment a, ${\nu }_{\mu \nu }^{F_a∕F_b}$ (or ${\nu }_{\mu \nu }^{F_a∕F_c},{\nu }_{\mu \nu }^{F_a∕F_d},\dots$, etc.) is included in the total Fock matrix of fragment a, $F_{\mu \nu }^{F_a,\mathrm{DFI}\text{‐}\mathrm{QM}∕\mathrm{MM}}$, which corresponds to the first and second terms in Eq. 5. However, the opposite contribution is not included in that of fragment b, $F_{\mu \nu }^{F_b,\mathrm{DFI}\text{‐}\mathrm{QM}∕\mathrm{MM}}$, therefore we need to consider this interaction. To overcome this issue, we adopt the self-consistent method. Figure 1c shows this method schematically. First, the self-consistent field (SCF) calculation of fragment a is performed by using $F_{\mu \nu }^{F_a,\mathrm{DFI}\text{‐}\mathrm{QM}∕\mathrm{MM}}$. Then the density matrix of fragment a is obtained. Next, this density matrix and the other fragment density matrices are used to calculate the Fock matrix of fragment b, $F_{\mu \nu }^{F_b,\mathrm{DFI}\text{‐}\mathrm{QM}∕\mathrm{MM}}$, and a similar SCF procedure on fragment b is carried out. The same process is continued until each fragment has been considered. Hence, a series of these calculations among all fragments is performed iteratively until the change in the total energy has converged below a threshold of 0.0001 a.u. In this way, the DFI approach with the self-consistent method becomes a mean-field treatment of the fragment interactions such that the HF method treats the electron interactions.

The most significant advantage of the present method is that the electronic polarization effects not only on fragment a but also on the other fragments are included equally. As noted above, the problem of the conventional QM∕MM method is in the ES interaction between the QM and MM subsystems, which results from the fixed point-charge approximation of the MM atoms. In other words, the QM∕MM method is able to describe the electronic polarization of the QM subsystem but not in the MM subsystem. On the other hand, the ES effects in the present method are based on the self-consistent interactions between the individual fragment densities. Therefore, the DFI method overcomes one of the major limitations of the conventional QM∕MM method by including explicit polarization of the protein and solvent.

Another way of performing a SCF procedure on the fragments is to make all fragment density matrices to converge at the same time. That is to say, at the ith SCF cycle for fragment a, the F_a∕F_b interaction $V_{\mu \nu }^{F_a∕F_b}$ is calculated using the density matrix elements of fragment b obtained at the ith SCF cycle for fragment b. Because we did not test such a synchronous scheme yet, we will leave the comparison of the convergences and the computational costs between the two schemes for future study.

Comparison with the DC method

The DC method developed by Yang^{26, 27, 28} is also based on the electron density interactions. In this section, we compare the DFI-QM∕MM method with the DC method to clarify the differences.

In the DC method, the total density matrix is calculated via two steps. In the first step, the total system is divided into subsystems S_a(a=1,2, …,N_subs) using the partition matrix $p_{\mu \nu }^{S_a}$. Here, the subsystem S_a is distinguished from the fragment F_a used above. Under the following normalization condition,

$$\sum _a{p}_{\mu \nu }^{S_a}=1,$$ (22)

the partition matrix $p_{\mu \nu }^{S_a}$ for the subsystem a is defined in the following way:

$$p_{\mu \nu }^{S_a}=\{\begin{array}{l}1,\text{if\hspace{0.5em}}\mu ,\nu ∊S_a\hfill \\ 1∕2,\text{if\hspace{0.5em}}\mu ∊S_a\cap \nu ∊S_b\text{\hspace{0.5em}or\hspace{0.5em}}\nu ∊S_a\cap \mu ∊S_b\hfill \\ 0,\text{if\hspace{0.5em}}\mu ,\nu \notin S_a.\hfill \end{array}\phantom{\}}$$ (23)

Then, the total density matrix P_μν can be divided into subsystems $P_{\mu \nu }^{S_a}$ as follows:

$$P_{\mu \nu }=\sum _a{p}_{\mu \nu }^{S_a}{P}_{\mu \nu }=\sum _a{P}_{\mu \nu }^{S_a}.$$ (24)

The second step is the direct calculation of the total density matrix P_μν. First, the following approximation

$$P_{\mu \nu }^{S_a}\cong 2p_{\mu \nu }^{S_a}\sum _i{f}_{\beta }\left({\epsilon }_F-{\epsilon }_i^{S_a}\right)C_{\mu i}^{S_a}{C}_{\nu i}^{S_a^{*}}$$ (25)

is assumed for each $P_{\mu \nu }^{S_a}$. Here, $C_{\mu i}^{S_a}$ represents the AO coefficient in the ith MO of subsystem a, and f_β(x) is the Fermi function with inverse temperature β, which is given as follows:

$$f_{\beta }\left(x\right)={\left[1+\text{exp}\left(-\beta x\right)\right]}^{-1}.$$ (26)

The ε_F and ${\epsilon }_i^{S_a}$ indicate the Fermi level (chemical potential) and the ith orbital energy in subsystem a, respectively. In order to obtain the total density matrix using Eqs. 24, 25, the value of ε_F is needed. Thus, the following normalization constraint is used,

$$N_{\text{elec}}=\sum _{\mu \nu }{P}_{\mu \nu }{S}_{\nu \mu }=2\sum _a\sum _{\mu \nu }{p}_{\mu \nu }^{S_a}\sum _i{f}_{\beta }\left({\epsilon }_F-{\epsilon }_i^{S_a}\right)C_{\mu i}^{S_a}{C}_{\nu i}^{S_a^{\ast }}{S}_{\nu \mu }^{S_a},$$ (27)

where N_elec and $S_{\nu \mu }^{S_a}$ show the number of electrons for the total system and the overlap matrix in the AO expression, respectively. In this way, the value of ε_F is determined, and then the total density matrix P_μν can be calculated.

In the DC method, the interactions between the subsystems are described by the partition matrix $p_{\mu \nu }^{S_a}$ and the Fermi level ε_F, which corresponds to Eqs. 23, 25, respectively. Using these two equations, we can include not only the polarization effects but also the charge-transfer (CT) effects between the subsystems. This is the advantage for the DC method, compared with the DFI-QM∕MM method. However, the DC method suffers from the problem that the orbital picture is broken, which is caused by the buffer treatment of the partition matrix [i.e., the second case in Eq. 23]. To maintain the orbital picture, we must exclude the buffer region.

In the DFI-QM∕MM method, the CT effects between the fragments cannot be described, and the interfragment exchange interactions are not included in DFT calculations. However, the orbital picture for each fragment is maintained since the total density matrix is divided into fragments with no buffer. In addition, the number of electrons for each fragment is maintained. Therefore, the DFI-QM∕MM method may also be easily applied to excited state calculations.

COMPUTATIONAL DETAILS

Reproducing reliable structures of KMG-20 in solution is the first important task in the present study. For this purpose, we used the QM∕MM-free energy (QM∕MM-FE) method⁵⁸ that has a good record in the previous studies of solution-phase and enzyme-catalyzed reactions.⁵⁹ In the first step, a gas-phase geometry optimization of KMG-20 without the bound Mg²⁺ ion was performed using DFT with the B3LYP functional. Next, this structure was solvated in a 20 Å sphere of classical MM water molecules described by the TIP3P model,⁶⁰ and a QM∕MM-FE optimization was carried out. During the optimization and subsequent molecular dynamics (MD) simulations, all atoms greater than 15 Å from the center of mass of KMG-20 were held fixed. In the QM∕MM-FE steps, a 10 ps MD simulation was run using a time step of 1 fs under NVT conditions, and the temperature was maintained at 300 K using a Berendsen thermostat.⁶¹ A 12 Å cutoff was used for nonbonding interactions. For the structure with a bound Mg²⁺ ion (KMG-20⋅Mg²⁺), four QM water molecules and the Mg²⁺ were coordinated with the carboxyl and carbonyl groups of KMG-20 to form an octahedral structure that was then used as an initial guess for the gas-phase geometry optimization. The rest of the procedure was the same as for KMG-20 with no Mg²⁺. The structures of KMG-20 and KMG-20⋅Mg²⁺ are shown in Fig. 3.

Figure 3.

Structure of (a) KMG-20 and (b) KMG-20⋅Mg²⁺ (the KMG-20 chromophore, Mg²⁺ ion, and four water molecules are shown).

In the DFI-QM∕MM computations, KMG-20 (and the Mg²⁺ ion and four water molecules) were treated as one fragment (active site), and the solvent was separated into an additional QM fragment (i.e., N_frag=2) and the MM subsystem. To investigate the dependence of the polarization effects on the size of the QM solvent fragment, we considered two different fragment sizes. We performed calculations on a system in which the radius of the QM water fragment was either 3 or 8 Å from the center of mass of KMG-20. To evaluate the polarization effects, single point QM∕MM calculations were also performed. The excitation energies and the oscillator strength for KMG-20 and KMG-20⋅Mg²⁺ were calculated using TD-DFT (Ref. ⁵⁵) with the B3LYP (Ref. ⁵⁶) functional. At that time, the final MD structures in the QM∕MM-FE optimizations were used for the excited state calculations. Therefore, these excitation energies do not contain the free energy effects.

To estimate the both polarization and long range ES effects, excitation energies for KMG-20 with and without Mg²⁺ were calculated using a continuum model [the COSMO-RS (Ref. ⁶²) option from GAUSSIAN03 (Ref. ⁶³)].

In all calculations, the 6–31G(d) basis set was used for all QM atoms. In the DFI-QM∕MM calculations for the KMG-20 system, a total of 1027 and 5036 basis functionals were used for the 3 and 8 Å fragments, respectively. In the KMG-20⋅Mg²⁺ calculations, a total of 932 and 4713 basis functions were used for the 3 and 8 Å fragments, respectively. The TIP3P model was used for the MM solvent molecules. This force field was also used for the single point QM∕MM calculations (i.e., point-charge model). For the QM∕MM-FE computations, the MD simulations and minimizations were carried out with the TINKER4.2 (Ref. ⁶⁴) program package, which was interfaced with GAUSSIAN03 to perform the QM calculations. The DFI-QM∕MM program with DFT∕TD-DFT was implemented in GAUSSIAN03.

RESULTS

Evaluation of the interfragment exchange contributions

In order to estimate the error associated with the approximation in Eq. 21, we calculated interaction energies between two water molecules using the full QM and the DFI methods. Figure 4 shows the interaction energies to the intermolecular O–H distance between two water molecules. As a result, the interaction energies of the full QM (B3LYP) and the DFI (B3LYP) methods at the equilibrium intermolecular distance (1.9 Å) were −0.0118 and −0.0646 a.u., respectively, which shows the error of −0.0528 a.u. ( −33.1 kcal∕mol) in the DFI method. At the short O–H distance(<1.9 Å), the behavior of the interaction energies are quite different between the two methods. The DFI method gives much larger gradient than the full QM method, which is due to the lack of the exchange interactions in the Fock matrix as approximated by Eq. 21. In other words, the Coulomb repulsions strongly contribute to the positive interaction energies. On the other hand, the errors gradually become small with the increase in the O–H distance (>1.9 Å). At 3.0 Å, the DFI method satisfies the 5.0 kcal∕mol accuracy in the interaction energy, and finally the DFI method (−0.0005 a.u.) gives almost the same interaction energy with the full QM method (−0.0001 a.u.) at 10.0 Å. From these results, we find that the exchange contributions are not dominant to the interaction energy at the distance more than 3.0 Å, and that the approximation in Eq. 21 is effective to describe the electronic structures in this region. Therefore, the KMG-20 chromophore and the water molecules within 3.0 Å from the chromophore are treated as one QM fragment (active site) in DFI-QM∕MM calculations.

Figure 4.

Interaction energies between two water molecules as a function of intermolecular O–H distance. (a) Full QM [B3LYP∕6–31G(d)] and (b) DFI [B3LYP∕6–31G(d)].

TD-DFT excitation energies with DFI-QM∕MM

TD-DFT calculations based on the DFI-QM∕MM method were performed for the KMG-20 and the KMG-20⋅Mg²⁺ systems with the 3 and 8 Å fragments, and the results are summarized in Table 1. For the KMG-20 calculations, the excitation energies using the 3 and 8 Å fragments were 3.21 and 3.17 eV, respectively. The excitation energies for the KMG-20⋅Mg²⁺ systems were 3.07 and 3.06 eV for the 3 and 8 Å fragments, respectively. In comparison, the experimental excitation energies are 2.92 and 2.79 eV for the KMG-20 and KMG-20⋅Mg²⁺ systems, respectively. From these results, we find that although the dependence of the excitation energy on the fragment size is not large for either system (0.04 and 0.01 eV for KMG-20 and KMG-20⋅Mg²⁺, respectively), the excitation energies become closer to the experimental values with the extension of the fragment size. Using the results of the 8 Å fragments, the deviations from the experimental values were 0.25 and 0.27 eV for KMG-20 and KMG-20⋅Mg²⁺, respectively. Although the absolute values of the excitation energies differ slightly from the experimental ones, the spectral shift between the two systems (0.11 eV) well reproduces the experimental results (0.13 eV).

Table 1.

Dependence of the fragment size on the excitation energies of KMG-20 and KMG-20⋅Mg²⁺(eV).

	Method	Fragment size (Å)	Main configuration |C|>0.3	fa (a.u.)	Eexb (eV)	Expt. (eV)c
KMG-20	DFI-QM∕MM	8.0	0.70(H→L) d	0.53	3.17
		3.0	0.70(H→L) d	0.54	3.21
	Point charge	⋯	0.70(H→L) d	0.50	3.30	2.92
	COSMO-RS	⋯	0.70(H→L) d	0.86	3.01
KMG-20⋅Mg2+	DFI-QM∕MM	8.0	0.69(H→L) d	0.57	3.06
		3.0	0.69(H→L) d	0.57	3.07	2.79
	Point charge	⋯	0.69(H→L) d	0.51	3.14
	COSMO-RS	⋯	0.70(H→L) d	0.89	2.90

^aOscilator strength.

^bExcitation.

^cExcitation energy.

^dπ-π^∗ excitation from HOMO to LUMO.

The observed absorption peaks for both systems are assigned to the first excited states that have the largest oscillator strength in the energy region. These transitions are π-π^* excitations from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO).

Evaluation of polarization effects

In order to evaluate the polarization effects included in the DFI-QM∕MM method, we also computed TD-DFT excitation energies with the point-charge model (i.e., single point QM∕MM calculations), which are listed in Table 1. Here, the same geometry optimized using the QM∕MM-FE method was used for the point-charge and DFI-QM∕MM calculations. In the KMG-20 system, the KMG-20 chromophore and four QM water molecules forming hydrogen bonds to the carboxyl and carbonyl groups of the chromophore were treated as a QM fragment. In the KMG-20⋅Mg²⁺ system, the chromophore, Mg²⁺ ion, and four QM water molecules were treated as a QM fragment. In the KMG-20 calculations, the excitation energies obtained with the DFI-QM∕MM method and the point-charge model were 3.17 and 3.30 eV, respectively, which corresponds to a spectral redshift of 0.13 eV. This value comes from the polarization effects described by the DFI-QM∕MM method. In the KMG-20⋅Mg²⁺ calculations, the polarization effects included in the DFI-QM∕MM method (3.06 eV) give rise to the spectral redshift of 0.08 eV from the excitation energy obtained with the point-charge model (3.14 eV). In both cases, the inclusion of polarization effects by the DFI-QM∕MM method brings about the spectral redshift, which yields excitation energies closer to the experimental values than the point-charge description.

To investigate not only the polarization effect but also the long range solvent ES effects, we performed continuum model (COSMO-RS) calculations for the KMG-20 and KMG-20⋅Mg²⁺ systems, and the results are also summarized in Table 1. The excitation energies obtained with the COSMO-RS method for the KMG-20 and KMG-20⋅Mg²⁺ systems were 3.01 and 2.90 eV, respectively, which corresponds to a spectral redshift of 0.11 eV. Compared with the results from DFI-QM∕MM, although the spectral shift caused by Mg²⁺ binding is the same, the absolute excitation energies obtained with COSMO-RS are closer to the experimental values for the both systems with the commonly used atomic radii. These results may be interpreted as long range solvent ES effects contribute to the spectral redshift of 0.16 eV from the excitation energies obtained with DFI-QM∕MM for the both systems. These effects need to be included to reproduce the experimental excitation energies.

As summarized in Table 1, the oscillator strength was also computed and the influence of the polarization effects on the oscillator strength is evident. In the point-charge model, the oscillator strengths of KMG-20⋅Mg²⁺ and KMG-20 were 0.51 and 0.50 a.u., respectively, which show a shift of 0.01 a.u. in the oscillator strength. On the other hand, the DFI-QM∕MM method gives a shift of 0.04 a.u. upon Mg²⁺ binding (KMG-20⋅Mg²⁺: 0.57 a.u., KMG-20: 0.53 a.u.), which shows a shift that is 0.03 a.u. larger than the value obtained with the point-charge model (0.01 a.u.). Hence, the results obtained with the DFI-QM∕MM method are quite similar to the experimental trend such that the intensity of the absorption spectrum is enhanced by Mg²⁺ binding. Here, it is interesting to note that the oscillator strength increases with Mg²⁺ binding even though there is a decrease in the excitation energy, and the increase in the oscillator strength is more evident in the case of the DFI-QM∕MM description than with the point-charge description. Therefore, we decided to investigate the origin of this behavior. The oscillator strength f is composed of two contributions as follows:

$$f=\frac{2}{3}{E}_{\text{ex}}{\mid ⟨{\Psi }_E\mid \hat{\mathbf{r}}\mid {\Psi }_G⟩\mid }^2=\frac{2}{3}{E}_{\text{ex}}\sum _{i=x,y,z}{\mid ⟨{\Psi }_E\mid {\widehat{r}}_i\mid {\Psi }_G⟩\mid }^2.$$ (28)

One is the excitation energy E_ex between two states (e.g., the ground and first excited states) and another is the square of the transition dipole moment ${\left|⟨{\Psi }_E|\widehat{\mathbf{r}}|{\Psi }_G⟩\right|}^2$ between the corresponding states. From this formula, an increase in the oscillator strength should be responsible for the increase in ${\left|⟨{\Psi }_E|\widehat{\mathbf{r}}|{\Psi }_G⟩\right|}^2$. Therefore, the values of ${\left|⟨{\Psi }_E|\widehat{\mathbf{r}}|{\Psi }_G⟩\right|}^2$ were compared, as summarized in Table 2. In both methods, the values of KMG-20⋅Mg²⁺ (6.60 a.u. with the point-charge model and 7.56 a.u. using DFI-QM∕MM) are larger than those of KMG-20 (6.14 a.u. with the point-charge model and 6.77 a.u. using DFI-QM∕MM). In the value of ${\left|⟨{\Psi }_E|\widehat{\mathbf{r}}|{\Psi }_G⟩\right|}^2$, the ratios of KMG-20⋅Mg²⁺ to KMG-20 (KMG-20⋅Mg²⁺∕KMG-20) are 1.12 and 1.08 in the DFI-QM∕MM and point-charge methods, respectively. On the other hand, the corresponding ratios in the excitation energies are 0.96 and 0.95 in the DFI-QM∕MM and point-charge methods, respectively. Therefore, the increase in the transition dipole moment overcomes the decrease in the excitation energy, which results in an increase in the oscillator strength. Comparing the values obtained from the two methods, the shift in ${\left|⟨{\Psi }_E|\widehat{\mathbf{r}}|{\Psi }_G⟩\right|}^2$ caused by Mg²⁺ binding is larger by 0.33 a.u. in the DFI-QM∕MM description (0.79 a.u.) than in the point-charge description (0.46 a.u.). Therefore, the square of the transition dipole moment mainly contributes to the difference in the oscillator strength between the two methods. As a result, we find that the solvent polarization effects significantly increase the shift in the transition dipole moment, and this effect directly contributes to the enhancement of the oscillator strength.

Table 2.

Oscillator strength and the square of the transition dipole moment of KMG-20 and KMG-20⋅Mg²⁺(a.u.).

	Method	⟨x⟩ a	⟨y⟩ b	⟨z⟩ c	|⟨r⟩|2d	fe
KMG-20	DFI-QM∕MMf	2.60	0.04	0.12	6.77	0.53
	Point chargeg	2.48	0.07	0.08	6.14	0.50
KMG-20⋅Mg2+	DFI-QM∕MMf	2.74	0.14	0.08	7.56	0.57
	Point chargeg	2.57	0.02	0.04	6.60	0.51

^ax-element of the transition dipole moment.

^by-element.

^cz-element.

^dSquare of the transition dipole moment.

^eOscillator strength.

^f8 Å fragment.

^gPoint-charge model.

Physical origin of spectral tuning

As mentioned above, the TD-DFT calculations with the DFI-QM∕MM method well reproduce the experimental spectral shift between KMG-20 and KMG-20⋅Mg²⁺. Based on these results, we analyzed the physical origin of the spectral tuning. The excitation energies obtained with the DFI-QM∕MM method were decomposed into six terms,

$$E_{\text{ex}}^X\left(\text{AS},\text{\hspace{0.5em}DFI-QM∕MM}\right)=E_{\text{ex}}^X\left(\text{CHR},\text{\hspace{0.5em}bare}\right)+{\text{ES}}_{\text{solv}}^X+{\text{Pol}}_{\text{solv}}^X+{\text{CT}}_{\text{CI}}^X+{\text{ES}}_{\text{CI}}^X+{\text{Pol}}_{\text{CI}}^X,$$$$\left(X=\text{KMG-20\hspace{0.5em}and\hspace{0.5em}KMG-}20\cdot {\text{Mg}}^{2+}\right).$$ (29)

Here, AS denotes the “active site” QM fragment used in the DFI-QM∕MM and point-charge calculations, and $E_{\mathrm{ex}}^X$ (CHR, bare) is the excitation energy of the “bare” KMG-20 chromophore (without the Mg²⁺ ion and the water environment). The term ${\mathrm{ES}}_{\mathrm{solv}}^X$, calculated from $E_{\mathrm{ex}}^X\left(\mathrm{AS},\text{\hspace{0.5em}point\hspace{0.5em}charge}\right)-E_{\mathrm{ex}}^X\left(\mathrm{AS},\text{\hspace{0.5em}bare}\right)$, represents the solvent ES contribution to the excitation energy. ${\mathrm{Pol}}_{\mathrm{solv}}^X$ represents the solvent polarization effects discussed above, which are calculated by $E_{\mathrm{ex}}^X(\mathrm{AS},\mathrm{DFI}\text{‐}\mathrm{QM}∕\mathrm{MM})-E_{\mathrm{ex}}^X(\mathrm{AS},\text{\hspace{0.5em}point\hspace{0.5em}charge})$. ${\mathrm{ES}}_{\mathrm{CI}}^X$, ${\mathrm{Pol}}_{\mathrm{CI}}^X$, and ${\mathrm{CT}}_{\mathrm{CI}}^X$ refer to the ES, polarization, and CT interactions between the chromophore and associated ligands (i.e., four water molecules for KMG-20, and Mg²⁺ and four water molecules for KMG-20⋅Mg²⁺), respectively, and are evaluated as $E_{\mathrm{ex}}^X(\mathrm{CHR},\text{\hspace{0.5em}point\hspace{0.5em}charge})-E_{\mathrm{ex}}^X(\mathrm{CHR},\text{\hspace{0.5em}bare})$, $E_{\mathrm{ex}}^X(\mathrm{CHR},\mathrm{DFI})-E_{\mathrm{ex}}^X(\mathrm{CHR},\text{\hspace{0.5em}point\hspace{0.5em}charge})$, and $E_{\mathrm{ex}}^X(\mathrm{AS},\text{\hspace{0.5em}bare})-E_{\mathrm{ex}}^X(\mathrm{CHR},\mathrm{DFI})$, respectively. The excitation energies obtained with each method are given in Table 3. To examine the physical origin of the spectral tuning, the six components in Eq. 29 were compared in Fig. 5 using the following formula:

$$\Delta E_{\text{ex}}^X=E_{\text{ex}}^X\left(\text{AS},\text{\hspace{0.5em}DFI-QM∕MM}\right)-E_{\text{ex}}^Y\left(\text{AS},\text{\hspace{0.5em}DFI-QM∕MM}\right)=\Delta E_{\text{ex}}^X\left(\text{CHR},\text{\hspace{0.5em}bare}\right)+\Delta {\text{ES}}_{\text{solv}}^X+\Delta {\text{Pol}}_{\text{solv}}^X+\Delta {\text{ES}}_{\text{CI}}^X+\Delta {\text{Pol}}_{\text{CI}}^X+\Delta {\text{CT}}_{\text{CI}}^X,$$ (30)

$$\left(X=\text{KMG-}20\cdot {\text{Mg}}^{2+},Y=\text{KMG-}20\right).$$

Figure 5 clearly shows that the main origin of spectral tuning is from the ES interactions between the KMG-20 chromophore and the Mg²⁺ and water ligands, which contribute 0.32 eV of the overall spectral redshift (0.11 eV). The effects of geometric changes in the chromophore structure upon Mg²⁺ binding are also of secondary importance in the spectral redshift (0.10 eV). On the other hand, the solvent ES and polarization effects and the CT effects between the chromophore and the ligands contribute 0.19, 0.05, and 0.07 eV to the spectral blueshift, respectively. This is because the contributions from the solvent ES and polarization effects and the CT effects are smaller in KMG-20⋅Mg²⁺ than in KMG-20. As a result, these three effects contribute to the cancellation of the overestimated redshift. From these results, we find that although the inclusion of the solvent polarization effects is necessary for obtaining the absolute excitation energy, the effects are not dominant in the spectral tuning between KMG-20 and KMG-20⋅Mg²⁺.

Table 3.

Comparison of the excitation energies of KMG-20 and KMG-20⋅Mg²⁺(eV).

	Bare (CHR)a	Bare(CHR)+Point charge	Bare(CHR)+DFI	Bare(AS)b	Point chargec	DFI-QM∕MMd	Expt.e
KMG-20	3.75	3.70f	3.70g	3.61	3.30	3.17	2.92
KMG-20⋅Mg2+	3.65	3.28h	3.28i	3.26	3.14	3.06	2.79

^aGas-phase calculation of isolated chromophore.

^bGas-phase calculation of isolated active site.

^cPoint-charge method.

^d8 Å fragment.

^eReference ⁵⁴.

^fIsolated chromophore (QM) and four water molecules (point-charge model).

^gIsolated chromophore (QM fragment 1) and four water molecules (QM fragment 2).

^hIsolated chromophore (QM) and Mg²⁺ ion and four water molecules (point-charge model).

ⁱIsolated chromophore (QM fragment 1) and Mg²⁺ ion and four water molecules (QM fragment 2).

Figure 5.

Physical origin of color tuning. Decomposition analysis of the excitation energy shift (eV). Results from KMG-20 were used for the references.

In addition to these results, we note the excitation energy obtained with the COSMO-RS method. As shown in Table 1, if we employ the COSMO-RS method, the absolute excitation energies become much closer to the experimental spectra than the values obtained with DFI-QM∕MM method. However, the contributions from the long range solvent ES effects are equal in the KMG-20 (−0.16 eV) and KMG-20⋅Mg²⁺ (−0.16 eV) calculations if these values are estimated as $E_{\mathrm{ex}}^X(\mathrm{AS},\mathrm{COSMO}\text{‐}\mathrm{RS})-E_{\mathrm{ex}}^X$(AS, DFI-QM∕MM). From these results, we find that the effects do not contribute to the spectral shift between KMG-20 and KMG-20⋅Mg²⁺.

CONCLUSIONS

We have developed here the DFI scheme for QM∕MM calculations. Taking advantage of the orbital picture and the number of electrons, we have applied this method to the excited states of the Mg²⁺-sensitive dye, KMG-20, and have determined that it is able to overcome one of the problems associated with the fixed point-charge treatment in the conventional QM∕MM method.

First, the efficiency on the approximation by Eq. 21 was tested using the interaction energies between two water molecules (DFI versus full QM). As a result, we found that the approximation is effective at the O–H distance more than 3.0 Å because the exchange contributions are not dominant to the interaction energy in this region. Based on this result, the KMG-20 chromophore and the water molecule within 3.0 Å from the chromophore were treated as one QM fragment in the DFI-QM∕MM calculations.

Second, the dependence of the fragment size on the excitation energy was examined. To determine this dependence, TD-DFT excitation energies with two fragment radii (3 and 8 Å) were performed for KMG-20 and KMG-20⋅Mg²⁺. As a result, we found that the dependence of the fragment size on the excitation energy is quite small, but the excitation energies become closer to the experimental values with an increased fragment size.

Third, the solvent polarization effects on the excitation energy were investigated. The polarization effects were evaluated by calculating the difference between the excitation energies using the DFI-QM∕MM and point-charge descriptions. As a result, we found that the polarization effects included in the DFI-QM∕MM method bring about a spectral redshift relative to the excitation energy obtained with the point-charge method, and yield excitation energies closer to the experimental values than the point-charge method.

Fourth, solvent polarization effects on the oscillator strength were also studied. Comparing the values from the DFI-QM∕MM and point-charge methods, we found that the DFI-QM∕MM method gives a larger shift in the oscillator strength upon binding of the Mg²⁺ ion than the point-charge treatment, and reproduces the experimental trend. Using the formula for the oscillator strength, the value of the square of the transition dipole moment was also compared. We found that solvent polarization effects contribute to the shift in the transition dipole moment more than the spectral shift and, as a result, the oscillator strength was increased with the binding of the Mg²⁺ ion.

Fifth, the physical origin of the spectral tuning in KMG-20 on Mg²⁺ binding was analyzed on the basis of the reproduction of the experimental spectral shift. As a result, we found that the main origin of the spectral redshift is from the ES interactions between the KMG-20 chromophore, Mg²⁺ ion, and the four QM water molecules, and that the solvent polarization effects are not dominant in the spectral tuning between KMG-20 and KMG-20⋅Mg²⁺.

Finally, we note that the DFI scheme developed here can be combined with other methods for ground and excited states, even though only the combination of DFT and TD-DFT with the B3LYP functional was employed in this paper. The DFI-QM∕MM method was successful in including solvent polarization effects. As a result, the experimental spectral shift between KMG-20 and KMG-20⋅Mg²⁺ was well reproduced. However, the absolute excitation energies had non-negligible errors (∼0.27 eV) compared to the experimental values. The lack of the long range solvent ES effects can be thought as one reason because the COSMO-RS method well reproduced the absolute experimental values. On the other hand, the errors may be due to the B3LYP functional as another reason. Therefore, we will extend the present scheme to other functionals such as CAM-B3LYP (Ref. ⁶⁵) and rCAM-B3LYP (Ref. ⁶⁶) in the future.