Abstract
We have implemented the serial replica exchange method (SREM) and simulated tempering (ST) enhanced sampling algorithms in a global distributed computing environment. Here we examine the helix-coil transition of a 21 residue α-helical peptide in explicit solvent. For ST, we demonstrate the efficacy of a new method for determining initial weights allowing the system to perform a random walk in temperature space based on short trial simulations. These weights are updated throughout the production simulation by an adaptive weighting method. We give a detailed comparison of SREM, ST, as well as standard MD and find that SREM and ST give equivalent results in reasonable agreement with experimental data. In addition, we find that both enhanced sampling methods are much more efficient than standard MD simulations. The melting temperature of the Fs peptide with the AMBER99φ potential was calculated to be about 310 K, which is in reasonable agreement with the experimental value of 334 K. We also discuss other temperature dependent properties of the helix-coil transition. Although ST has certain advantages over SREM, both SREM and ST are shown to be powerful methods via distributed computing and will be applied extensively in future studies of complex bimolecular systems.
INTRODUCTION
Adequately sampling the conformational space of biomolecules is important for understanding molecular functions. Computer simulation, such as molecular dynamics (MD) and Monte Carlo (MC), is a powerful technique for exploring conformation space. However, such simulations often become trapped in local energy minima when applied to complex biomolecular systems.1, 2 Recently, it has been shown that a large ensemble of individual MD trajectories generated by a distributed computing network makes it possible to study the folding of some miniproteins in explicit solvent.3, 4, 5, 6, 7, 8 Unfortunately, due to the local trapping problem, it is still difficult to satisfactorily sample the entire configuration space of a biomolecule in explicit solvent even with a distributed computing effort. Tempering methods such as simulated tempering9, 10 (ST) and parallel tempering [or replica exchange method (REM)]11, 12, 13, 14 were developed to overcome this kinetic trapping problem by inducing a random walk in temperature space. At high temperatures the free energy landscape is more or less flat, allowing broad sampling of configuration space. Conformations found at high temperatures may then be exchanged to lower temperatures in order to explore the relevant free energy minima. Both ST and parallel tempering have proved useful for sampling phase space and have been widely used to simulate biomolecular systems.2, 15, 16, 17, 18, 19, 20, 21 Therefore, the combination of the tempering methods and a distributed computing network such as FOLDING@HOME (FAH), currently with more than 200 000 computer processors (CPU’s), should greatly enhance our ability to sample the conformation space of complex biomolecular systems.
In the REM, independent MD or MC simulations are performed in parallel at different temperatures. Exchanges of configurations between neighboring temperatures are attempted periodically and accepted according to the detailed balance condition.13, 14 The standard REM scheme requires synchronization and frequent communication between different processors, which makes it unsuitable for a heterogeneous distributed computing environment lacking direct communication between hosts. Rhee and Pande developed the multiplexed replica exchange method (MREM) for running replica exchange on distributed computers.22 In MREM, multiplexed replicas with more than one independent simulation at each temperature are run, and exchanges of configurations between these multiplexed replicas are attempted periodically. This algorithm still requires synchronization between multiplexed replicas, resulting in short idle times, as in another serial algorithm called Asynchronous Replica Exchange.23 Recently, Hagen et al. proposed another method called serial replica exchange method (SREM) that is suitable for distributed computing.24 In SREM, a single, independent simulation performs a random walk in temperature space by making regular attempts to change temperatures. The transition probability for this move is determined by one potential energy from the simulation and a second one from a prestored potential energy distribution function (PEDF) at the new temperature. In contrast to MREM, SREM does not require any synchronization between different simulations, so no CPUs are left idle. Thus SREM is substantially more efficient than MREM. The main difficulty with SREM is determining the PEDFs because SREM is only approximately correct unless the exact PEDFs are adopted.
ST, an inherent serial algorithm, is another enhanced sampling method suitable for distributed computing environments.9, 10 In ST, an expanded canonical ensemble, where canonical ensembles at different temperatures are weighted differently, is used to sample the conformation space. A single simulation is performed, again making periodic attempts to change temperatures according to a well defined transition probability determined by the detailed balance condition. In contrast to SREM, ST is an exact method. Each temperature is assigned a weight and the difference between the weights of neighboring temperatures determines the probability of making an exchange between them. If these weights are not determined properly then simulations will be constrained to a subset of temperature space and become inefficient.9, 10, 25, 26 Therefore, determining a good set of weights is essential for ST. A number of attempts have been made to obtain weights allowing the system to perform a random walk in temperature space.27, 28, 29, 30, 31, 32, 33 However, these algorithms normally require an interactive procedure and relatively expensive trial simulations such as REM. In this study, we propose a simple method to compute good initial weights from short trial MD simulations. The combination of this scheme with an adaptive weighing method is shown to efficiently determine a set of weights enabling the system to perform a random walk in temperature space.31
In this paper, we apply both SREM and ST to the Fs peptide in order to study the helix-coil transition using a distributed computing network. Our aim is to make an exact comparison between SREM, ST, and MD. We show that both enhanced sampling methods outperform standard MD and give reasonable agreement with experimentally determined thermodynamic properties of the Fs peptide.
SYSTEM AND METHODS
Serial replica exchange
The SREM algorithm,24 a serial version of the REM, is designed to run asynchronously on a worldwide distributed computing environment such as FAH.34 We will first review the original REM. REM, also referred to as parallel tempering, involves running independent MD or MC simulations in parallel at different temperatures.13, 14 After a certain interval, an attempt is made to exchange the configurations of the neighboring replicas (closest neighbors in temperature space), typically as shown by the following
| (1) |
where Xi and Ti are the configuration and the temperature of the ith replica, respectively. In the current study, we will focus on using MD to propagate each replica.
The transition probability for exchanging adjacent replicas i and j must satisfy the detailed balance condition,
| (2) |
where P(i→j) is the transition probability for the exchange i→j and Pi(Xj,pj) is the probability of finding configuration Xj with momenta pj at temperature i.
The equilibrium probability of state i for the canonical ensemble is
| (3) |
where βi=1∕(kBTi), pi is the momenta, and Zi is the partition function. The Hamiltonian Hi(Xi,pi) is the sum of the kinetic energy (K) and potential energy (U) (Hi(Xi,pi)=K(pi)+U(Xi)).
A rescaling of the momenta13 following the exchange causes the kinetic energy to cancel out in the detailed balance equation, and the transition probably can be rewritten as
| (4) |
where
| (5) |
If the Metropolis criteria is applied then one of the transition probabilities will always be one. Thus, they can be written as
| (6) |
From Eq. 6, it is easy to show that the average acceptance ratios for the forward and backward transitions in REM are equal,
| (7) |
The above REM scheme requires synchronization and frequent communication between different processors. This requirement is not suitable for a distributed computing environment which consists of a heterogeneous network of distributed computers that are unable to communicate directly with one another. Recently, Hagen et al.noticed that in REM energy is the only property involved in the detailed balance condition, They derived the SREM based on this property.24 In SREM, PEDFs, P(E,Tn), are stored at different temperatures. The algorithm works as follows: A single replica is propagated with MC or MD at temperature Tn using a single processor. After a certain interval, it attempts to move to the neighboring temperature Tn+1. At this time, two potential energies En and En+1 are required to determine the transition probability as shown in Eq. 5. En is the potential energy of the current simulation system and En+1 is sampled from the energy distribution P(E,Tn+1) at Tn+1. If the move is accepted, the replica will continue propagating at the new temperature Tn+1, otherwise the replica will stay at the initial temperature Tn. In this way, a single replica can walk through the whole temperature space and thermodynamic averages can be computed at different temperatures.
The main difficulty with SREM is determining the PEDFs. SREM is only approximately correct unless the exact PEDFs are used. Hagen et al.suggest that the PEDFs be updated iteratively until they are stationary.24 We apply SREM on a distributed computing network to study the helix-coil transition. In Sec. 3, we will discuss the convergence of the PEDFs and show that SREM predicts correct thermodynamic properties for the Fs peptide system.
Simulated Tempering
ST is another enhanced sampling method suitable for a distributed computing environment because it is inherently a serial algorithm.9, 10 In ST, configurations are sampled from an expanded canonical ensemble in which the canonical ensemble with different temperatures are weighted differently. A generalized hamiltonian Ξn(X,p) is defined as
| (8) |
where βn=1∕(kBTn), H(X,p) is the Hamiltonian for the canonical ensemble at temperature Tn, and the a priori determined constant gn is the weight for the temperature Tn.
In practice, ST works as follows: A single simulation is performed at a particular temperature using MC or MD, and after a certain interval, an attempt is made to change the configuration to another temperature among a list of choices (T1,…,Tn) as shown by the following:
| (9) |
where Xi is the configuration of the system and Ti is the temperature.
The transition probability for moving from Ti to Tj has to satisfy the following detailed balance condition:
| (10) |
The probability of state i for the expanded canonical ensemble is
| (11) |
where βi=1∕(kBTi), pi is the momenta, and Z is the partition function for the expanded canonical ensemble.
The momenta are rescaled just as in REM, again causing them to drop out of the detailed balance condition. The transition probabilities after applying the metropolis criteria are shown by the following:
| (12) |
where Ui(x) and Uj(x) are potential energies sampled from the canonical ensembles at Ti and Tj, respectively.
In contrast to SREM, which is an approximate method unless the exact PEDFs are employed, ST is an exact method regardless of the selection of the weights. However, without proper weighting, ST will only explore a subset of temperature space and becomes inefficient. In ST, the “optimal” weights are typically defined to be a set of weights which lead the system to perform a random walk in temperature space, resulting in uniform sampling of each temperature.9, 10, 25, 26, 30, 31, 32, 33 In Sec. 3, we show that suchuniform sampling does not necessarily produce optimal sampling, and could oversample at high temperatures and undersample at low temperatures or around the melting temperature. Thus, we refer to weights leading to uniform sampling as “free energy” weights rather than optimal weights in this study, for reasons explained in the next section.
How to choose weights leading to uniform sampling? In ST, the probability that temperature Ti is visited in the expanded canonical ensemble is
| (13) |
where Zi and Z are partition functions for the canonical ensemble at Ti and for the expanded ensemble, respectively.
In the canonical ensemble, the partition function is related to the Helmholtz free energy,
| (14) |
Uniform sampling where P1=P2=…=Pn can be achieved if
| (15) |
Since the weights leading to uniform sampling equal the unitless free energies at different temperatures, we refer to them as free energy weights. It is not an easy task to determine these free energy weights. In principle, these unitless free energies can be estimated from trial simulations using the weighted histogram analysis method.27, 28, 31 However, this still requires an interactive procedure and relatively expensive trial simulations such as REM.31
In this study, we propose a simple method to compute approximate free energy weights from short trial MD simulations. Our method is based on the following property:25 The “free energy” weights leading to uniform sampling must yield the same acceptance ratios for both forward and backward transitions from Ti to Tj as shown by the following:
| (16) |
From Eq. 13, we can compute the average acceptance ratios,
| (17) |
where P(Ui) is the PEDF at Ti and U0=(gi−gj)∕(βi−βj).
PEDFs for each temperature are estimated from the short trial MD simulations by assuming the distributions are Gaussian.
| (18) |
where ⟨Ui⟩ and σi can be computed from the trial simulations.
By solving Eq. 16, we can obtain a set of near free energy weights with a given temperature list. This scheme is an extension of the method proposed by Park and Pande,25 in which the weights were also computed by ensuring equal average acceptance ratios for the forward and backward transitions. However, in their original scheme, they only considered the average potential energy at each temperature. By taking into account the potential energy distribution our method provides greater efficiency, especially around the melting temperature where PEDFs are normally wider. To gain this advantage we assume that the PEDFs are Gaussian. This assumption has been shown to be valid in a variety of biological systems26, 35 including the Fs peptide studied here. More generally, we believe that the central limit theorem36 implies the overall PEDFs are nearly Gaussian for any biological system in explicit solvent due to the large number of degrees of freedom.
Recently, Park26 showed that the two methods for obtaining approximate free energy weights discussed above are consistent, i.e., ⟨P(i→j)⟩ and ⟨P(j→i)⟩ become identical only if gi=βifi. These near free energy weights are still approximate considering the limited length of the trial MD simulations. For example, it is particularly difficult for these simulations to capture slow conformational changes, e.g., protein folding∕unfolding. Therefore, in our study we combined the above scheme with an adaptive weighing method. The latter regularly updates the weights during the ST simulations using an adaptive weighted histogram analysis method (WHAM) by Bartels and Karplus.31
In ST, choosing free energy weights only ensures ⟨P(i→j)⟩=⟨P(j→i)⟩. But the value of the acceptance ratio is determined by the temperature gap ΔTij=Ti−Tj. Transition probabilities diminish quickly with increasing temperature gap. For example, when Ti⪢Tj, ⟨P(i→j)⟩=⟨P(j→i)⟩≈0, thus it will take forever to achieve uniform sampling even if the equilibrium probabilities are equal for the two states (Pi=Pj). Therefore, the attempted moves in ST are usually between neighboring temperatures and a good temperature list will yield relatively large and equal acceptance ratios between them.
Simulation details
In this study we examined the capped Fs (Acc-A5[AAAR+A]3A-NMe) peptide. The AMBER-99ϕ potential,5 a modified version of AMBER99,37 was selected because it was found to better reproduce experimental helix-coil properties compared to earlier AMBER potentials.5 Both the ST and SREM algorithms were implemented in a version of the GROMACS molecular dynamics simulation package38 modified for the FAH (Ref. 34) infrastructure (http://folding.stanford.edu).
Two initial configurations are used, as shown in Fig. 1. The first is a prehelix structure with a helical content of 58% and the second is a random coil structure with no helical content. Each system is solvated in a 42 Å cubic box using 2039 TIP3P water molecules.39 Three Cl− counterions were included to neutralize the charged peptide. The simulation systems were minimized using a steepest descent algorithm, followed by a 100 ps MD simulation applying a position restraint potential to the peptide heavy atoms. All simulations were conducted using constant NVT with a Nosé-Hoover thermostat having a coupling constant of 0.02 ps−1.40 Long-range electrostatic interactions were treated using the reaction field method with a dielectric constant of 80. 9 Å cutoffs were imposed on nonbonded interactions. Neighbor lists were updated every ten steps. A 2 fs time step was used and covalent bonds involving hydrogen atoms were constrained with the LINCS algorithm.41
Figure 1.
The two initial configurations used for simulations of the capped Fs peptide (Ace-A5[AAAR+A]3A-NMe): (a) A prehelical structure and (b) a random-coil structure.
Starting from the two initial configurations, 1300 simulations were performed on a distributed computing environment using both the SREM and ST enhanced sampling methods. The total simulation time was aggregated to more than 250 μs. The same 50 element, roughly exponentially distributed temperature list covering a range from 285 to 592 K was used for both SREM and ST. The initial temperatures were uniformly selected from the temperature list. Thus, there are 26 simulations starting from each temperature, each with a different set of initial velocities. In both SREM and ST simulations, exchanges were attempted every 2 ps. In SREM, potential energies were saved every 0.4 ps. To obtain initial estimates of the PEDFs in SREM, we performed two hundred 500 ps SREM simulations where every move was accepted, resulting in a continuous walk in temperature space. The above simulations were first equilibrated for 2.5 ns at different initial temperatures. In a subsequent updating phase, slightly different from what was suggested by Hagen et al.,24 we continued updating the PEDFs, though the updates became less frequent with time. The PEDFs were updated every 40 ns for about 40 iterations at first, then every 400 ns for about 20 iterations, and at last every 1000 ns. In ST, the initial weights were computed using the data obtained from 50 short 100 ps trial simulations. Subsequently, the weights were updated approximately every 400 ns by an adaptive weighing scheme.31
In the SREM∕ST simulations run on a distributed computing environment described above, PEDFs or weights were updated based on data gathered from a heterogeneous network of computers with different rates of progress for each of a number of parallel simulations. Thus, it is difficult to do an exact comparison of the efficiency of SREM and ST using distributed computing data. To overcome this issue, we performed additional SREM, ST, and MD simulations on a local computer cluster. To ensure these simulations could be compared exactly, they were run with the same parameters and for the same duration. In addition, the same protocol was used for updating the SREM PEDFs and the ST weights. To be more specific, 50 24 ns simulations were run with SREM and ST. For MD 50 simulations were run with constant NVT at each of the three temperatures: 285, 308, and 592 K. For SREM and ST a 1 ns MD simulation with constant NVT was run for each of the 50 temperatures in our temperature list. We obtained initial weights for ST by solving Eq. 16 and PEDFs for SREM from these 1 ns simulations. These simulations were then extended using the SREM and ST algorithms. The PEDFs or weights were updated every 500 ps for six iterations. Then they were updated every 4 ns for five iterations. Thus, just as for MD at each of the three temperatures, a total of 50 24 ns simulations were run for both SREM and ST. The first 4 ns of each simulation was disregarded for equilibration purposes regardless of the algorithm used.
Lifson-Roig helix-coil counting theory
Helical properties were computed using the Lifson–Roig helix-coil counting theory.42, 43 In this model, a residue is considered to be helical if ϕ∊(−60±x)° and ψ∊(−47±x)°, where x is typically 30 (Refs. 5, 18) but may be varied. We set x to 40°, and show that this choice gives the best agreement with the melting temperature using the AMBER-99ϕ potential in Sec. 3C. Following the Lifson–Roig model, a helical segment is defined as three or more consecutive helical residues because a minimum of three residues are required to form a helical hydrogen bond. Each segment has a length of n−2, where n is the total number of consecutive helical residues. Thus, the maximum helical length of our 21 residue Fs peptide system is 19. This maximum is used to calculate the helical content as
| (19) |
where Nc is the helical content, Ns is the number of helical segments, Nh is the length of segment h, and Nmax is the maximum possible helical length.
The Lifson–Roig model also gives average helix nucleation and propagation parameters called ⟨ν⟩ and ⟨ω⟩, respectively. Mathematically, ⟨ν⟩ is the average statistical weight of a residue being in a helical state and is found as follows:
| (20) |
where F(ϕ,ψ) is the free energy of the given ϕ,ψ angles.5 The ⟨ω⟩ parameter is the statistical weight of a residue participating in a helical segment and thus requires a residue to be helical itself and belong to a group of at least three consecutive helical residues. It can be calculated as
| (21) |
where W(ϕ,ψ) is similar to F(ϕ,ψ) but includes the interaction of the given residue with its neighbors when they form a helical segment.5
RESULTS AND DISCUSSION
Comparison of SREM, ST, and MD
To demonstrate the usefulness of the generalized ensemble methods examined in this work we first discuss the results of an exact comparison between SREM, ST, and standard MD. This comparison is based on simulation data generated using each of the algorithms with the same amount of sampling, as described in the Methods section. We also investigate the rate of the convergence for PEDFs in SREM and weights in ST. The data generated by the distributed computing network are shown to be well converged and used as the gold standard for this comparison.
Convergence of the PEDF in SREM
As stated in Sec. 2A, the main obstacle for SREM is determining the PEDFs. This algorithm cannot be used for production unless the PEDFs are converged. Thus, we first investigate the convergence of the PEDFs.
χ2convergence measure. The χ2 convergence measure was proposed by Hagen et al.24 to verify the convergence of PEDFs. χ2 is defined to be an integrated error,
| (22) |
where N is the number of bins in the potential histogram, Pi(t) is the value of the ith bin of the potential energy histogram generated by potential energies collected over time t at a particular temperature, and is the reference PEDF.
Reference PEDFs. In order to demonstrate convergence we need a set of converged PEDFs as a reference. Figure 2a shows two nearly identical sets of SREM PEDFs from massive distributed computing simulations. Each set is from one of the two starting configurations. To quantitatively test their convergence we applied an integrated difference measure (D2(T)) which is analogous to the χ2 measure.24. The D2(T) values at different temperatures are close to zero (∼10−9 or smaller), indicating strong convergence of the two sets of PEDFs. Section 3B also shows that these massive distributed computing SREM simulations generate converged thermodynamics properties. We thus use these well converged PEDFs as our reference point.
Figure 2.
(a). Potential energy distribution functions (PEDFs) generated from FOLDING@HOME data at each of the 50 temperatures used. The black and red curves show the converged PEDFs from simulations starting from a prehelix structure and a coil structure, respectively. (See Fig. 1 for the two initial configurations.) (b). Heat capacity (Cv=∂U∕∂T) as a function of temperature generated from Folding@home simulations starting from the two initial configurations.
Convergence of PEDFs. When the well converged PEDFs from distributed computing simulations are used as the reference distributions, χ2(t) should decay to zero. On the other hand, when PEDFs from initial trial are used as the reference, χ2(t) should grow to a plateau value. Using as the reference distribution has certain advantages, since it does not require a prior knowledge of the correct PEDFs.
In a previous study, Hagen et al. showed that the average χ2(t) over all temperatures is a good convergence measure for the alanine dipeptide system they studied.24 However, we show here that such an average χ2(t) measure misrepresents the convergence of PEDFs for the Fs peptide system because PEDFs at different temperatures do not converge at the same rate. Figure 3 displays the average χ2(t) measures using both and as reference distributions. Although PEDFs obtained from simulations starting from a helical structure converge slightly faster than those obtained from simulations starting from a coil structure, both sets of average χ2(t) curves seem to converge after about 6 ns. Curves using as the reference distribution decay to a value very close to zero (<10−7) while curves using as the reference distribution start to reach a plateau. However, not all the PEDFs have converged within 6 ns, as shown in Fig. 4. This figure shows PEDFs from SREM simulations performed on the cluster as well as PEDFs from our distributed computing simulations at three representative temperatures: 285, 308, and 592 K. When T=308 K, PEDFs obtained from 50 6 ns cluster simulations display a visible deviation from the corresponding curves obtained from distributed computing. In particular, the whole potential distribution corresponding to the coil starting structure [the center column of Fig. 4b] is clearly shifted to higher energy. On the other hand, all the PEDFs at 285 and 592 K have nearly converged. Most of the PEDFs at other temperatures are also converged, except a few around T=308 K.
Figure 3.
The χ2 convergence measure averaged over all temperatures as a function of time. Triangles correspond to using as the reference point while circles are used when is the reference. The black curves are from simulations starting from a prehelical structure, while gray (red) curves are obtained from simulations starting from a coil structure.
Figure 4.
Potential energy distribution functions (PEDFs) for three temperatures: 285 K (left column), 308 K (middle column), and 592 K (right column). (a) Rough PEDFs from the 1 ns trial MD simulations performed on the local cluster. The black and red curves correspond to simulations starting from a prehelix structure and a coil structure, repetitively. (b) Comparison of PEDFs obtained from 6 ns SREM simulations at each of the 50 temperatures on the local cluster with those from distributed computing simulations. The black and red curves show results from the local cluster simulations starting from the prehelix and coil structures, respectively. The green and blue curves show the results from FOLDING@HOME simulations again starting from a prehelix and coil structure, respectively. (c) The same as (b) except that 50 24 ns SREM simulations are used to compute the PEDFs.
In Fig. 5, we show χ2(t) and average χ2(t) curves for our cluster simulations at three representative temperatures using as the reference distribution. At 285 and 592 K all the χ2(t) curves are similar to the average χ2(t) plot and decay to a value below 10−7 within 6 ns regardless of the initial configuration. However, the χ2(t) plot at 308 K decays much slower than those at other temperatures. At 308 K the χ2(t) plot starting from the prehelical structure converges at about 10 ns [see Fig. 5a] while the plot starting from the coil structure decays even slower and never falls below 10−7 during our 24 ns SREM simulations [see Fig. 5b].
Figure 5.
χ2 convergence measure of the PEDFs as a function of time at three representative temperatures, 285 (green triangles), 308 (blue diamonds), and 592 K (red asterisks) are shown and compared to the averaged χ2 (black circles). The plots are averaged over 50 SREM simulations, and are used as the reference distributions. (a). χ2 convergence measure obtained form simulations starting from a prehelical structure. (b) The same as (a) except that the results are obtained form simulations starting from a coil structure.
A further investigation shows that the melting temperature occurs around 308 K, which explains the slow convergence of the PEDFs at this temperature. At the melting temperature, the potential energy distribution is likely to be wider due to the more or less equal probability of finding the folded and unfolded states. As shown in Fig. 2a, potential energy distributions around T=308 K (the seventh curve from the left) are indeed wider than adjacent distributions. In addition, the value of the melting temperature is confirmed by the location of the dominant peak in the heat capacity plot, which occurs at around 310 K as shown in Fig. 2b.
Uniform sampling convergence measure. As stated above, PEDFs at different temperatures do not necessarily converge at the same rate. Furthermore, PEDFs converge slower around the protein melting temperature. Thus, the average χ2(t) is not a good convergence measure, and all 50 χ2(t) plots must be monitored instead. In this section, we describe a new convergence measure based on how uniform the sampling is across temperature space.
As shown in Eq. 7, the average forward and backward transition probabilities from Ti to Tj in SREM are equal, implying that each simulation should spend an equal amount of time at each temperature given infinite sampling. Given finite sampling, approximately uniform sampling would also be achieved if there are no large gaps in the acceptance ratios between neighboring temperatures. Since all the acceptance ratios in our SREM simulations are between 20% and 40%, approximately equal sampling at each temperature should be obtained if the exact PEDFs are applied (see Fig. 11 for the acceptance ratios). However, if the PEDFs are not converged then ⟨Pij⟩≠⟨Pji⟩, resulting in nonuniform sampling. Thus, uniform sampling could serve as an indirect convergence measure for PEDFs. We define u(t), the average deviation from uniform sampling, as
| (23) |
where N denotes the number of temperatures, ni represents the total amount of time spent at temperature Ti in a window of time centered at t over all the simulations, and ⟨ni⟩ is the average of ni over all the temperatures. Given this definition, u(t)=0 when the sampling is perfectly uniform and increases the more nonuniform the data are.
Figure 11.
Comparison of acceptance ratios from SREM and ST.
Figure 6 shows the amount of time our SREM simulations spent at each temperature during a series of 4 ns windows as well as the corresponding u(t) curves. When starting from a prehelical structure, the sampling is already roughly uniform in the second window (from 4 to 8 ns) but slightly more time is still spent at low temperatures before t=16 ns. The corresponding u(t) plot is always below 0.4 and even falls below 0.2 after 16 ns, indicating that the PEDFs are converged. The convergence time predicted by u(t) (16 ns) is slightly longer than that predicted by the average χ2(t) (10 ns) since uniform sampling can only be achieved after the converged PEDFs have been applied for a while. On the other hand, Fig. 6b clearly shows more sampling at low temperatures for simulations starting from a coil structure, though the sampling starts to become uniform as time progresses. The u(t) curve for these simulations decrease from 0.8 to 0.3, but never falls below 0.2, indicating that not all the PEDFs have converged within the 24 ns simulations. This observation is consistent with the prediction from the temperature specific χ2(t) measures (as opposed to the average χ2(t)).
Figure 6.
(a). The amount of time each of the SREM simulations starting from a helical structure spent at each temperature. (b). The same as (a) except that data is collected from SREM simulations starting from a coil structure. (c). The uniform sampling convergence measure u(t) as a function of time obtained from simulations starting from a helical structure (black curve) and a coil structure (red curve). Each data point is averaged over the 50 SREM simulations using a time window of 4 ns.
The uniform sampling (u(t)) measure has the advantage that only one function is necessary to evaluate the convergence of all of the PEDFs, whereas the χ2(t) measure requires the user to monitor one curve for each temperature. For the u(t) measure to be valid, the time window has to be long enough for the system to explore the whole temperature space. One additional caveat is that there should not be any large gaps in the acceptance ratios, otherwise it will take a long time for the system to reach uniform sampling. Finally, we note that the u(t) measure is still an average measure and, therefore, may smooth out one or two deviant temperatures. However, the above analysis demonstrates that it is a more sensitive measure than the χ2(t) metric and should provide a reasonable gauge of the level of convergence.
Convergence of the weights in ST
As stated in Sec. 2B, ST is an exact method regardless of the selection of the weights. However, ST simulations will be constrained to a subset of temperature space without proper weighing. A set of free energy weights will lead the system to perform a random walk in temperature space. In this study, we combined a method to obtain near free energy weights from trial simulations as described in Sec. 2B with an adaptive weighting scheme using WHAM (Ref. 31) to determine the free energy weights. In this section, we investigate the convergence properties of the weights in our ST simulations.
Figure 7 shows the time evolution of Δg=gi+1−gi during simulations on the cluster for three pairs of neighboring temperatures: One at low temperature, one at high temperature, and one around the melting temperature. The differences between weights are plotted rather than the weights themselves as it is the differences that determine the acceptance ratios, as shown in Eq. 13. The weights obtained from our massive distributed computing ST simulations starting from different initial configurations are well converged, as shown in Table 1. We note that the weights for temperatures below the melting temperature are not converged as well as the other weights. Differences of up to 0.42 KJ∕mol in free energy differences (Δfji=gj∕βj−gi∕βi) are observed below the melting temperature but differences of not more than 0.1 KJ∕mol occur elsewhere. This difference indicates that thermodynamic properties are more difficult to converge below the melting temperature. Regardless, the differences in Δfji are still much less than a KT so we consider them to be well converged (see Table 1). Thus, we chose to use the weights from our distributed computing simulations starting from a prehelical configuration as our reference point for the convergence of weights from our cluster simulations. As shown in Fig. 7, the weights computed from short trial MD simulations are already close to the correct values (within 0.5%) for three temperature pairs. However, weights around the melting temperature (T=308 K) still converge slower than those at other temperatures.
Figure 7.
Δg=gi+1−gi from ST simulations as a function of time for three pairs of neighboring temperatures: 285 and 288 K (left column), 304 and 308 K (center column), and 583 and 592 K (right column). Black and gray (red) curves correspond to Δg values obtained from simulations starting from a helical and a coil structure, respectively. The well converged weights from distributed computing simulations are used as a reference (blue curve without symbols).
Table 1.
Δg=gj−gi obtained from distributed computing simulations starting from a helical structure (third column) and a coil structure (fourth column) at representative temperature pairs. In the fifth column, differences between free energy differences Δfji=gj∕βj−gi∕βi obtained from simulations starting from a helical structure and a coil structure are displayed. KT at temperature i is shown in the sixth column. Δfji(helical)−Δfji(coil) is much smaller than KT at all temperature pairs.
| Ti | Tj | Δgji(helical) | Δgji(coil) | Δfji(helical)−Δfji(coil) (KJ∕mol) | KTi (KT∕mol) |
|---|---|---|---|---|---|
| 285 | 288 | 360.36 | 360.38 | −0.06 | 2.37 |
| 288 | 292 | 466.48 | 466.39 | 0.22 | 2.39 |
| 292 | 296 | 451.13 | 450.95 | 0.42 | 2.43 |
| 296 | 300 | 436.41 | 436.30 | 0.28 | 2.46 |
| 300 | 304 | 422.25 | 422.29 | −0.09 | 2.49 |
| 304 | 308 | 408.41 | 408.45 | −0.09 | 2.53 |
| 308 | 312 | 394.65 | 394.69 | −0.11 | 2.56 |
| 312 | 317 | 475.35 | 475.37 | −0.06 | 2.59 |
| 317 | 322 | 457.33 | 457.33 | −0.02 | 2.63 |
| 322 | 327 | 440.48 | 440.48 | 0.00 | 2.68 |
| 347 | 352 | 368.18 | 368.18 | −0.01 | 2.88 |
| 399 | 405 | 314.38 | 314.39 | −0.01 | 3.32 |
| 447 | 454 | 277.36 | 277.35 | 0.04 | 3.71 |
| 497 | 506 | 273.58 | 273.57 | 0.04 | 4.13 |
| 583 | 592 | 184.33 | 184.33 | 0.00 | 4.84 |
As discussed above, a set of converged weights will produce uniform sampling in ST. In Figs. 8a, 8b, we again plot the amount of time spent at each temperature over a series of 4 ns windows. It is clear that the sampling is not uniform before 12 ns for simulations starting from either of the initial configurations. Before 12 ns, the system spends considerably more time exploring high temperatures. This biased exploration of temperature space results from the fact that the weights are not converged. When the weights are not converged, ⟨Pij⟩≠⟨Pji⟩, resulting in nonuniform sampling. In Fig. 9, we plot Pi→i−1−Pi−1→i for the transitions between all neighboring temperatures. When t<12 ns there is a significant difference between the forward and backward transition probabilities, especially around the melting temperature where i=6. After 12 ns the differences appear to be more randomly distributed around 0. These differences are probably due to the limitations of finite sampling rather than unconverged weights. To quantify the convergence of the weights we apply the same uniform sampling measure (u(t)) as used for SREM. As shown in Fig. 8c, the u(t) curves for each of the starting configurations decrease to a value below 0.2 after 16 ns, indicating that the weights are converged.
Figure 8.
(a). Amount of time the 50 ST simulations starting from a helical structure spent at each of the 50 temperatures. (b). The same as (a) except that data are collected from simulations starting from a coil structure. (c). The uniform sampling convergence measure u(t) as a function of time obtained from simulations starting from a helical structure (black curve) and a coil structure (red curve). Each data point is averaged over 50 ST simulations using a time window of 4 ns.
Figure 9.
Average probability difference (ΔP) between transitions to lower and higher temperatures over 50 ST simulations. ΔP=Pi→i−1−Pi−1→i. (a) ΔP obtained from simulations starting from a helical structure. (b). The same as (a) except that ΔP is obtained from simulations starting from a coil structure.
Convergence of helical properties
The convergence of various thermodynamic properties serves as another indirect measure of the convergence of our simulations. In theory, any thermodynamic property will depend on the underlying PEDFs in SREM or weights in ST. In practice, however, thermodynamic properties may not converge at the same rate as these underlying variables. They are an attractive measure of convergence because, at least in this study, they are the primary quantities of interest. Measuring the convergence of thermodynamic properties also allows a direct comparison to MD.
In this study we will focus on the helical content. Other measures, such as number of helical residues, number of helical segments, and the maximum length of a single helix were also examined and showed similar trends (data not shown). To visualize the convergence of our simulations we plot the average helical content as a function of time for simulations starting from extended configurations and prehelical configurations, as shown in Fig. 10 for a few representative temperatures. Each point in Fig. 10 shows the average helical content over a 4 ns window with error bars corresponding to one standard deviation. The first 4 ns are omitted to allow for equilibration. The mean values and statistical uncertainties are computed by using WHAM (Ref. 28).
Figure 10.
Comparison of helical content as a function of time between SREM, ST, and standard MD using the same amount of sampling at three temperatures: (a). 285, (b). 308, and (c) 592 K. (Black curve) Data obtained from simulations starting from a prehelical structure. (Gray∕red curve) Data obtained from simulations starting from a prehelical structure. (Blue curve without symbols) The converged value from distributed computing simulations. The mean values and statistical uncertainties are estimated using WHAM. (Ref. 30).
From Fig. 10c it is clear that both SREM and ST converge quickly at high temperatures and yield very small error bars. However, neither converges as quickly as the high temperature MD simulations. The small error bars make sense in light of the fact that the free energy surface is more smooth at higher temperatures. In addition, the high fidelity of the convergence of MD compared to SREM and ST is probably due to the fact that the MD plot is for 50 24 ns simulations at constant temperature while 50 24 ns simulations are performed for all temperatures in SREM or ST.
At low temperatures SREM appears to converge more quickly than ST. This is not an inherent advantage of SREM, however. Rather, this phenomenon is the result of SREM being biased towards lower temperatures and ST being biased towards higher temperatures before their PEDFs and weights converge, as shown in Figs. 68. The fact that SREM converges faster than ST at lower temperatures in this case indicates that uniform sampling of temperature space may not be optimal. Various methods of exploiting this observation are now being implemented.
MD simulations starting from the prehelical configuration at low temperatures converge to the correct value quickly, most likely because the system tends to explore the free energy basin around the native structure. MD simulations starting from an extended configuration fail to converge to the correct value, however, because of the presence of large free energy barriers at low temperatures. The much faster convergence of our SREM and ST simulations starting from an extended state demonstrates that configurations accepted from high temperatures do indeed help sampling at lower temperatures.
Around the melting temperature both SREM and ST converge more slowly than at higher temperatures. SREM also converges more slowly than at lower temperatures, and this would probably be true for ST as well if it were not initially biased towards higher temperatures in this system. As for the PEDFs and weights, this slow convergence results from the broad energy distribution, more or less equal occurrence of the folded and unfolded states, and slow folding∕unfolding transitions. Even at the melting temperature SREM and ST still converge within 10 ns, whereas MD fails to converge within the 24 ns simulations. Thus, both SREM and ST provide faster and more accurate thermodynamic predictions than MD. In this case they converge at least twice as quickly, though we cannot exactly quantify the advantage provided since our MD simulations fail to converge at all. Interestingly, the thermodynamic properties also converge faster than the PEDFs and weights (10 ns as opposed to 16 ns). Thus, convergence of the PEDFs and weights in SREM and ST is not necessarily a prerequisite for the convergence of thermodynamic properties of interest.
The weights in ST are converged after 16 ns regardless of the starting configuration. PEDFs from our SREM simulations converge after 16 ns starting from the prehelical configuration but take more than 24 ns to converge when started from a coil configuration. Regardless of these small differences, both algorithms are capable of reaching convergence within a small number of short simulations for this system (50 24 ns simulations here). More interestingly, certain thermodynamic properties such as helical content converge even faster than the PEDFs and weights. Given the utility of these short simulations, a large number of simulations run in a distributed computing environment should be able to yield converged weights or PEDFs, even for a larger system. Thus, both of the enhanced sampling methods studied here should prove useful for studying the folding free energy landscapes of biomolecules in a distributed environment.
ST does have certain advantages over SREM. First, ST is an exact method, while SREM is only approximately correct unless the exact PEDFs are used. Second, ST has higher acceptance ratios than SREM as shown in Fig. 11. This observation is in agreement with Park’s recent analytic proof that ST should give higher acceptance ratios than SREM for any system given the same temperature list.26 The primary difficulty with ST is determining the free energy weights. As discussed above, we show that obtaining initial weights from short trial simulations followed by refinement by an adaptive weighing method such as an adaptive WHAM (Ref. 31) very efficiently determines a set of free energy weights, which allows the system to perform a random walk in temperature space.
Study of helical-coil transitions by SREM∕ST in a distributed computing network
Distributed computing environments are able to generate a massive amount of sampling. Thus, converged PEDFs and weights can be more readily achieved, as shown in Fig. 2 and Table 1. The convergence of these underlying variables leads to better convergence of thermodynamic properties. For example, Fig. 12 shows helical content melting curves demonstrating that simulations starting from the prehelical and unfolded states converge excellently for both SREM and ST. Such exact convergence was not possible on our local computer cluster, where curves starting from different initial configurations converged only within very large error bars (data not shown).
Figure 12.
Helical content as a function of temperature obtained from distributed computing simulations. (Black curve) SREM starting from a helical structure. (Red curve) SREM starting from a coil structure. (Blue curve) ST starting from a helical structure. (Green curve) ST starting from a coil structure. The mean values and statistical uncertainties are estimated using WHAM (Ref. 28).
In fact, Fig. 12 also shows that SREM and ST simulations run on a distributed computing environment give almost identical results. Each gives a melting temperature of about 310 K, in reasonable agreement with the experimental value of 334 K.44 Again, this level of agreement was not found in our cluster simulations (data not shown). Thus, it appears that large-scale SREM simulations are able to yield converged PEDFs, leading to thermodynamic predictions with the same level of accuracy as ST even though SREM is an approximate method. However, for larger systems where converging the PEDFs may be more difficult, ST is probably still more useful since it is an exact method. Regardless, it is clear that SREM and ST are both powerful tools when employed on a distributed computing network.
At present there is no straightforward way to apply the u(t) convergence measure to FAH data due to its asynchronous nature. To ensure that uniform sampling was achieved 50 short 4 ns simulations were performed uniformly starting from different temperatures on a local cluster using the final FAH PEDFs in the case of SREM and the final FAH weights in the case of ST. Application of the u(t) metric to these data sets yielded values of 0.10 and 0.18 for SREM simulations starting from helical and coil structures, respectively, and values of 0.11 and 0.17 for ST simulations. These values are below the empirically determined cutoff of 0.2 used previously, indicating that near uniform sampling is achieved.
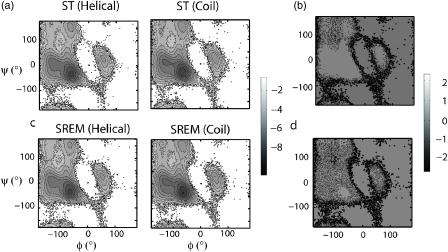
In addition to the average thermodynamic properties such as helical content, we also demonstrate the convergence of the free energy landscape starting from different initial configurations as projected onto the ϕ and ψ axis. Figure 13 shows the convergence of the ϕ-ψ free energy landscape for both SREM and ST simulations at 308 K. Visual inspection of Fig. 13a shows that the free energy landscapes computed from ST simulations started from both prehelical and random coil states are almost identical. Figure 13b shows the difference map between the two free energy landscapes and quantitatively demonstrates the agreement between the two landscapes. Differences larger than kT mostly appear at the edges where the probability is low and therefore more variable. Results from SREM simulations are also converged as shown in Figs. 13c, 13d. Furthermore, these free energy landscapes are in agreement with those from an earlier work employing ensemble MD simulations.5
Figure 13.
Free energy landscape projected onto the Φ and Ψ axis in units of kcal∕mol at 308 K. (a) Obtained from ST simulations started from the prehelical state (left figure) and from a random coil state (right figure). (b) The difference map between the free energy landscapes in (a). (c) The same as (a) except that free energy landscapes are obtained from SREM simulations. (d). The difference map between the free energy landscapes in (c).
The utility of the SREM and ST algorithms may be further increased by moving away from uniform sampling. Relative to short cluster simulations, our distributed simulations are approaching infinite sampling. In this case our melting curves are based on 12 times as much sampling while still throwing out 6 times as much data for equilibration. In fact, these numbers give an underestimate since other simulations not included in these calculations still contributed to the convergence of the PEDFs and weights. Aggregate simulation times for SREM and ST were 64.3 and 185.8 μs, respectively. Even so, the error bars at lower temperatures, the primary area of interest, are still greater than those at higher temperatures as shown in Fig. 12. Adaptive sampling methods may serve to decrease the uncertainty at temperatures of interest even on a distributed computing network. One possibility would be to start more simulations from regions of temperature space that are not well converged. Another possibility would be to update the temperature list and or weights in order to bias simulations towards a specific set of temperatures.
Temperature dependent properties
Sorin and Pande5 define a helical residue as having ϕ∊(−60±30)° and ψ∊−47±30°. They chose a cutoff of 30° because slight variations in this number caused the least difference in their results. Basing their cutoff on this variance relies on the assumption that the Fs peptide is a two state folder. Two distinct state would imply some range of cutoffs that would give more or less the same results.
In this work, we use a cutoff of 40°. To arrive at this cutoff we started with the definition of the transition temperature, which is the temperature at which half the population is folded and the other half is unfolded. We assume that the folded state is completely helical while the unfolded state has no helical content, thus the helical content at the transition temperature would be 0.5. The helical content was then plotted as a function of temperature using cutoffs of 30°, 35°, 40°, 45°, and 50°, as shown in Fig. 14. Both curves obtained from simulations starting from a helical structure and a coil structure converge well at every cutoff angle. The plots using a 40° cutoff are found to give 0.5 helical content at the transition temperature of 310 K, so 40° was selected as the optimal cutoff.
Figure 14.
Helical content as a function of temperature obtained from distributed computing ST simulations starting from a helical structure or a coil structure. Each curve uses a different cutoff angles to define a helical residue.
We also calculated the Lifson–Roig average helix nucleation and propagation propensity parameters, ⟨ν⟩ and ⟨ω⟩, respectively, for our simulations. Our values for ⟨ν⟩ were an order of magnitude greater than the experimentally measured values (data not shown), in agreement with previous calculations.5, 45 This overestimate may be attributed to the AMBER99φ force field over stabilizing helices. As shown in Fig. 15, our results for ⟨ω⟩ are converged well for simulations starting from different configurations and more promising. At low temperatures we find reasonable agreement with the experimentally measured values. The overall trend of our ⟨ω⟩ curve is qualitatively similar to the experimentally measured curve, although our values fall off less quickly with increasing temperature. This can probably be attributed to some combination of the poor temperature dependence of the force field and the overstabilization of alpha helices at high temperatures.
Figure 15.
Average helix propagation parameters as a function of temperature obtained from distributed computing ST simulations starting from a helical structure (black circles), ST simulations starting from a coil structure (red squares), and from experiments (Ref. 47) (blue diamonds).
CONCLUSION
Generalized ensemble methods such as the replica exchange method (REM) and simulated tempering (ST) have led to important advances in the sampling of conformations of biomolecular systems on computer clusters of all sizes. As demonstrated in this work, they can significantly speedup convergence relative to ensemble MD for the helical peptide studied here. However, it is still difficult to get convergence within the constraints of the computing power available on most local clusters. One common way of testing the convergence of such simulations is to determine whether the sampling is Boltzmann weighted. However, a simple thought experiment shows that it is possible to achieve Boltzmann weighted sampling of only a subset of the conformational space. A good measure of convergence is to achieve “reversible folding”46 (i.e., multiple unfolding and refolding events in the same trajectory). However, even for a small protein, it is extremely difficult to achieve enough sampling to simulate reversible folding with all-atom force field in the explicit solvent. The difficulty is mostly due to the limit of the computing resources. With the large-scale distributed computing, we are able to gain higher level of convergence than those work using local clusters. Another less strict measure for the convergence is to run simulations starting from very different conformations, such as the prehelical and random coil states used in this work and compare the results as it demonstrates their robustness. Furthermore, it is important to look at a number of properties as some may converge faster than others. Besides thermodynamic properties, two obvious candidates are the PEDFs in SREM and the weights in ST.
Generalized ensemble methods have proved extremely powerful when taking these considerations into account in the context of a massive distributed computing environment. For ST, we demonstrate the efficacy of a new scheme for determining weights allowing the system to perform a random walk in temperature space that employs short trial simulations to make an initial estimate of the weights followed by massive simulations with an adaptive weighting method using WHAM. By making use of the extensive sampling capabilities of such an environment we are able to obtain converged energy distributions, weights, and temperature dependent thermodynamic properties. Both relatively short cluster simulations and large-scale distributed computing simulations demonstrate that SREM and ST converge to equivalent results within error on a small system. The performance of these methods may be improved through judicious use of nonuniform sampling. Thus, both methods could serve as powerful tools for further studies of more complicated systems on distributed computing networks. However, we note that ST may be more appropriate for larger systems because it is an exact solution, yielding valuable results even if a set of unconverged weights are used whereas SREM may not provide accurate predictions until after its PEDFs have converged.
ACKNOWLEDGMENTS
This work would not have been possible without the FOLDING@HOME users who contributed invaluable processor time (http://folding.stanford.edu). We would like to thank Dr. Sanghyun Park, Dr. Guha Jayachandran, Dan Ensign, and Dr. Eric Sorin for their help on setting up SREM and ST at FOLDING@HOME. We would like to thank Dr. Morten Hagen and Professor Bruce Berne at Columbia University for helpful discussions. We would also like to thank A. Kulp for her excellent advice on comma placement and other editorial comments. This work was funded by NIH R01-GM062868 and NSF MCB-0317072. Cluster resources were provided by NSF Award No. CNS-0619926. X.H. is supported by the National Institutes of Health through the NIH Roadmap for Medical Research, Grant No. U54 GM072970. G.R.B. is supported by the NSF Graduate Research Fellowship Program. X.H. would also like to thank Professor Michael Levitt for his support.
References
- Hukushima K. and Nemoto K., J. Phys. Soc. Jpn. 10.1143/JPSJ.65.1604 65, 1604 (1996). [DOI] [Google Scholar]
- Hansmann U. and Okamoto Y., Curr. Opin. Struct. Biol. 10.1016/S0959-440X(99)80025-6 9, 177 (1999). [DOI] [PubMed] [Google Scholar]
- Snow C., Nguyen H., Pande V. S., and Gruebele M., Nature (London) 10.1038/nature01160 420, 102 (2002). [DOI] [PubMed] [Google Scholar]
- Rhee Y., Sorin E., Jayachandran G., Lindahl E., and Pande V. S., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0307898101 101, 6456 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorin E. and Pande V. S., Biophys. J. 10.1529/biophysj.104.051938 88, 2472 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jayachandran G., Vishal V., Garcia A. E., and Pande V. S., J. Struct. Biol. 10.1016/j.jsb.2006.10.001 157, 491 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jayachandran G., Vishal V., and Pande V. S., J. Chem. Phys. 10.1063/1.2171194 124, 164902 (2006). [DOI] [PubMed] [Google Scholar]
- Sorin E. J. and Pande V. S., J. Am. Chem. Soc. 10.1021/ja060917j 128, 6316 (2006). [DOI] [PubMed] [Google Scholar]
- Lyubartsev A. P., Martsinovski A. A., Shevkunov S. V., and Vorontsov-Velyainov P. N., J. Chem. Phys. 10.1063/1.462133 96, 1776 (1992). [DOI] [Google Scholar]
- Marinari E. and Parisi G., Europhys. Lett. 10.1209/0295-5075/19/6/002 19, 451 (1992). [DOI] [Google Scholar]
- Geyer C. J. and Thompson E. A., J. Am. Stat. Assoc. 10.2307/2291325 90, 909 (1995). [DOI] [Google Scholar]
- Hansmann U. H. E., Chem. Phys. Lett. 10.1016/S0009-2614(97)01198-6 281, 140 (1997). [DOI] [Google Scholar]
- Sugita Y. and Okamoto Y., Chem. Phys. Lett. 10.1016/S0009-2614(99)01123-9 314, 141 (1999). [DOI] [Google Scholar]
- Swendsen R. H. and Wang J. S., Phys. Rev. Lett. 10.1103/PhysRevLett.57.2607 57, 2607 (1986). [DOI] [PubMed] [Google Scholar]
- Zhou R., Berne B. J., and Germain R., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.201543998 98, 14931 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou R., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.2233312100 100, 13280 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmerling C., Strockbine B., and Roitberg A. E., Proc. Natl. Acad. Sci. U.S.A. 124, 11258 (2002). [DOI] [PubMed] [Google Scholar]
- Garcia A. E. and Sanbonmatsu K. Y., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.042496899 99, 2782 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin C., Hu C., and Hansmann U., Proteins 10.1002/prot.10351 52, 436 (2003). [DOI] [PubMed] [Google Scholar]
- Schug A., Herges T., and Wenzel W., Proteins 10.1002/prot.20290 57, 792 (2004). [DOI] [PubMed] [Google Scholar]
- Zheng W., Andrec M., Gallicchio E., and Levy R., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0704418104 104, 15340 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhee Y. and Pande V., Biophys. J. 84, 775 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E., Levy R. M., and Parashar M., J. Comput. Chem. 10.1002/jcc.20839, 29, 788 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagen M., Kim B., Liu P., Friesner R. A., and Berne B. J., J. Phys. Chem. B 10.1021/jp064479e 111, 1416 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S. and Pande V. S., Phys. Rev. E 10.1103/PhysRevE.76.016703 76, 016703 (2007). [DOI] [PubMed] [Google Scholar]
- Park S., “Weights and acceptance ratios in generalized ensemble simultations,” Phys. Rev. E (submitted).
- Kumar S., Bouzida D., Swendsen R. H., Kollman P. A., and Rosenberg J. M., J. Comput. Chem. 10.1002/jcc.540130812 13, 1011 (1992). [DOI] [Google Scholar]
- Chodera J. D., Swope W. C., Pitera J. W., Seok C., and Dill K. A., J. Chem. Theory Comput. 10.1021/ct0502864 3, 26 (2007). [DOI] [PubMed] [Google Scholar]
- Mitsutake A. and Okamoto Y., Chem. Phys. Lett. 10.1016/S0009-2614(00)01262-8 332, 131 (2000). [DOI] [Google Scholar]
- Park S., Ensign D. L., and Pande V. S., Phys. Rev. E 10.1103/PhysRevE.74.066703 74, 066703 (2006). [DOI] [PubMed] [Google Scholar]
- Bartels C. and Karplus M., J. Comput. Chem. 12, 1450 (1997). [DOI] [Google Scholar]
- Wang F. and Landau D. P., Phys. Rev. Lett. 10.1103/PhysRevLett.86.2050, 86, 2050 (2001). [DOI] [PubMed] [Google Scholar]
- Li H., Fajer M., and Yang W., J. Chem. Phys. 10.1063/1.2424700 126 024106 (2007). [DOI] [PubMed] [Google Scholar]
- Shirts M. and Pande V. S., Science 10.1126/science.290.5498.1903 290, 1903 (2000). [DOI] [PubMed] [Google Scholar]
- Rathore N., Chopra M., and de Pablo J. J., J. Chem. Phys. 10.1063/1.1831273 122, 024111 (2005). [DOI] [PubMed] [Google Scholar]
- Tijms H., Understanding Probability: Chance Rules in Everyday Life (Cambridge University Press, Cambridge, 2004). [Google Scholar]
- Wang J., Cieplak P., and Kollman P. A., J. Comput. Chem. 21, 1049 (2000). [DOI] [Google Scholar]
- Lindahl E., Hess B., and van der Spoel D., J. Mol. Model. 7, 306 (2001). [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 10.1063/1.445869 79, 926 (1983). [DOI] [Google Scholar]
- Hoover W., Phys. Rev. A 10.1103/PhysRevA.31.1695 31, 1695 (1985). [DOI] [PubMed] [Google Scholar]
- Hess B., Bekker H., Berendsen H. J. C., and Fraaije J. G. E. M., J. Comput. Chem. 18, 1463 (1997). [DOI] [Google Scholar]
- Lifson S. and Roig A., J. Chem. Phys. 10.1063/1.1731802 34, 1963 (1961). [DOI] [Google Scholar]
- Qian H. and Schellman J. A., J. Phys. Chem. 10.1021/j100189a015 96, 3987 (1992). [DOI] [Google Scholar]
- Williams S., Causgrove T. P., Gilmanshin R., Fang K. S., Callender R. H., Woodruff W. H., and Dyer R. B., Biochemistry 10.1021/bi952217p 35, 691 (1996). [DOI] [PubMed] [Google Scholar]
- Nymeyer H. and Garcia A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.2232868100 100, 13934 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao F. and Caflish A., J. Chem. Phys. 10.1063/1.1591721 119, 4035 (2003). [DOI] [Google Scholar]
- Rohl C. A. and Baldwin R. L., Biochemistry 10.1021/bi9706677 36, 8435 (1997). [DOI] [PubMed] [Google Scholar]