Abstract
Middle-ear sound transmission was evaluated as the middle-ear transfer admittance HMY (the ratio of stapes velocity to ear-canal sound pressure near the umbo) in gerbils during closed-field sound stimulation at frequencies from 0.1 to 60 kHz, a range that spans the gerbil’s audiometric range. Similar measurements were performed in two laboratories. The HMY magnitude (a) increased with frequency below 1 kHz, (b) remained approximately constant with frequency from 5 to 35 kHz, and (c) decreased substantially from 35 to 50 kHz. The HMY phase increased linearly with frequency from 5 to 35 kHz, consistent with a 20–29 μs delay, and flattened at higher frequencies. Measurements from different directions showed that stapes motion is predominantly pistonlike except in a narrow frequency band around 10 kHz. Cochlear input impedance was estimated from HMY and previously-measured cochlear sound pressure. Results do not support the idea that the middle ear is a lossless matched transmission line. Results support the ideas that (1) middle-ear transmission is consistent with a mechanical transmission line or multiresonant network between 5 and 35 kHz and decreases at higher frequencies, (2) stapes motion is pistonlike over most of the gerbil auditory range, and (3) middle-ear transmission properties are a determinant of the audiogram.
INTRODUCTION
This paper continues an inquiry into high-frequency sound transmission through the external and middle ear (ME) of the Mongolian gerbil Meriones unguiculatus that began with a study of the distribution of ear canal (EC) sound pressure (Ravicz et al., 2007). In that study, we established that sound pressure could be measured in the EC over the tympanic membrane (TM) near the umbo over a broad frequency range and that sound pressure at that point provided an adequate characterization of ME input up to 60 kHz. In this paper, we use similar EC sound measurements to characterize the ME input and measurements of stapes velocity to characterize the ME output. The transfer function computed as the ratio of these two variables describes sound transmission through the ME over a frequency range that spans the range of gerbil hearing.
The nature of high-frequency ME sound transmission has recently been a matter of considerable debate. Though simple models suggest that ME sound transmission should be bandpass in nature and limited at high frequencies by the mass of the ossicles and the cochlear fluids (see, e.g., Zwislocki, 1962; Hemilä et al., 1995), most data suggest that sound transmission is broadband (see, e.g., Johnstone and Sellick, 1972; Ruggero and Temchin, 2002). A pertinent question is whether sound transmission is maintained at high levels at high sound frequencies, as in lossless transmission through a matched transmission line (Puria and Allen, 1998; Ruggero and Temchin, 2002), or decreases at some high-frequency limit. Published data in gerbil do not resolve this debate: Some measurements of the stapes velocity (normalized by EC sound pressure) show a bandpass characteristic (Rosowski et al., 1999), while others show scala vestibuli sound pressure or stapes velocity (normalized as above) that remains roughly constant to the highest frequency of measurement (e.g., Olson, 1998; Overstreet and Ruggero, 2002).
A complication in nearly all of these previous studies of ME sound transmission is adequate characterization of the ME input, sound pressure stimulus in the EC, at high frequencies (Rosowski et al. 1999; Overstreet and Ruggero, 2002; Dong and Olson, 2006). The similarity between the wavelength λ of sound in air at high frequencies and the dimensions of the gerbil EC and TM (λ∕10 is less than the length of even a surgically shortened EC (∼4 mm) above 8 kHz) suggests that the sound pressure produced by stimuli at higher frequencies will vary substantially along the EC and, to a lesser extent, over the surface of the TM (Ravicz et al., 2007). In the earlier study, we explored possible causes of error in estimating ME input (Ravicz et al., 2007) and concluded that sound pressure measurements made within 1 mm of the umbo were a good estimate of the sound pressure at the TM over the umbo and therefore of ME input at frequencies up to at least 60 kHz. In this study, we use such sound pressure measurements as the normalization for stapes velocity to evaluate ME sound transmission.
Another complication in using stapes velocity to evaluate ME sound transmission is that the ME output, stapes velocity, has components in all three dimensions, especially at high frequencies (Decraemer et al., 2000; Decraemer et al., 2006b, 2007). Though evidence suggests that stapes motion in the piston direction is the effective stimulus to the cochlea (Decraemer et al., 2006a, 2007) and therefore the effective ME output, the three dimensionality of stapes motion means that the velocity of a single point may not be a good descriptor of stapes piston motion. In this study, we compute the motion of a measured point on the stapes posterior crus in three dimensions and estimate the accuracy of this motion in describing piston stapes motion.
Determining ME sound transmission helps address another question: whether the frequency range of hearing is determined primarily by cochlear limitations or whether ME limitations could also play a role. Several investigators (e.g., Khanna and Tonndorf, 1969; Khanna and Sherrick, 1981; Rosowski et al., 1986, 1988; Rosowski, 1991a, 1991b) have postulated that cochlear sensitivity is approximately constant across frequency and that the audiogram is determined by the sound transmission properties of the ME. Other investigators (e.g., Overstreet and Ruggero, 2002; Ruggero and Temchin, 2002) have pointed out that the frequency sensitivity of the ensemble of cochlear sensory cells spans only the auditory range and claim that (1) efficient ME sound transmission spans a wider frequency range than cochlear sensitivity and hence (2) the audiogram is determined only by cochlear sensitivity. A weakness of all previous studies is that the highest frequency examined is still within the gerbil auditory range.
In this paper, we evaluate ME transmission by a transfer function between stapes velocity and EC sound pressure from 100 to 60 kHz. This frequency range spans the gerbil’s range of hearing.1 We define the ME transfer admittance HMY(f) as the ratio of the stapes velocity spectrum VS(f) (the ME output) to the spectrum of sound pressure PU(f) near the umbo (the ME input) by
| (1) |
where VS(f), PU(f), and HMY(f) are functions of frequency f.2 Stapes velocity is described by the velocity of a point on the stapes posterior crus measured in a direction as close to the piston direction as practicable. (Henceforth, velocities, sound pressures, and admittances will be understood to be functions of f unless otherwise noted.)
We present measurements from two laboratories in which somewhat different techniques were used: the Eaton-Peabody Laboratory at MEEI (Ravicz and Rosowski) and an auditory physiology laboratory at the University of Bristol (where Cooper was at the time). We show that the ME transfer admittance has features of a simple resonant system at low frequencies, is representative of a multiresonant network or a transmission line below about 35 kHz, and decreases rapidly with frequency above that, consistent with a multiresonant network. These results confirm and extend conclusions of other recent studies of stapes motion and ME transmission (Decraemer et al., 2007; de la Rochfoucauld et al., 2008). We present evidence that errors in specifying cochlear input from single-point stapes velocity measurements versus whole-stapes measurements are small below 50 kHz. We compute cochlear input impedance from HMY and previous measurements of scala vestibuli sound pressure measured in a similar fashion (Olson, 2001) and show that cochlear input, as evaluated by VS or by cochlear sound power transmission, is a fairly good predictor of the entire gerbil audiogram.
METHODS
Animal preparation
The preparation and use of the experimental animals were approved by the Institutional Animal Care and Use Committees at MEEI and Bristol as applicable and have been described in detail previously (Ravicz et al., 2007). Briefly, 19 young adult Mongolian gerbils (13 at MEEI, the same as those used in the 2007 study; 6 at Bristol) were anesthetized, the pinna flange and cartilaginous EC were removed, and the soft tissue was removed from the surface of the skull around the opening of the bony EC and for some distance posteriorly. One or more holes were made in the exposed wall of the auditory bulla to preclude a buildup of static pressure within the ME air spaces and to provide visual access to the stapes. A coupling tube was cemented around the bony EC opening with dental cement or cyanoacrylate glue to permit a high-frequency sound source to be coupled and recoupled reliably to the ear.
Experimental methods
The experiments were conducted in a sound-isolation booth. Heart rate was monitored throughout the experiment, and body temperature was maintained at (37±1) °C with a heating pad. Anesthesia boosters at half the initial surgical dose were provided as necessary to suppress the pedal withdrawal reflex. The animal’s head was clamped securely in a custom holder. At Bristol, the animal and holder were mounted in nested goniometers such that the axis of the outer goniometer was parallel to the interaural axis (transverse), the axis of the inner goniometer was approximately anterior-posterior (longitudinal), and the intersection of the goniometer axes was at the stapes of the measured ear (cf., Decraemer et al., 1994, 2007). At the conclusion of the live experiment, the animal was euthanized with a fatal dose of anesthesia.
Stapes velocity
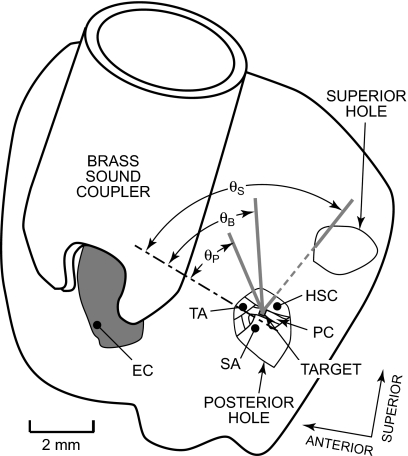
To assess stapes velocity, a small target comprising four to six retroreflective balls was placed on the posterior crus of the stapes, and the velocity VS of this stapes target in response to chirp or tone sound stimuli presented in the EC was measured with a laser-Doppler vibrometer [MEEI: OPV 501∕2600, Polytec PI, Waldbronn, Germany; Bristol: custom (Cooper, 1999)]. Both velocity magnitude |VS| and phase ∠VS relative to the stimulus were measured. Visual access to the stapes was through the small hole(s) in the bulla wall posterior to the EC opening (Fig. 1; see also Rosowski et al., 1999). At MEEI, most measurements were made through an ∼2 mm diameter hole located approximately in the same horizontal plane as the EC opening—the “posterior hole” (Fig. 1). The vibrometer laser beam (thick gray line in Fig. 1) was oriented in a direction as close to the direction of pistonlike stapes motion (dot-dashed line) as permitted by the edge of the hole and the anatomical structures within the ME: the angle θ between this “baseline” measurement direction and the piston direction (θP in Fig. 1) was 27°–37°. At Bristol, the access hole was larger (4–5 mm diameter), and the vibrometer laser was oriented in a baseline direction somewhat further from the direction of pistonlike stapes motion than the MEEI measurements: θ≈47° (θB in Fig. 1). Each vibrometer measured velocity only in the direction of its line of sight.
Figure 1.
View of the left side of a gerbil head showing the locations of measurement access holes and the view of the stapes through the posterior hole used for most stapes velocity measurements. The skin and soft tissue were removed from the superior and lateral aspects of the auditory bulla. A brass sound coupler was cemented about the opening of the bony ear canal (EC). A hole was made in the bulla wall posterior to the bony EC (“posterior hole”). A retroreflective target (gray square) was placed on the stapes posterior crus (PC). The view of the stapes was limited by the tympanic annulus (TA), the horizontal semicircular canal (HSC), and the stapedial artery (SA). At MEEI, stapes velocity was measured from a direction as close to the piston direction (dot-dashed line) as possible. The angle θ between the measurement direction (the baseline direction, thick gray line) and the piston direction (labeled θP) was 27°–37°. (Note that angles are foreshortened in this view and appear larger or smaller than they actually were.) At Bristol, this hole was larger, and θ between this baseline measurement direction and the piston direction (labeled θB) was approximately 47°. Another hole (“superior hole”) was made in the bulla superior to the posterior hole to vent the ME and (in some bones) to provide an alternate view of the posterior crus target for stapes velocity measurements: θ for this measurement direction (solid and dashed gray line, labeled θS) was 61°–65°.
To estimate VS in three-dimensional (3D) space, additional velocity measurements were made as the direction of the line of sight was changed. At MEEI, VS was also measured in three ears in another direction through a second similar-size hole superior to the original hole (the “superior hole”), θS in Fig. 1. Components of stapes motion could then be computed within a plane defined by the two measurement directions (see the Appendix). At Bristol, VS was also measured in three ears from a range of directions permitted by the edges of the wider access hole. Velocities measured from five to six different directions were used to compute components of stapes motion in three dimensions (as in Decraemer et al., 1994, 2007; see the Appendix).
The measurement directions were determined differently at MEEI and Bristol, with differing degrees of precision. At MEEI, directions were estimated postmortem by separating the head from the body and orienting it so the stapes footplate was nearly horizontal. An operating microscope was oriented along each measurement direction (as determined by the hole and anatomical limits described above), and the angles from the measurement direction to the horizontal plane and the plane defined by the stapes crura were measured with a protractor. Repeatability was within 5°. At Bristol, the goniometers enabled the measurement direction to be changed in 0.1° increments. Determination of the orientation of the stapes relative to the measurement direction was estimated visually and so was less precise (±20°) than at MEEI.
Ear-canal sound pressure
EC sound pressure PEC was measured simultaneous to stapes target velocity: Both magnitude |PEC| and phase ∠PEC relative to the stimulus were measured. At MEEI, PEC was measured at various locations within the bony EC remnant with a custom probe tube microphone (based on a Larson–Davis 2520 1∕4–in. condenser microphone, Provo, UT—see Ravicz et al., 2007; 1.27 mm outer diameter) that was advanced ∼0.5–1 mm down the bony EC toward the TM along an approximately longitudinal trajectory [see Ravicz et al., 2007, Fig. 2b]. In the last four ears measured at MEEI, EC sound pressure was also measured over the TM at a point near the umbo PU (Ravicz et al., 2007). At Bristol, PEC was measured with a probe tube microphone (based on a Brüel+Kjær 4134 1∕4-in. condenser microphone, Denmark) near the border of pars tensa and pars flaccida, within 1 mm of the EC remnant opening and 2.5–3 mm from the umbo.
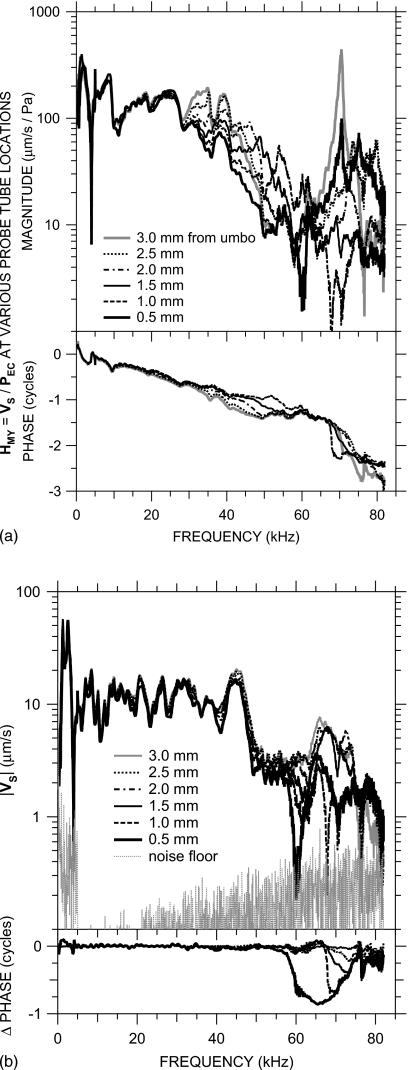
Figure 2.
(a) Transfer admittance HMY=VS∕PEC with the probe tube at various locations along an approximately longitudinal trajectory. Legend indicates the approximate distance from the probe tube tip to a point on the TM over the umbo. Top: magnitude; bottom: phase. (b) VS with the probe tube at the various locations. The relative invariance of VS with probe tube location below 58 kHz shows that variations in HMY with probe tube location are due primarily to variations in PEC among those locations. Also shown is a typical VS measurement noise floor (gray dots). Top: magnitude; bottom: phase relative to ∠VS with the probe tube approximately 3.0 mm from the umbo.
Stimulus generation and response measurement
Computer-controlled experimental systems at MEEI and Bristol were used for stimulus generation and measurement of sound pressure and velocity responses. The system used at MEEI is described in Ravicz et al. (2007). Stimuli were broadband chirps 0.05–99 kHz, and vibrometer and microphone responses were digitized at 225 kHz. Some stimuli were deemphasized by 20 dB below 5 kHz to allow higher stimulus levels to be used to deliver more high-frequency sound energy into the EC. Broadband sound levels (summed across frequency) were 90–95 dB sound pressure level (SPL). The system used at Bristol is described in Cooper and Rhode (1992) and comprised a Tucker–Davis Technologies (Alachua, FL) System II digital to analog converter and attenuators and a fast (1 MHz) Analogic (Peabody, MA) analog to digital converter to digitize vibrometer and microphone responses. The system presented tones in the EC at 80 dB SPL with a logarithmic frequency spacing of eight points per octave.
Computation of transfer admittance from stapes velocity and ear canal sound pressure
Because the transfer admittance used to describe ME function and facilitate comparisons among ears in this study and to other studies depends on both stapes velocity and EC sound pressure, the accuracy of EC sound pressure measurement is important. We have shown in a previous paper that, even with the EC shortened by removing the cartilaginous EC (leaving only the bony EC), EC sound pressure PEC varies substantially between the opening of the bony EC and the TM over the umbo at frequencies above 30 kHz (Ravicz et al., 2007).
The effect of this variation in PEC on the transfer admittance is shown for one ear (0402R) in Fig. 2a. The curves show HMY computed from VS and PEC measured with the probe tube at various positions between the EC entrance and the umbo. Though there are small variations in HMY between probe tube positions at sound frequencies less than 30 kHz, above that frequency, |HMY| varies by a factor of 3 or more depending on the probe tube position. A plot of the stapes velocity (not normalized by PEC) measured with the probe tube at these various positions [Fig. 2b] demonstrates that VS is nearly invariant with probe tube position below 58 kHz; hence, the HMY variations below 58 kHz in Fig. 2a are almost entirely attributable to variations in PEC. Consequently, we will use PU for HMY computations in those ears in which PU measurements are available. The technique for computing HMY in other ears is described below.
Figure 2b also shows that there are variations in VS with probe tube position at higher frequencies. Below 58 kHz, VS varied by less than a factor of 1.2 when the probe tube position was varied. Above 58 kHz VS varied substantially (|VS| decreased by a factor of 3, ∠VS decreased by almost 0.5 cycles) when the probe tube approached to within 0.5 mm of the umbo, which suggests that the presence of the probe tube affected the sound field at the umbo at higher frequencies.3 To minimize the effects of the probe tube on HMY computations, we use VS measured with the probe tube near the EC entrance, where there was minimal effect on VS.
Both VS and PEC were measured at frequencies up to 99 kHz at MEEI, but sound pressure measurements were valid only up to 82 kHz, and sound pressure variations in the microphone calibration setup limited accurate PEC measurements to 60 kHz and below (Ravicz et al., 2007; see Sec. 1). For these reasons and because of the probe-tube-induced variation in VS near 60 kHz described above, we limit our presentation of VS, PEC, and HMY to frequencies below 60 kHz.
In the four later MEEI ears (including the one shown in Fig. 2), measurements of EC sound pressure within 0.5 mm of the umbo (and throughout the EC) were available, and HMY in those ears was computed from VS normalized by PU as described above. In the nine early MEEI ears and the six Bristol ears, the only PEC data available were measured closer to the bony EC canal entrance, 2–3 mm from the umbo. For these 15 ears, we correct HMY computed from VS and PEC in each ear by an appropriate sound pressure transformation PU∕PEC between the umbo and the PEC measurement location, computed from measurements in the four later MEEI ears mentioned above.
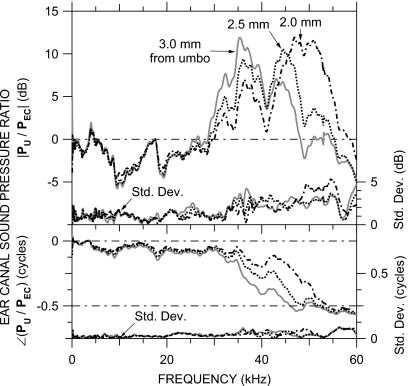
Figure 3 shows the mean PU∕PEC ratio for the four later MEEI ears at three EC locations that span the range of PEC measurement locations in the other ears: approximately 3.0 mm from the umbo, near the bony EC entrance; and approximately 2.5 and 2.0 mm from the umbo. PU∕PEC at each of these three locations was remarkably similar among ears [as revealed by the small standard deviations (s.d.)—right axis], consistent with previous acoustical measurements in gerbil (see, for example, Ravicz et al., 1992, 1996; Teoh et al., 1997). The variance in |PU∕PEC| at each location was due primarily to broadband differences—the overall frequency dependence and the frequencies of magnitude peaks and notches varied little among ears. The magnitude ratio was significantly4 greater than 0 dB between 30 and 45–55 kHz (depending on location) and differed significantly between the three locations from 28 to 35 kHz and from 48 to 52 kHz. (|PU∕PEC| was also significantly less than 0 dB from 8 to 17 kHz at all three locations, perhaps due to effects of the opening in the EC wall). The phase difference decreased to −0.5 cycles between 30 and 50 kHz (depending on location) and differed significantly between the three locations over this frequency range. In the 30–55 kHz range where |PU∕PEC| was significantly different from unity, differences in PU∕PEC between locations were greater than the PU∕PEC differences between ears.
Figure 3.
Ratios of sound pressure near the umbo PU to sound pressure in the bony EC PEC at various distances from the umbo. Each curve is the mean (in dB) of measurements in four ears. Top: magnitude ratio in dB; bottom: phase difference. At the bottom of each panel is the s.d. (right-hand vertical scale). VS∕PEC in the other 15 ears (see Figs. 56) was corrected by the mean PU∕PEC curve corresponding to the PEC measurement location in that ear.
For each of the other ears, the particular PU∕PEC for the correction was chosen as the curve for which the frequency of the |PU∕PEC| peak (35, 44, or 47–51 kHz) was closest to the frequency of the first |PEC| minimum in that ear (29–50 kHz). Except for a minor mismatch near the frequency of the first |PEC| minimum, HMY in the other ears was quite similar to HMY in the four later ears.
RESULTS
In this paper, we present results from independent experiments in two laboratories. The results from the two laboratories (MEEI and Bristol) have complementary strengths and considerable similarities. Stapes velocity was measured to higher frequencies at MEEI than at Bristol. At MEEI, VS and PEC were measured with a broadband chirp stimulus; at Bristol, pure-tone stimuli were used. The baseline measurement direction for VS at MEEI was generally closer to the direction of piston stapes motion than that at Bristol, and PEC was measured closer to the umbo at MEEI than at Bristol. For investigations of the 3D motion of the stapes posterior crus, VS was measured from five or six directions at Bristol but at most two directions at MEEI.
The HMY data shown in Figs. 4567 were computed from VS measured in the baseline direction normalized by sound pressure near the umbo PU (directly or indirectly) as described in Sec. 2C. As such, they show HMY in an “experimental” reference frame (along the line of sight of the laser vibrometer) rather than in a direction defined by the stapes orientation (an “intrinsic” reference frame; Decraemer et al., 2007). Later (in Sec. 4A), we will discuss the extent to which HMY estimates the ME transfer admittance in the piston direction in the intrinsic reference frame.
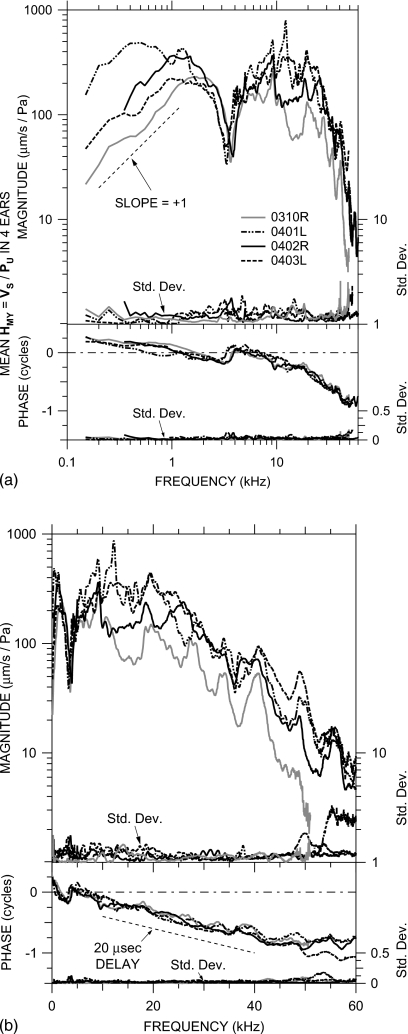
Figure 4.
Mean HMY=VS∕PU in four ears at MEEI in which PU was measured, shown in the experimental reference frame of the vibrometer. Each curve is the logarithmic mean of 11–22 VS measurements normalized by PU. Top: magnitude; bottom: phase. At the bottom of each panel is the s.d. (right-hand vertical scale). The |HMY| dip and ∠HMY ripple near 3–4 kHz are due to a resonance between the compliance of the air in the bulla and the mass of the bulla hole. (a) Logarithmic frequency scale; (b) linear frequency scale. The thin dashed line in panel (a) shows a log-log slope of +1. The thin dashed line in panel (b) indicates the phase slope corresponding to a 20–μs delay.
Figure 5.
Mean HMY=VS∕PU in nine ears at MEEI in which PEC was measured 2–3 mm from the umbo (black lines), corrected by a PU∕PEC curve from Fig. 3. Each curve is the logarithmic mean of two to six measurements. HMY in the four ears in Fig. 4 is shown by gray lines. An outlier (0309L) is shown by a dashed line. Top: magnitude; bottom: phase. (a) Logarithmic frequency scale; (b) linear frequency scale. The thin dashed line in panel (b) indicates the phase slope corresponding to a 25–μs delay.
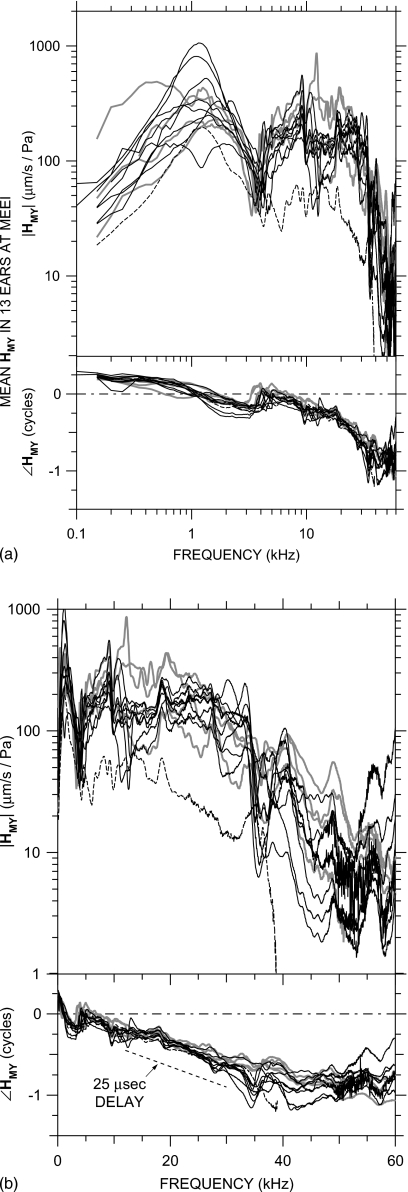
Figure 6.
Means±s.d. of HMY in 6 ears at Bristol (black line, error bars) and 13 ears at MEEI (gray line, shading). Top: magnitude; bottom: phase. (a) Logarithmic frequency scale; (b) linear frequency scale. The dashed line indicates the phase slope corresponding to a 29 μs delay.
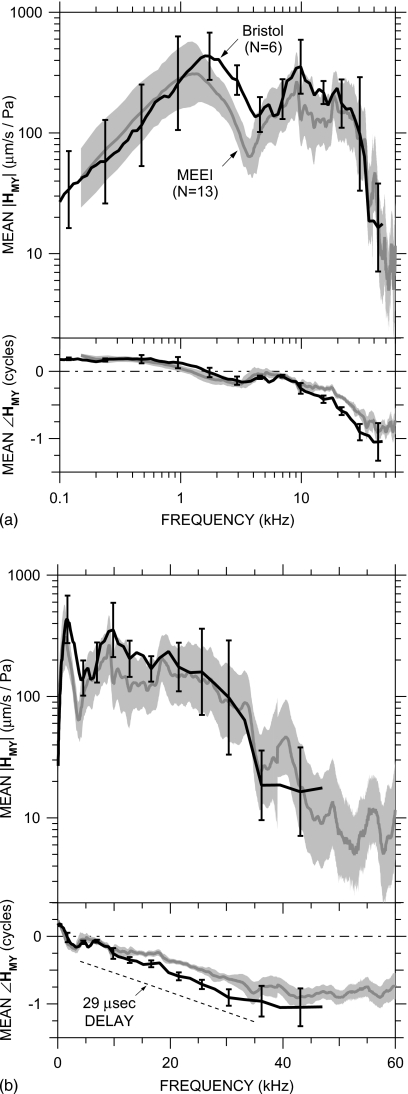
Figure 7.
HMY in a representative ear (0306L) at MEEI with the inner ear intact (solid line), with the round window punctured and open (dashed line), and with the inner ear drained (dot-dashed gray line). Results in two other MEEI ears were similar. Top: magnitude; bottom: phase.
Middle-ear transfer admittance at MEEI
The stapes velocity transfer function HMY is shown for four ears in Fig. 4: against a logarithmic frequency scale (to show low-frequency data more clearly) in panel (a) and against a linear frequency scale (to show high-frequency data more clearly) in panel (b). The HMY curve for each ear is the logarithmic mean5 of several VS measurements normalized by PU. HMY is shown for frequencies at which |VS| was above the measurement noise and motion artifact estimated from measurements of the sound-induced motion of the bone of the cochlear promontory [see Fig. 2b].6 The s.d. of measurements in each ear is plotted against the right-hand axis: as a magnitude ratio and as a phase addend. Both VS and PU were linear with stimulus level over at least a 40 dB range in these ears and those shown in Fig. 5.
In all ears, HMY shows a magnitude slope with frequency (d|HMY|∕df) of ∼+1 (on a log-log scale) and phase angle near +0.25 cycles at frequencies below 0.5–1 kHz, consistent with a compliance-dominated admittance [Fig. 4a]. The value of this compliance varies considerably (a factor of 10) among ears. The magnitude of HMY in all ears has a peak in the 0.5–2 kHz range and ∠HMY crosses zero at about the same frequency, consistent with a ME resonance. The relatively flat |HMY| peak and shallow ∠HMY slope indicate that the resonance is highly damped. Above the resonance, |HMY| decreases sharply to a notch near 3 kHz, and there is a positive ∠HMY ripple at the notch frequency. This |HMY| notch and ∠HMY ripple pair is consistent with a resonance between the compliance of the air in the ME and the mass of the air in the bulla hole (see, e.g., Ravicz et al., 1992; also Sec. 3C below). Above the notch frequency, |HMY| increases to a peak near 10 kHz (ear 0401L has a second peak at a slightly higher frequency), and ∠HMY has a small ripple at the frequency of the peak.
At frequencies above the peak(s), |HMY| is approximately constant with frequency (±a factor of 2) up to 30–35 kHz. ∠HMY continues to accumulate approximately linearly with frequency above the ripple [Fig. 4b], consistent with a delay. Below 35 kHz, the slope of ∠HMY with frequency (d∠HMY∕df) suggests a delay of 20 μs. At higher frequencies, |HMY| decreases sharply, and the rate of ∠HMY accumulation slows. Between about 40 and 60 kHz, d∠HMY∕df suggests a group delay of zero.
In addition to the four ears shown in Fig. 4, HMY was computed from VS∕PEC in nine earlier MEEI ears and corrected by an appropriate mean PU∕PEC as described in Sec. 2C. Logarithmic means of multiple estimates of HMY (computed from two to six VS and PEC measurement pairs) in each of these nine ears are shown as black lines in Fig. 5; HMY in the four ears in Fig. 4 is shown by gray lines. HMY in the earlier ears shows nearly all of the same features as HMY in the later ears. In all ears at low frequencies d|HMY|∕df is near +1 and ∠HMY is near +0.25 cycles; there is a broad |HMY| peak near 1–1.5 kHz (except in ear 0301L) and a shallow ∠HMY zero crossing at the same frequency; there is a |HMY| notch and ∠HMY ripple near 3 kHz, and there is a |HMY| peak and ∠HMY ripple near 10 kHz.7 At higher frequencies, up to 30–35 kHz, |HMY| is approximately constant (±a factor of 2 as above) in all ears (except 0309L, dashed line), and ∠HMY accumulates with frequency with a slope that implies a delay of about 25 μs. At still higher frequencies, above 35 kHz, |HMY| decreases sharply and ∠HMY flattens. (The magnitude and phase ripples near 35–40 kHz may be artifacts of the PU∕PEC correction; see Sec. 2C.) Except for the outliers above, |HMY| and ∠HMY have the same spectral shape among ears, and HMY in these earlier ears generally falls within the range of the HMY measured in the four ears of Fig. 4.
Middle-ear transfer admittance at Bristol
At Bristol, stapes velocity was measured on the posterior crus and PEC was measured near the EC entrance in a manner similar to that described above for measurements in the earlier nine ears at MEEI. Figure 6 shows the logarithmic mean of HMY in six ears, computed from VS and PEC measurements and the PU∕PEC correction for a probe tube location 2.5–3 mm from the umbo as described above and in Sec. 2C. The mean HMY (black line) is plotted against a logarithmic frequency scale in panel (a) and against a linear frequency scale in panel (b); the s.d. is shown at representative points by error bars. These data are compared to the mean HMY±s.d. in all MEEI ears (gray line and shading).
There is a marked similarity among the mean HMY measured at Bristol and MEEI: Both show a |HMY| slope of approximately +1 and ∠HMY near +0.25 cycles below 1 kHz [Fig. 6a], a broad |HMY| peak near 1–1.5 kHz, a |HMY| notch and ∠HMY ripple near 3–5 kHz, a |HMY| peak and ∠HMY ripple near 10 kHz, approximately constant |HMY| and linearly accumulating ∠HMY up to 30 kHz [Fig. 6b], and a fairly sharp rolloff in |HMY| and a flattening of ∠HMY above 35 kHz. There were some minor differences, but these differences were not statistically significant except in narrow frequency ranges: ∠HMY between 1 and 2 kHz, due to ∠HMY>0.25 cycles in two Bristol ears; |HMY| between 2 and 4 kHz, around the |HMY| dip due to the bulla hole resonance in MEEI measurements described above; ∠HMY around 5 kHz from a local ∠HMY dip probably due to a bulla hole resonance in Bristol measurements; and ∠HMY between 15 and 30 kHz, due to more delay in the Bristol ears (29 μs) than the MEEI ears (20–25 μs). The results from the two laboratories are sufficiently similar that conclusions about stapes motion from results in one laboratory should apply to all measurements.
Effect of middle-ear air spaces on middle-ear transfer admittance
The HMY measurements shown in Figs. 456 include two assumptions (one stated explicitly, one implied) about the effect of opening the ME on HMY: (1) the dip in |HMY| near 3–5 kHz was due to a resonance between the compliance of the ME air space and the mass of the air in the bulla hole, and (2) the open ME had no other effect on HMY. We tested these assumptions in three ears by measuring VS and PEC while the posterior hole was sealed with a small transparent window (piece of polycarbonate cover slip) and the ME was vented with a long thin polyethylene tube in the superior bulla hole (Ravicz et al., 1992; see Fig. 1). Only a few measurements could be taken, as the window quickly became fogged with condensation. Consistent effects were seen in two ears: the |HMY| notch and ∠HMY ripple at 3–4 kHz disappeared when the posterior hole was sealed, but the |HMY| notch and ∠HMY ripple at ∼10 kHz remained. The change was in stapes velocity; PEC did not vary. This result verifies that the |HMY| dips and ∠HMY ripples near 3 kHz in the MEEI data set were produced by the bulla opening and that the open bulla holes did not affect HMY at higher frequencies. Differences between Bristol and MEEI data in the 2–6 kHz range can be explained by the difference in the size of the bulla hole in the two preparations: The smaller acoustic mass associated with the larger bulla hole used in Bristol measurements would be expected to resonate with the ME air space compliance at a higher frequency (Ravicz et al., 1992).
Effect of removing inner-ear load on middle-ear transfer admittance
The extent to which cochlear load influences HMY was examined by measuring VS and PEC in three ears after the cochlear load was irreversibly removed by puncturing the round window and suctioning the cochlear fluids. Results from a representative ear are shown in Fig. 7; results from the other two ears were similar. Removing the cochlear load had several effects on HMY that were consistent among the three ears: (1) The |HMY| peak near 1 kHz was much greater (by a factor of 3–5) and sharper. |HMY| was elevated over the intact case between 800 Hz and 10 kHz. The sharper |HMY| peak was accompanied by an abrupt ∠HMY transition from about +0.2 to −0.2 cycles at the frequency of the |HMY| peak. This peak was unrelated to the |HMY| notch and ∠HMY peak near 3 kHz associated with the bulla hole. (2) Another comparable-size |HMY| peak and smaller ∠HMY transition were observed at 15–20 kHz. (3) In two of the three ears, a third |HMY| peak and ∠HMY transition were observed at a frequency approximately twice the frequency of the second |HMY| peak. These |HMY| peaks and ∠HMY transitions are consistent with removal of damping from a multiresonant network. These results show that the cochlear load is a significant influence on HMY at frequencies up to at least 40 kHz.
The observations of increased |HMY| excursion and less-damped HMY behavior after draining the cochlear fluids are consistent with measurements of cochlear input impedance in cat and human with the inner ear open (Lynch et al., 1982; Merchant et al., 1996) and ME input admittance or impedance in cat with the inner-ear lymphs drained (Lynch, 1981; Allen, 1986). The similarity of these observations to the accentuation of multiple admittance maxima and minima seen in cat (Puria and Allen, 1998) suggests that the gerbil ME also can be described as a multiresonant network or distributed system at frequencies up to 40 kHz.
Stapes velocity measured from other directions
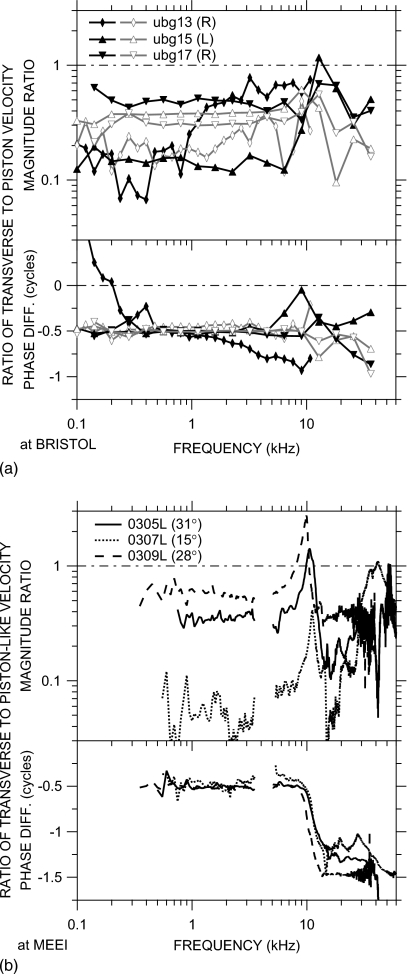
The unidirectional stapes velocity measurements used in the computed HMY shown in Figs. 4567 describe the motion of the stapes target only along the line of measurement. Additional measurements are needed to determine stapes motion in the piston direction. Besides the baseline VS measurements described above, all of which were made from approximately the same direction (the angle θ between the baseline direction and the piston direction was 28°–47°; see Sec. 2B1), additional measurements were made from different directions for the purpose of describing the motion of the stapes target in 3D space.
At Bristol, stapes velocity was measured in three ears from several well-controlled directions within 28° of the baseline direction. The measurement direction was varied from the baseline by rotating the animal with one or both of the goniometers: Moving the animal approximately about the longitudinal axis through an angle L from its baseline position varied θ substantially, while moving the animal about the transverse axis through an angle T from its baseline position had little effect on θ. At MEEI, stapes velocity was measured in three ears through a superiorly-located bulla hole (θ=61°–65°) in addition to the posterior bulla hole used for baseline measurements (θ=27°–37°; see Sec. 2B1 and Fig. 1).
Figure 8a shows the ratio of VS measured from five other directions in one ear (ugb15) at Bristol to the mean of three VS measurements from the baseline direction. Below 7 kHz, changing the measurement direction through an angle L caused regular variations in |VS|: for negative L that decreased θ (closer to the piston direction, solid line), |VS| increased, and for positive L that increased θ (long-dashed lines), |VS| decreased. These variations were larger than the range of variation among baseline measurements (about ±10% for |VS|, shading). Changes through an angle T (dotted lines) had virtually no effect on |VS| in this frequency range. No values of L or T caused any substantive change in ∠VS below 7 kHz. These trends were common to variations in L and T in the two other ears.
Figure 8.
Variations in VS with measurement direction. (a) Magnitude ratios (top) and phase differences (bottom) for a typical ear at Bristol as the measurement direction was varied from the baseline direction through goniometer angles L and T about longitudinal and transverse axes, respectively (see Sec. 2B). Effects of various L (which correspond approximately to changes in the angle θ between the measurement direction and the piston direction) are shown as solid and long-dashed lines; effects of various T (which had little effect on θ) are shown by dotted lines. The range of measurements from the baseline direction is shown by the shading. (b) Ratio of VS measured through the superior vs posterior bulla holes in three ears at MEEI. Top: magnitude ratio; bottom: phase difference.
Near 10 kHz, both |VS| and ∠VS in all three ears varied with changes in L or T. The variations in |VS| with changes in L described above were larger, and ∠VS varied as well. Changes in T caused a change in |VS| just below 10 kHz and a change in the opposite direction in |VS| just above. ∠VS was also more variable with changes in T just above the frequency of maximum |VS| variability. Between 15 and 36 kHz (the highest frequency in this series), changes in |VS| were similar to those described above at low frequencies but smaller, and ∠VS varied very little with changes in L or T.
Figure 8b shows the ratio of stapes velocity measured through the superior bulla hole to the mean of baseline measurements in each of the three ears at MEEI. Similar to Fig. 8a, |VS| measured from a direction further from the piston direction was smaller than |VS| measured from a direction closer to the piston direction (the ratio was <1), and the difference was greater at low frequencies (below 7–10 kHz) than at frequencies above 15 kHz (except above 50 kHz). Both |VS| and ∠VS varied with measurement direction near 10 kHz. The variations with direction were larger than those in Fig. 8a, perhaps because θ for superior hole measurements was larger, the angle between measurement directions was greater (39°–78° at MEEI versus 23°–28° at Bristol), or the frequency resolution was finer.
The changes in |VS| and ∠VS as θ varied are similar to those seen in human temporal bones but occur at higher frequencies. As in gerbil, increasing θ in human caused a monotonic decrease in |VS| and no change in ∠VS at low frequencies below a critical frequency, a decrease in |VS| variation and increase in ∠VS variation near the critical frequency, and a smaller dependence of |VS| on θ above the critical frequency (Chien et al., 2006), but the break frequency was higher in gerbil (∼10 kHz) than that in human (∼1.5 kHz). The higher critical frequency in gerbil might be related to the smaller size of the gerbil TM and ossicular chain, but the common frequency dependence suggests that similar mechanisms influence stapes motion.
DISCUSSION
Estimates of piston stapes motion from measurements
The ME transfer admittance estimates of Figs. 456 were computed from the motion of the stapes target along the line of measurement in the baseline direction (the experimental reference frame). To relate any single-point stapes motion measurements (such as ours) to stapes piston motion (the assumed input to the cochlea; Decraemer et al. 2007), two fundamental assumptions must be made: (1) the motion in the baseline measurement direction is proportional to piston motion and (2) the motion of the posterior crus is representative of the motion of the stapes footplate; i.e., the stapes acts as a rigid body without bending. By using measurements from various directions in addition to the baseline direction (see Fig. 8), we compute the motion in three dimensions (Bristol data) and estimate the relative importance of transverse motion components relative to the baseline direction (MEEI and Bristol data). We use the geometric relationship between the baseline direction and the direction of stapes piston motion to express the motion of the stapes target in an intrinsic (stapes-centered) reference frame, , by using the transformations described in the Appendix. We use a rigid-body assumption to predict footplate piston motion from target piston motion, and we show that the difference between our measured VS and this footplate motion is sufficiently small that HMY computed from VS is a good estimate of the effective cochlear input.
We define the intrinsic coordinate system with its origin at the center of the stapes footplate; x is defined by the long footplate axis, z is defined by the short footplate axis, and y is in the direction of piston motion, orthogonal to the plane defined by the x and z axes (Decraemer et al., 2007). For consistency with Decraemer et al. (2007), we define +x as the posterior direction and +z as the inferior direction; so, for a right-hand coordinate system, +y is into the cochlea in the right ear. For ease of comparison of results in the left and right ears, we use a left-hand coordinate system for left ears, so +y is into the cochlea in the left ear also. We use stapes dimensions from Decraemer et al., 2007 (one ear). The target was located ∼0.9 mm from the footplate and ∼0.3 mm from the y axis in the +x direction. Translational velocities are unchanged by a translation of the reference frame; so (assuming that contributions of stapes rotations to y-direction motion are negligible, see the Appendix), for rigid-body motion, at the target is equal to at the footplate.
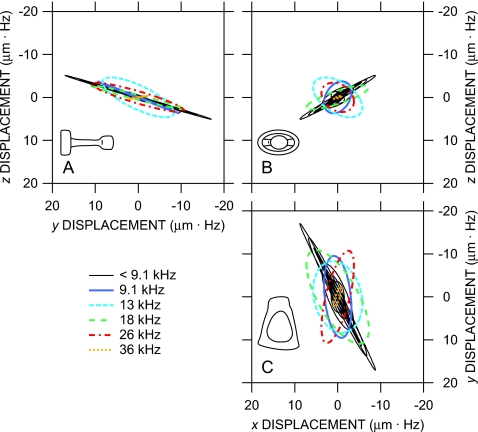
The computed 3D motion of the stapes target in one ear at Bristol in the intrinsic reference frame is shown in Fig. 9 as Lissajous figures of target displacement in time at several frequencies. The motion is viewed along the three principal directions: Panels (a) and (c) are side views to compare the relative amplitude and phase of transverse to piston components, and panel (b) is a “top” view looking along the y axis toward the stapes footplate showing the relative amplitudes and phases of the two transverse components. The displacement amplitude is multiplied by the stimulus frequency for easier comparison at different frequencies.8 Several points are evident: (1) At low frequencies below 9 kHz, stapes motion is consistent with simple translation in the piston direction—the deviation of the motion from the y direction is within the 20° measurement error of the baseline measurement direction in the y-z plane [Fig. 9a] and nearly within the measurement error in the x-y plane [Fig. 9c]. Nonpiston components are small and in phase with piston motion—the Lissajous figures resemble straight lines, so quadrature components are insignificant—and are largest in the direction of the long footplate axis [x; Fig. 9b]. (2) At 9 and 13 kHz, transverse components become more significant, and substantial phase differences occur between the different components—the Lissajous figures in Figs. 9a and (especially) 9c open up into ellipses. (3) At higher frequencies (18, 26, and 36 kHz), stapes motion is again generally consistent with piston-direction translation, as at low frequencies, but the primary direction of motion (ellipse major axis) is different than that at low frequencies. Transverse components are out of phase with piston motion (ellipses are open) and are approximately equal [Fig. 9b]. Similar results were obtained from the two other ears.
Figure 9.
(Color online) Reconstructed Lissajous figures of the displacement of the stapes posterior crus target (normalized by frequency) at several frequencies in three dimensions in an intrinsic reference frame aligned with the stapes (insets) from one right ear (ubg17) at Bristol; two other ears (one left, one right) were similar. (a) Looking in the −x direction (approximately anterior); (b) looking in the +y direction (from the stapes head into the cochlea); (c) looking in the −z direction (approximately superior).
These results and the results from the two other ears are presented in a different way in Fig. 10a: Each curve in Fig. 10a is the ratio of stapes target motion in a transverse direction (black curves) or (gray curves) to piston motion . Below 9 kHz, transverse components in all ears were generally between 0.1× and and were 0.5 cycle out of phase with inward stapes motion: Inward stapes piston motion was accompanied by transverse motion anteriorly and superiorly. In two of the ears, the magnitude ratios and phase differences were approximately constant across frequency; in the third, the ratios and x-direction phase were more variable. Between 9 and 13 kHz, transverse components in each ear were larger than those at other frequencies (in one ear, larger than the piston motion), and phase differences were more variable. At higher frequencies, the transverse component ratios were similar to their low-frequency values, though phase differences remained variable. Except in a fairly narrow frequency range around 10 kHz, stapes motion is mostly pistonlike in the range 0.1–36 kHz.
Figure 10.
Ratio of transverse to pistonlike stapes motion. (a) (black lines and filled symbols) and (gray lines and open symbols) in three ears at Bristol (in the intrinsic reference frame), where is the motion in the piston direction. (b) VS,t∕VS,p in three ears at MEEI, where VS,p is the direction in the measurement plane (defined by the two measurement directions) closest to the piston direction and VS,t is in the orthogonal direction. The legend indicates the angle between VS,p and . Noisy data at 3.5–5.5 kHz are omitted. Top: magnitude ratio; bottom: phase difference.
Because we measured VS at only a single point, we can draw only limited conclusions about the nature of transverse stapes motion: we cannot distinguish transverse stapes translation from rocking about a footplate axis, and we cannot distinguish rotation about the piston axis. It seems reasonable to assume, based on ME geometry and observations in other species (von Békésy, 1960; Guinan and Peake, 1967; Decraemer et al., 2000), that most of the transverse target motion is due to stapes rocking about the footplate axes.9 If we assume that all transverse motion at the target 0.9 mm from the stapes footplate is due to rocking, we compute an angular footplate displacement considerably less than that observed by Decraemer et al. (2007). In general, the transverse motion we observed was lower and more uniform among ears than that observed by Decraemer et al. (2007).
A different estimate of transverse stapes target motion in ears at MEEI is presented in Fig. 10b: In these experiments, target velocity was measured in only two directions, so we are limited to computing motion in the plane defined by the measurement directions. We computed in-plane velocity components in the direction closest to the piston direction, VS,p, and transverse to that direction, VS,t. Figure 10b shows the relative amplitude and phase of transverse motion in three left ears. (Data are omitted between 3.5 and 5.5 kHz where low stimulus levels caused computed VS,t to be noisy.) In all three ears, |VS,t| is lower than |VS,p| (by a factor of 0.05–0.5) below 7–8 kHz and 0.5 cycles out of phase with inward stapes motion as in Fig. 10a. |VS,t| peaks near 10–12 kHz, higher than |VS,p| in two of the three ears, and ∠VS,t accumulates approximately 1 cycle relative to ∠VS,p. [The frequency spacing in Figs. 910a is sufficiently large that a phase cycle could have been missed.] At higher frequencies, transverse motion is generally lower again and the phase is near −1.5 cycle, though motion becomes more complex above 40 kHz. These results are consistent with Fig. 10a, and together, these data indicate that gerbil stapes motion is primarily pistonlike to high frequencies except for a narrow frequency band near 10 kHz.
It is also interesting to note in Fig. 10b that the lowest transverse components were observed in ear 0307L, in which the measurement direction was closest to the piston direction (15°). The highest transverse components were observed in ear 0309L, which had the lowest |VS| among the 19 ears measured (dashed curve in Fig. 5). Perhaps the low |VS| in this ear was due to some anomaly in the ossicular chain that allowed higher transverse motion.
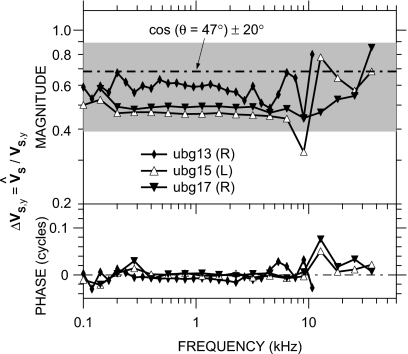
The aspect of 3D stapes motion of most practical interest to us is the degree to which our measured VS estimates the piston stapes velocity . Figure 11 compares VS to in the three Bristol ears of Fig. 10a. The difference between VS and , denoted as , is mostly in magnitude and relatively small: |ΔVS,y| is approximately constant with frequency up to 8–10 kHz at about a factor of 0.5–0.6, slightly lower than what might be expected from a simple cosine correction (dividing by the cosine of the angle between the measurement direction and the y axis, namely, 47°; dot-dashed line) but within the range expected from the ±20° error in baseline direction (shading). This value of |ΔVS,y| is also consistent with the observation in Fig. 9 that the primary direction of stapes motion is consistent with piston motion. |ΔVS,y| is more variable between 8 and 13 kHz and then gradually increases toward 1 as frequency increases further. Differences in phase are extremely small (generally <0.02 cycle) except in the 8–13 kHz range; the largest values of ∠ΔVS,y occur in two of the three ears near the frequency of the maximum |ΔVS,y|. Results were similar among the three ears. This result suggests that VS measured within 47° of the piston direction is a good estimate of at nearly all frequencies from 100 Hz to 36 kHz.
Figure 11.
ΔVS,y, the ratio of measured VS to the piston component , in three ears at Bristol in the intrinsic reference frame. The dot-dashed line is the cosine of the angle (∼47°±20°, shading) between the measurement direction and the y axis. Top: magnitude; bottom: phase.
A recent study has shown that scala vestibuli pressure in gerbil tracks very closely from 0.2 to 50 kHz (de la Rochefoucauld et al., 2008), even though transverse stapes velocity can be significant at those frequencies (Decraemer et al., 2007). This close tracking with is further support for the idea that transverse components do not affect cochlear input and VS should be an adequate estimate of cochlear input. A more cautionary note was sounded by Decraemer et al. (2006a, Fig. 11), but even they show (from reconstructions) that (1) the velocity of a point on the anterior aspect of the stapes head along a direction within 20° of the piston direction differs from piston stapes motion by less than a factor of 2 in magnitude and ∼0.1 cycle at any frequency between 0.1 and 40 kHz and (2) stapes velocity measured within 40° of the piston direction differs by more than a factor of 2 in magnitude at only a few frequencies (∼3, 7–10, and ∼30 kHz) over the same range.10 Because VS is not much different from , we will continue to use VS in subsequent HMY calculations and comparisons.
Comparison of middle-ear transfer admittance to earlier measurements
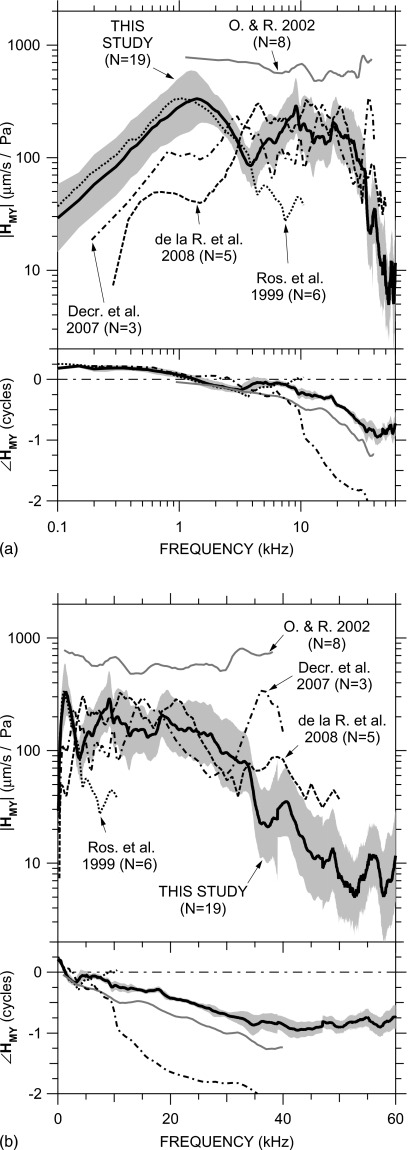
Our HMY measurements are summarized in Fig. 12. The thick black line is the mean of the MEEI and Bristol measurements weighted by the number of ears measured at each laboratory; the shaded area is the s.d. in HMY at MEEI from Fig. 6. The small jump in ∠HMY near 47 kHz is due to the differing delays in the MEEI and Bristol measurements (20–25 versus 29 μs). As mentioned in the previous section, the |HMY| shown (computed from VS) probably underestimates in the piston direction (computed from ) by no more than a factor of 2 below 10 kHz, less at higher frequencies, and ∠HMY should provide a close estimate of .
Figure 12.
Comparison of our mean HMY (thick black line)±s.d. (shaded area) to previously published measurements: Rosowski et al. (1999) (logarithmic mean; “Ros. et al.;” dotted); Overstreet and Ruggero (2002) (median; “O. & R.;” gray line), de la Rochefoucauld et al., 2008 (in piston direction; linear mean; “de la R. et al.;” dashed), and Decraemer et al., (2007) (piston, computed in an intrinsic reference frame; logarithmic mean; “Decr. et al.;” dot-dashed). Top: magnitude; bottom: phase. (a) Logarithmic frequency scale; (b) linear frequency scale.
Figure 12 also includes data from four previous studies in gerbil: the mean HMY in six ears measured by Rosowski et al. (1999; dotted line), the medianHMY of eight ears measured by Overstreet and Ruggero (2002; gray line), the mean computed from three ears measured by Decraemer et al. (2007; dot-dashed line), and the mean |HMY| in five ears in the piston direction by de la Rochefoucauld et al. (2008); magnitude only; dashed line). The data of Decraemer et al. were computed from whole-stapes rigid-body motion calculated for the piston direction from measurements in other directions (as in Figs. 89); the data of de la Rochefoucauld et al. were computed from VS,y measured on the incus long process above the incudostapedial joint through a hole in the pars flaccida; and the data from the other studies were measured on a single point on the stapes posterior crus from a direction similar to ours.
Our data show similarities to most previous measurements, but the similarities are to different measurements over different frequency ranges. Our mean HMY is similar to that of Rosowski et al. (1999) below 4 kHz, but at higher frequencies, our |HMY| remains roughly constant and our ∠HMY continues to decrease. Our mean ∠HMY has a slope similar to that of Overstreet and Ruggero (2002) up to 40 kHz, but their ∠HMY is ∼0.25 periods lower than ours and their |HMY| is considerably higher than ours and those of other studies. Our |HMY| shows rough similarities to that of Decraemer et al. up to 30 kHz, but their accumulation is much greater. Our |HMY| is most similar to that of de la Rochefoucauld et al. (2008) above 5 kHz. (Below 5 kHz, the open pars flaccida hole in the experiments of de la Rochefoucauld et al. influenced their measured HMY.) In general, most studies (including this one) are consistent with the idea that |HMY| and phase delay remain roughly constant as frequency increases above 2–3 kHz. This study shows that the range of roughly constant |HMY| and phase delay extends up to about 35 kHz, above which |HMY| decreases rapidly with frequency.
The middle ear as a mechanical transmission line?
Several investigators have suggested that the ME acts as a lossless mechanical transmission line matched to its terminating impedance, in that the magnitude of sound transmission is fairly constant at low and high frequencies but a delay is introduced (Wilson and Bruns, 1983; Olson, 1998; Puria and Allen, 1998; Overstreet and Ruggero, 2002). Others (e.g., Zwislocki, 1962; Hemilä et al., 1995) have suggested that the ME acts as a second- (or higher-) order resonant system in which high-frequency sound transmission is limited by the mass of the system, though little evidence has been offered in support (see Rosowski, 1994; Overstreet and Ruggero, 2002). A matched lossless transmission line would produce constant |HMY| and a constant delay (constant negative ∠HMY slope with frequency) at all frequencies, while a simple second-order resonant system would show stiffness-domination characteristics (|HMY| slope=+1 on a log-log plot, ∠HMY=+0.25 cycle) at low frequencies, a resonant |HMY| peak with a ∠HMY zero crossing, and mass-domination characteristics (|HMY| slope=−1, ∠HMY=−0.25 cycle) at higher frequencies.
Our measurements and most previous measurements of gerbil ME sound transmission (Fig. 12) suggest that the behavior of the gerbil ossicular system cannot be described as either a matched lossless transmission line or a simple resonant system but includes aspects of both. Our HMY clearly shows low-frequency stiffness dominance, a rather broad resonant |HMY| peak with ∠HMY zero crossing, and a continued decrease in |HMY| and ∠HMY as frequency increases to about 3 kHz [as does HMY measured by Rosowski et al. (1999) and, to a lesser extent, Decraemer et al. (2007)], but our |HMY| also shows approximately constant |HMY| and approximately linear ∠HMY decrease with frequency from 5 to 35 kHz [as does HMY measured by Overstreet and Ruggero (2002), Decraemer et al. (2007; to 10 kHz only), and de la Rochefoucauld et al. (2008); |HMY| only)] consistent with a transmission line. This behavior in the 5–35 kHz range is also consistent with a multiresonant network whose resonances are distributed in frequency (see, e.g., Decraemer et al., 1990).11 Above 35 kHz, our data show a definite change in behavior: |HMY| decreases sharply [also seen in some ears by de la Rochefoucauld et al. (2008)] and ∠HMY levels off [as does ∠HMY of Overstreet and Ruggero (2002)], consistent with a multiresonant network but inconsistent with a transmission line. These results indicate that the gerbil ME behaves as a simple resonant system at low frequencies and as a distributed multiresonant network at higher frequencies. ME behavior is consistent with a transmission line from 5 to 35 kHz but not at higher frequencies.
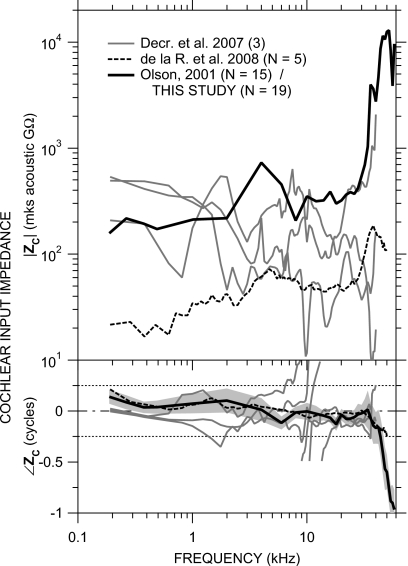
Estimates of gerbil cochlear input impedance
Our ME transfer admittance data (=VS∕PU) are used with measurements of the ME-to-scala-vestibuli sound pressure gain GMP=PSV∕PU (where PSV is the sound pressure in scala vestibuli) and the stapes footplate area Afp to compute the cochlear acoustic input impedance ZC (the ratio of PSV to stapes volume velocity US=Afp⋅VS) by
| (2) |
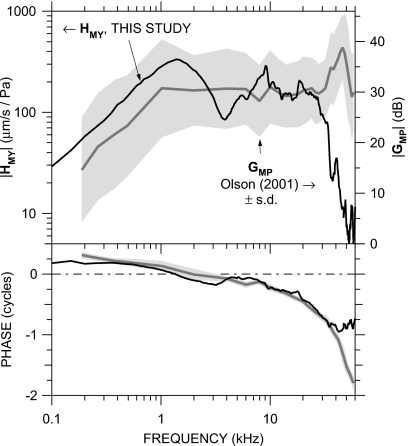
We use the mean scala vestibuli sound pressure from Olson (2001) (Fig. 2, in 14 ears, normalized by PU) rather than more recent measurements because they were taken in a similar fashion to our VS data: closed-field sound stimulus, with PU measured concurrently very near the umbo. The mean |GMP| (Olson, 2001) and ∠GMP±1 s.d. (not presented in that paper)12 are compared to our mean HMY in Fig. 13. There is a marked similarity in the frequency dependence of GMP and HMY below 30 kHz: Both |GMP| and |HMY| are roughly constant with frequency and ∠GMP and ∠HMY are similar. [A comparable relationship was observed below 30 kHz by de la Rochefoucauld et al. (2008).] Above 30 kHz, |GMP| increases while |HMY| decreases, and ∠GMP continues to accumulate while ∠HMY becomes roughly constant.
Figure 13.
Comparison of our mean HMY (thick black line; left axis) to the mean scala vestibuli pressure gain GMP described by Olson (2001) (N=15; gray line)±s.d. (shading; right axis). Top: magnitude; bottom: phase. The relative positions of the left and right magnitude axes were chosen for the closest alignment of midfrequency |HMY| and |GMP|.
The s.d. of |GMP| is high, but the spectral shape of |GMP| is nearly constant among the ears: in all ears, |GMP| was roughly constant at frequencies between 1 and 30 kHz but increased by a factor of 2-3 between about 30 and 50 kHz. Most of the variance in |GMP| may be due to frequency-independent changes in the sensitivity of the fiber-optic pressure sensor used for GMP measurements (Dong and Olson, 2005; de la Rochefoucauld et al., 2008). The fact that most of the |GMP| variance is frequency independent allows us to draw conclusions about the frequency dependence of quantities computed from GMP.
The cochlear input impedance computed by Eq. 2 from the mean GMP and HMY in Fig. 13 and Afp=0.62 mm2 (Lay, 1972) is shown in Fig. 14. The magnitude and phase of ZC (black line) are consistent with a resistance over most of the frequency range: |ZC| is roughly constant with frequency and ∠ZC is approximately zero below 30 kHz. Above 30 kHz |ZC| increases, and above 35 kHz, ∠ZC decreases sharply. Above 43 kHz, ∠ZC is less than −0.25 cycle, which results from the flattening of ∠HMY with frequency (Fig. 13).
Figure 14.
Cochlear input impedance ZC (thick black line) computed from the mean HMY and GMP in Fig. 13. Top: magnitude; bottom: phase angle. Dotted lines indicate ±0.25 cycle limits of ∠ZC for a passive system. S.d of |ZC| (not shown) is about a factor of 12; s.d. of ∠ZC is shown by shading. Also shown are ZC in three ears by Decraemer et al. (2007, gray lines, phase-wrapped as suggested in that publication) and the mean ZC in five ears by de la Rochefoucauld et al., 2008, dashed line).
There are some similarities among our computed ZC and ZC computed for gerbil by de la Rochefoucauld et al., 2008; dashed line) and by Decraemer et al. (2007; gray lines): Our |ZC| is similar to |ZC| in one of the ears of Decraemer et al., and our ∠ZC is similar to ∠ZC in another of the ears of Decraemer et al. The high-frequency increase in |ZC| and decrease in ∠ZC computed from our VS measurements are hinted at by the ZC of de la Rochefoucauld et al. but our higher-frequency data suggest that the |ZC| increase and ∠ZC decrease continue at frequencies above the limit of the measurements of de la Rochefoucauld et al. The frequency dependence of our ZC below 30 kHz is similar to ZC measured in other species (reviewed by de la Rochefoucauld et al., 2008).
The s.d. in |ZC| is rather high (about a factor of 12 across frequency) due mostly to the high variance in |GMP|. However, as mentioned above, even though the |GMP| variance is high, the spectral dependence of |GMP| is fairly uniform among those ears; so even though the |ZC| variance is high, most of the variance can be explained by a frequency-independent variability in sensitivity.
The decrease in ∠ZC above 35 kHz suggests that the cochlear input impedance becomes more reactive at high frequencies, i.e., less input power is absorbed by the cochlea and more is reflected. This increased power reflectance is consistent with (a) the idea by Lighthill (1981)13 that reactance and reflectance increase above the maximum frequency where a cochlear traveling wave can form and (b) the increase in EC sound power reflectance REC above 50 kHz observed by Ravicz et al. (2007).
Some features of our computed ZC above 35 kHz are inconsistent with a driving-point impedance: The decrease in ∠ZC associated with the increase in |ZC| above 35 kHz is inconsistent with a minimum-phase driving-point impedance, and the continued decrease in ∠ZC to <−0.25 cycle above 43 kHz implies a negative resistance inconsistent with a passive system (see, e.g., Oppenheim and Schafer, 1989). Possible explanations for these inconsistencies include (a) a significant phase delay in PSV between the stapes and the PSV measurement location such that GMP∕HMY no longer describes a driving-point impedance (see de la Rochefoucauld et al., 2008 for a detailed discussion of this and other possibilities) and (b) a change in the primary mode of stapes motion that would contribute significant transverse components to the measured VS. Nevertheless, the appearance of the |ZC| increase and ∠ZC decrease above 35 kHz in both our and some previous ZC measurements by different methods suggests that there is in fact an increase in ZC magnitude and reactance at high frequencies.
The flatness of |GMP| with frequency has been cited as an indication that ME sound transmission is constant across frequency (Overstreet and Ruggero, 2002; Ruggero and Temchin, 2002). In fact, the flatness could also arise from an increase in |ZC| at high frequencies such that a given stapes velocity produces a higher |PSV| or, conversely, a constant |GMP| results from lower |HMY|. Our ZC computations suggest that the constant |GMP| is due to an increase in |ZC| and is not indicative of constant cochlear input at high frequencies.
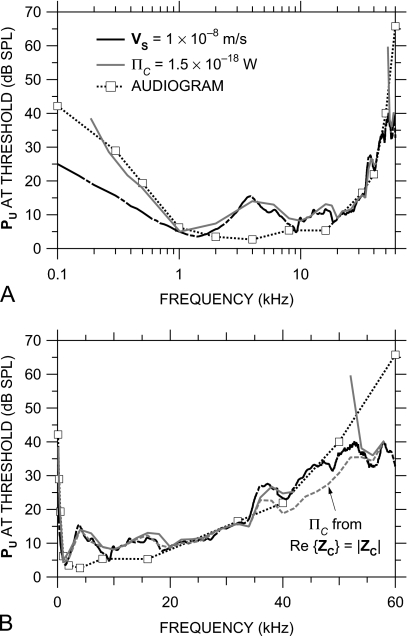
Contribution of middle-ear transmission to the limits of the audiometric range
The acoustic power entering the cochlea ΠC for a given sound pressure at the umbo can be computed from HMY, ZC, and the stapes footplate area Afp by
| (3) |
(Rosowski et al., 1986). Equation 3 can be rearranged to yield the umbo sound pressure PU,th necessary to provide a given constant level of sound power into the cochlea across frequency. If we assume that the auditory threshold is a cochlear isopower curve (as suggested by several authors, e.g., Khanna and Tonndorf, 1969; Khanna and Sherrick, 1981; Rosowski et al., 1986; Rosowski, 1991a, 1991b) or an isovelocity curve across frequency, PU,th provides an estimate of the audiogram with closed-field stimulus.
Figure 15 plots the sound pressure at the umbo necessary to provide a baseline level of acoustic input to the cochlea. The black curve is PU,th that produces a cochlear isovelocity input of 10 nm∕s across frequency (which corresponds to a cochlear volume velocity input of 6×10−15 m3∕s), and the gray curve is PU,th that produces a cochlear isopower input of 1.5×10−18 W across frequency.14 These values were chosen to match (by eye) the most sensitive portion of the gerbil free-field audiogram (dashed line and squares; Ryan, 1976). Because Re{ZC} is negative at some frequencies above 43 kHz (Fig. 14), we show PU,th for constant ΠC only at those frequencies where Re{ZC} is positive, and for comparison, we also show PU,th for ΠC computed assuming that Re{ZC}=|ZC| (gray dashed line). The spectral shape of the audiogram is matched remarkably well from 1 kHz to above 40 kHz by the isopower curve and to above 50 kHz by the isovelocity curve. At low frequencies [below 1 kHz, Fig. 15a], the isopower curve is a better audiogram predictor than the isovelocity curve. At intermediate frequencies, where ZC is constant in magnitude and resistive, PU,th for constant ΠC and PU,th for constant VS are similar. As frequency increases above 50 kHz [Fig. 15b], the isovelocity curve flattens while the audiogram continues upward. To the extent that PU is a good estimate of the free-field sound pressure used to measure the audiogram, the match between the audiogram and PU,th for constant sound power (0.2–40 kHz) or VS input (1–40 kHz) supports the idea that the audiogram is determined by a constant level of cochlear input.
Figure 15.
Sound pressure at the umbo required to produce a constant level of cochlear input across frequency. Shown are PU,th that produces a constant stapes velocity of 10 nm∕s (equivalent to a constant stapes volume velocity of 6×10−15 m3∕s) (black line) and PU,th that provides a constant cochlear sound power input ΠC of 1.5×10−18 W (solid gray line, only at frequencies where Re{ZC} is positive). Also shown is PU,th for ΠC=1.5×10−18 W computed by assuming that ZC is purely resistive (dashed gray line). The mean gerbil audiogram (Ryan, 1976) is shown by the dotted line and squares. (a) Logarithmic frequency scale; (b) linear frequency scale.
The conclusions above, drawn from mean HMY and ZC data, are of course affected by potential high-frequency errors and the variance in HMY and ZC, but we believe that the influence of these factors is relatively small. The negative real part of ZC between 43 and 52 kHz (as ∠ZC cycles; see Fig. 14) implies that power is injected into the cochlea at these frequencies from some other source or that there are errors in VS measurements in this frequency range. The PU,th for constant ΠC computed from Re{ZC}=|ZC| [assuming ∠ZC=0; gray dashed line in Fig. 15b] is therefore a lower bound on PU,th; if ZC becomes reactive at high frequencies (see previous section), Re{ZC}<|ZC|, and the PU,th for constant cochlear power input is somewhat higher. The variance in HMY can be expected to cause about a 6 dB s.d. in ΠC. Because the variance in ZC is due mostly to variance in |ZC| and because the |ZC| variance is primarily a variance in sensitivity (see Sec. 4D above), the variance in cochlear input power is primarily in the magnitude and not in the frequency dependence. Hence, the |ZC| variance could cause the baseline power level to be different for different ears, but the spectral shape would be similar.
As mentioned above, the isopower curve in Fig. 15 relates cochlear input power to sound pressure near the TM; yet the audiogram was measured in the free field. The only data of which we are aware that relate gerbil PEC to free-field sound pressure PFF are free-field-to-eardrum transfer functions (FETFs) measured from several directions by Maki and Furukawa (2005, Fig. 2). Below 20 kHz, their FETFs show a direction-independent EC gain that peaks at about 20 dB near 8 kHz, but since the TM was stiffened for these measurements (thereby increasing REC; see Ravicz et al., 2007), the EC gain in an unmodified ear is probably less. Above 20 kHz, the situation is more complicated—their EC gain is direction dependent, their FETFs vary with the measurement location in the EC, and their innermost measurement location [“3 mm,” Fig. 2(i)] is still probably several millimeters away from the TM (based on the gain notch at 30 kHz; see Ravicz et al., 2007); but, assuming that the highest EC gain among measurement locations at a given frequency is a good estimate of |PU∕PFF| at that frequency (see Ravicz et al., 2007), the EC gain is approximately unity from about 20 to 50 kHz, the highest frequency measured.
Two pieces of evidence suggest that the amount of free-field sound power entering the ME decreases at high frequencies: (1) The diffuse-field effective area , which is a measure of the sound power-collecting ability of the external ear and ME (Rosowski et al., 1986, 1988; Rosowski, 1991a, 1991b), is approximately 25 mm2 at 12 kHz but is limited by the ideal EADF=λ2∕4π at higher frequencies (Ravicz et al., 1996). Since EADF decreases as the square of frequency as frequency increases, this result suggests that the cochlear power produced by a constant diffuse-field sound pressure PDF decreases more rapidly at high frequencies than does ΠC for a constant PU. (2) REC increases from about 0.5 near 30 kHz to at least 0.8 above 55 kHz (Ravicz et al., 2007). Each of these pieces of evidence suggests that the free-field sound pressure necessary for a constant cochlear input power is higher at high frequencies than the PU,th estimated in Fig. 15.
Figure 15 shows that the high-frequency increase in auditory threshold that forms the upper audiometric limit is accompanied by a reduction in cochlear input. These results do not support the idea (Olson, 2001; Overstreet and Ruggero, 2002; Ruggero and Temchin, 2002) that ME sound transmission remains high even at high frequencies where cochlear response is low. These results support the idea that the limitations of ME transmission contribute to the limits of hearing.
SUMMARY AND CONCLUSIONS
We were able to measure stapes velocity independently in two laboratories over a frequency range that spans the gerbil auditory range, to higher frequencies than previously published measurements. These velocity measurements, when combined with reliable measurements of ME input PU in the same ears to form the ME transfer admittance HMY=VS∕PU, provide a broadband view of ME function.
Stapes motion is consistent with simple translational motion in the piston direction below 9 kHz, and the piston component of stapes motion is dominant up to at least 36 kHz except in a narrow range near 10 kHz. Single-point measurements from a direction within 45° of the piston direction can provide a reasonably good estimate of piston motion to at least 36 kHz.
The ME exhibits different behaviors over different frequency ranges. HMY is compliance-dominated at low frequencies, and the ME behaves as a simple second-order resonant system below about 3 kHz. Above a peak near 10 kHz up to 30–35 kHz, ME transmission is consistent with a multiresonant network or a mechanical transmission line: |HMY| is approximately constant and d∠HMY∕df is consistent with a delay of 26–29 μs.
At higher frequencies (above 35 kHz), ME transmission does not remain constant at high frequencies: |HMY| decreases steeply with frequency and |HMY| flattens.
The high-frequency decrease in |HMY| corresponds to an increase in cochlear input impedance.
The increase in gerbil auditory threshold at high frequencies coincides with a decrease in |HMY| and sound power entering the cochlea. Therefore, reductions in cochlear input contribute to the rise in auditory thresholds at high frequencies.
Other peripheral mechanisms, e.g., decreases in external-ear sound power collection (Ravicz et al. 1996) and increases in EC power reflectance (Ravicz et al., 2007), may also contribute to the rise in auditory thresholds at high frequencies.
ACKNOWLEDGMENTS
The authors thank Elizabeth Olson, Wei Dong, Ombeline de la Rochefoucauld, and Willem Decraemer for many helpful discussions, and William Peake, Melissa Wood, Kelly Brinsko, Heidi Nakajima, and the staff of the Eaton-Peabody Laboratory for greatly appreciated assistance. This work was supported by NIDCD R01-DC00194 (M.E.R. and J.J.R.) and The Royal Society and the Wellcome Trust (N.P.C.).
APPENDIX: METHOD OF COMPUTING PISTON AND TRANSVERSE STAPES MOTION FROM VELOCITY MEASUREMENTS
Estimation of stapes motion in the piston direction and transverse directions from measurements of stapes posterior crus target velocity VS requires three steps: (1) Determine the velocity of the target in a coordinate system defined by the measurement setup (an “experimental” reference frame); (2) transform that velocity into a coordinate system aligned with the stapes (an “intrinsic” reference frame, see, e.g., Decraemer et al., 1994, 2007); and (3) estimate the velocity of the entire stapes from velocity measured at one point (the target). Different methods of estimation were used at MEEI and Bristol. In both cases, the origin of the experimental reference frame was at the posterior crus target, and target velocity was measured along the −z′ axis. The x′ axis was approximately anterior-posterior, and the y′ axis was approximately transverse.
At Bristol, VS was measured repeatedly from a baseline direction VS,z′ and also from four to five different directions relatively similar to the baseline direction. These seven to eight measurements were used to compute the velocity of the posterior crus target in directions transverse to the baseline direction in the experimental reference frame (x′,y′,z′) VS,x′ and VS,y′ by
| (A1) |
where the elements of D(d1x,d1y,d1z,d2x,…,dnx,dny,dnz) describe rotations L and T from the baseline direction that define the directions of the measurements M={m1,m2,…,mn} in the experimental reference plane. A minimum of three measurements are necessary; for the Bristol experiments, n=7–8 (as mentioned above), and Eq. A1 describes an overdetermined system. A singular value decomposition technique (see, e.g., Decraemer et al., 1994) was used to minimize errors in solving for VS,x′, VS,y′, and VS,z′:
| (A2a) |
and
| (A2b) |
The velocities computed above in the experimental reference frame were then converted to velocities in the intrinsic reference frame (x,y,z). The origin of the intrinsic reference frame is at the center of the stapes footplate; the x axis is the long footplate axis (approximately anterior-posterior), the y axis is in the piston direction (inward – a left-hand coordinate system was used for left ears), and the z axis is the short footplate axis (approximately superior-inferior). First, rotations were applied about the three experimental axes: +45° about the +x′ axis, +15° about the +y′ axis (for right ears; −15° for left ears), and −10° about the +z′ axis, in that order. These manipulations produced the velocity of the posterior crus target in the piston direction VS,y and transverse directions VS,x and VS,z.
The piston velocity of the posterior crus target was assumed to be indicative of the piston velocity of the stapes footplate: We assume that the stapes moves as a rigid body and that the y components of motion at the posterior crus due to rotations about the x and z axes are negligible. Then the transformation of target velocity to stapes footplate involves only a simple translation of the origin from the target to the center of the stapes footplate. Because translations of the origin do not affect translational velocities, .
Estimates of transverse motion were performed at MEEI in a different way because velocity was measured from only two directions and there are insufficient data to compute the components of VS in all directions. This technique is insensitive to motion out of the plane defined by the two measurement directions. The two measurements were used to compute the motion of the posterior crus target in the direction in the plane closest to piston motion and in the perpendicular direction in the plane. Target velocity was transformed to stapes footplate velocity as described above.
Portions of this work were presented by Olson and Cooper (2000) and Ravicz and Rosowski (2004).
Footnotes
The gerbil auditory threshold is 60 dB above its most sensitive value by 60 kHz (see Ryan, 1976).
Note that HMY has units of a specific acoustic admittance.
The reduction in VS with the probe tube within 0.5 mm of the umbo may be due to shadowing of the location of effective ME input by the probe tube: λ at 60 Hz (∼6 mm) is only about four times the diameter of the probe tube, and sound might not diffract completely around the probe tube tip when the distance between it and the TM is small.
p(0)<0.05 as evaluated by Student’s t test.
The logarithmic mean is frequently used with data that span a wide range. An advantage is that the variance is symmetric about the mean when plotted on a logarithmic scale.
The data sets in panels (A) and (B) are slightly different: the mean HMY in panel (A) includes some measurements in which VS was above the noise floor at low frequencies but not high; the mean HMY in panel (B) includes some measurements in which VS was above the noise floor at high frequencies but not low. Factors that influenced VS signal-to-noise ratio include the seal around the probe tube in the EC (which affected low-frequency stimulus levels) and the strength of the laser signal reflected from the target (which affected noise levels, especially at high frequencies: lower signal strength produced higher noise).
Note that this |HMY| peak is unaffected by the notch in |PU∕PEC| near 10 kHz (Fig. 3).
The product of displacement and frequency is equivalent to velocity. We chose to describe the figure in terms of displacement to make it easier to grasp intuitively.
Forces are exerted on the stapes head by the incus and resisted by the stapedius muscle and tendon, inertial forces at the stapes center of gravity, and the annular ligament at the footplate edges. Neglecting reaction forces from the stapedius muscle and tendon and inertial forces, any forces applied along a line that does not include both the stapes head and the stapes centroid (coincident with the center of gravity for a uniform mass distribution), i.e., different from the piston direction, must cause a rocking moment.
In that study, velocity phase accumulated an extra cycle at the magnitude notch near 3 kHz.
A transmission line can be modeled as an infinite sum of discrete matched compliant and inertial elements below its cutoff frequency (a ladder-network delay line, see e.g., Magnusson et al., 2001). A multiresonant network with distributed resonant frequencies can therefore be considered a discretized, truncated, and not-so-well-matched transmission line.
Data generously provided by Elizabeth Olson.
As suggested by Elizabeth Olson.
This threshold value for ΠC is consistent with the estimate of power entering the ME ΠT=5×10−17 W by Ravicz et al. (1992): It is expected that some power would be lost in the ME and, as mentioned above, our method of measuring stapes motion might underestimate |VS| and hence ΠC by about a factor of 2. This threshold value for ΠC is also consistent with estimates for other species (Rosowski et al., 1986).
References
- Allen, J. B. (1986). “Measurement of eardrum acoustic impedance,” in Peripheral Auditory Mechanisms, edited by Allen J. B., Hall J. L., Hubbard A., Neely S. T., and Tubis A. (Springer-Verlag, New York: ), pp. 44–51. [Google Scholar]
- von Békésy, G. (1960). Experiments in Hearing, edited by Wever E. G. (McGraw-Hill, New York: ). [Google Scholar]
- Chien, W., Ravicz, M. E., Merchant, S. N., and Rosowski, J. J. (2006). “The effect of methodological differences in the measurement of stapes motion in live and cadaver ears,” Audiol. Neuro-Otol. 10.1159/000091815 11, 183–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper, N. P. (1999). “An improved heterodyne laser interferometer for use in studies of cochlear mechanics,” J. Neurosci. Methods 10.1016/S0165-0270(99)00017-588, 93–102. [DOI] [PubMed] [Google Scholar]
- Cooper, N. P., and Rhode, W. S. (1992). “Basilar membrane mechanics in the hook region of cat and guinea-pig cochleae: Sharp tuning and nonlinearity in the absence of baseline position shifts,” Hear. Res. 10.1016/0378-5955(92)90083-Y 63, 163–190. [DOI] [PubMed] [Google Scholar]
- Decraemer, W. F. S., Khanna, S. M., and Dirckx, J. J. J. (2006a). “Estimation of stapes piston motion from uniaxial interferometer measurements along observation directions at an angle with the piston axis is prone to substantial errors,” in Vibration Measurements by Laser Techniques: Advances and Applications, edited by Tomasini E. P. (SPIE, Bellingham, WA: ), Vol. 6345, Paper No. 63450C.
- Decraemer, W. F., Khanna, S. M., and Funnell, W. R. J. (1990). “Heterodyne interferometer measurements of the frequency response of the manubrium tip in cat,” Hear. Res. 10.1016/0378-5955(90)90152-F 47, 205–218. [DOI] [PubMed] [Google Scholar]
- Decraemer, W. F., Khanna, S. M., and Funnell, W. R. J. (1994). “A method for determining three-dimensional vibration in the ear,” Hear. Res. 10.1016/0378-5955(94)90250-X 77, 19–37. [DOI] [PubMed] [Google Scholar]
- Decraemer, W. F., Khanna, S. M., and Funnell, W. R. J. (2000). “Measurement and modeling of the three-dimensional vibration of the stapes in cat,” in Recent Developments in Auditory Mechanics, edited by Wada H., Takasaka T., Ikeda K., Ohyama K., and Koike T. (World Scientific, Singapore: ), pp. 36–43. [Google Scholar]
- Decraemer, W. F., de la Rochefoucauld, O., Dong, W., Khanna, S. M., Dirckx, J. J. J., and Olson, E. S. (2007). “Scala vestibuli pressure and three-dimensional stapes velocity measured in direct succession in gerbil,” J. Acoust. Soc. Am. 10.1121/1.2709843 121, 2774–2791. [DOI] [PubMed] [Google Scholar]
- Decraemer, W. F., de la Rochefoucauld, O., Dong, W., Khanna, S. M., Dirckx, J. J. J., and Olson, E. S., and (2006b). “Do non-piston components contribute to scala vestibuli pressure behind the footplate in gerbil?,” in Middle Ear Mechanics in Research and Otology, edited by Huber A. and Eiber A. (World Scientific, Singapore: ), pp. 116–122. [Google Scholar]
- Dong, W., and Olson, E. S. (2005). “Two-tone distortion in intracochlear pressure,” J. Acoust. Soc. Am. 10.1121/1.1880812 117, 2999–3015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong, W., and Olson, E. S. (2006). “Middle ear forward and reverse transmission in gerbil,” J. Neurophysiol. 10.1152/jn.01214.2005 95, 2951–2961. [DOI] [PubMed] [Google Scholar]
- Guinan, J. J., Jr., and Peake, W. T. (1967). “Middle-ear characteristics of anesthetized cats,” J. Acoust. Soc. Am. 10.1121/1.1910465 41, 1237–1261. [DOI] [PubMed] [Google Scholar]
- Hemilä, S., Nummela, S., and Reuter, T. (1995). “What middle ear parameters tell about impedance matching and high frequency hearing,” Hear. Res. 10.1016/0378-5955(95)00031-X 85, 31–44. [DOI] [PubMed] [Google Scholar]
- Johnstone, B. M., and Sellick, P. M. (1972). “The peripheral auditory apparatus,” Q. Rev. Biophys. 5, 1–57. [DOI] [PubMed] [Google Scholar]
- Khanna, S., and Sherrick, C. (1981). “The comparative sensitivity of selected receptor systems,” in The Vestibular System: Function and Morphology, edited by Gualtierotti T. (Springer-Verlag, New York: ), pp. 337–348. [Google Scholar]
- Khanna, S. M., and Tonndorf, J. (1969). “Middle ear power transfer,” Arch. Klin. Exp. Ohren Nasen Kehlkopfheilkd 193, 78–88. [DOI] [PubMed] [Google Scholar]
- Lay, D. M. (1972). “The anatomy, physiology, functional significance and evolution of specialized hearing organs of gerbilline rodents,” J. Morphol. 10.1002/jmor.1051380103 138, 41–120. [DOI] [PubMed] [Google Scholar]
- Lighthill, J. (1981). “Energy flow in the cochlea,” J. Fluid Mech. 10.1017/S0022112081001560 106, 149–213. [DOI] [Google Scholar]
- Lynch, T. J., III (1981). “Signal processing by the cat middle ear: Admittance and transmission, measurements and models,” Ph.D. thesis, Massachusetts Institute of Technology. [Google Scholar]
- Lynch, T. J., III, Nedzelnitsky, V., and Peake, W. T. (1982). “Input impedance of the cochlea in cat,” J. Acoust. Soc. Am. 10.1121/1.387995 72, 108–130. [DOI] [PubMed] [Google Scholar]
- Magnusson, P. C., Alexander, G. C., Tripathi, V. K., and Weisshaar, A. (2001). Transmission Lines and Wave Propagation, 4th ed. (CRC, Boca Raton: ). [Google Scholar]
- Maki, K., and Furukawa, S. (2005). “Acoustical cues for sound localization by the Mongolian gerbil, Meriones unguiculatus,” J. Acoust. Soc. Am. 10.1121/1.1944647 118, 872–886. [DOI] [PubMed] [Google Scholar]
- Merchant, S. N., Ravicz, M. E., and Rosowski, J. J. (1996). “Acoustic input impedance of the stapes and cochlea in human temporal bones,” Hear. Res. 10.1016/0378-5955(96)00023-8 97, 30–45. [DOI] [PubMed] [Google Scholar]
- Olson, E. S. (1998). “Observing middle and inner ear mechanics with novel intracochlear pressure sensors,” J. Acoust. Soc. Am. 10.1121/1.423083 103, 3445–3463. [DOI] [PubMed] [Google Scholar]
- Olson, E. S. (2001). “Intracochlear pressure measurements related to cochlear tuning,” J. Acoust. Soc. Am. 10.1121/1.1369098 110, 349–367. [DOI] [PubMed] [Google Scholar]
- Olson, E. S., and Cooper, N. P. (2000). “Stapes motion and scala vestibuli pressure in gerbil,” Abstracts of the 23rd Midwinter Meeting of the Association for Research in Otolaryngology, Abstract No. 399.
- Oppenheim, A. V., and Schafer, R. W. (1989). Discrete-Time Signal Processing (Prentice-Hall, Englewood Cliffs, NJ: ). [Google Scholar]
- Overstreet, E. H., and Ruggero, M. A. (2002). “Development of wide-band middle ear transmission in the Mongolian gerbil,” J. Acoust. Soc. Am. 10.1121/1.1420382 111, 261–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puria, S., and Allen, J. B. (1998). “Measurements and model of the cat middle ear: Evidence of tympanic membrane delay,” J. Acoust. Soc. Am. 10.1121/1.423930 104, 3463–3481. [DOI] [PubMed] [Google Scholar]
- Ravicz, M. E., Olson, E. S., and Rosowski, J. J. (2007). “Sound pressure distribution and power flow within the gerbil ear canal from 100 Hz to 80 kHz,” J. Acoust. Soc. Am. 10.1121/1.2769625 122, 2154–2173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravicz, M. E., and Rosowski, J. J. (2004). “High-frequency sound transmission through the gerbil middle ear,” Abstracts of the 27th Midwinter Meeting of the Association for Research in Otolaryngology, Abstract No. 817.
- Ravicz, M. E., Rosowski, J. J., and Voigt, H. F. (1992). “Sound-power collection by the auditory periphery of the mongolian gerbil Meriones unguiculatus. I. Middle-ear input impedance,” J. Acoust. Soc. Am. 10.1121/1.404280 92, 157–177. [DOI] [PubMed] [Google Scholar]
- Ravicz, M. E., Rosowski, J. J., and Voigt, H. F. (1996). “Sound-power collection by the auditory periphery of the mongolian gerbil Meriones unguiculatus. II. External-ear radiation impedance and power collection,” J. Acoust. Soc. Am. 10.1121/1.414793 99, 3044–3063. [DOI] [PubMed] [Google Scholar]
- de la Rochefoucauld, O., Decraemer, W. F., Khanna, S. M., and Olson, E. S. (2008). “Simultaneous measurements of stapes motion and intracochlear pressure in gerbil from 0.5–50 kHz,” J. Assoc. Res. Otolaryngol. 9, 161–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosowski, J. J. (1991a). “The effects of external- and middle-ear filtering on auditory threshold and noise-induced hearing loss,” J. Acoust. Soc. Am. 10.1121/1.401306 90, 124–135. [DOI] [PubMed] [Google Scholar]
- Rosowski, J. J. (1991b). “Erratum: The effects of external- and middle-ear filtering on auditory threshold and noise-induced hearing loss,” J. Acoust. Soc. Am. 10.1121/1.402408 90, 3373. [DOI] [PubMed] [Google Scholar]
- Rosowski, J. J. (1994). “Outer and middle ear,” in The Springer Series in Auditory Research, Volume IV: Comparative Mammalian Hearing (Springer-Verlag, New York: ), pp. 172–247. [Google Scholar]
- Rosowski, J. J., Carney, L. H., Lynch, T. J., III, and Peake, W. T. (1986). “The effectiveness of external and middle ears in coupling acoustic power into the cochlea,” in Peripheral Auditory Mechanisms, edited by Allen J. B., Hall J. L., Hubbard A., Neely S. T., and Tubis A. (Springer-Verlag, New York: ), pp. 3–12. [Google Scholar]
- Rosowski, J. J., Carney, L. H., and Peake, W. T. (1988). “The radiation impedance of the external ear of cat: Measurements and applications,” J. Acoust. Soc. Am. 10.1121/1.397185 84, 1695–1708. [DOI] [PubMed] [Google Scholar]
- Rosowski, J. J., Ravicz, M. E., Teoh, S. W., and Flandermeyer, D. (1999). “Measurements of middle-ear function in the Mongolian gerbil, a specialized mammalian ear,” Audiol. Neuro-Otol. 10.1159/000013831 4, 129–136. [DOI] [PubMed] [Google Scholar]
- Ruggero, M. A., and Temchin, A. N. (2002). “The roles of the external, middle, and inner ears in determining the bandwidth of hearing,” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.202492699 99, 13206–13210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryan, A. (1976). “Hearing sensitivity of the mongolian gerbil, Meriones unguiculatis,” J. Acoust. Soc. Am. 10.1121/1.380961 59, 1222–1226. [DOI] [PubMed] [Google Scholar]
- Teoh, S. W., Flandermeyer, D. T., and Rosowski, J. J. (1997). “Effects of pars flaccida on sound conduction in ears of Mongolian gerbil: Acoustic and anatomical measurements,” Hear. Res. 10.1016/S0378-5955(97)00002-6 106, 39–65. [DOI] [PubMed] [Google Scholar]
- Wilson, J. P., and Bruns, V. (1983). “Middle-ear mechanics in the CF-bat Rhinolophus ferrumequinum,” Hear. Res. 10.1016/S0378-5955(97)00059-2 10, 1–13. [DOI] [PubMed] [Google Scholar]
- Zwislocki, J. J. (1962). “Analysis of the middle-ear function. Part I. Input impedance,” J. Acoust. Soc. Am. 10.1121/1.1918382 34, 1514–1523. [DOI] [Google Scholar]